Research on Deformation Failure Mechanism and Stability of Bedding Cataclastic Rock Slope Containing Multi-Muddy Interlayers
Abstract
1. Introduction
2. Methods
2.1. Strength Reduction Method
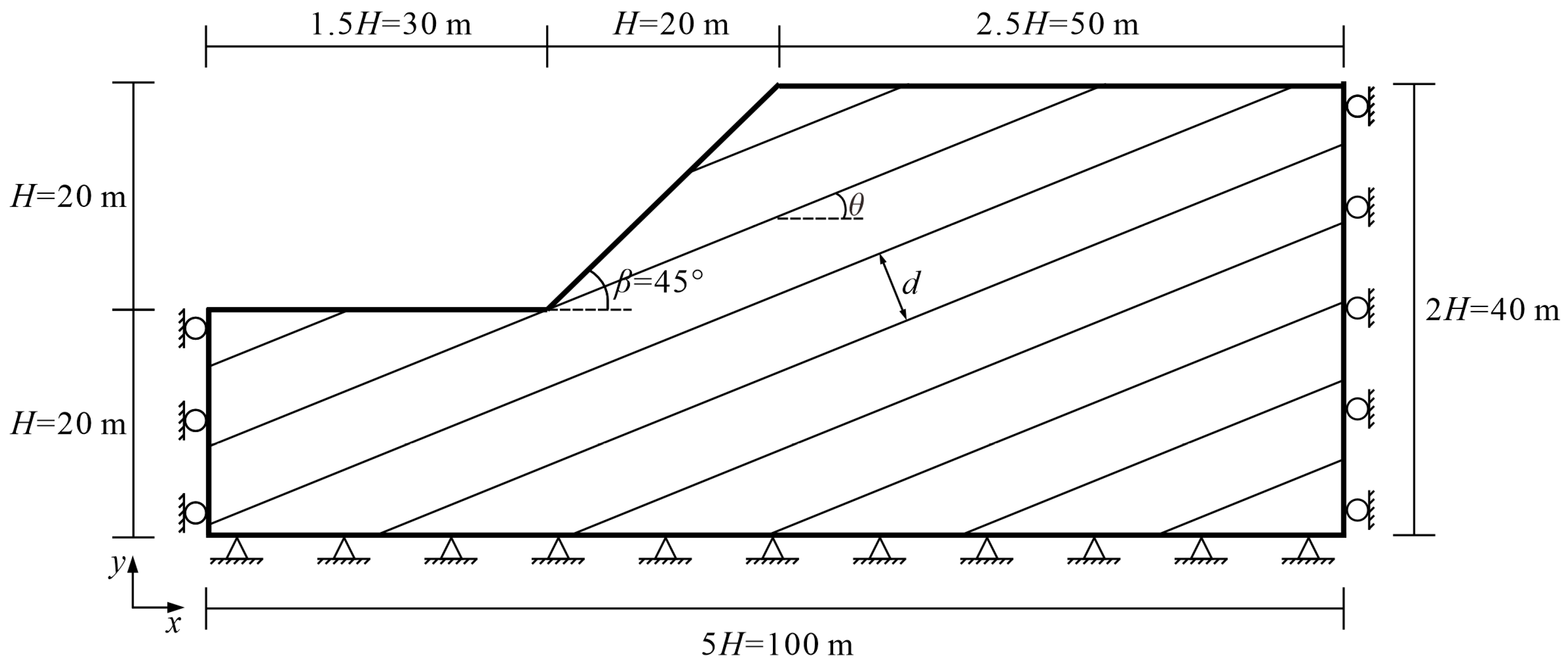
2.2. Calculation Model and Parameter Selection
2.3. Scheme of the Calculation Model
3. Results and Discussion
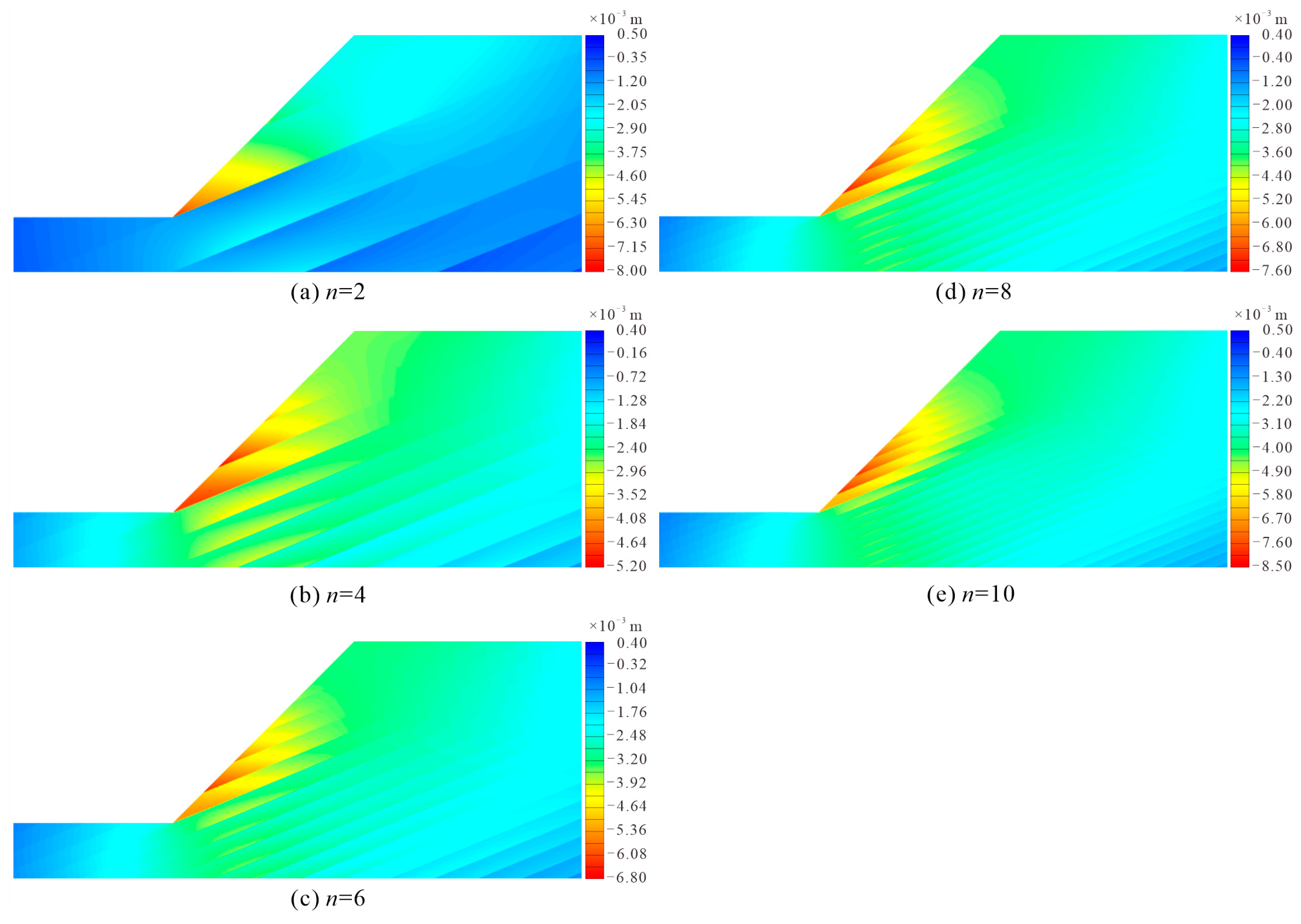
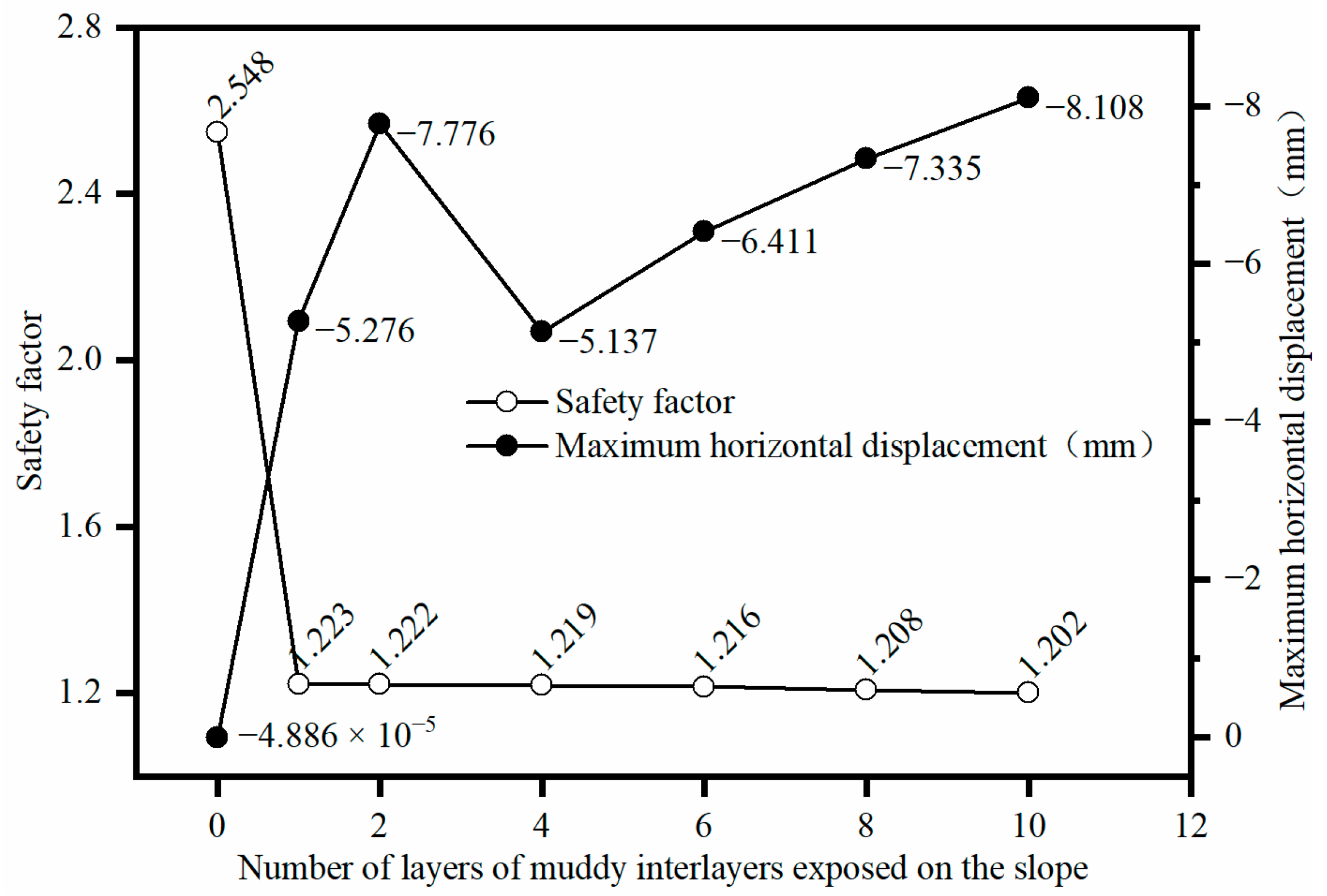
3.1. The Impact of the Number of Exposed Muddy Interlayers on the Slope Surface
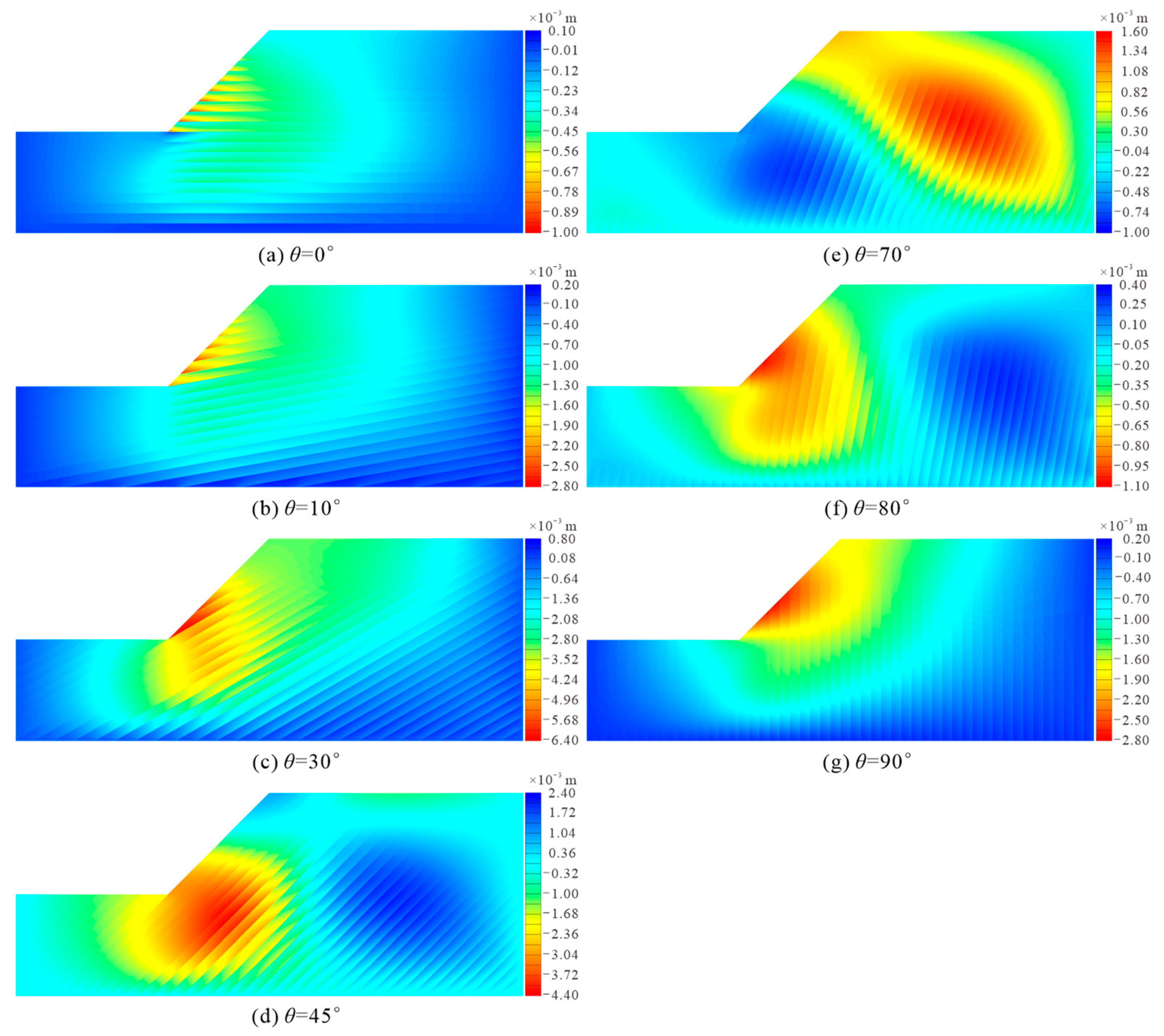
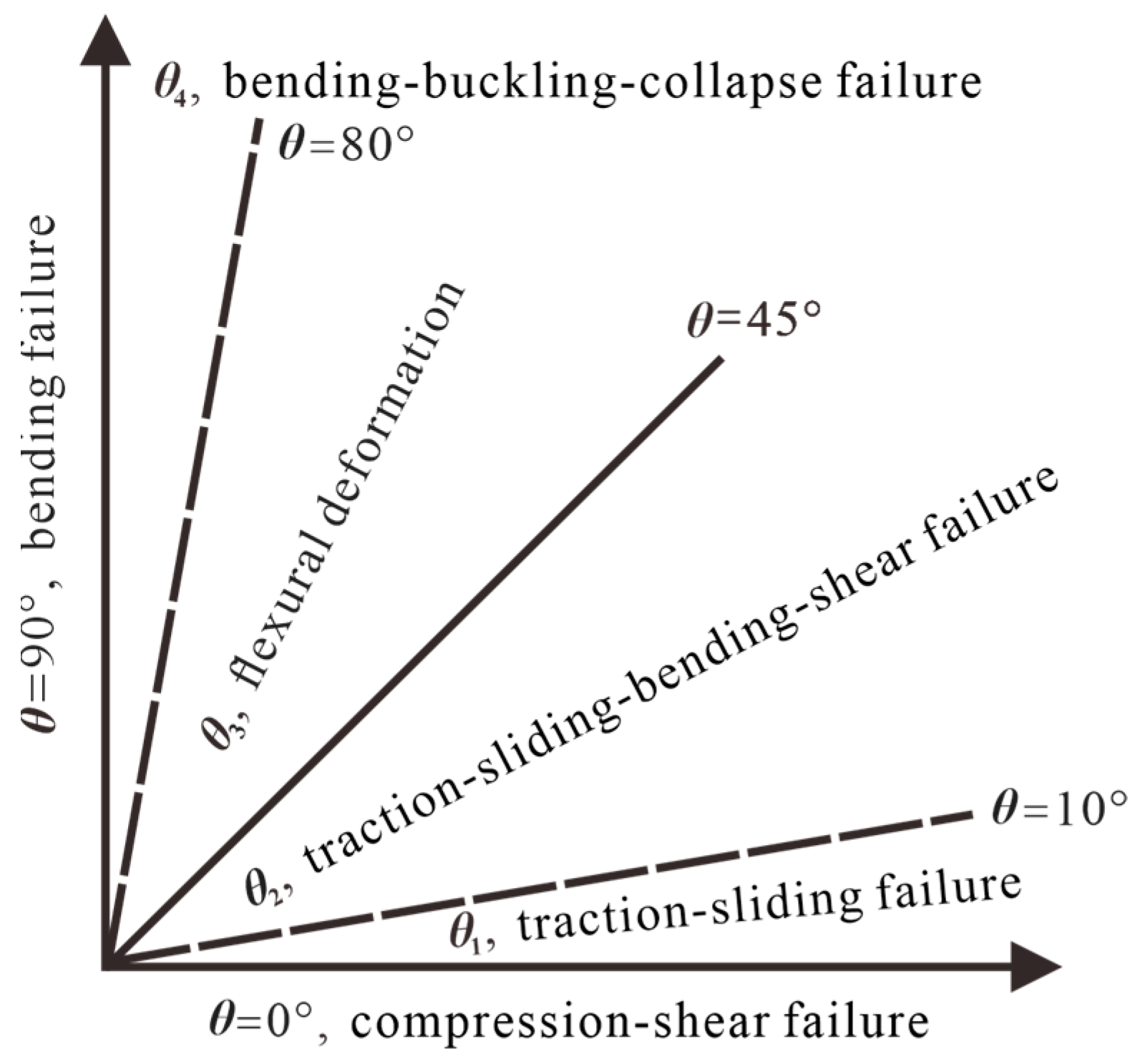
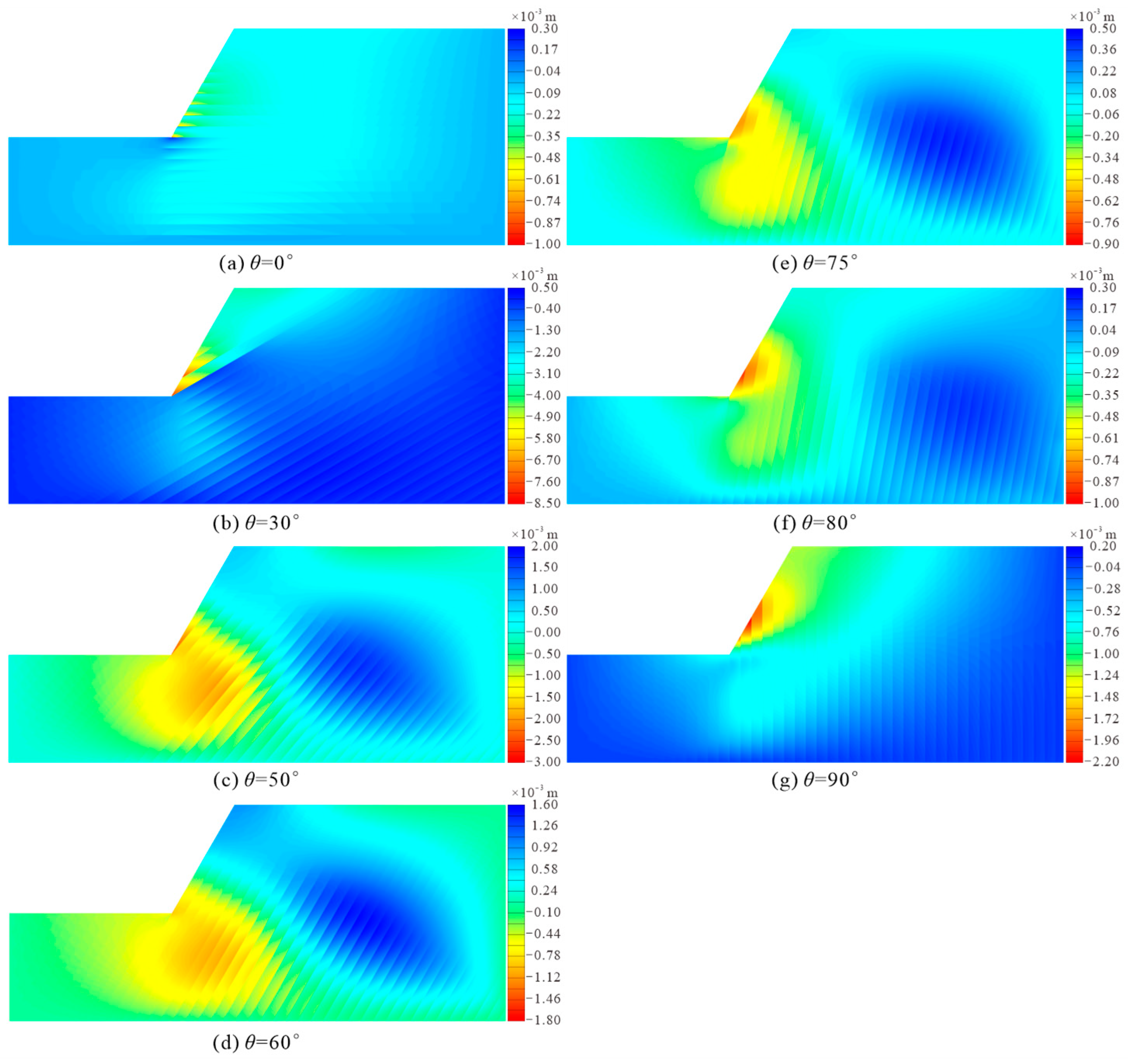
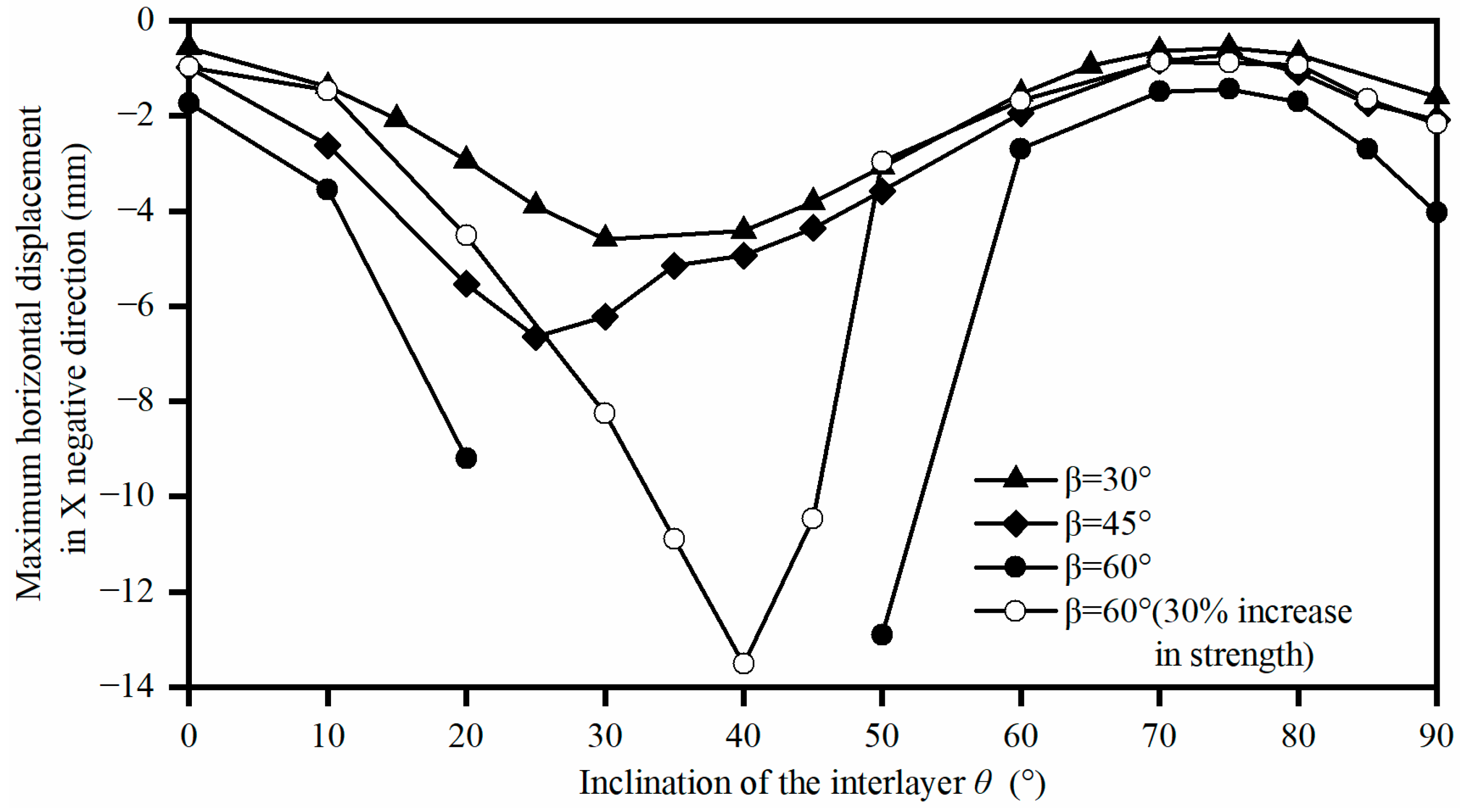
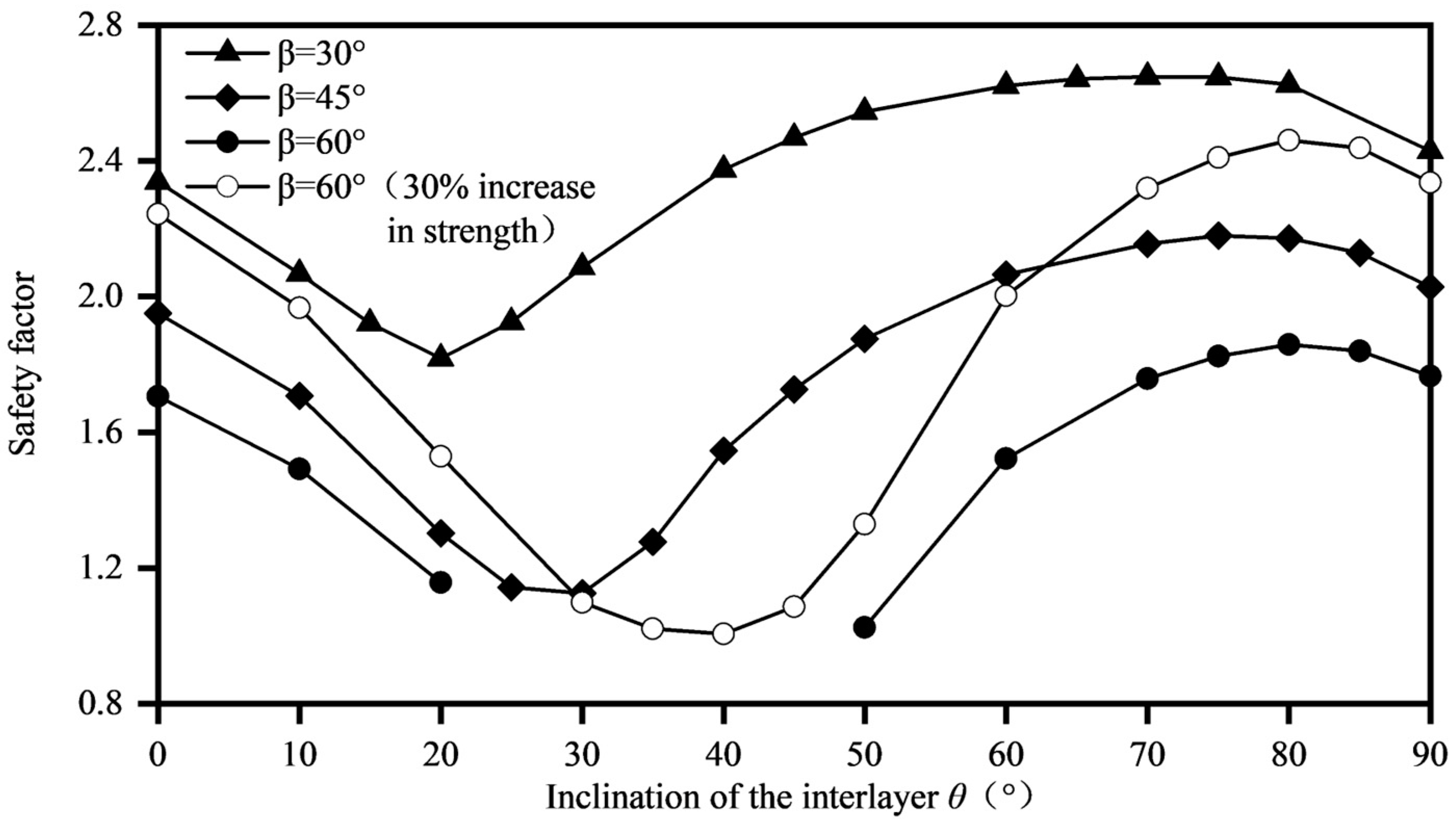
3.2. The Impact of the Dip Angle of Muddy Interlayers
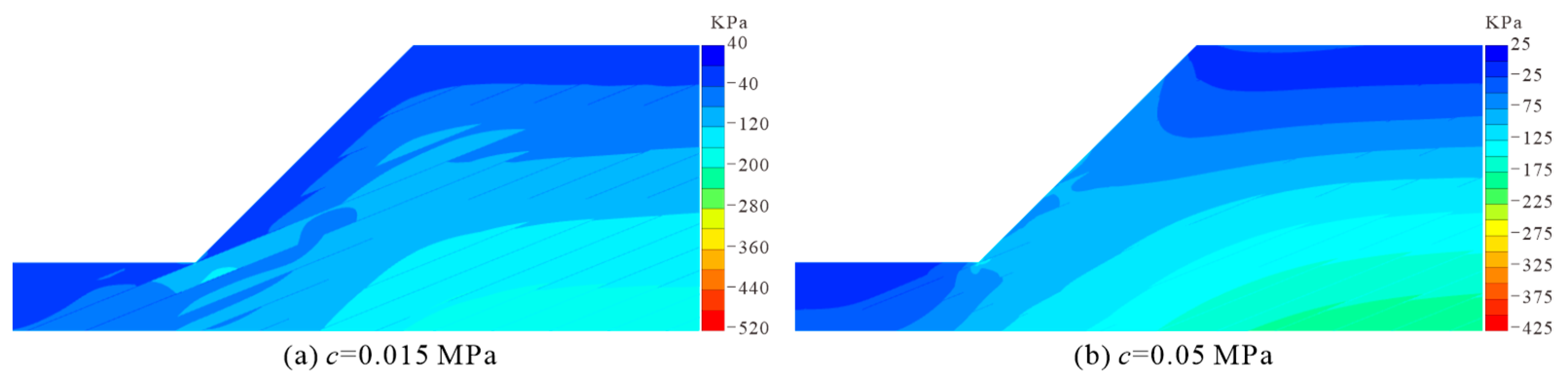
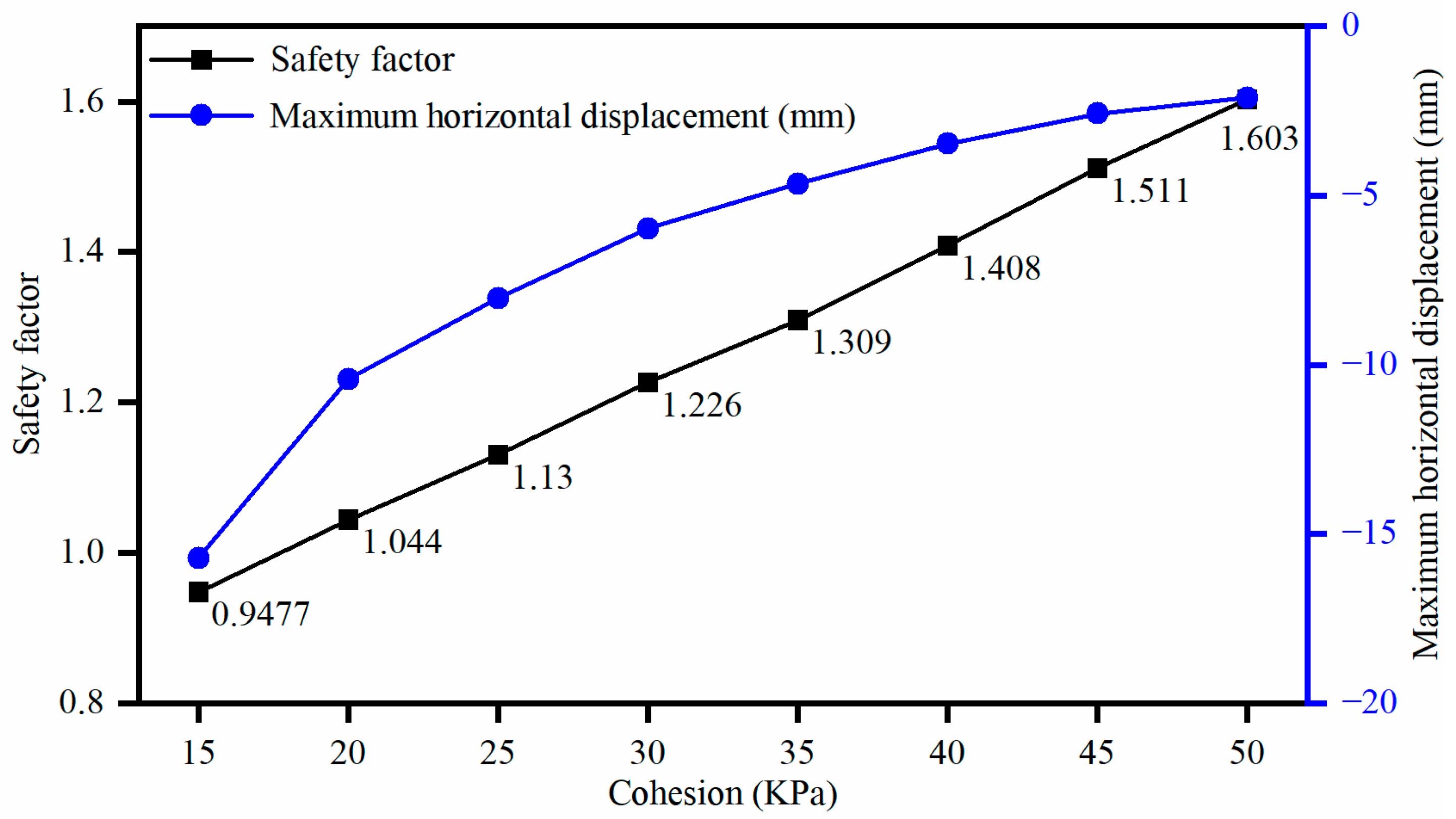
3.3. The Influence of the Cohesion of the Muddy Interlayers
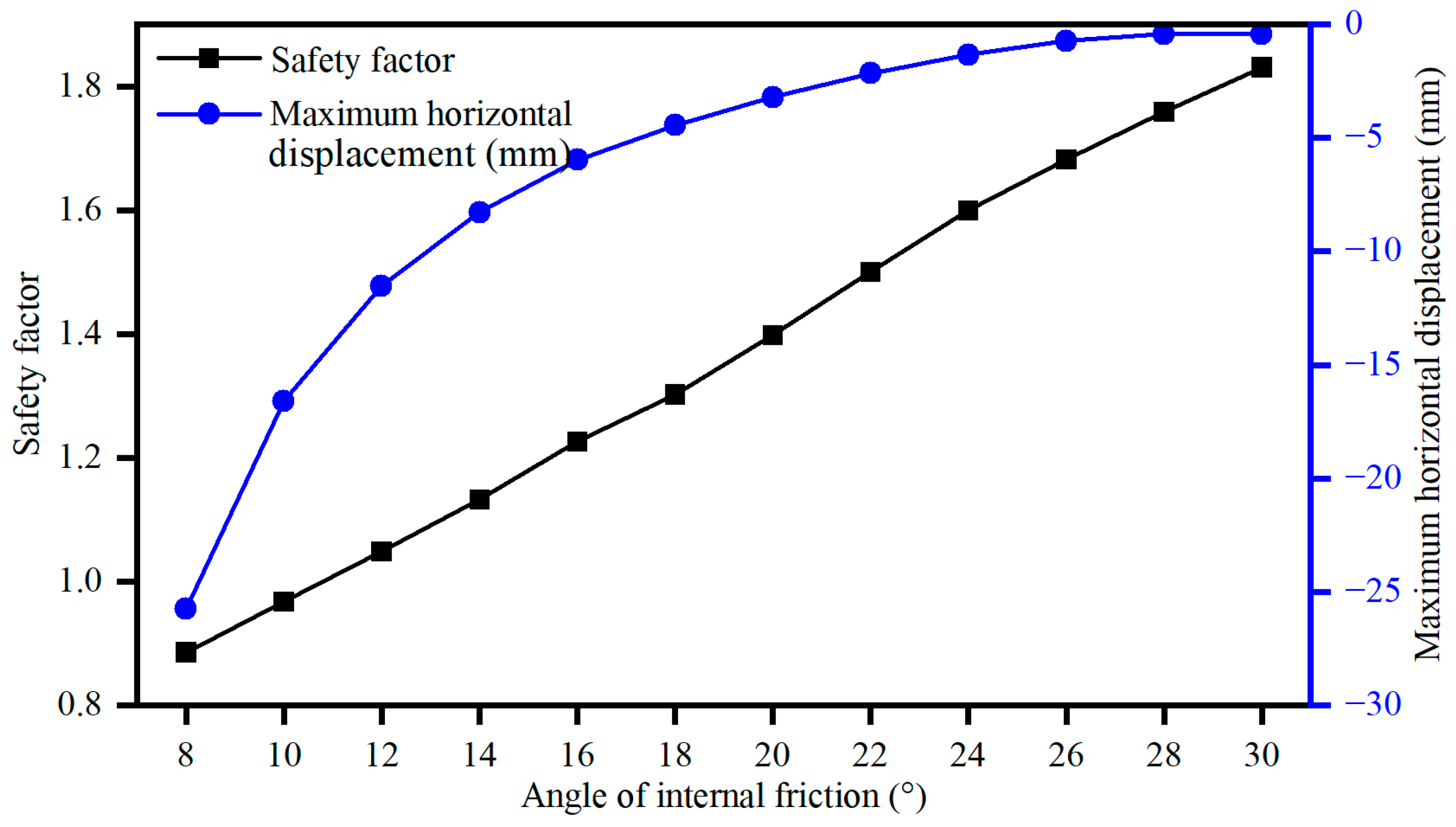
3.4. The Influence of the Internal Friction Angle of the Muddy Interlayers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaiswal, A.; Verma, A.K.; Singh, T.N. Evaluation of slope stability through rock mass classification and kinematic analysis of some major slopes along NH-1A from Ramban to Banihal. J. Rock Mech. Geotech. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Shou, K.; Wang, C. Analysis of the Chiufengershan landslide triggered by the 1999 Chi-Chi earthquake in Taiwan. Eng. Geol. 2003, 68, 237–250. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Yamanaka, M.; Dhakal, S.; Bhandary, N.P.; Yatabe, R. Comparative analysis of contributing parameters for rainfall-triggered landslides in the Lesser Himalaya of Nepal. Environ. Geol. 2008, 58, 567–586. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, H.; Wan, Y.; Yu, X. Reliability and parameter sensitivity analysis on geosynthetic-reinforced slope with considering spatially variability of soil properties. Constr. Build. Mater. 2022, 350, 128806. [Google Scholar] [CrossRef]
- Sazid, M. Analysis of rockfall hazards along NH-15: A case study of Al-Hada road. Int. J. Geo-Eng. 2019, 10, 1. [Google Scholar] [CrossRef]
- Ansari, T.; Kainthola, A.; Singh, K.H.; Singh, T.N.; Sazid, M. Geotechnical and micro-structural characteristics of phyllite derived soil; implications for slope stability, Lesser Himalaya, Uttarakhand, India. Catena 2021, 196, 104906. [Google Scholar] [CrossRef]
- Singh, P.K.; Wasnik, A.B.; Kainthola, A.; Sazid, M.; Singh, T.N. The stability of road cut cliff face along SH-121: A case study. Nat. Hazards 2013, 68, 497–507. [Google Scholar] [CrossRef]
- Kainthola, A.; Singh, P.K.; Wasnik, A.B.; Sazid, M.; Singh, T.N. Finite Element Analysis of Road Cut Slopes using Hoek & Brown Failure Criterion. Int. J. Earth Sci. Eng. 2012, 5, 1100–1109. [Google Scholar]
- Siddique, T.; Sazid, M.; Khandelwal, M.; Varshney, H.; Irshad, S. Application of Slope Mass Rating and Kinematic Analysis Along Road Cut Slopes in the Himalayan Terrain. In Proceedings of Geotechnical Challenges in Mining, Tunneling and Underground Infrastructures; Springer: Singapore, 2022; Volume 10, pp. 697–708. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, P.; Xu, L.; Li, W.; Sun, Y.; Sun, W.; Yuan, Z. Mechanism of Roof Deformation and Support Optimization of Deeply Buried Roadway under Mining Conditions. Appl. Sci. 2022, 12, 12090. [Google Scholar] [CrossRef]
- Yao, E.; Li, W.; Miao, Y.; Ye, L.; Yang, Z. Study on the Influence of a Soft Soil Interlayer on Spatially Varying Ground Motions. Appl. Sci. 2022, 12, 1322. [Google Scholar] [CrossRef]
- Zhang, S.; Tan, Y.; Wang, C.; Wang, K. Research on deformation failure mechanism and stability of slope rock mass containing multi-weak interlayers. Rock Soil Mech. 2014, 35, 1695–1702, (In Chinese with English Abstract). [Google Scholar]
- Lu, B. The Research on The Stability of Rock Slope with Weak Interlayer. Doctoral Dissertation, Hebei University of Engineering, Handan, China, 2013. (In Chinese). [Google Scholar]
- Zhang, D. The Research on the Stability Analysis and Reinforcement Measures of Slope with Weak Interlayer. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2010. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD2010&filename=2010160815.nh (accessed on 10 April 2010). (In Chinese).
- Qin, H. Analysis of deformation characteristics and its influencing factors of slope with soft interlayer. Nat. Sci. 2011, 30, 282, (In Chinese with English Abstract). [Google Scholar]
- Zuo, W.R.; Liu, P. Creep properties of carbonaceous shale and slope stability analysis of soft interlayer. Hunan Commun. Sci. Technol. 2014, 40, 1–4. (In Chinese) [Google Scholar]
- Liu, X.; Dai, Y.; Chen, X.; Xu, Z. Stability analysis of cutting slope with carbonaceous shale weak interlayer. J. Hunan Univ. Arts Sci. (Sci. Technol.) 2015, 27, 69–74. [Google Scholar]
- Chai, J. The Stability Analysis of Rock Slope with Weak Interlayer under the Unloading Influence. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2016. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201701&filename=1017018993.nh (accessed on 1 December 2016). (In Chinese).
- Liu, P.; Bao, T.; Yin, B. Application of butterfly catastrophe theory in stability of slope with weak interlayer. J. Guizhou Univ. (Nat. Sci.) 2019, 36, 109–112. [Google Scholar] [CrossRef]
- Tian, L.; Liu, W.; Zhang, J.; Gao, H. Cataclastic Characteristics and Formation Mechanism of Dolomite Rock Mass in Yunnan, China. Appl. Sci. 2023, 13, 6970. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, J.; Wang, Z.; Xu, Z. Spatial Distribution and Geometrical Morphology of Muddy Interlayer in Rock Slopes Based on Three-Dimensional Laser Scanning Technique. J. Jilin Univ. Earth. Sci. Ed. 2021, 51, 1139–1151. [Google Scholar] [CrossRef]
- Zhang, J. Advances in the engineering geological properties of weak intercalation. J. Geol. Hazards Environ. Preserv. 2020, 31, 104–112. (In Chinese) [Google Scholar]
- Xu, D.P.; Feng, X.T.; Cui, Y.J. A simple shear strength model for interlayer shear weakness zone. Eng. Geol. 2012, 147, 114–123. [Google Scholar] [CrossRef]
- Xu, B.; Qian, Q.; Yan, C.; Xu, H. Stability and strengthening analyses of slope rock mass containing multi-weak interlayers. Chin. J. Rock Mech. Eng. 2009, 28, 3959–3964. [Google Scholar]
- Chen, Z.; Hu, X.; Bu, X. Effect of weak intercalation on failure mode of rock slopes under seismic excitation. Nat. Hazards 2020, 105, 363–381. [Google Scholar] [CrossRef]
- Zhang, J. State of art and trends of rock slope stability with soft interlayer. J. Eng. Geol. 2020, 28, 626–638. (In Chinese) [Google Scholar] [CrossRef]
- Deng, D.; Li, L.; Zhao, L. Limit equilibrium method (LEM) of slope stability and calculation of comprehensive factor of safety with double strength-reduction technique. J. Mt. Sci. 2017, 14, 2311–2324. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W.; Zheng, H. Investigation of slope stability based on strength-reduction-based numerical manifold method and generalized plastic strain. Int. J. Rock Mech. Min. Sci. 2023, 164, 105358. [Google Scholar] [CrossRef]
- Lin, H.-D.; Wang, W.-C.; Li, A.-J. Investigation of dilatancy angle effects on slope stability using the 3D finite element method strength reduction technique. Comput. Geotech. 2020, 118, 103295. [Google Scholar] [CrossRef]
- Sun, G.; Lin, S.; Zheng, H.; Tan, Y.; Sui, T. The virtual element method strength reduction technique for the stability analysis of stony soil slopes. Comput. Geotech. 2020, 119, 103349. [Google Scholar] [CrossRef]
- Peng, S.; Liao, W.; Liu, E. Pipe–soil interaction under the rainfall-induced instability of slope based on soil strength reduction method. Energy Rep. 2020, 6, 1865–1875. [Google Scholar] [CrossRef]
- Zhang, L.-Y.; Zheng, Y.-R.; Zhao, S.; Shi, W. The feasibility study of strength-reduction method with FEM for calculating safety factors of soil slope stability. J. Hydraul. Eng. 2003, 1, 21–26, (In Chinese with English Abstract). [Google Scholar]
- Zheng, Y.-R.; Zhao, S.-Y. Application of strength reduction FEM in soil and rock slope. Chin. J. Rock Mech. Eng. 2004, 23, 3381–3388, (In Chinese with English Abstract). [Google Scholar]
- Pei, L.; Qu, B.; Qian, S. Uniformity of slope instability criteria of strength reduction with FEM. Rock Soil Mech. 2010, 31, 3337–3341, (In Chinese with English Abstract). [Google Scholar]
- Zhao, Z.; Liu, W.; Wang, Z. Investigation Report on Side (Slip) Slope Management Project for Yuxi City Domestic Waste Incineration Power Generation Project; Kunming Prospecting Design Institute of China Nonferrous Metals Industry Co., Ltd.: Kunming, China, 2019. (In Chinese) [Google Scholar]









| Materials | Density (g∙cm−3) | Modulus of Elasticity (MPa) | Poisson’s Ratio | Cohesion (MPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|
| rock body | 2.15 | 500 | 0.25 | 0.12 | 26 |
| interlayer | 2.73 | 20 | 0.35 | 0.03 | 16 |
| Materials | Density (g∙cm−3) | Modulus of Elasticity (MPa) | Poisson’s Ratio | Cohesion (MPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|
| rock body | 2.15 | 500 | 0.25 | 0.156 | 33.8 |
| interlayer | 2.73 | 20 | 0.35 | 0.039 | 20.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, P.; Long, Y.; Zhang, J. Research on Deformation Failure Mechanism and Stability of Bedding Cataclastic Rock Slope Containing Multi-Muddy Interlayers. Appl. Sci. 2023, 13, 8459. https://doi.org/10.3390/app13148459
Qiu P, Long Y, Zhang J. Research on Deformation Failure Mechanism and Stability of Bedding Cataclastic Rock Slope Containing Multi-Muddy Interlayers. Applied Sciences. 2023; 13(14):8459. https://doi.org/10.3390/app13148459
Chicago/Turabian StyleQiu, Peicheng, Yunkai Long, and Jiaming Zhang. 2023. "Research on Deformation Failure Mechanism and Stability of Bedding Cataclastic Rock Slope Containing Multi-Muddy Interlayers" Applied Sciences 13, no. 14: 8459. https://doi.org/10.3390/app13148459
APA StyleQiu, P., Long, Y., & Zhang, J. (2023). Research on Deformation Failure Mechanism and Stability of Bedding Cataclastic Rock Slope Containing Multi-Muddy Interlayers. Applied Sciences, 13(14), 8459. https://doi.org/10.3390/app13148459





