3.3. Agreement Phase
The EPRQDBA protocol achieves detectable agreement during its third and last phase, aptly named agreement phase. Alice, Bob and Charlie initiate the agreement phase by measuring their quantum registers. The distribution scheme, as analyzed in
Section 3.1, leads to some crucial correlations among the contents of Alice, Bob and Charlie’s registers.
Definition 3. Let the bit vectors , , and denote the contents of Alice, Bob and Charlie’s registers after the measurement, and assume that their explicit form is as given below:The pair of , , is the pair of bits , and is designated by . Similarly, the pairs of and are designated by and . Hence, , , and can be written succinctly as:We also define a special type of pair, termed the uncertain
pair, that is denoted by , where ⊔
is a new symbol, different from 0
and 1
. In contrast, pairs consisting of BITS 0
and/or 1
are called definite
pairs. When we want refer to either Bob’s or Charlie’s bit vector, but without specifying precisely which one, we will designate it by
According to the distribution scheme, Alice and Bob share the odd-numbered pairs, and Alice and Charlie share the even-numbered pairs. Therefore, the next Lemma 1 holds. Its proof is trivial and is omitted.
Lemma 1 (Pair Differentiation Property). The next property, termed pair differentiation property, characterizes the corresponding bits and pairs of the bit vectors , , and .
For every odd-numbered bit
in
, where
, it holds that
For every even-numbered bit
in
, where
, it holds that
Every
pair, where
, differs from the corresponding pairs
and
.
In the above relations (
14) and (
15),
is the negation of
.
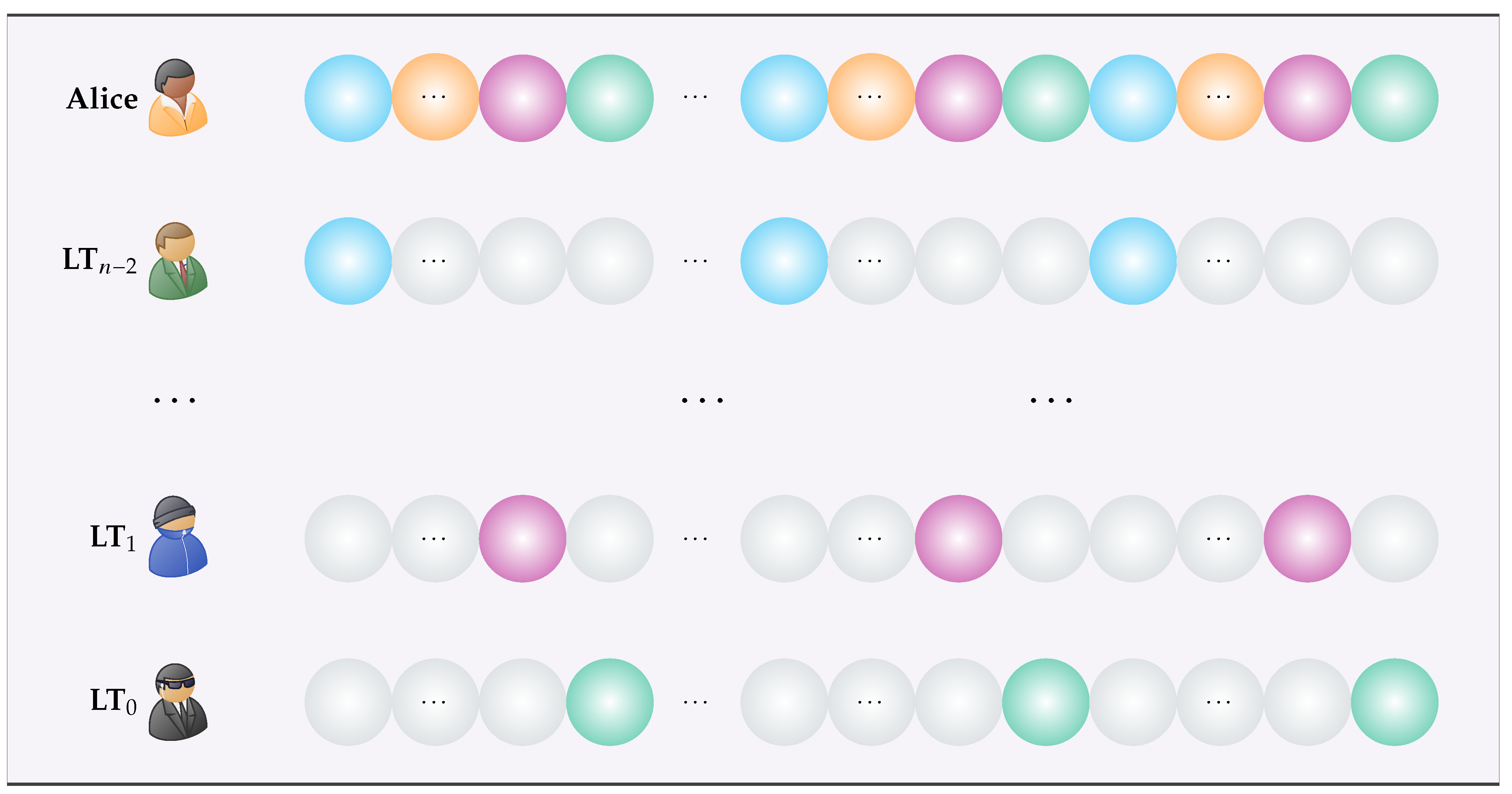
Visually, the situation regarding the correlations among corresponding bits is shown in
Figure 2. Again bits resulting from the same EPR pair are shown in the same color.
Definition 4 (Command Vectors)
. Alice sends to Bob and Charlie either the command 0
or the command 1
. Besides her command, as a “proof”, she also sends an appropriate command vector
. The idea is that the command vector for Bob is always different from the command vector for Charlie, even when the command is the same. For the command 0
, the command vectors for Bob and Charlie are and , respectively, whereas for the command 1
the corresponding command vectors are and . The explicit form of the command vectors is the following.A command vector, besides pairs containing 0
and 1
bits, also contains an approximately equal number of pairs consisting of ⊔
characters. When we want refer to a command vector, but without providing further details, we will designate it by Given a command vector or a bit vector, we define the set containing the positions of the pairs that consist of a given combination of bits.
Definition 5 (Pair Designation). Given a command vector or a bit vector , we define the set and , respectively, of the positions of those pairs consisting precisely of the bits .
Example 1 (Illustrating the concepts)
. This first example is designed to illustrate all the previous concepts. For practical purposes, i.e., to fit in a page, we take . In a real implementation m should certainly be greater (see Table 1). Let us assume that the contents of Alice, Bob and Charlie’s registers are those shown in Figure 3.By Definition 3, we may write thatwhere the bit vectors , , and denote the contents of Alice, Bob and Charlie’s registers after the measurement. In Figure 3, the correlated pairs of bits are drawn with the same color. Specifically, as in all previous figures, red is used to indicate the pairs of bits that originated from the measurement of the EPR pairs shared between Alice and Bob, and which occupy the odd-numbered positions in their registers. Analogously, green depicts the pairs of bits that originated from the measurement of the EPR pairs shared between Alice and Charlie, which occupy the even-numbered positions in their registers. The remaining gray bits that appear in Bob and Charlie’s registers come from qubits that were initially in the state. By a simple observation of the red and green pairs of bits, we immediately see that Lemma 1 is verified. In every red pair, the two bits are complementary, i.e., the second bit is the negation of the first. This is due to the fact that their values are the result of the measurement of a pair. The red pairs correlate Alice and Bob’s registers. Exactly the same holds for the green pairs, which correlate Alice and Charlie’s registers. The initial presence of the pairs in the entanglement distribution phase, has manifested into classical correlation among the contents of Alice, Bob, and Charlie’s registers during the agreement phase.
There are 12
pairs in , , and . In each of them, the pair, , contains the bits that occupy positions and , as shown in Figure 3. The bit in position is the most significant bit of the pair and the bit in position is the least significant bit. Let us suppose that Alice sends the order 0. According to Definition 4, Alice must prove her order by sending the command vectors and to Bob and Charlie, respectively. The command vector is constructed by including the pairs in with most significant bit 0
(irrespective of what the least significant bit is) and filling the gaps with the uncertain pair. Symmetrically, is constructed by including the pairs in with least significant bit 0
(irrespective of what the most significant bit is) and filling the gaps with the uncertain pair. Thus, and are as given below (we have also repeated to facilitate the comparison).Recalling Definition 5, we see that the sets and contain the positions in and , respectively, of the pairs consisting of the bits . In view of (26) and (27), we derive that Let us now suppose that Alice sends the order 1
. In this case, Alice must prove her order by sending the command vectors and to Bob and Charlie, respectively. The command vector is constructed by including the pairs in with most significant bit 1
(irrespective of what the least significant bit is) and filling the gaps with the uncertain pair. Symmetrically, is constructed by including the pairs in with least significant bit 1
(irrespective of what the most significant bit is) and filling the gaps with the uncertain pair. The resulting and are shown below (again, we have also repeated to facilitate the comparison).The sets and contain the positions in and , respectively, of the pairs. Taking into account (29) and (30), we see that In the present example, the value of the parameter m is 12, which implies that . The cardinality of all the sets , , , , , , , and is , which verifies the next Lemma 2. Of course, the exact cardinality of some of these sets deviates slightly from the expected value 3, but this is not unexpected. As m increases, the ratio of the deviation to m will tend to 0. ◃
Based on Definition 5, it is trivial to see that the next Lemma 2 holds. The notation is employed to designate the cardinality, i.e., the number of elements, of an arbitrary set S.
Lemma 2 (Loyal Command Vector Properties). If Alice is loyal, her command vectors , , and satisfy the following properties.
The agreement phase of the EPRQDBA protocol evolves in rounds. The actions taken by the Alice, Bob and Charlie in each round are described below.
Algorithms 1–3 apply Lemmata 1 and 2 to determine whether a command vector is consistent, in which case they return TRUE. If they determine inconsistencies, they terminate and return FALSE. The names of Algorithms 2 and 3 are mnemonic abbreviations for “Check with Command Vector” and “Check with Bit Vector.” It is important to explain their difference.
Without loss of generality, let us suppose that Bob received the order 0 and a consistent command vector from Alice, while Charlie claims that he received the order 1. Charlie must convince Bob by sending Bob the command vector he claims he received from Alice. Bob checks for inconsistencies against his own by invoking the Algorithm 2. Now, imagine that Bob received an inconsistent command vector from Alice and his initial decision is to abort, while Charlie claims that he received the order 1. Charlie must convince Bob by sending Bob the command vector he claims he received from Alice. In this situation, Bob does not have a consistent command vector that he could use, so Bob must check for inconsistencies against his own bit vector by invoking the Algorithm 3.
In Algorithms 1–3, we employ the following notation.
are the indices of Bob (1) and Charlie (0).
c, where or , is the command being checked for consistency.
is the command vector sent by Alice.
, is the command vector sent by Bod to Charlie (or vice versa).
is the bit vector of Bod (Charlie) who does the consistency checking.
△ is the symmetric difference of two sets, i.e., , for given sets S and .
| Algorithm 1 CheckAlice (i, c, , ) |
![Applsci 13 08405 i001 Applsci 13 08405 i001]() |
| Algorithm 2 CheckWCV (i, j, c, , ) |
![Applsci 13 08405 i002 Applsci 13 08405 i002]() |
| Algorithm 3 CheckWBV (i, j, c, , ) |
![Applsci 13 08405 i003 Applsci 13 08405 i003]() |
In order to streamline the exposition of the text, all lengthy proofs are relocated in the
Appendix A.
In the literature, all works focusing on the 3 player setting, assume that there is exactly one traitor among the 3, who can either be the commanding general or one of the lieutenant generals. If we assume that there is precisely one traitor among the 3, we can prove the following Propositions 1 and 2.
Proposition 1 (Loyal Alice). If Alice is loyal, the 3 player EPRQDBA protocol will enable the loyal lieutenant general to agree with Alice. Specifically, if Alice and Bob are loyal and Charlie is a traitor, Bob will follow Alice’s order. Symmetrically, if Alice and Charlie are loyal and Bob is a traitor, Charlie will follow Alice’s order.
Proposition 2 (Traitor Alice). If Bob and Charlie are loyal and Alice is a traitor, the 3 player EPRQDBA protocol will enable Bob and Charlie to reach agreement, in the sense of both following the same order or both aborting.
Example 2 (Illustrating the 3 player protocol). This second example is a continuation of the first. It aims to illustrate the operation of the 3 Player EPRQDBA Protocol and give an intuitive explanation of why Propositions 1 and 2 are true.
Let us continue Example 1, and examine first the scenario where a loyal Alice sends order 0 to both Bob and Charlie accompanied by the command vectors and as given by (26) and (27), respectively. We may distinguish the following cases.
Both Bob and Charlie are loyal. Then, according to Rule of the 3 player EPRQDBA Protocol 1, all 3 players agree to execute order 0.
There is one traitor among Bob and Charlie. Without loss of generality we may assume that Charlie is the traitor, who tries to sabotage the agreement. What can he do?
- ⋄
Charlie may claim that he decided to abort because Alice sent him an inconsistent command vector. Then, according to Rule of the 3 player EPRQDBA Protocol 1, Bob will stick to his initial decision, and, together with Alice, will agree to execute order 0. In this way, assumption (DBA) of the detectable Byzantine Agreement protocol, stipulating that commanding general is loyal, then either all loyal lieutenant generals follow the commanding general’s order or abort the protocol (recall Definition 2), is satisfied. The rationale behind this rule is that Bob, having already received a consistent command vector from Alice, is suspicious of Charlie’s decision to abort, and decides to cling to his preliminary decision.
- ⋄
Charlie may claim that Alice gave the order 1
, along with a consistent command vector . Bob will then use the C
heckWCV
Algorithm 2 to check Charlie’s command vector against his own command vector for inconsistencies. If Bob finds no inconsistencies, then, according to Rule of the 3
player EPRQDBA Protocol 1, he will abort. Obviously, in such a case, Charlie will have won in sabotaging the agreement. Let’s analyze the probability of this event. First, let’s recall from (27) what Charlie knows with certainty.He partially knows given by (26), and in particular only the pairs consisting of 00
,and his problem is to construct something resembling the real , as given from (30). Charlie knows that the least significant bit of the uncertain pairs in is 1
and the most significant bit is 0
or 1
, with equal probability . However, Charlie cannot know with certainty if the most significant bit of a specific uncertain pair is 0
or 1
. Therefore, when guessing , Charlie can make two detectable mistakes: (i) place a 0
in a wrong pair that is not actually contained in , e.g., set the pair 10
as 01
, or (ii) place a 1
in a wrong pair that appears in , e.g., set pair 7 as 11
. The situation from a probabilistic point of view resembles the probability of picking the one correct configuration out of many. The total number of configurations is equal to the number of ways to place 2
or 3
identical objects (0
) into 5
distinguishable boxes. The probability that Charlie places all the 0
s correctly is Thus, the probability that Charlie cheats successfully is just , even in this toy scale example with . Consequently, Bob is bound to detect inconsistencies, which will lead him to apply Rule of the 3 player EPRQDBA Protocol 1, cling to his initial decision, and, ultimately, achieve agreement with Alice.
The situation where a loyal Alice sends order 1 to both Bob and Charlie is identical.
Let us now examine the second major scenario where a traitor Alice intends to prevent the loyal Bob and Charlie from recanting agreement. In view of Definition 2, this precludes the cases where Alice sends to both of them inconsistent command vectors, or the same order, accompanied by appropriate consistent command vectors. In reviewing her remaining options, we distinguish the following cases.
Alice sends an order, say 0, along with a consistent command vector to Bob and an inconsistent one to Charlie
. In this case, Bob will stick to his initial decision, but Charlie will use the C
heckWBV
Algorithm 3 to verify Bob’s command vector. In doing so, Charlie will crosscheck , given by (26), with his own bit vector from (24).Charlie will count the 00 and 01 pairs in to find that they are 4 and 2, pretty close to the expected value 3, and in all these pairs the least significant bit is the negation of his corresponding bit, as dictated by the original entanglement. Hence, Charlie will successfully verify Bob’s command vector, and, according to the Rule of the 3 player EPRQDBA Protocol 1, he will change his decision to that of Bob, thereby reaching the desired agreement. The rationale behind this rule is that Charlie, having already received an inconsistent command vector from Alice, is suspicious of Alice. His suspicion is confirmed when he verifies Bob’s command vector, considering that it high unlikely for Bob to have forge a consistent command vector. Thus, he decides to change his preliminary decision to that of Bob.
Alice sends to Bob and Charlie different orders with consistent command vectors. Let us assume, without loss of generality, that Alice sends the order 0 together with a consistent command vector to Bob and the order 1 together with a consistent command vector to Charlie. Bob knows the positions of almost all 00 and 01 pairs in . If Alice had forged even a single 10 or 11 pair, claiming to be either 00 or 01, then Bob, when using the CheckAlice Algorithm 1, he would have immediately detected the inconsistency. Symmetrically, Charlie knows the positions of almost all 01 and 11 pairs in . According to the rules of the protocol, Bob will sent to Charlie the command vector , and, simultaneously, Charlie will send to Bob the command vector . Both will use the CheckWCV Algorithm 2 to verify the consistency of the others’ command vector. Then, according to Rule, both Bob and Charlie will abort, again fulfilling the requirements of DBA. ◃
Let us ponder the question of what will happen if there are 2 traitors and only one loyal general. It might be that the 2 traitors are the 2 lieutenant generals, or the commanding general and one of the lieutenant generals. This case is actually very easy as explained in the next Corollary 1.
| Protocol 1: The 3 Player EPRQDBA Protocol. |
- (Round1)
Alice sends to Bob and Charlie her order and the appropriate command vector as proof. - (Round2)
Bob uses the CheckAlice Algorithm 1 to check the received command vector against his own bit vector for inconsistencies. - ★
If no inconsistencies are found, Bob preliminary accepts the received order. - ★
Otherwise, Bob’s preliminary decision is to abort (⊥).
Upon completion of the verification procedure, Bob sends to Charlie his preliminary decision together with the received command vector. Symmetrically and in parallel, Charlie performs the same actions. - (Round3)
Bob compares his own initial decision with that of Charlie’s. - ★
Rule: If Charlie’s decisions coincides with Bob’s preliminary decision, then Bob accepts as final his preliminary decision and terminates the protocol on his end. - ★
In case Charlie’s initial decision is different, then the following cases are considered. - □
Rule: If Bob’s decision is 0 (1) and Charlie’s decision is to abort, then Bob sticks to his initial decision and terminates the protocol. - □
If Bob’s decision is 0 (1) and Charlie’s decision is 1, then Bob uses the CheckWCV Algorithm 2 to check Charlie’s command vector against his own command vector for inconsistencies. - ⋄
Rule: If no inconsistencies are detected, then Bob aborts and terminates the protocol. - ⋄
Rule: Otherwise, Bob sticks to his preliminary decision and terminates the protocol.
- □
If Bob’s decision is to abort and Charlie’s decision is 0 (or 1), then Bob uses the CheckWBV Algorithm 3 to check Charlie’s command vector against his own bit vector for inconsistencies. - ⋄
Rule: If no inconsistencies are found, then Bob changes his final decision to 0 (1) and terminates the protocol. - ⋄
Rule: Otherwise, Bob sticks to his initial decision to abort and terminates the protocol.
Charlie’s actions mirror Bob’s actions.
|
Corollary 1 (The case of 2 traitors). The 3 player EPRQDBA protocol achieves detectable Byzantine Agreement even when there are 2 traitors among the 3 generals.
Proof. The fundamental assumption (DBA) of any detectable Byzantine Agreement protocol, stipulates that all loyal generals either follow the same order or abort the protocol (recall Definition 2). When there is only one loyal general, no matter whether he is the commanding general or a lieutenant general, whatever he decides is perfectly fine, as there is no other loyal party that he must agree with. □
The next theorem is an obvious consequence of Propositions 1 and 2, and Corollary 1.
Theorem 1 (3 Player Detectable Byzantine Agreement). The 3 player EPRQDBA protocol achieves detectable Byzantine Agreement in any eventuality.