Biothermal Heating on Human Skin by Millimeter and Sub-Terahertz Waves in Outdoor Environment—A Theoretical Study
Abstract
1. Introduction
2. Dielectric Properties and Channel Modeling
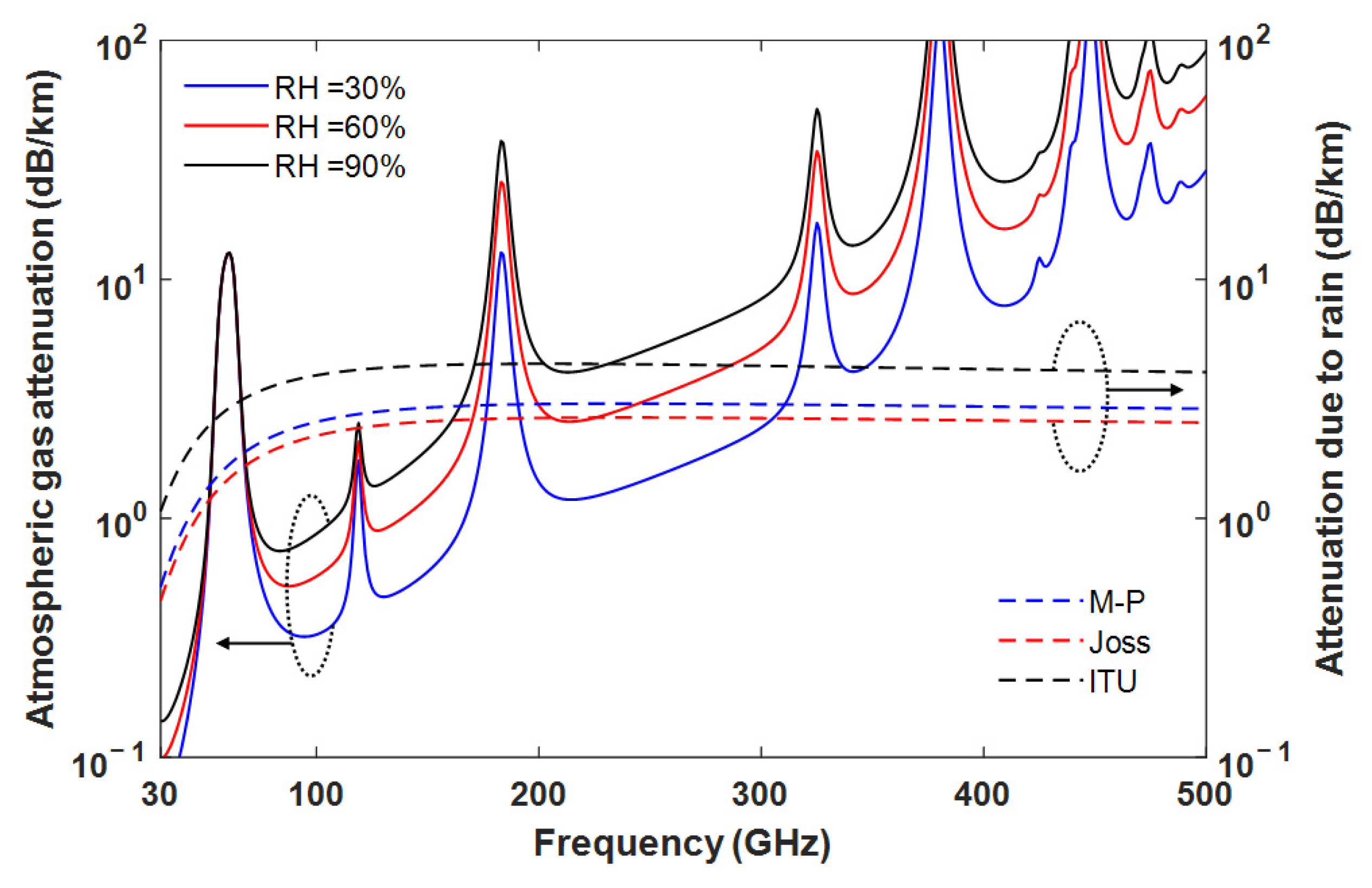
2.1. Dielectric Properties of Skin and Rainwater
2.2. Channel Models
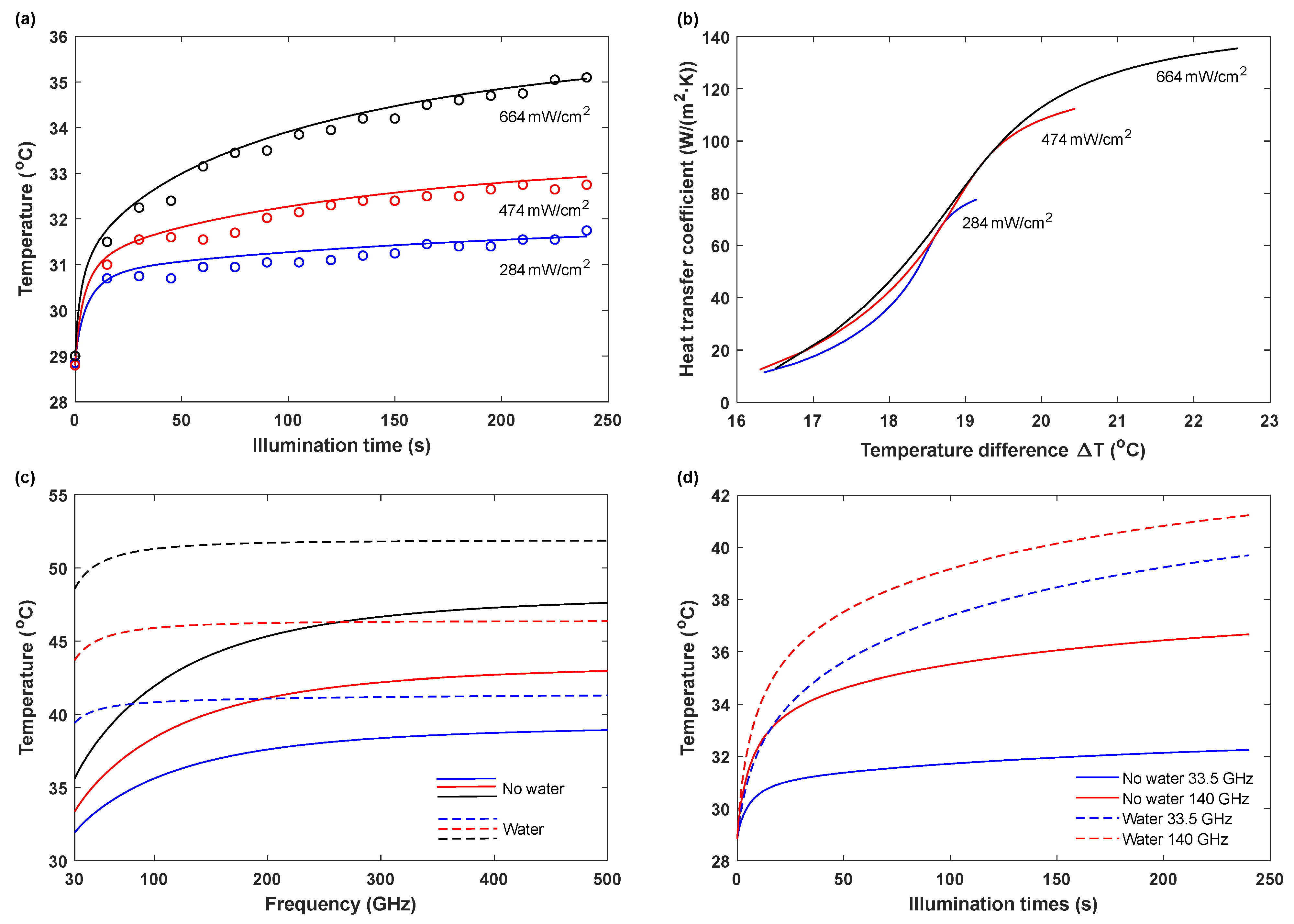
3. Thermal Heat Modeling
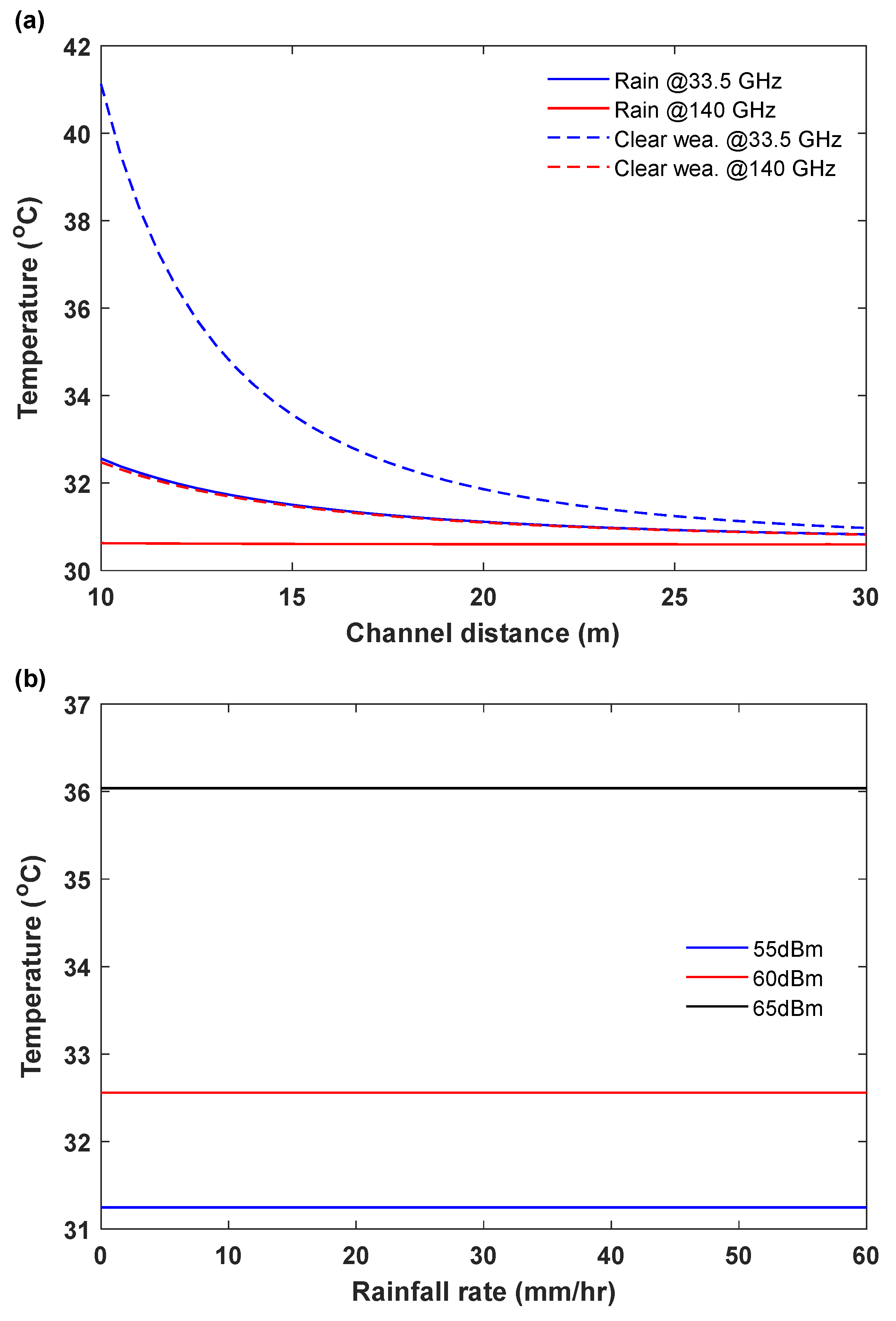
4. Outdoor Thermal Heating Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Popov, V.; Shevchenko, A. Analysis of standards and norms of electromagnetic irradiation levels in wireless communication systems on railway transport. Procedia Comput. Sci. 2019, 149, 239–245. [Google Scholar] [CrossRef]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines for limiting exposure to electromagnetic fields (100 kHz to 300 GHz). Health Phys. 2020, 118, 483–524. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Diao, Y.; Onishi, T.; Sasaki, K.; Ahn, S.; Colombi, D.; Santis, V.D.; Laakso, I.; Giaccone, L.; Joseph, W.; et al. Assessment of human exposure to electromagnetic fields: Review and future directions. IEEE Trans. Electromagn. Compat. 2021, 63, 1619–1630. [Google Scholar] [CrossRef]
- Bailey, W.H.; Bodemann, R.; Bushberg, J.; Chou, C.; Cleveland, R.; Faraone, A.; Foster, K.R.; Gettman, K.E.; Graf, K.; Harrington, T.; et al. Synopsis of IEEE Std C95. 1™-2019 “IEEE Standard for Safety Levels with Respect to Human Exposure to Electric, Magnetic, and Electromagnetic Fields, 0 Hz to 300 GHz”. IEEE Access 2019, 7, 171346–171356. [Google Scholar] [CrossRef]
- Sasaki, K.; Mizuno, M.; Wake, K.; Watanabe, S. Monte Carlo simulations of skin exposure to electromagnetic field from 10 GHz to 1 THz. Phys. Med. Biol. 2017, 62, 6993–7010. [Google Scholar] [CrossRef]
- Kanezaki, A.; Hirata, A.; Watanabe, S.; Shirai, H. Effects of dielectric permittivities on skin heating due to millimeter wave exposure. Biomed. Eng. Online 2009, 8, 20. [Google Scholar] [CrossRef]
- Hashimoto, Y.; Hirata, A.; Morimoto, R.; Aonuma, S.; Laakso, I.; Jokela, K.; Foster, K.R. On the averaging area for incident power density for human exposure limits at frequencies over 6 GHz. Phys. Med. Biol. 2017, 62, 3124. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Zhao, L.; Ma, J.; Sun, H.; Moeller, L.; Federici, J.F. Performance degradation of terahertz channels in emulated rain. Nano Commun. Netw. 2023, 35, 100431. [Google Scholar] [CrossRef]
- Wang, R.; Mei, Y.; Meng, X.; Ma, J. Secrecy performance of terahertz wireless links in rain and snow. Nano Commun. Netw. 2021, 28, 100350. [Google Scholar] [CrossRef]
- Amarasinghe, Y.; Zhang, W.; Zhang, R.; Mittleman, D.M.; Ma, J. Scattering of Terahertz Waves by Snow. J. Infrared Millim. Terahertz Waves 2020, 41, 215–224. [Google Scholar] [CrossRef]
- Ma, J.; Adelberg, J.; Shrestha, R.; Moeller, L.; Mittleman, D.M. The Effect of Snow on a Terahertz Wireless Data Link. J. Infrared Millim. Terahertz Waves 2018, 39, 505–508. [Google Scholar] [CrossRef]
- Ma, J.; Shrestha, R.; Moeller, L.; Mittleman, D.M. Invited Article: Channel performance for indoor and outdoor terahertz wireless links. APL Phontonics 2018, 3, 51601. [Google Scholar] [CrossRef]
- Federici, J.F.; Ma, J.; Moeller, L. Review of weather impact on outdoor terahertz wireless communication links. Nano Commun. Netw. 2016, 10, 13–26. [Google Scholar] [CrossRef]
- Ma, J.; Vorrius, F.; Lamb, L.; Moeller, L.; Federici, J.F. Experimental Comparison of Terahertz and Infrared Signaling in Laboratory-Controlled Rain. J. Infrared Millim. Terahertz Waves 2015, 36, 856–865. [Google Scholar] [CrossRef]
- Ma, J.; Vorrius, F.; Lamb, L.; Moeller, L.; Federici, J.F. Comparison of Experimental and Theoretical Determined Terahertz Attenuation in Controlled Rain. J. Infrared Millim. Terahertz Waves 2015, 36, 1195–1202. [Google Scholar] [CrossRef]
- Hirata, A.; Yamaguchi, R.; Takahashi, H.; Kosugi, T.; Murata, K.; Kukutsu, N.; Kado, Y. Effect of Rain Attenuation for a 10-Gb/s 120-GHz-Band Millimeter-Wave Wireless Link. IEEE Trans. Microw. Theory Technol. 2009, 57, 3099–3105. [Google Scholar] [CrossRef]
- Yang, Y.; Mandehgar, M.; Grischkowsky, D.R. Broadband THz Signals Propagate Through Dense Fog. IEEE Photonics Technol. Lett. 2015, 27, 383–386. [Google Scholar] [CrossRef]
- Nikitkina, A.I.; Bikmulina, P.Y.; Gafarova, E.R.; Kosheleva, N.V.; Efremov, Y.M.; Bezrukov, E.A.; Butnaru, D.V.; Dolganova, I.N.; Chernomyrdin, N.V.; Cherkasova, O.P.; et al. Terahertz radiation and the skin: A review. J. Biomed. Opt. 2021, 26, 43005. [Google Scholar] [CrossRef]
- Wu, T.; Rappaport, T.S.; Collins, C.M. Safe for Generations to Come: Considerations of Safety for Millimeter Waves in Wireless Communications. IEEE Microw. Mag. 2015, 16, 65–84. [Google Scholar] [CrossRef]
- Gandhi, O.P.; Riazi, A. Absorption of Millimeter Waves by Human Beings and its Biological Implications. IEEE Trans. Microw. Theory Technol. 1986, 34, 228–235. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Pickwell, E.; Cole, B.E.; Fitzgerald, A.J.; Wallace, V.P.; Pepper, M. Simulation of terahertz pulse propagation in biological systems. Appl. Phys. Lett. 2004, 84, 2190–2192. [Google Scholar] [CrossRef]
- Alekseev, S.I.; Ziskin, M.C. Human skin permittivity determined by millimeter wave reflection measurements. Bioelectromagnetics 2007, 28, 331–339. [Google Scholar] [CrossRef]
- Chahat, N.; Zhadobov, M.; Augustine, R.; Sauleau, R. Human skin permittivity models for millimetre-wave range. Electron. Lett. 2011, 47, 427–428. [Google Scholar] [CrossRef]
- Hasgall, P.A.; Gennaro, F.D.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Klingenbock, A.; Kuster, N. IT’ IS Database for Thermal and Electromagnetic Parameters of Biological Tissues. Available online: https://itis.swiss/virtual-population/tissue-properties/overview/ (accessed on 10 July 2023).
- Tripathi, S.R.; Miyata, E.; Ishai, P.B.; Kawase, K. Morphology of human sweat ducts observed by optical coherence tomography and their frequency of resonance in the terahertz frequency region. Sci. Rep. 2015, 5, 9071. [Google Scholar] [CrossRef]
- Kristensen, T.T.; Withayachumnankul, W.; Jepsen, P.U.; Abbott, D. Modeling terahertz heating effects on water. Opt. Express 2010, 18, 4727–4739. [Google Scholar] [CrossRef]
- Barthel, J.; Bachhuber, K.; Buchner, R.; Hetzenauer, H. Dielectric spectra of some common solvents in the microwave region. Water and lower alcohols. Chem. Phys. Lett. 1990, 167, 62–66. [Google Scholar] [CrossRef]
- Kindt, J.T.; Schmuttenmaer, C.A. Far-Infrared Dielectric Properties of Polar Liquids Probed by Femtosecond Terahertz Pulse Spectroscopy. J. Phys. Chem. 1996, 100, 10373–10379. [Google Scholar] [CrossRef]
- Stogryn, A.P.; Bull, H.T.; Rubayi, K.; Iravanchy, S. The microwave permittivity of sea and freshwater. In Arrojet Internal Report; GenCorp Aerojet: Sacramento, CA, USA, 1996. [Google Scholar]
- Ronne, C.; Thrane, L.; Astrand, P.O.; Wallqvist, A.; Mikkelsen, K.V.; Keiding, S.R. Investigation of the temprerature dependence of dielectric relaxation in liquid water by THz reflection spectroscopy and molecular dynamics simulation. J. Chem. Phys. 1997, 107, 5319–5331. [Google Scholar] [CrossRef]
- Mätzler, C. Thermal Microwave Radiation: Applications for Remote Sensing; Institution of Engineering & Technology: Stevenage, UK, 2007. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Actice and Passive. In Radar Remote Sensing and Surface Scattering and Emission Theory; Artech House: Norwood, MA, USA, 1982; Volume 2. [Google Scholar]
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1 THz. Int. J. Infrared Millim. Waves 1991, 12, 659–675. [Google Scholar] [CrossRef]
- Nakagawa, N.; Matsumoto, M.; Sakai, S. In vivo measurement of the water content in the dermis by confocal Raman spectroscopy. Skin Res. Technol. 2010, 16, 137–141. [Google Scholar] [CrossRef] [PubMed]
- You, B.; Chen, C.; Yu, C.; Wang, P.; Lu, J. Frequency-dependent skin penetration depth of terahertz radiation determined by water sorption–desorption. Opt. Express 2018, 26, 22709–22721. [Google Scholar] [CrossRef] [PubMed]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Actice and Passive. In Fundamentals and Radiometry; Artech House: Norwood, MA, USA, 1981; Volume 1. [Google Scholar]
- ITU-R Recommendation P.676-13: Attenuation by Atmospheric Gases and Related Effects. Available online: https://www.itu.int/rec/R-REC-P.676-13-202208-I/en (accessed on 10 July 2023).
- Liebe, H.J.; Hufford, G.A.; Cotton, M.G. Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz. In Proceedings of the AGARD 52th Specialists’ Meeting of the Electromagnetic Wave Propagation Panel, Palma de Mallorca, Spain, 17–20 May 1993. [Google Scholar]
- O’Hara, J.F.; Grischkowsky, D.R. Comment on the Veracity of the ITU-R Recommendation for Atmospheric Attenuation at Terahertz Frequencies. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 372–375. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Deirmendjian, D. Electromagnetic Scattering on Spherical Polydispersions; American Elsevier Publishing: New York, NY, USA, 1969. [Google Scholar]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Joss, J.; Thams, J.C.; Waldvogel, A. The variation of rain drop size distribution at Locarno. Bull. Am. Meteorol. Soc. 1968, 49, 2. [Google Scholar]
- ITU-R Recommendation P.838-3: Specific Attenuation Model for Rain for Use in Prediction Methods. 2005. Available online: https://www.itu.int/rec/R-REC-P.838/en (accessed on 10 July 2023).
- 3GPP TS 38.104. Base Station (BS) Radio Transmission and Reception. Available online: https://www.3gpp.org/ftp/Specs/archive/38_series/38.104 (accessed on 10 July 2023).
- Wang, W.Y. Study on Animal Surface Temperature Irradiated by Millimeter Wave; University of Electronic Science and Technology of China: Chengdu, China, 2005. [Google Scholar]
- Foster, K.R.; Kritikos, H.N.; Schwan, H.P. Effect of Surface Cooling and Blood Flow on the Microwave Heating of Tissue. IEEE Trans. Biomed. Eng. 1978, 25, 313–316. [Google Scholar] [CrossRef]
- Song, W.J.; Weinbaum, S.; Jiji, L.M. A Theoretical Model for Peripheral Tissue Heat Transfer Using the Bioheat Equation of Weinbaum and Jiji. J. Biomech. Eng. 1987, 109, 72–78. [Google Scholar] [CrossRef]
- Liu, J.; Ren, Z.P.; Wang, C.C. Interpretation of living tissue’s temperature oscillations by thermal wave theory. Chin. Sci. Bull. 1995, 12, 1493–1495. [Google Scholar]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1984, 85, 5–34. [Google Scholar] [CrossRef]
- Wang, H.; Burgei, W.A.; Zhou, H. Analytical solution of one-dimensional Pennes’ bioheat equation. Open Phys. 2020, 18, 1084–1092. [Google Scholar] [CrossRef]
- Musat, R.; Helerea, E. Parameters and Models of the Vehicle Thermal Comfort. Acta Univ. Sapientiae 2009, 1, 215–226. [Google Scholar]
- Benedict, F.G.; Miles, W.R.; Johnson, A. The Temperature of the Human Skin. Proc. Natl. Acad. Sci. USA 1919, 5, 218–222. [Google Scholar] [CrossRef]
- Torvi, D.A.; Dale, J.D. A Finite Element Model of Skin Subjected to a Flash Fire. J. Biomech. Eng. 1994, 116, 250–255. [Google Scholar] [CrossRef]
- Deng, Z.S.; Liu, J. Parametric studies on the phase shift method to measure the blood perfusion of biological bodies. Med. Eng. Phys. 2000, 22, 693–702. [Google Scholar] [CrossRef]
- Ishigaki, H.; Horikoshi, T.; Uematsu, T.; Sahashi, M.; Tsuchikawa, T.; Mochida, T.; Hieda, T.; Isoda, N.; Kubo, H. Experimental study on convective heat transfer coefficient of the human body. J. Therm. Biol. 1993, 18, 455–458. [Google Scholar] [CrossRef]
- Gilhar, A.; Etzioni, A. The nude mouse model for the study of human skin disorders. Dermatology 1994, 189, 5–8. [Google Scholar] [CrossRef]
- Tolgyessy, J. Chemistry and Biology of Water, Air and Soil: Environmental Aspects; Elsevier: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Asada, M.; Suzuki, S. Terahertz emitter using resonant-tunneling diode and applications. Sensors 2021, 21, 1384. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, M.; Li, P.; Lei, Y.; Bao, X.; Ma, J. Biothermal Heating on Human Skin by Millimeter and Sub-Terahertz Waves in Outdoor Environment—A Theoretical Study. Appl. Sci. 2023, 13, 8305. https://doi.org/10.3390/app13148305
Wei M, Li P, Lei Y, Bao X, Ma J. Biothermal Heating on Human Skin by Millimeter and Sub-Terahertz Waves in Outdoor Environment—A Theoretical Study. Applied Sciences. 2023; 13(14):8305. https://doi.org/10.3390/app13148305
Chicago/Turabian StyleWei, Menghan, Peian Li, Yuanshuai Lei, Xiue Bao, and Jianjun Ma. 2023. "Biothermal Heating on Human Skin by Millimeter and Sub-Terahertz Waves in Outdoor Environment—A Theoretical Study" Applied Sciences 13, no. 14: 8305. https://doi.org/10.3390/app13148305
APA StyleWei, M., Li, P., Lei, Y., Bao, X., & Ma, J. (2023). Biothermal Heating on Human Skin by Millimeter and Sub-Terahertz Waves in Outdoor Environment—A Theoretical Study. Applied Sciences, 13(14), 8305. https://doi.org/10.3390/app13148305









