The Efficacy and Utility of Lower-Dimensional Riemannian Geometry for EEG-Based Emotion Classification
Abstract
1. Introduction
- (i)
- Direct computations on the covariance matrices of EEG signals through applying differential geometry tools and algorithms, such as minimum distance to Riemannian mean (MDRM). Thus, it facilitates the classification of covariance matrices within the Riemannian space to help enhance EEG signal analysis [10].
- (ii)
- Riemannian geodesic distance metric accounts for the geometry of the space of covariance matrices. It is invariant by projection, allowing the use of dimensionality reduction techniques, such as principal component analysis (PCA), to compute the space of covariance matrices without losing essential information or distorting the structure of the space, which is crucial for accurate analysis of EEG signals [10,15,16].
- (iii)
- The dimensionality reduction performed on Riemannian spaces offers a means to exploit high dimensional and more discriminative features, subsequently improving accuracy in classification or clustering [17].
- (iv)
- The Riemannian framework can handle intra-individual variability by modeling individual-specific covariance matrices, which can capture variations in brain activity patterns over time. Similarly, it can address inter-individual variability by employing population-based covariance models that capture commonalities across individuals.
- (v)
- The Riemannian framework is robust to changes in electrode placement and noise handling, allowing for reliable and accurate analysis of EEG signals [16].
- (vi)
- The Riemannian framework is insensitive to spatial filtering of the data, resulting in improved classification accuracy.
- (1)
- Integration of traditional feature extraction techniques, specifically principal component analysis (PCA), into a dynamic feature extraction process. By representing the extracted features as covariance matrices and leveraging their distinctive characteristics in the Riemannian manifold space, our proposed method effectively addresses variabilities observed across different instances.
- (2)
- Demonstration of the generalizability and robustness of the proposed method through a successful application to four well-known datasets with varying characteristics. The achieved results outperformed state-of-the-art methods, highlighting the considerable potential of this approach for practical applications.
2. Related Work
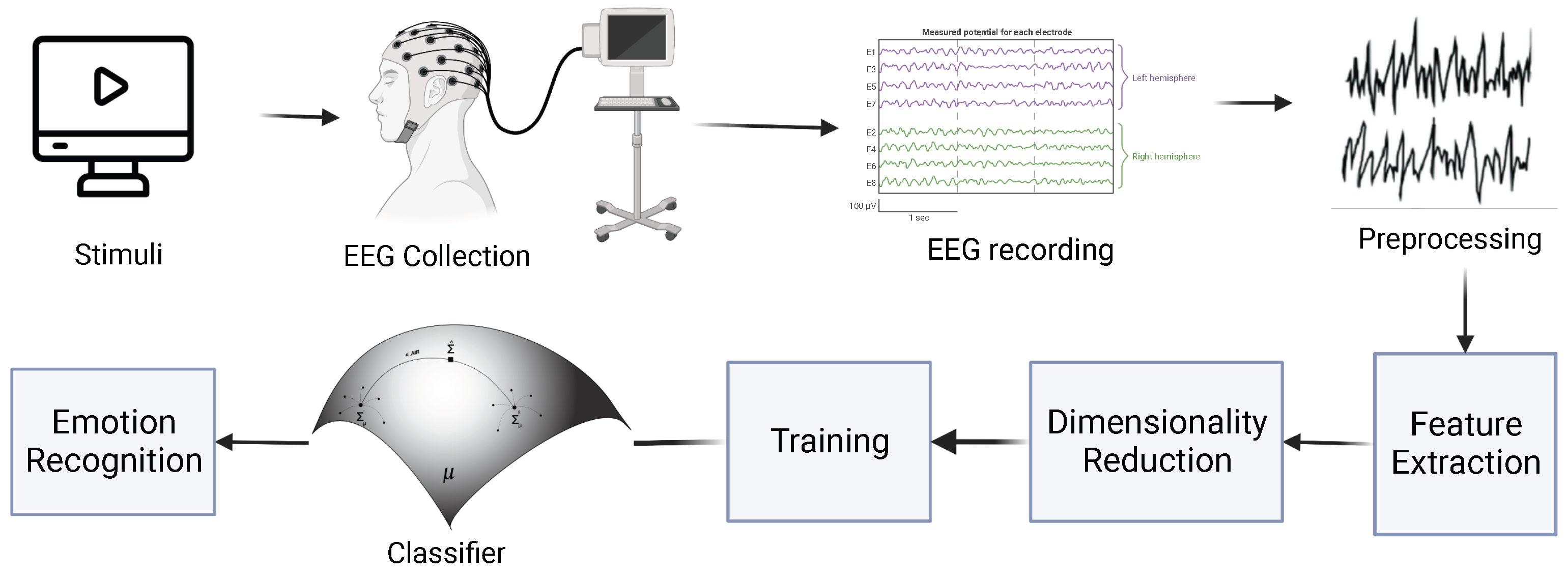
3. Methods
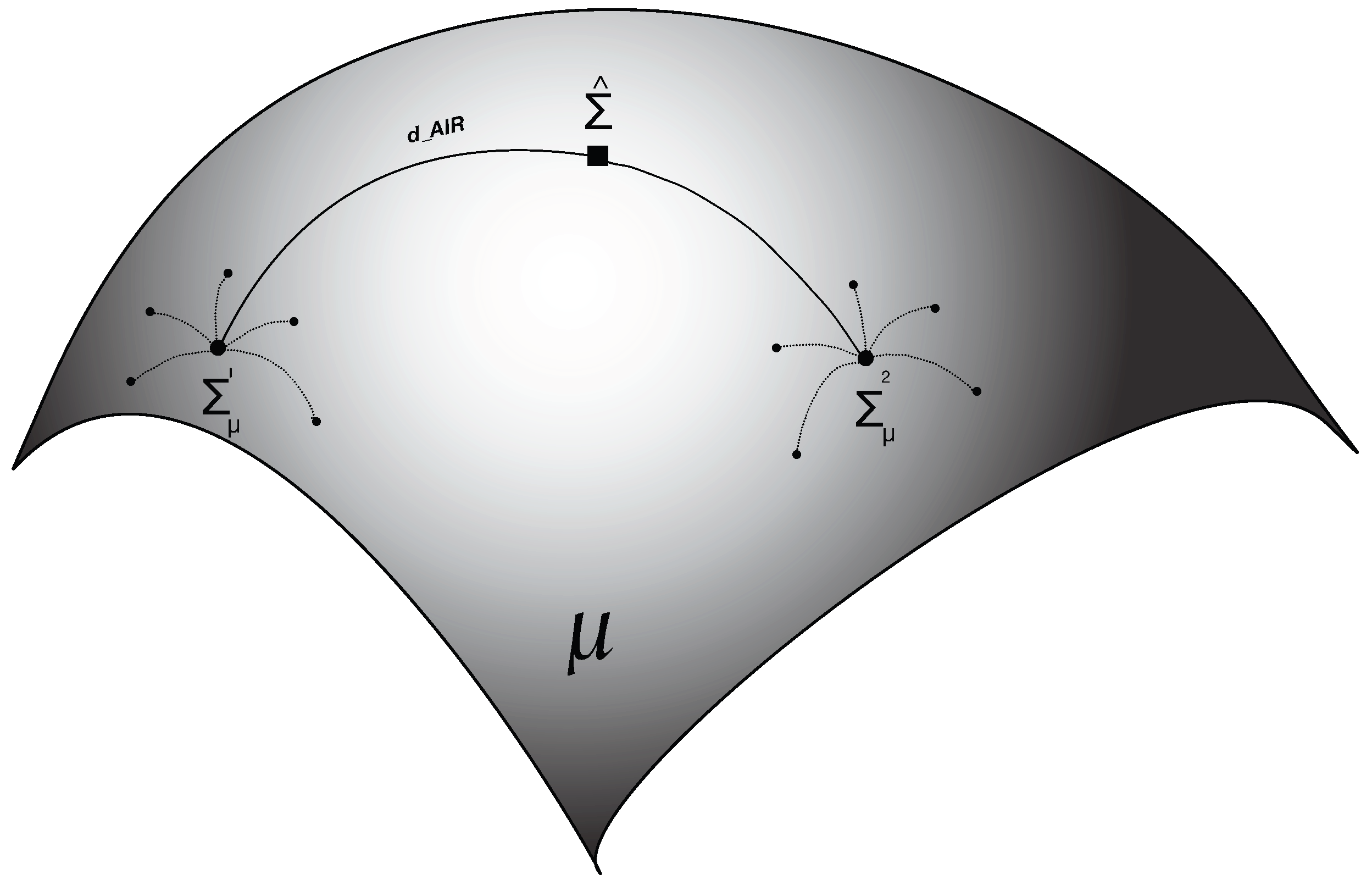
3.1. Riemannian
3.2. Classification Algorithms
| Algorithm 1 Estimation of Riemannian centers of classes. |
Input: a set of labeled trials for . Input: , a set of indices of trials of class k. Output: , k = 1,...,K, centers of classes.
|
| Algorithm 2 Minimum distance to Riemannian mean. |
Input: a set of of K different known classes. Input: X an EEG trial of unknown class. Input: , K centers of classes from Algorithm 1. Output: the predicted class of test trial X
|
3.3. Methods
3.3.1. Method 1 (MDRM)
3.3.2. Method 2 (MDRM plus PCA)
3.3.3. Method 3 (MDRM plus PCA plus Hyperparameter Tuning)
| Algorithm 3 Feature extraction and hyperparameter tuning. |
Input: = outer folds, = inner folds. Input: D, the subject dataset. Input: , hyperparameters pairs. Output: Accuracy
|
3.4. Pre-Processing and Feature Extraction
3.5. Datasets
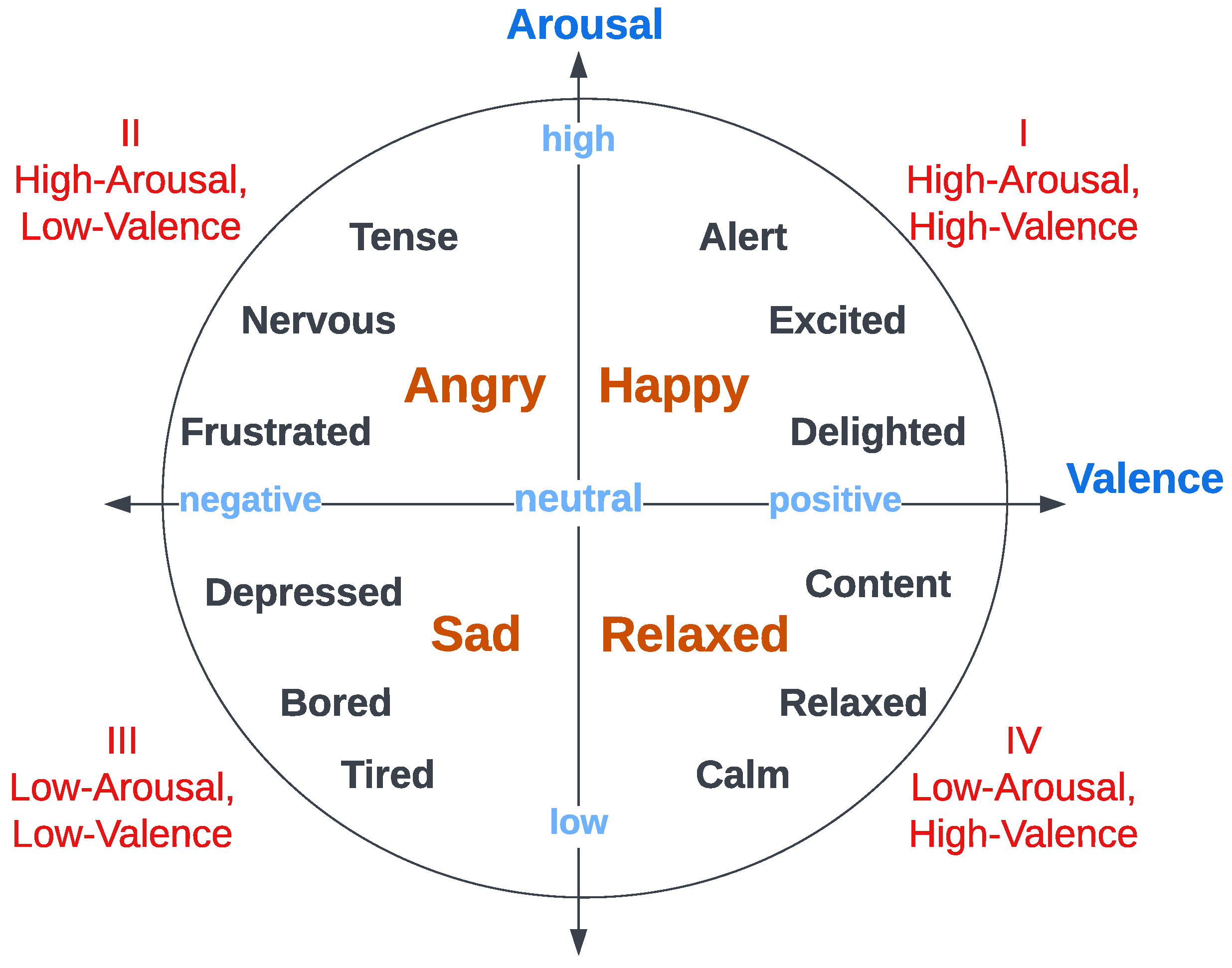
3.5.1. DEAP Dataset
3.5.2. DREAMER Dataset
3.5.3. MAHNOB Dataset
3.5.4. SEED Dataset
4. Results
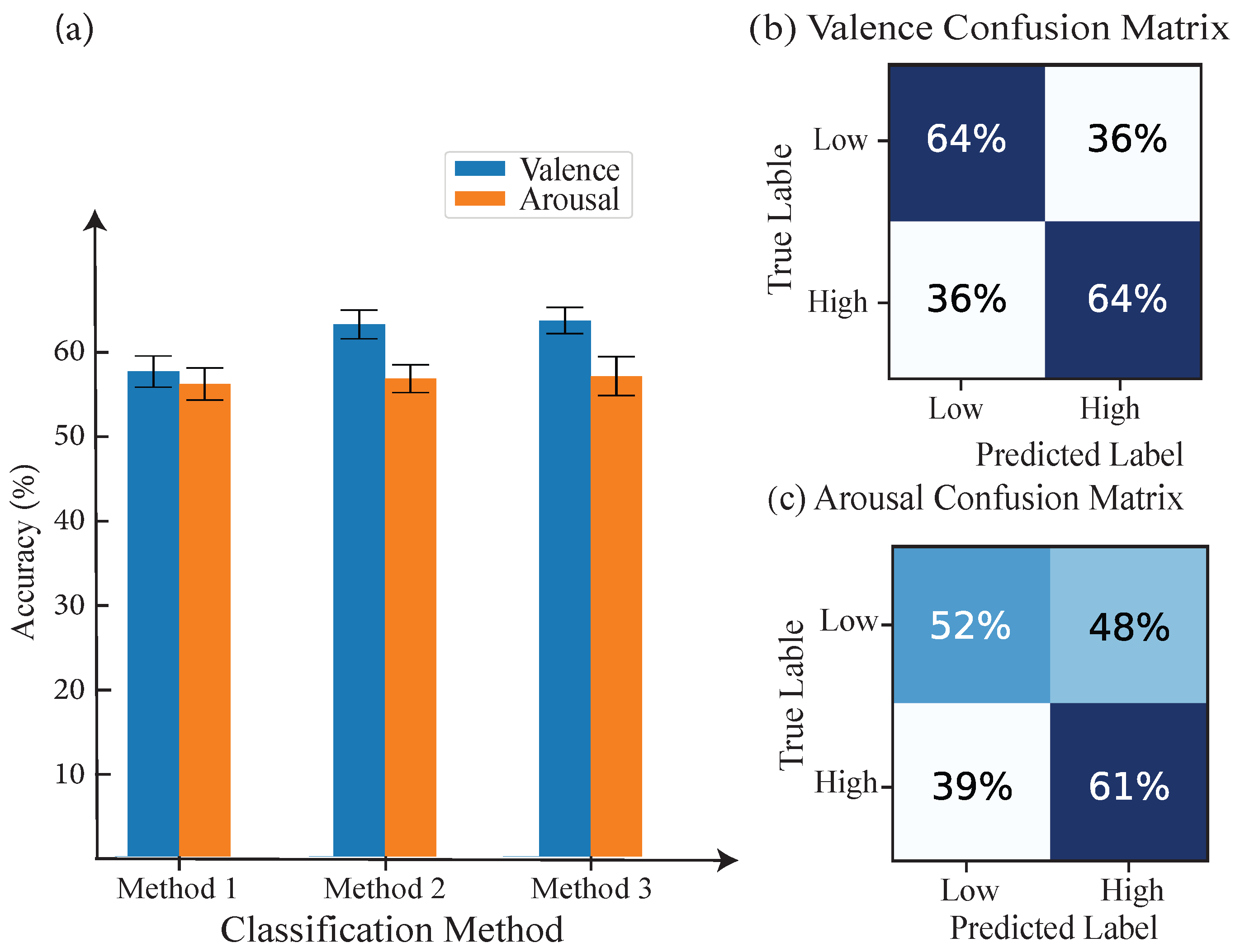
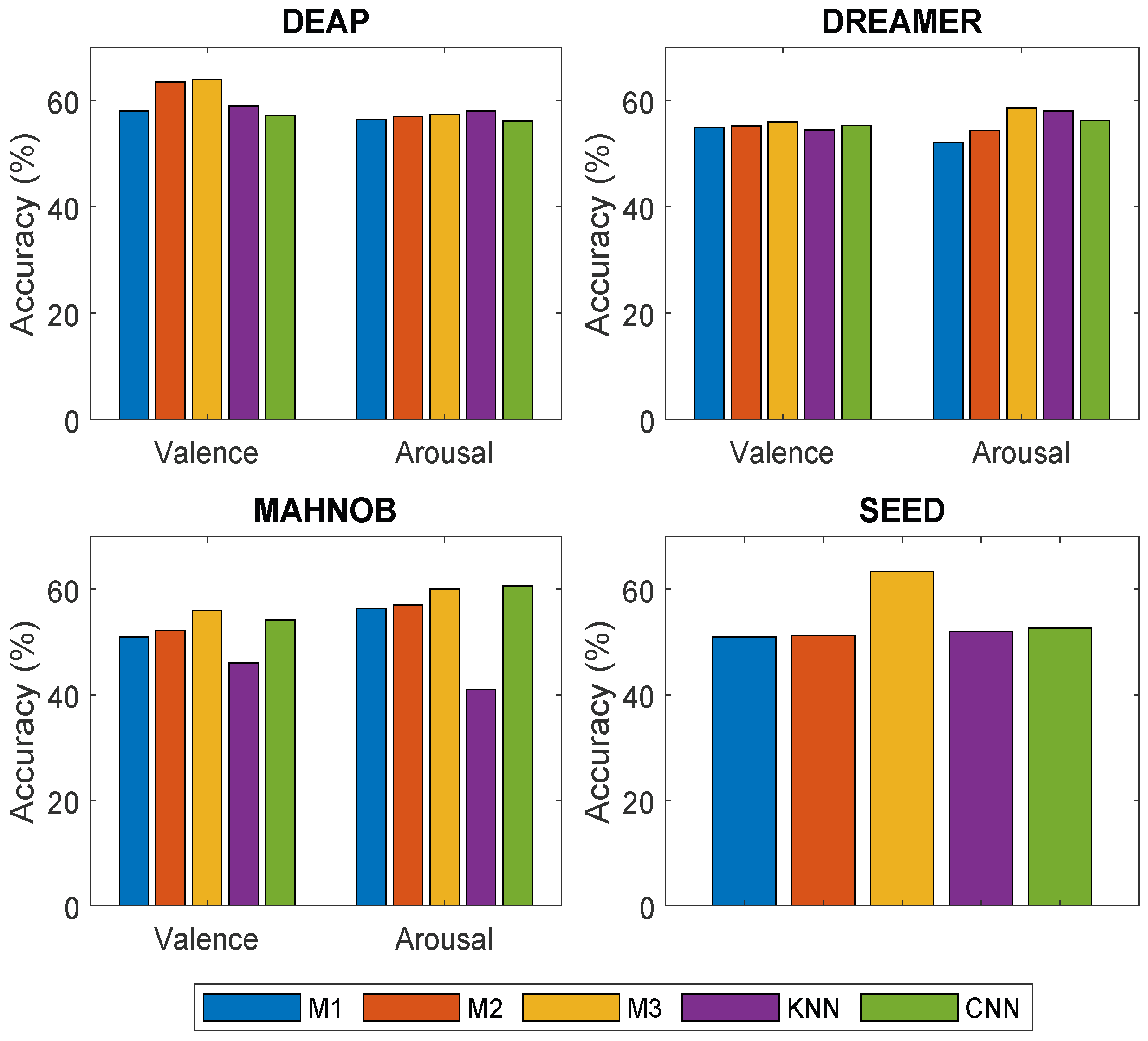
4.1. DEAP Dataset
4.2. DREAMER Dataset
4.3. MAHNOB Dataset
4.4. SEED Dataset
4.5. Overall Performance Comparison of Proposed Methods and Baseline Models on Multiple Datasets
5. Discussion and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koelstra, S.; Muhl, C.; Soleymani, M.; Lee, J.S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. DEAP: A Database for Emotion Analysis; Using Physiological Signals. IEEE Trans. Affect. Comput. 2012, 3, 18–31. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Li, Y.; Kong, X. Review on emotion recognition based on electroencephalography. Front. Comput. Neurosci. 2021, 15, 758212. [Google Scholar] [CrossRef]
- Zheng, W.L.; Lu, B.L. Investigating Critical Frequency Bands and Channels for EEG-Based Emotion Recognition with Deep Neural Networks. IEEE Trans. Auton. Ment. Dev. 2015, 7, 162–175. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hammad, A.; Ali, A.A. Human Emotion Recognition from EEG-Based Brain-Computer Interface Using Machine Learning: A Comprehensive Review. Neural Comput. Appl. 2022, 34, 12527–12557. [Google Scholar] [CrossRef]
- Davis, M.; Whalen, P.J. The amygdala: Vigilance and emotion. Mol. Psychiatry 2001, 6, 13–34. [Google Scholar] [CrossRef]
- Nguyen, T.; Zhou, T.; Potter, T.; Zou, L.; Zhang, Y. The cortical network of emotion regulation: Insights from advanced EEG-fMRI integration analysis. IEEE Trans. Med. Imaging 2019, 38, 2423–2433. [Google Scholar] [CrossRef]
- Abdel-Ghaffar, E.A.; Wu, Y.; Daoudi, M. Subject-Dependent Emotion Recognition System Based on Multidimensional Electroencephalographic Signals: A Riemannian Geometry Approach. IEEE Access 2022, 10, 14993–15006. [Google Scholar] [CrossRef]
- Mei, H.; Xu, X. EEG-based emotion classification using convolutional neural network. In Proceedings of the 2017 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Shenzhen, China, 15–17 December 2017; pp. 130–135. [Google Scholar] [CrossRef]
- Lv, Z.; Qiao, L.; Wang, Q.; Piccialli, F. Advanced Machine-Learning Methods for Brain-Computer Interfacing. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 1688–1698. [Google Scholar] [CrossRef]
- Barachant, A.; Bonnet, S.; Congedo, M.; Jutten, C. Multiclass Brain-Computer Interface Classification by Riemannian Geometry. IEEE Trans. Biomed. Eng. 2012, 59, 920–928. [Google Scholar] [CrossRef]
- Navarro-Sune, X.; Hudson, A.L.; Fallani, F.D.V.; Martinerie, J.; Witon, A.; Pouget, P.; Raux, M.; Similowski, T.; Chavez, M. Riemannian Geometry Applied to Detection of Respiratory States From EEG Signals: The Basis for a Brain-Ventilator Interface. IEEE Trans. Biomed. Eng. 2017, 64, 1138–1148. [Google Scholar] [CrossRef]
- Islam, M.R.; Tanaka, T.; Molla, M.K.I. Multiband tangent space mapping and feature selection for classification of EEG during motor imagery. J. Neural Eng. 2018, 15, 046021. [Google Scholar] [CrossRef]
- Liang, J.; Wong, K.M.; Zhang, J.K. Detection of narrow-band sonar signal on a Riemannian manifold. In Proceedings of the 2015 IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, Canada, 3–6 May 2015; pp. 959–964. [Google Scholar] [CrossRef]
- Wu, D.; Lance, B.J.; Lawhern, V.J.; Gordon, S.; Jung, T.P.; Lin, C.T. EEG-Based User Reaction Time Estimation Using Riemannian Geometry Features. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2157–2168. [Google Scholar] [CrossRef]
- Barachant, A.; Bonnet, S.; Congedo, M.; Jutten, C. Common Spatial Pattern revisited by Riemannian geometry. In Proceedings of the 2010 IEEE International Workshop on Multimedia Signal Processing, Saint Malo, France, 4–6 October 2010; pp. 472–476. [Google Scholar] [CrossRef]
- Chevallier, S.; Kalunga, E.K.; Barthélemy, Q.; Monacelli, E. Review of Riemannian distances and divergences, applied to SSVEP-based BCI. Neuroinformatics 2021, 19, 93–106. [Google Scholar] [CrossRef]
- Harandi, M.; Salzmann, M.; Hartley, R. Dimensionality Reduction on SPD Manifolds: The Emergence of Geometry-Aware Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 48–62. [Google Scholar] [CrossRef]
- Arsigny, V.; Fillard, P.; Pennec, X.; Ayache, N. Geometric means in a novel vector space structure on symmetric positive-definite matrices. SIAM J. Matrix Anal. Appl. 2007, 29, 328–347. [Google Scholar] [CrossRef]
- Smith, A.; Laubach, B.; Castillo, I.; Zavala, V.M. Data analysis using Riemannian geometry and applications to chemical engineering. Comput. Chem. Eng. 2022, 168, 108023. [Google Scholar] [CrossRef]
- Nam, C.S.; Nijholt, A.; Lotte, F. Brain-Computer Interfaces Handbook: Technological and Theoretical Advances; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Soleymani, M.; Lichtenauer, J.; Pun, T.; Pantic, M. A Multimodal Database for Affect Recognition and Implicit Tagging. IEEE Trans. Affect. Comput. 2012, 3, 42–55. [Google Scholar] [CrossRef]
- Katsigiannis, S.; Ramzan, N. DREAMER: A Database for Emotion Recognition Through EEG and ECG Signals From Wireless Low-cost Off-the-Shelf Devices. IEEE J. Biomed. Health Inform. 2018, 22, 98–107. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Christensen, L.R. EEG Emotion Detection Using Multi-Model Classification. In Proceedings of the 2018 International Conference on Bioinformatics and Systems Biology (BSB), Allahabad, India, 26–28 October 2018; pp. 178–182. [Google Scholar] [CrossRef]
- Wyczesany, M.; Kaiser, J.; Coenen, A. Subjective mood estimation co-varies with spectral power EEG characteristics. Acta Neurobiol. Exp. 2008, 68, 180–192. [Google Scholar]
- Revanth, B.; Gupta, S.; Dubey, P.; Choudhury, B.; Kamble, K.; Sengupta, J. Multi-Channel EEG-based Multi-Class Emotion Recognition From Multiple Frequency Bands. In Proceedings of the 2023 2nd International Conference on Paradigm Shifts in Communications Embedded Systems, Machine Learning and Signal Processing (PCEMS), Nagpur, India, 5–6 April 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, G.; Zhao, X.; Yang, F. Cross-subject emotion recognition with a decision tree classifier based on sequential backward selection. In Proceedings of the 2019 11th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 24–25 August 2019; Volume 1, pp. 309–313. [Google Scholar]
- Wang, R.; Wu, X.J.; Chen, K.X.; Kittler, J. Multiple Riemannian Manifold-Valued Descriptors Based Image Set Classification with Multi-Kernel Metric Learning. IEEE Trans. Big Data 2022, 8, 753–769. [Google Scholar] [CrossRef]
- Tang, J.; Jirayucharoensak, S.; Pan-Ngum, S.; Israsena, P. EEG-Based Emotion Recognition Using Deep Learning Network with Principal Component Based Covariate Shift Adaptation. Sci. World J. 2014, 2014, 627892. [Google Scholar] [CrossRef]
- Artoni, F.; Delorme, A.; Makeig, S. Applying dimension reduction to EEG data by Principal Component Analysis reduces the quality of its subsequent Independent Component decomposition. NeuroImage 2018, 175, 176–187. [Google Scholar] [CrossRef]
- Pereira, E.T.; Martins Gomes, H. The role of data balancing for emotion classification using EEG signals. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 555–559. [Google Scholar] [CrossRef]
- Kraljević, L.; Russo, M.; Sikora, M. Emotion classification using linear predictive features on wavelet-decomposed EEG data. In Proceedings of the 2017 26th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Lisbon, Portugal, 28 August–1 September 2017; pp. 653–657. [Google Scholar] [CrossRef]
- Ben Henia, W.M.; Lachiri, Z. Emotion classification in arousal-valence dimension using discrete affective keywords tagging. In Proceedings of the 2017 International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Muhammad, F.; Hussain, M.; Aboalsamh, H. A Bimodal Emotion Recognition Approach through the Fusion of Electroencephalography and Facial Sequences. Diagnostics 2023, 13, 977. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Yin, Y.; Xu, P. A Customized ECA-CRNN Model for Emotion Recognition Based on EEG Signals. Electronics 2023, 12, 2900. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, M.; Feng, G. Study on Driver Cross-Subject Emotion Recognition Based on Raw Multi-Channels EEG Data. Electronics 2023, 12, 2359. [Google Scholar] [CrossRef]
- Ye, C.; Liu, J.; Chen, C.; Song, M.; Bu, J. Speech emotion classification on a Riemannian manifold. In Proceedings of the Advances in Multimedia Information Processing-PCM 2008: 9th Pacific Rim Conference on Multimedia, Tainan, Taiwan, 9–13 December 2008; Proceedings 9. Springer: Berlin/Heidelberg, Germany, 2008; pp. 61–69. [Google Scholar]
- Liu, M.; Wang, R.; Li, S.; Huang, Z.; Shan, S.; Chen, X. Video modeling and learning on Riemannian manifold for emotion recognition in the wild. J. Multimodal User Interfaces 2016, 10, 113–124. [Google Scholar] [CrossRef]
- Kim, B.H.; Choi, J.W.; Lee, H.; Jo, S. A Discriminative SPD Feature Learning Approach on Riemannian Manifolds for EEG Classification. Pattern Recognit. 2023, 143, 109751. [Google Scholar] [CrossRef]
- Zhang, G.; Etemad, A. Spatio-temporal EEG representation learning on Riemannian manifold and Euclidean space. arXiv 2020, arXiv:2008.08633. [Google Scholar]
- Fletcher, P.T.; Venkatasubramanian, S.; Joshi, S. Robust statistics on Riemannian manifolds via the geometric median. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Tang, F.; Fan, M.; Tiňo, P. Generalized Learning Riemannian Space Quantization: A Case Study on Riemannian Manifold of SPD Matrices. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 281–292. [Google Scholar] [CrossRef]
- Fletcher, P.; Lu, C.; Pizer, S.; Joshi, S. Principal Geodesic Analysis for the Study of Nonlinear Statistics of Shape. IEEE Trans. Med. Imaging 2004, 23, 995–1005. [Google Scholar] [CrossRef]
- Chavan, A.; Kolte, M. Improved EEG signal processing with wavelet based multiscale PCA algorithm. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 1056–1059. [Google Scholar] [CrossRef]
- Gursoy, M.I.; Subast, A. A comparison of PCA, ICA and LDA in EEG signal classification using SVM. In Proceedings of the 2008 IEEE 16th Signal Processing, Communication and Applications Conference, Aydin, Turkey, 20–22 April 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Patel, R.; Senthilnathan, S.; Janawadkar, M.; Gireesan, K.; Radhakrishnan, T.; Narayanan, M. Ocular artifact suppression from EEG using ensemble empirical mode decomposition with principal component analysis. Comput. Electr. Eng. 2015, 54, 78–86. [Google Scholar] [CrossRef]
- Morris, J.D. Observations: SAM: The Self-Assessment Manikin; an efficient cross-cultural measurement of emotional response. J. Advert. Res. 1995, 35, 63–68. [Google Scholar]
- Kalunga, E.K.; Chevallier, S.; Barthélemy, Q.; Djouani, K.; Hamam, Y.; Monacelli, E. From Euclidean to Riemannian means: Information geometry for SSVEP classification. In Proceedings of the Geometric Science of Information: Second International Conference, GSI 2015, Palaiseau, France, 28–30 October 2015; Proceedings 2. Springer: Cham, Switzerland, 2015; pp. 595–604. [Google Scholar]

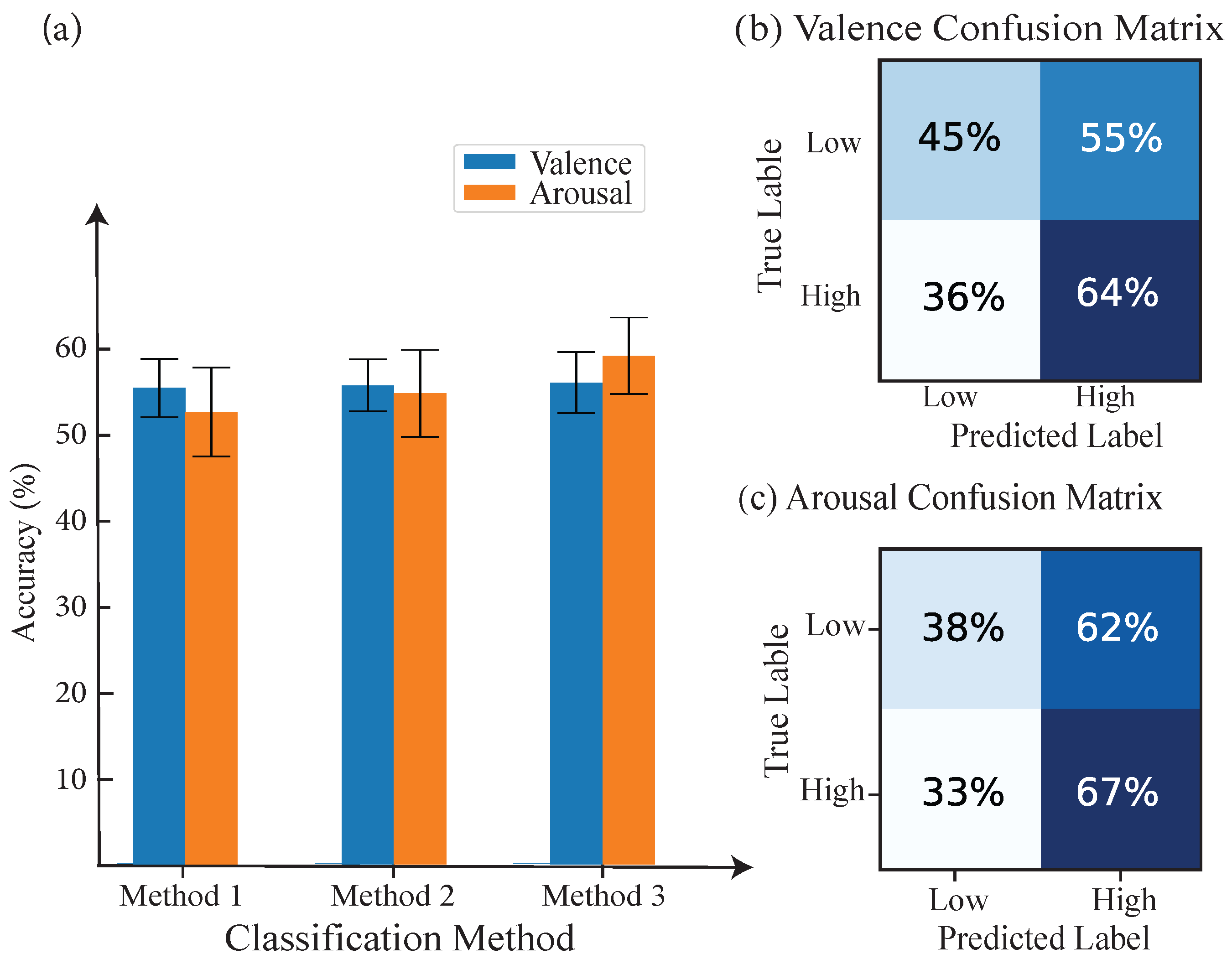
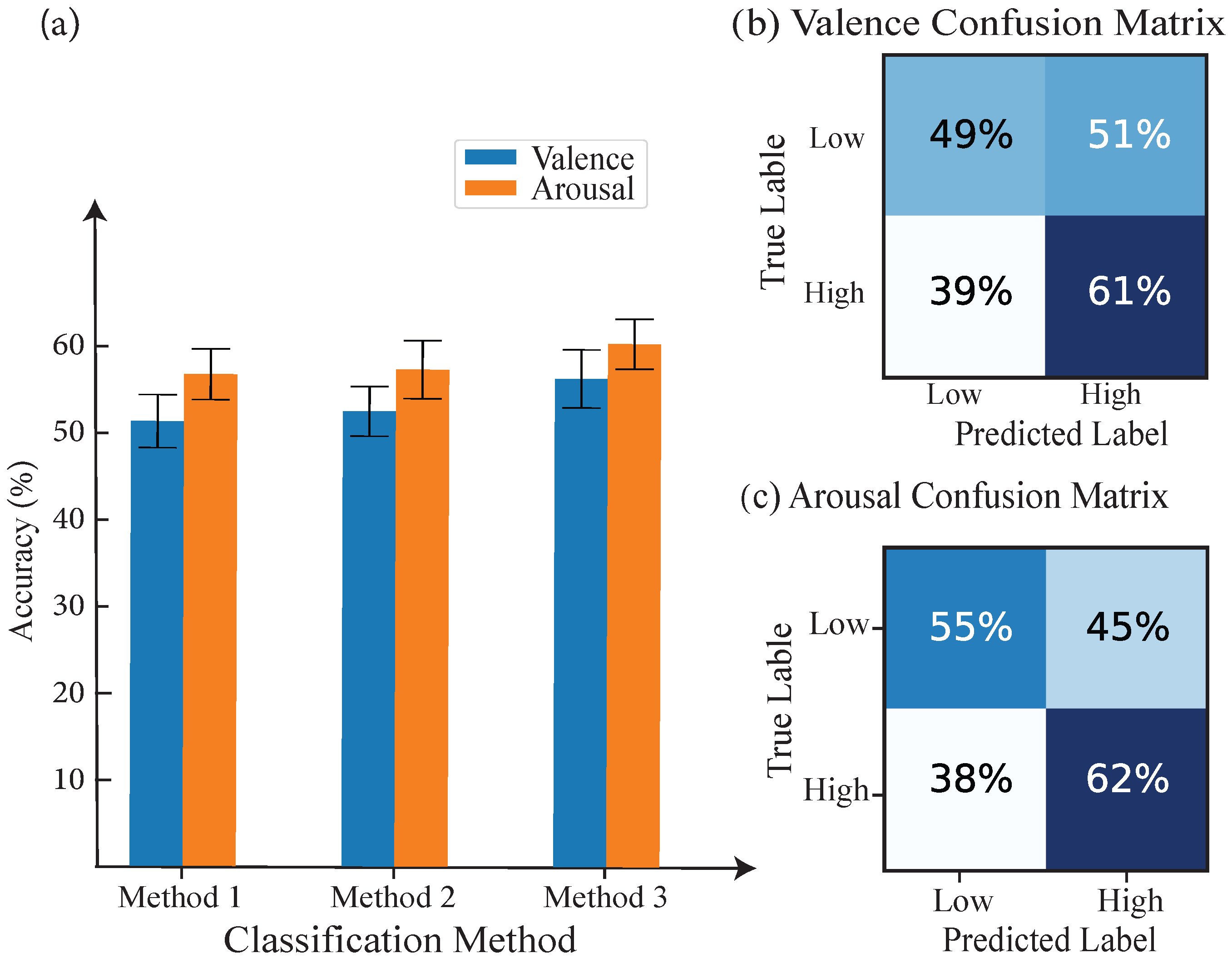

| Class | Proposed Methods | KNN | CNN | ||
|---|---|---|---|---|---|
| M1 | M2 | M3 | K = 5 | EEGNet | |
| Valence | 58% | 63.5% | 64% | 59% | 57.24% |
| Arousal | 55.48% | 57.1% | 57.4% | 58% | 56.21% |
| Class | Proposed Methods | KNN | CNN | ||
|---|---|---|---|---|---|
| M1 | M2 | M3 | K = 5 | EEGNet | |
| Valence | 54.94% | 55.25% | 56% | 54.4% | 55.34% |
| Arousal | 52.16% | 54.32% | 58.64% | 58% | 56.27% |
| Class | Proposed Methods | KNN | CNN | ||
|---|---|---|---|---|---|
| M1 | M2 | M3 | K = 5 | EEGNet | |
| Valence | 51% | 52.2% | 56% | 46% | 54.24% |
| Arousal | 56.4% | 57% | 60% | 41% | 60.62% |
| Class | Proposed Methods | KNN | CNN | ||
|---|---|---|---|---|---|
| M1 | M2 | M3 | K = 5 | EEGNet | |
| Accuracy | 51% | 51.26% | 63.4% | 52% | 52.66% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Mashhadani, Z.; Bayat, N.; Kadhim, I.F.; Choudhury, R.; Park, J.-H. The Efficacy and Utility of Lower-Dimensional Riemannian Geometry for EEG-Based Emotion Classification. Appl. Sci. 2023, 13, 8274. https://doi.org/10.3390/app13148274
Al-Mashhadani Z, Bayat N, Kadhim IF, Choudhury R, Park J-H. The Efficacy and Utility of Lower-Dimensional Riemannian Geometry for EEG-Based Emotion Classification. Applied Sciences. 2023; 13(14):8274. https://doi.org/10.3390/app13148274
Chicago/Turabian StyleAl-Mashhadani, Zubaidah, Nasrin Bayat, Ibrahim F. Kadhim, Renoa Choudhury, and Joon-Hyuk Park. 2023. "The Efficacy and Utility of Lower-Dimensional Riemannian Geometry for EEG-Based Emotion Classification" Applied Sciences 13, no. 14: 8274. https://doi.org/10.3390/app13148274
APA StyleAl-Mashhadani, Z., Bayat, N., Kadhim, I. F., Choudhury, R., & Park, J.-H. (2023). The Efficacy and Utility of Lower-Dimensional Riemannian Geometry for EEG-Based Emotion Classification. Applied Sciences, 13(14), 8274. https://doi.org/10.3390/app13148274






