Application-Specific Integrated Circuit of an Inter-IC Sound Digital Filter for Audio Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Noise-Cancellation Algorithms
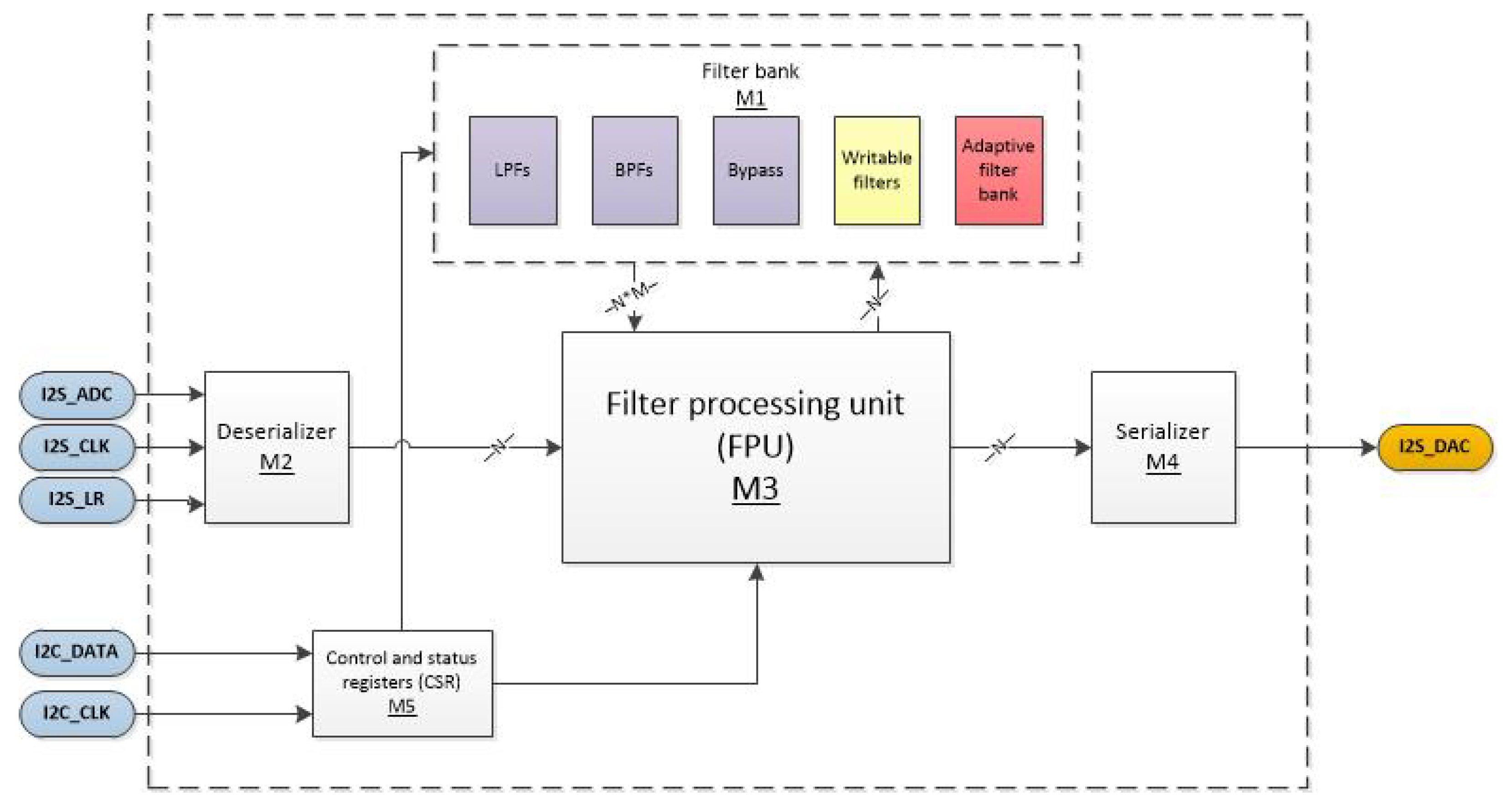
2.2. Digital Filter Architecture
2.2.1. Filter Bank (M1)
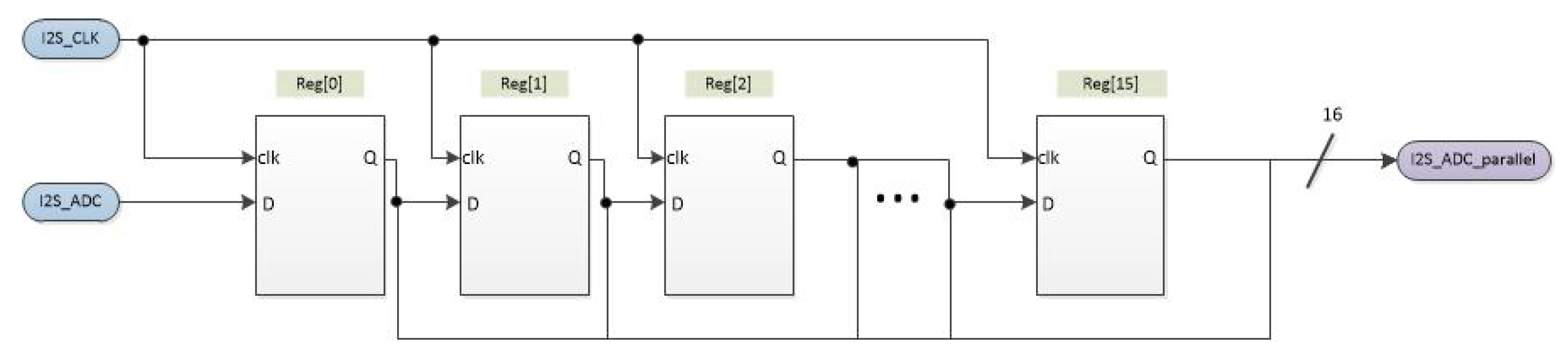
2.2.2. Deserializer (M2)
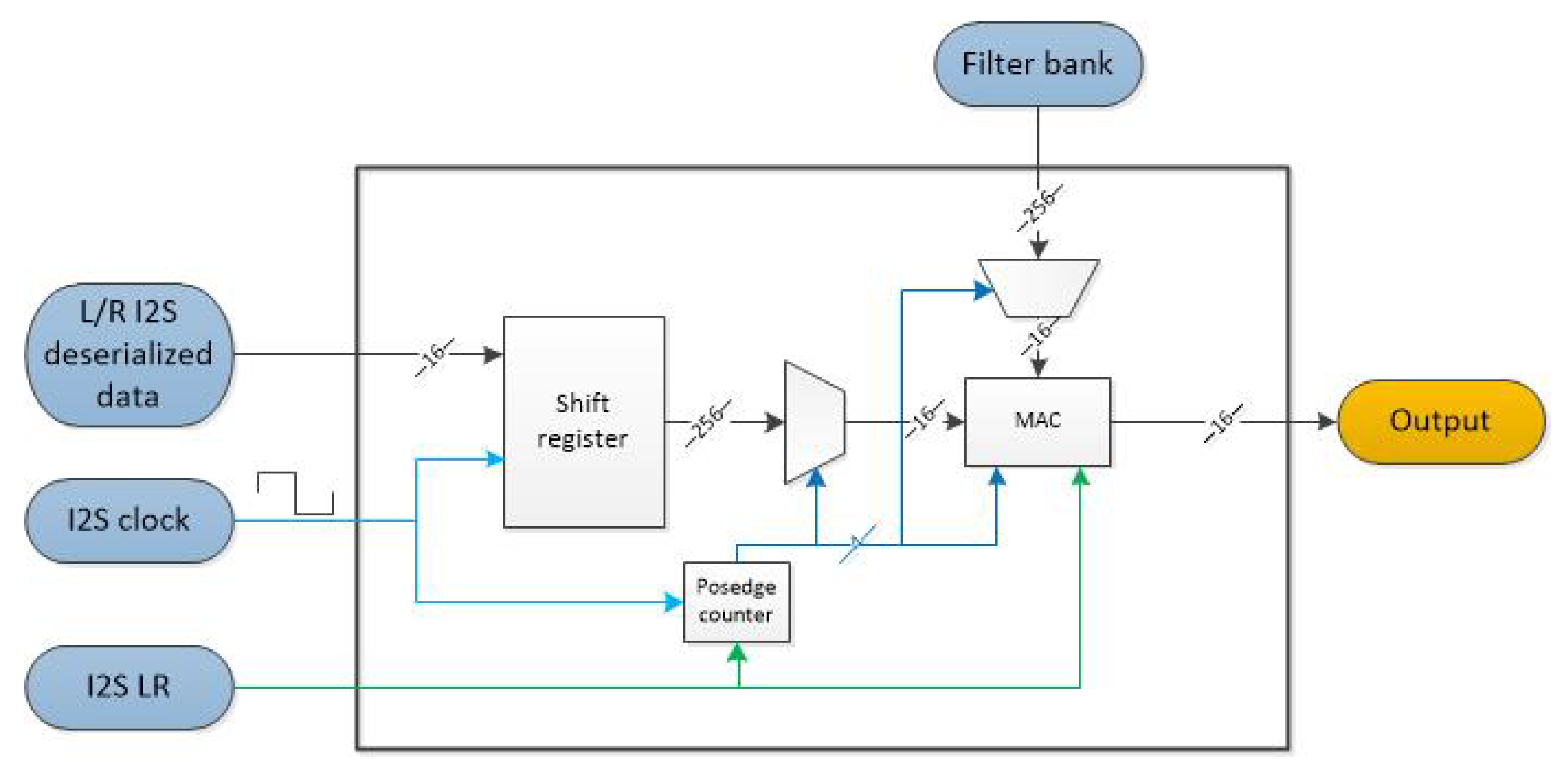
2.2.3. FPU (M3)
2.2.4. Serializer (M4)
2.2.5. Control and Status Register (M5)
Main Control Register
I2C
Sensitivity Numerator Constant Register and Sensitivity Denominator Constant Register
User-Defined Filters
2.2.6. Process Timing
3. Implementation Results and Discussion
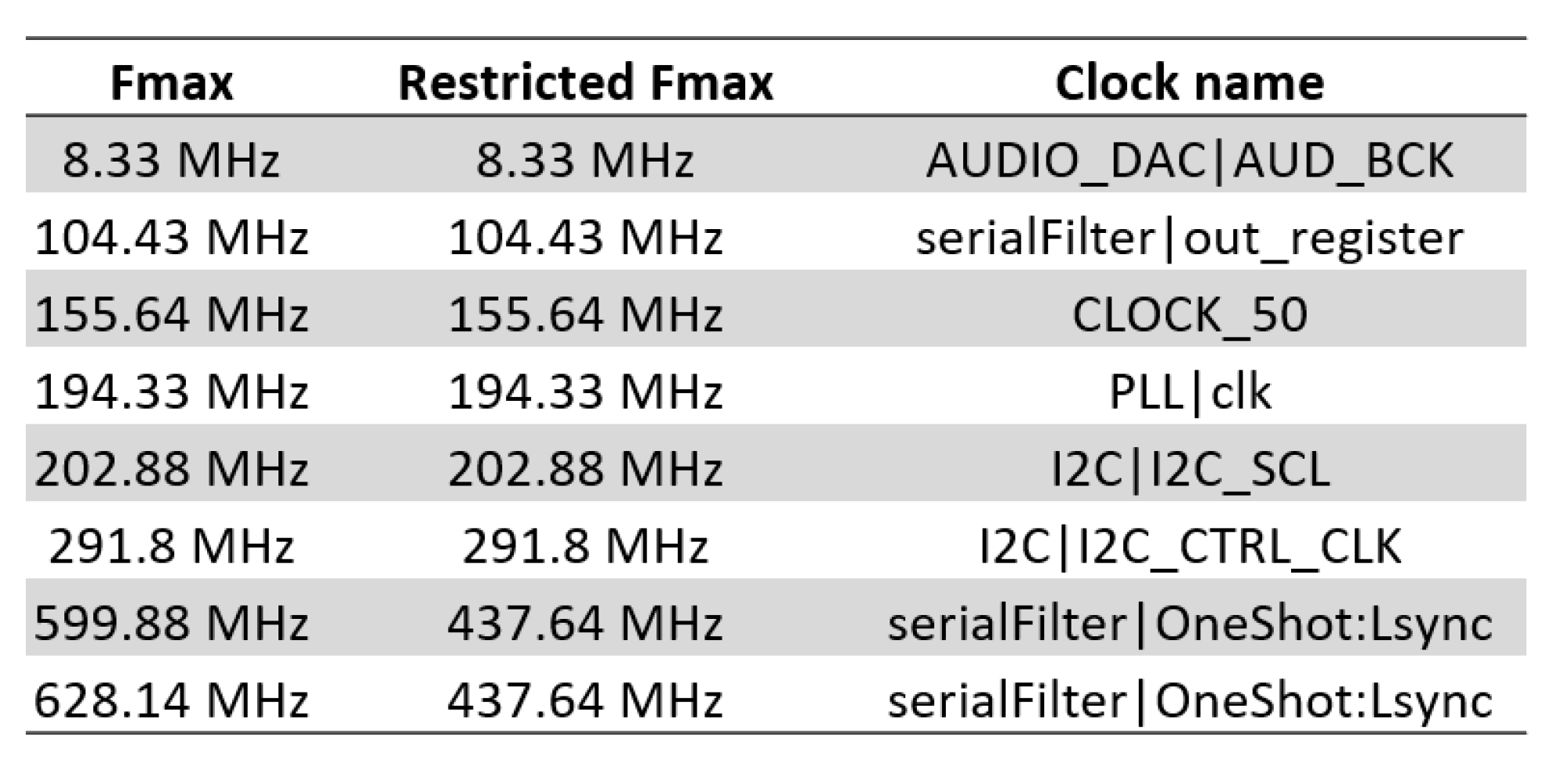
3.1. FPGA Implementation
3.2. Physical Implementation
3.3. Validation and Testing
- I2C master to select the working filter;
- I2S master to provide sound data;
- I2S slave to read the data after filtering;
- Logic analyzer to debug serial protocols.
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Adaptive filter mode |
| BPF | Band-pass filter |
| CLK | CLK |
| CS | Channel side |
| DRC | Design rules check |
| DSP | Digital signal processor |
| EQ | Equalizer |
| FIR | Finite impulse response |
| FOPT | Filter option |
| FPGA | Field-programmable gate array |
| IC | Integrated circuit |
| IO | Input–output |
| I2C | Inter-integrated circuits |
| I2S | Inter-IC sound |
| LEC | Logical equivalence checking |
| LMS | Least mean square |
| LPF | Low-pass filter |
| LR | Left–right |
| LSB | Least-significant bit |
| MAC | Multiply–accumulate |
| MCR | Main control register |
| MSB | Most-significant bit |
| MUX | Multiplexer |
| NLMS | Normalized least mean square |
| NU | Not used |
| OUTC | Output configuration |
| RAM | Random access memory |
| ROM | Read-only memory |
| rst | Reset |
| RTL | Register transfer level |
| SDC | Sensitivity denominator constant |
| SNC | Sensitivity numerator constant |
| UDF | User-defined filter |
| VLSI | Very-large-scale integration |
References
- Pepe, G.; Gabrielli, L.; Squartini, S.; Cattani, L. Designing Audio Equalization Filters by Deep Neural Networks. Appl. Sci. 2020, 10, 2483. [Google Scholar] [CrossRef]
- Kwon, S.; Kim, B.-S.; Park, J. Active Noise Reduction with Filtered Least-Mean-Square Algorithm Improved by Long Short-Term Memory Models for Radiation Noise of Diesel Engine. Appl. Sci. 2022, 12, 10248. [Google Scholar] [CrossRef]
- Lee, S.-K.; An, K.; Cho, H.-Y.; Hwang, S.-U. Prediction and Sound Quality Analysis of Tire Pattern Noise Based on System Identification by Utilizing an Optimal Adaptive Filter. Appl. Sci. 2019, 9, 3995. [Google Scholar] [CrossRef]
- Singh, G.; Panda, G. A novel ANC system using nonlinear error LMS algorithm. In Proceedings of the 2015 IEEE Power, Communication and Information Technology Conference (PCITC), Bhubaneswar, India, 15–17 October 2015; pp. 539–544. [Google Scholar] [CrossRef]
- Gupta, D.K.; Gupta, V.K.; Chandra, M.; Mishra, A.N.; Srivastava, P.K. Hardware Co-Simulation of Adaptive Noise Cancellation System using LMS and Leaky LMS Algorithms. In Proceedings of the 2019 4th International Conference on Internet of Things: Smart Innovation and Usages (IoT-SIU), Ghaziabad, India, 18–19 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ramakrishna, V.; Kumar, T.A. Low Power VLSI Implementation of Adaptive Noise Canceller based on Least Mean Square Algorithm. In Proceedings of the IEEE 2013 4th International Conference on Intelligent Systems, Modelling and Simulation, Bangkok, Thailand, 29–31 January 2013; pp. 276–279. [Google Scholar]
- Sharma, L.; Mehra, R. Adaptive Noise Cancellation using Modified Normalized Least Mean Square Algorithm. Int. J. Eng. Trends Technol. 2016, 34, 215–219. [Google Scholar] [CrossRef]
- Schlichthãrle, D. Digital Filters; Springer: Berlin/Heidelberg, Germany, 2011; Volume 2, ISBN 978-3-642-14324-3. [Google Scholar]
- Mehrnia, A.; Willson, A.N. A Lower Bound for the Hardware Complexity of FIR Filters. IEEE Circuits Syst. Mag. 2018, 18, 10–28. [Google Scholar] [CrossRef]
- Ramos-Contreras, R.; Davila-Velarde, R.; Pizano-Escalante, L. Configurable/Adaptive FIR Filter. Available online: https://rei.iteso.mx/handle/11117/6176 (accessed on 17 May 2023).
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]







| Type | Name | Description |
|---|---|---|
| Input | I2C_SCL | I2C bus clock |
| Input | I2S_CLK | I2S bus clock |
| Input | I2S_ADC | I2S serial data from the ADC |
| Input | I2S_LR | I2S bus data left/right selector |
| Input | rst | Global reset |
| Inout | I2C_SDA | I2C bus serial data |
| Output | I2S_DAC | I2S bus serial data to the DAC |
| Name | HPF | LPF |
|---|---|---|
| LPF0 | - | 1.894 kHz |
| LPF1 | - | 3.057 kHz |
| BPF0 | 1 kHz | 20 kHz |
| BPF1 | 4 kHz | 10 kHz |
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 | Name |
|---|---|---|---|---|---|---|---|---|---|
| 0h0 | NU | CS | AFM | FOPT | OUTC | MCR | |||
| 0h1 | NU | I2C_SLAVE | I2C | ||||||
| 0h2 | LOW | SNCL | |||||||
| 0h3 | HIGH | SNCH | |||||||
| 0h4 | LOW | SDCL | |||||||
| 0h5 | HIGH | SDCH | |||||||
| 0h6 | LOW | UDF0_L00 | |||||||
| 0h7 | HIGH | UDF0_H00 | |||||||
| 0h8 | LOW | UDF0_L01 | |||||||
| 0h9 | HIGH | UDF0_H01 | |||||||
| … | … | UDF0_LHnn | |||||||
| 0h24 | LOW | UDF0_L15 | |||||||
| 0h25 | HIGH | UDF0_H15 | |||||||
| 0h26 | LOW | UDF1_L00 | |||||||
| 0h27 | HIGH | UDF1_H00 | |||||||
| 0h28 | LOW | UDF1_L01 | |||||||
| 0h29 | HIGH | UDF1_H01 | |||||||
| … | … | UDF1_LHnn | |||||||
| 0h44 | LOW | UDF1_L15 | |||||||
| 0h45 | HIGH | UDF1_H15 | |||||||
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|
| 0h0 | NU | CS | AFM | FOPT | OUTC | |||
| Binary | Hex | Configuration | Details |
|---|---|---|---|
| 00 | 0h0 | No output | The output is set to 0 at any time |
| 01 | 0h1 | Bypass | The input data are connected directly to the output |
| 10 | 0h2 | Filter output | Outputs the filter result |
| 11 | 0h3 | Not used | Set to 0 |
| Binary | Hex | Configuration | Details |
|---|---|---|---|
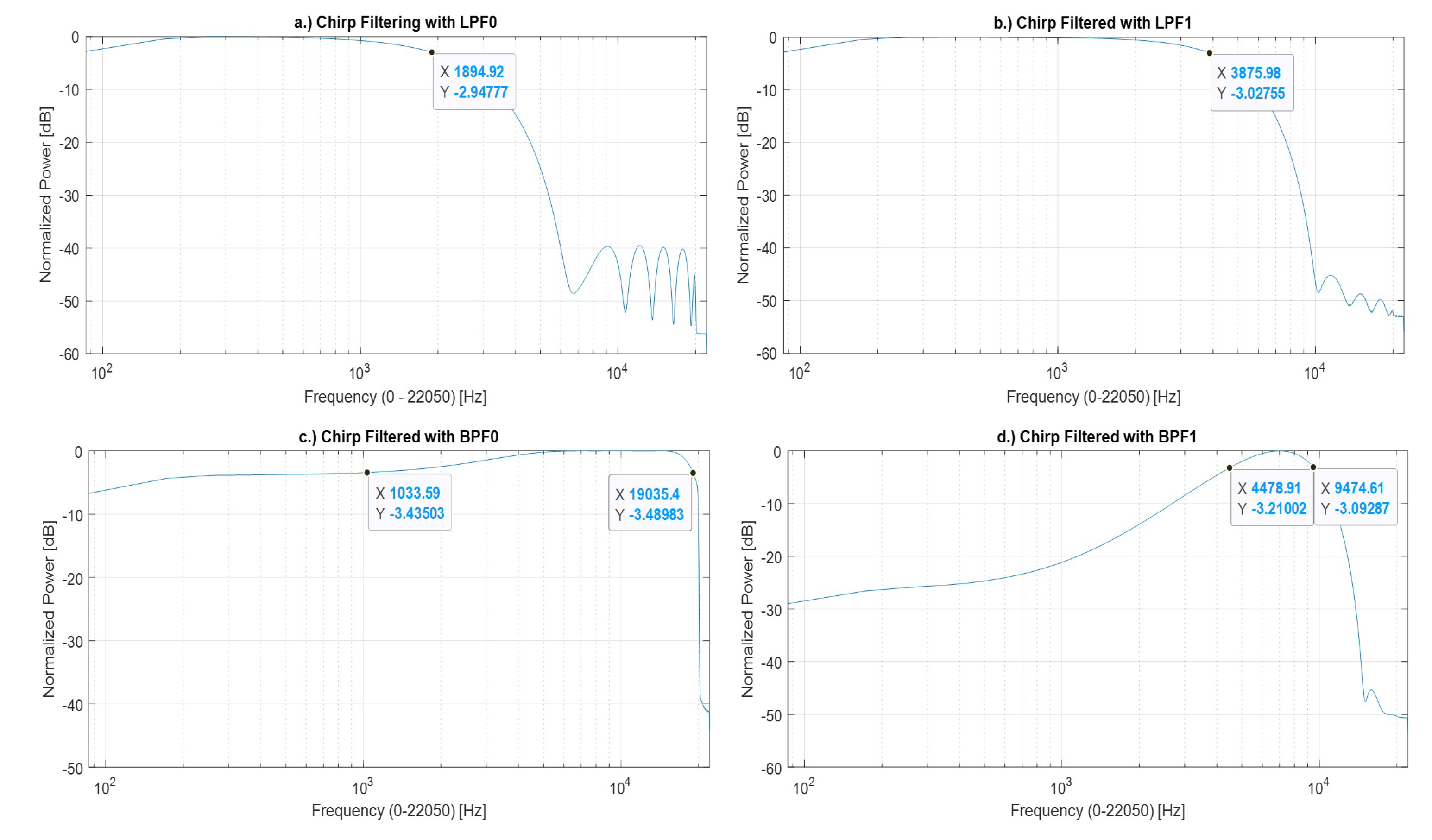
| 000 | 0h0 | LPF0 | Low-pass filter, calculated for 500 Hz; the minimum cutoff frequency for WL = 16 bits and N = 16 coefficients is 1894.92 Hz |
| 001 | 0h1 | LPF1 | Low-pass filter, calculated for 5 kHz |
| 010 | 0h2 | BPF0 | Band-pass filter, calculated for 1 kHz–20 kHz |
| 011 | 0h3 | BPF1 | Band-pass filter, calculated for 4 kHz–10 kHz |
| 100 | 0h4 | UDF0 | First I2C user-writable filter |
| 101 | 0h5 | UDF1 | Second I2C user-writable filter |
| 110 | 0h6 | AF | Adaptive filtering function |
| 111 | 0h7 | NU | Not used |
| Binary | Hex | Configuration | Details |
|---|---|---|---|
| 000 | 0h0 | LMS | Least-mean-squares algorithm |
| 001 | 0h1 | NLMS | Normalized least-mean-squares algorithm |
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|
| 0h1 | NU | I2C SLAVE | ||||||
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|
| 0h2 | SNC LOW | |||||||
| 0h3 | SNC HIGH | |||||||
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|
| 0h4 | SDC LOW | |||||||
| 0h5 | SDC HIGH | |||||||
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|
| 0h6 | UDF0 LOW 0 | |||||||
| 0h7 | UDF0 HIGH 0 | |||||||
| 0h8 | UDF0 LOW 1 | |||||||
| 0h9 | UDF0 HIGH 1 | |||||||
| 0h… | UDF0… | |||||||
| 0h24 | UDF0 LOW 15 | |||||||
| 0h25 | UDF0 HIGH 15 | |||||||
| Address | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|
| 0h26 | UDF1 LOW 0 | |||||||
| 0h27 | UDF1 HIGH 0 | |||||||
| 0h28 | UDF1 LOW 1 | |||||||
| 0h29 | UDF1 HIGH 1 | |||||||
| 0h… | UDF1… | |||||||
| 0h44 | UDF1 LOW 15 | |||||||
| 0h45 | UDF1 HIGH 15 | |||||||
| Process | Description |
|---|---|
| Deserialize | I2S data come from the serialized DAC; this process converts it to a parallel bus of 16 bits. |
| Push | Once there is parallel data available, they are entered into the shift register, shifting all previously entered data to the right and overflowing the oldest data. |
| Multiply | Perform the 16 words’ calculation given by: . |
| Serialize | Serializes the output parallel data to be written to the DAC. |
| Save bus | As seen in Figure 5 and Figure 6, it takes two full cycles of I2S_LR for the input to be deserialized and pushed into the shift register; therefore, the shift register needs to be saved before the next data are pushed in, and the subsequent calculations match with the actual processed data. |
| Power | Calculates the actual quadratic power of the shift register: , to be used in the adaptive filter (only used in the adaptive filtering mode). |
| Write new coefficient | Calculates and updates the next coefficient given by (2) (only used in the adaptive filtering mode). |
| Repeat the left channel | When using deterministic filtering, the right and left channels are filtered by using the same coefficients, but when using adaptive filtering mode, the left channel (data and noise) will be filtered based on the right channel (noise); this creates a mono output signal; this module delays the left channel output 16 clocks to the right channel, replicating the data and converting them once more to a stereo signal (only used in the adaptive filtering mode). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davila-Velarde, R.; Ramos-Contreras, R.; Pizano-Escalante, L.; Longoria-Gandara, O.; Aguilera-Galicia, C. Application-Specific Integrated Circuit of an Inter-IC Sound Digital Filter for Audio Systems. Appl. Sci. 2023, 13, 8182. https://doi.org/10.3390/app13148182
Davila-Velarde R, Ramos-Contreras R, Pizano-Escalante L, Longoria-Gandara O, Aguilera-Galicia C. Application-Specific Integrated Circuit of an Inter-IC Sound Digital Filter for Audio Systems. Applied Sciences. 2023; 13(14):8182. https://doi.org/10.3390/app13148182
Chicago/Turabian StyleDavila-Velarde, Rene, Ricardo Ramos-Contreras, Luis Pizano-Escalante, Omar Longoria-Gandara, and Cuauhtémoc Aguilera-Galicia. 2023. "Application-Specific Integrated Circuit of an Inter-IC Sound Digital Filter for Audio Systems" Applied Sciences 13, no. 14: 8182. https://doi.org/10.3390/app13148182
APA StyleDavila-Velarde, R., Ramos-Contreras, R., Pizano-Escalante, L., Longoria-Gandara, O., & Aguilera-Galicia, C. (2023). Application-Specific Integrated Circuit of an Inter-IC Sound Digital Filter for Audio Systems. Applied Sciences, 13(14), 8182. https://doi.org/10.3390/app13148182







