Global Dynamics of a Predator–Prey System with Cooperative Hunting

Abstract

We consider a predator–prey system with cooperative hunting. The parameter space of the system is divided into several mutually exclusive regions. Based on the investigation of the dynamical properties in each parameter region, we provide a complete description of the global dynamics, including stability, Hopf bifurcation and its directions, and the existence of limit cycles. By comparing this system’s dynamics to those of a system without cooperative hunting, it is found that cooperative hunting is beneficial to the coexistence of the prey and predator. When the mortality of the predator is small, hunting cooperation does not affect the coexistence of populations but it affects the pattern of coexistence.

1. Introduction

In an ecosystem, cooperative hunting behavior among predators is an important biological phenomenon [1] that is frequently observed in carnivores [2] such as African wild dogs [3], wolves [4], lions [5,6,7], chimpanzees [8], and other organisms such as spiders [9], birds [10,11], and ants [12]. Cooperative hunting has many advantages for the evolution of predator populations. For example, cooperation increases hunting success, prey mass, and the probability of multiple kills. It also decreases the chase distance [3], increases the probability of capturing large prey [13], enables the population to find food more quickly [14], and allows individuals in large packs to accrue foraging advantages by helping prevent the carcass from being stolen by other predators [15].

In recent years, various predator–prey mathematical models with hunting cooperation have been proposed and studied. Cosner et al. [16] proposed a predator–prey model with a functional response for predators that forage in a spatially linear formation and aggregate when they encounter a cluster of prey. Berec [17] derived a predator–prey model with cooperative foraging, which is described by a Holling type II-like functional response, and investigated the impacts of foraging facilitation among predators. Due to this functional response, it was presented in [17] that hunting cooperation has a destabilizing effect on predator–prey dynamics and the populations exhibit oscillatory behavior. Duarte et al. [18] proposed a three-species food chain model with hunting cooperation for the predator and analyzed the dynamics of the species under several degrees of cooperative hunting. Pal et al. [19] considered a modified Leslie–Gower predator–prey model, where predators cooperate during hunting and prey populations show anti-predator behavior due to fear of predation risk. It was observed that in the absence of the fear effect, hunting cooperation can induce both supercritical and subcritical Hopf bifurcations. Recently, Du et al. [20] proposed a predator–prey model with a non-differentiable functional response, where the prey exhibits group defense and the predator exhibits cooperative hunting, and explored the effect of cooperative hunting in the predator and aggregation in the prey on the existence and stability of the coexistence state, as well as the dynamics of the system. We also refer the reader to [21,22,23,24,25,26,27,28,29,30,31] for models of ordinary differential equations, reaction–diffusion equations, and difference equations with hunting cooperation.

Alves and Hilker [32] studied the following predator–prey model with cooperative hunting in predators

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}N}{\mathrm{d}t}=rN\left(1-\frac{N}{K}\right)-(\lambda +aP)NP,\hfill \\ \hfill & \frac{\mathrm{d}P}{\mathrm{d}t}=e(\lambda +aP)NP-mP.\hfill \end{array}$$

(1)

where N and P represent the population density of the prey and predator, respectively; r and K are the intrinsic growth rate and carrying capacity of the prey population, respectively; e is the conversion coefficient; m is the mortality of the predator; $\lambda$ is the attack rate of each predator on the prey; and a is a parameter describing predator cooperation in hunting. All these parameters are positive. By introducing the dimensionless variables $n=\frac{e\lambda }{m}N$, $p=\frac{\lambda }{m}P,$ and $\tau =mt$, and the dimensionless parameters $\sigma =\frac{r}{m},k=\frac{e\lambda K}{m},$ and $\alpha =\frac{am}{{\lambda }^2}$, and still using t for $\tau$, Model (1) is written as the following three-parameter system

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}n}{\mathrm{d}t}=\sigma n\left(1-\frac{n}{k}\right)-(1+\alpha p)np,\hfill \\ \hfill & \frac{\mathrm{d}p}{\mathrm{d}t}=(1+\alpha p)np-p.\hfill \end{array}$$

(2)

The study of Alves and Hilker [32] indicates that Model (2) has more complex dynamics than the well-known Lotka–Volterra model (i.e., when $\alpha =0$), and hunting cooperation can be beneficial to the predator population by increasing the attack rate brought about by the cooperation. In [32], through numerical simulations, the stability of the equilibria and the various bifurcation behaviors of (2), including the Hopf bifurcation, homoclinic bifurcation, and Bogdanov–Takens bifurcation, were investigated for one-parameter cases (bifurcation parameter is taken as $\alpha$ and $\sigma$, respectively) and two-parameter cases (bifurcation parameter is taken as $(\alpha ,\sigma )$ and $(k,\alpha )$, respectively). However, in [32], the important parameter conditions that describe the dynamical behavior of (2) were not provided mathematically. For example, the exact parameter regions such that Model (2) has zero, one, and two interior equilibria, the parametric conditions for the stability of equilibria, and the critical parameter value for the Hopf bifurcation were not explicitly presented.

Motivated by the works of Alves and Hilker [32], in this paper, we also study the dynamics of (1) but apply changes to the variables $x=\frac{\lambda }{r}P,y=\frac{N}{K},$ and $\tilde{t}=rt$, and define the constants as $c=\frac{e\lambda K}{r},\beta =\frac{ra}{{\lambda }^2},$ and $d=\frac{m}{r}$. After dropping the “tilde” on $\tilde{t}$, we rewrite Model (1) in the following non-dimensional form

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}x}{\mathrm{d}t}=c(1+\beta x)xy-dx,\hfill \\ \hfill & \frac{\mathrm{d}y}{\mathrm{d}t}=y(1-y)-(1+\beta x)xy.\hfill \end{array}$$

(3)

where the population density of the predator and prey are represented by x and y, respectively. In order to better understand the dynamics of (3), such as the number of interior equilibria, stability of the equilibria, and Hopf bifurcation, we divide the two-parameter space

$$\Lambda =\{(\beta ,c)\in {\mathbb{R}}_{+}^2:c\beta >0\}.$$

(4)

into several mutually exclusive regions. The idea and method of the division are motivated by [33] and are described in this paper, along with an analysis of the dynamic behaviors of (3). In each parameter region, by choosing d as the bifurcation parameter, the dynamics of (3) are explored in detail. Based on the dynamics of (3), we investigate the following two questions: (i) What are the parameter regions in which both species coexist? (ii) How does hunting cooperation affect the coexistence of the two species and the pattern of coexistence?

The rest of the paper is organized as follows. First, we show the positivity and boundedness of the solutions to System (3) in Section 2. In Section 3 and Section 4, as d varies, the existence and stability of equilibria are investigated in each parameter region. The Hopf bifurcation of (3) and its directions, together with the stability of bifurcating periodic orbits, are discussed. It is presented that there is a critical surface $d=H(\beta ,c)$ under which a supercritical and backward Hopf bifurcation occurs. In Section 5, through theoretical analysis and numerical simulations, the global stability and the existence of periodic solutions are considered, and a complete description of the global dynamic behaviors of (3) is presented for each parameter region. Finally, in Section 6, we summarize our main results and compare the dynamics of (3) to those of the well-known Lotka–Volterra model (i.e., when the predator has no cooperative hunting). It turns out that due to cooperative hunting, System (3) has a richer and more complex dynamic behavior than the Lotka–Volterra model, such as various bifurcation phenomena and oscillation behavior. Cooperative hunting by predators is beneficial to the coexistence of the prey and predator. When the mortality of the predator is small ($d<c$), the hunting cooperation term $-\beta x^{2}y$ does not affect the coexistence of populations but it affects the pattern of coexistence.

2. Positivity and Boundedness

We define the state space of (3) as $X={\mathbb{R}}_{+}^2$, with its interior $\mathring{X}=\{(x,y)\in {\mathbb{R}}_{+}^2:xy>0\}$.

Theorem 1.

1.   Both X and $\mathring{X}$ are positively invariant sets of System (3).

2.   System (3) is uniformly and ultimately bounded in X and $\underset{t\to \infty }{lim\; sup}y\left(t\right)\le 1$.

Proof. 

1. For $x\ge 0$ and $y\ge 0$, we have $x^{\prime }{|}_{x=0}=0$ and $y^{\prime }{|}_{y=0}=0$, which implies that $x=0$ and $y=0$ are invariant manifolds, respectively. Due to the continuity of the system, we can conclude that System (3) is positively invariant in ${\mathbb{R}}_{+}^2$.

2. From the positivity of System (3), the second equation of (3) implies that $y^{\prime }{{|}_{y=1}=-(1+\beta x)x\le 0,y^{\prime }|}_{y>1}<0$. So, $\underset{t\to \infty }{lim\; sup}y\left(t\right)\le 1$. Now, let $N=x+cy$. Then,

$$N^{\prime }\left(t\right)=c[(1+d)y-y^2]-dN\le \frac{c{(1+d)}^2}{4}-dN,$$

which implies that $\underset{t\to \infty }{lim\; sup}N\left(t\right)\le \frac{c{(1+d)}^2}{4d}$ and hence (3) is uniformly and ultimately bounded in X. □

3. Equilibria

In this section, we consider the number of equilibria in System (3). Clearly, System (3) always has two boundary equilibria $E_0(0,0)$ and $E_1(0,1)$. Below, we discuss the existence of interior equilibria.

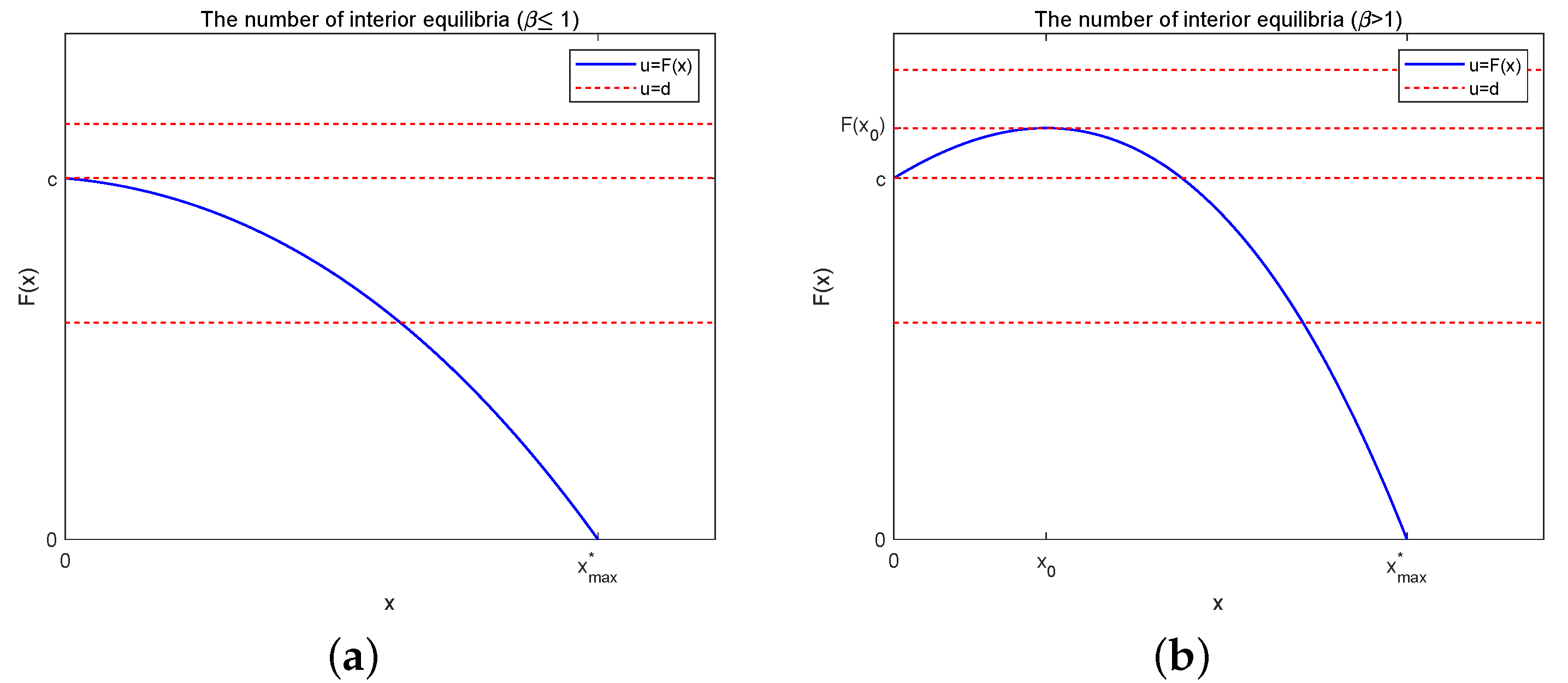
System (3) has the x-nullcline

$$y={\varphi }_1\left(x\right):=\frac{d}{c(1+\beta x)}$$

and the y-nullcline

$$y={\varphi }_2\left(x\right):=-\beta x^2-x+1.$$

It is easy to see that $y={\varphi }_1\left(x\right)$ decreases to zero as x increases on $[0,\infty )$ with ${\varphi }_1\left(0\right)=\frac{d}{c}$. $y={\varphi }_2\left(x\right)$ is a parabola with ${\varphi }_2\left(0\right)=1$ and has a unique positive zero, denoted as

$$x_{max}^{*}=\frac{-1+\sqrt{1+4\beta }}{2\beta }.$$

(5)

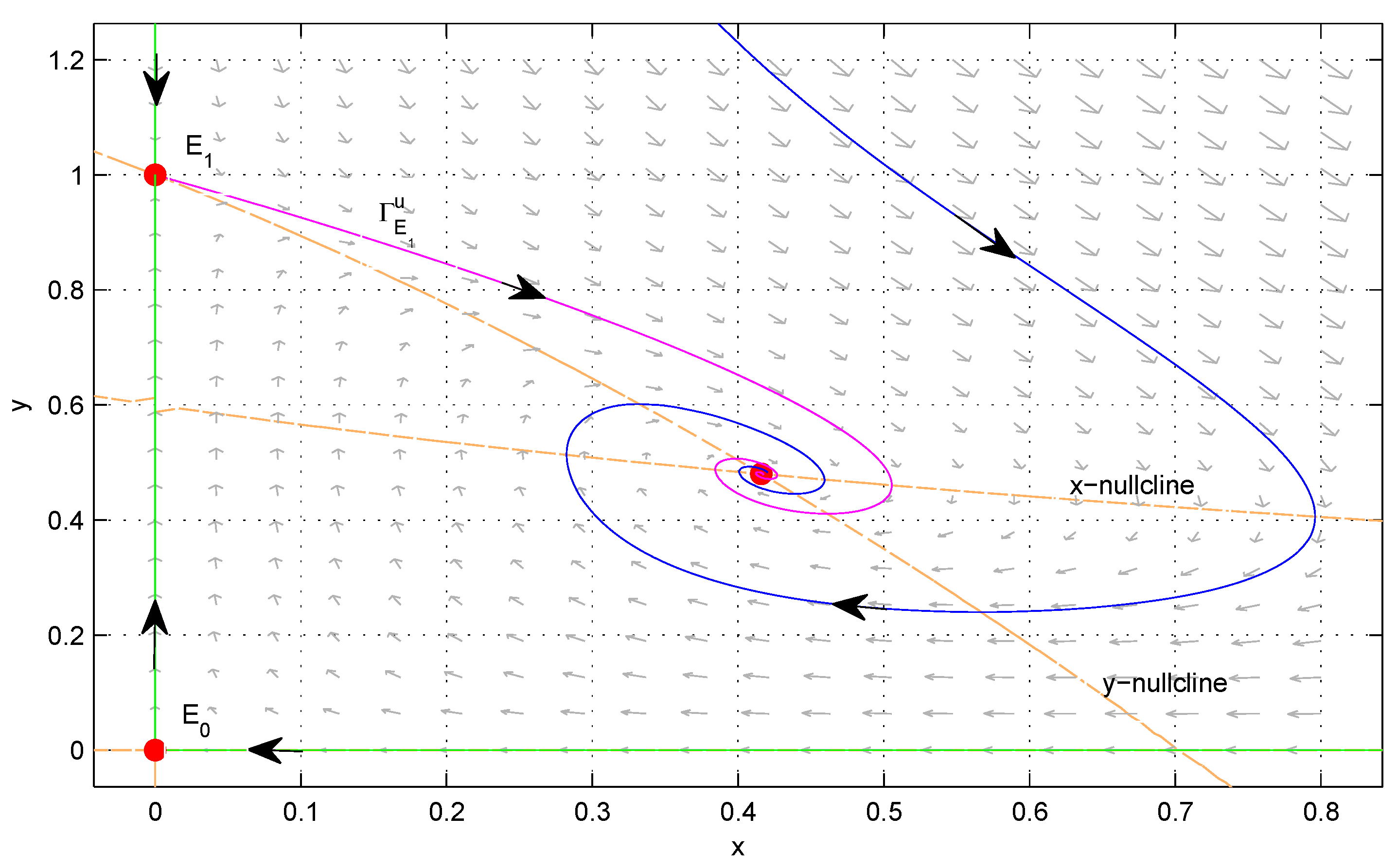
$(x^{*},y^{*})$ is an interior equilibrium point of (3) if and only if it is the intersection point of $y={\varphi }_1\left(x\right)$ and $y={\varphi }_2\left(x\right)$ in the first quadrant of the $(x,y)$-plane (see Figure 1). Therefore, System (3) has at most two interior equilibria.

Figure 1. The x-nullcline and y-nullcline.

That is, $(x^{*},y^{*})$ is an interior equilibrium point if and only if $x^{*}$ is a positive root of ${\varphi }_1\left(x\right)-{\varphi }_2\left(x\right)=0$, i.e., $x^{*}$ satisfies $F\left(x\right)=d$, and $y^{*}={\varphi }_1\left(x^{*}\right)$. Here,

$$F\left(x\right)=c(1+\beta x){\varphi }_2\left(x\right)=c(-{\beta }^2{x}^3-2\beta x^2+(\beta -1)x+1).$$

(6)

Clearly, $F\left(0\right)=c$. Therefore, we only need to discuss the positive intersection point of the functions $u=F\left(x\right)$ and $u=d$. When there are two interior equilibria, the larger one of the predator is denoted as $E_2^{*}(x_2^{*},y_2^{*})$, and the other one is denoted as $E_1^{*}(x_1^{*},y_1^{*})$.

In (6), the sign of the coefficient $\beta -1$ is important for determining the graph of the function $F\left(x\right)$ and the range of the parameter d such that System (3) has zero, one, and two interior equilibria. So, we choose d as the bifurcation parameter. Based on the sign of $\beta -1$, the coefficient of the first-order term of $F\left(x\right)$, we divide the parameter space $\Lambda$ given in (4) into

$${\Lambda }_1=\{(\beta ,c)\in \Lambda :\beta \le 1\},\mathrm{and}{\Lambda }_2=\{(\beta ,c)\in \Lambda :\beta >1\}.$$

(7)

If $(\beta ,c)\in {\Lambda }_1$, from

$$F^{\prime }\left(x\right)=c(-3{\beta }^2{x}^2-4\beta x+\beta -1)$$

we know that $F\left(x\right)$ is decreasing on $[0,\infty )$, and for all $x>0$, $F\left(x\right)<F\left(0\right)=c$ (see Figure 2a). If $(\beta ,c)\in {\Lambda }_2$, then at the point $x=x_0$, where

$$x_0=\frac{-2+\sqrt{3\beta +1}}{3\beta },$$

(8)

$F\left(x\right)$ has a positive local maximum value

$$F\left(x_0\right)=\frac{c(2{(3\beta +1)}^{\frac{3}{2}}+9\beta +2)}{27\beta }.$$

When $x\in (0,x_0)$, $F\left(x\right)$ increases and $c=F\left(0\right)<F\left(x\right)<F\left(x_0\right)$; when $x>x_0$, $F\left(x\right)$ decreases and $F\left(x\right)<F\left(x_0\right)$ (see Figure 2b).

Figure 2. The number of interior equilibria is determined by the number of intersection points of $u=F\left(x\right)$ and $u=d$ in the first quadrant. (a) The case of $\beta \le 1$. (b) The case of $\beta >1$.

Thus, we can obtain the following result.

Theorem 2.

System (3) may have zero, one, or two interior equilibria. More precisely:

1 

If $(\beta ,c)\in {\Lambda }_1$, then System (3) has a unique interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ when $d<c$, and no interior equilibrium when $d\ge c$ (see Figure 2a).

2 

If $(\beta ,c)\in {\Lambda }_2$, then System (3) has two interior equilibria $E_1^{*}(x_1^{*},y_1^{*})$ and $E_2^{*}(x_2^{*},y_2^{*})$, with $x_1^{*}<x_0<x_2^{*}$ when $c<d<F\left(x_0\right)$; one interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ when $d\le c$; and no interior equilibrium when $d>F\left(x_0\right)$. When $d=F\left(x_0\right)$, $E_1^{*}$ and $E_2^{*}$ coincide and System (3) has a unique interior equilibrium ${\tilde{E}}^{*}(x_0,{\varphi }_1\left(x_0\right))$ (see Figure 2b).

Remark 1.

Based on the above arguments, we can make the following statements.

1 

When the cooperative predation rate of the predator is small ($\beta \le 1$), (3) has at most one coexistence equilibrium, whereas if β is large ($\beta >1$), there may exist two coexistence equilibria.

2 

If $d<c$, then for each $\beta >0$, System (3) always has a unique interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$.

3 

If $E_2^{*}(x_2^{*},y_2^{*})$ (or $E_1^{*}(x_1^{*},y_1^{*})$) exists, then $F^{\prime }\left(x_2^{*}\right)<0$ (or $F^{\prime }\left(x_1^{*}\right)>0$).

4 

It is easy to check that $x_1^{*}=x_1^{*}\left(d\right)$ and $x_2^{*}=x_2^{*}\left(d\right)$ are continuously differentiable functions with respect to the parameter d. As d increases, $x_1^{*}$ increases while $x_2^{*}$ decreases.

5 

$x_2^{*}<x_{max}^{*}$ and $x_2^{*}{|}_{d\to 0^{+}}=x_{max}^{*}$. When $\beta \le 1$, $x_2^{*}{|}_{d\to c^{-}}=0$; when $\beta >1$, $x_2^{*}{|}_{d\to F{\left(x_0\right)}^{-}}=x_0$.

4. Stability of Equilibria

In this section, we consider the stability of the equilibria of (3). The Jacobian matrix of (3) is

$$\begin{array}{c}\hfill J=\left(\begin{array}{cc}c(1+2\beta x)y-d& c(1+\beta x)x\\ -(1+2\beta x)y& 1-2y-(1+\beta x)x\end{array}\right).\end{array}$$

(9)

4.1. Stability of Boundary Equilibria

In this subsection, we show the local qualitative behaviors of System (3) near the boundary equilibria $E_0=(0,0)$ and $E_1=(0,1)$.

Theorem 3.

1 

$E_0=(0,0)$ is always a saddle.

2 

$E_1=(0,1)$ is a stable node if either $d>c$ or $d=c$ and $\beta =1$, whereas it is a saddle if $d<c$, with its stable manifold along the y-axis and its unstable manifold (denoted by ${\Gamma }_{E_1}^u$) entering the interior of ${\mathbb{R}}_{+}^2$. If $d=c$ and $\beta \ne 1$, $E_1$ is a saddle node:

(i) 

When $\beta <1$, $E_1$ has a parabolic sector in the first quadrant and it is an attracting saddle node;

(ii) 

When $\beta >1$, $E_1$ has two hyperbolic sectors in the first quadrant.

Proof. 

From the Jacobian matrix (9) at $E_0$, it is easy to see that $E_0$ is always a saddle.

At $E_1=(0,1)$, the eigenvalues of the Jacobian matrix (9) are ${\kappa }_1=c-d$ and ${\kappa }_2=-1$. Therefore, $E_1$ is a stable node if $d>c$ and a saddle if $d<c$. Now, we discuss the critical case $d=c$, where $E_1$ becomes a non-hyperbolic equilibrium. We use the center manifold theorem and the polar blow-up technique [34] to determine the type of $E_1$.

By performing a transformation of $x=X,y=Y+1$ and then setting $X=u,Y=-u+v$, System (3) becomes

$$\begin{array}{cc}\hfill & u^{\prime }=c(\beta -1)u^2+cuv-c\beta u^3+c\beta u^{2}v,\hfill \\ \hfill & v^{\prime }=-v+(\beta (c-1)-c)u^2+(c+1)uv-v^2-\beta (c-1)u^3+\beta (c-1)u^{2}v.\hfill \end{array}$$

(10)

It is easy to check that the flow on the center manifold is given by

$$u^{\prime }=c(\beta -1)u^2+c(\beta c-2\beta -c)u^3+O\left(u^4\right).$$

Thus, we know from the center manifold theorem [34] that $E_1$ is a saddle node when $\beta \ne 1$, whereas it is a stable node when $\beta =1$. In order to determine the qualitative behavior of the solutions near $E_1$ in ${\mathbb{R}}_{+}^2$ when $\beta \ne 1$, the blow-up technique [34] is applied to System (10) below. By applying the polar coordinate transformation $u=\rho cos\left(\eta \right),$$v=\rho sin\left(\eta \right)$ to (10), we obtain the following system of polar coordinates

$$\frac{\mathrm{d}\rho }{\mathrm{d}t}=-\rho {sin}^2\left(\eta \right)+{\rho }^{2}p\left(\eta \right)+O\left({\rho }^3\right),\frac{\mathrm{d}\eta }{\mathrm{d}t}=-cos\left(\eta \right)sin\left(\eta \right)+O\left(\rho \right),$$

(11)

where

$$\begin{array}{cc}\hfill p\left(\eta \right)=& cos\left(\eta \right)\left[c(\beta -1){cos}^2\left(\eta \right)+ccos\left(\eta \right)sin\left(\eta \right)\right]\hfill \\ \hfill & +sin\left(\eta \right)\left[(\beta c-\beta -c){cos}^2\left(\eta \right)+(c+1)cos\left(\eta \right)sin\left(\eta \right)-{sin}^2\left(\eta \right)\right].\hfill \end{array}$$

(12)

On the unit circle $\left\{0\right\}\times \mathbb{S}$, System (11) clearly has four singular points $(0,{\eta }_i),{\eta }_i=0,\pi ,\frac{\pi }{2},\frac{3\pi }{2}$, corresponding to $i=1,2,3,4$. When $0<\rho \ll 1$, we have $\frac{\mathrm{d}\rho }{\mathrm{d}t}<0$ along the directions $\eta ={\eta }_3$ and ${\eta }_4$. If $\beta >1$, then $\frac{\mathrm{d}\rho }{\mathrm{d}t}>0$ along the direction $\eta ={\eta }_1$ and $\frac{\mathrm{d}\rho }{\mathrm{d}t}<0$ along the direction $\eta ={\eta }_2$. If $\beta <1$, then $\frac{\mathrm{d}\rho }{\mathrm{d}t}<0$ along the direction $\eta ={\eta }_1$ and $\frac{\mathrm{d}\rho }{\mathrm{d}t}>0$ along the direction $\eta ={\eta }_2$. Therefore, when $\beta >1$, $E_1$ is a saddle node that consists of two hyperbolic sectors and one parabolic sector, and its hyperbolic sectors are in the first quadrant; when $\beta <1$, $E_1$ has its parabolic sector in the first quadrant, and it is an attracting saddle node. □

4.2. Stability of Interior Equilibria and Hopf Bifurcation

Now, we consider the local stability of the interior equilibria of (3). At an interior equilibria $E^{*}=(x^{*},y^{*})$, the Jacobian matrix (9) becomes

$$\begin{array}{c}\hfill {J|}_{E^{*}}=\left(\begin{array}{cc}c\beta x^{*}{y}^{*}& c(1+\beta x^{*})x^{*}\\ -(1+2\beta x^{*})y^{*}& -y^{*}\end{array}\right).\end{array}$$

(13)

The characteristic equation is given by

$${\kappa }^2-{\omega }_1\kappa +{\omega }_2=0.$$

(14)

where ${\omega }_1=TrJ{{|}_{E^{*}},{\omega }_2=DetJ|}_{E^{*}}$. By using $y^{*}={\varphi }_1\left(x^{*}\right)=\frac{d}{c(1+\beta )x^{*}}$ and $y^{*}={\varphi }_2\left(x^{*}\right)=-\beta {\left(x^{*}\right)}^2-x^{*}+1$, we have

$${\omega }_1=(c\beta x^{*}-1)y^{*}=d-(c+1)y^{*}=(c\beta x^{*}-1){\varphi }_2\left(x^{*}\right),$$

(15)

and

$${\omega }_2=-x^{*}{y}^{*}(c\beta y^{*}-c(1+\beta x^{*})(1+2\beta x^{*}))=-x^{*}{y}^{*}{F}^{\prime }\left(x^{*}\right).$$

(16)

Note that it is very important to observe that the determinant ${DetJ|}_{E^{*}}$ is expressed by $F^{\prime }\left(x^{*}\right)$, that is, ${DetJ|}_{E^{*}}=-x^{*}{y}^{*}{F}^{\prime }\left(x^{*}\right)$. If $E_1^{*}(x_1^{*},y_1^{*})$ exists, it is a saddle since $F^{\prime }\left(x_1^{*}\right)>0$; if $E_2^{*}(x_2^{*},y_2^{*})$ exists, its stability is determined by the sign of ${\omega }_1{=TrJ|}_{E_2^{*}}$ since $F^{\prime }\left(x_2^{*}\right)<0$ (see Remark 1). Thus, from (15), we can directly obtain the following result.

Lemma 1.

$E_2^{*}(x_2^{*},y_2^{*})$ is a sink if $x_2^{*}<\frac{1}{c\beta }$ and a source if $x_2^{*}>\frac{1}{c\beta }$.

Lemma 1 does not explicitly reveal whether $E_2^{*}(x_2^{*},y_2^{*})$ is stable or unstable in explicit parameter regions. For this reason, we need to conduct an in-depth analysis of different parameter regions.

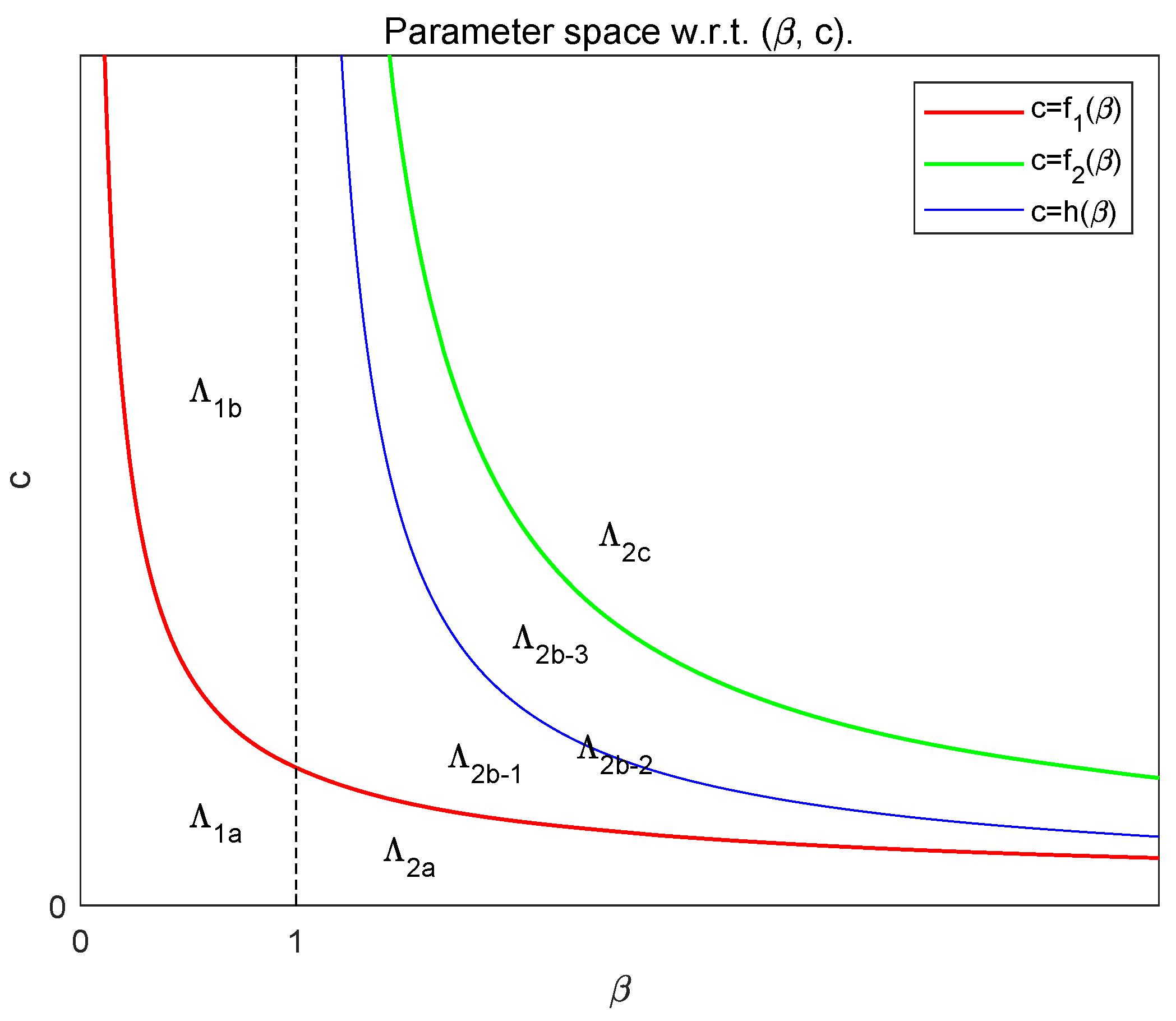
Obviously, for $\beta >0$,

$$\frac{1}{c\beta }<x_{max}^{*}\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}c>f_1\left(\beta \right):=\frac{2}{\sqrt{1+4\beta }-1},$$

(17)

and for $\beta >1$,

$$\frac{1}{c\beta }<x_0=\frac{-2+\sqrt{3\beta +1}}{3\beta }\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}c>f_2\left(\beta \right):=\frac{3}{\sqrt{1+3\beta }-2}$$

(18)

Based on (17) and (18), we divide the parameter region ${\Lambda }_1$ into the following two subregions (see Figure 3):

$${\Lambda }_{1a}=\{(\beta ,c)\in {\Lambda }_1:c\le f_1\left(\beta \right)\},{\Lambda }_{1b}=\{(\beta ,c)\in {\Lambda }_1:c>f_1\left(\beta \right)\}.$$

(19)

Also, the parameter region ${\Lambda }_2$ is divided into the following three subregions (see Figure 3):

$$\begin{array}{cc}\hfill & {\Lambda }_{2a}=\{(\beta ,c)\in {\Lambda }_2:c\le f_1\left(\beta \right)\},{\Lambda }_{2b}=\{(\beta ,c)\in {\Lambda }_2:f_1\left(\beta \right)<c<f_2\left(\beta \right)\},\hfill \\ \hfill & {\Lambda }_{2c}=\{(\beta ,c)\in {\Lambda }_2:c\ge f_2\left(\beta \right)\}.\hfill \end{array}$$

(20)

Figure 3. Parameter space $\Lambda$, where $\Lambda ={\Lambda }_1\cup {\Lambda }_2$, ${\Lambda }_1={\Lambda }_{1a}\cup {\Lambda }_{1b}$, ${\Lambda }_2={\Lambda }_{2a}\cup {\Lambda }_{2b}\cup {\Lambda }_{2c}$, and ${\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}\cup {\Lambda }_{2b-3}$. When $(\beta ,c)\in {\Lambda }_1$, System (3) only has the interior equilibrium $E_2^{*}$ for $d\in (0,c)$; when $(\beta ,c)\in {\Lambda }_2$, there exists one interior equilibrium $E_2^{*}$ for $d\in (0,c]$ and two interior equilibria $E_1^{*}$ and $E_2^{*}$ for $d\in (c,F\left(x_0\right))$. When $(\beta ,c)\in {\Lambda }_{1a}\cup {\Lambda }_{2a}$, $E_2^{*}$, if it exists, is a sink; when $(\beta ,c)\in {\Lambda }_{2c}$, $E_2^{*}$ is a source. If $(\beta ,c)\in {\Lambda }_{1b}\cup {\Lambda }_{2b}$, the Hopf bifurcation occurs at $d=d^{*}$ and the stability of $E_2^{*}$ switches from unstable to stable as d increases near $d^{*}$. When $(\beta ,c)\in {\Lambda }_{1b}\cup {\Lambda }_{2b-1}$, $d^{*}<c$; when $(\beta ,c)\in {\Lambda }_{2b-2}$, $d^{*}=c$; when $(\beta ,c)\in {\Lambda }_{2b-3}$, $d^{*}>c$.

Now, we apply the monotonicity of $x_2^{*}$ on d (see Remark 1) to analyze the stable parameter region of the interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$. Define $d^{*}=F\left(\frac{1}{c\beta }\right)$, that is,

$$\begin{array}{c}\hfill d^{*}=H(\beta ,c):=(1+c)\left(1-\frac{1}{c\beta }-\frac{1}{c^2\beta }\right).\end{array}$$

(21)

Note that $d^{*}>0$ is equivalent to $c>f_1\left(\beta \right)$.

First, we consider the stability of $E_2^{*}(x_2^{*},y_2^{*})$ for the case of $(\beta ,c)\in {\Lambda }_1$. According to Theorem 2, System (3) has the unique interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ when $d\in (0,c)$.

(1)

Let $(\beta ,c)\in {\Lambda }_{1a}$, then $x_{max}^{*}\le \frac{1}{c\beta }$, as indicated by (17). According to Remark 1, if $E_2^{*}(x_2^{*},y_2^{*})$ exists, then $x_2^{*}<x_{max}^{*}$. Hence, for all $d\in (0,c)$, $E_2^{*}(x_2^{*},y_2^{*})$ is a sink according to Lemma 1.

(2)

Let $(\beta ,c)\in {\Lambda }_{1b}$, then $\frac{1}{c\beta }<x_{max}^{*}$. In addition, (21) implies that when $d=d^{*}$, $x_2^{*}=\frac{1}{c\beta }$. Then, from the monotonicity of $x_2^{*}$ on d (see Remark 1), we know that $x_2^{*}>\frac{1}{c\beta }$ for $d\in (0,d^{*})$ and $x_2^{*}<\frac{1}{c\beta }$ for $d\in (d^{*},c)$. It follows from Lemma 1 that $E_2^{*}(x_2^{*},y_2^{*})$ is a source for $d\in (0,d^{*})$ and a sink for $d\in (d^{*},c)$.

Now, we consider the stability of $E_2^{*}(x_2^{*},y_2^{*})$ for the case of $(\beta ,c)\in {\Lambda }_2$. According to Theorem 2, when $d\in (0,F\left(x_0\right))$, the interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ exists.

(1)

Let $(\beta ,c)\in {\Lambda }_{2a}$, then, similar to the case of $(\beta ,c)\in {\Lambda }_{1a}$, $E_2^{*}(x_2^{*},y_2^{*})$, if it exists, is a sink.

(2)

Let $(\beta ,c)\in {\Lambda }_{2b}$, then $x_0<\frac{1}{c\beta }<x_{max}^{*}$, as indicated by (17) and (18). From the monotonicity of $x_2^{*}$ on d, we know that $x_2^{*}>\frac{1}{c\beta }$ for $d\in (0,d^{*})$ and $x_2^{*}<\frac{1}{c\beta }$ for $d\in (d^{*},F\left(x_0\right))$. It follows from Lemma 1 that $E_2^{*}(x_2^{*},y_2^{*})$ is a source for $d\in (0,d^{*})$ and a sink for $d\in (d^{*},F\left(x_0\right))$.

(3)

Let $(\beta ,c)\in {\Lambda }_{2c}$, then $\frac{1}{c\beta }\le x_0$, as indicated by (18), which implies from the monotonicity of $x_2^{*}$ on d that for all $d\in (0,F\left(x_0\right))$, the corresponding interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ satisfies $x_2^{*}>\frac{1}{c\beta }$. So, $E_2^{*}(x_2^{*},y_2^{*})$ is a source for all $d\in (0,F\left(x_0\right))$.

Then, we obtain the following conclusive result on the local stability of the interior equilibria.

Theorem 4.

1 

$E_1^{*}(x_1^{*},y_1^{*})$, if it exists, is always a saddle.

2 

At $E_2^{*}(x_2^{*},y_2^{*})$, we have the following statements:

(i) 

If $(\beta ,c)\in {\Lambda }_{1a}\cup {\Lambda }_{2a}$, then $E_2^{*}$, if it exists, is a sink.

(ii) 

If $(\beta ,c)\in {\Lambda }_{1b}$, then $E_2^{*}$ is a source for $d\in (0,d^{*})$ and a sink for $d\in (d^{*},c)$.

(iii) 

If $(\beta ,c)\in {\Lambda }_{2b}$, then $E_2^{*}$ is a source for $d\in (0,d^{*})$ and a sink for $d\in (d^{*},F\left(x_0\right))$.

(iv) 

If $(\beta ,c)\in {\Lambda }_{2c}$, then $E_2^{*}$ is a source for all $d\in (0,F\left(x_0\right))$.

According to Theorem 4, if $(\beta ,c)\in {\Lambda }_{1b}$ or $(\beta ,c)\in {\Lambda }_{2b}$, i.e., $\beta \le 1$ and $c>f_1\left(\beta \right)$, or $\beta >1$ and $f_1\left(\beta \right)<c<f_2\left(\beta \right)$, there exists a unique $d^{*}$ ($d^{*}<c$ or $d^{*}<F\left(x_0\right)$) such that when $d=d^{*}$, System (3) may undergo the Hopf bifurcation at $E_2^{*}(x_2^{*},y_2^{*})$, where $d^{*}$ is given by (21), and $x_2^{*}=\frac{1}{c\beta }$. Below, we discuss the Hopf bifurcation of (3) and its directions, together with the stability of bifurcating periodic orbits.

We say that a Hopf bifurcation with respect to the parameter d at $d=d^{*}$ is backward (respectively, forward) if there is a small amplitude periodic orbit for each $d\in (d^{*}-ϵ,d^{*})$ (respectively, $d\in (d^{*},d^{*}+ϵ)$), where $ϵ>0$ is a small constant. Additionally, we say that a Hopf bifurcation is supercritical (respectively, subcritical) if the bifurcating periodic solutions are orbitally asymptotically stable (respectively, unstable).

To compare d to c, we first determine the location of $d^{*}$. If $(\beta ,c)\in {\Lambda }_{1b}$, i.e., $\beta \le 1$ and $c>f_1\left(\beta \right)$, we have $d^{*}<c$ since the interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ exists only for $d\in (0,c)$ according to Theorem 4.

Let $(\beta ,c)\in {\Lambda }_{2b}$, i.e., $\beta >1$ and $f_1\left(\beta \right)<c<f_2\left(\beta \right)$. According to Theorem 2, System (3) has the unique interior equilibrium $E_2^{*}$ for $d\le c$ and two interior equilibria $E_1^{*}$ and $E_2^{*}$ for $c<d<F\left(x_0\right)$. From the equation $F\left(x\right)=d$, one can deduce that the first component of the interior equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ corresponding to $d=c$ is given by $x_2^{*}=\frac{-1+\sqrt{\beta }}{\beta }$. It is easy to see that

$$\begin{array}{c}\hfill \frac{-1+\sqrt{\beta }}{\beta }<x_2^{*}{\mid }_{d=d^{*}}=\frac{1}{c\beta }\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}c<h\left(\beta \right):=\frac{1}{\sqrt{\beta }-1},\beta >1.\end{array}$$

Clearly, for $\beta >1$, $f_1\left(\beta \right)<h\left(\beta \right)$. Thus, from the monotonicity of $x_2^{*}$ on d, $d^{*}=c$ if and only if $c=h\left(\beta \right)$, $d^{*}>c$ if and only if $c>h\left(\beta \right)$, and $d^{*}<c$ if and only if $c<h\left(\beta \right)$.

It is easy to see that $h\left(\beta \right)<f_2\left(\beta \right)=\frac{3}{\sqrt{1+3\beta }-2}$ if and only if $\tilde{h}\left(\beta \right):=3\sqrt{\beta }-\sqrt{1+3\beta }-1>0$. Since $\tilde{h}\left(1\right)=0$ and

$${\tilde{h}}^{\prime }\left(\beta \right)=\frac{3}{2}\left(\frac{1}{\beta }-\frac{1}{\sqrt{1+3\beta }}\right)>0,\beta >1,$$

we know that for $\beta >1$, $\tilde{h}\left(\beta \right)>0$. It follows that for $\beta >1$, $h\left(\beta \right)<f_2\left(\beta \right)$. So, conclusively, we have

$$f_1\left(\beta \right)<h\left(\beta \right)<f_2\left(\beta \right),\beta >1.$$

(22)

Based on (22), we divide the region ${\Lambda }_{2b}$ into the following three subregions (see Figure 3):

$$\begin{array}{cc}\hfill & {\Lambda }_{2b-1}:=\{(\beta ,c)\in {\Lambda }_{2b}:f_1\left(\beta \right)<c<h\left(\beta \right)\},\hfill \\ \hfill & {\Lambda }_{2b-2}:=\{(\beta ,c)\in {\Lambda }_{2b}:c=h\left(\beta \right)\},\hfill \\ \hfill & {\Lambda }_{2b-3}:=\{(\beta ,c)\in {\Lambda }_{2b}:h\left(\beta \right)<c<f_2\left(\beta \right)\},\hfill \end{array}$$

(23)

Theorem 5.

If $(\beta ,c)\in {\Lambda }_{1b}\cup {\Lambda }_{2b}$, then a supercritical and backward Hopf bifurcation occurs at $E_2^{*}(x_2^{*},y_2^{*})$ when $d=d^{*}$. The Hopf bifurcation surface $d=H(\beta ,c)$ is given by (21). In addition, we have the following statements:

1 

If $(\beta ,c)\in {\Lambda }_{1b}$, then $d^{*}<c$;

2 

If $(\beta ,c)\in {\Lambda }_{2b-1}$, then $d^{*}<c$;

3 

If $(\beta ,c)\in {\Lambda }_{2b-2}$, then $d^{*}=c$;

4 

If $(\beta ,c)\in {\Lambda }_{2b-3}$, then $d^{*}>c$.

Proof. 

When $d=d^{*}$, $x_2^{*}=\frac{1}{c\beta }$. Hence, ${\omega }_1=(c\beta x_2^{*}-1){\varphi }_2\left(x_2^{*}\right)=0$ and the characteristic Equation (14) at $E_2^{*}$ has a pair of imaginary eigenvalues ${\kappa }_{1,2}=\pm \sqrt{{\omega }_2}$. Let $\kappa ={\varrho }_1\left(d\right)\pm i\sqrt{{\varrho }_2\left(d\right)}$ be the root of (14) when d is near $d^{*}$. Then, ${\varrho }_1\left(d\right)=\frac{1}{2}{\omega }_1=\frac{1}{2}(c\beta x_2^{*}-1){\varphi }_2\left(x_2^{*}\right)$, ${\varrho }_2\left(d\right)=\frac{1}{2}({\omega }_1^2-4{\omega }_2)$. Clearly,

$$\frac{\partial {\varrho }_1\left(d\right)}{\partial d}=\frac{1}{2}c\beta {\varphi }_2\left(x_2^{*}\right)\frac{\partial x_2^{*}}{\partial d}+\frac{1}{2}(c\beta x_2^{*}-1){\varphi }^{\prime }\left(x_2^{*}\right)\frac{\partial x_2^{*}}{\partial d}.$$

Noticing that $x_2^{*}{\mid }_{d=d^{*}}=\frac{1}{c\beta }$ and $\frac{\partial x_2^{*}}{\partial d}<0$ (see Remark 1), we observe that for $(\beta ,c)\in {\Lambda }_{1b}\cup {\Lambda }_{2b}$,

$$\frac{\partial {\varrho }_1\left(d\right)}{\partial d}{\mid }_{d=d^{*}}={\left[\frac{1}{2}c\beta {\varphi }_2\left(x_2^{*}\right)\frac{\partial x_2^{*}}{\partial d}\right]}_{d=d^{*}}<0.$$

From the Poincaré-Hopf Bifurcation Theorem [35], it follows that System (3) undergoes a Hopf Bifurcation when $d=d^{*}$.

Below, we calculate the first Lyapunov coefficient at $d=d^{*}$, which determines the direction of the Hopf bifurcation and the stability of the bifurcating periodic orbits. Let $X=x-x_2^{*}$, $Y=y-y_2^{*}$. For simplicity, we still use the variables x and y instead of X and Y, respectively. Then, System (3) becomes

$$\begin{array}{c}\hfill \frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}=a_{11}x+a_{12}y+g_1(x,y),\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}=a_{21}x+a_{22}y+g_2(x,y),\end{array}$$

where

$$\begin{array}{cc}\hfill & a_{11}=c\beta x_2^{*}{y}_2^{*},a_{12}=c(1+\beta x_2^{*})x_2^{*},a_{21}=-(1+2\beta x_2^{*})y_2^{*},a_{22}=-y_2^{*},\hfill \\ \hfill & g_1(x,y)=c\beta y_2^{*}{x}^2+c(1+2\beta x_2^{*})xy+c\beta x^{2}y,\hfill \\ \hfill & g_2(x,y)=-\beta y_2^{*}{x}^2-(1+2\beta x_2^{*})xy-y^2-\beta x^{2}y.\hfill \end{array}$$

By setting $u=y,v=-\frac{a_{21}}{w}x-\frac{a_{22}}{w}y$, where $w=\sqrt{{\omega }_2}$, we obtain

$$\frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=-wv+p(u,v),\frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}=wu+q(u,v),$$

where

$$\begin{array}{cc}\hfill p(u,v)& =-\frac{uvw}{y_2^{*}}-\beta \frac{{(wv-y_2^{*}u)}^2(y_2^{*}+u)}{{(1+2\beta x_2^{*})}^2{\left(y_2^{*}\right)}^2},\hfill \\ \hfill q(u,v)& =\frac{y_2^{*}}{w}p(u,v)+\frac{y_2^{*}(1+2\beta x_2^{*})}{w}\left[\frac{uvw}{y_2^{*}}-c{u}^2+c\beta \frac{{(wv-y_2^{*}u)}^2(y_2^{*}+u)}{{(1+2\beta x_2^{*})}^2{\left(y_2^{*}\right)}^2}\right]\hfill \\ \hfill & =[c(1+\beta x_2^{*})-1]uv-\frac{c{y}_2^{*}(1+2\beta x_2^{*})u^2}{w}+\frac{\beta y_2^{*}{(wv-y_2^{*}u)}^2(y^{*}+u)[c(1+2\beta x_2^{*})-1]}{w{(1+2\beta x_2^{*})}^2{\left(y_2^{*}\right)}^2}.\hfill \end{array}$$

Let

$$\mu =\frac{1}{16}[p_{uuu}+p_{uvv}+q_{uuv}+q_{vvv}]+\frac{1}{16w}[p_{uv}(p_{uu}+p_{vv})-q_{uv}(q_{uu}+q_{vv})-p_{uu}{q}_{uu}+p_{vv}{q}_{vv}],$$

where $p_{uv}$ denotes $({\partial }^2/(\partial u\partial v))(0,0),$ etc. Through careful calculation, we have

$$\begin{array}{c}\hfill \begin{array}{cc}& p_{uuu}=-\frac{6\beta }{{(1+2\beta x_2^{*})}^2},p_{uvv}=-\frac{2\beta w^2}{{(1+2\beta x_2^{*})}^2{\left(y_2^{*}\right)}^2},q_{uuv}=-\frac{2\beta [c(1+2\beta x_2^{*})-1]}{{(1+2\beta x_2^{*})}^2},\hfill \\ & q_{vvv}=0,p_{uv}=-\frac{w}{y_2^{*}}+\frac{2\beta w}{{(1+2\beta x_2^{*})}^2},p_{uu}=-\frac{2\beta y_2^{*}}{{(1+2\beta x_2^{*})}^2},\hfill \\ & p_{vv}=-\frac{2\beta w^2}{{(1+2\beta x_2^{*})}^2{y}_2^{*}},q_{vv}=\frac{2\beta w[c(1+2\beta x_2^{*})-1]}{{(1+2\beta x_2^{*})}^2},\hfill \\ & q_{uu}=-\frac{2c{y}_2^{*}(1+2\beta x_2^{*})}{w}-\frac{2\beta {\left(y_2^{*}\right)}^2[c(1+2\beta x_2^{*})-1]}{w{(1+2\beta x_2^{*})}^2},\hfill \\ & q_{uv}=[c(1+2\beta x_2^{*})-1]-\frac{2\beta y_2^{*}[c(1+2\beta x_2^{*})-1]}{{(1+2\beta x_2^{*})}^2}.\hfill \end{array}\end{array}$$

At $d=d^{*}$, we obtain

$$\begin{array}{cc}\hfill \mu & =-\frac{1}{16w^2}\left[\frac{4c\beta {\left(y_2^{*}\right)}^2}{1+2\beta x_2^{*}}+\frac{2\beta w^2(3+c)}{{(1+2\beta x_2^{*})}^2}+\frac{c^2\beta {\left(y_2^{*}\right)}^2(1+5\beta x_2^{*}+5{\beta }^2{\left(x_2^{*}\right)}^2)}{{(1+2\beta x_2^{*})}^3}\right.\hfill \\ \hfill & {\left.+\frac{4\beta y_2^{*}[w^4(1+c\beta +\beta )+\beta (w^2+c{\left(y_2^{*}\right)}^2+{\left(y_2^{*}\right)}^2)]}{{(1+2\beta x_2^{*})}^4}\right]}_{d=d^{*}}<0.\hfill \end{array}$$

Thus, the Hopf bifurcation is supercritical and backward (see Theorem 3.4.2 and Formula (3.4.11) of Guckenheimer and Holmes [36]). The proof is complete. □

4.3. Saddle Node and Cusp

According to Theorem 2, when $(\beta ,c)\in {\Lambda }_2$ and $d=F\left(x_0\right)$, System (3) has the unique interior equilibrium ${\tilde{E}}^{*}(x_0,y_0)$, where $x_0=\frac{-2+\sqrt{3\beta +1}}{3\beta }$ (see (8)), $y_0={\varphi }_1\left(x_0\right)$. Below, we discuss the dynamic behavior near ${\tilde{E}}^{*}(x_0,y_0)$.

Theorem 6.

Let $(\beta ,c)\in {\Lambda }_2$ and $d=F\left(x_0\right)$.

(1) 

If $c>f_2\left(\beta \right)$, then ${\tilde{E}}^{*}(x_0,y_0)$ is a repelling saddle node of codimension one.

(2) 

If $c<f_2\left(\beta \right)$, then ${\tilde{E}}^{*}(x_0,y_0)$ is an attracting saddle node of codimension one.

(3) 

If $c=f_2\left(\beta \right)$, then ${\tilde{E}}^{*}(x_0,y_0)$ is a Bogdanov–Takens-type cusp of codimension two.

Proof. 

At ${\tilde{E}}^{*}(x_0,y_0)$, it is easy to see that ${\omega }_2=0$ and the characteristic Equation (14) has two roots: ${\kappa }_1=0$ and ${\kappa }_2={\omega }_1$. Therefore, ${\tilde{E}}^{*}$ is a non-hyperbolic equilibrium. We use the center manifold theorem and the blow-up technique [34] to determine the type of ${\tilde{E}}^{*}$.

Let $c\ne f_2\left(\beta \right)$, which implies that ${\omega }_1=(c\beta x_0-1)y_0\ne 0$. Perform a transformation of $X=x-x_0$, $Y=y-y_0$ to translate ${\tilde{E}}^{*}=(x_0,y_0)$ to the origin. For simplicity, we still use the variables x and y instead of X and Y, respectively. Then, System (3) becomes

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}=c\beta x_0{y}_{0}x+c(1+\beta x_0)x_{0}y+c\beta y_0{x}^2+c(1+2\beta x_0)xy+c\beta x^{2}y,\hfill \\ \hfill & \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}=-(1+2\beta x_0)y_{0}x-y_{0}y-\beta y_0{x}^2-(1+2\beta x_0)xy-y^2-\beta x^{2}y.\hfill \end{array}$$

(24)

Let $x=-u+c{x}_0(1+\beta x_0)v$ and $y=(1+2\beta x_0)u-y_{0}v$. Then, System (24) becomes

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=a_1{u}^2+a_{2}uv+a_3{v}^2+{O\left(\right|(u,v)|}^3),\hfill \\ \hfill & \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}={\omega }_{1}v+b_1{u}^2+b_{2}uv+b_3{v}^2+{O\left(\right|(u,v)|}^3).\hfill \end{array}$$

(25)

Here,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill a_1& =-\frac{c\beta x_0{y}_0}{{\omega }_1}(2+3\beta x_0),a_2=-\frac{c{y}_0}{{\omega }_1}[{\omega }_1+3\beta x_0{y}_0+c\beta x_0^2(1+\beta x_0)],\hfill \\ \hfill a_3& =\frac{c{x}_0{y}_0(1+\beta x_0)}{{\omega }_1}[c^2\beta x_0^2{(1+\beta x_0)}^2+{\omega }_1],\hfill \\ \hfill b_1& =\frac{1+2\beta x_0}{{\omega }_1}\left(c\beta x_0(1+2\beta x_0)+(1+\beta x_0)\right),\hfill \\ \hfill b_2& =-\frac{1}{{\omega }_1}[c{y}_0(1+2\beta x_0)(1+2\beta x_0-c\beta x_0)+y_0(c\beta x_0+\beta x_0+1)],\hfill \\ \hfill b_3& =-\frac{1}{{\omega }_1}[c^2\beta x_0{y}_0(1+2\beta x_0)(c{x}_0(1+\beta x_0)-y_0)-c^2\beta x_0^2{y}_0{(1+\beta x_0)}^2-y_0{\omega }_1].\hfill \end{array}\end{array}$$

It is clear that the flow on the center manifold is given by $\frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=-\frac{c\beta x_0{y}_0}{{\omega }_1}(2+3\beta x_0)u^2+O\left(u^3\right)$. So, according to the center manifold theorem, ${\tilde{E}}^{*}$ is a saddle node, i.e., half of ${\tilde{E}}^{*}$ is a node and the other half is a saddle. In order to determine the stability of the half node of ${\tilde{E}}^{*}$, below, the blow-up technique [34] is applied to System (25). By applying the polar coordinate transformation $u=\rho cos\left(\theta \right)$, $v=\rho sin\left(\theta \right),$ System (25) is transformed into the following system

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}\rho }{\mathrm{d}t}=\rho {\omega }_1{sin}^2\left(\theta \right)+{\rho }^2[cos\left(\theta \right)(a_1{cos}^2\left(\theta \right)+a_{2}cos\left(\theta \right)sin\left(\theta \right)+a_3{sin}^2\left(\theta \right))\hfill \\ \hfill & +sin\left(\theta \right)(b_1{cos}^2\left(\theta \right)+b_{2}cos\left(\theta \right)sin\left(\theta \right)+b_3{sin}^2\left(\theta \right))]+o\left({\rho }^2\right),\hfill \\ \hfill & \frac{\mathrm{d}\theta }{\mathrm{d}t}={\omega }_{1}cos\left(\theta \right)sin\left(\theta \right)+O\left(\rho \right).\hfill \end{array}$$

(26)

On the unit circle $\left\{0\right\}\times \mathbb{S}$, System (26) clearly has four singular points $(0,{\theta }_i)$ corresponding to ${\theta }_i=0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}$, $i=1,2,3,4$. If $c<f_2\left(\beta \right)$, then ${\omega }_1<0$ and $a_1>0$. Then, when $0<\rho \ll 1$, we have $\frac{\mathrm{d}\rho }{\mathrm{d}t}>0$ along the direction $\theta ={\theta }_1$ and $\frac{\mathrm{d}\rho }{\mathrm{d}t}<0$ along the directions $\theta ={\theta }_2$, ${\theta }_3$, and ${\theta }_4$, which implies that the half node of ${\tilde{E}}^{*}$ is stable, i.e., ${\tilde{E}}^{*}$ is an attracting saddle node of codimension one. If $c>f_2\left(\beta \right)$, then, when $0<\rho \ll 1$, we have $\frac{\mathrm{d}\rho }{\mathrm{d}t}<0$ along the direction $\theta ={\theta }_1$ and $\frac{\mathrm{d}\rho }{\mathrm{d}t}>0$ along the directions $\theta ={\theta }_2$, ${\theta }_3$, and ${\theta }_4$, which implies that the half node of ${\tilde{E}}^{*}$ is unstable, i.e., ${\tilde{E}}^{*}$ is a repelling saddle node of codimension one.

Now, we assume that $c=f_2\left(\beta \right)$, which implies that ${\omega }_1=0$. Then, ${\kappa }_1={\kappa }_2=0$. In this case, we set $x=-u-\frac{1}{y_0}v$, $y=(1+2\beta x_0)u$. Then, System (24) becomes

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=v-(1+\beta x_0)u^2-\frac{1}{y_0}uv-\frac{\beta }{y_0(1+2\beta x_0)}{v}^2+O\left(3\right),\hfill \\ \hfill & \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}=y_0(2+3\beta x_0)u^2-(1+c)uv-\frac{\beta (1+c)}{1+2\beta x_0}{v}^2.\hfill \end{array}$$

(27)

Let $u={\phi }_1+\frac{1}{2}\left(-\frac{1}{y_0}-\frac{\beta (1+c)}{1+2\beta x_0}\right){\phi }_1^2-\frac{\beta }{y_0(1+2\beta x_0)}{\phi }_1{\phi }_2$, $v={\phi }_2+(1+\beta x_0){\phi }_1^2-\frac{\beta (c+1)}{1+2\beta x_0}{\phi }_1{\phi }_2$. Then, System (27) is transformed into

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{\phi }_1\left(t\right)}{\mathrm{d}t}& ={\phi }_2+o\left(\right|({\phi }_1,{\phi }_2){|}^2),\hfill \\ \hfill \frac{\mathrm{d}{\phi }_2\left(t\right)}{\mathrm{d}t}& ={\delta }_1{\phi }_1^2-{\delta }_2{\phi }_1{\phi }_2+o\left(\right|({\phi }_1,{\phi }_2){|}^2),\hfill \end{array}$$

(28)

where

$${\delta }_1=y_0(2+3\beta x_0)>0,{\delta }_2=(1+c)+2(1+\beta x_0)>0.$$

So, ${\tilde{E}}^{*}$ is a Bogdanov–Takens-type cusp of codimension two (see [34,37]). The proof is complete. □

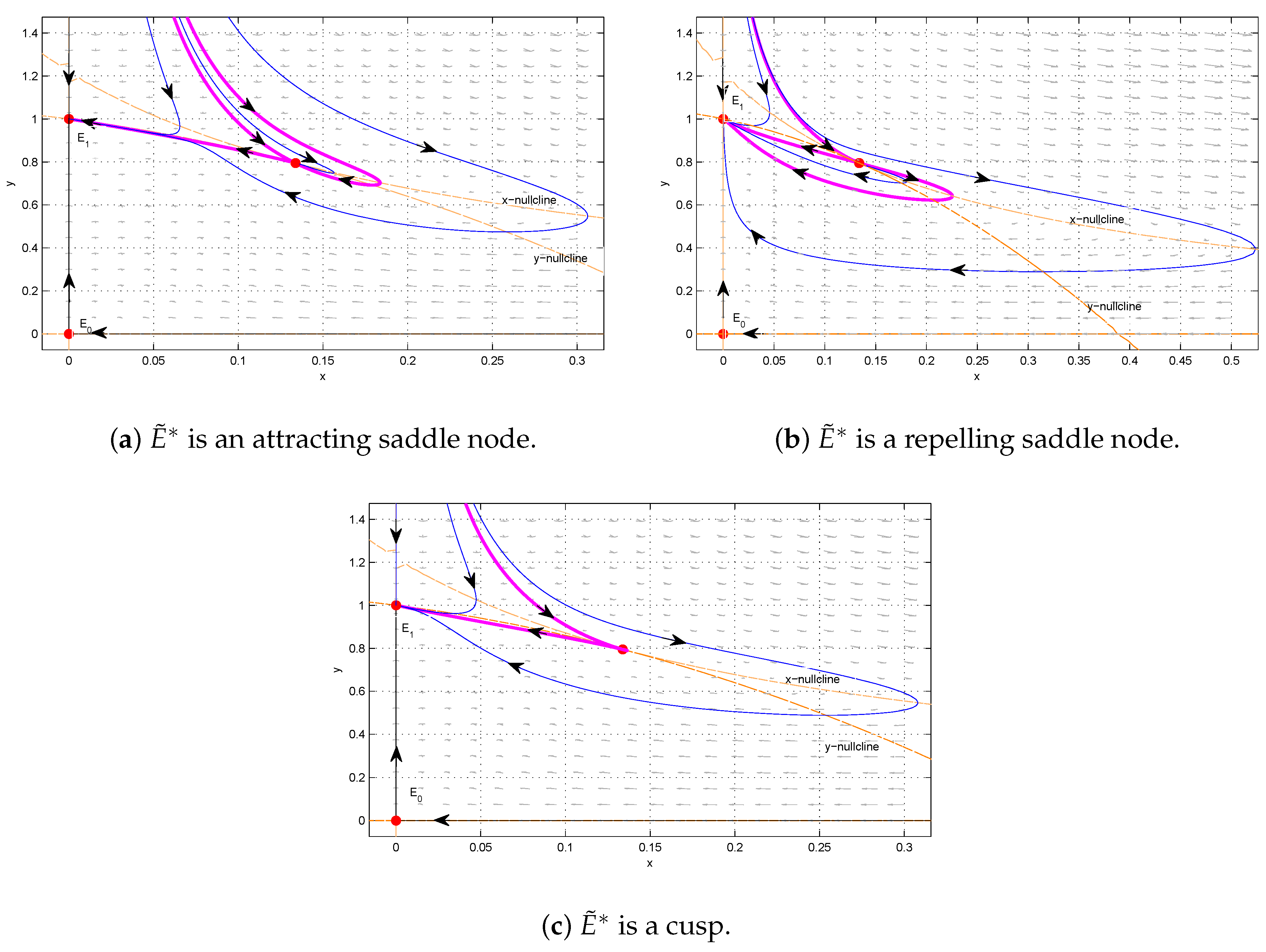
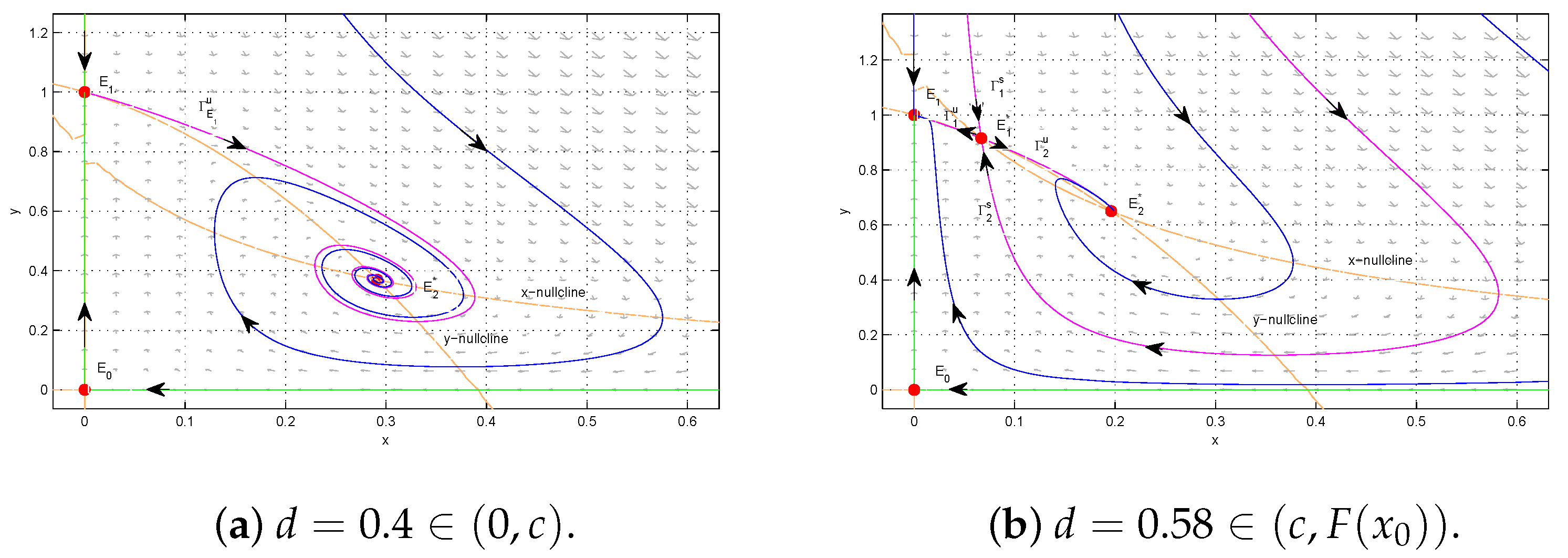
For example, we take $\beta =4$, then, $x_0\approx 0.1337959395$. We consider the dynamics of System (3) when $(\beta ,c)=(4,c)\in {\Lambda }_2$ and $d=F\left(x_0\right)$.

(1)

In Figure 4a, we choose $c=1<f_2\left(\beta \right)\approx 1.868517092$. When $d=F\left(x_0\right)\approx 1.2198549364$, System (3) has the unique interior equilibrium ${\tilde{E}}^{*}(x_0,y_0)$, which is an attracting saddle node. There are three separatrices, two approaching ${\tilde{E}}^{*}$ and one connecting ${\tilde{E}}^{*}$ and $E_1(0,1)$ and entering $E_1$. The three separatrices divide ${\mathbb{R}}_{+}^2$ into three parts, two of which are hyperbolic sectors and one of which is a parabolic sector. The solutions initiated in the hyperbolic sectors converge to $E_1$, whereas the solutions initiated in the parabolic sector tend to ${\tilde{E}}^{*}$.

Figure 4. Phase portraits of System (3): (a) Taking $\beta =4,c=1<f_2\left(\beta \right),f_2\left(\beta \right)\approx 1.868517092,$$d=F\left(x_0\right)\approx 1.2198549364$, ${\tilde{E}}^{*}$ is an attracting saddle node. (b) Taking $\beta =4,c=3>f_2\left(\beta \right),$$d=F\left(x_0\right)\approx 3.6595648104$, ${\tilde{E}}^{*}$ is a repelling saddle node. (c) Taking $\beta =4,c=f_2\left(\beta \right),$$d=F\left(x_0\right)\approx 2.2793198$, ${\tilde{E}}^{*}$ is a Bogdanov–Takens-type cusp.

(2)

In Figure 4b, we choose $c=3>f_2\left(\beta \right)$. When $d=F\left(x_0\right)\approx 3.6595648104$, the unique interior equilibrium ${\tilde{E}}^{*}$ is a repelling saddle node. ${\tilde{E}}^{*}$ consists of two hyperbolic sectors, one parabolic sector, and three separatrices. Only one of the separatrices approaches ${\tilde{E}}^{*}$ and all the other solutions approach $E_1$.

(3)

In Figure 4c, we choose $c=f_2\left(\beta \right)$. When $d=F\left(x_0\right)\approx 2.2793198$, the unique interior equilibrium ${\tilde{E}}^{*}$ is a Bogdanov–Takens-type cusp. Cusp ${\tilde{E}}^{*}$ consists of two hyperbolic sectors and two separatrices. Only one of the separatrices approaches ${\tilde{E}}^{*}$ and all the other solutions approach $E_1$.

4.4. Summary

Our main results obtained in the previous arguments can be summarized in Figure 5a,b, where the parameter $\beta$ is chosen as $\beta =0.6<1$ and $\beta =4>1$, respectively. The red curve denotes the Hopf bifurcation curve $d=H(\beta ,c)$, and the blue and green straight lines are $d=c$ and $d=F\left(x_0\right)=\frac{c(2{(3\beta +1)}^{\frac{3}{2}}+9\beta +2)}{27\beta }$ ($x_0\approx 0.1337959395$), respectively.

Figure 5. Bifurcation diagram with respect to $(c,d)$. (a) The case of $\beta =0.6<1$. (b) The case of $\beta =4>1$.

1.

As d decreases, Figure 5a ($\beta =0.6<1$) indicates the following implications:

(1)

When $d>c$, there is no interior equilibrium and $E_1(0,1)$ is a sink; when $d=c$, $E_1$ becomes a half-stable equilibrium (a saddle-node point; see Theorem 3); when d decreases from $d=c$, the saddle-node bifurcation occurs, and $E_1$ becomes a saddle and a stable interior equilibrium $E_2^{*}$ appears (see Theorem 4).

(2)

When d continues to decrease, according to Theorem 4, if $c\le f_1\left(\beta \right)(f_1\left(\beta \right)\approx 2.3699)$, i.e., $(\beta ,c)\in {\Lambda }_{1a}$, $E_2^{*}$ is a sink for all $d<c$; if $c>f_1\left(\beta \right)$ (i.e., $(\beta ,c)\in {\Lambda }_{1b}$), as d decreases to the red curve, i.e., $d=H(\beta ,c)$ ($\beta =0.6$), a supercritical Hopf bifurcation occurs. Below it, i.e., $d<H(\beta ,c)$, $E_2^{*}$ becomes a source.

2.

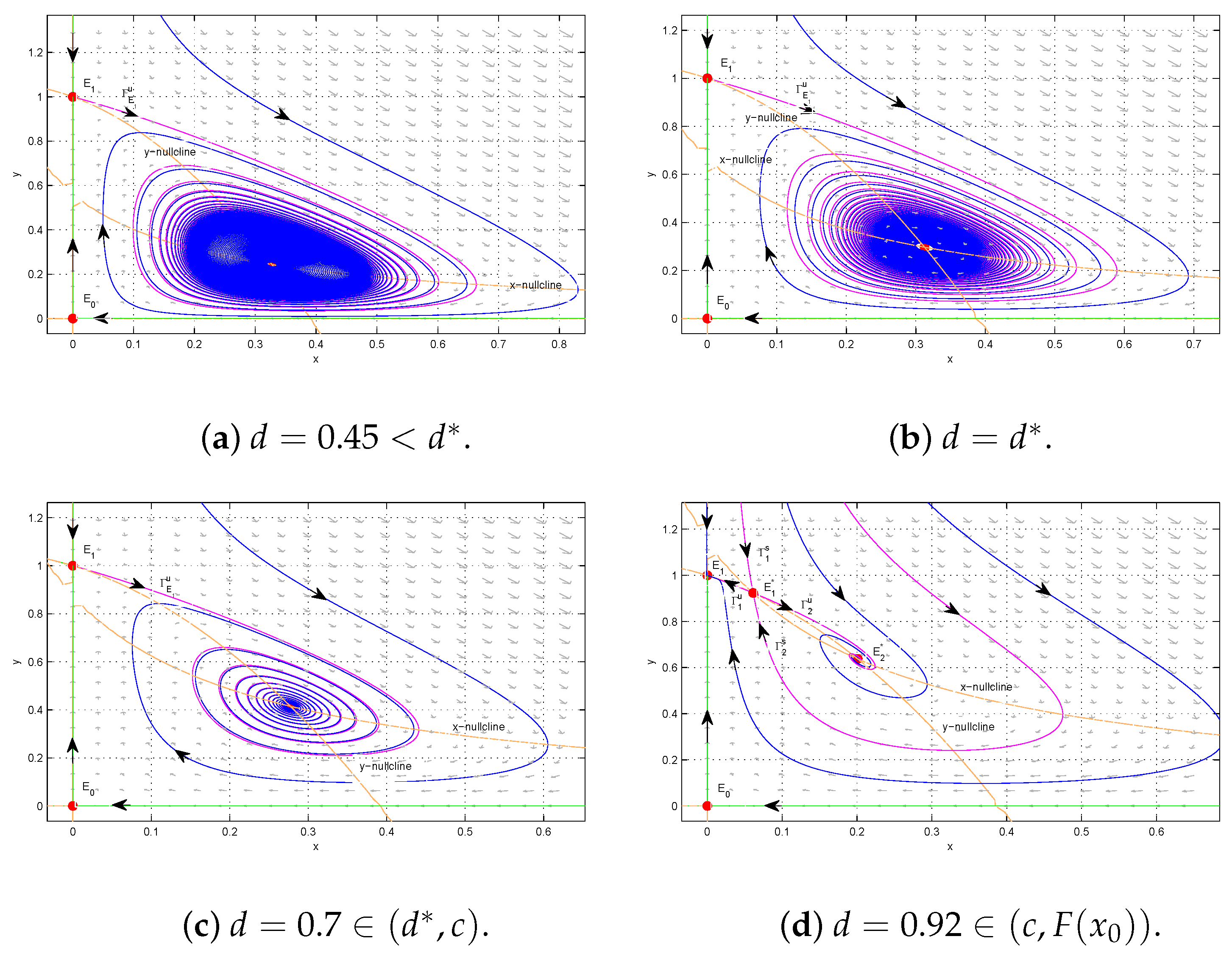
As d decreases, Figure 5b ($\beta =4>1$) indicates the following implications:

(1)

According to Theorem 2, when $d>F\left(x_0\right)$, System (3) has no interior equilibrium and $E_1$ is stable node. According to Theorems 2 and 6, when d decreases to the green line $d=F\left(x_0\right)$, System (3) has a unique interior equilibrium ${\tilde{E}}^{*}(x_0,{\varphi }_1\left(x_0\right))$, which is an attracting saddle node when $c<f_2\left(\beta \right)(f_2\left(\beta \right)\approx 1.868517092)$, a repelling saddle node when $c>f_2\left(\beta \right)$, and a Bogdanov–Takens-type cusp when $c=f_2\left(\beta \right)$ (see Figure 4). Note that when $c=f_2\left(\beta \right)$, the line $d=F\left(x_0\right)$ is tangent to the Hopf bifurcation curve $d=H(\beta ,c)$.

(2)

According to Theorems 2 and 4, as d continues to decrease from $F\left(x_0\right)$ ($d<F\left(x_0\right)$ but near $F\left(x_0\right)$), two interior equilibria $E_1^{*}$ and $E_2^{*}$ appear, where $E_1^{*}$ is a saddle and $E_2^{*}$ is a sink when $c<f_2\left(\beta \right)$ (i.e., $(\beta ,c)\in {\Lambda }_{2a}\cup {\Lambda }_{2b}$), whereas it is a source when $c\ge f_2\left(\beta \right)$ (i.e., $(\beta ,c)\in {\Lambda }_{2c}$). When $d>c$, $E_1$ is a stable node.

(3)

When $c\le f_1\left(\beta \right)(f_1\left(\beta \right)\approx 0.6404)$, i.e., $(\beta ,c)\in {\Lambda }_{2a}$, and d continues to decrease to $d=c$, the stability of $E_1$ switches from a stable node to a half-stable equilibrium (a saddle node), $E_1^{*}$ disappears, and System (3) has the unique interior equilibrium $E_2^{*}$. When $d<c$, $E_1$ becomes a saddle and $E_2^{*}$ remains asymptotically stable.

(4)

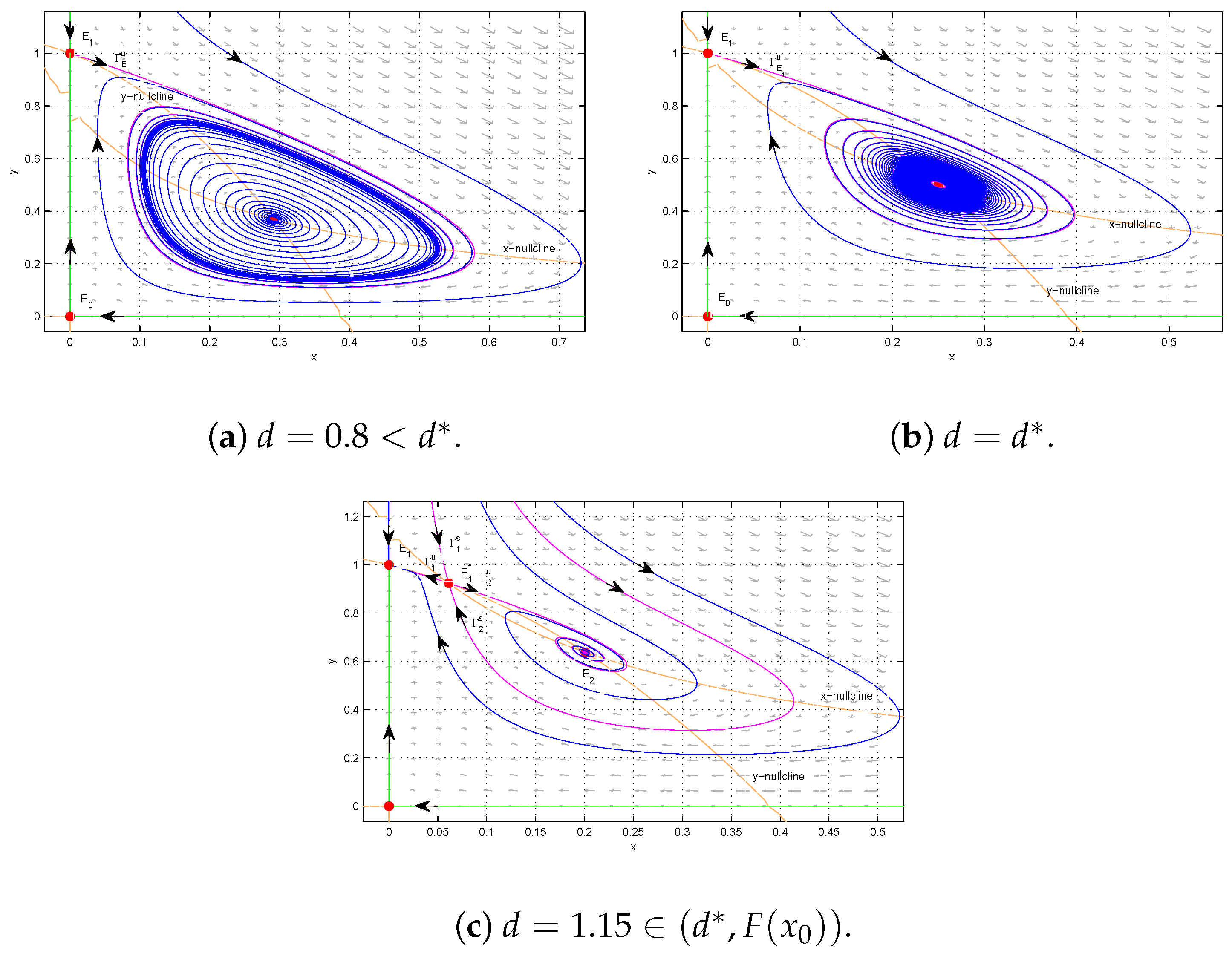
When $f_1\left(\beta \right)<c<h\left(\beta \right)$ (here, $h\left(\beta \right)=1$), i.e., $(\beta ,c)\in {\Lambda }_{2b-1}$, and d continues to decrease to $d=c$, similar to the case $(\beta ,c)\in {\Lambda }_{2a}$, the stability of $E_1$ switches from a stable node to a saddle node, $E_1^{*}$ disappears, and System (3) has the unique interior equilibrium $E_2^{*}$. When d decreases from $d=c$ and passes the Hopf bifurcation curve $d=H(\beta ,c)(\beta =4$), $E_1$ becomes a saddle and $E_2^{*}$ goes from a sink to a source.

(5)

When $c=h\left(\beta \right)=1$, i.e., $(\beta ,c)=(4,1)\in {\Lambda }_{2b-2}$, and d decreases to $d=c=1$, $E_1$ becomes a saddle node, $E_1^{*}$ disappears, and System (3) has the unique interior equilibrium $E_2^{*}$. The Hopf bifurcation curve $d=H(\beta ,c)$ intersects the line $d=c$ when $c=h\left(\beta \right)=1$. Therefore, when $(\beta ,c)\in {\Lambda }_{2b-2}$ and $d=c$, the Hopf bifurcation and saddle-node bifurcation occur simultaneously. After that, as d continues to decrease from $d=c$, $E_1$ becomes a saddle and $E_2^{*}$ becomes a source.

(6)

When $h\left(\beta \right)<c<f_2\left(\beta \right)$, i.e., $(\beta ,c)\in {\Lambda }_{2b-3}$, and d decreases from $d=F\left(x_0\right)$ and passes the Hopf bifurcation curve $d=H(\beta ,c)$, $E_2^{*}$ goes from a sink to a source. As d continues to decrease and passes the line $d=c$, $E_1$ goes from a stable node and a saddle node to a saddle, while $E_2^{*}$ remains a source.

(7)

When $c\ge f_2\left(\beta \right)$, i.e., $(\beta ,c)\in {\Lambda }_{2c}$, and d decrease from $d=F\left(x_0\right)$, $E_2^{*}$ is always a source. If d continues to decrease and passes the line $d=c$, $E_1$ goes from a stable node, a saddle node to a saddle.

5. Complete Description of the Dynamic Behaviors

In this section, we consider the global features of System (3) through theoretical analysis and numerical simulations. First, we show the following result, which indicates that when the death rate d of the predator is large, the predator species becomes extinct while the prey species survives.

Theorem 7.

$E_1(0,1)$ is globally asymptotically stable if either $(\beta ,c)\in {\Lambda }_1$ and $d\ge c$, or $(\beta ,c)\in {\Lambda }_2$ and $d>F\left(x_0\right)$ (see Figure 6).

Figure 6. Phase portraits of System (3) when (a) $(\beta ,c)=(0.6,1)\in {\Lambda }_1$ and $d=1.5>c$, and (b) $(\beta ,c)=(4,1)\in {\Lambda }_2$ and $d=1.3>F\left(x_0\right)\approx 1.2$.

Proof. 

According to Theorem 2, when either $(\beta ,c)\in {\Lambda }_1$ (i.e., $\beta \le 1$) and $d\ge c$, or $(\beta ,c)\in {\Lambda }_2$ (i.e., $\beta >1$) and $d>F\left(x_0\right)$, System (3) has no positive equilibrium and only has two boundary equilibria $E_1(0,1)$ and $E_0(0,0)$, where $E_0(0,0)$ is a saddle. According to Theorem 3, when either $d>c$ and $\beta \le 1$ or $d=c$ and $\beta =1$, $E_1(0,1)$ is a stable node so $E_1(0,1)$ is globally asymptotically stable. When $d=c$ and $\beta <1$, $E_1$ is an attracting saddle node and has its parabolic sector in the first quadrant so it is globally attracting. If $d>F\left(x_0\right)$ and $\beta >1$, then, noticing that $F\left(x_0\right)>c$, we know from Theorem 3 that $E_1(0,1)$ is a stable node and hence it is globally asymptotically stable. □

5.1. Global Dynamics for $(\beta ,c)\in {\Lambda }_1$

In this subsection, we consider the global dynamics of the case $(\beta ,c)\in {\Lambda }_1={\Lambda }_{1a}\cup {\Lambda }_{1b}$. In this case, System (3) has the positive equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ only for $d<c$, as indicated by Theorem 2. According to Theorems 3 and 5, when $(\beta ,c)\in {\Lambda }_{1a}$, $E_2^{*}$ is a sink; when $(\beta ,c)\in {\Lambda }_{1b}$, there exists a $d^{*}:d^{*}<c$ such that $E_2^{*}$ is a source for $d\in (0,d^{*})$, a sink for $d\in (d^{*},c)$, and a Hopf bifurcation occurs at $E_2^{*}$ for $d=d^{*}$, where $d^{*}=H(\beta ,c)$ and $H(\beta ,c)$ is given by (21).

Theorem 8.

If $(\beta ,c)\in {\Lambda }_{1a}$ and $d<c$, then $E_2^{*}(x_2^{*},y_2^{*})$ is globally asymptotically stable (see Figure 7).

Figure 7. The global stability of $E_2^{*}$ when $(\beta ,c)\in {\Lambda }_{1a}$ and $d<c$. Here, $\beta =0.6,c=1<f_1\left(\beta \right)\approx 2.3699$ and $d=0.6$.

Proof. 

When $\lambda \in {\Lambda }_{1a}$ and $d<c$, both $E_0(0,0)$ and $E_1(0,1)$ are saddles according to Theorem 3, and $E_2^{*}(x_2^{*},y_2^{*})$ is the unique interior equilibrium and is locally asymptotically stable, as indicated by Theorem 4. The stable and unstable manifolds of $E_0$ are along the x-axis and y-axis, respectively. The stable manifold of $E_1$ is along the y-axis and its unstable manifold enters the interior of ${\mathbb{R}}_{+}^2$. If System (3) has no limit cycle, according to the Poincaré-Bendixson theorem [36], we can conclude that $E_2^{*}(x_2^{*},y_2^{*})$ is globally asymptotically stable. On the contrary, we assume that System (3) has a periodic orbit $\left(x\right(t),y(t\left)\right)$ with the period T. Then, by integrating the equations of (3) on $[0,T]$, we have

$$\begin{array}{c}\hfill {\int }_0^T((1+\beta x)y-d)dt=0,{\int }_0^T(1-y-(1+\beta x)x)dt=0.\end{array}$$

(29)

Denote the right-hand sides of (3) by $P_1(x,y)$ and $P_2(x,y)$, respectively. Using (29), we obtain the integral of the divergence of (3):

$$\begin{array}{c}\hfill \begin{array}{c}{\int }_0^T\left(\frac{\partial P_1}{\partial x}+\frac{\partial P_2}{\partial y}\right)dt={\int }_0^T(d-(c+1)y\left(t\right))dt.\hfill \end{array}\end{array}$$

(30)

Since $E_2^{*}(x_2^{*},y_2^{*})$ is locally asymptotically stable, we know that ${\omega }_1=d-(c+1)y_2^{*}<0$ (see (15)), that is, $y_2^{*}>\frac{d}{c+1}$. Let $M_1(0,\frac{d}{c+1})$. The line $y=\frac{d}{c+1}$ must intersect the y-nullcline $y={\varphi }_2\left(x\right)$ at some point $M_2$ below $y={\varphi }_1\left(x\right)$. We consider the negative half-trajectory ${\gamma }^{-}\left(M_2\right)$ passing the point $M_2$.

If ${\gamma }^{-}\left(M_2\right)$ intersects the line $y=1$ at some point $M_3$ above the y-nullcline $y={\varphi }_2\left(x\right)$, we can construct a region $\mathcal{R}$ with the vertices $M_1,M_2,M_3$, and $E_1=(0,1)$ as follows: between $M_2$ and $M_3$, the boundary of $\mathcal{R}$ is the orbit ${\gamma }^{-}\left(M_2\right)$, and all other parts of the boundary of $\mathcal{R}$ are the line segments connecting $M_3\to E_1\to M_1\to M_2$. It is easy to see that $\mathcal{R}$ is positively invariant. Since $E_2^{*}(x_2^{*},y_2^{*})$ is the unique equilibrium point in the first quadrant, any periodic orbit, if it exists, must encircle it and lie wholly in the region $\mathcal{R}$. Assume that System (3) has a T-periodic orbit $\left(x\right(t),y(t\left)\right)$. Then, $y\left(t\right)>\frac{d}{c+1}$ and ${\int }_0^T\left(\frac{\partial P_1}{\partial x}+\frac{\partial P_2}{\partial y}\right)dt<0$. It follows that the periodic orbit $\left(x\right(t),y(t\left)\right)$ is asymptotically stable. However, it is impossible since $E_2^{*}$ is locally asymptotically stable.

If ${\gamma }^{-}\left(M_2\right)$ does not meet the line $y=1$, by examining the direction of the vector field in System (3), it enters the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y<{\varphi }_2\left(x\right)\}$. After that, if ${\gamma }^{-}\left(M_2\right)$ always stays above the line $y=\frac{d}{c+1}$, its $\alpha$-limit set must be a periodic orbit. In (30), the periodic orbit is stable. But it is also impossible since $E_2^{*}$ is locally asymptotically stable. So, ${\gamma }^{-}\left(M_2\right)$ intersects the line $y=\frac{d}{c+1}$ at some point $M_3$. Thus, we can construct the region $\mathcal{R}$ with the vertices $M_2$ and $M_3$ as follows: the boundaries of $\mathcal{R}$ are composed of the orbit ${\gamma }^{-}\left(M_2\right)$ above the line $y=\frac{d}{c+1}$ and the line segment $y=\frac{d}{c+1}$ between $M_3$ and $M_2$. It is easy to see that $\mathcal{R}$ is positively invariant. Similar to the above arguments, System (3) has no periodic orbit. □

Remark 2.

For the case $(\beta ,c)\in {\Lambda }_{1a}$, according to Theorems 7 and 8, the global features of System (3) are described as follows: when the degree of cooperative hunting of the predator species x and the predator conversion c are both low such that $\beta \le 1$ and $c\le f_1\left(\beta \right)$, the high mortality of the predator population ($d\ge c$) drives the predator to extinction (see Figure 6a). On the contrary, if the mortality of the predator population is small such that $d<c$, two species coexist (see Figure 7).

Theorem 9.

If $(\beta ,c)\in {\Lambda }_{1b}$, then we can make the following statements:

1 

If $d\in (0,d^{*})$, then (3) has a stable limit cycle (see Figure 8a).

Figure 8. The dynamics of System (3) as $d\in (0,c)$ in the case $(\beta ,c)\in {\Lambda }_{1b}$. Here, $\beta =0.6,c=4>f_1\left(\beta \right)\approx 2.3699$. The Hopf bifurcation value $d^{*}=H(\beta ,c)\approx 2.39583333$. In (a), $d\in (0,d^{*})$, $E_2^{*}$ is a source and surrounded by a stable limit cycle. In (b), $d=d^{*}$ and a backward and supercritical Hopf bifurcation occurs. In (c), $d\in (d^{*},c)$ and $E_2^{*}$ is globally asymptotically stable.

2 

If $d\in (d^{*},c)$, then $E_2^{*}(x_2^{*},y_2^{*})$ is globally asymptotically stable (see Figure 8c).

Proof. 

When $d\in (d^{*},c)$, similar to the proof of Theorem 8, one can prove that $E_2^{*}(x_2^{*},y_2^{*})$ is globally asymptotically stable.

Now, let $d\in (0,d^{*})$. According to Theorem 5, $E_2^{*}$ is a source. Let $M_1$ be the intersection point of the lines $y=1$ and $x=x_2^{*}$, i.e., $M_1=(x_2^{*},1)$. We consider the positive half-trajectory ${\gamma }^{+}\left(M_1\right)$ passing the point $M_1$. By examining the direction of the vector field in System (3), ${\gamma }^{+}\left(M_1\right)$ must intersect the nullcline $y={\varphi }_2\left(x\right)$ at some point $M_2(x_{M_2},y_{M_2})$ below $y={\varphi }_1\left(x\right)$. Denote $M_3=(x_{M_2},0)$. Then, we construct a region $\mathcal{R}$ with the vertices $M_1,M_2,M_3$, and $E_1$ as follows: between $M_1$ and $M_2$, the boundary of $\mathcal{R}$ is the orbit ${\gamma }^{+}\left(M_1\right)$, and all other parts of the boundary of $\mathcal{R}$ are the line segments connecting $M_2\to M_3\to E_1\to M_1$. It is easy to see that $\mathcal{R}$ is positively invariant. Thus, from the Poincaré-Bendixson theorem [36], System (3) has a stable limit cycle since $E_2^{*}$ is unstable. □

Remark 3.

For the case $(\beta ,c)\in {\Lambda }_{1b}$, Theorems 7 and 9 indicate that although the conversion efficiency c is high such that $c>f_1\left(\beta \right)$, when the degree of cooperative hunting is low ($\beta \le 1$), the high mortality of the predator population ($d\ge c$) still drives the predator to extinction and the prey to survival (see Figure 6a). On the contrary, if the mortality of the predator is small ($d<c$), both species coexist. However, unlike the case $(\beta ,c)\in {\Lambda }_{1a}$, the coexistence of the two species in the case $(\beta ,c)\in {\Lambda }_{1b}$ takes two different forms: when $d\in (0,d^{*})$, the coexistence exhibits an oscillatory mode (there is a stable limit cycle; see Figure 8a); when $d\in (d^{*},c)$, the coexistence exhibits a steady mode ($E_2^{*}$ is globally asymptotically stable; see Figure 8c).

5.2. Global Dynamics of the Case $(\beta ,c)\in {\Lambda }_2$

In this subsection, we consider the global dynamics for the case $(\beta ,c)\in {\Lambda }_2$, i.e., $\beta >1$ and $f_1\left(\beta \right)<c<f_2\left(\beta \right)$. When $d\le c$, System (3) has the unique positive equilibrium $E_2^{*}(x_2^{*},y_2^{*})$ according to Theorem 2, and according to Theorem 2, $E_1(0,1)$ is a saddle or saddle node with its hyperbolic sectors in the first quadrant. When $c<d<F\left(x_0\right)$, there are two positive equilibria $E_1^{*}(x_1^{*},y_1^{*})$ and $E_2^{*}(x_2^{*},y_2^{*})$, where $E_1^{*}$ is always a saddle and the stability of $E_2^{*}$ is dependent on parameters and $E_1$ becomes a sink.

Lemma 2.

Let $(\beta ,c)\in {\Lambda }_2$ and $c<d<F\left(x_0\right)$.

1 

One branch of the stable manifolds of $E_1^{*}$, denoted by ${\Gamma }_1^s$, enters $E_1^{*}$ from the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y>{\varphi }_1\left(x\right),y>{\varphi }_2\left(x\right)\}$; another one, denoted by ${\Gamma }_2^s$, enters $E_1^{*}$ from the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y<{\varphi }_1\left(x\right),y<{\varphi }_2\left(x\right)\}$.

2 

One branch of the unstable manifolds of $E_1^{*}$, denoted by ${\Gamma }_1^u$, is the heteroclinic orbit connecting $E_1^{*}$ and $E_1(0,1)$ entering the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y<{\varphi }_1\left(x\right),y<{\varphi }_2\left(x\right)\}$ and then approaching $E_1$. Another one, denoted by ${\Gamma }_2^u$, enters the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y>{\varphi }_1\left(x\right),$$y>{\varphi }_2\left(x\right)\}$.

Proof. 

At $E_1^{*}(x_1^{*},y_1^{*})$, the eigenvalues of (13) are ${\kappa }_1=\frac{{\omega }_1-\sqrt{{\omega }_1^2-4{\omega }_2}}{2}<0,{\kappa }_2=\frac{{\omega }_1+\sqrt{{\omega }_1^2-4{\omega }_2}}{2}>0$. The eigenvector corresponding to ${\kappa }_1$ is $\left(-\frac{c(1+\beta x_1^{*})x_1^{*}}{c\beta x_1^{*}{y}_1^{*}-{\kappa }_1},1\right)$. Then, the tangential direction of the stable manifold at $E_1^{*}$ is

$$k_1=-\frac{c\beta x_1^{*}{y}_1^{*}-{\kappa }_1}{c(1+\beta x_1^{*})x_1^{*}}<-\frac{c\beta y_1^{*}}{c(1+\beta x_1^{*})}=-\frac{d\beta }{c{(1+\beta x_1^{*})}^2}={\varphi }_1^{\prime }\left(x_1^{*}\right)<{\varphi }_2^{\prime }\left(x_1^{*}\right)$$

since $y_1^{*}={\varphi }_1\left(x_1^{*}\right)=\frac{d}{c(1+\beta x_1^{*})}$. So, ${\Gamma }_1^s$ enters from the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y>{\varphi }_1\left(x\right),$$y>{\varphi }_2\left(x\right)\}$, and ${\Gamma }_2^s$ approaches $E_1^{*}$ from the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y<{\varphi }_1\left(x\right),y<{\varphi }_2\left(x\right)\}$.

The eigenvector corresponding to ${\kappa }_2$ is $\left(-\frac{y_1^{*}+{\kappa }_2}{(1+2\beta x_1^{*})y_1^{*}},1\right)$. Then, the tangential direction of the unstable manifold at $E_1^{*}$ is

$$k_2=-\frac{(1+2\beta x_1^{*})y_1^{*}}{y_1^{*}+{\kappa }_2}>-(1+2\beta x_1^{*})={\varphi }_2^{\prime }\left(x_1^{*}\right)>{\varphi }_1^{\prime }\left(x_1^{*}\right).$$

So, ${\Gamma }_1^u$ enters the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y<{\varphi }_1\left(x\right),y<{\varphi }_2\left(x\right)\}$, and ${\Gamma }_2^u$ enters the region $\{(x,y)\in {\mathbb{R}}_{+}^2:y>{\varphi }_1\left(x\right),y>{\varphi }_2\left(x\right)\}$. From the direction of the vector field in (3), ${\Gamma }_1^u$ is the heteroclinic orbit connecting $E_1^{*}$ and $E_1(0,1)$. □

Below, we consider the global dynamics for the following scenarios: $(\beta ,c)\in {\Lambda }_{2a}$, $(\beta ,c)\in {\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}\cup {\Lambda }_{2b-3}$, and $(\beta ,c)\in {\Lambda }_{2c}$. When $d\in (c,F\left(x_0\right))$, the dynamics of (3) are complex and are described through numerical simulations.

5.2.1. Scenario $(\beta ,c)\in {\Lambda }_{2a}$

For the scenario $(\beta ,c)\in {\Lambda }_{2a}$, i.e., $c<f_1\left(\beta \right)$ and $\beta >1$, we have the following result.

Theorem 10.

If $(\beta ,c)\in {\Lambda }_{2a}$ and $d\le c$, then $E_2^{*}(x_2^{*},y_2^{*})$ is globally asymptotically stable (see Figure 9a).

Figure 9. The dynamics of System (3) as $d\in (0,F\left(x_0\right))$ in the case $(\beta ,c)\in {\Lambda }_{2a}$. Here, $\beta =4>1,$$c=0.5<f_1\left(\beta \right)\approx 0.6404$, $F\left(x_0\right)\approx 0.6099$. In (a), $d=0.4\in (0,c)$ and $E_2^{*}$ is globally asymptotically stable. In (b), $d=0.58\in (c,F\left(x_0\right))$ and there are two attractors $E_1(0,1)$ and $E_2^{*}$ (bistability).

Proof. 

When $d\le c$, from Theorem 2, we know that System (3) has the unique interior equilibrium $E_2^{*}$, which is locally asymptotically stable according to Theorem 4. According to Theorem 3, $E_0(0,0)$ is a saddle, and $E_1(0,1)$ is also a saddle when $d<c$ and a saddle node when $d=c$ but its two hyperbolic sectors lie in the first quadrant. So, similar to the proof of Theorem 8, $E_2^{*}$ is globally asymptotically stable. □

Remark 4.

For the case $(\beta ,c)\in {\Lambda }_{2a}$, Theorem 10 indicates that when the mortality of the predator is small ($d\le c$), both species coexist (see Figure 9a). When d is large such that $c<d<F\left(x_0\right)$, System (3) has no limit cycle and there are two attractors: $E_1(0,1)$ and $E_2^{*}$ (bistability). The separatrices of the attracting basins of $E_1$ and $E_2^{*}$ are the stable manifolds ${\Gamma }_1^s$ and ${\Gamma }_2^s$ of the saddle $E_1^{*}$ (see Figure 9b). So, when $c<d<F\left(x_0\right)$, the coexistence of the two populations depends on the initial values. As d becomes larger ($d>F\left(x_0\right)$), System (3) only has the attractor $E_1$; the predator becomes extinct and the prey survives (see Theorem 7 and Figure 6b).

5.2.2. Scenario $(\beta ,c)\in {\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$

We consider the global dynamics for the scenario $(\beta ,c)\in {\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$. When $(\beta ,c)\in {\Lambda }_{2b-1}$, i.e., $\beta >1$ and $f_1\left(\beta \right)<c<h\left(\beta \right)$, the Hopf bifurcation occurs at $E_2^{*}$ for $d=d^{*}$, where $d^{*}=H(\beta ,c)$ and $d^{*}<c$ (see Theorem 5). When $(\beta ,c)\in {\Lambda }_{2b-2}$, i.e., $\beta >1$ and $c=h\left(\beta \right)$, the Hopf bifurcation value $d^{*}=c$. According to Theorem 3, $E_2^{*}$ is a source for $d<d^{*}$ and a sink for $d\in (d^{*},F\left(x_0\right))$.

Theorem 11.

Let $(\beta ,c)\in {\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$.

1 

If $(\beta ,c)\in {\Lambda }_{2b-1}$, we can make the following statements:

(i) 

When $d\in (0,d^{*})$, System (3) has a stable limit cycle (see Figure 10a).

Figure 10. The dynamics of System (3) as $d\in (0,F\left(x_0\right))$ in the case $(\beta ,c)\in {\Lambda }_{2b-1}$. Here, $\beta =4>1,$$c=0.8\in (f_1\left(\beta \right),h\left(\beta \right)),f_1\left(\beta \right)\approx 0.6404,h\left(\beta \right)=1$, $F\left(x_0\right)\approx 0.9758$. The Hopf bifurcation value $d^{*}=H(\beta ,c)\approx 0.534375$. In (a), $d=0.45<d^{*}$ and $E_2^{*}$ is a source and surrounded by a stable limit cycle. In (b), $d=d^{*}$ and a backward and supercritical Hopf bifurcation occurs. In (c), $d=0.7\in (d^{*},c)$ and $E_2^{*}$ is globally asymptotically stable. In (d), $d=0.92\in (c,F\left(x_0\right))$ and there are two attractors $E_1(0,1)$ and $E_2^{*}$ (bistability).

(ii) 

When $d\in (d^{*},c]$, $E_2^{*}(x_2^{*},y_2^{*})$ is globally asymptotically stable (see Figure 10c).

2 

If $(\beta ,c)\in {\Lambda }_{2b-2}$ and $d\in (0,c)$, System (3) has a stable limit cycle (see Figure 11a).

Figure 11. The dynamics of System (3) as $d\in (0,F\left(x_0\right))$ in the case $(\beta ,c)\in {\Lambda }_{2b-2}$. Here, $\beta =4>1,$$c=h\left(\beta \right)=1$, $F\left(x_0\right)\approx 1.220$. The Hopf bifurcation value $d^{*}=H(\beta ,c)=h\left(\beta \right)=1$. In (a), $d=0.8<d^{*}$ and $E_2^{*}$ is a source and surrounded by a stable limit cycle. In (b), $d=d^{*}$ and the Hopf bifurcation and saddle-node bifurcation occur simultaneously. In (c), $d=1.15\in (d^{*},F\left(x_0\right))$ and there are two attractors $E_1(0,1)$ and $E_2^{*}$ (bistability).

Remark 5.

For the scenario $(\beta ,c)\in {\Lambda }_{2b-1}$, Theorem 11 indicates that when the mortality of the predator is small ($d\le c$), both species coexist (see Figure 10a–c). The coexistence exhibits two different forms: an oscillatory mode (when $d\in (0,d^{*})$. see Figure 10a) and a steady mode (when $d\in (d^{*},c)$; see Figure 10c). When d is large such that $c<d<F\left(x_0\right)$, through numerical simulations, System (3) has no limit cycle and there are two attractors $E_1(0,1)$ and $E_2^{*}$ (bistability). The separatrices of the attracting basins of $E_1$ and $E_2^{*}$ are the stable manifolds ${\Gamma }_1^s$ and ${\Gamma }_2^s$ of the saddle $E_1^{*}$ (see Figure 10c). So, when $c<d<F\left(x_0\right)$, the coexistence of the two populations depends on the initial values. As d becomes larger ($d>F\left(x_0\right)$), System (3) only has the attractor $E_1$, the predator becomes extinct, and the prey survives (see Theorem 7 and Figure 6b).

For the scenario $(\beta ,c)\in {\Lambda }_{2b-2}$, the Hopf bifurcation curve $d=H(\beta ,c)$ intersects the line $d=c$ (see Figure 5b) so the Hopf bifurcation and the saddle-node bifurcation occur simultaneously at $d^{*}=c$. In this scenario, the coexistence of two species exhibits only an oscillatory mode for $d<c$ (see Figure 11a). When $c<d<F\left(x_0\right)$, (3) has no limit cycle, two attractors $E_1$ and $E_2^{*}$ (bistability) appear, and the coexistence of the two populations depends on the initial values (see Figure 11c).

5.2.3. Scenario $(\beta ,c)\in {\Lambda }_{2b-3}$

We consider the global dynamics for the scenario $(\beta ,c)\in {\Lambda }_{2b-3}$, i.e., $\beta >1$ and $h\left(\beta \right)<c<f_2\left(\beta \right)$. The Hopf bifurcation occurs at $E_2^{*}$ for $d=d^{*}$, where $d^{*}=H(\beta ,c)$ and $d^{*}>c$ (see Theorem 5 and Figure 5). According to Theorem 3, $E_2^{*}$ is a source for $d<d^{*}$ and a sink for $d\in (d^{*},F\left(x_0\right))$.

Theorem 12.

If $(\beta ,c)\in {\Lambda }_{2b-3}$ and $d\in (0,c]$, System (3) has a stable limit cycle (see Figure 12a).

Figure 12. The dynamics of System (3) as $d\in (0,F\left(x_0\right))$ in the case $(\beta ,c)\in {\Lambda }_{2b-3}$. Here, $\beta =4>1,$$c=1.2\in (h\left(\beta \right),f_2\left(\beta \right)),h\left(\beta \right)=1,f_2\left(\beta \right)\approx 1.8685$, $F\left(x_0\right)\approx 1.4638$. The Hopf bifurcation value $d^{*}=H(\beta ,c)\approx 1.35972222>c$. In (a), $d=1<d^{*}$ and $E_2^{*}$ is a source and surrounded by a stable limit cycle. In (b), $d=1.35\in (c,d^{*})$, $E_2^{*}$ still is a source, and there are two attractors (bistability): one is the boundary equilibrium $E_1(0,1)$ and the other is the stable limit cycle surrounding $E_2^{*}$. In (c), $d=d^{*}$ and a backward and supercritical Hopf bifurcation occurs. In (d), $d=1.42\in (d^{*},F\left(x_0\right))$, $E_2^{*}$ becomes a sink and there are two attractors $E_1(0,1)$ and $E_2^{*}$ (bistability).

Remark 6.

For the scenario $(\beta ,c)\in {\Lambda }_{2b-3}$, Theorem 12 and the numerical simulations indicate that when the mortality of the predator is small ($d\le c$), two species coexist in an oscillatory mode (see Figure 12a). When d is large such that $c<d<F\left(x_0\right)$, System (3) has two attractors: one is the boundary equilibrium $E_1(0,1)$ and the other is the stable limit cycle surrounding $E_2^{*}$ or the stable interior equilibrium $E_2^{*}$ (bistability). The separatrices of the attracting basins of these two attractors are the stable manifolds ${\Gamma }_1^s$ and ${\Gamma }_2^s$ of the saddle $E_1^{*}$ (see Figure 12b–d). When $d\in (c,d^{*})$, the interior attractor in the state space ${\mathbb{R}}_{+}^2$ is the stable limit cycle surrounding $E_2^{*}$ (see Figure 12b). When $d\in (d^{*},F\left(x_0\right))$, the limit cycle disappears and the interior attractor in the state space ${\mathbb{R}}_{+}^2$ becomes the interior equilibrium $E_2^{*}$ (see Figure 12d). As d becomes larger ($d>F\left(x_0\right)$), System (3) only has the attractor $E_1$, the predator becomes extinct, and the prey survives (see Theorem 7 and Figure 6b).

5.2.4. Scenario $(\beta ,c)\in {\Lambda }_{2c}$

We consider the global dynamics for the scenario $(\beta ,c)\in {\Lambda }_{2c}$, i.e., $\beta >1$ and $c\ge f_2\left(\beta \right)$. According to Theorem 3, $E_2^{*}$ is always a source for all $d\in (0,F\left(x_0\right))$. Similar to Theorem 12, when $d\in (0,c]$, we have the following result.

Theorem 13.

If $(\beta ,c)\in {\Lambda }_{2c}$ and $d\in (0,c]$, System (3) has a stable limit cycle (see Figure 13a).

Figure 13. The dynamics of System (3) as $d\in (0,F\left(x_0\right))$ in the case $(\beta ,c)\in {\Lambda }_{2c}$. Here, $\beta =30>1,$$c=0.4>f_2\left(\beta \right),f_2\left(\beta \right)\approx 0.3979$, $F\left(x_0\right)\approx 0.9917$. When $d\in (0,F\left(x_0\right))$, $E_2^{*}$ is always a source. There exists a $d^{♯}\approx 0.53074832\in (c,F\left(x_0\right))$ such that System (3) has a homoclinic cycle of the saddle $E_1^{*}$. In (a), $d=0.39\in (0,c)$ and $E_2^{*}$ is surrounded by a stable limit cycle. In (b), $d=0.48\in (c,d^{♯})$ and there are two attractors (bistability): one is the boundary equilibrium $E_1(0,1)$ and the other is the stable limit cycle surrounding $E_2^{*}$. In (c), $d=d^{♯}$ and a homoclinic cycle appears. In (d), $d=0.8\in (d^{♯},F\left(x_0\right))$, the homoclinic loop is broken, and all trajectories (except the stable manifolds of $E_1^{*}$) converge to the boundary equilibrium $E_1$.

When $d\in (c,F\left(x_0\right))$, the dynamics of (3) are very complex. Through the numerical simulation, there exists $d^{♯}\in (c,F\left(x_0\right))$ such that

(1)

When $d\in (c,d^{♯})$, (3) has a stable limit cycle surrounding $E_2^{*}$, which is the $\omega$-limit set of the unstable manifold ${\Gamma }_2^u$ of $E_1^{*}$ (see Figure 13b).

(2)

When $d=d^{♯}$, ${\Gamma }_2^u={\Gamma }_2^s$, that is, System (3) has a homoclinic loop of the saddle $E_1^{*}$ (see Figure 13c). Outside the homoclinic loop, trajectories converge to the boundary equilibrium $E_1$, whereas inside the homoclinic loop, trajectories converge toward it (see Figure 13c);

(3)

When $d\in (d^{♯},F\left(x_0\right))$, the homoclinic loop is broken and all trajectories (except the stable manifolds of $E_1^{*}$) converge to the boundary equilibrium $E_1$ (see Figure 13d).

Remark 7.

For the scenario $(\beta ,c)\in {\Lambda }_{2c}$, Theorem 13 and the numerical simulation (see Figure 13) imply the following biological implications:

(1) 

When the mortality of the predator is small ($d\le c$), two species coexist (see Figure 13a) in an oscillatory mode.

(2) 

When d is large such that $c<d<d^{♯}$, System (3) has two attractors: one is the boundary equilibrium $E_1(0,1)$ and the other is the stable limit cycle surrounding $E_2^{*}$. The separatrices of the attracting basins of these two attractors are the stable manifolds ${\Gamma }_1^s$ and ${\Gamma }_2^s$ of the saddle $E_1^{*}$ (see Figure 12b). As d increases from c to $d^{♯}$, the attracting basin of the limit cycle dwindles and eventually shrinks into a homoclinic loop of $E_1^{*}$ (see Figure 12c). So, when $c<d\le d^{♯}$, the coexistence of the prey and predator depends on the initial values.

(3) 

As d becomes larger ($d>d^{♯}$), System (3) only has one boundary attractor $E_1(0,1)$ and the coexistence of the prey and predator becomes impossible (see Figure 4b,c, Figure 6b, and Figure 12d).

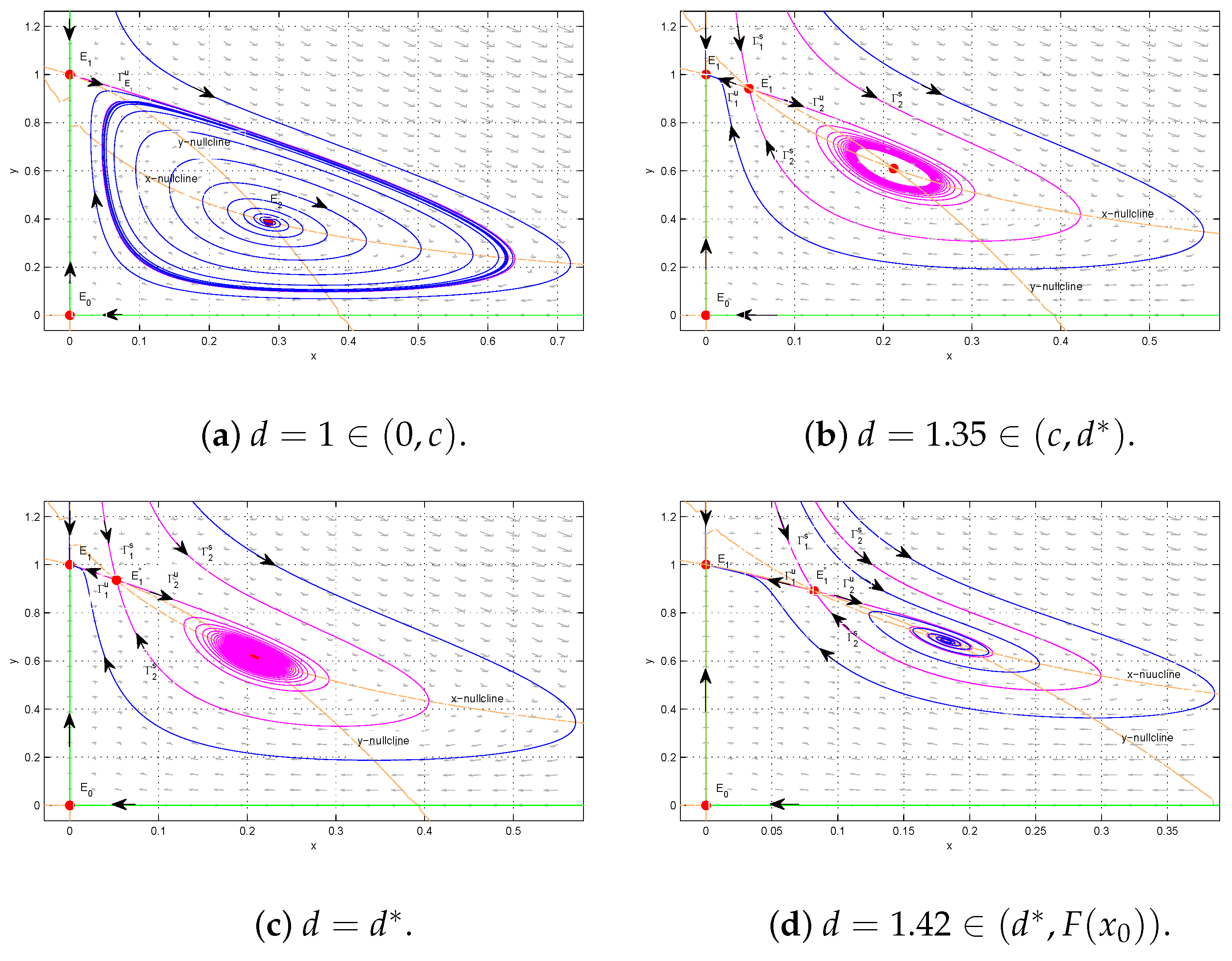
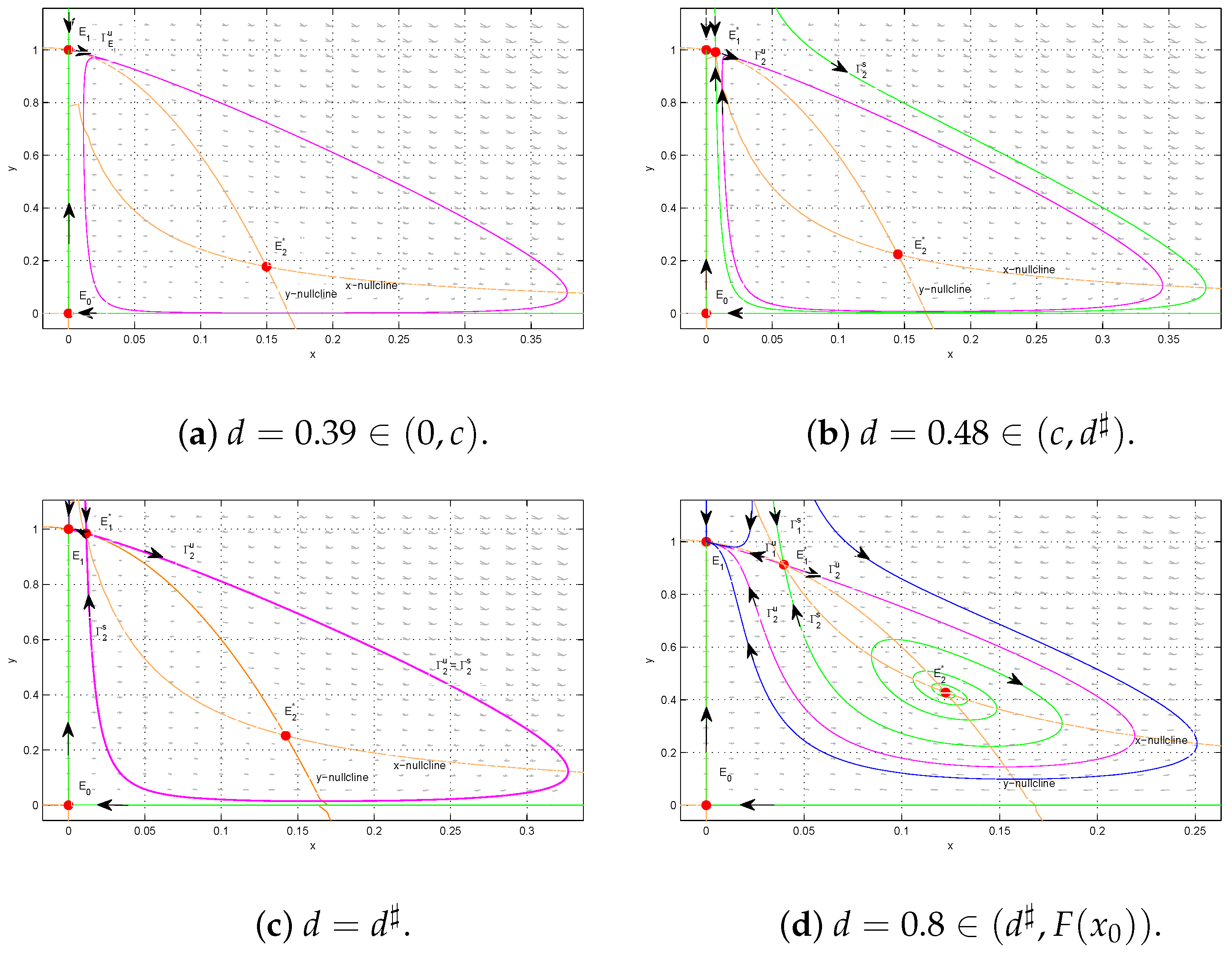
6. Discussion

In this paper, the dynamics of the predator–prey model (3) with cooperative hunting are considered. The parameter space $\Lambda$ of $(\beta ,c)$ involved in (3) is divided into different regions: $\Lambda ={\Lambda }_1\cup {\Lambda }_2$, ${\Lambda }_1={\Lambda }_{1a}\cup {\Lambda }_{1b}$, ${\Lambda }_2={\Lambda }_{2a}\cup {\Lambda }_{2b}\cup {\Lambda }_{2c}$, ${\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}\cup {\Lambda }_{2b-3}$ (see Figure 3). The division is very important for the dynamic analysis of System (3). In each region, as d changes, the dynamic behaviors of (3) are presented through theoretical analysis and numerical simulations, including the number of equilibria (see Theorem 2 and Figure 2); the stability of equilibria (see Theorems 3 and 4); the bifurcation phenomena, including the Hopf bifurcation (see Theorem 5), saddle-node bifurcation and Bogdanov–Takens bifurcation (see Theorem 6 and Figure 4), and homoclinic bifurcation (see Figure 13); and the existence and non-existence of limit cycles (see Theorems 9–13 and Figure 8 and Figure 10, Figure 11, Figure 12 and Figure 13). Based on the theoretical analysis and numerical simulations, a complete description of the dynamic behaviors of (3) for d, along with the corresponding biological explanations, is presented for each region.

If the predator is without cooperative hunting, then (3) becomes the following well-known Lotka–Volterra model:

$$\frac{\mathrm{d}x}{\mathrm{d}t}=cxy-dx,\frac{\mathrm{d}y}{\mathrm{d}t}=y(1-y)-xy.$$

(31)

The dynamics of System (31) are quite clear. System (31) has two boundary equilibria: $E_0=(0,0)$, which is always a saddle, and $E_1=(0,1)$, which is locally asymptotically stable if $d\ge c$ and a saddle if $d<c$. If $d<c$, there exists a unique interior equilibrium $E^{*}=(1-\frac{d}{c},\frac{d}{c})$, which is globally asymptotically stable. If $d\ge c$, $E_1$ is globally asymptotically stable, which implies that the high death rate of the predator leads it to become extinct. Comparing Model (3) to the Lotka–Volterra model (31), we find that System (3) has exactly the same dynamics as the Lotka–Volterra model (31) only when $(\beta ,c)\in {\Lambda }_{1a}$ (see Theorem 8). When $(\beta ,c)\in {\Lambda }_{2a}\cup {\Lambda }_2$, due to the nonlinearity of the cooperative hunting term $-\beta x^{2}y$, Model (3) exhibits more complex dynamic behavior than (31), including rich bifurcation phenomena such as the Hopf bifurcation (see Theorem 5), saddle-node bifurcation and Bogdanov–Takens bifurcation (see Theorems 6), and homoclinic bifurcation (see Figure 13). Moreover, we can make the following statements, which answer the questions posed in Section 1.

1

If the mortality of the predator is small such that $d<c$, then both species coexist regardless of the intensity of hunting cooperation. The coexistence of the two species exhibits either a steady mode or an oscillatory mode. If the Hopf bifurcation occurs, it only changes the coexistence mode. Therefore, compared to the Lotka–Volterra model (31), when $d<c$, the hunting cooperation term $-\beta x^{2}y$ does not affect the coexistence of populations but it affects the pattern of coexistence.

2

When $(\beta ,c)\in {\Lambda }_{2a}\cup {\Lambda }_{2b}$ and $c<d<F\left(x_0\right)$, or $(\beta ,c)\in {\Lambda }_{2c}$ and $c<d<d^{♯}$, Model (3) has two attractors (bistability): one is the boundary equilibrium $E_1(0,1)$ and the other is the interior equilibrium $E_2^{*}$ or the stable limit cycle surrounding $E_2^{*}$. The separatrices of the attracting basins of these two attractors are the stable manifolds of the interior equilibrium $E_1^{*}$. This indicates that two species may coexist but this depends on the initial values. For the Lotka–Volterra model (31), when $d>c$, the predator becomes extinct regardless of the initial value. Therefore, hunting cooperation is beneficial to the coexistence of the prey and predator.

Conclusively, in comparison to the Lotka–Volterra model (without cooperative hunting), hunting cooperation brings benefits to the predator population and plays an important role in ecosystem stability and persistence.

Generally, the extinction of a predator is induced by its high mortality or due to the extinction of its prey. Du et al. [20] studied a predator–prey model with cooperative hunting in the predator and group defense in the prey. It was presented that too strong cooperation caused the extinction of the prey and, consequently, the extinction of the predator. In contrast, our results indicate that strong cooperation has a positive effect on the predator, and the extinction of the predator is induced by the high mortality of the species. However, if the cooperation of the predator is strong, the size of the predator in the coexistence state will be small. This also implies that hunting cooperation can enable a predator of a small size to survive.