scCGImpute: An Imputation Method for Single-Cell RNA Sequencing Data Based on Similarities between Cells and Relationships among Genes
Abstract
1. Introduction
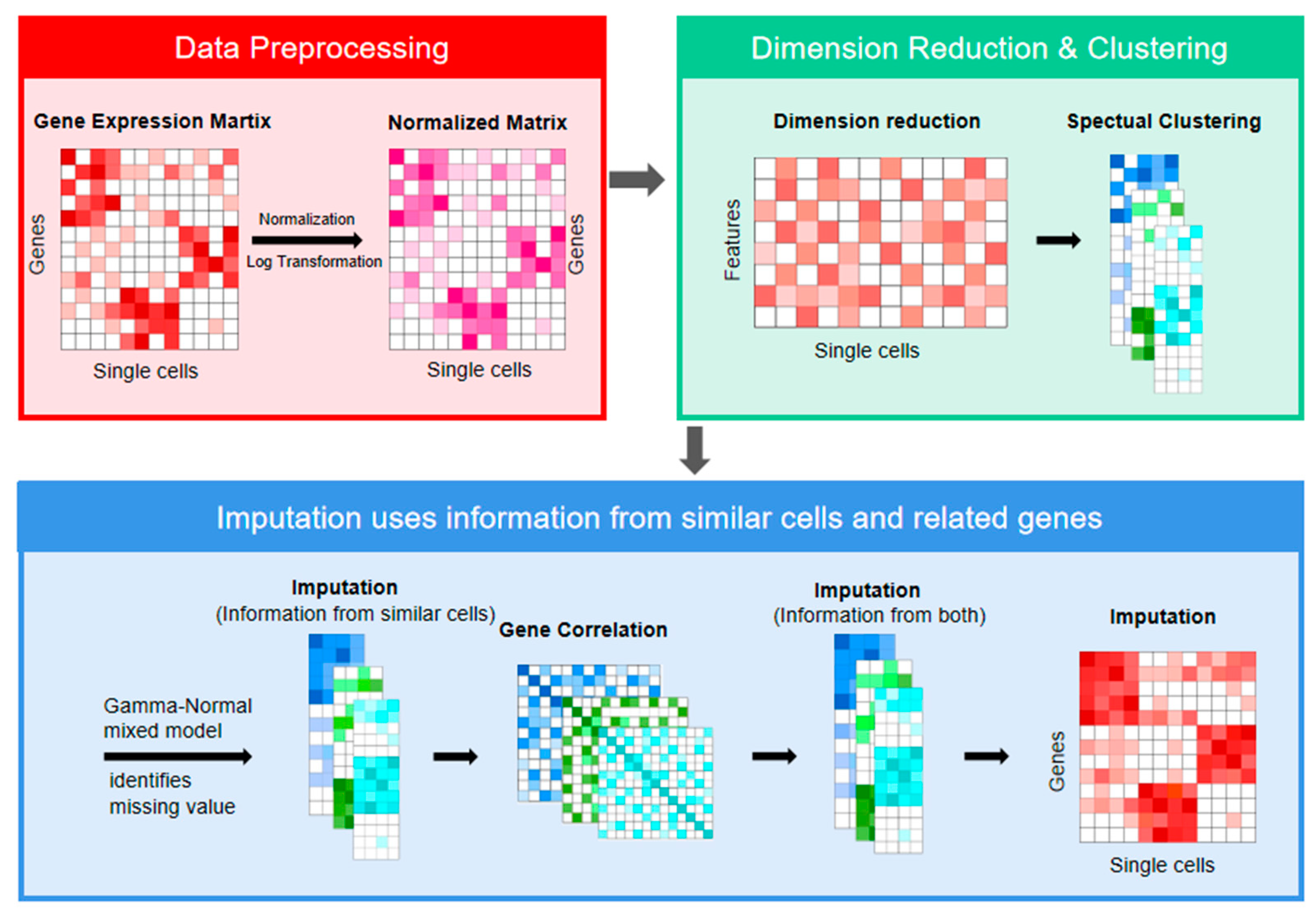
2. Materials and Methods
2.1. Data Preprocessing
2.2. Dimension Reduction and Clustering
2.3. Imputation Strategy
- For each gene i, the data in set A were averaged, and its average value was used as the imputation of gene i in low confidence set B. We denoted the imputation matrix as Y. The information across cells was already incorporated into matrix Y at this stage, but this is not the final imputation. And then, correlations between genes are calculated by the Pearson correlation coefficient for each cell subpopulation. The genes with an absolute value of the correlation coefficient greater than 0.5 were selected for the next step of the calculation.
- For each gene i, as shown in Figure 2, based on the matrix Y and the high correlation genes we filter out, random forest regression is used for regression training on data with high confidence cells. Then, predictions are made for data with low confidence cells. Thus, it preserves the heterogeneity across cells and does not impute all zeros. At the beginning of the regression with random forest, the low confidence set B is imputed with information from similar cells. When the gene i which has been predicted by random forest regression, is used to calculate other genes, the gene expression level of gene i corresponds to the value predicted by random forest; that is, after calculating gene i, the set B of gene i is retained for the subsequent random forest regression of the next gene. The random forest regression model establishes several uncorrelated decision trees by randomly extracting samples and features. Each decision tree can obtain a prediction result based on the extracted samples and features. The regression model of the whole forest can be obtained by taking the average value of all the results. Using random forests, we can learn nonlinear relationships between genes.
2.4. Evaluation Strategies of Clustering
2.5. Simulate scRNA-Seq Data
2.6. Real Data Used to Evaluate Clustering Result
3. Results
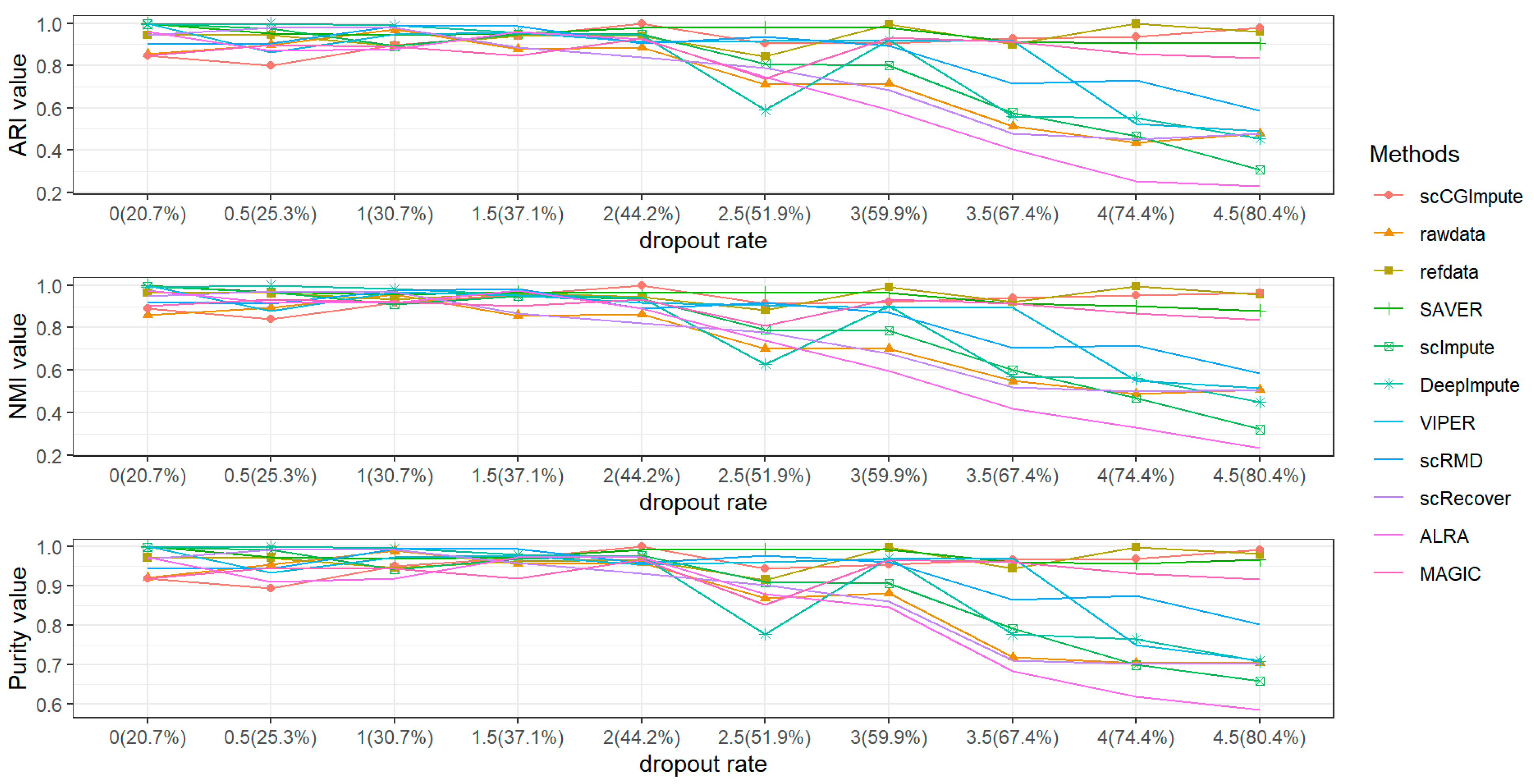
3.1. Simulation Analysis
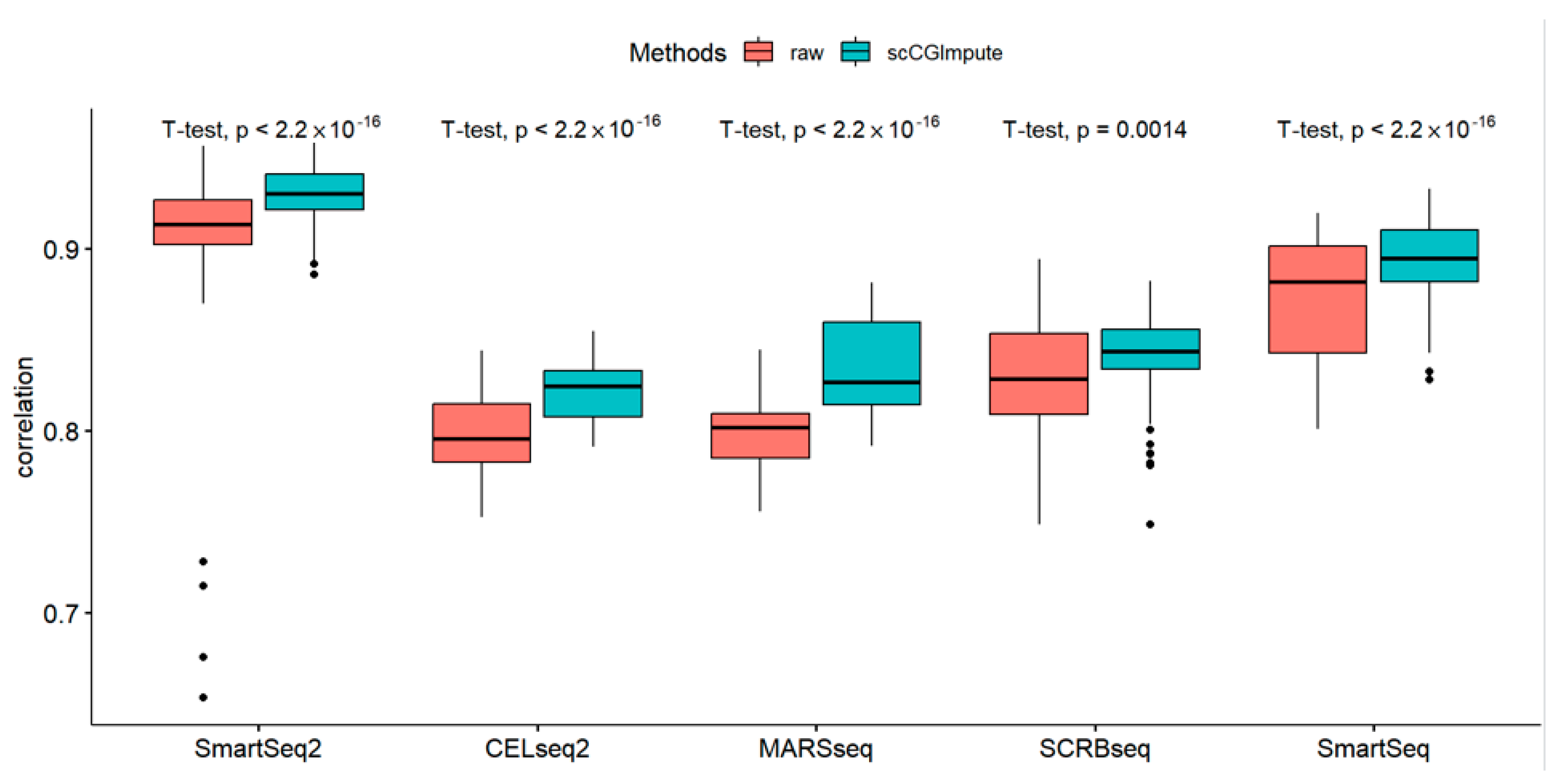
3.2. scCGImpute Recovers Gene Expression in Real Data
3.3. scCGImpute Enhances the Ability to Identify Cell Types in Real Data
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jovic, D.; Liang, X.; Zeng, H.; Lin, L.; Xu, F.; Luo, Y. Single-cell RNA sequencing technologies and applications: A brief overview. Clin. Transl. Med. 2022, 12, e694. [Google Scholar] [CrossRef] [PubMed]
- Tang, F.; Barbacioru, C.; Wang, Y.; Nordman, E.; Lee, C.; Xu, N.; Surani, M.A. mRNA-Seq whole-transcriptome analysis of a single cell. Nat. Methods 2009, 6, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Grün, D.; Lyubimova, A.; Kester, L.; Wiebrands, K.; Basak, O.; Sasaki, N.; Clevers, H.; van Oudenaarden, A. Single-cell messenger RNA sequencing reveals rare intestinal cell types. Nature 2015, 525, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Zeisel, A.; Muñoz-Manchado, A.B.; Codeluppi, S.; Lönnerberg, P.; La Manno, G.; Juréus, A.; Marques, S.; Munguba, H.; He, L.; Betsholtz, C.; et al. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 2015, 347, 1138–1142. [Google Scholar] [CrossRef]
- Keren-Shaul, H.; Spinrad, A.; Weiner, A.; Matcovitch-Natan, O.; Dvir-Szternfeld, R.; Ulland, T.K.; David, E.; Baruch, K.; Lara-Astaiso, D.; Toth, B.; et al. A Unique Microglia Type Associated with Restricting Development of Alzheimer’s Disease. Cell 2017, 169, 1276–1290.e17. [Google Scholar] [CrossRef]
- Kim, K.T.; Lee, H.W.; Lee, H.O.; Kim, S.C.; Seo, Y.J.; Chung, W.; Park, W.Y. Single-cell mRNA sequencing identifies subclonal heterogeneity in anti-cancer drug responses of lung adenocarcinoma cells. Genome Biol. 2015, 16, 127. [Google Scholar] [CrossRef]
- Finak, G.; McDavid, A.; Yajima, M.; Deng, J.; Gersuk, V.; Shalek, A.K.; Gottardo, R. MAST: A flexible statistical framework for assessing transcriptional changes and charac-terizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 2015, 16, 278. [Google Scholar] [CrossRef]
- Satija, R.; A Farrell, J.; Gennert, D.; Schier, A.F.; Regev, A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 2015, 33, 495–502. [Google Scholar] [CrossRef]
- Qian, J.; Liao, J.; Liu, Z.; Chi, Y.; Fang, Y.; Zheng, Y.; Shao, X.; Liu, B.; Cui, Y.; Guo, W.; et al. Reconstruction of the cell pseudo-space from single-cell RNA sequencing data with scSpace. Nat. Commun. 2023, 14, 2484. [Google Scholar] [CrossRef]
- Moignard, V.; Woodhouse, S.; Haghverdi, L.; Lilly, A.J.; Tanaka, Y.; Wilkinson, A.C.; Buettner, F.; Macaulay, I.C.; Jawaid, W.; Diamanti, E.; et al. Decoding the regulatory network of early blood development from single-cell gene expression measurements. Nat. Biotechnol. 2015, 33, 269–276. [Google Scholar] [CrossRef]
- Herring, C.A.; Banerjee, A.; McKinley, E.T.; Simmons, A.J.; Ping, J.; Roland, J.T.; Franklin, J.L.; Liu, Q.; Gerdes, M.J.; Coffey, R.J.; et al. Unsupervised Trajectory Analysis of Single-Cell RNA-Seq and Imaging Data Reveals Alternative Tuft Cell Origins in the Gut. Cell Syst. 2018, 6, 37–51.e9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, S. Comparison of computational methods for imputing single-cell RNA-sequencing data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 17, 376–389. [Google Scholar] [CrossRef] [PubMed]
- Kharchenko, P.V.; Silberstein, L.; Scadden, D.T. Bayesian approach to single-cell differential expression analysis. Nat. Methods 2014, 11, 740–742. [Google Scholar] [CrossRef] [PubMed]
- Eraslan, G.; Simon, L.M.; Mircea, M.; Mueller, N.S.; Theis, F.J. Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun. 2019, 10, 390. [Google Scholar] [CrossRef] [PubMed]
- Jiang, R.; Sun, T.; Song, D.; Li, J.J. Statistics or biology: The zero-inflation controversy about scRNA-seq data. Genome Biol. 2022, 23, 31. [Google Scholar] [CrossRef]
- Lähnemann, D.; Köster, J.; Szczurek, E.; McCarthy, D.J.; Hicks, S.C.; Robinson, M.D.; Vallejos, C.A.; Campbell, K.R.; Beerenwinkel, N.; Mahfouz, A.; et al. Eleven grand challenges in single-cell data science. Genome Biol. 2020, 21, 31. [Google Scholar] [CrossRef]
- Huang, M.; Wang, J.; Torre, E.; Dueck, H.; Shaffer, S.; Bonasio, R.; Murray, J.I.; Raj, A.; Li, M.; Zhang, N.R. SAVER: Gene expression recovery for single-cell RNA sequencing. Nat. Methods 2018, 15, 539–542. [Google Scholar] [CrossRef]
- Lin, P.; Troup, M.; Ho, J.W.K. CIDR: Ultrafast and accurate clustering through imputation for single-cell RNA-seq data. Genome Biol. 2017, 18, 59. [Google Scholar] [CrossRef]
- Li, W.V.; Li, J.J. An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat. Commun. 2018, 9, 997. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, X. VIPER: Variability-preserving imputation for accurate gene expression recovery in single-cell RNA se-quencing studies. Genome Biol. 2018, 19, 196. [Google Scholar] [CrossRef]
- Miao, Z.; Li, J.; Zhang, X. scRecover: Discriminating true and false zeros in single-cell RNA-seq data for imputation. BioRxiv 2019, 665323. [Google Scholar] [CrossRef]
- Van Dijk, D.; Sharma, R.; Nainys, J.; Yim, K.; Kathail, P.; Carr, A.J.; Pe’er, D. Faculty Opinions recommendation of Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell 2018, 174, 716–729.e27. [Google Scholar] [CrossRef]
- Gong, W.; Kwak, I.-Y.; Pota, P.; Koyano-Nakagawa, N.; Garry, D.J. DrImpute: Imputing dropout events in single cell RNA sequencing data. BMC Bioinform. 2018, 19, 220. [Google Scholar] [CrossRef]
- Chen, C.; Wu, C.; Wu, L.; Wang, X.; Deng, M.; Xi, R. scRMD: Imputation for single cell RNA-seq data via robust matrix decomposition. Bioinformatics 2020, 36, 3156–3161. [Google Scholar] [CrossRef] [PubMed]
- Linderman, G.C.; Zhao, J.; Roulis, M.; Bielecki, P.; Flavell, R.A.; Nadler, B.; Kluger, Y. Zero-preserving imputation of single-cell RNA-seq data. Nat. Commun. 2022, 13, 192. [Google Scholar] [CrossRef] [PubMed]
- Arisdakessian, C.; Poirion, O.; Yunits, B.; Zhu, X.; Garmire, L.X. DeepImpute: An accurate, fast, and scalable deep neural network method to impute single-cell RNA-seq data. Genome Biol. 2019, 20, 211. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhang, Z.; You, L.; Liu, J.; Fan, Z.; Zhou, X. scIGANs: Single-cell RNA-seq imputation using generative adversarial networks. Nucleic Acids Res. 2020, 48, e85. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ma, A.; Chang, Y.; Gong, J.; Jiang, Y.; Qi, R.; Wang, C.; Fu, H.; Ma, Q.; Xu, D. scGNN is a novel graph neural network framework for single-cell RNA-Seq analyses. Nat. Commun. 2021, 12, 1882. [Google Scholar] [CrossRef] [PubMed]
- Peng, T.; Zhu, Q.; Yin, P.; Tan, K. SCRABBLE: Single-cell RNA-seq imputation constrained by bulk RNA-seq data. Genome Biol. 2019, 20, 88. [Google Scholar] [CrossRef]
- Ronen, J.; Akalin, A. netSmooth: Network-smoothing based imputation for single cell RNA-seq. bioRxiv 2017, 234021. [Google Scholar] [CrossRef]
- Wang, J.; Agarwal, D.; Huang, M.; Hu, G.; Zhou, Z.; Ye, C.; Zhang, N.R. Data denoising with transfer learning in single-cell transcriptomics. Nat. Methods 2019, 16, 875–878. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Yan, X.; Zheng, R.; Li, M. Bubble: A fast single-cell RNA-seq imputation using an autoencoder constrained by bulk RNA-seq data. Briefings Bioinformat. 2023, 24, bbac580. [Google Scholar] [CrossRef] [PubMed]
- Zappia, L.; Phipson, B.; Oshlack, A. Splatter: Simulation of single-cell RNA sequencing data. Genome Biol. 2017, 18, 174. [Google Scholar] [CrossRef] [PubMed]
- Blakeley, P.; Fogarty, N.M.E.; del Valle, I.; Wamaitha, S.E.; Hu, T.X.; Elder, K.; Snell, P.; Christie, L.; Robson, P.; Niakan, K.K. Defining the three cell lineages of the human blastocyst by single-cell RNA-seq. Development 2015, 142, 3151–3165. [Google Scholar] [CrossRef]
- Ting, D.T.; Wittner, B.S.; Ligorio, M.; Jordan, N.V.; Shah, A.M.; Miyamoto, D.T.; Aceto, N.; Bersani, F.; Brannigan, B.W.; Xega, K.; et al. Single-Cell RNA Sequencing Identifies Extracellular Matrix Gene Expression by Pancreatic Circulating Tumor Cells. Cell Rep. 2014, 8, 1905–1918. [Google Scholar] [CrossRef]
- Baron, M.; Veres, A.; Wolock, S.L.; Faust, A.L.; Gaujoux, R.; Vetere, A.; Ryu, J.H.; Wagner, B.K.; Shen-Orr, S.S.; Klein, A.M.; et al. A Single-Cell Transcriptomic Map of the Human and Mouse Pancreas Reveals Inter- and Intra-cell Population Structure. Cell Syst. 2016, 3, 346–360.e4. [Google Scholar] [CrossRef]
- Ziegenhain, C.; Vieth, B.; Parekh, S.; Reinius, B.; Guillaumet-Adkins, A.; Smets, M.; Leonhardt, H.; Heyn, H.; Hellmann, I.; Enard, W. Comparative Analysis of Single-Cell RNA Sequencing Methods. Mol. Cell 2017, 65, 631–643.e4. [Google Scholar] [CrossRef]


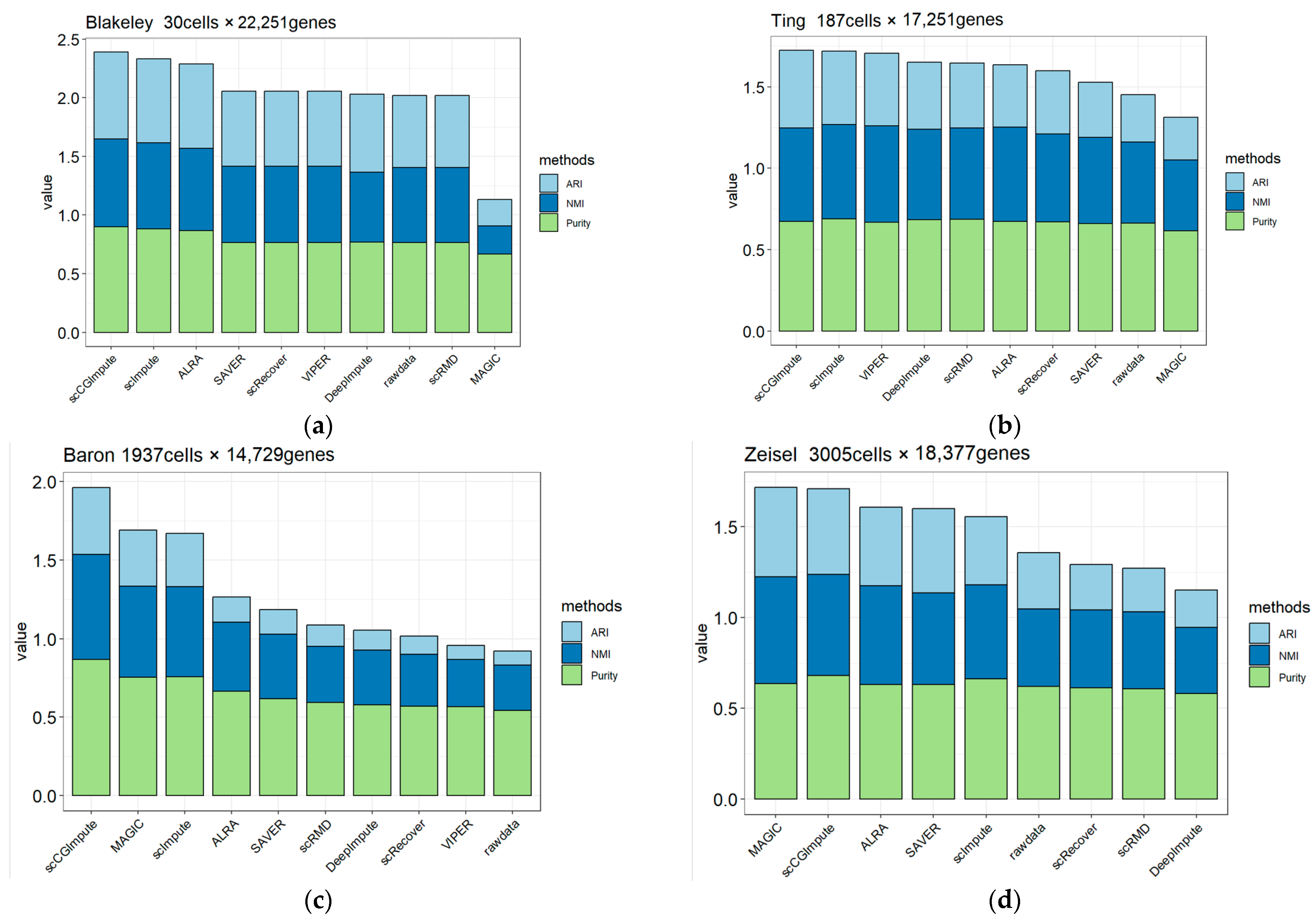
| Datasets | Number of Cell Types | Number of Cells | Number of Genes | Cell Source | Dropout Rate | References |
|---|---|---|---|---|---|---|
| Blakeley | 3 | 30 | 22,251 | Human Blastocyst | 38.2% | [34] |
| Ting | 7 | 187 | 17,251 | Mouse Pancreatic Circulating Tumor Cells | 66.7% | [35] |
| Baron | 14 | 1937 | 20,125 | human pancreatic islets | 86.9% | [36] |
| Zeisel | 9 | 3005 | 18,378 | Mouse cortex and hippocampus | 79.6% | [4] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Li, Y. scCGImpute: An Imputation Method for Single-Cell RNA Sequencing Data Based on Similarities between Cells and Relationships among Genes. Appl. Sci. 2023, 13, 7936. https://doi.org/10.3390/app13137936
Liu T, Li Y. scCGImpute: An Imputation Method for Single-Cell RNA Sequencing Data Based on Similarities between Cells and Relationships among Genes. Applied Sciences. 2023; 13(13):7936. https://doi.org/10.3390/app13137936
Chicago/Turabian StyleLiu, Tiantian, and Yuanyuan Li. 2023. "scCGImpute: An Imputation Method for Single-Cell RNA Sequencing Data Based on Similarities between Cells and Relationships among Genes" Applied Sciences 13, no. 13: 7936. https://doi.org/10.3390/app13137936
APA StyleLiu, T., & Li, Y. (2023). scCGImpute: An Imputation Method for Single-Cell RNA Sequencing Data Based on Similarities between Cells and Relationships among Genes. Applied Sciences, 13(13), 7936. https://doi.org/10.3390/app13137936






