Effects of Diamond-like Carbon and Tungsten-Carbide Carbon Coatings on Tribological Performance of Cam–Tappet Conjunction

Abstract

Cam–tappet contacts are responsible for ~7.5% of the internal combustion engine’s (ICE) total frictional losses. The application of coatings can improve the tribological performance of these contacts. In this paper, the application of a WC-C coating as a novel approach for cam–tappets in comparison with DLC coating is investigated. The tribological performance of the coated contacts are evaluated by a novel model comprising combined implicit analytical and explicit numerical methods. This model considers the coupled tribo-dynamic behaviour whilst obtaining detailed tribological performance. The combined approach provides a computationally efficient platform. The results show that application of DLC or WC-C can improve the film thickness value by up to 41%. They can improve boundary friction, whilst increasing the viscous friction.

1. Introduction

To reduce global greenhouse emissions, legislations and directives regarding vehicle emissions are becoming significantly more stringent. With the introduction of the “Euro 6” directive by the European Union in 2014, NOx allowable emissions were reduced by 94% compared to 1992, when the “Euro 1” directive was first introduced [1]. To meet the imposed limits without performance sacrifices, various approaches were adopted by car manufacturers including engine downsizing, forced induction methods and hybridisation. Nevertheless, the need for improved engine efficiency in any newly designed vehicle is paramount and can be a key contributor in achieving the emission standards as well as market success.

It is estimated that under steady conditions (coasting), 33% of the input fuel energy which is converted to mechanical work is consumed to overcome the frictional losses experienced by the vehicle, 11.5% of which being attributed to the engine. The valvetrain system of an engine is a major contributor to these frictional energy losses, as research has shown that it is accountable for 6–15% of the engine’s total frictional losses [2,3]. It therefore becomes apparent that improvements in the efficiency of the valvetrain system is critical, both in fulfilling the legislation criteria and improving the performance and longevity of the vehicle.

Further analysis of the valvetrain system suggests that nearly 70% of the system’s frictional losses arise from the cam–tappet sliding contact [4], a conjunction that experiences elastohydrodynamic and boundary lubrication regimes as shown experimentally by Tayyab et al. [5]. Under such conditions, frictional losses are heavily dependent on the lubricating fluid film thickness existing between the cam and the tappet, as well as the surface characteristics of the contacting components and their interaction with the lubricant. To accurately predict the tribological behaviour of the cam–tappet conjunction and subsequently optimise the system for reductions in frictional losses, a simultaneous solution of the flexible dynamics, together with the solution of the elastohydrodynamic formulation for the concentrated contact of the conjunction is necessary. This is because the presence of the oil film induces a frictional damping effect that can affect the system’s frictional and dynamic behaviour [6]. The dynamic solution in return provides realistic load and kinematics of the conjunction to the tribological model. This system of coupled models is referred to as tribo-dynamics.

Different approaches to couple the aforementioned solutions are present throughout the literature. In the formulation followed by Rahnejat et al. [7], an approximate quasi-static EHL solution for the cam–tappet lubricated contact was embedded into the Lagrangian dynamics model addressing the non-linear constrained system [7]. The cam–tappet contact was considered to be equivalent to a cylinder of the same instantaneous radius with the cam in contact with an elastic half-space, and thus, the Hertzian theory was applied for calculations of deflection, contact half-width, maximum pressure and contact pressure profile. An extrapolated formula obtained by Rahnejat [8] was used for the calculation of the central film thickness to avoid the high computational times necessary when calculating the fluid film thickness using an analytical approach. This study did not provide a detailed EHL solution for the pressure and film thickness distributions.

In another study by Kushwaha and Rahnejat [9], the evaluation of the fluid film thickness and the pressure distribution under transient conditions along the finite line contact conjunction was approached analytically and numerically. Solutions were obtained through the normalised Reynolds’ equation by the effective influence of the Newton–Raphson (EIN) method [9]. Lubricant rheological properties were also considered by use of the relationship of the fluid’s density with variations in pressure as derived by Dowson and Higginson [10]. The model was extended by Teodorescu et al. [11], and the principles were applied to a four-cylinder engine, with results being validated experimentally. In these studies, the effects of tribo-dynamic couplings were neglected.

Another model was developed and validated experimentally by Nakahara et al. [12], which allowed the effects of surface roughness as well as thermal effects arising from asperity contacts to be considered. The results highlighted a direct correlation between frictional power losses and surface roughness.

Further work was carried out by Meuter et al. [6], where a full EHL line contact was coupled with a multi-body dynamics-based full engine simulation and solved iteratively at every point in time. This method was developed for incorporation into simulation software. For this reason, the Reynolds equation and the film thickness equation were treated as modular decoupled systems so that the formulation could provide coverage of various load cases and versatility of hydrodynamic implementation whilst the results remain consistently accurate. Despite the significant development in this work, leading to a fully numerical implicit EHL solution in the tribo-dynamic formulation, the computational cost of the system was a limitation.

One of the practical approaches to enhance the tribological performance of cam–tappet conjunctions is to apply appropriate coatings to control the surface behaviour. DLC (Diamond-like Carbon)-type coatings were first introduced on high-performance racing vehicles. However, in recent years, increasingly more manufacturers are incorporating DLC-coated components in commercial vehicles for their superior tribological behaviour compared to uncoated steel [13]. Their frictional benefits have been demonstrated experimentally in several studies [14,15], whereby reductions in frictional losses of up to 40% were observed [16] depending on lubrication conditions. WC-C (Tungsten-Carbide Carbon) coatings are a type of metal-doped DLC coatings that have also shown further reductions in frictional losses, improvements in lubricity [17] as well as higher resistance to wear under heavily loaded conditions of sliding or rolling contact [18]. However, the application of WC-C coatings in automotive valvetrain applications is not reported in the literature.

One of the first advancements was made in the field of the contact mechanics of coated surfaces in a study by Gupta and Walowit [19], whereby a numerical solution was obtained for the case of a cylindrical elastic body being in a loaded contact with a coated elastic substrate. Numerical methods were derived for the evaluation of the actual contact pressure and halfwidth, which originated from the Hertzian solution. This work was further developed by Gupta [20], with modifications being made to the formulation to incorporate an EHL film within the conjunction. Numerical results were tabulated for EHL film thickness depending on various contact parameters. Both studies, however, did not relate their findings to the dynamic behaviour of the cam–tappet conjunction. Teodorescu and Rahnejat [13] proposed a mathematical model that facilitated the evaluation of the behaviour of a cam–tappet conjunction when a thin-film DLC coating layer was introduced on the tappet. However, the model assumed dry contact conditions between the two components for a faster convergence to a solution. Hence, the tribo-dynamic coupling was missing.

In this paper, considering the reported benefits of DLC and WC-C coatings in an EHL conjunction, their tribological behaviour in the cam–tappet application is evaluated numerically. The tribological benefits of a WC-C coating in cam–tappets have not been reported in the literature hitherto. The numerical solution comprises an explicit full numerical coated EHL of the contacts, coupled with an implicit analytical tribo-dynamic model. The implicit model which employs analytical EHL methods delivers realistic dynamically achieved load and speed conditions for the explicit method. The explicit method, on the other hand, computes detailed contact conditions including pressure, film thickness and shear distributions with the coating effects. This combined approach enables the detailed effects of lubricated coated surfaces on the tribological performance of cam–tappet contacts in a computationally efficient method to be obtained. Such a comprehensive numerical method for a tribo-dynamic solution of a coated EHL contacts has not been reported hitherto. Hence, the outcome of this paper will provide novel knowledge of applying WC-C-coated surfaces (in comparison with DLC coatings) in cam–tappet contacts using a novel and time-efficient numerical method.

2. Methodology

2.1. The Multi-Physics Workflow

As suggested in the literature, to precisely predict the behaviour of system at the cam–tappet conjunction, a simultaneous solution of dynamic problem together with the tribological model is required. Hence, a multi-physics approach is necessary.

Additional computational load would be introduced by the integration of appropriate models, necessary for the evaluation of the effects of the coating layer on the behaviour of the system. To circumvent the high computational loads that would be created with such an approach, the detailed tribological model comprising lubricant film thickness and the frictional calculations are simulated explicitly. In this approach, the kinematic and dynamic outputs produced from the multibody-dynamic valvetrain system is provided to this explicit tribological model. The multi-body dynamic system includes an implicit simple tribological approach in order to predict frictional dissipation as a source of damping. This approach relies on extrapolated film thickness equations and add negligible computation time to the dynamic solution. The validity of this explicit–implicit modelling platform had been shown for other applications such as gears [21] and roller bearings [22] and is investigated and discussed for cam–tappet contacts in the results section of this paper.

The tribological model itself requires input from experimental measurements to consider the realistic surface and interfacial characteristics such as topography and boundary friction. An overview of the methodology utilised in this study is provided in Figure 1, while thorough descriptions are provided in the following sections.

2.2. Experimental Characterisation

To construct the 3D profiles of the surfaces of uncoated polished steel as well as DLC and WC-C-coated surfaces (See Figure 2), surface topography measurements were performed using a “Bruker (Billerica, MA, USA) NPFlex 3D Surface Metrology System”. The system utilises white light interferometry so that no physical contact is made with the specimens. The investigated coatings were “Diamolith-DLC™” and “Nitron-MC™” (DLC and WC-C, respectively) and were deposited onto the substrates using Physical Vapour Deposition (PVD) approach. Several topography measurements were taken from the surfaces of the samples to facilitate averaging of the results and exclusion of any outliers. The settings used for the measurements are shown in

Table 1. “Bruker NPFlex 3D Surface Metrology System” parameters.

Magnifying Lens	50×
Optical Zoom	2×
Sample Area	2984.63 μm2
Lateral Resolution	0.099 μm

.

To obtain the necessary surface characteristics and subsequently observe their tribological effects on the cam–tappet conjunction, the obtained topographies were post-processed with a band-pass filter with a wavelength range from 0.25 μm to 250 μm, to eliminate possible waviness and surface singularities from the measurements. A sample surface profile is shown in Figure 3. The above procedure was performed using the Micro-Contact Analysis tool in AVL (Graz, Austria) EXCITE™ Power Unit.

2.3. Flexible Multi-Body Dynamic Model

For the purpose of this investigation, a single valvetrain model was used, thus facilitating efficient evaluation of the dynamic and tribological behaviour of the cam–tappet conjunction under coated and un-coated conditions. A 3D view of the system is shown in Figure 4, which was produced using EXCITE^TM (Graz, Austria) Multi-Body Environment. All bodies comprising the system are flexible, thus allowing the incorporation of localised deformation in bodies. Contact deformations in the system are considered as restrains to account for deformations in the conjunction. Additional constraints and restraints are applied using joints, limiting the degrees of freedom of each body while also facilitating their motions and interactions. A list of bodies and their global degrees of freedom (DoF) are presented in

Table 2. Single valvetrain model bodies.

Body	Global DOF
Cam	One rotational
Follower (Flat Tappet)	Three translations
Valve Spring	Three translations
Valve	Three translations
Cylinder Head	None

. As mentioned above, these bodies are flexible. Hence, additional DoF are present due to the flexibility and localised deformations. The flexibility of the system is implemented using Component Synthesis Method [23]. Joints utilised to facilitate constraining the system are shown in Table 2 and

Table 3. Single valvetrain model joints.

Joint	Type	Connected Bodies	No. of Constrains	No. of Restrains
Cam Follower	Contact	Cam and Follower	5	1 translational
Push Contact	AXBE	Follower and Spring	5	1 translational
Spring Seat	AXBE	Valve and Spring	5	1 translational
Spring Support	AXBE	Cylinder Head and Spring	5	1 translational
Valve Seat	AXBE	Cylinder Head and Valve	5	1 translational

.

The “Axial Thrust Bearing” (AXBE) joints enable the pairs of bodies to be constrained in three rotational and two translational DOFs. The remaining single translational DOF is restrained with discrete stiffness and damping parameters provided from experimental characterisation. The contact joint can be represented by a dry or lubricated model. In case of dry representation, the restrained DOF is governed by the contact stiffness. If the contact represents the presence of lubricant, the restrained DOF should consider the effective stiffness comprising contact and lubricant film compliances. Due to the load–speed combinations in the cam–tappet conjunction, the behaviour of the lubricated contact falls within the EHL regime. This will be shown in the results section using a “Greenwood Chart” [24]. Under this regime of lubrication, the stiffness of the lubricant film is several orders of magnitude higher than the one from contacting bodies. Since the lubricant film is in series with this contact, the effect of lubricant film stiffness can be neglected in the dynamic system [21,22]. Consequently, the only coupling between dynamics and tribology will be via friction in the contact. This implies that implicit simulation of the full numerical EHL model within the flexible multi-body dynamics environment can be avoided. Comparison of the implicit and explicit EHL with multi-body dynamics is presented in the results section, justifying the choice of an explicit approach.

2.4. Coated EHL Model

As explained above, the EHL model can be included in the workflow either explicitly or implicitly. The former is selected in the current study. The developed methodology should be able to model EHL regime of lubrication for coated surfaces which exhibit different contact mechanics to uncoated ones. The fluid film in EHL contact is governed and modelled by Reynolds equation. The one-dimensional form of this equation, neglecting any side-leakage for the cam and follower lubrication, is presented below [25]:

$$\frac{\partial }{\partial x}\left(\frac{\rho h^3}{\mu }\frac{\partial p}{\partial x}\right)-12u\frac{\partial \left(\rho h\right)}{\partial x}-12\frac{\partial \left(\rho h\right)}{\partial t}=0$$

(1)

In above equation, both viscosity $\left(\mu \right)$ and density $\left(\rho \right)$ are functions of the hydrodynamic pressure. In this study, Dowson and Higginson equation is used to model the pressure–density relationship [10].

$$\frac{\rho }{{\rho }_0}=1+\frac{0.6p}{1+1.7p}$$

(2)

For the pressure–viscosity relationship (piezo-viscosity), Roeland’s equation [26] is employed:

$$\frac{\mu }{{\mu }_0}=\exp \left(\left(\ln {\mu }_0+9.67\right)\left(-1+{\left(1+5.1\times {10}^{-9}\times p\right)}^{{\rm Z}}\right)\right)$$

(3)

$${\rm Z}=\frac{\alpha }{5.1\times {10}^{-9}\left(\ln \left({\mu }_0\right)+9.67\right)}$$

where ${\rho }_0$ and ${\mu }_0$ are the density and viscosity at atmosphere pressure, respectively.

The Reynolds boundary condition is assumed for Equation (1) as [27]:

$$p=0|{}_{x_{in}}, p=0|{}_{x_{out}}, \frac{dp}{dx}=0|{}_{x_{out}}$$

(4)

In an explicit approach, the force equilibrium should be satisfied between the conjunction load resulted from the dynamic solution (which includes inertial forces) and the EHL pressure distribution obtained through Equations (1)–(4). For this purpose, the hydrodynamic load-carrying capacity, provided by fluid film pressure is calculated as:

$$W_h=l{\displaystyle {\int }_{x_{in}}^{x_{out}}p\left(x\right)} dx$$

(5)

Under the EHL regime of lubrication in a cam–tappet conjunction, the presence of asperity interactions from both surfaces is likely. This interaction which contributes to the boundary friction and load-carrying capacity is usually characterised by the Stribeck parameter ($\lambda$), which is the ratio of lubricant film thickness over the composite roughness value of the surfaces. To consider this boundary interaction, the Greenwood and Tripp method is utilised [28]. In this method, the share of contact load carried by the asperities is calculated as (boundary load-carrying capacity):

$$W_a=\frac{8\sqrt{2}}{15} \pi {\left(n\beta \sigma \right)}^2 \sqrt{\frac{\sigma }{\beta }} \acute{E}A{F}_{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\lambda \right) \lambda =\frac{h}{\sigma }$$

(6)

The statistical function $F_{\frac{5}{2}}\left(\lambda \right)$ can be expressed through the below polynomial function, which is based on the Gaussian distribution of surface asperity heights:

$$F_{\frac{5}{2}}\left(\lambda \right)=\left\{\begin{array}{c}0.000421{\lambda }^6-0.008538{\lambda }^5+0.07162{\lambda }^4-0.3193{\lambda }^3+\\ 0.802{\lambda }^2-1.082\lambda +0.6166for \lambda \le 2.5 \\ 0for \lambda >2.5\end{array}\right.$$

(7)

Hence, the abovementioned force equilibrium is obtained as:

$$W=W_h+W_a$$

(8)

where $W$ is the total load on the contact (obtained from dynamics). The film thickness equation of lubricant utilised in Reynolds equation is presented as a function of geometry and the elastic deformation of surfaces [25]:

$$h=h_0+\frac{x^2}{2R}+V(x)$$

(9)

The main difference between the coated and uncoated model lies in deformation and contact mechanics. For an uncoated line contact (half plain), the normal displacement by a pressure distribution (elastic deformation) is controlled by the Flamant solution [29]:

$$V(x)=-\frac{4}{\pi E^{\prime }}{\displaystyle {\int }_{-\infty }^{\infty }\ln \left|x-x^{\prime }\right|}p(x^{\prime })d{x}^{\prime }$$

(10)

where $1/E^{\prime }=0.5 \left[\left(1-{{\upsilon }_1}^2\right)/E_1+\left(1-{{\upsilon }_2}^2\right)/E_2\right]$.

The Green’s function in the convolution of Equation (10) is [29]:

$$g(x)=-\frac{4}{\pi E^{\prime }}\ln \left|x\right|$$

(11)

Then, the corresponding frequency response function (FRF) in the frequency domain can be presented as [29]:

$$\tilde{g}(\omega )=\frac{4}{E^{\prime }\left|\omega \right|}$$

(12)

For the coated line contact conjunctions, an explicit Green’s function is not achievable for deformation in the space domain. However, its frequency response function is available as [29]:

$$\tilde{g}(m)=\frac{1-{\upsilon }_c}{{\mu }_{c}m}\frac{1+4m{h}_c\kappa \theta -\lambda \kappa {\theta }^2}{1-(\lambda +\kappa +4\kappa m^2{h}_c{}^2)\theta +\lambda \kappa {\theta }^2}m=\left|\omega \right|$$

(13)

where $\theta =\mathit{exp}(-2m{h}_c)$.

The tilde represents Fourier transform with respect to $x$. ${\mu }_c$ is the shear modulus of the coating material (${\mu }_c=\frac{E_c}{2(1+{\upsilon }_c)}$), and $h_c$ is the coating thickness. $m$ is the frequency domain counterpart of radius in the space domain. ${\upsilon }_c$ is the Poisson’s ratio of the coating material. Other parameters in Equation (13) are expressed as [30]:

$$\lambda =1-\frac{4(1-{\upsilon }_c)}{1+\zeta (3-4{\upsilon }_s)}, \kappa =\frac{\zeta -1}{\zeta +(3-4{\upsilon }_c)}, \zeta =\frac{E_c(1+{\upsilon }_s)}{E_s(1+{\upsilon }_c)}$$

(14)

There is a singularity problem of FRF at $m=0$ [29]. This problem is resolved by the Gaussian quadrature. Deriving the FRF of Green function, the elastic deformation of coated contact can be obtained utilising the Discrete Convolution—Fast Fourier Transform (DC-FFT) fast algorithm and influence coefficients [31]. The deformation of the coated line contact can be ultimately calculated through the below formula:

$$V=\mathrm{IFFT}(\widehat{D}.\widehat{P})$$

(15)

where $\widehat{D}$ is the discrete response function of pressure displacement, and $\mathrm{IFFT}$ is the Inverse Discrete Fourier Transform. Figure 5 shows dry pressure distributions obtained for different ratios of coating modulus of elasticity to the one for steel using Equation (15). It is clear that by increasing the coefficient of friction in the coating, the contact area is reduced, and higher pressure values are experienced. The pressure distributions of the same contact under the EHL regime are presented in Figure 6.

2.5. Friction Calculation

The friction in contact comprises boundary and viscous terms. Viscous friction is calculated based on pressure and film thickness distributions as [32]:

$$F_v=\int \left[\pm \frac{h}{2}\frac{dp}{dx}+\frac{\mu u}{h}\right] d{A}_v$$

(16)

Greenwood and Tripp [28] method is utilised to calculate the boundary friction as:

$$F_b={\tau }_l{A}_a$$

(17)

where ${\tau }_l={\tau }_{l_0}+{\beta }_m\raisebox{1ex}{$W_a$}\!\left/ \!\raisebox{-1ex}{$A_a$}\right.$ is the lubricant’s limiting shear stress. $W_a$ is obtained from Equation (6). Based on a Gaussian distribution assumption and Greenwood and Tripp method, the asperity contact area, $A_a$, is:

$$A_a={\pi }^2{\left(n\sigma \beta \right)}^{2}A{F}_2\left(\lambda \right)$$

(18)

where the statistical functions $F_2\left(\lambda \right)$ can be expressed in a polynomial form as:

$$F_2\left(\lambda \right)=\left\{\begin{array}{c}-0.002 {\lambda }^5+0.028 {\lambda }^4-0.173 {\lambda }^3+0.526 {\lambda }^2-0.804 \lambda +0.5 for \lambda \le 3\\ 0for \lambda >3\end{array}\right.$$

(19)

3. Results and Discussion

In this section, the proposed methodology is used to assess the effect of DLC and WC-C coatings on the tribological performance of a single cam–tappet conjunction shown in Figure 4. The single valvetrain case study is outlined in the methodology section in detail. As explained above, an experimental characterisation of surfaces is required to inform the numerical models with input values for boundary friction calculations. The summary of the combined topographical characteristics obtained through post-processing of measured data is presented in

Table 4. Combined surface characteristics.

Uncoated Tappet
Asperity Density per unit Area, ζ	8.3 × 109 m−2
Composite RMS Surface Roughness, σ12	0.408 μm
Mean Composite Radius of Curvature of Asperity Peaks, β12	0.669 μm
DLC-Coated Tappet
Asperity Density per unit Area, ζ	3.8 × 109 m−2
Composite RMS Surface Roughness, σ12	0.358 μm
Mean Composite Radius of Curvature of Asperity Peaks, β12	0.332 μm
WC-C-Coated Tappet
Asperity Density per unit Area, ζ	2.7 × 109 m−2
Composite RMS Surface Roughness, σ12	0.347 μm
Mean Composite Radius of Curvature of Asperity Peaks, β12	0.217 μm

. These data are directly used in the boundary interaction model of Section 2.5.

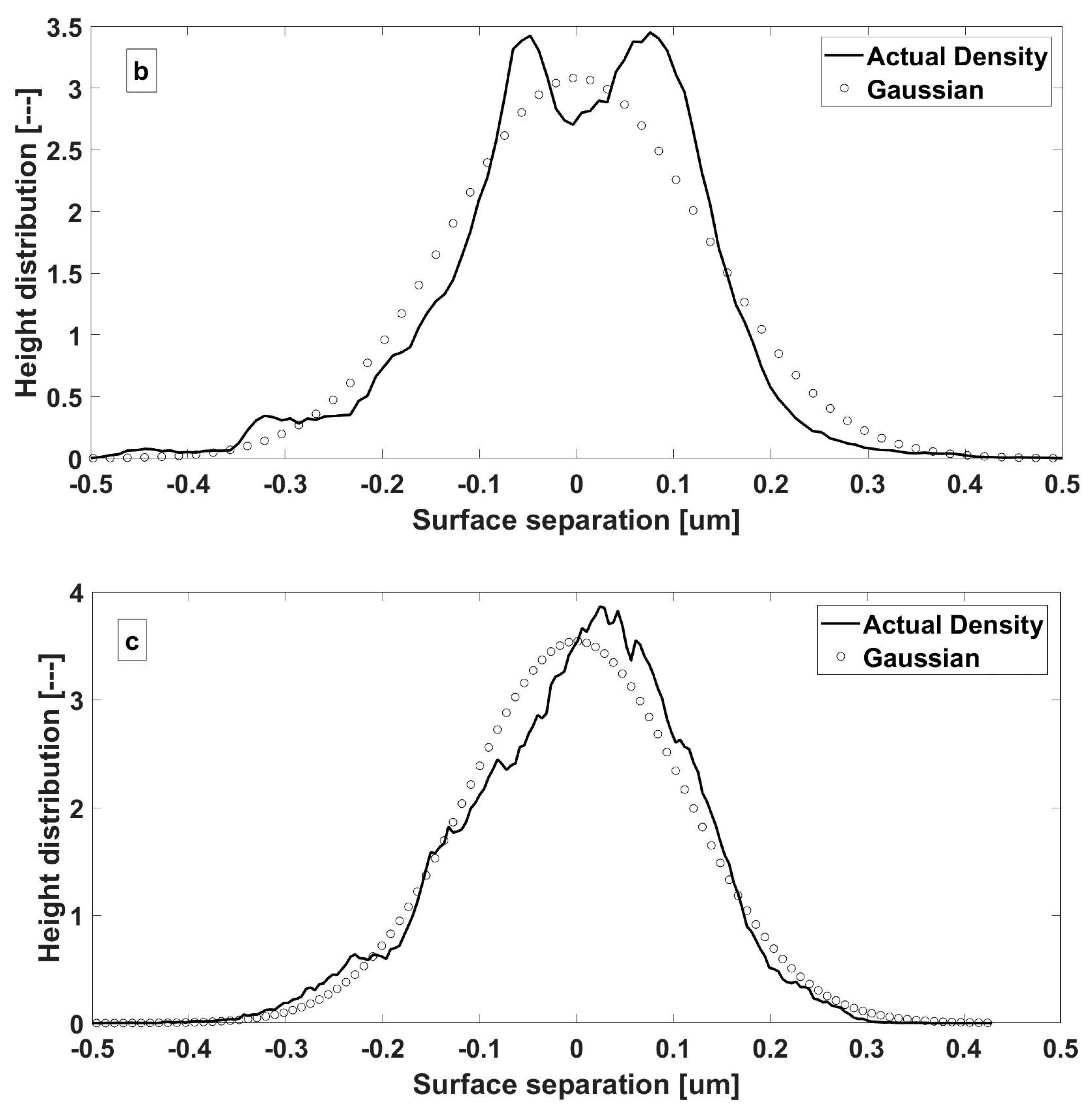
The boundary interaction model assumes a Gaussian of surface asperity heights. This can be verified using experimentally obtained surface topographies. Figure 7 shows the real asperity height distributions for steel, DLC and WC-C surfaces. The results reveal that there is a reasonable conformity to a Gaussian distribution. Hence, the application of statistical functions for boundary interaction, assuming this distribution, is justified.

The rheological properties used throughout the investigation can be found in

Table 5. Lubricant rheological properties.

Dynamic Viscosity	0.055 Pa. s
Limiting Shear Strength Coefficient	0.08
Eyring Shear Stress	2 Mpa
Pressure–Viscosity Coefficient	1.05 × 10−8 Pa−1

, which correspond to a standard SAE 5W-20 lubricant. These properties were kept constant for all simulations performed. Other material properties necessary for the formulation can be found in

Table 6. Material properties.

Steel
Modulus of Elasticity	210 MPa
Poisson’s Ratio	0.300
Pressure coefficient of boundary shear strength of asperities [31]	0.185
DLC Coating
Modulus of Elasticity	185 MPa
Poisson’s Ratio	0.300
Pressure coefficient of boundary shear strength of asperities [31]	0.440
Coating layer thickness	4 μm
WC-C Coating
Modulus of Elasticity	175 MPa
Poisson’s Ratio	0.300
Pressure coefficient of boundary shear strength of asperities [31]	0.540
Coating layer thickness	4 μm

. The pressure coefficient of boundary shear strength of asperities is required for boundary friction calculation. It is the asperity level equivalent of the coefficient of friction which is expanded to macro-level (conjunction level) using the Greenwood and Tripp approach presented in Section 2.5. The values of this coefficient for surfaces of this study are investigated and obtained using an Atomic Force Microscope (AFM) by Laderou et al. [33].

The simulations performed are representative of a four-stroke engine at a speed of 3000 RPM and evaluate the behaviour of the system over two complete engine cycles. Since the simulation algorithm assumes a fully flooded cam–tappet conjunction as an initial condition, only the second engine cycle (720 to 1440 degrees) is presented, where the solution is considered to be settled after removing all transient effects. Simulation conditions are shown in

Table 7. Additional model parameters.

Engine Speed	3000 RPM
Valve Mass	0.07 kg
Spring Mass	0.036 kg
Spring Constant	33750 N·m−1
Cam Base Circle Radius	0.015 m
Cam Length	0.012 m
Maximum Cam Lift	0.0093 m

.

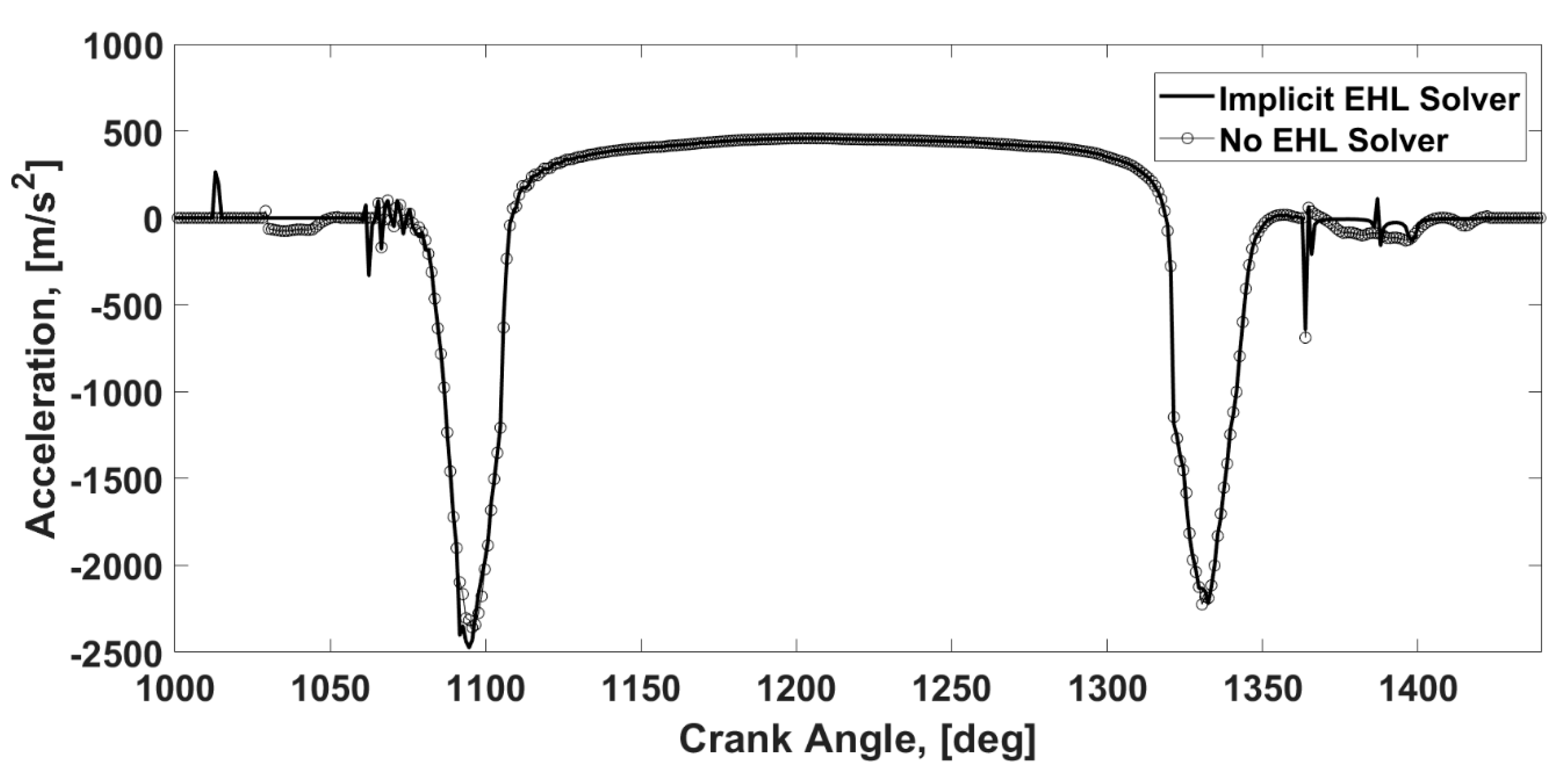
As the first step, the validity of using a full numerical EHL contact explicitly is investigated. For this purpose, two versions of multi-body dynamic model are simulated. The first model (referred to as “implicit EHL model” or “implicit” in figures) implicitly solves the numerical EHL model within the multi-body formulation. The second model (referred to as “no EHL solver” or “explicit” in figures) represents the multi-body dynamic model with a simple analytical tribology model instead of full numerical EHL solution. The tappet velocity and contact force from implicit and explicit models are plotted in Figure 8 and Figure 9, respectively. The results show the insignificant effect of using the implicit solution in comparison with the explicit one. The slight variation is observed in lightly loaded regions where the nature of the EHL regime is less pronounced, and the film thickness stiffness approached comparable values to those from solid contact. These are regions where the cam and tappet come into loaded contact or they are about to cease contact. They are shown schematically in Figure 8. This effect is more pronounced in acceleration presented in Figure 10. Overall, considering the insignificant effect of these regions as well as expected major effect of coatings in the highly loaded region, the explicit model is used for this investigation.

For the EHL solution, the contact load from Figure 9 and speed of entertaining motion in Figure 11 are used as inputs to the explicit coated EHL model. These results are used quasi-dynamically to simulate the behaviour of the lubricated contact during a complete cycle. For each case, the effects of coating are compared with uncoated steel. In addition, the effect of coating thickness is investigated.

The main reason for the insignificant effect of implicit modelling can be explained by significantly smaller contribution of the lubricant film to contact stiffness under elasticity domination regimes on the Greenwood Chart, such as EHL [24]. For this purpose, the regimes of lubrication can be ascertained and verified using the Greenwood Chart [24]. This chart utilises working conditions (mainly speed–load combinations) to summarise the contribution of elasticity and piezo-viscosity effects in the form of two dimensionless numbers, $G_v=\frac{{W^{*}}^{3/2}{G}^{*}}{{U^{*}}^{1/2}}$ and $G_e=\frac{W^{*}}{{U^{*}}^{1/2}}$. The combination of these numbers specifies if the regime of lubrication is piezo viscos/elastic (PE), piezo viscos/rigid (PR), iso viscos-elastic (IE) or iso viscos-rigid (IR). PE corresponds to the classical EHL, and IR corresponds to the classical hydrodynamic regimes. IE is the regime for so-called “soft-EHL”. Figure 12 shows the working conditions of this study on the Greenwood chart. It should be noted that the boundaries in this graph are indicative and based on simplified analytical formulas [24]. However, they roughly show the dominant effects. It is observed that some working points in the studies cycle fall in the hydrodynamic regime. Hydrodynamic condition corresponds to lightly loaded contacts. These points show the biggest difference between implicit and explicit models in Figure 8, Figure 9 and Figure 10. Under higher loads, the working conditions approach PE and IE where the effect of film stiffness is diminished, and the implicit and explicit approached show a good agreement.

To further investigate the results of Figure 12, the pressure and film thickness distributions of six points along a cycle are provided in Figure 13. These points are considered at points 1 to 6 on Figure 9 to show a variety of speed–load combinations. Each graph in Figure 13 shows pressure and film thickness distributions for uncoated and WC-C-coated samples with 4 $\mathsf{\mu }\mathrm{m}$ coating thickness. The results clearly show a variety of contact regimes from EHL, such as point 1 and 6, under high loads to the moderately deformed point 2. Under EHL conditions, the flattened film thickness as well as the secondary spike of the pressure distribution is apparent. It should be noted that the shape of pressure and film thickness distributions, as well as their values depend on both load and speed. Point 2, for example, resembles a near-zero velocity, leading to significantly lower film thickness.

It is also clear that the application of a WC-C coating leads to an expanded contact area, which in turn supports a thicker film thickness. This effect is due to the lower modulus of elasticity of the coated surfaces, which agrees with the generic results in Figure 6. The expansion of the contact area and consequent increase in the film thickness value can be seen as a benefit of WC-C application, since it significantly affects the frictional and wear behaviour (the latter is not the subject of this study). This benefit is more pronounced under lightly loaded conditions such as points 2, 3, 4 and 5, which are away from the PE region on the Greenwood Chart.

Figure 14a shows the pressure and film thickness distributions of the DLC-coated surfaces in comparison with the WC-C-coated cam–tappets. The effect of coating thickness is also analysed by comparing the results of 1 $\mathsf{\mu }\mathrm{m}$ coating thickness to those from 4 μm coating thickness. It is seen that the results for DLC and WC-C, as well as the behaviour of different coating thicknesses, are similar. This is due to the negligible effect of the coating thickness in comparison to the ratio of modulus of elasticity, as shown in Figure 5 and Figure 6. Similar values of modulus of elasticities from DLC and WC-C also yield similar pressure and film thickness distributions. The zoomed-in view in Figure 14b shows the minute level of variation from DLC to WC-C and between coating thickness values.

Figure 15 is the variation of central film thickness during one cycle for 4 $\mathsf{\mu }\mathrm{m}$ thickness of coatings. It is revealed that the major effect of coatings is observed in the moderately loaded region, as shown in Figure 13 and Figure 14. It accounts for a maximum increase of 41%, mainly observed at the centre of the high-load section. The consequence of this variation in the film thickness will be on durability as well as frictional performance. The former is not the subject of this study; hence, the effect of coatings on friction will be further investigated. It is also revealed that the difference between DLC and WC-C on the central film thickness is minute, as can also be observed in Figure 14b. This will mean that any potential variation in friction between DLC and WC-C will be less related to the variation in the film thickness.

Figure 16 and Figure 17 present the boundary contact load and boundary friction variations along a cycle. The results show a significant reduction in the boundary contact load (share of load carried by asperities) in coated samples. This is also reflected in the value of boundary friction force, which accounts for more than 95% at the moderately loaded region. This can be related to the improved (increased) film thickness in Figure 15, which reduces the asperity interactions from both surfaces. Comparing two types of coating, WC-C reveals superior behaviour in terms of boundary friction with values which are ~70% lower in comparison with DLC. This comparative improvement can be attributed to minor differences in the values of pressure and film thickness.

Although boundary friction values are important, the absolute value of this quantity in comparison with viscous friction is lower. Hence, the value of viscous friction over a cycle is shown in Figure 18 for different surfaces. The values in this figure are governed by the level of pressure as well as shear, which are in turn affected by film thickness and contact area. The results show that unlike boundary friction (governed by film thickness), the viscous friction in coated surfaces is higher than that in an uncoated surface. WC-C again reveals better frictional behaviour compared to DLC. The increased viscous friction can be attributed to the extended contact area, which is subject to the shear stress. Comparing the performance of WC-C as the better-performing coating with the uncoated surface, it gains a maximum of 0.44 N in boundary friction, whilst losing maximum of 0.43 N of viscous friction. Consequently, compared with DLC as a commonly used coating for cam–tappet contacts leading to an overall loss in the frictional values, the gain from WC-C coatings outweighs the loss.

4. Conclusions

The effect of a WC-C coating compared to DLC and uncoated surfaces in a cam–tappet contact is investigated. The analysis is performed using a combination of implicit and explicit models, leading to a time-efficient simulation workflow. The following conclusions can be drawn from this research:

• The results show an insignificant contribution of EHL film stiffness in the overall stiffness of the contact. The elastic deformation and piezo-viscous effects are present throughout the cycle, supporting the drawn conclusion. The presented workflow can be used to analyse detailed tribological effects in a coated cam–tappet conjunction and in a time-efficient manner.
• During a complete cycle of the investigated cam–tappet, the contact area is extended under WC-C and DLC coatings due to their lower modulus of elasticity. However, the difference between pressure and film thickness distributions from DLC and WC-C surfaces are negligible.
• The effect of coating layer thickness is less than the effect of material properties of the coating, although it is present and measurable.
• The application of coatings increases the lubricant film thickness by up to 41%. This gain is mainly in the middle section of the cycle under moderate loads.
• The boundary friction is reduced by applying WC-C and DLC coatings. This is due to the increase in the film thickness values. A greater than 95% reduction is achieved by applying WC-C on a steel tappet, which showed a superior performance in this case.
• The viscous friction increases by applying WC-C or DLC, mainly due to the increased contact area. This increase is lower for WC-C, putting this coating in a better position compared with DLC. Overall, WC-C can balance its increased and reduced viscous and boundary frictions, respectively, whereas DLC causes increased friction in overall comparison with the uncoated surface.