A Novel Secondary Side Series LCD Forward Converter with High Efficiency and Magnetic Reset
Abstract
:1. Introduction
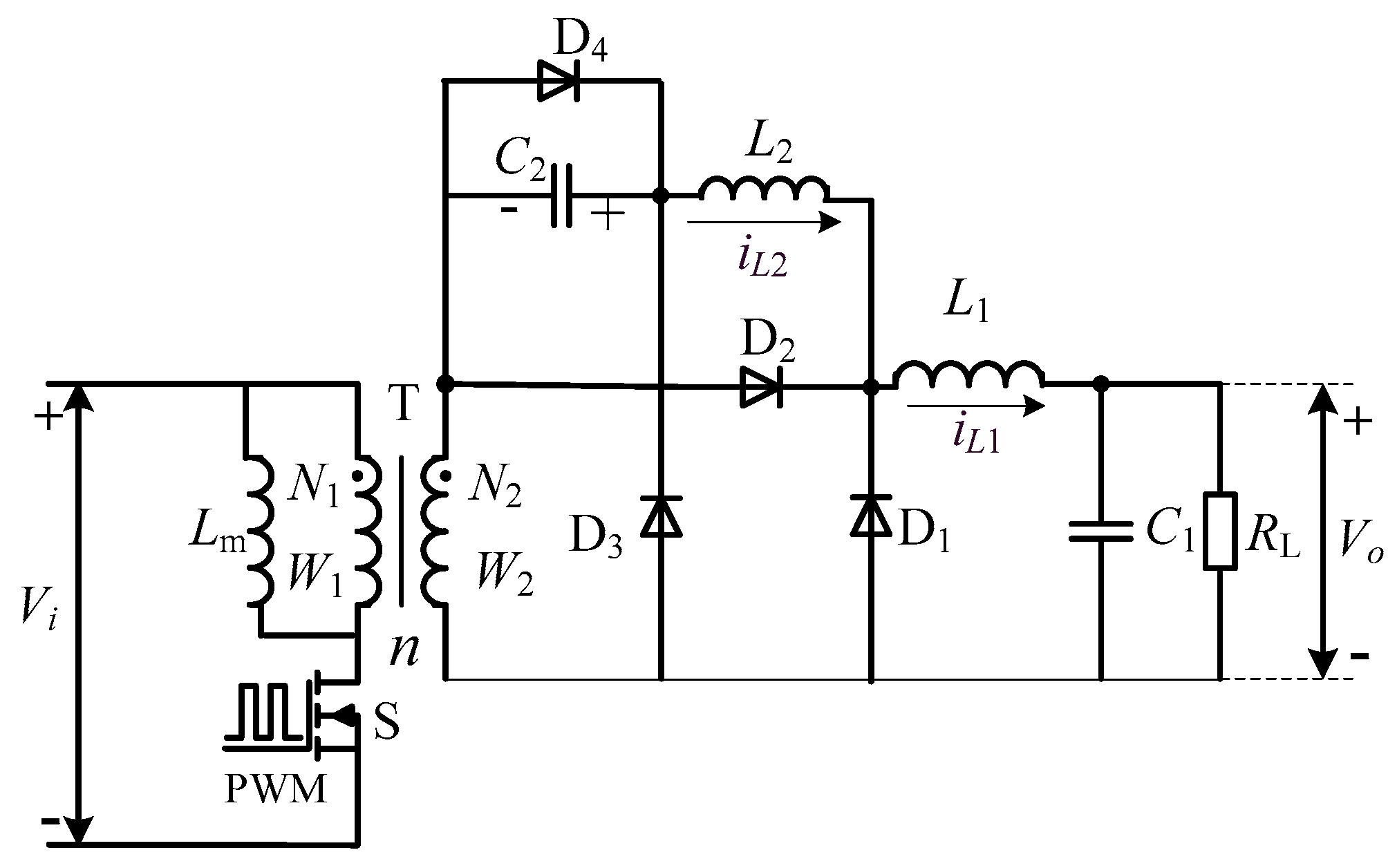
2. Circuit Composition and Energy Transmission Process of a Novel of Secondary Side Series LCD Forward Converter
2.1. Composition and Principle of a Circuit
2.2. Analysis of the Working Mode and Energy Transfer Process of the Converter
3. Selection and Analysis of the Additional Capacitance Parameters When the Excitation Inductor Works in the DCM
4. Analysis of the Voltage Characteristics of the Switch and the Selection of the Forward Inductance Parameter
4.1. Analysis of the Turn-Off Characteristics of the Switch
4.2. Analysis of the Switching Characteristics of the Switch
4.3. Parameter Design of the Forward Inductor L1
5. Simulation and Experimental Analysis
5.1. Simulation Analysis
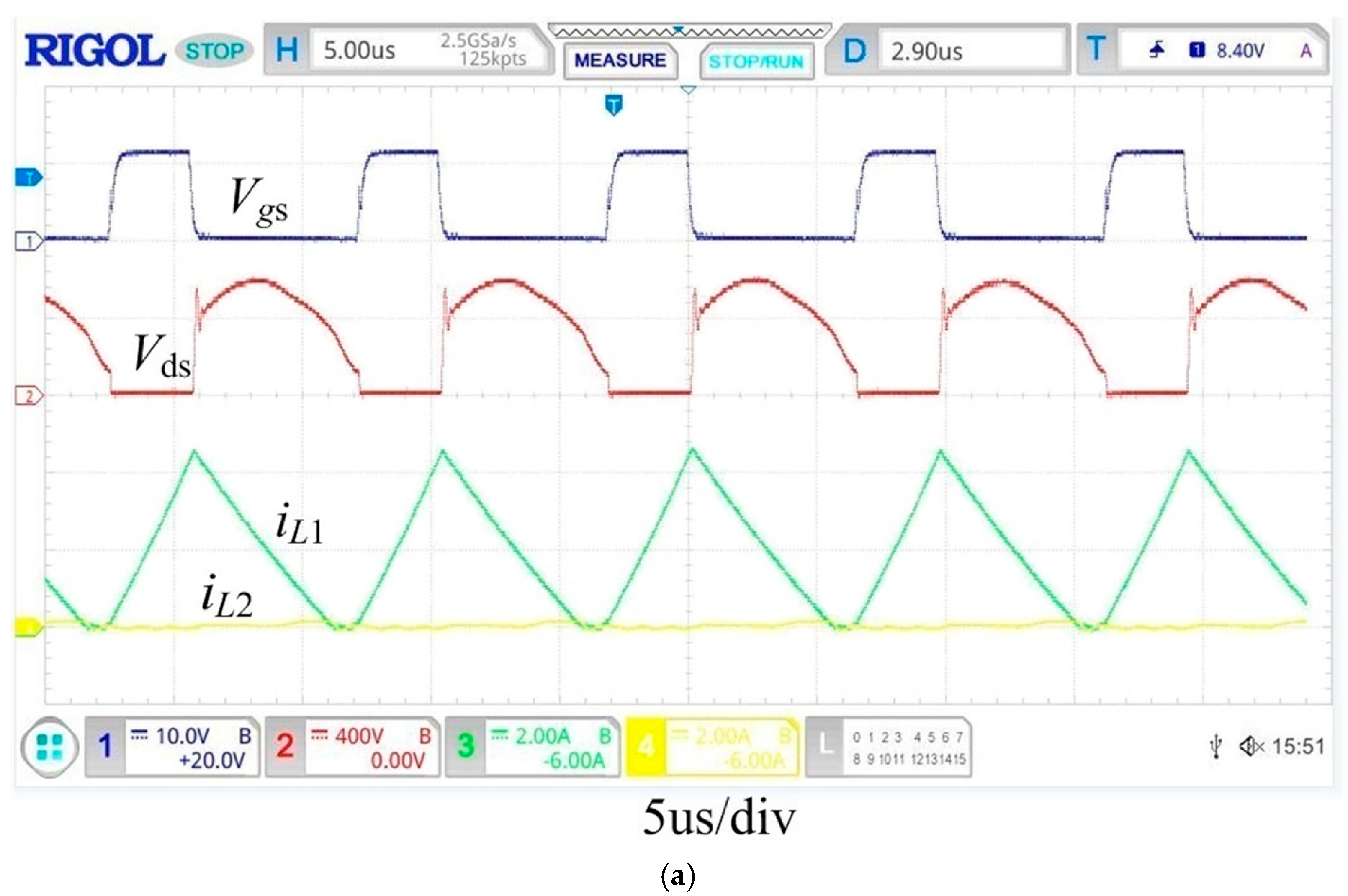
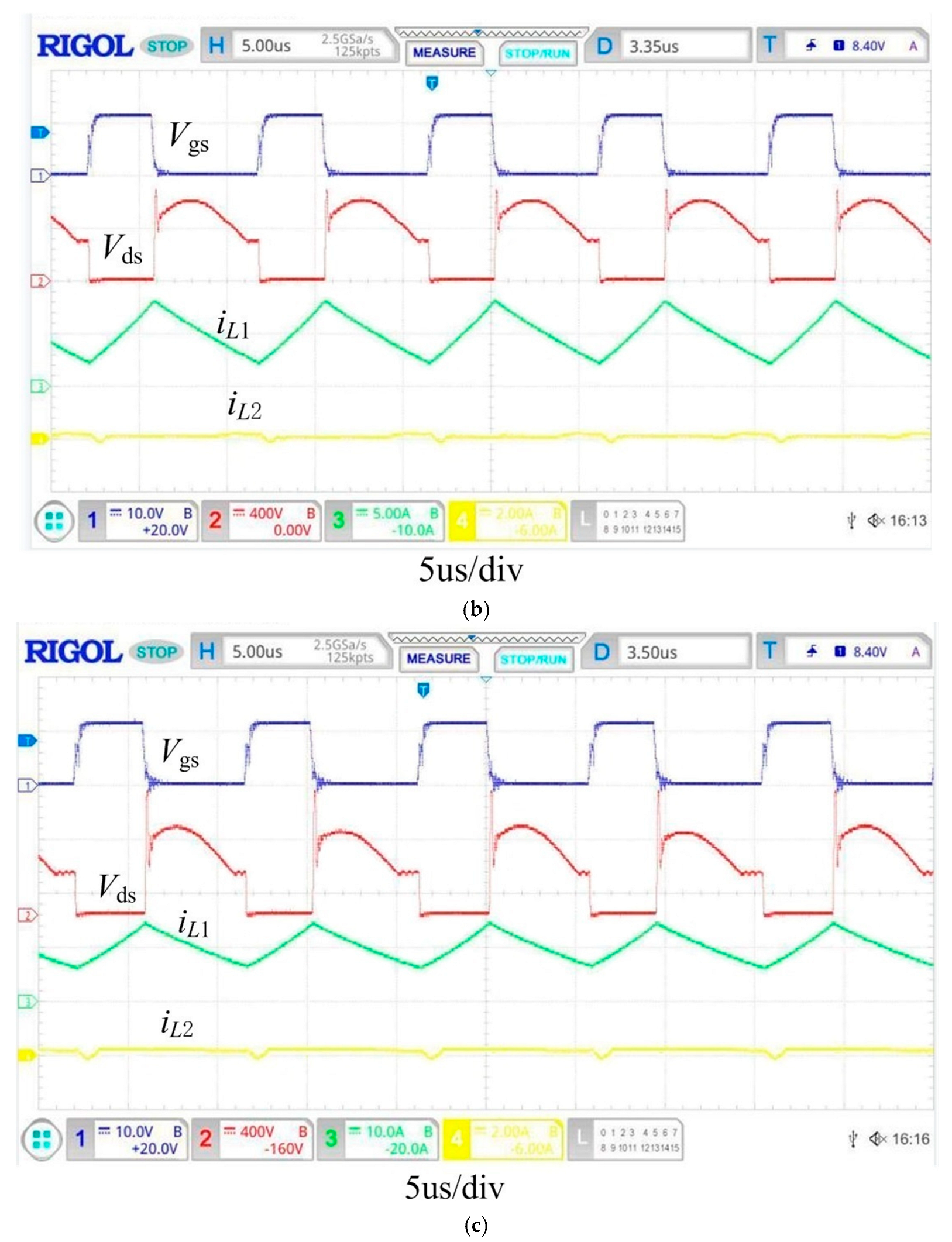
5.2. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pol, P.V.; Patil, S.L. A High Efficiency Modified Forward Converter for Solar Photovoltaic Applications. Electr. Power Compon. Syst. 2023, 51, 525–537. [Google Scholar] [CrossRef]
- Kim, C.E.; Baek, J.; Lee, J.B. Improved Three Switch-Active Clamp Forward Converter With Low Switching and Conduction Losses. IEEE Trans. Power Electron. 2019, 34, 5209–5216. [Google Scholar] [CrossRef]
- Abareshi, M.; Hamzeh, M.; Farhangi, S.; Alavi, S.M. Robust control of a forward-converter active battery cell balancing. IET Power Electron. 2023, 16, 1271–1280. [Google Scholar] [CrossRef]
- Ghorbanian, M.; Maghsoudi, M.; Esteki, M.; Farzanehfard, H. Forward converter using a resonant auxiliary circuit to provide soft-switching and reset the magnetic core. IET Power Electron. 2022, 15, 1713–1724. [Google Scholar] [CrossRef]
- Phillips, A.; Cook, T.; West, B.; Grainger, B.M. Gallium Nitride Efficacy for High-Reliability Forward Convertersin Spacecraft. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5357–5370. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Liao, M.Y.; Jiang, D.R.; Yang, X.B.; Li, S. High step-up isolated forward-flyback DC/DC converter based onresonance with pulse frequency modulation. J. Power Electron. 2021, 21, 483–493. [Google Scholar] [CrossRef]
- Li, H.Z.; Liu, X.Y.; Li, H.F.; Lan, T.W. Analysis and Design Criteria of Integrated Magnetics in Forward Converter. Proc. CSEE 2019, 39, 3667–3675. [Google Scholar]
- Gao, S.S.; Song, H.K.; Wang, Y.; Xu, R.; Xu, D.G. A Secondary-Resonance MHz Active-Clamp Flyback Converter with Partial Power Processing. IEEE Trans. Ind. Appl. 2022, 58, 7988–7997. [Google Scholar] [CrossRef]
- Ghazali, M.; Adib, E.; Ting, C.Y. Efficient Soft Switching Single-Stage PFC for Low-Power Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 818–825. [Google Scholar] [CrossRef]
- Li, H.Z.; Fan, L.L. Dual-tube Forward Converter with Electromagnetic Integration of Various Magnetic Materials. J. Electr. Eng. 2022, 17, 148–155. [Google Scholar]
- Chen, D.L.; Fan, Y.P.; Yan, Y.G. Research on Magnetic Reset Technique of Forward Converters. Power Electron. 1998, 1, 36–41. [Google Scholar]
- Wu, H.F.; Xing, Y. Families of Forward Converters Suitable for Wide Input Voltage Range Applications. IEEE Trans. Power Electron. 2014, 29, 6006–6017. [Google Scholar] [CrossRef]
- Santosh, S.G. Study Of RCD Clamp Forward Converter. Int. J. Adv. Electron. Commun. Syst. 2014, 3, 246–250. [Google Scholar]
- Gao, M.Y.; Gao, X.L. Research on the Design Range of RCD Clamping Circuit Parameters. Electr. Autom. 2019, 41, 65–67. [Google Scholar]
- Ning, P.H.; Chen, L.Z.; Ding, X.L.; Xia, X.G. Research on Dual Switch Forward Converter with Dual RCD Clamp. J. Power Supply 2016, 14, 124–130. [Google Scholar]
- Wang, L.; He, N.Y.; Chen, Z.H.; Hu, J.; Guo, Q.L. Analysis and Design of Passive Dissipative RCD Clamping Circuit for Flyback Converter. J. Lanzhou Inst. Technol. 2021, 28, 66–71. [Google Scholar]
- Tan, F.D. The forward converter: From the classic to the contemporary. In Proceedings of the APEC Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.02CH37335), Dallas, TX, USA, 10–14 March 2002; pp. 857–863. [Google Scholar]
- Kim, M.H.; Lee, S.H.; Lee, B.S.; Kim, J.Y.; Kim, J.K. Double-Ended Active-Clamp Forward Converter with Low DC Offset Current of Transformer. IEEE Trans. Ind. Electron. 2020, 67, 1036–1047. [Google Scholar] [CrossRef]
- Wu, K.; Qian, T.; Wang, H. Analysis, Design, and Implementation of a Soft-Switched Active-Clamped Forward Converter with a Current-Doubler Rectifier. Trans. China Electrotech. Soc. 2018, 33, 4771–4779. [Google Scholar]
- Liu, S.L.; Cao, J.; Hu, C.Y.; Yan, J.Z.; Wang, C.L. Energy Transmission Modes and Output Ripple Voltage of Forward-Flyback Converter. Trans. China Electrotech. Soc. 2019, 34, 1647–1656. [Google Scholar]
- Peng, Y.Q.; Liu, S.L.; Wu, H.; Lu, B. Optimized design of transformer of forward-flyback converter. Trans. China Electrotech. Soc. 2020, 35, 470–476. [Google Scholar]
- Hu, Y.; Ge, L.A.; Lin, W.M. A Novel Forward-flyback Converter. Power Electron. 2011, 45, 38–39. [Google Scholar]
- Khorasani, R.R.; Adib, E.; Farzanehfard, H. ZVT Resonant Core Reset Forward Converter With a Simple Auxiliary Circuit. IEEE Trans. Ind. Electron. 2018, 65, 242–250. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Input voltage | AC 165~265 V |
| Input frequency | 40~60 Hz |
| Switching frequency | 100 kHz |
| Maximum efficiency | ≥90% |
| Output ripple | ≤1% Vo |
| Output voltage | 48 V |
| Output current | 10 A |
| Load adjustment rate | ±2% |
| Components | Part Number |
|---|---|
| Power switch S | 80R280P7 |
| Diodes D1–D4 | MM60F060PC |
| Transformer core T | EE/42/21/15 |
| Control chip | UC3845 |
| Load (A) | Output Voltage (V) | Load (A) | Output Voltage (V) |
|---|---|---|---|
| 1 | 48.14 | 6 | 48.01 |
| 2 | 48.11 | 7 | 47.99 |
| 3 | 48.08 | 8 | 47.97 |
| 4 | 48.06 | 9 | 47.94 |
| 5 | 48.03 | 10 | 47.91 |
| Topology | Converter in [17] | Converter in [18] | Converter in [21] | Proposed Converter |
|---|---|---|---|---|
| Switch | 2 | 3 | 1 | 1 |
| Inductors | 3 | 2 | 2 | 2 |
| Diodes | 4 | 3 | 4 | 4 |
| Voltage stress of the Switch | High | High | High | Adjustable |
| Low-voltage turn-off | No | No | Yes | Yes |
| Excitation energy | Consumed | Input | Output | Output |
| Efficiency | Low | High | Medium | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Liu, S. A Novel Secondary Side Series LCD Forward Converter with High Efficiency and Magnetic Reset. Appl. Sci. 2023, 13, 7640. https://doi.org/10.3390/app13137640
Zhu G, Liu S. A Novel Secondary Side Series LCD Forward Converter with High Efficiency and Magnetic Reset. Applied Sciences. 2023; 13(13):7640. https://doi.org/10.3390/app13137640
Chicago/Turabian StyleZhu, Gaozhong, and Shulin Liu. 2023. "A Novel Secondary Side Series LCD Forward Converter with High Efficiency and Magnetic Reset" Applied Sciences 13, no. 13: 7640. https://doi.org/10.3390/app13137640
APA StyleZhu, G., & Liu, S. (2023). A Novel Secondary Side Series LCD Forward Converter with High Efficiency and Magnetic Reset. Applied Sciences, 13(13), 7640. https://doi.org/10.3390/app13137640







