1. Introduction
Cybersecurity has become a significant concern due to frequent and complex cyberattacks and a changing threat landscape, creating an emergency for organizations worldwide [
1], such as an increase of up to 62% in cyberattacks to organization’s supply chain, and up to 75% in the number of general cyberattacks directly received by organizations [
2]. To address this challenge, a holistic management approach and unity of action [
3] are required, involving a cross-functional cybersecurity workforce from tactical and operational levels, with a sense of urgency. However, in today’s organizational landscape, managing cybersecurity from a holistic perspective poses significant challenges. One of the most crucial obstacles is the lack of methodological development to manage cybersecurity at lower organizational levels, which can lead to improper organization and alignment with strategic cybersecurity goals, hindering the organization’s ability to respond quickly to changing cyber threats. While frameworks such as the Framework for Improving Critical Infrastructure Cybersecurity [
4] or the International Organization for Standardization (ISO) 27000 [
5,
6] family of standards are commonly used at the strategic level, they fail to provide procedural foundations for tactical and operational levels. Another challenge lies in achieving holism [
7] when collaborating in cross-functional internal–external teams with different chains of command at lower organizational levels, which necessitates the development of suitable mechanisms. Additionally, the absence of standardized and homogeneous cybersecurity evaluation criteria [
8] at lower levels poses a significant challenge to assessing the current and expected cybersecurity status in a holistic manner.
To address this set of difficulties, CyberTOMP [
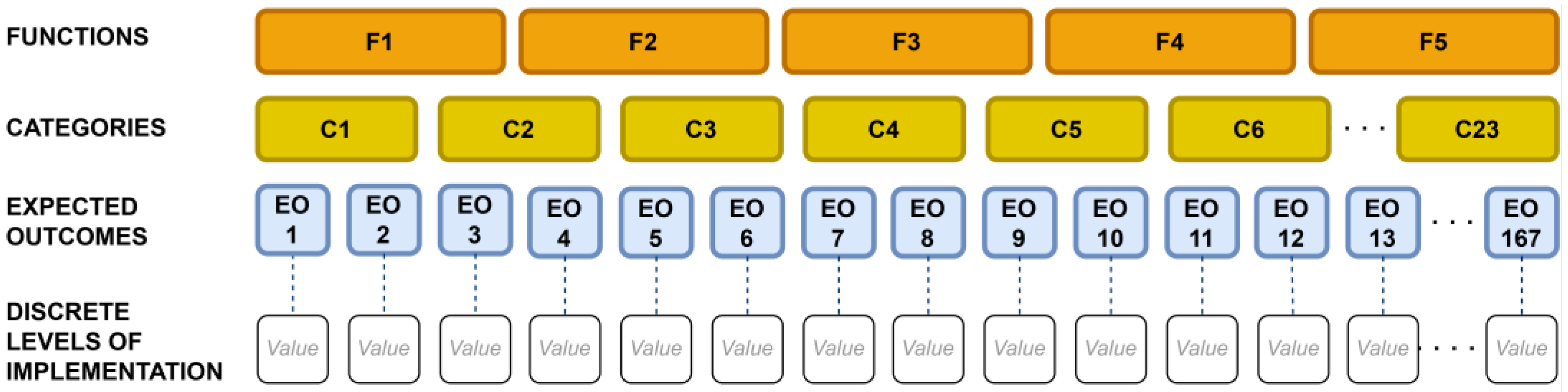
9] was designed. It is a framework to manage holistic cybersecurity at tactical and operational levels. The CyberTOMP framework comprises various components that collectively provide organizations with what is necessary for the holistic management of cybersecurity at tactical and operational levels. One of these components is the Unified List of Expected Outcomes (ULEO), which is an organized list of cybersecurity actions in a four-level tree-structure format (asset level at the top, then function level, category level, and expected outcome level at the bottom). It is a common and homogeneous list that represents all the cybersecurity actions that should be implemented to protect a specific asset. Along with this, it defines a set of metrics that can be aggregated and that, together, allow for the evaluation of the current cybersecurity status of assets or their evolution over time, or the establishment of cybersecurity objectives at any level of the organization.
This list and set of metrics have been developed by combining cybersecurity actions from different de facto standards in this area [
4,
10,
11]. None of these standards need to be implemented in the organization, but the application of CyberTOMP will allow for their implementation in a much faster and simpler way, if necessary. Furthermore, if any of these standards are already implemented in the organization, the application of CyberTOMP will already be partially achieved. Moreover, the complete list of cybersecurity actions (also called expected outcomes) are grouped in three different implementation groups (IGs) that allow organizations to apply proportionate cybersecurity actions depending on the criticality of assets (e.g., the minimum subset, the intermediate subset, or the whole list of cybersecurity actions). Each outcome has a discrete level of implementation (DLI) assigned to it [
12], based on the deployment degree of the required actions to achieve the corresponding expected outcome (
Figure 1). This ensures an impartial evaluation of an organization’s cybersecurity posture and avoids conflicts, bias, or misinterpretations.
In addition to this component, CyberTOMP defines the process by which the cybersecurity workforce of the organization, consisting of different functional and multidisciplinary teams, must coordinate and work together to achieve the desired cybersecurity state in an orchestrated, holistic, and simultaneously aligned manner with the organization’s strategic objectives.
In general, the whole CyberTOMP framework has been designed in a way that guarantees that the implementation of the actions defined in the ULEO addresses a significant proportion of the current documented cyber threats [
13].
The ULEO determines an asset’s cybersecurity status based on the expected outcomes and their level of implementation. It also enables the assessment of cybersecurity status through hierarchical metrics and supports the establishment of strategic goals in the form of constraints for these metrics.
To comply with the strategic cybersecurity constraints, various combinations of expected outcomes, their implementation levels, and cybersecurity actions are possible and therefore must be evaluated. This is important because each expected outcome is translated into a set of required cybersecurity actions that have to be implemented. Consequently, each combination affects functional areas and can be influenced by previous or future investments in cybersecurity. Selecting a suitable combination requires determining the level of implementation for each outcome, ideally as close as possible to the current cybersecurity status. Metrics should be calculated to determine if the chosen solution meets the required constraints. If not, a new combination must be proposed. To attain the desired implementation levels, a thorough analysis of the work required must be conducted. Agreement among all functional areas is crucial, and if necessary, a new combination must be proposed to reach it.
CyberTOMP offers a guided process to coordinate cross-functional cybersecurity teams at all levels for the consecution of the expected outcomes at the desired level, achieving practical cybersecurity holism within the organization, easing the task list described in the previous paragraph. The process involves decision-makers meeting to agree on the asset’s required cybersecurity status, the cybersecurity actions to be implemented, and their levels of implementation, metrics, and indicators. This is where holism is guaranteed in CyberTOMP.
In practical applications of CyberTOMP, selecting the set of cybersecurity actions and implementation levels that allows achieving a desired cybersecurity status for the asset is complex due to the vast number of potential solutions. For low criticality assets, there are 1.98 × 1028 possibilities, and for high criticality, there are 3.5 × 10100 options. Manually identifying the right combination of expected outcomes and levels of implementation is time-consuming and often unacceptable, making it challenging to reach an agreed-upon cybersecurity status during the management gatherings where decisions must be made. Meeting strategic constraints while aligning with current cybersecurity status is difficult, especially when the number of constraints increases. This results in a process that only targets the first feasible combination instead of exploring more possibilities, making it challenging to hold a productive discussion.
Natural selection is a biological concept that explains how species evolve based on their ability (or inability) to adapt to their surrounding environment. Each individual (a single specimen) within a population possesses specific characteristics that are determined by its genetic composition. A chromosome contains a defined number of genes, with each gene encoding information about a specific characteristic of the individual. The characteristics of an individual, which are defined by the alleles of each gene, are more or less beneficial to the individual depending on the specific value of the alleles. The level of adaptation of an individual within a species to their surrounding environment is determined by their particular characteristics, which are defined by the alleles of each of their genes. Individuals with better characteristics are more likely to reproduce and give rise to new individuals, while those who are less adapted are likely to become extinct without reproducing.
It is common for the offspring of well-adapted individuals to have even better characteristics, resulting in a better-adapted population through the process of reproduction and genetic exchange. Another way in which a population can evolve is through mutation. While gene mutation in the natural world can often have fatal consequences, in certain cases, it can lead to a beneficial characteristic that enables an individual to unexpectedly prosper and become better adapted.
This natural evolutionary process has been transferred to the field of computing by designing algorithms, called genetic algorithms [
14], that mimic the way nature works in order to solve complex optimization problems. To do so, a problem is usually defined as the context to which individuals (potential solutions to the problem) must adapt, and mechanisms similar to those existing in nature are applied [
15]: mutation, crossover, adaptation, etc. Each individual is defined by a set of genes and alleles (variables and their respective values) that provide specific characteristics and determine their level of adaptation to the problem. In this context, being better adapted means being a better solution to the problem, while being less adapted means the opposite. Through a computationally accelerated process, genetic algorithms enable obtaining high-quality solutions to the proposed problem in a short amount of time in multiple applications.
Genetic algorithms are metaheuristic techniques useful in solving complex optimization problems [
16], such as tactical–operational cybersecurity management. These problems involve a large search space and a multitude of constraints that must be satisfied simultaneously. Genetic algorithms are useful tools to manage the processes of the organization and decision-making in different areas as presented in [
17], in which the authors review the operations management problems solved by genetic algorithms and suggest future research directions from the point of view of researchers and practitioners. Furthermore, [
18] focuses on the application of genetic algorithms in the eight processes of supply chain management. In the field of cybersecurity, [
19] presents a decision support system using a genetic algorithm to calculate uncertain cyberattack risk and determine the optimal combination of security countermeasures based on threat rates, costs, and asset impacts, whereas [
20] introduces an approach to optimize cyber security investments using various methods for risk-averse organizations, aiming to reduce the cost of cyber insurance while improving self-protection. Finally, it is worth mentioning [
21], which introduces a semi-automated approach based on Pareto optimality for selecting appropriate cybersecurity controls to minimize risks and address conflicting goals among stakeholders. To the best of our knowledge, there have been no prior studies employing genetic algorithms to support decision-making in the tactical and operational management of cybersecurity, specifically in the selection of cybersecurity actions applicable to business assets, from a holistic and cross-functional perspective.
By applying genetic algorithms to the exposed cybersecurity management optimization problem, organizations can improve their ability to choose faster, more accurately, and more easily the required cybersecurity actions to detect and respond to cyber threats, reduce vulnerability, and minimize risk.
This work contributes to tactical–operational cybersecurity management by means of a genetic algorithm that aids cross-functional cybersecurity teams in decision-making for the selection of the cybersecurity actions required to fulfill the strategic cybersecurity constraints/goals within the CyberTOMP framework. As a result of this, the decision-making process is boosted and made easier, leading to a reduction in the workload of cybersecurity personnel. The two most significant contributions of our study are as follows:
An appropriate mechanism for searching feasible sets of cybersecurity actions for their application to the CyberTOMP framework.
The demonstration of the application of evolutionary computing to decision-making in cybersecurity management.
These contributions are directly applicable to all organizations that deploy the CyberTOMP framework and are being validated by two different entities. Furthermore, they can be promptly adapted for use with other frameworks, with the National Institute of Standards and Technology (NIST) framework being particularly well-suited.
The subsequent sections of this document are organized as follows: In
Section 2, a description of the relevant features and parameters of our algorithm is provided.
Section 3 outlines the set of experiments that we conducted to assist decision-makers in selecting the appropriate cybersecurity actions to achieve strategic cybersecurity objectives. The results of these experiments are presented and discussed. The paper concludes with a summary and conclusions in
Section 4.
2. Problem Modeling and Formulation
To achieve a comprehensive and effective cybersecurity strategy, it is essential to foster collaboration among the different functional areas that comprise the cross-functional cybersecurity workforce within an organization. In the CyberTOMP framework, this collaboration is facilitated through a series of meetings where the necessary cybersecurity safeguards required to achieve strategic cybersecurity constraints are established. However, in practice, these meetings can be ineffective as the number of possible combination of actions is too large to be manually or nearly manually identified and analyzed within a reasonable period.
The main objective of our research is to provide a technological solution to address this managerial challenge. Specifically, our study aims to develop a Fast, Lightweight, and Efficient Cybersecurity Optimization (FLECO) mechanism consisting of an adaptive, constrained and multi-objective genetic algorithm. This algorithm will enable the swift identification of high-quality solutions or sets of solutions that can be discussed among all cybersecurity participants, thus facilitating the applicability of tactical–operational cybersecurity management processes within the organization.
As stated, the field of evolutionary algorithms, and genetic algorithms in particular, has been used broadly to solve not only technical aspects, but also, often, managerial challenges in a broad range of disciplines. In this case our proposal consists of applying this approach to a cybersecurity management problem, thus contributing to enhancing the procedural basis for cybersecurity management at organizations’ lower levels.
2.1. Determining Value of FLECO Parameters
In the course of designing and developing FLECO, multiple adjustments were required to ensure that the algorithm operated as intended and yielded valuable solutions. FLECO is designed for organizations that are implementing the CyberTOMP framework to manage cybersecurity at the tactical and operational levels, and to ensure its comprehensive validity, we collaborated with two organizations in the design and validation process. The first organization is a non-technological small or medium-sized enterprise (SME), consisting of fewer than 40 employees and only 2 departments. The meetings held to discuss the cybersecurity actions to be implemented include only three to five individuals. The second organization is a public entity with over 300 direct employees, 5 departments, and 11 primary functional areas. This organization has several outsourcing contracts, and its teams comprise in-house as well as external personnel. Meetings held to determine the set of cybersecurity actions involve 15–20 individuals. Both organizations are implementing CyberTOMP to varying degrees and have encountered the challenges outlined in
Section 1. During the multifunctional cybersecurity workforce meetings, where the different teams must reach an agreement on which cybersecurity actions to implement and to what depth, these teams were unable to find a solution in these two companies. The main reason is the large number of existing combinations, which is unmanageable manually; a secondary reason is that the different teams were unable to search for combinations that simultaneously satisfied more than one objective: complying with the constraints defined at the strategic level related to CyberTOMP metrics; maximizing similarity with respect to the currently enforced combination to leverage previously completed work; and maximizing all the assets’ global cybersecurity state. Without the possibility of finding valid combinations that maintain a balance between all objectives, the work meetings planned in CyberTOMP to ensure the required holism are meaningless. Therefore, the main motivation of our work is the design of a technological mechanism that enables the quick obtainment of solutions that can be shared in the meetings planned in CyberTOMP, and thus, achieve the necessary holism in these organizations.
During the design phase of FLECO, we conducted hundreds of executions, most of which were unsuccessful. We made numerous modifications and decisions in collaboration with the aforementioned organizations, such as determining the value of the weights, defining strategic constraints, specifying the requirements for a solution to be deemed acceptable, and defining the genetic operators, among others [
22]. At the end of the experimentation phase, these organizations participated in validating the efficacy of the proposal and testing its effectiveness in their specific use cases.
2.2. Formulation of the Multi-Objective Optimization Problem
Let P be the multi-objective optimization problem [
23,
24]. Let
be the set of feasible solutions for the optimization problem. Let
be the vector representation of an asset’s cybersecurity status, where each element
denotes the degree to which the required cybersecurity measures have been implemented to achieve the expected outcome
. The length of the vector is determined by
, which varies depending on the cybersecurity criticality of the asset. We define
as a real-valued function that quantifies the number of strategic cybersecurity constraints satisfied by the vector
. Similarly, we define
as a real-valued function that captures the similarity between the current asset’s cybersecurity state and a previously recorded state. Finally, we define
as a real-valued function that characterizes the overall level of cybersecurity achieved by the asset, as determined by its current cybersecurity status represented by
.
Formally, we express , , and as functions that belong to the set of real numbers (ℝ), such that . These functions are designed to satisfy mathematical properties that allow for their effective use in the optimization process, which ensures that their values are meaningful and can be used to compare different solutions in a mathematically rigorous manner.
FLECO computes the individual fitness by means of a scalarization function, as shown in Equation (1). Specifically, the weighted sum scalarization function used is , where is the weight associated to each objective (). The values of , , and were determined after an extensive analysis process. During this period, hundreds of FLECO executions were performed with different initial statuses and various strategic constraints. These executions were supervised by the organizations’ decision-makers, who worked together with experts and the rest of the team to tune the weights until the convergence time of FLECO was deemed acceptable, and the generated solutions met the requirements of the organization. Finally, the values of , , and were established as , , and , which were deemed to be the optimal weights for the FLECO algorithm.
We define the multi-objective problem as follows:
The function denoted by
serves to amalgamate the set of strategic cybersecurity constraints [
25]. This approach was chosen to provide guidance to the algorithm towards generating a high-quality set of feasible solutions. Consequently, while non-feasible solutions persist within the population, they are not regarded as solutions.
2.3. Representation of Individuals
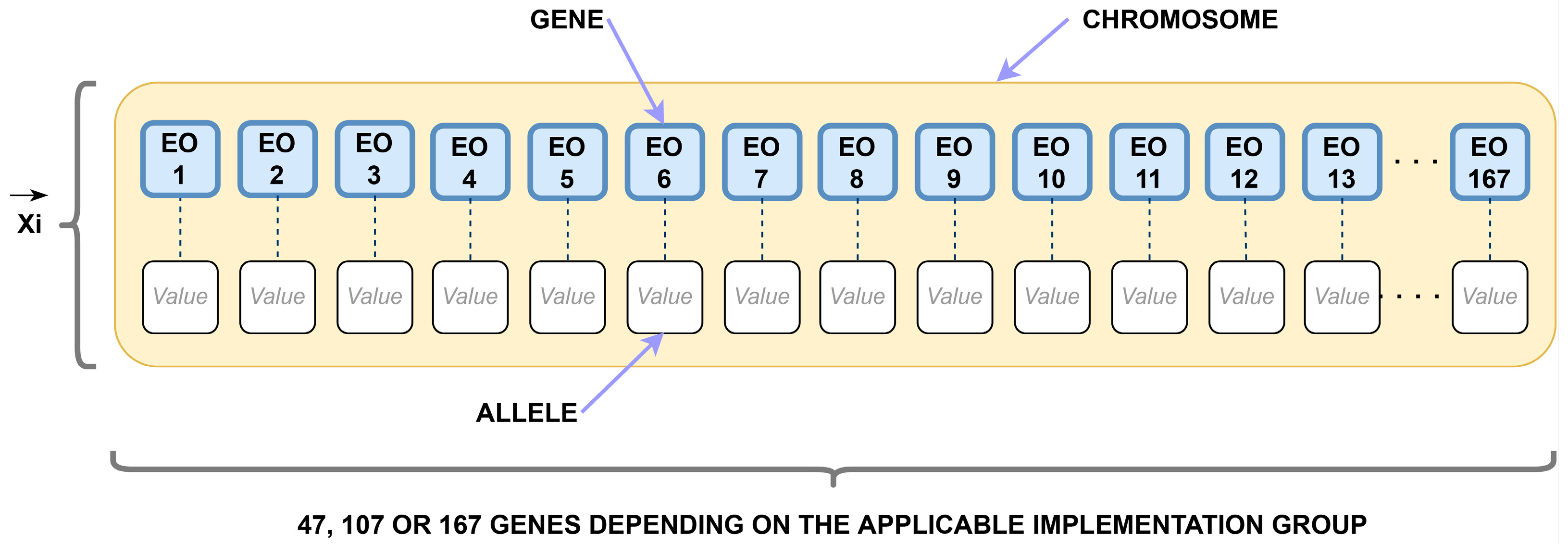
The present study considers the expected outcome level resulting from the structure of the ULEO, as depicted in
Section 1,
Figure 1. This expected outcome level will be treated as a chromosome in the problem under consideration [
26]. Due to the three distinct implementation groups, the expected outcomes are clustered accordingly. Hence, there are three possible chromosome lengths, as not all expected outcomes are applicable to every implementation group. Based on the cybersecurity criticality of the asset and its corresponding implementation group, the FLECO is capable of handling individuals with 47, 107, or 167 genes. Each gene represents an expected outcome from the ULEO.
In practical deployment, achieving the mentioned outcome would necessitate a set of cybersecurity actions to be implemented. Depending on the extent to which these actions are accomplished, a discrete level of implementation is assigned to each gene. These four discrete levels of implementations are the alleles in our proposal (
Figure 2).
Finally, the number of genes (decision variables) and alleles (values for those decision variables) determine the number of potential solutions that could be explored, depending on the applicable implementation group. The number of possibilities to explore for implementation group 1, 2, and 3 are 1.98070 × 10
28, 2.63281 × 10
64, and 3.4996 × 10
100, respectively, as shown in
Table 1.
2.4. Crossover and Mutation Operators
Our proposal uses a standard two-point crossover operator with a crossover rate of 0.90 that was chosen based on previous ranges in the literature [
27,
28] and experimentation. The objective is to balance chromosome recombination with preserving genetic material from highly fit individuals. When triggered, two new offspring are generated from each set of two parents.
The mutation phase uses a predetermined rate of 1/L, where L is the number of decision variables (the chromosome length). This rate is widely used in the related literature [
29] and is known to provide significant diversity. FLECO applies this mutation rate to every gene in each chromosome, ensuring that, when applicable, the new allele is different from the current one. If the mutation is triggered for any gene, an additional new individual is generated from the corresponding chromosome.
2.5. Population and Selection Method
FLECO’s initial population includes high-quality and randomly selected individuals to reach the designated population size. Subsequent populations are generated through a selection process, followed by the application of the crossover and mutation mechanisms until the population reaches the defined value. Individuals are then sorted based on fitness, and the top 30 individuals are selected to maintain the predetermined population size after each generation. A population size of 30 individuals was chosen based on an examination of various alternatives within the range provided in [
30] for population size, mutation, and crossover rates. During each generation, the algorithm identifies the most suitable individuals for the reproduction phase. Twins are excluded from the population as they possess identical genetic material, which detracts from the quality of the population [
31,
32]. The top 1/5 (20%) of individuals are selected for reproduction, while the remainder are discarded, based on a threshold established through micro-experiments to promote FLECO’s convergence time and produce feasible solutions of remarkable quality.
2.6. Algorithm Stopping Criteria
The business challenge that FLECO aims to solve, as described in
Section 1, requires the swift response of a feasible solution. A feasible solution in this context must satisfy the following requirements:
The solution is provided in a timely manner. Since the solution must be discussed in a meeting to reach agreements, it is necessary that the solution is provided to the cross-functional cybersecurity workforce by FLECO within a reasonable timeframe, no longer than 5 min. This requirement has been established by the organization’s decision-maker responsible for deploying the CyberTOMP framework. Subsequently, the proposed solution can be deliberated upon amongst various functional domains, ultimately accepted upon consensus, or rejected outright.
The solution must fulfill all the specific cybersecurity constraints, which is ultimately achieved if
as described in
Section 2.2.
The algorithm will terminate when either of the two conditions is met.
In the event that the algorithm terminates due to time constraints (the limit of five minutes), the population may not have converged, and the resulting solutions may not be feasible. This can occur when the algorithm reaches a stagnation point and is unable to escape it, but it is more likely to happen when the strategic constraints are highly stringent or even contradictory, rendering it impossible to identify a solution that satisfies all of them.
Furthermore, in the process of designing and developing FLECO, it was determined that the algorithm must be able to run on general-purpose hardware, comparable to the ones employed in the organizations’ operational setting, such as a standard laptop or desktop personal computer, rather than on specialized hardware.
2.7. Stagnation Detection and Scape
The FLECO algorithm incorporates a mechanism to detect stagnation and, if possible, escape it in order to converge towards a high-quality solution (Algorithm 1). To do so, a time threshold (2.5%) is defined as a percentage of the maximum allowed time (five minutes). At the beginning of the algorithm, the current time is recorded and updated every time the best individual fitness is improved. If there is no improvement, the time remains the same. This approach enables the computation of the consumed amount of time from the last improvement of the best chromosome’s fitness. If the time reaches the defined threshold and the population has not yet converged, the stagnation warning is triggered.
| Algorithm 1. Pseudo-code of the mechanism for stagnation detection and scape. |
| 1: | Set default values for FLECO parameters |
| 2: | While conditions to stop FLECO are not met |
| 3: | | Update last time the best individual’s fitness changed |
| 4: | | Compute period from last time best individual’s fitness changed to “now” |
| 5: | | Estimate whether FLECO seems to be in a local minimum |
| 6: | | Estimate whether FLECO is deeply stagnated |
| 7: | | If seems to be in a local minimum |
| 8: | | | Apply increased mutation rate |
| 9: | | | If it is deeply stagnated |
| 10: | | | | Remove current 50% of population’s best individuals (soft reset)
Regenerate the population with random individuals |
| 11: | | | End if |
| 12: | | | Increase diversity by adding extra random individuals |
| 13: | | Else |
| 14: | | | Reset FLECO parameters to their default values |
| 15: | | End if |
| 16: | End while |
Under stagnation, the FLECO algorithm adapts dynamically to try to escape from local minimums:
The “raw” population size, which is typically 30 in our proposal or very close to it, is enlarged up to 50% more, resulting in a total of 45 individuals [
33,
34]. This size adjustment aims to help the algorithm explore alternative regions of the solution space.
Additionally, the mutation rate, usually fixed at 0.05, is dynamically increased [
35] 20-fold to yield a value of 1.0, which helps the algorithm evade potential sub-optimal solutions.
If the entrapment situation persists despite these adaptive adjustments, a secondary threshold (3.13%) is used to detect it. In this case, the top 1/2 (50%) of the best fitted individuals in the population are removed from the population and replaced by random individuals. This adjustment functions as a soft reset for the algorithm [
36], preserving part of the already mature population while eliminating the most problematic individuals. This approach enables FLECO to escape from low-quality solutions in most situations and explore alternative regions of the solution space.
This parameter adjustment process implemented in FLECO to prevent stagnation improves upon its adaptive capabilities [
37], enabling it to effectively respond to the evolving problem context. The activation of the jamming alert does not inherently impact the quality of the solution identified by FLECO. It serves solely as a mechanism to detect the potential occurrence of the algorithm becoming trapped in a local minimum. If such a situation arises, the alert aids in the algorithm’s escape from this state and facilitates the continued exploration of the solution space for potential alternatives. Once the local minimum is successfully bypassed, the dynamic parameters are reset to their predetermined values.
3. Experiments Design and Result
The management of tactical and operational aspects of cybersecurity is of paramount importance in achieving comprehensive and effective cybersecurity. To this end, and in response to the needs of the organizations’ decision-makers, our experiments were designed to assess whether FLECO could deliver a meaningful enhancement in terms of efficiency and effectiveness, thereby significantly improving the decision-making process in cybersecurity management meetings and ultimately optimizing cybersecurity outcomes.
3.1. Definition of Initial Statuses
In order to ensure uniformity in all experiments, we deemed it appropriate to utilize a set of randomly chosen chromosomes that would serve as the initial cybersecurity status for hypothetical assets, where their criticality level necessitates the application of IG1, IG2, or IG3. To prevent any potential bias in the operation of FLECO stemming from the use of specific initial statuses, we generated 15 unique, randomized initial statuses for each implementation group, allowing for testing under diverse circumstances.
3.2. Definition of Strategic Constraints
In a manner analogous to the configuration of initial states, a series of strategic constraints were devised in order to test each scenario under equivalent conditions. The primary objective of these strategic constraints was to encompass a minimum of 10% of the metrics outlined in the CyberTOMP proposal, at all levels (i.e., asset, function, category, or expected outcome). Notably, in practical applications of CyberTOMP, average metric coverage was observed to be below 1% for all cases, as it is highly unusual for personnel operating in the strategic sphere to establish constraints that fall beneath the level of asset or cybersecurity function. Nonetheless, in order to rigorously evaluate FLECO under challenging conditions, we opted to apply four sets of constraints that were 10 times greater in scale (
Table 2) to assess the effectiveness at asset, function, category, or expected outcome levels.
The strategic objectives are established in a fixed and proportionate manner to equally influence the exploration of potential solutions, regardless of the implementation group or the length of the chromosome.
In
Table 3, the strategic constraints that have been established for our experiments are presented in conjunction with their applicability to each implementation group. Each constraint has been defined as an operator and a value that references a metric that is defined in CyberTOMP.
3.3. Definition of Analysis Cases
The test suite comprises twelve combinations derived from the amalgamation of the three implementation groups and the four sets of predetermined strategic constraints at asset (A), function (F), category (C), and expected outcomes (EO) levels. The strategic constraints are clustered into four hierarchical levels, namely A, A-F, A-F-C, and A-F-C-EO levels that aggregate the corresponding constraints. These experiments focused on the evaluation of the convergence, convergence time, and solution quality, as well as the ability of FLECO to navigate the constrained region of solutions. To ensure comprehensiveness, 15 initial statuses are employed (
Section 3.1) and executed 15 times for each combination of implementation group and constraint type, resulting in a set of 225 executions per combination and a total of 2700 FLECO executions.
3.4. Execution and Experiment Results
The time required by FLECO to generate solutions after executing the test suite is shown in
Table 4. Every row represents a combination where 225 FLECO executions are summarized. The table shows, hence, the whole 2700 FLECO executions. The time mean, standard deviation, and median of every test case are presented in columns
,
, and
, respectively.
It is noteworthy that the FLECO algorithm demonstrated a 100% convergence rate in all 2700 executions (225 per case of analysis) conducted. This is of significant importance for the practical application of the algorithm to the real-world problem it is designed to address. Notably, despite being permitted a convergence time up to five minutes, the average time required by FLECO was s in the worst-case scenario. However, in the majority of the analysis cases, the minimum time to obtain a feasible solution was less, reaching s in the most favorable case. The convergence time tends to increase with an escalation in the number of constraints in the implementation group, i.e., when the chromosomes are larger, but even in these cases it is maintained below (and far from) the defined limit. Thus, the requirement of achieving a solution in less than five minutes is greatly accomplished by FLECO, which has been demonstrated to be fast. Moreover, all the experiments have been executed in hardware below the specified requirements, achieving the mentioned values, which reveals also that FLECO is efficient in the use of resources.
Regarding the quality of the generated solutions, in
Table 5 and
Table 6, the fitness means,
, for each optimization function and for the weighted function are shown, together with the median,
, and also the corresponding standard deviation,
, that indicates the dispersion degree of the 225 solutions for each analysis case. The average measurements of the functions
,
,
, and
, along with the corresponding disaggregated measurements, exhibit close proximity to the solution anticipated by the decision-makers of the organizations. These measurements align with the requirements of FLECO for recognizing a solution as feasible, where
, and, moreover, the observation of closely similar values across the various scenarios tested is indicative of FLECO’s ability to obtain solutions of comparable quality, regardless of the situation.
The computed standard deviation for each case is kept around for all analysis cases, which denotes that FLECO is able to reach solutions with similar quality regarding the surrounding conditions. The test suite was purposefully designed and implemented to validate FLECO, incorporating diverse conditions for each run. These conditions include variations in starting points, restrictions on metrics, implementation groups, random populations, and other factors. As a result, we have been able to gather results from a total of 2700 executions. Although each execution possesses unique characteristics, they all exhibit a similar level of quality and completion time. This achievement is attributed to the meticulous fine-tuning of various algorithm parameters, guided by decision-makers from different domains from the collaborating companies. Weeks of testing have facilitated the enhancement of FLECO’s capability to effectively explore the solution space and discover high-quality solutions. This serves as a positive indication of the algorithm’s efficacy and consistency in generating solutions, and its ability to comply with the requirement of generating valuable solutions for the cybersecurity workforce to discuss.
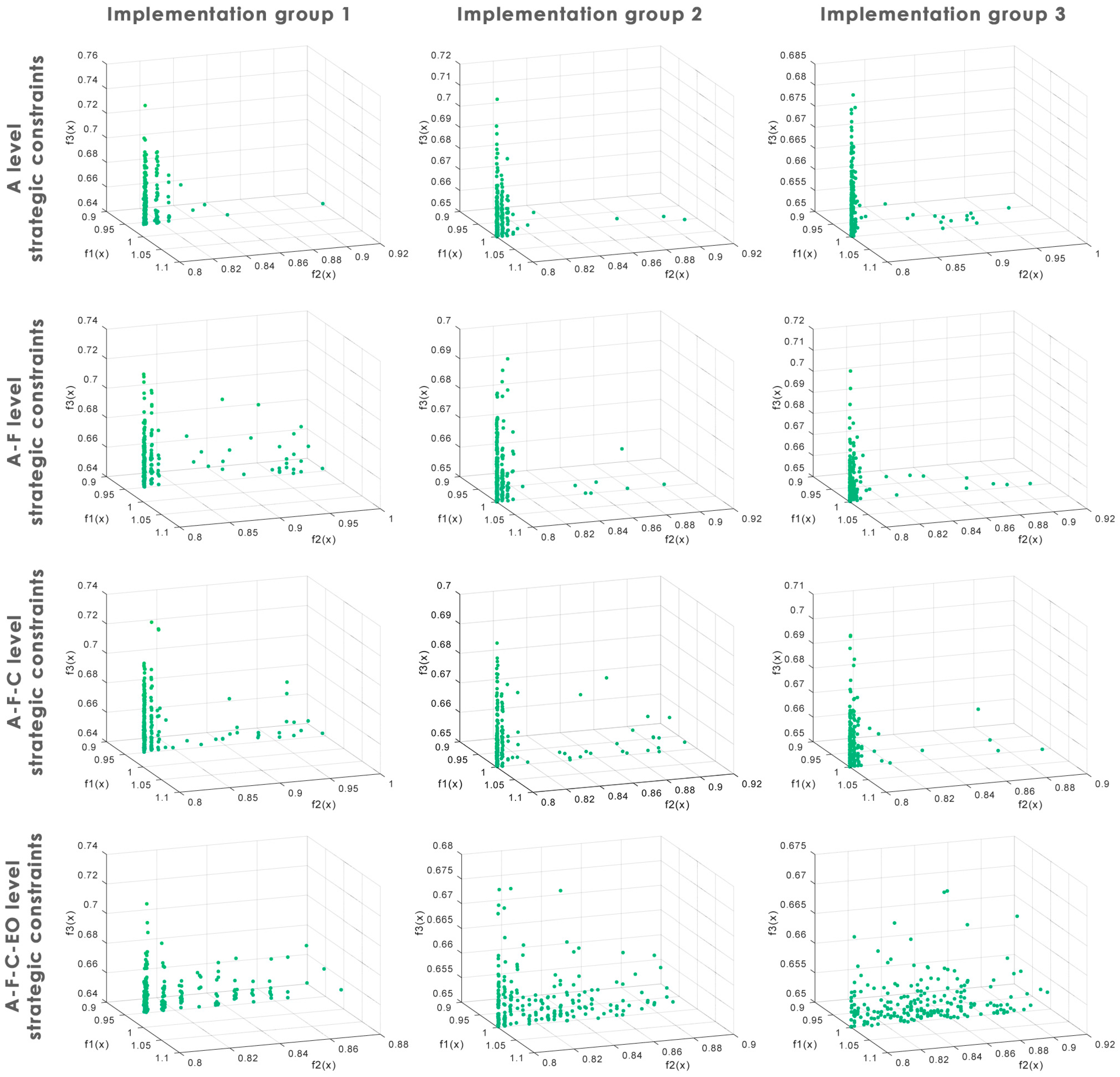
Regarding FLECO’s ability to explore the solution space,
Figure 3 presents 12 charts, each corresponding to an analysis case where 225 solutions are displayed (2700 in total).
These charts depict the impact of applying constraints to the problem and its consequent effect on the constrained solution space. The results indicate that the feasible solution space becomes more fragmented as the number of decision variables is increased (which is the same as increasing the corresponding IG) and when more constraints are imposed on the problem, ranging from 1 to 22 in the designed experiments. Nonetheless, what is noteworthy is that the FLECO algorithm managed to explore these narrow segments of the constrained solutions space, in search of solutions, at an adequate level.
4. Conclusions and Future Work
In this research work, we address the potential of evolutionary computation for solving an optimization problem related to cybersecurity management. To this end, we have developed FLECO, a multi-objective, constrained, and adaptive genetic algorithm that assists the cybersecurity workforce in selecting the set of actions that must be implemented to comply with the cybersecurity restrictions required from the strategic sphere. The multidisciplinary cybersecurity teams, consisting of 3–5 and 15–20 members, respectively, from the collaborating companies in this study encountered difficulties in finding feasible combinations of cybersecurity actions without the aid of FLECO. These combinations were essential for their discussions and the achievement of comprehensive agreements as mandated by the CyberTOMP framework. Despite numerous attempts over the course of a month while the design of FLECO was in progress, the teams were unsuccessful in identifying a feasible set of cybersecurity actions that met the requirements within the specified timeframe of less than 5 min, as stipulated by the decision-makers of these companies. In fact, they were unable to find a suitable set even after dedicating significant additional time. Addressing this need, FLECO provides feasible sets of cybersecurity actions that fulfill the multiple established objectives in a significantly shorter time than what is required by the decision-makers of the participating companies. This capability has enabled them to conduct tactical–operational management meetings, explore different combinations, and achieve holistic cybersecurity starting from the lower levels of the organization. The specific contributions of our work to this scenario are as follows:
An effective mechanism, as it discovers solutions that comply with all business-level constraints.
A rapid mechanism, as it achieves this within a timeframe of less than 5 min, facilitating the smooth implementation of the CyberTOMP framework.
An efficient mechanism, as it operates using general-purpose hardware similar to the workstations commonly found in contemporary companies.
A predictable mechanism, as it exhibits stable behavior regardless of search conditions, consistently delivering solutions of comparable quality.
The practical demonstration of the application of evolutionary computing to decision-making in cybersecurity management.
The algorithm has been designed based on the specifications of the CyberTOMP framework, which makes it useful and directly applicable to organizations that are using this framework for tactical and operational cybersecurity management. However, it is easily modifiable to adapt to similar frameworks, the NIST framework being particularly well-suited. Furthermore, the set of test cases designed to validate FLECO has also aimed to minimize bias and the influence that the participation of two specific organizations may have on the results.
FLECO has demonstrated its speed, efficiency, and effectiveness in finding solutions in a wide variety of contexts, meeting the expectations set by decision-makers in the participating organizations regarding the quality of the solutions provided, the speed with which those solutions are generated, and the positive effect this has on the holistic, tactical–operational cybersecurity management process and meetings that CyberTOMP foresees to discuss and jointly agree on cybersecurity actions to execute.
In summary, we can say that evolutionary computation in general, and genetic algorithms such as FLECO in particular, can positively make a difference in decision-making in a poorly explored area such as tactical–operational cybersecurity management.
As part of our research we have also identified some lines for future work we deem necessary to expose. Firstly, although we have made every effort to design both the algorithm and experiments to avoid bias, it is difficult to eliminate it completely given the subjectivity inherent in defining a solution as good or bad for each organization and its reflection in the weights and ratios that serve as a parameter for the algorithm. For that reason, we intend to address this by conducting further tests with different types of organizations focused on increasing the validity of FLECO in any situation. We also believe that it is important to explore alternatives that require less intervention by decision-makers for their final adjustment, such as algorithms based on Pareto dominance. Secondly, while FLECO represents a qualitative and quantitative leap in the application of the principles indicated by the CyberTOMP framework, we believe that this contribution could be much greater if optimization functions were defined that covered more complex business objectives and whose outcome was to minimize the human effort required to select the set of cybersecurity actions. As a consequence, we plan to expand the solution by including economic or effort aspects required for each expected cybersecurity outcome, which could significantly enhance the assistance that FLECO provides to the teams responsible for selecting and designing cybersecurity actions.