Study of Electrical Neural Stimulation Effects Using Extraneural and Intraneural Electrodes

Abstract

Sensory feedback restoration in upper-limb neuroprosthetics can significantly enhance amputees’ quality of life. Neural interfaces allow the elicitation of sensory information through current stimuli. Stimulation studies can be useful to evaluate the electric potential distribution into the nerve in response to a current stimulus and therefore the activation of fibers. In this paper, hybrid FEM-Neuron computational models are used to study nerve fiber activation in different nerve models that resemble the human median nerve. To conduct a comprehensive study, the variability in fascicular topography and different configurations of active sites of two types of electrodes (intraneural and extraneural) has been considered. Furthermore, the simulation results (in terms of the percentage of fiber activation in nerve fascicles, their location in the nerve section models, and the order of their activation when the stimulus increases) are evaluated according to the sensation intensity perceived by a human amputee in an experimental trial. The obtained results let us infer the effect of using intraneural and extraneural electrodes on the number and position of activated fascicles when the minimum values of electric charges considered in the experimental trial are used, and the dependence of the order of fiber activation into the fascicles on the current stimulus.

1. Introduction

Upper-limb amputees’ quality of life can be greatly improved with neuroprosthetic devices. In this field, different solutions allowing interaction between these devices and the nervous system have been proposed. Commercial myoelectric upper-limb prostheses do not enable information to be derived from interactions with the environment [1]. These devices can be controlled by the users by means of electromyographic (EMG) sensors, positioned on the forearm, which can decode muscular signals. The principal motivation for the abandonment of myoelectric prostheses by amputees is the lack of afferent information. To improve dexterity, the embodiment of the prosthesis, and the interaction with the environment, restoring sensory feedback is among the main properties to be included in new generations of upper-limb prosthesis [2].

There are several approaches for restoring sensory feedback in upper-limb amputees. Electrical nerve stimulation, utilizing neural or surface electrodes on peripheral nerves, is one of the most effective. The use of neural electrodes can provide forms of sensory feedback, in terms of tactile sensations, that are more similar to natural ones because of the high selectivity. In 2019, Zollo et al. conducted an experimental study on sensory feedback restoration via invasive electrical neural stimulation on an upper-limb amputee [2]. Force and slippage sensations were elicited using extraneural (i.e., cuff) and intraneural (i.e., ds-FILE) electrodes implanted for 11 weeks in a woman with transradial amputation. The approach demonstrated natural-like force and slippage sensations, allowing the user to enhance handling abilities with the hand prosthesis. However, these devices, both intraneural and extraneural, are quite invasive for patients. For this reason, it is very important to study the problem in a simulation environment, considering the interaction between nerve and electrode to estimate the efficacy and safety of the implant. To this purpose, computational multiscale approaches have been used in the literature, also to evaluate stimulation parameters and waveforms [3] and to study the interaction between nerve and electrode [4]. To perform a computational multiscale study, the finite element method (FEM) and mathematical axon models have been considered [4,5,6,7,8,9].

1.1. Hybrid FEM-Neuron Simulation to Study Nerve–Electrode Interaction

Kent et al. [10] investigated the impact of the cuff electrode design in a simulation environment. Flat interface nerve electrode (FINE) cuffs and single-ring round cuff electrodes are considered to evaluate selectivity on the pudendal nerve. When the nerve is deformed due to cuff electrode positioning, nerve segment reshaping is also considered. To evaluate fiber activation, a hybrid FEM-Neuron computational model is used. The main achievement of this study is related to the comparison of nerve fiber selectivity using FINEs and single-ring cuff electrodes to asses an appropriate electrode design for pudendal nerve stimulation in the restoration of bladder function. The hybrid FEM-Neuron approach is a valuable tool that could be used to study the electric stimulation of the median nerve using different types of electrode models in different active site configurations.

Another study in the literature [4], in which the same hybrid FEM-Neuron approach was used, studied fiber activation and selectivity related to human sciatic and median nerves subjected to electrical current stimulation sent by FINEs and Transverse Intrafascicular Multicontact Electrodes (TIME). Some general effects are studied related to fibrotic reaction, the location of active sites in the nerve section (close to a nerve fascicle or into it), and monopolar and bipolar stimulation. From simulation results about the optimal number of active sites to send current stimulus to in a single TIME model, the optimal number of TIME implants and monopolar and bipolar stimulations using FINEs and TIMEs are studied. Some limitations of this work are related to the consideration of a single nerve topography of inner fascicles and the usage of only the specific models of TIMEs and FINEs. Important aspects remain unaddressed regarding other electrode models (with different active site configurations, for example, bipolar stimulation with active sites located longitudinally along the nerve) and the nerve fascicle’s behavior considering the fascicle’s topography variability when it is subjected to the electric stimulus.

Looking at the literature about experimental studies on human median nerve stimulation to restore sensory feedback, it is evident that there is a lack of simulation analysis to evaluate the nerve fascicle activation according to the location of electrode active sites and the nerve fascicle’s topography.

1.2. Aims of the Study

This paper wants to fill this gap by proposing a simulation study, based on experimental trials on humans, on the interaction of the human median nerve with extraneural neural electrodes (i.e., cuff) and intraneural electrodes (i.e., ds-FILE) considering two specific configurations of active sites from which the stimulus is sent. The hybrid FEM-Neuron approach resembles the one used and validated in the literature [4,8]. It can be a useful approach to investigate different stimulation techniques and quantitatively analyze the effect of changing stimulation parameters on the behavior of the nerve fibers. In particular, the number of fascicles activated and their position in the nerve with respect to current sources active sites are analyzed. More specifically, this work wants to

(i)

Study the activation properties of nerve fibers in the two cases (using an intraneural electrode and an extraneural cuff electrode sending stimuli from active sites located as shown in Section 2.2), using stimulation parameters, in terms of electric charge quantity, pulse width, and frequency, based on experimental results [2];

(ii)

Relate the number of fibers activated, taking into account the location of fascicles and active sites from which the stimulus is sent in simulation, with the intensity index reported by the subject in the experimental work in [2].

2. Materials and Methods

To account for the anatomical inter-subject variability, different 3D finite element conductor models of the human median nerve were developed. In particular, five 3D models of the nerve with the ds-FILE intraneural electrode and five 3D nerve models with the CUFF electrode were generated. On the basis of the results obtained in [7], all the models were considered in a simplified way, i.e., the nerve fascicle section was approximated to a circular section. In each model, circular section fascicles were randomly located into the nerve. The number and dimension of the fascicles were considered according to values found in the literature [11].

The two different electrode models, developed in a simulation environment, were implanted in different regions of the nerve, at different heights of the median nerve above the elbow, according to the study in [2]. Hence, the surface areas of the nerve with the two types of electrodes are different: the surface area of the nerve with the cuff electrode is smaller than the one of the nerve with ds-FILE electrode.

More details about the dimension of nerve sections are reported in Section 2.1. The electric potential distributions into the nerve subjected to a current stimulus by the two electrode types were analyzed and processed in Matlab. These values were interpolated on different sections of the axon model in Neuron [12] to study the activation of nerve fibers. Simulations were performed on a computer with an Intel Core i7-8750H CPU at 2.20 GHz, 16 GB RAM.

2.1. FEM Models of the Human Median Nerve and Neural Electrodes

The human median nerve simplified models were obtained starting from the anatomical image used in our previous works [3,5]. In Figure 1, a schematic view of the used procedure is shown. According to the considered electrode type, two different nerve dimensions were modeled, depending on the median nerve region where the electrodes were implanted. Geometrical properties of the human median nerve related to nerve and fascicle dimensions were set according to the data reported in [11]. To create and locate circle-section inner fascicles in the nerve boundary model, the nerve model with the ds-FILE electrode had an anatomical boundary shape. The nerve model with the cuff had a circular shape section according to the electrode section. The 3D nerve models were developed in Comsol Multiphysics^® v.5.3 (Comsol S.r.l., Brescia, Italy); all the models had a length of 15 mm. Different tissue classes were assigned to each region of the nerve model according to the human anatomy. Three tissues were considered: endoneurium, perineurium, and epineurium. Conductivities related to each tissue were 0.00088 S/m and 0.0826 S/m for perineurium and epineurium. Endoneurium has an anisotropic conductivity tensor with a transverse value of 0.00826 S/m and a longitudinal value of 0.0571 S/m [6]. A cylindrical region with saline solution properties and a diameter of 76 mm was considered to simulate the intraoperative environment. Maxwell’s equations in media were solved using finite element methods, using Dirichlet boundary conditions with V = 0 at infinity. To implement this approximation in Comsol, the diameter of the saline cylindrical region was set larger than the nerve dimension. The AC/DC module of Comsol Multiphysics^®, physics of Electric Currents, was used. A quasi-static approximation of Maxwell’s equations was considered [13] for the study of the electric potential in the tissues

$$\nabla ·(\sigma \nabla V)=0$$

(1)

where V and $\sigma$ are the electric potential and the conductivity of the medium, respectively. Comsol Multiphysics^® allows us to solve the following equations:

$$\nabla ·\overrightarrow{J}=Q_J$$

(2)

where $\overrightarrow{J}$ is the current density and $Q_j$ is the current source,

$$\overrightarrow{J}=\sigma \overrightarrow{E}+{\overrightarrow{J}}_e$$

(3)

where $\overrightarrow{E}$ is the electric field and ${\overrightarrow{J}}_e$ is the external current density,

$$\overrightarrow{E}=-\nabla V$$

(4)

$Q_j$ and $J_e$ are set to zero in all the space in the model and Maxwell’s equations are solved in quasi-static approximation. Tethraedral elements are used to mesh the geometry of the model.

Nerve dimensions in the models with ds-FILE and CUFF electrodes are different according to their dimensions and to the region of the nerve where the electrode was implanted in experimental studies. Two different nerve regions were considered at two different heights along the median nerve, those regions have section dimensions of minor and major diameters of 2.99 ± 0.66 mm and 6.27 ± 0.85 mm for the first region and 3.35 ± 1.39 mm and 7.07 ± 1.29 mm for the second region, as reported in [11].

2.2. Electrode Models

The ds-FILE electrode model and the cuff electrode model (Figure 2) were developed in Comsol Multiphysics^®. The active sites shown in Figure 2 were used to send electric stimuli, according to the procedure used in experimental trials on human subject described in [2]. The electrode model adopted in simulation, and whose CAD has been developed, is for human use and is characterized by 4 rings and 16 contacts.

The ds-FILE electrode model is described in [7,14]. It has a 20 µm thick polymide body and 360 µm height. The model has sixteen active sites. It is located at the middle length of the nerve model and its longitudinal axis is perpendicular to the longitudinal axis of the nerve (Figure 1). The current intensity is set to an arbitrary value that will be subsequently modified in the Neuron axon model.

A similar procedure was followed to develop the cuff electrode. A sixteen-active-sites cuff model was built. In total, 14 active contacts and 2 ground are distributed on 4 rings according to the geometrical properties of the electrode model by Ardiem Medical. This model presents 16 platinum active sites with dimensions 2.5 mm × 0.5 mm × 0.125 mm. The material of the body is polymide and has a conductivity of 6.7 × 10${}^{-14}$ S/m. The active sites have a conductivity of 8.9 × 10${}^6$ S/m. These last two properties are the same for cuff and ds-FILE electrodes.

2.3. Axon Mathematical Model

A double-cable axon model is considered to study the activation properties of nerve fibers. The McIntyre–Richardson–Grill (MRG) axon model [15], with channel mechanisms of Ranvier nodes and imperfect insulation for other compartments, is used. Ten internodal, two paranodal, and two myelin sections are in between two nodes as reported in [16].

Electrical membrane dynamics is described by the different properties of ion channels. Membrane capacitance and conductances related to slow potassium, nonlinear fast sodium, persistent sodium, and linear leakage have to be considered to model the node of Ranvier. Information about geometrical and electrical properties is the same as our previous study [3]. Data on electric potential distribution were exported from Comsol Multiphysics to Matlab and then processed and exported to Neuron to study the fibers’ activation. A number of fibers randomly located into the fascicles according to a density of 240 fibers/mm² are considered in each nerve fascicle of the models [8]. Their diameters were modeled with different values randomly extracted from two gaussian distributions [4]. Moreover, the first Ranvier node was also randomly placed between 0 and $\mathrm{\Delta }$x of the arclength of the nerve fiber. $\mathrm{\Delta }$x is the node-to-node distance for a defined fiber. Other axon compartments were located along all of the fiber between two nodes of Ranvier. The axon was ended by a Ranvier node. Electric potential values were interpolated in Matlab on different regions of the nerve fibers and used in Neuron as extracellular potential. The stimulus waveform, defined as extracellular potential, is a biphasic charge-balanced waveform, with 60 µs and 200 µs pulse duration for ds-FILE and CUFF electrodes, respectively, and 50 Hz frequency, according to the type of electrode used, based on [2]. The defined geometric properties of nerve and axons were used in Comsol to perform the simulation.

2.4. Experimental Data

The stimulation parameters used in human trials [2] were considered to replicate, in the simulation environment, the nerve behavior when the electric stimulation was performed. All the data obtained from the experimental trials were related to the intensity index of sensation perceived by the human subject. They show that the sensation intensity increases with the stimulus intensity. On the human subject, a wide range of electric charge values was used in the first mapping session. However, only a narrow range, which elicited specific sensation with increasing intensity, was selected to perform the subsequent trials. A representative sample of the experimental data is reported in

Table 1. Set of stimulation parameters used in the experimental trials [2]. To each current intensity value, a different intensity sensation elicited in the amputee expressed in arbitrary units (a.u.) corresponds.

Electrode Model	Frequency (Hz)	Pulse Width (µs)	Electric Current (µA)	Sensation Elicited	Intensity Index of Sensation (a.u.)
ds-FILE	50	60	40	middle finger metacarpophalangeal flexion	0
			60		3
			80		7
			100		7
Cuff	50	200	400	middle finger flexion	2
			600		3
			800		6

, and the intensity of tactile sensations perceived by humans is defined by means of intensity index in arbitrary units.

3. Results

A biphasic charge-balanced waveform was used to stimulate nerve fibers alternatively using a cuff electrode and an intraneural ds-FILE electrode. All the stimulation parameters (pulse width, frequency, and electric charge) were the same as those used in the experimental study on a human amputee [2]. The electric charge values used in the computational models were included in the range from 7 nC to 192 nC and from 60 nC to 1200 nC for the nerve models with ds-FILE and cuff electrode, respectively [2]. These wider ranges were used during the time period (around 11 weeks) of an experimental study on a human amputee. The ranges tested in the simulation environment were from 0.3 nC to 198 nC and from 12 nC to 1320 nC for the nerve models with ds-FILE and cuff electrode, respectively (percentage of activated fibers in fascicles when the electric charge was increased are in Figures S1 and S2 of Supplementary Materials). The reason is that, from previous experimental trials, it is noticed that not all the electric charge values are related to a perceived sensation from the human subject. Hence, in this study, the attention was restricted to two narrow ranges of electric charge that correspond to specific sensations perceived by the human subject in an experimental trial, as reported in the subsequent paragraphs.

In experimental data on the human amputee, signals directly comparable with the percentage of activation (PA) of fibers are not available, but the intensity of sensation perceived by the subject is recorded.

A nerve fiber is considered activated if an action potential propagates along the fiber length, i.e., the action potential is observed on the first and last node of Ranvier of the considered fiber. In each nerve fascicle, according to its surface area, a different number of fibers is located. Therefore, a different value of the percentage of activated fibers is computed for each fascicle according to a different value of the stimulus intensity. The electrical parameters are shown in Table 1 and they are related to data described in Tables S1–S4 in the Supplementary Material of [2]. To test and validate the hybrid FEM-Neuron approach, the results shown in the literature are replicated [4], and as a consequence, the FEM model is adapted for the study using the defined nerve section and electrode models.

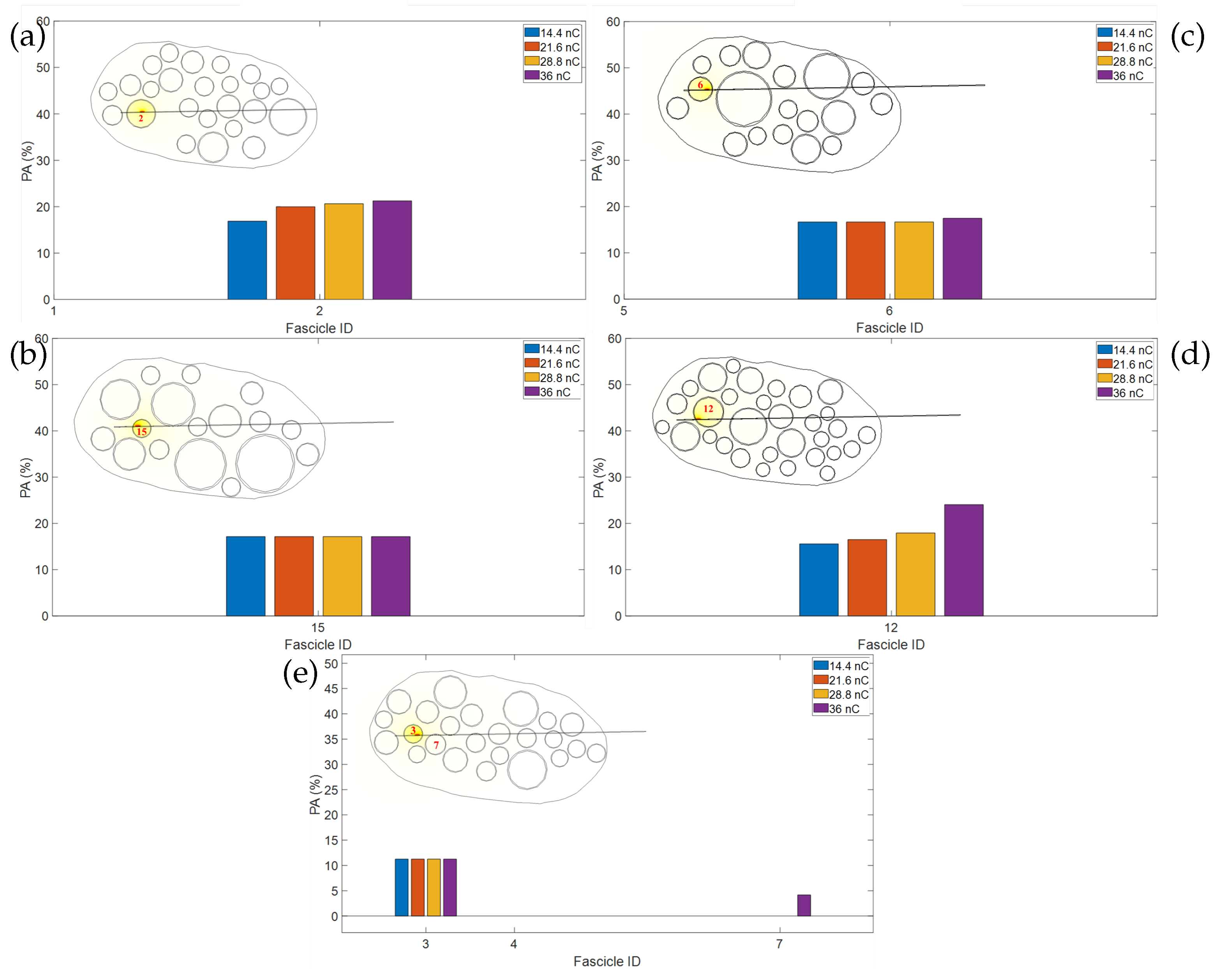
Figure 3 (where intensity is expressed in terms of electric charge) shows the percentage of fiber activation in different nerve fascicles for the three values of injected electric charge used in the experimental session on the human being, Table 1. Figure 3a–e are related to the simulation results of five nerve models different in fascicle topography. On the right of each plot, the corresponding nerve section is shown. The labels of fascicles are in different colors to show the gradual activation of fascicles when the electric charge increases. The fascicles labeled indicate a percentage of activation above 10%. In the literature [8], the electric charge threshold is defined as the value at which 10% of fibers are activated. So, it is possible to assume that 10% of fibers activated leads to efficient nerve stimulation.

The PA can be exploited to relate the number of fascicles that have activated fibers with the sensation intensity observed in the experimental trial on a human amputee. In simulations with the cuff electrode, a longitudinal bipolar configuration of active sites is considered (the active sites highlighted in Figure 2 are activated). The order of activation of fascicles depends on their number and dimension, their location in the nerve section, and the configuration of active sites.

In Figure 3, it is possible to observe that for some nerve fascicles, when the electric charge intensity increases, no increase in PA is observed (one example is fascicle 1 in Figure 3a for the electric charge values of 720 nC and 960 nC, but analogue observations can be performed for other subplots). Two cases have to be considered related to the fascicles involved: (i) fascicles that have a value below 100% PA; and (ii) fascicles that have values of 100% PA when electric charge values different from the maximum value considered in the experimental study (960 nC) are used. Regarding the first case, we can observe that, for a given fascicle, the PA does not increase, but an increase in PA can be observed in other different fascicles. This behavior can be related to the non-uniform distribution of electric potential into the nerve because of the different electric properties of tissue and the particular location of active sites. Another reason can be due to the threshold process of axons to generate action potentials and as a consequence consider that axon as activated. Probably, the increase in stimulus intensity in some fascicles does not suffice to generate action potential in some axons, and no increase in PA is observed in the corresponding fascicle. About the second case, if one fascicle has a PA of 100%, and there is an increase in stimulus intensity, all the fibers of that fascicle are already activated, so it can be only verified that for other fascicles there is an increase in PA.

The simulation results of neural stimulation using a ds-FILE neural electrode are shown in Figure 4, for the corresponding electric charge intensity values used in the experimental trial in a human amputee. In particular, the inner of Figure 4 shows the electric potential color map, in a section plane through the active site, observed in five different nerve models, when the current stimulus is sent by an active site located in the inner of a nerve fascicle. Figure 4 shows the histograms of the fiber’s PA related to the electric charge values used in the experimental test on a human amputee (see Table 1).

Figure 4a,d show that only the fascicle with the active site located in it has activated fibers above the 10% PA threshold and that the PA increases according to the electric charge intensity. In Figure 4b,c,e, nerve fibers in a single fascicle are activated and the PA has small variations above the threshold value when the stimulus intensity increases. Only Figure 4e shows an increase in PA in a fascicle close to the fascicle with an active site (label 7 in the Figure) when an electric charge value of 36 nC is used (the maximum intensity used in the considered experimental trial). Nevertheless, the fascicle 7 has activated fibers with a PA below the 10% efficacy threshold. The PA, in all the data observed, is above the threshold of 10% starting from the minimum electric charge intensity used in the experiments, 14.4 nC. For each nerve model, the PA increases according to the electric charge intensity.

In the case of intraneural electrodes, i.e., in the case of active sites located in a specific fascicle, when the stimulus intensity increases, it is possible to observe an activation of the fibers belonging not only to the fascicle where the active site is located, but also to the surrounding fascicles.

4. Discussion

Computer simulation using a hybrid FEM-Neuron model is a useful approach for studying the electrical response of neural tissues subjected to electric current stimulation. This work adopts the same modeling approach as the literature [4,8], to investigate different stimulation approaches and to evaluate the effects of the stimulation configuration of two different types of electrodes, taking into account the topography of the nerve. For this purpose, FEM simulation was used to evaluate electric potential distribution into the nerve model subjected to a current stimulus from neural electrodes and the MRG axon model was adopted to evaluate the nerve fiber activation in terms of the generation and propagation of action potential. The main differences are related to the different types of electrode models used (i.e., ds-FILE intraneural and CUFF with four rings and four active sites on each ring) and to the purposes of our study. The aims were to compare the activation properties of nerve fibers in the fascicles using the two different electrodes, accounting also for the nerve fascicle topography and to observe the relation between the fascicles that have activated fibers and the sensation intensity reported by a human subject in an experimental trial.

Considering a given configuration of electrode active sites, it is possible to find how the nerve fascicles that have activated fibers are located, how many nerve fascicles they are, and their order of activation according to their position compared with the location of active sites. Moreover, by comparing simulation results with experimental data, for an increase in intensity sensation perceived by a human subject, it is possible to know where the activated fascicles are located and in which order they are activated when the stimulus increases.

Therefore, the percentage of activation in nerve fascicles has been studied by considering a different number of fibers randomly located in each fascicle.

From the simulation results obtained using cuff electrodes in five different models (Figure 3), different maps of activation can be observed. Observing the fiber percentage of activation in each fascicle, it is possible to note that more than one fascicle has a PA above 10% for the minimum value used in the experimental trials of 480 nC (blue−labeled fascicles), for all the five models considered. The other fascicles related to a PA above 10% when the electric current of active sites reaches amplitudes of 720 nC and 960 nC are, respectively, labeled in orange and yellow.

The PA of fascicles in each one of the five nerve models with cuff also depends on the fascicle’s dimension and location. For this reason, it is possible to observe in Figure 3a–e that 7, 17, 13, 11, and 14 fascicles are activated, respectively, with a PA above 10%, when the minimum value is 480 nC, at which the patient perceived the sensation in the experimental trial.

These observations can be made for the electrode stimulation configuration considered in our experimental trials, i.e., electric current is sent through two active sites, one close and the other located longitudinally along the nerve, Figure 2a.

This configuration type, of bipolar stimulation with active sites located longitudinally along the nerve length, could also be the reason for the particular fascicle activation behavior shown in Figure 3. For example, observing in detail Figure 3b, (similar behavior can be observed in other subplots of Figure 3), and it is possible to note that at the minimum value considered of electric charge (i.e., 480 nC), fascicle 19, that is far from the active sites, has a PA value around 80%, fascicle 15 around 40%, and fascicle 12 has a PA value below 10%. This behavior can be related to the longitudinal configuration of the active sites to perform bipolar stimulation. The two different active sites are positive and negative current sources. Close to the active sites, there is a higher strength both for positive and negative current compared with locations far from the active sites. So, the high-intensity current of the opposite sign affects the fiber activation, inducing depolarization in one region along the z-axis and polarization in another region (results are shown in Figures S3–S5 in Supplementary Materials). For this reason, an increase in PA for the nerve fascicles far from the active sites could be therefore induced by the more uniform distribution of electric potential compared with the values found in the region close to the active sites.

Until now, it has not been possible to study directly the nerve section model of a patient, so different simulations accounting for fascicle variability can be useful to understand how the fibers could be activated when the nerve is subjected to electric stimulation. The five different models of the nerve, with fascicles of different dimensions and positions in the nerve section, are considered to account for the morphological variability in human subject fascicles.

From the results shown in Figure 4 about the percentage of fiber activation obtained from the simulations of the five nerve models with the intraneural ds-FILE electrode, a different behavior is observed.

In Figure 4a–d, an increase im PA with an increase in electric charge intensity is evident. This is the expected behavior of nerve fibers in a fascicle when an intraneural electrode is used and its active site from which is sent the electric stimulus is located within that fascicle. The PA behavior shown in Figure 4b,c,e could also be related to the different topography of the nerve fascicles (their dimensions and location in the nerve section): the return active site is located out of the nerve, so the electric potential between the two active sites is also affected by the fascicles and the tissue between them.

From experimental data, it is possible to see that the patient perceived sensation at increasing intensity according to the increasing electric current stimulus. In our computational model of the intraneural electrode, we are assuming the most advantageous case, i.e., that the active site providing the stimulation current is in the inner of a fascicle. For this reason, a nerve fiber can be activated at a lower electric charge value than the condition where the active site is located outside of a fascicle.

If we assume the experimental trial had the same, most advantageous, conditions as the simulation, the results of the models with intraneural electrodes show that when the current intensity increases, the PA increases in a single fascicle. The co-activation of fascicles will be observed for higher current values. When the active sites that provide the present stimulus are outside of a fascicle, there is a decreased proportion of fiber activation in the fascicle closest to the active site and a contemporaneous activation of several surrounding fascicles.

Differently from the previous analysis on cuff electrodes, in this case, only one fascicle has activated fibers in four of the five models when the current increases. Comparing the simulation results with the experimental data, we could assume that, considering a generic median nerve also in the experimental trial, one fascicle that has a percentage of activated fibers above the threshold of 10% is sufficient to evoke sensations.

The computational simulation approach that is validated in the literature [17] can be a useful tool to evaluate in depth the possible fascicles activated when electrical stimulation is performed. In this study, we analyzed two types of electrodes using one active site configuration for each one and observed the fascicle activation shown in the results. The same approach can be used to test other different configurations of active sites to evaluate the corresponding fascicle activation and design the stimulation protocol in experimental trials. At the same time, neural interfaces can be designed and optimized in a simulation environment to test their efficacy before experimental trials.

4.1. Limitations of the Study

The findings of this study have to be seen in light of minor limitations. In building the computational FEM models, the shape of the nerve and inner fascicles were considered constant along the z-axis (i.e., the longitudinal direction of the nerve); however, from experimental data about the anatomy of peripheral nerves, the shape of the fascicles section varies along the longitudinal axis. Therefore, the nerve models considered in this study assume the approximation of topographic stability along the z-axis, which is valid if the hypothesis that the implant is performed in a nerve section of topographical stability is assumed. Some studies showed that to have fascicles branching in the median nerve is not common in the range of length of a few millimeters [18]. According to these considerations and to previous works found in the literature [4], the assumption considered in this paper could be considered valid.

4.2. Applicability

The results obtained in this paper can be useful to obtain an estimation of the nerve fibers’ behavior when subjected to neural stimulation, through different electrode models and configurations. The obtained results can be used as guidelines to be used during experimental sessions to improve the implantation of the electrodes in the human median nerve and the active sites configuration to have suitable recruitment of the nerve fibers.

5. Conclusions

In this paper, the activation of neural fibers by electric current stimulation using ds-FILE and cuff electrodes has been analyzed by means of the FEM-Neuron computational approach. According to two different electrode models, five different FEM simulations using Comsol Multiphysics were performed for each electrode model. Each nerve model differs by the dimension and location of its inner fascicles: the nerve models with cuff have a circular nerve section and the ds-FILE ones have an elliptical-shaped nerve section based on an anatomical image. Differences between using the two different electrode configurations in terms of fiber activation are shown using the same electrical parameters used in the experimental trials. From the results, fascicles located in different regions of the nerve are activated in each model at different electric charge intensities. The use of the simulation approach permits us to observe which fascicle can be activated according to stimulation parameters and electrode configurations in terms of active sites providing current stimulus. Furthermore, this approach makes it possible to test different electric charge values for each electrode configuration to obtain a quantitative estimation of the parameters to be used on human subjects.

Considering the simulation results, at different values of electric charge it is possible to relate fascicles with activated fibers located in a specific region of the nerve section. Future perspectives could be devoted to performing other simulations activating different sites of the electrode and considering different nerve variability. These could be useful for (i) a priori investigating possible sensations arising from the stimulation by observing the number of fascicles activated in simulation; (ii) forecasting the sensations that could be perceived by a human subject before the implantation of the electrodes. The FEM computational approach could also be useful to estimate the optimal positioning of the electrode with respect to the nerve and to improve the electrode design for a more efficient activation of nerve fascicles, for example varying the shape, the size, and the position of the active sites.