Figure 1.
Flowchart of the methodology.
Figure 1.
Flowchart of the methodology.
Figure 2.
Downscaled cement–rock sample (a) and its CT image (b) and simplified binarized CT image (c).
Figure 2.
Downscaled cement–rock sample (a) and its CT image (b) and simplified binarized CT image (c).
Figure 3.
The binarized CT images. (a–c): rock phase, cement phase, interface between cement and rock.
Figure 3.
The binarized CT images. (a–c): rock phase, cement phase, interface between cement and rock.
Figure 4.
Shapes of the simulated microchannels with a 64 pixel2 (0.2273 mm2) cross-sectional area. (a–e): circular, oval, square, rectangular, triangular.
Figure 4.
Shapes of the simulated microchannels with a 64 pixel2 (0.2273 mm2) cross-sectional area. (a–e): circular, oval, square, rectangular, triangular.
Figure 5.
Modified CT images for different shapes of simulated microchannels with a cross-sectional area of 64 pixel2 (0.2273 mm2). (a–e): circular, oval, square, rectangular, triangular.
Figure 5.
Modified CT images for different shapes of simulated microchannels with a cross-sectional area of 64 pixel2 (0.2273 mm2). (a–e): circular, oval, square, rectangular, triangular.
Figure 6.
Modified CT images for different quantities of simulated microchannel with square shape and cross-sectional area of 64 pixel2 (0.2273 mm2). (a–e): microchannel quantity = 1, 2, 3, 4, 5.
Figure 6.
Modified CT images for different quantities of simulated microchannel with square shape and cross-sectional area of 64 pixel2 (0.2273 mm2). (a–e): microchannel quantity = 1, 2, 3, 4, 5.
Figure 7.
Graphical description of forming a slanted microchannel in the interface region. (a–d): first CT image, intermediate CT image, last CT image, 3D view of slanted microchannel.
Figure 7.
Graphical description of forming a slanted microchannel in the interface region. (a–d): first CT image, intermediate CT image, last CT image, 3D view of slanted microchannel.
Figure 8.
Moving distances of the microchannel to form different inclination angles.
Figure 8.
Moving distances of the microchannel to form different inclination angles.
Figure 9.
Physical geometry and boundary conditions for a 3D model with a circular simulated microchannel with a cross-sectional area of 64 pixel2 (0.2273 mm2). (a) physical geometry, (b) boundary conditions.
Figure 9.
Physical geometry and boundary conditions for a 3D model with a circular simulated microchannel with a cross-sectional area of 64 pixel2 (0.2273 mm2). (a) physical geometry, (b) boundary conditions.
Figure 10.
Meshes with different densities: (a) medium mesh, (b) better mesh, (c) fine mesh and (d) finer mesh.
Figure 10.
Meshes with different densities: (a) medium mesh, (b) better mesh, (c) fine mesh and (d) finer mesh.
Figure 11.
Positions of selected velocity measuring points (a) and corresponding velocity profiles under different meshes (b).
Figure 11.
Positions of selected velocity measuring points (a) and corresponding velocity profiles under different meshes (b).
Figure 12.
Effects of the presence of microchannels with different shapes on velocity streamlines through a cement–rock sample. (a–f): circular, oval, square, rectangular, triangular, base case.
Figure 12.
Effects of the presence of microchannels with different shapes on velocity streamlines through a cement–rock sample. (a–f): circular, oval, square, rectangular, triangular, base case.
Figure 13.
Effect of the microchannel contact area on the volume flow rate: data for cases with 64 pixel2 (0.2273 mm2) microchannel.
Figure 13.
Effect of the microchannel contact area on the volume flow rate: data for cases with 64 pixel2 (0.2273 mm2) microchannel.
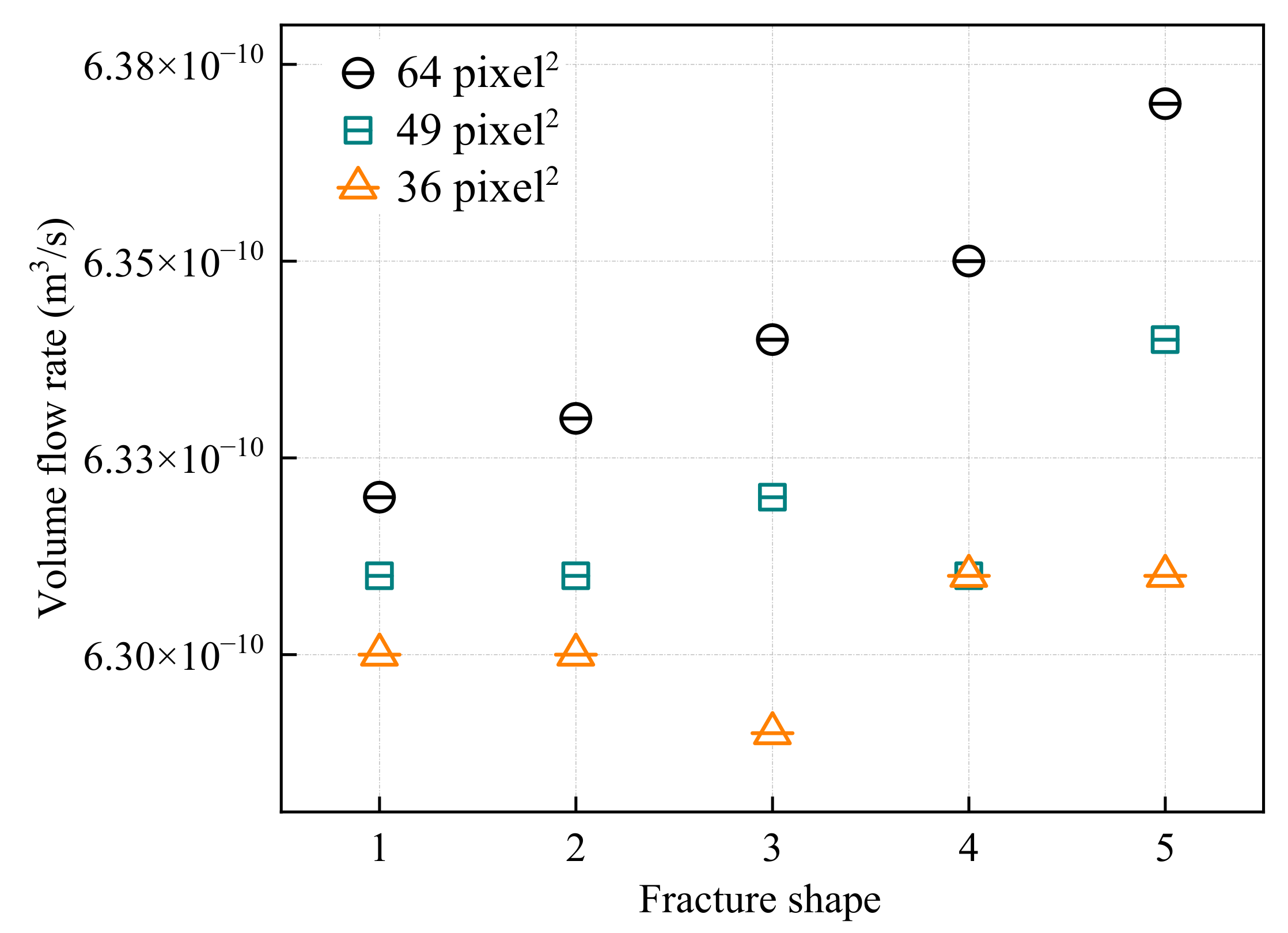
Figure 14.
Volume flow rate through a cement–rock sample: effect of variable microchannel shape and cross-sectional area.
Figure 14.
Volume flow rate through a cement–rock sample: effect of variable microchannel shape and cross-sectional area.
Figure 15.
The velocity streamlines for cases with multiple microchannels and base case. (a–f): microchannel quantity = 1, 2, 3, 4, 5, 0 (base case).
Figure 15.
The velocity streamlines for cases with multiple microchannels and base case. (a–f): microchannel quantity = 1, 2, 3, 4, 5, 0 (base case).
Figure 16.
(a) Percentage of increase in the volume flow rate vs. number of microchannels, and (b) effect of increasing number of microchannels on the volume flow rate.
Figure 16.
(a) Percentage of increase in the volume flow rate vs. number of microchannels, and (b) effect of increasing number of microchannels on the volume flow rate.
Figure 17.
The velocity streamlines for vertical and slanted microchannel cases: (a) circular 0°, (b) circular 13.89°, (c) circular 25.82°, (d) square 0°, (e) square 13.89°, (f) square 25.82°.
Figure 17.
The velocity streamlines for vertical and slanted microchannel cases: (a) circular 0°, (b) circular 13.89°, (c) circular 25.82°, (d) square 0°, (e) square 13.89°, (f) square 25.82°.
Figure 18.
(a) Contact area vs. inclination angle for slanted microchannel models with a 16 pixel2 (0.1279 mm2) circular microchannel and a 16 pixel2 (0.1279 mm2) square microchannel, respectively; (b) volume flow rate vs. contact area for slanted microchannel models with a 16 pixel2 (0.1279 mm2) circular microchannel and a 16 pixel2 (0.1279 mm2) square microchannel, respectively.
Figure 18.
(a) Contact area vs. inclination angle for slanted microchannel models with a 16 pixel2 (0.1279 mm2) circular microchannel and a 16 pixel2 (0.1279 mm2) square microchannel, respectively; (b) volume flow rate vs. contact area for slanted microchannel models with a 16 pixel2 (0.1279 mm2) circular microchannel and a 16 pixel2 (0.1279 mm2) square microchannel, respectively.
Figure 19.
The velocity streamlines for cases with different rock permeability. (a–c): k1(krock < kinterface), k2 (krock = kinterface), k3 (krock > kinterface).
Figure 19.
The velocity streamlines for cases with different rock permeability. (a–c): k1(krock < kinterface), k2 (krock = kinterface), k3 (krock > kinterface).
Table 1.
Mineral and chemical composition of the Notikewin rock [
19].
Table 1.
Mineral and chemical composition of the Notikewin rock [
19].
| Properties | Details |
|---|
| Lithology | Quartzose sandy siltstone |
| Mineralogical composition | High amount of quartz with small amounts of dolomite, ankerite, muscovite, and albite |
| Major element composition (unit: ppm) | Si (340136), Ca (33333), Al (31364), Fe (14598), K (9092), Mg (6883) |
Table 2.
Primary simulation parameters.
Table 2.
Primary simulation parameters.
| Parameters | Values |
|---|
| Fluid flow regime | Laminar |
| Fluid type | Water at 25 °C |
| Domain type of the cement matrix | Porous |
| Domain type of the rock | Porous |
| Domain type of the interface | Porous |
| Domain type of microchannel | Fluid |
| Porosity of the cement matrix | 0.011 |
| Porosity of the rock matrix | 0.04 |
| Porosity of the interface | 0.014 |
| Permeability of the cement matrix | 9.86923 × 10−19 m2 |
| Permeability of the rock | 6.908461 × 10−17 m2 |
| Permeability of the interface | 4.9346 × 10−16 m2 |
| Initial velocity | U = 0, V = 0.1, W = 0 m/s |
| Max iterations | 1000 |
| RMS residual level | 1 × 10−5 |
| Boundary condition | Total inlet pressure (stable) = 10 psi
Static outlet pressure (relative) = 0 psi |
Table 3.
Rock permeability values used for three cases of simulation studies.
Table 3.
Rock permeability values used for three cases of simulation studies.
| Case | Rock Permeability (m2) |
|---|
| k1 (krock < kinterface) | 6.908461 × 10−17 |
| k2 (krock = kinterface) | 4.9346 × 10−16 |
| k3 (krock > kinterface) | 1.70737 × 10−15 |
Table 4.
Effect of micro channel shape on the volume flow rate through cement–rock sample: comparison of the base case (no microchannel) and case with 64 pixel2 (0.2273 mm2) microchannel.
Table 4.
Effect of micro channel shape on the volume flow rate through cement–rock sample: comparison of the base case (no microchannel) and case with 64 pixel2 (0.2273 mm2) microchannel.
| Section | Volume Flow Rate (m3/s) |
|---|
| Base Case | Circle 64 | Oval 64 | Square 64 | Rectangle 64 | Triangle 64 |
|---|
| Cement | 6.31 × 10−13 | 5.13 × 10−13 | 5.10 × 10−13 | 5.12 × 10−13 | 5.03 × 10−13 | 5.02 × 10−13 |
| Interface | 2.19 × 10−10 | 1.82 × 10−10 | 1.80 × 10−10 | 1.81 × 10−10 | 1.79 × 10−10 | 1.78 × 10−10 |
| Rock | 3.59 × 10−10 | 3.55 × 10−10 | 3.55 × 10−10 | 3.56 × 10−10 | 3.54 × 10−10 | 3.55 × 10−10 |
| Microchannel | / | 9.51 × 10−11 | 9.75 × 10−11 | 9.60 × 10−11 | 1.02 × 10−11 | 1.04 × 10−10 |
| Total | 5.79 × 10−10 | 6.32 × 10−10 | 6.33 × 10−10 | 6.34 × 10−10 | 6.35 × 10−10 | 6.37 × 10−10 |
| Percentage of increase | / | 9.15% | 9.33% | 9.50% | 9.67% | 10.02% |
Table 5.
Effect of the microchannel contact area on the volume flow rate: data for cases with a 64 pixel2 (0.2273 mm2) microchannel.
Table 5.
Effect of the microchannel contact area on the volume flow rate: data for cases with a 64 pixel2 (0.2273 mm2) microchannel.
| Case | Contact Area (m2) | Volume Flow Rate (m3/s) | Percentage Increase in Volume Flow Rate |
|---|
| Circle 64 | 1.02 × 10−5 | 6.32 × 10−10 | 9.15% |
| Oval 64 | 1.17 × 10−5 | 6.33 × 10−10 | 9.33% |
| Square 64 | 1.13 × 10−5 | 6.34 × 10−10 | 9.50% |
| Rectangle 64 | 1.43 × 10−5 | 6.35 × 10−10 | 9.67% |
| Triangle 64 | 1.60 × 10−5 | 6.37 × 10−10 | 10.02% |
| Base Case | / | 5.79 × 10−10 | / |
Table 6.
Volume flow rate through cement–rock sample: comparison of the base case (no microchannel) and microchannels with a 49 pixel2 (0.1741 mm2) cross-sectional area.
Table 6.
Volume flow rate through cement–rock sample: comparison of the base case (no microchannel) and microchannels with a 49 pixel2 (0.1741 mm2) cross-sectional area.
| Section | Volume Flow Rate (m3/s) |
|---|
| Base Case | Circle 49 | Oval 49 | Square 49 | Rectangle 49 | Triangle 49 |
|---|
| Cement | 6.31 × 10−13 | 5.15 × 10−13 | 5.11 × 10−13 | 5.15 × 10−13 | 5.12 × 10−13 | 5.09 × 10−13 |
| Interface | 2.19 × 10−10 | 1.82 × 10−10 | 1.81 × 10−10 | 1.82 × 10−10 | 1.81 × 10−10 | 1.80 × 10−10 |
| Rock | 3.59 × 10−10 | 3.55 × 10−10 | 3.53 × 10−10 | 3.55 × 10−10 | 3.53 × 10−10 | 3.55 × 10−10 |
| Microchannel | / | 9.36 × 10−11 | 9.58 × 10−11 | 9.40 × 10−11 | 9.54 × 10−11 | 9.77 × 10−11 |
| Total | 5.79 × 10−10 | 6.31 × 10−10 | 6.31 × 10−10 | 6.32 × 10−10 | 6.31 × 10−10 | 6.34 × 10−10 |
| % of increase | / | 8.98% | 8.98% | 9.15% | 8.98% | 9.50% |
Table 7.
Volume flow rate through cement–rock sample: comparison of the base case (no microchannel) and microchannels with a 36 pixel2 (0.1279 mm2) cross-sectional area.
Table 7.
Volume flow rate through cement–rock sample: comparison of the base case (no microchannel) and microchannels with a 36 pixel2 (0.1279 mm2) cross-sectional area.
| Section | Volume Flow Rate (m3/s) |
|---|
| Base Case | Circle 36 | Oval 36 | Square 36 | Rectangle 36 | Triangle 36 |
|---|
| Cement | 6.31 × 10−13 | 5.18 × 10−13 | 5.17 × 10−13 | 5.17 × 10−13 | 5.16 × 10−13 | 5.16 × 10−13 |
| Interface | 2.19 × 10−10 | 1.83 × 10−10 | 1.83 × 10−10 | 1.83 × 10−10 | 1.83 × 10−10 | 1.83 × 10−10 |
| Rock | 3.59 × 10−10 | 3.56 × 10−10 | 3.55 × 10−10 | 3.54 × 10−10 | 3.56 × 10−10 | 3.56 × 10−10 |
| Microchannel | / | 9.07 × 10−11 | 9.11 × 10−11 | 9.14 × 10−11 | 9.20 × 10−11 | 9.20 × 10−11 |
| Total | 5.79 × 10−10 | 6.30 × 10−10 | 6.30 × 10−10 | 6.29 × 10−10 | 6.31 × 10−10 | 6.31 × 10−10 |
| % of increase | / | 8.81% | 8.81% | 8.64% | 8.98% | 8.98% |
Table 8.
Volume flow rate through a cement–rock sample: effect of variable microchannel shape and the size of the cross-sectional area.
Table 8.
Volume flow rate through a cement–rock sample: effect of variable microchannel shape and the size of the cross-sectional area.
| Microchannel Shape | Volume Flow Rate (m3/s) |
|---|
| 0.2273 mm2 (64 Pixel2) | 0.1741 mm2 (49 Pixel2) | 0.1279 mm2 (36 Pixel2) |
|---|
| 1. Circle | 6.32 × 10−10 | 6.31 × 10−10 | 6.30 × 10−10 |
| 2. Oval | 6.33 × 10−10 | 6.31 × 10−10 | 6.30 × 10−10 |
| 3. Square | 6.34 × 10−10 | 6.32 × 10−10 | 6.29 × 10−10 |
| 4. Rectangle | 6.35 × 10−10 | 6.31 × 10−10 | 6.31 × 10−10 |
| 5. Triangle | 6.37 × 10−10 | 6.34 × 10−10 | 6.31 × 10−10 |
Table 9.
Contact area of microchannels with variable shape and cross-sectional area.
Table 9.
Contact area of microchannels with variable shape and cross-sectional area.
| Microchannel Shape | Contact Area (m2) |
|---|
| 0.2273 mm2 (64 Pixel2) | 0.1741 mm2 (49 Pixel2) | 0.1279 mm2 (36 Pixel2) |
|---|
| 1. Circle | 1.02 × 10−5 | 9.37 × 10−6 | 7.43 × 10−6 |
| 2. Oval | 1.17 × 10−5 | 1.05 × 10−5 | 7.77 × 10−6 |
| 3. Square | 1.13 × 10−5 | 9.73 × 10−6 | 8.19 × 10−6 |
| 4. Rectangle | 1.43 × 10−5 | 1.00 × 10−5 | 8.17 × 10−6 |
| 5. Triangle | 1.60 × 10−5 | 1.14 × 10−5 | 9.18 × 10−6 |
Table 10.
Effects of the number of microchannels on the volume flow rate.
Table 10.
Effects of the number of microchannels on the volume flow rate.
| Number of Microchannels | Cross-Sectional Area (m2) | Contact Area (m2) | Total Volume Flow Rate (m3/s) | Percentage of Increase |
|---|
| 0 | 0 | 0 | 5.79 × 10−10 | / |
| 1 | 2.44 × 10−7 | 1.13 × 10−5 | 6.34 × 10−10 | 9.50% |
| 2 | 4.92 × 10−7 | 2.25 × 10−5 | 6.85 × 10−10 | 18.31% |
| 3 | 7.41 × 10−7 | 3.37 × 10−5 | 7.32 × 10−10 | 26.42% |
| 4 | 9.85 × 10−7 | 4.51 × 10−5 | 7.65 × 10−10 | 32.12% |
| 5 | 1.27 × 10−6 | 5.91 × 10−5 | 7.89 × 10−10 | 36.27% |
Table 11.
Volume flow rate and contact area of slanted microchannels with circular shape.
Table 11.
Volume flow rate and contact area of slanted microchannels with circular shape.
| Case | Inclination Angle, α (Degree) | Volume Flow Rate (m3/s) | Cross-Sectional Area (m2) | Contact Area (m2) |
|---|
| Circle-i2 | 25.82 | 6.29 × 10−10 | 3.22 × 10−8 | 4.40 × 10−6 |
| Circle-i4 | 13.89 | 6.28 × 10−10 | 3.20 × 10−8 | 4.33 × 10−6 |
| Base case | 0 | 6.25 × 10−10 | 3.18 × 10−8 | 4.31 × 10−6 |
Table 12.
Volume flow rate and contact area of slanted microchannels with square shape.
Table 12.
Volume flow rate and contact area of slanted microchannels with square shape.
| Case | Inclination Angle, α (Degree) | Volume Flow Rate (m3/s) | Cross-Sectional Area (m2) | Contact Area (m2) |
|---|
| Square-i2 | 25.82 | 6.30 × 10−10 | 4.84 × 10−8 | 5.28 × 10−6 |
| Square-i4 | 13.89 | 6.29 × 10−10 | 4.64 × 10−8 | 5.18 × 10−6 |
| Base case | 0 | 6.28 × 10−10 | 4.84 × 10−8 | 5.12 × 10−6 |
Table 13.
Volume flow rate through cement–rock samples with microchannels and variable rock permeability.
Table 13.
Volume flow rate through cement–rock samples with microchannels and variable rock permeability.
| Section | Volume Flow Rate (m3/s) |
|---|
| k1 (Krock < Kinterface) | k2 (Krock = Kinterface) | k3 (Krock > Kinterface) |
|---|
| Cement | 5.12 × 10−13 | 9.02 × 10−13 | 1.02 × 10−12 |
| Interface | 1.81 × 10−10 | 3.50 × 10−10 | 4.13 × 10−10 |
| Rock | 3.56 × 10−10 | 2.73 × 10−9 | 9.70 × 10−9 |
| Microchannel | 9.60 × 10−11 | 3.28 × 10−10 | 5.75 × 10−10 |
| Total | 6.34 × 10−10 | 3.41 × 10−9 | 1.07 × 10−8 |
Table 14.
Average outflow velocity through a cement–rock sample with microchannels and variable rock permeability.
Table 14.
Average outflow velocity through a cement–rock sample with microchannels and variable rock permeability.
| Section | Average Outflow Velocity (m/s) |
|---|
| k1 (Krock < Kinterface) | k2 (Krock = Kinterface) | k3 (Krock > Kinterface) |
|---|
| Cement | 1.19 × 10−8 | 2.11 × 10−8 | 2.39 × 10−8 |
| Interface | 7.72 × 10−6 | 1.49 × 10−5 | 1.76 × 10−5 |
| Rock | 6.32 × 10−6 | 4.84 × 10−5 | 1.72 × 10−4 |
| Microchannel | 3.94 × 10−4 | 1.35 × 10−3 | 2.36 × 10−3 |
| Total | 5.16 × 10−6 | 2.77 × 10−5 | 8.70 × 10−5 |