Knowledge Representation and Reasoning with an Extended Dynamic Uncertain Causality Graph under the Pythagorean Uncertain Linguistic Environment
Abstract
:1. Introduction
2. Literature Review
3. Preliminaries
3.1. Pythagorean Uncertain Linguistic Sets
- (1)
- The set is ordered:, if;
- (2)
- Negation operator:;
- (3)
- Max operator: max, if;
- (4)
- Min operator: min, if.
- (1)
- (2)
- (3)
- (4)
- (1)
- If, then;
- (2)
- If, then:
- (a)
- If, then;
- (b)
- If, then.
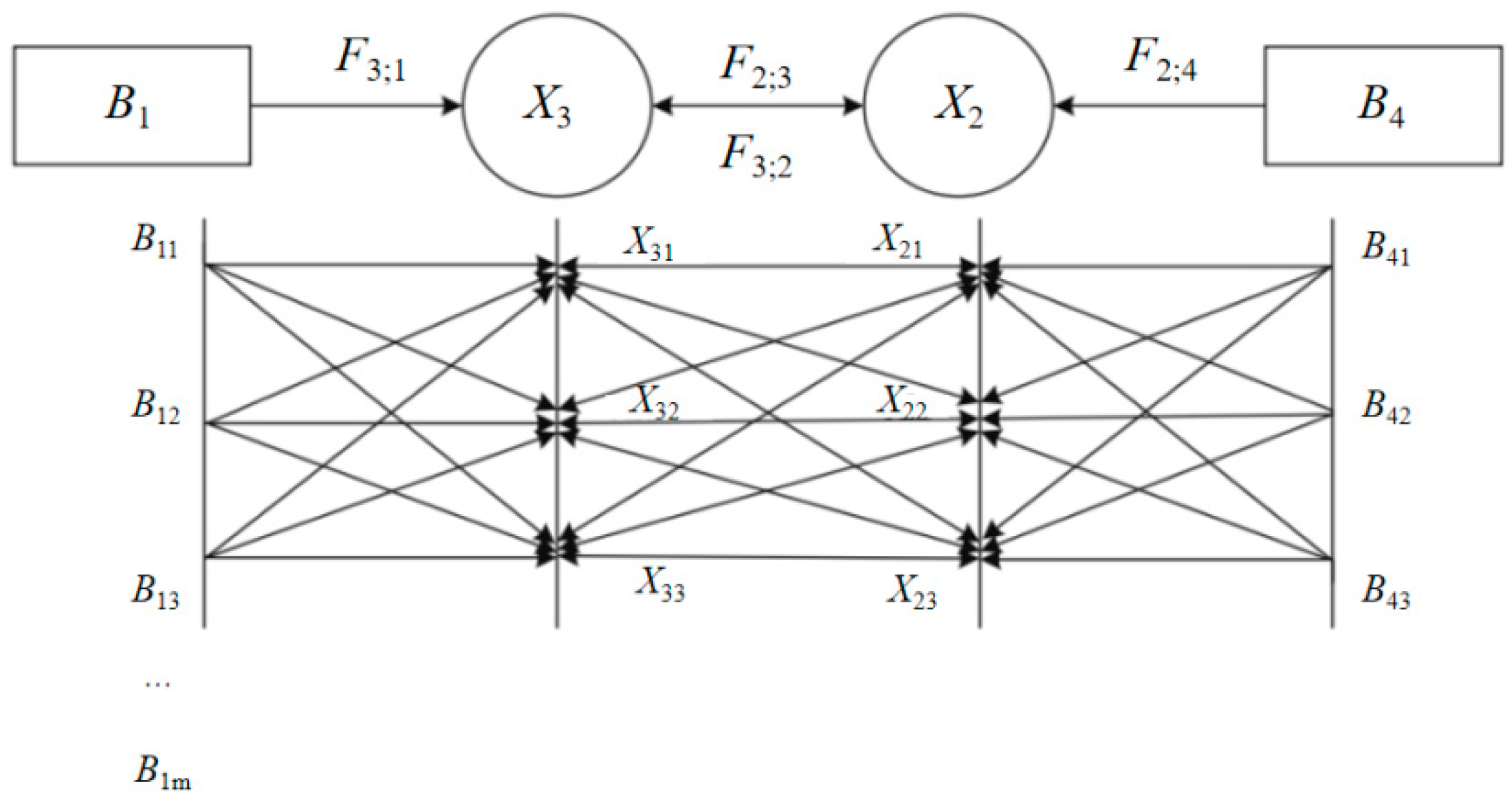
3.2. The DUCG Model
- (1)
- The root variable B, which can be drawn as a square, represents the root cause;
- (2)
- The intermediate variable X, which can be drawn as a circle, represents the consequence and can also be a cause variable;
- (3)
- The variable F, which can be written as in text, represents a connection event variable and is represented by a certain probability between 0 and 1.
4. The Proposed PUL-DUCG Model
4.1. Definition of the PUL-DUCG
4.2. Knowledge Acquisition and Representation
- Step 1: Construct the collective knowledge assessment matrix .
- Step 2: Obtain the first-order cut-set expression of the target event.
4.3. Reasoning Algorithm
- Step 3: Compute the occurrence probabilities of target child events.
- Step4: Obtain the average probability vector .
- Step5: Determine the positive distance matrix and the negative distance matrix of probabilities to the average probability vector .
- Step 6: Calculate the weighted sum of the probability assessment positive distance and negative distance for each target child event.
- Step 7: Normalize the values of SPi and SNi for each event.
- Step 8: Obtain the ranking order of target child events.
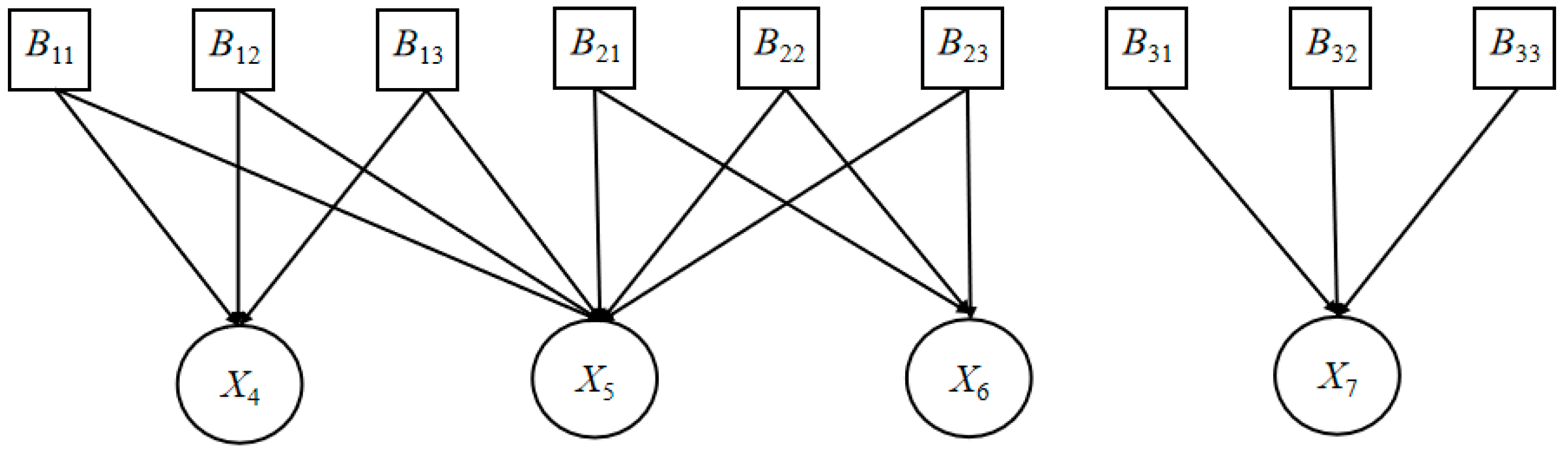
5. Case Study
5.1. Problem Description
5.2. Implementation and Results
- Step 1: By applying Equation (12), the collective knowledge assessment matrix is derived as shown in Table 3.
- Step2: The expression of target child events Xnk under different states could be simplified as
- Step 3: Via Equation (17), the occurrence probabilities of target child events Xnk under different states are calculated as listed in Table 4.
- Step 4: Via Equation (19), the average probability vector is established as
- Step 5: With Equations (20) and (21), the positive distance matrix and the negative distance matrix of target child events to the average probability vector are determined as
- Step 6: By using Equations (22)–(23), the weighted sums of SP and SN for each target child event SPi (i = 1, 2, ..., 9) and SNi (i = 1, 2, ..., 9) are determined as expressed in Table 5.
- Step 7: Via Equations (24) and (25), the normalized values of (i = 1, 2, ..., 9) and (i = 1, 2,..., 9) for each target child event are computed and shown in Table 5.
5.3. Comparisons and Discussions
- 1.
- The model used the membership degree and non-membership degree of PULSs to express the fuzzy knowledge of experts. The fuzziness of initial information will be retained, which can avoid information loss and distortion in the process of causal analysis. Hence, the proposed model is more capable of representing and reasoning uncertain information.
- 2.
- Based on a correction algorithm for solving the contradictory opinions of specialists, the proposed model can manage the conflicts and inconsistencies among expert evaluations in knowledge parameters. Thus, it can determine the knowledge parameters more precisely when acquiring knowledge.
- 3.
- By means of the modified EDAS method, the proposed model can obtain rational and distinguishing occurrence probabilities and select the maximal probability event. Therefore, it is more accurate and effective in the practical utilization of causal analysis problems.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: Directed cyclic graph and joint probability distribution. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1503–1517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Geng, S. Dynamic uncertain causality graph applied to dynamic fault diagnoses of large and complex systems. IEEE Trans. Reliab. 2015, 64, 910–927. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Z.; Zhang, T.; Shi, W.; Zhu, Y.; Hu, J.; Zhang, Q. Development of an artificial intelligence diagnostic model based on dynamic uncertain causality graph for the differential diagnosis of dyspnea. Front. Med. 2020, 14, 488–497. [Google Scholar] [CrossRef] [PubMed]
- Mou, X.; Mao, L.X.; Liu, H.C.; Zhou, M. Spherical linguistic Petri nets for knowledge representation and reasoning under large group environment. IEEE Trans. Artif. Intell. 2022, 1. [Google Scholar] [CrossRef]
- Liu, H.C.; Luan, X.; Zhou, M.C.; Xiong, Y. A new linguistic Petri net for complex knowledge representation and reasoning. IEEE Trans. Knowl. Data Eng. 2022, 36, 1011–1020. [Google Scholar] [CrossRef]
- Dong, C.; Zhao, Y.; Zhang, Q. Assessing the influence of an individual event in complex fault spreading network based on dynamic uncertain causality graph. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1615–1630. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Z. Dynamic uncertain causality graph applied to dynamic fault diagnoses and predictions with negative feedbacks. IEEE Trans. Reliab. 2016, 65, 1030–1044. [Google Scholar] [CrossRef]
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Continuous variable, uncertain evidence, and failure forecast. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 990–1003. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiao, Y.; Zhang, M.; Wei, B.; Liu, X.; Zhao, J.; Tian, F.; Hu, J.; Zhang, Q. AI-aided general clinical diagnoses verified by third-parties with dynamic uncertain causality graph extended to also include classification. Artif. Intell. Rev. 2022, 1–37. [Google Scholar] [CrossRef]
- Deng, N.; Zhang, Q. The application of dynamic uncertain causality graph based diagnosis and treatment unification model in the intelligent diagnosis and treatment of hepatitis B. Symmetry 2021, 13, 1185. [Google Scholar] [CrossRef]
- Dong, C.; Zhang, Q. The cubic dynamic uncertain causality graph: A methodology for temporal process modeling and diagnostic logic inference. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4239–4253. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Ren, Y.; Yang, D.; Feng, Q.; Sun, B.; Qian, C. Reliability analysis of dynamic reliability block diagram based on dynamic uncertain causality graph. J. Loss Prev. Process Ind. 2019, 62, 103947. [Google Scholar] [CrossRef]
- Yao, Q.; Yang, B.; Zhang, Q. Dynamic uncertain causality graph applied to the intelligent evaluation of a shale-gas sweet spot. Energies 2021, 14, 5228. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, Q. Model event/fault trees with dynamic uncertain causality graph for better probabilistic safety assessment. IEEE Trans. Reliab. 2017, 66, 178–188. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Utilization of statistical data and domain knowledge in complex cases. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1637–1651. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Dong, C.; Cui, Y.; Yang, Z. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: Statistics base, matrix, and application. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 645–663. [Google Scholar] [CrossRef]
- Mou, X.; Zhang, Q.Z.; Liu, H.C.; Zhao, J. Knowledge representation and acquisition using R-numbers Petri nets considering conflict opinions. Expert Syst. 2021, 38, 12660. [Google Scholar] [CrossRef]
- Liu, H.C.; Xu, D.H.; Duan, C.Y.; Xiong, Y. Pythagorean fuzzy Petri nets for knowledge representation and reasoning in large group context. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5261–5271. [Google Scholar] [CrossRef]
- Xu, X.G.; Xiong, Y.; Xu, D.H.; Liu, H.C. Bipolar fuzzy Petri nets for knowledge representation and acquisition considering non-cooperative behaviors. Int. J. Mach. Learn. Cybern. 2020, 11, 2297–2311. [Google Scholar] [CrossRef]
- Li, L.; Yue, W. Dynamic uncertain causality graph based on Intuitionistic fuzzy sets and its application to root cause analysis. Appl. Intell. 2020, 50, 241–255. [Google Scholar] [CrossRef]
- Li, L.; Xie, Y.; Chen, X.; Yue, W.; Zeng, Z. Dynamic uncertain causality graph based on cloud model theory for knowledge representation and reasoning. Int. J. Mach. Learn. Cybern. 2020, 11, 1781–1799. [Google Scholar] [CrossRef]
- Li, L.; Xie, Y.; Chen, X. A method for root cause diagnosis with picture fuzzy sets based dynamic uncertain causality graph. J. Intell. Fuzzy Syst. 2021, 41, 387–397. [Google Scholar] [CrossRef]
- Shi, H.; Wang, L.; Li, X.Y.; Liu, H.C. A novel method for failure mode and effects analysis using fuzzy evidential reasoning and fuzzy Petri nets. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2381–2395. [Google Scholar] [CrossRef]
- Liu, H.C.; Luan, X.; Lin, W.; Xiong, Y. Grey reasoning Petri nets for large group knowledge representation and reasoning. IEEE Trans. Fuzzy Syst. 2020, 28, 3315–3329. [Google Scholar] [CrossRef]
- Xu, X.G.; Shi, H.; Xu, D.H.; Liu, H.C. Picture fuzzy Petri nets for knowledge representation and acquisition in considering conflicting opinions. Appl. Sci. 2019, 9, 983. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Liu, P.; Liu, W.; Pang, J. Pythagorean uncertain linguistic partitioned Bonferroni mean operators and their application in multi-attribute decision making. J. Intell. Fuzzy Syst. 2017, 32, 2779–2790. [Google Scholar] [CrossRef]
- Xian, S.; Guo, H.; Dong, Y. A novel outranking sorting approach based on interval-valued Pythagorean uncertain linguistic Euclidean distance for material supplier grading. Int. J. Intell. Syst. 2019, 34, 2872–2899. [Google Scholar] [CrossRef]
- Gao, H.; Wei, G.W. Multiple attribute decision making based on interval-valued Pythagorean uncertain linguistic aggregation operators. Int. J. Knowl.-Based Intell. Eng. Syst. 2018, 22, 59–81. [Google Scholar] [CrossRef]
- Zhang, Q.; Bu, X.; Zhang, M.; Zhang, Z.; Hu, J. Dynamic uncertain causality graph for computer-aided general clinical diagnoses with nasal obstruction as an illustration. Artif. Intell. Rev. 2021, 54, 27–61. [Google Scholar] [CrossRef]
- Qiu, K.; Zhang, Q. The M-DUCG methodology to calculate the joint probability distribution of directed cycle graph with local data and domain causal knowledge. IEEE Access 2021, 9, 36087–36099. [Google Scholar] [CrossRef]
- Bu, X.; Lu, L.; Zhang, Z.; Zhang, Q.; Zhu, Y. A general outpatient triage system based on dynamic uncertain causality graph. IEEE Access 2020, 8, 93249–93263. [Google Scholar] [CrossRef]
- Zhao, Y.; Di Maio, F.; Zio, E.; Zhang, Q.; Dong, C.L.; Zhang, J.Y. Optimization of a dynamic uncertain causality graph for fault diagnosis in nuclear power plant. Nucl. Sci. Tech. 2017, 28, 34. [Google Scholar] [CrossRef]
- Nie, H.; Zhang, Q. A new inference algorithm of dynamic uncertain causality graph based on conditional sampling method for complex cases. IEEE Access 2021, 9, 94523–94536. [Google Scholar] [CrossRef]
- Dong, C.; Zhou, Z.; Zhang, Q. Cubic dynamic uncertain causality graph: A new methodology for modeling and reasoning about complex faults with negative feedbacks. IEEE Trans. Reliab. 2018, 67, 920–932. [Google Scholar] [CrossRef]
- Hao, S.R.; Geng, S.C.; Fan, L.X.; Chen, J.J.; Zhang, Q.; Li, L.J. Intelligent diagnosis of jaundice with dynamic uncertain causality graph model. J. Zhejiang Univ. Sci. B 2017, 18, 393–401. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.S. Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Inf. Sci. 2004, 168, 171–184. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Some results for Pythagorean fuzzy sets. Int. J. Intell. Syst. 2015, 30, 1133–1160. [Google Scholar] [CrossRef]
- Liu, H.C.; Wu, S.M.; Wang, Z.L.; Li, X.Y. A new method for quality function deployment with extended prospect theory under hesitant linguistic environment. IEEE Trans. Eng. Manag. 2021, 68, 442–451. [Google Scholar] [CrossRef]
- Xu, Z.S. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Xu, Z. Induced uncertain linguistic OWA operators applied to group decision making. Inf. Fusion 2006, 7, 231–238. [Google Scholar] [CrossRef]
- Lu, M.; Wei, G.W. Pythagorean uncertain linguistic aggregation operators for multiple attribute decision making. Int. J. Knowl.-Based Intell. Eng. Syst. 2017, 21, 165–179. [Google Scholar] [CrossRef]
- Liu, C.; Tang, G.; Liu, P. An approach to multicriteria group decision-making with unknown weight information based on Pythagorean fuzzy uncertain linguistic aggregation operators. Math. Probl. Eng. 2017, 2017, 6414020. [Google Scholar] [CrossRef] [Green Version]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Ding, X.F.; Liu, H.C. A new approach for emergency decision-making based on zero-sum game with Pythagorean fuzzy uncertain linguistic variables. Int. J. Intell. Syst. 2019, 34, 1667–1684. [Google Scholar] [CrossRef]
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Discrete DAG cases. J. Comput. Sci. Technol. 2012, 27, 1–23. [Google Scholar] [CrossRef]
- Deng, N.; Zhang, Q. Towards dynamic uncertain causality graphs for the intelligent diagnosis and treatment of hepatitis B. Symmetry 2020, 12, 1690. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Yue, W.; Chen, X.; Gui, W.; Xie, Y.; Zhang, H. A knowledge reasoning Fuzzy-Bayesian network for root cause analysis of abnormal aluminum electrolysis cell condition. Front. Chem. Sci. Eng. 2017, 11, 414–428. [Google Scholar] [CrossRef]
- Yue, W.; Gui, W.; Xie, Y. Experiential knowledge representation and reasoning based on linguistic Petri nets with application to aluminum electrolysis cell condition identification. Inf. Sci. 2020, 529, 141–165. [Google Scholar] [CrossRef]
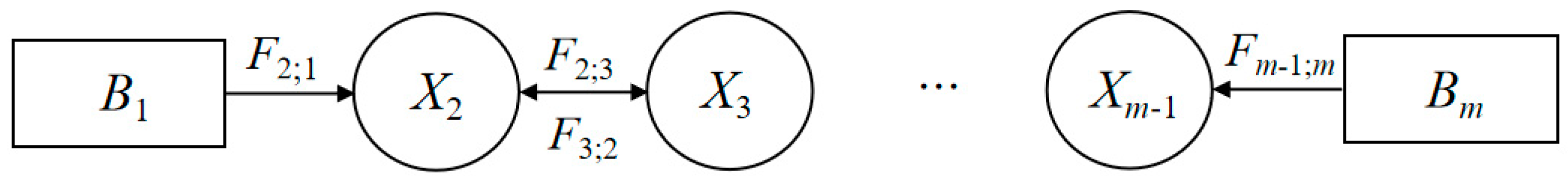
| Technical Parameter | Role Analysis |
|---|---|
| Aluminum height (AH) | AH can stabilize battery voltage. |
| Electrolyte level (EL) | EL maintains cell energy stability. |
| Molecular ratio (MR) | MR will influence the dissolution of alumina in electrolyte. |
| Heat insulation capacity (IP) | Heat insulation performance of aluminum reduction cell. |
| Electrolyte temperature (ET) | The appropriate temperature to ensure the normal operation of aluminum batteries. |
| Voltage fluctuation (VF) | VF is influenced by AH. |
| Crystallization temperature (CT) | The primary temperature of crystallization. |
| Experts | States | |||
|---|---|---|---|---|
| High | Normal | Low | ||
| AH | E1 | <[s4, s5], (0.18,0.82)> | <[s2, s3], (0.72,0.28)> | <[s1, s2], (0.00,1.00)> |
| E2 | <[s5, s6], (0.18,0.82)> | <[s3, s4], (0.65,0.57)> | <[s1, s2], (0.02,0.99)> | |
| E3 | <[s4, s5], (0.18,0.82)> | <[s3, s4], (0.71,0.37)> | <[s2, s3], (0.01,0.98)> | |
| E4 | <[s4, s5], (0.18,0.82)> | <[s3, s4], (0.61,0.39)> | <[s2, s3], (0.00,1.00)> | |
| E5 | <[s4, s5], (0.18,0.82)> | <[s3, s4], (0.71,0.37)> | <[s2, s3], (0.00,1.00)> | |
| EL | E1 | <[s3, s4], (0.10,0.70)> | <[s2, s3], (0.75,0.20)> | <[s1, s2], (0.00,1.00)> |
| E2 | <[s5, s6], (0.27,0.82)> | <[s2, s3], (0.18,0.82)> | <[s2, s3], (0.03,0.89)> | |
| E3 | <[s5, s6], (0.18,0.82)> | <[s1, s2], (0.18,0.82)> | <[s2, s3], (0.01,0.98)> | |
| E4 | <[s5, s6], (0.10,0.80)> | <[s2, s3], (0.18,0.82)> | <[s2, s3], (0.03,0.89)> | |
| E5 | <[s5, s6], (0.18,0.82)> | <[s1, s2], (0.18,0.82)> | <[s2, s3], (0.01,0.98)> | |
| MR | E1 | <[s3, s4], (0.20,0.20)> | <[s5, s6], (0.85,0.15)> | <[s1, s2], (0.01,0.98)> |
| E2 | <[s3, s4], (0.13,0.18)> | <[s3, s4], (0.56,0.31)> | <[s2, s3], (0.01,0.98)> | |
| E3 | <[s4, s5], (0.25,0.28)> | <[s3, s4], (0.67,0.35)> | <[s1, s2], (0.18,0.82)> | |
| E4 | <[s3, s4], (0.30,0.30)> | <[s3, s4], (0.56,0.31)> | <[s2, s3], (0.01,0.98)> | |
| E5 | <[s3, s4], (0.11,0.11)> | <[s2, s3], (0.67,0.35)> | <[s2, s3], (0.11,0.72)> | |
| States | High | Normal | Low |
|---|---|---|---|
| AH | <[s4, s5], (0.18,0.82)> | <[s2, s3], (0.72,0.28)> | <[s1, s2], (0.00,1.00)> |
| EL | <[s5, s6], (0.18,0.82)> | <[s3, s4], (0.65,0.57)> | <[s1, s2], (0.02,0.99)> |
| MR | <[s4, s5], (0.18,0.82)> | <[s3, s4], (0.71,0.37)> | <[s1, s2], (0.01,0.98)> |
| Target Child Events | Occurrence Probabilities |
|---|---|
| <[s1, s2], (0.18,0.82)> | |
| <[s1, s2], (0.70,0.23)> | |
| <[s5, s6], (0.00,1.00)> | |
| <[s3, s4], (0.70,0.10)> | |
| <[s5, s6], (0.70,0.18)> | |
| <[s1, s2], (0.00,1.00)> | |
| <[s5, s6], (0.88,0.01)> | |
| <[s3, s4], (0.79,0.08)> | |
| <[s1, s2], (0.00,1.00)> |
| Target Child Events | Ranking | |||||
|---|---|---|---|---|---|---|
| 0.000 | 0.021 | 0.000 | 0.925 | 0.462 | 6 | |
| 0.122 | 0.000 | 0.411 | 1.000 | 0.705 | 4 | |
| 0.000 | 0.282 | 0.000 | 0.000 | 0.000 | 9 | |
| 0.190 | 0.000 | 0.640 | 1.000 | 0.820 | 2 | |
| 0.000 | 0.074 | 0.000 | 0.734 | 0.367 | 7 | |
| 0.027 | 0.025 | 0.090 | 0.909 | 0.500 | 5 | |
| 0.297 | 0.000 | 1.000 | 1.000 | 1.000 | 1 | |
| 0.129 | 0.000 | 0.4360 | 1.000 | 0.718 | 3 | |
| 0.000 | 0.173 | 0.0000 | 0.384 | 0.192 | 8 |
| Group | Results Given by Model | Actual Result | Consistency | ||||
|---|---|---|---|---|---|---|---|
| FBN | DUCG | IFDUCG | CDUCG | PUL-DUCG | |||
| 1 | AH Low | SV Low | AH Low | AH Low | AH Low | AH Low | Y |
| 2 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Normal | N |
| 3 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Low | Y |
| 4 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Low | Y |
| 5 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Low | Y |
| 6 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Low | Y |
| 7 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Low | Y |
| 8 | AH Low | AH Low | AH Low | AH Low | AH Low | AH Low | Y |
| 9 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 10 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 11 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 12 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 13 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 14 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 15 | AH Normal | AH High | AH High | AH High | AH High | AH High | Y |
| 16 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 17 | AH High | AH High | AH High | AH High | AH High | AH High | Y |
| 18 | AH Normal | AH High | AH High | AH High | AH High | AH High | Y |
| 19 | EL High | EL High | EL High | EL High | EL High | EL High | Y |
| 20 | EL High | EL High | EL High | EL High | EL High | EL High | Y |
| Accuracy | 91.10% | 93.30% | 95.60% | 95.60% | 95.60% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.-J.; Guo, W.; Liu, H.-C. Knowledge Representation and Reasoning with an Extended Dynamic Uncertain Causality Graph under the Pythagorean Uncertain Linguistic Environment. Appl. Sci. 2022, 12, 4670. https://doi.org/10.3390/app12094670
Zhu Y-J, Guo W, Liu H-C. Knowledge Representation and Reasoning with an Extended Dynamic Uncertain Causality Graph under the Pythagorean Uncertain Linguistic Environment. Applied Sciences. 2022; 12(9):4670. https://doi.org/10.3390/app12094670
Chicago/Turabian StyleZhu, Yu-Jie, Wei Guo, and Hu-Chen Liu. 2022. "Knowledge Representation and Reasoning with an Extended Dynamic Uncertain Causality Graph under the Pythagorean Uncertain Linguistic Environment" Applied Sciences 12, no. 9: 4670. https://doi.org/10.3390/app12094670
APA StyleZhu, Y.-J., Guo, W., & Liu, H.-C. (2022). Knowledge Representation and Reasoning with an Extended Dynamic Uncertain Causality Graph under the Pythagorean Uncertain Linguistic Environment. Applied Sciences, 12(9), 4670. https://doi.org/10.3390/app12094670






