Abstract
In crane safety assessment, both quantitative and qualitative indicators are inevitably influenced by the subjective influence of the evaluator, which is unfavorable to the objective requirements of safety assessment. In response to these problems, this study proposes a crane safety assessment method based on the cloud model and the improved combination weighting method of game theory (ICWGT). This evaluation method constructs a multi-level assessment index system for crane safety status by selecting suitable indicators in layers and groups, according to the crane safety assessment rules, and gives a method for constructing the cloud model of the commentary set, the selection and derivation of the membership function, and the determination of the fuzzy relationship matrix. When performing fuzzy synthetic calculations based on the cloud model, the synthetic operator enhances the effect of expectation on entropy and makes the cloud image significantly deformed; this method uses a fine-tuned synthetic operator to improve the algorithm. Compared with the traditional crane fuzzy synthesis assessment method, this method combines the cloud model and ICWGT to achieve finding a balance between expert experience and sample data information, calculating the combined optimization weights of each index and component layer by layer. In order to verify the effectiveness of the method, we take the metal structure system of the shipyard portal crane as an example to explore the applicability of the method in crane safety assessment. The results show that the assessment method can accurately reflect the safety level of the crane and can provide reference material for crane safety assessment.
1. Introduction
As an important piece of loading and unloading equipment in the port, the safety of cranes and their operation is a key concern. Inevitably, there are some port cranes where the safety performance cannot meet the standards in terminals around the world, which is the main reason for the frequent occurrence of safety violations and accidents. The current focus of crane safety management research is to study more advanced crane safety assessment methods so that the crane safety assessment results obtained are intuitive and accurate.
At present, the research direction of the crane safety assessment methods is mainly focused on three perspectives: the probabilistic approach, fuzzy mathematics, and machine learning, which include human factors, crane structure, the working environment, etc. Shepherd et al. [1] used statistical theory to analyze and summarize a large number of crane accident fatality reports provided by the U.S. Occupational Safety and Health Administration (OSHA), to establish a crane focus checklist. Aneziris et al. [2] quantified the occupational risks and accident triggers in the event of a crane accident, aggregated the risk factors that cause accidents, and integrated them into a logical system to guide their fieldwork. Tam et al. [3] analyzed the typical accident cases involving tower cranes and concluded that the main cause of accidents was found to be human factors. Shapira, A. et al. [4] analyzed the safety accidents caused by the operation of tower cranes on construction sites and proposed a model that can calculate the overall safety level index, in order to be able to truly reflect the impact it brings. Furthermore, Shin Jae I [5] found that the main factors of accidents in tower cranes during installation and dismantling are site safety management and the workers’ cooperation and familiarity. Sunaryo et al. [6] used risk identification and risk assessment (HIRA) to determine the root causes of potential accidents in container terminals, then used fault tree analysis (FTA) to determine the factors with the highest risk level. Han S. et al. [7] designed a comprehensive decision support model to perform a simulation evaluation, based on the impact of the project’s equipment, cost, and environmental aspects on known crane operations and presented two suggested approaches. Zhou W. et al. [8] studied the safety problem of tower cranes from the perspective of the social technology system, determined the influencing factors of tower crane safety by combining qualitative and quantitative methods, established a general safety model of tower crane qualitatively by using AcciMap technology and quantitatively analyzed the safety system. Ancione, G. et al. [9] designed a risk index evaluation system to evaluate the dynamic risks of crane operation in the oil and gas industry so that the coefficient could reflect the effects of safety equipment. Sadeghi, S. et al. [10] compared the risk factors studied in the literature with those that have received less or no attention and identified eight neglected areas in the crane safety body of knowledge that are critical to the safe management of cranes.
The safety assessment of cranes shares some similarities with the safety assessment of offshore wind turbines. Chen, W. et al. [11] demonstrated that wind loads can have an impact on the safety assessment of tower cranes by calculating their effect, and Lin Pan et. al. conducted work researching the variable pitch control strategy of a direct-driven offshore wind turbine using a KELM windspeed soft sensor, variable pitch control on direct-driven PMSG for an offshore wind turbine using a Repetitive-TS fuzzy PID control, and wind energy conversion systems analysis of PMSG on offshore wind turbines using improved SMC and the Extended State Observer, etc. [12,13,14,15,16].
For more manufacturing and control technology aspects of crane safety, perhaps we should refer to the innovative ideas in these studies [17,18,19,20,21]. In their paper, X. Xiao et al. introduced an automated method that allowed reorienting the parts during their building, using a five-axis machine. The reorientations still allowed the part to be built using traditional planar deposition but without the use of supports. These research works have had some beneficial effects on the crane safety assessment process.
In the crane safety assessment research, assessment methods based on machine learning have a high demand for standard database samples. Limited by the differences in the relevant safety standards of each country, scholars have difficulty in obtaining a large volume of valid crane safety accident data to accurately calculate the relevant risk probability. The relevant research methods encounter harsh conditions in practical applications. Therefore, the research on crane safety assessment methods is mostly based on fuzzy mathematical theory. Related methods are the traditional empirical method, based on probability [22,23,24,25], and the fuzzy synthesis assessment method, based on fuzzy mathematics [26,27,28]. These assessment methods offer expert experience for the theoretical basis in terms of the weight assignment, which better deals with the fuzzy problem existing in the process of crane safety level classification and determination. However, in the process of quantification, the evaluation level interval value is given a large subjective factor, which will lead to the decision result not being enough to fully express the current safety status of the crane.
Thus, considering the fuzziness and randomness of the crane safety assessment index, this study uses the cloud model [29] to realize the quantitative simulation of uncertainty problems to improve the crane safety assessment method. This method improves the crane safety assessment system based on the cloud model and the ICWGT [30,31,32]. Firstly, the assessment cloud model is established according to the crane safety level assessment standard. Secondly, the membership cloud model matrix of the system index is calculated using the assessment value of the sample index, while the combination optimization weight coefficient matrix of the system index is calculated using the improved ICWGT, based on the cloud model. Then, the improved fuzzy synthesis algorithm is used to synthesize the membership cloud relationship matrix and the combination optimization weight coefficient matrix, to obtain the characteristic parameters corresponding to the cloud model of the assessment results. Finally, the forward cloud generator is used to generate the cloud image of the assessment result cloud model and the commentary set cloud model, then the cloud drops in the image are analyzed to judge the safety assessment result of the crane and verify the feasibility of the method.
2. Methodology
2.1. The Crane Safety Assessment System, Based on the Cloud Model and ICWGT
The crane safety assessment process, based on the cloud model and ICWGT (as shown in Figure 1), mainly includes the establishment of the commentary set cloud model, the determination of the fuzzy relationship matrix, and the determination of the combined optimization weight cloud. The calculation of the comprehensive assessment results is conducted using the fuzzy synthesis algorithm and the assessment results are compared with the commentary set cloud model.
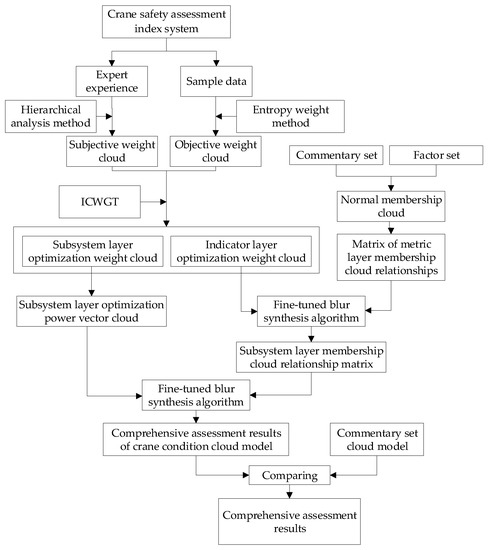
Figure 1.
The process of the crane safety assessment, based on the cloud model and ICWGT.
2.1.1. Fuzzy Integrated Assessment Method, Based on the Cloud Model
Cloud model theory can address the problem of a combination of qualitative concepts and quantitative values; its fuzziness and randomness are characterized by three numerical features: expectation (), entropy () and super entropy ().
The fuzzy comprehensive assessment algorithm, based on the cloud model, uses the cloud model theory to improve the membership function and uses the membership cloud model of the index to calculate the weight matrix and the comprehensive assessment matrix. The data are collected in the form of an expert scoring system and the weight coefficient is obtained by statistics. The reverse cloud generator is used to obtain the characteristic parameters of the cloud model. The membership cloud relationship matrix and combinatorial optimization weight coefficient matrix of the system index can be expressed as:
2.1.2. Commentary Set Cloud Model
The crane commentary set is established according to the crane safety level assessment standard. It describes the risk classification level of the object to be evaluated in the qualitative concept, defines the scope of each assessment level in the quantitative domain, and forms the commentary set cloud model to make the boundary of the assessment safety level fuzzy. The schematic cloud image of the commentary set cloud model determination process is shown in Figure 2.
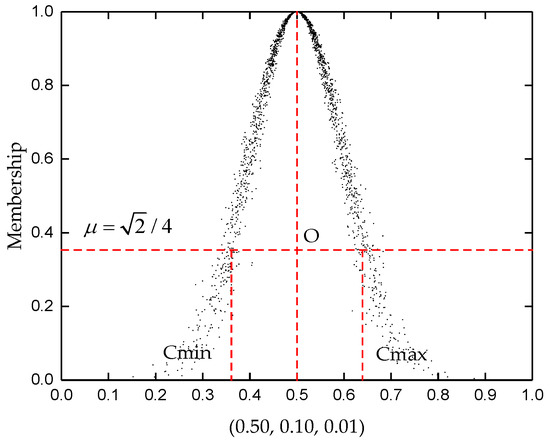
Figure 2.
The schematic cloud image of the commentary set cloud model determination process.
The centroid of the normal cloud model is located at the center of the cloud and its abscissa is the value of the expected , while the ordinate is . When the cloud image is divided into cloud models by a straight line , the number of the cloud drops above this line is high and the density is high, while below the line, the cloud drops are sparse. According to the characteristics of cloud droplet distribution in the cloud model and the position of the centroid, it is necessary to quantitatively represent the intermediate level variables constrained to in the assessment criteria, when establishing the commentary set cloud model. The cloud model digital feature calculation method can be expressed as:
where is an empirical value that is adjusted according to the ambiguity of the comment standard.
2.1.3. Determination of the Fuzzy Relationship Matrix
This fuzzy assessment method uses the membership degree to express the uncertainty of the indicator sample values attributed to different criteria levels. However, the determination of the membership function transforms the uncertainty in the evaluation process into exact values, which conflicts with the randomness and dispersion that exists in the crane safety evaluation process. This evaluation method uses the membership cloud model to represent the uncertainty of the current status of indicators attributed to different criteria levels, which can avoid translating the membership into specific values. This can ensure that the uncertainty of the sample indicators is maintained in the derivation process and that the evaluation results accurately represent the current safety status of the crane.
It is known from the fuzzy theory that the expectation curve of the membership cloud model is the membership curve of its characteristics. When the assigned value of indicator is known, the numerical characteristic calculation process, based on the corresponding membership cloud model, can be expressed as:
where is an empirical value, which is adjusted according to the ambiguity of the comment standard.
2.2. Determination of Optimization Weights for the Crane Assessment System
2.2.1. Determination of Subjective Weight Cloud
Different from the traditional analytic hierarchy process in which experts use the Satty scale to express the relative importance of the two indicators, this evaluation method uses the analytic hierarchy process, based on the cloud model, to determine the subjective weight cloud. An improved cloud model scale method is constructed. The corresponding scale table, based on the improved cloud model, is shown in Table 1, and the cloud model image is shown in Figure 3.

Table 1.
Improved scale table based on cloud model.
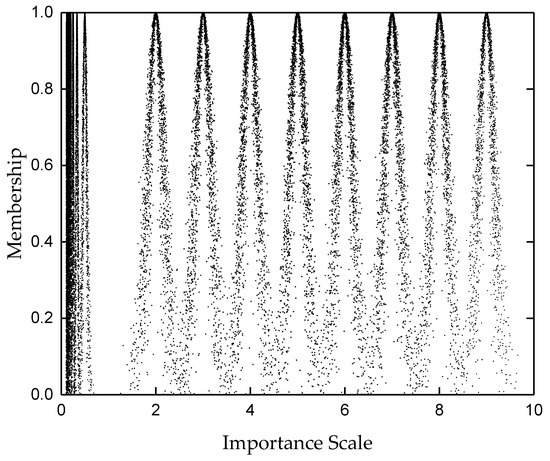
Figure 3.
Scale graph based on the improved cloud model.
The square root method is used to calculate the subjective weight cloud and the subjective weight cloud of is noted as ; its numerical feature calculation formulas can be expressed as:
2.2.2. Determination of the Objective Weight Cloud
Using the entropy weight method based on the cloud model improvement to determine the objective weight cloud, according to the cloud model theory, the objective weight cloud of indicator is , and its numerical feature calculation formulas can be expressed as:
where is taken to indicate a low dispersion of the objective weights.
2.2.3. Determination of the Weight Cloud for ICWGT-Based Portfolio Optimization
Using ICWGT to optimize the weights obtained by different assignment methods, we assume that the weight vectors obtained using methods are , . Any linear combination of weight vectors can be expressed as:
where is a linear combination coefficient, while , represents all possible weight vectors.
The game theory is used to optimize the linear combination in the above formula, to minimize the deviation between the combination weight vector and all possible weight vectors ; the resulting allocation coefficients are normalized to obtain . The solution of the combination coefficient can be expressed as:
The cloud model theory is introduced to replace the traditional subjective and objective weights, with the expected values of the subjective and objective weight clouds; the distribution coefficients and of the weight clouds are obtained through the calculation of Formulas (17) and (18) to minimize the deviation of the obtained optimized weights. Therefore, the objective weight cloud of indicator can be expressed as:
2.3. Improved Fuzzy Synthesis Algorithm
Many studies on reliability evaluation using the cloud model use multiplicative operators for fuzzy synthetic calculations to obtain the evaluation results. However, this expands the influence of the expectation of indicators affiliated with the cloud model on entropy and super entropy. This causes large deviations in the computational results and a significant distortion of the cloud images with respect to the indicator membership cloud model and the commentary set cloud model. Thus, the algorithm is improved using a fine-tuned synthetic operator to reduce the influence of the expectation on the results.
If we suppose that the assessment unit has assessment indicators, the indicator set is , the weight is ; each indicator generates the corresponding security cloud , whose matrix is denoted as . The weight of the indicator generates the corresponding weight cloud , whose matrix is . The fine-tuning synthesis operator is calculated as follows:
This evaluation method uses a fine-tuned synthesis operator to improve the fuzzy synthesis algorithm so as to calculate the crane safety level fuzzy comprehensive assessment results; the assessment results can be expressed as:
3. Results
In this study, the data from the metal structure safety assessment of the shipyard portal crane in paper [32] are used for case analysis to verify the effectiveness of the fuzzy comprehensive assessment method of crane safety levels, based on the cloud model and ICWGT. The assessment index system of the metal structure system of the shipyard portal crane is shown in Figure 4. The test data and assessment values of the structural sample indexes are shown in Table 2. The safety assessment level classification standard adopts a five-level assessment standard. The structural safety assessment level is shown in Table 3 and the safety assessment level classification standard is shown in Table 4. MATLAB will be used to implement the computational processing of the data and the construction of the cloud model, while Origin will be used to present the data results in the form of cloud images.
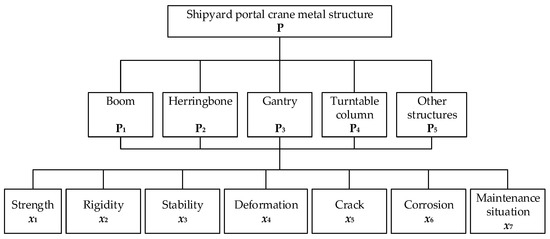
Figure 4.
Shipyard portal crane metal structure system assessment index system.

Table 2.
Test data and assessment values of sample indicators of the shipyard portal crane [32].

Table 3.
Shipyard portal crane structural safety assessment levels.

Table 4.
Shipyard portal crane safety assessment level classification standards.
3.1. Fuzzy Integrated Assessment
3.1.1. Determination of the Membership Cloud Model Matrix
Referring to the test data and assessment value of the sample indexes of the metal structure of the shipyard portal crane, the assessment value of the sample indexes of each subsystem is substituted into Formulas (7) and (8) to determine the expectation and entropy of the indexes of each subsystem belonging to the cloud model. According to the characteristics that the indexes of the system are quantitative indexes, the value of the super entropy is positioned at 0.01, so as to determine the indexes of each subsystem belonging to the cloud model matrix. The membership cloud model matrix of the complete system is obtained by synthesizing the cloud model of the assessment results of each subsystem. The membership cloud model matrix of each subsystem and the complete system obtained by calculation are shown in Table 5.

Table 5.
The membership cloud model matrix of each subsystem and the complete system.
3.1.2. Determination of the Weight Cloud for the ICWGT-Based Portfolio Optimization
- (1)
- Determination of the subjective and objective weight cloud model matrix
The subjective weight cloud model of each subsystem and the metal structure of the complete machine is determined by the improved analytic hierarchy process, based on the cloud model. This evaluation method refers to the subjective weight of the assessment index of the portal crane structure of the shipyard in reference and uses Formulas (10)–(12) to calculate this.
The objective weight cloud model of each subsystem and the metal structure of the complete machine is determined by the improved entropy weight method, based on the cloud model. In this study, the objective weight is determined by the information entropy–unascertained measure theory and is calculated by Formulas (13)–(15).
The subjective and objective weight cloud model matrix of each subsystem and the complete system obtained by calculation are shown in Table 6.

Table 6.
The subjective and objective weight cloud model matrix.
- (2)
- Determination of the weight cloud model matrix for combinatorial optimization
The weight cloud model matrix of crane metal structure combination optimization is determined by an improved game theory combination weighting method based on the cloud model. Firstly, the distribution coefficients of the combined optimization weight cloud are determined by the expected values of the subjective weight cloud and the objective weight cloud. The expected values of the subjective and objective weight cloud are brought into Formulas (17) and (18) to calculate the distribution coefficients and of the combined optimization weight cloud. The obtained distribution coefficients are substituted into Formulas (19)–(21), to determine the combined optimization weight cloud model matrix of the metal structure of each subsystem and the complete machine system.
The combination optimization weight cloud model matrix of each subsystem and the complete system obtained by calculation are shown in Table 7.

Table 7.
The combination optimization weight cloud model matrix.
3.1.3. Determination of the Assessment Results
The membership cloud relationship matrix of each subsystem, the complete machine system, and the combination optimization weight cloud model matrix are combined by the fuzzy synthesis algorithm improved by the fine-tuning synthesis operator. The membership cloud relationship matrix and the combination optimization weight cloud are substituted into Formulas (23)–(25) to determine the cloud model of the assessment results of each subsystem and the complete machine system. The cloud image of the assessment results is obtained using the positive cloud generator. The cloud model of the assessment results of each subsystem and the complete system obtained by calculation are shown in Table 8, and the cloud image of the assessment results is shown in Figure 5.

Table 8.
The cloud model of the assessment results.
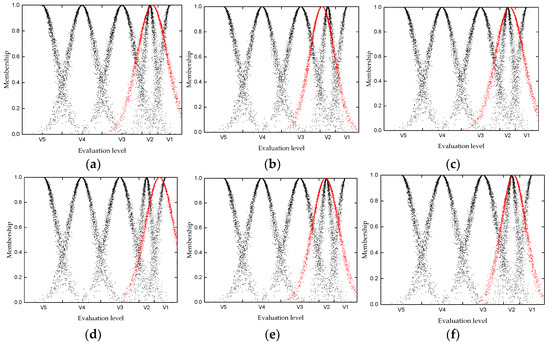
Figure 5.
The cloud images of the assessment results: (a) the boom system; (b) the herringbone system; (c) the gantry system; (d) the turntable column system; (e) other structures; (f) the complete machine system.
4. Discussion and Conclusions
4.1. Discussion
According to the cloud model and cloud images of crane fuzzy comprehensive assessment results, based on the cloud model and ICWGT, the expected value of the cloud model of the known boom system assessment results is , which is the center value of the results. The safety assessment level of each subsystem is consistent with that of the whole machine. Therefore, according to Table 4, the expected value of the boom system is (0.75, 0.85), and the corresponding assessment level is II. By analyzing the cloud morphology thickness and cloud droplet dispersion in Figure 5a, it can be seen that cloud droplets are mostly concentrated in the level V2 region, and a small number of cloud droplets are distributed in the level V1 region. Therefore, it is concluded that the safety level of the boom system is II. This assessment result indicates that the metal structure of the boom system is in good condition. Using the same judging method, it can be established that the safety level of the herringbone frame system is II, the safety level of the portal frame system is II, the safety level of the turntable column system is II, and the safety level of other structures is I.
For the whole system, the index assignment is the assessment result cloud model of each subsystem, so the fuzzy relationship matrix of the complete machine system is obtained according to the calculation results of each subsystem in Table 8. Then, the expected value of the complete machine system assessment results is calculated to be . According to Table 4, the expected value of the complete machine system is (0.75, 0.85), and the corresponding assessment level is II. By analyzing the cloud morphology in Figure 5f, it can be concluded that the metal structure safety level of the crane is II, which means that the shipyard portal crane is in good condition and it is recommended to strengthen maintenance.
The assessment results are compared with those obtained by the fuzzy analytic hierarchy process (FAHP), the method approximating the ideal solution ordering, and ICWGT combined with gray correlation analysis. The comparison of the results is shown in Table 9.

Table 9.
The comparison of the results of the four assessment models.
As shown in Table 9, the FAHP used in the literature [21] is to judge the safety level of the crane using the calculated level characteristic values, and the final assessment results of the crane depend on the range in which the level characteristic values are located. Approximating the ideal solution ordering method used in the literature [23] judges the safety level of the crane based on the ranking of the combined prospect values. The ICWGT, combined with the gray correlation analysis method, used in the literature [26] gives the results of the crane safety assessment by a more accurate description of the stage change trend of the crane’s safety condition, based on the calculated results. However, these three methods evaluate the sample values only through theoretical calculations to obtain the assessment results and have the problem of not being able to accurately describe the safety condition of the crane. In the crane fuzzy integrated assessment model, based on the cloud model and ICWGT, the assessment results of the overall safety and subsystems of the shipyard portal crane will be reflected by the cloud model. Its digital characteristics, , reflect the central value, fuzziness, and randomness. The final assessment results of this method can be displayed in the form of cloud images, which are more intuitive and accurate.
The assessment results obtained by this method are basically consistent with those obtained by the other three methods, which proves that the method is accurate. Compared with those, this method can achieve multi-level and quantitative modeling and analysis of the crane state. Adding the cloud model theory to the crane safety assessment can give a more reasonable combination optimization weight cloud. The fuzzy synthesis algorithm is improved by fine-tuning the synthesis operator to make the assessment result more reasonable and judge the safety level of the crane more accurately. The assessment results obtained by this method can be shown by its cloud model and cloud images, which have three digital characteristics of expectation, entropy, and hyper-entropy. The cloud images of the assessment results obtained by the forward cloud generator can intuitively reflect the center value of the assessment results and their randomness and fuzziness. This study can provide a more comprehensive theory for the safety assessment of cranes, which can help in further use and maintenance.
4.2. Conclusions
- (1)
- The cloud model theory can convert the qualitative concept of safety levels into a quantitative representation with mathematics. The randomness and fuzziness of the crane safety assessment indexes are handled by this theory. Based on the cloud model to improve the fuzzy comprehensive assessment method, the numerical characteristics of the cloud model are used to represent the fuzzy relationship matrix, the weight coefficient matrix, and the final assessment results. Then, the cloud map is generated by a forward cloud generator to make the presentation of assessment results more intuitive.
- (2)
- In this study, a new crane safety assessment method is obtained by combining ICWGT with cloud model theory. In calculating the combination optimized weight cloud of the crane metal structure, based on the sample values, the game theory idea is applied to optimize the combination coefficients, which makes the allocation of subjective and objective weight clouds more reasonable. In the synthesis calculations, the synthesis algorithm is improved by using a fine-tuned synthesis operator. The method not only takes expert experience and currently available sample information into account but also overcomes the influence of human subjective factors and the fluctuation of data information in weight assignment.
- (3)
- The crane safety assessment method based on the cloud model and ICWGT has been applied to a comprehensive assessment of the operation condition and safety level of the shipyard portal crane. The assessment results match the engineering reality. This validation result proves the accuracy of the method and has a theoretical reference value for a comprehensive assessment study of crane safety levels.
This crane safety assessment method is based on the central limit theorem and the universality of the cloud model. The normal cloud model is selected as the basis to improve the commentary set, fuzzy relationship matrix, combination weighting method, and fuzzy synthesis algorithm. However, methods of choosing different cloud models for different state indicators need to be further explored. Moreover, the set of risk factors for crane operation used in this study is derived from the analysis of crane safety issues and investigation of crane-related studies, but this set will be affected by the development of crane-related technologies. With the gradual quantification of qualitative indicators, the set of crane-related risk factors needs to be supplemented and improved.
Author Contributions
Conceptualization, Z.Z., Y.L. and C.C.; methodology, Z.Z., Y.L. and C.X.; software, Z.Z. and Y.L.; validation, Z.Z., Y.L., H.X., C.X. and C.C.; formal analysis, Z.Z. and Y.L.; investigation, Z.Z. and Y.L.; resources, Z.Z., Y.L. and C.C.; data curation, Z.Z. and Y.L.; writing—original draft preparation, Z.Z. and Y.L.; writing—review and editing, Z.Z., Y.L., H.X., C.X. and C.C.; visualization, Z.Z. and Y.L.; supervision, Z.Z., Y.L., H.X., C.X. and C.C.; project administration, Z.Z., Y.L., H.X., C.X. and C.C.; funding acquisition, Z.Z., Y.L., H.X., C.X. and C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shepherd, G.W.; Kahler, R.J.; Cross, J. Crane fatalities—A taxonomic analysis. Saf. Sci. 2000, 36, 83–93. [Google Scholar] [CrossRef]
- Aneziris, O.N.; Papazoglou, I.A.; Mud, M.L.; Damen, M.; Kuiper, J.; Baksteen, H.; Ale, B.J.; Bellamy, L.J.; Hale, A.R.; Bloemhoff, A.; et al. Towards risk assessment for crane activities. Saf. Sci. 2008, 46, 872–884. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Fung, I.W.H. Tower crane safety in the construction industry: A Hong Kong study. Saf. Sci. 2011, 49, 208–215. [Google Scholar] [CrossRef]
- Shapira, A.; Simcha, M.; Goldenberg, M. Integrative Model for Quantitative Evaluation of Safety on Construction Sites with Tower Cranes. J. Constr. Eng. Manag. 2012, 138, 1281–1293. [Google Scholar] [CrossRef]
- Shin, I.J. Factors that affect safety of tower crane installation/dismantling in construction industry. Saf. Sci. 2015, 72, 379–390. [Google Scholar] [CrossRef]
- Sunaryo; Hamka, M.A. Safety Risks Assessment on Container Terminal Using Hazard Identification and Risk Assessment and Fault Tree Analysis Methods. In Proceedings of the 10th International Conference on Marine Technology (MARTEC), Dhaka, Bangladesh, 9–10 December 2016; pp. 307–314. [Google Scholar]
- Han, S.; Hasan, S.; Bouferguene, A.; Al-Hussein, M.; Kosa, J. An integrated decision support model for selecting the most feasible crane at heavy construction sites. Autom. Constr. 2018, 87, 188–200. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, T.S.; Liu, W.; Tang, J.J. Tower crane safety on construction sites: A complex sociotechnical system perspective. Saf. Sci. 2018, 109, 95–108. [Google Scholar] [CrossRef]
- Ancione, G.; Paltrinieri, N.; Milazzo, M.F. Integrating Real-Time Monitoring Data in Risk Assessment for Crane Related Offshore Operations. J. Mar. Sci. Eng. 2020, 8, 532. [Google Scholar] [CrossRef]
- Sadeghi, S.; Soltanmohammadlou, N.; Rahnamayiezekavat, P. A systematic review of scholarly works addressing crane safety requirements. Saf. Sci. 2021, 133, 105002. [Google Scholar] [CrossRef]
- Chen, W.; Qin, X.R.; Yang, Z.G.; Zhan, P.M. Wind-induced tower crane vibration and safety assessment. J. Low Freq. Noise Vib. Act. Control. 2020, 39, 297–312. [Google Scholar] [CrossRef]
- Pan, L.; Shao, C.P. Wind energy conversion systems analysis of PMSG on offshore wind turbine using improved SMC and Extended State Observer. Renew. Energy 2020, 161, 149–161. [Google Scholar] [CrossRef]
- Pan, L.; Wang, X.D. Variable pitch control on direct-driven PMSG for offshore wind turbine using Repetitive-TS fuzzy PID control. Renew. Energy 2020, 159, 221–237. [Google Scholar] [CrossRef]
- Pan, L.; Zhu, Z.; Shi, Z.; Wang, L. Modeling and Investigation of Blade Trailing Edge of Vertical Axis Offshore Wind Turbine. Sustainability 2021, 13, 10905. [Google Scholar] [CrossRef]
- Pan, L.; Zhu, Z.; Xiao, H.D.; Wang, L.C. Numerical Analysis and Parameter Optimization of J-Shaped Blade on Offshore Vertical Axis Wind Turbine. Energies 2021, 14, 6426. [Google Scholar] [CrossRef]
- Pan, L.; Zhu, Z.; Xiong, Y.; Shao, J.K. Integral Sliding Mode Control for Maximum Power Point Tracking in DFIG Based Floating Offshore Wind Turbine and Power to Gas. Processes 2021, 9, 1016. [Google Scholar] [CrossRef]
- Xiao, X.; Joshi, S. Process planning for five-axis support free additive manufacturing. Addit. Manuf. 2020, 36, 101569. [Google Scholar] [CrossRef]
- Xiao, X.; Joshi, S.; Cecil, J. Critical assessment of Shape Retrieval Tools (SRTs). Int. J. Adv. Manuf. Technol. 2021, 116, 3431–3446. [Google Scholar] [CrossRef]
- Xiao, X.; Roh, B.-M.; Zhu, F. Strength Enhancement in Fused Filament Fabrication via the Isotropy Toolpath. Appl. Sci. 2021, 11, 6100. [Google Scholar] [CrossRef]
- Zou, S.; Pang, L.; Xu, C.; Xiao, X. Effect of Process Parameters on Distortions Based on the Quantitative Model in the SLM Process. Appl. Sci. 2022, 12, 1567. [Google Scholar] [CrossRef]
- Zou, S.; Xiao, H.; Ye, F.; Li, Z.; Tang, W.; Zhu, F.; Chen, C.; Zhu, C. Numerical analysis of the effect of the scan strategy on the residual stress in the multi-laser selective laser melting. Results Phys. 2020, 16, 103005. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Jiang, L.; Zhao, T.S. Identification of Critical Causes of Tower-Crane Accidents through System Thinking and Case Analysis. J. Constr. Eng. Manag. 2020, 146, 04020071. [Google Scholar] [CrossRef]
- Zhang, W.; Xue, N.N.; Zhang, J.R.; Zhang, X. Identification of Critical Causal Factors and Paths of Tower-Crane Accidents in China through System Thinking and Complex Networks. J. Constr. Eng. Manag. 2021, 147, 04021174. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, W. Multi-criteria decision analysis for tower crane layout planning in high-rise modular integrated construction. Autom. Constr. 2021, 127, 103709. [Google Scholar] [CrossRef]
- Huang, S.P. Application of the Evidence Theory in the Safety Assessment of Tower Cranes. In Proceedings of the 2nd International Conferene on Structures and Building Materials, Hong Kong, China, 17–18 November 2012; Volume 446–449, pp. 2162–2167. [Google Scholar]
- Shen, G.; Xiang, D.; Liu, N.; Mou, P.; Yang, Y. Application of the Fuzzy-AHP Method in Bridge The crane safety assessment. Appl. Mech. Mater. 2013, 496–500, 2788–2794. [Google Scholar]
- Li, A.H.; Zhao, Z.Y. An Improved Model of Variable Fuzzy Sets with Normal Membership Function for The crane safety assessment. Math. Probl. Eng. 2017, 2017, 3190631. [Google Scholar]
- Li, A.H.; Zhao, Z.Y. The crane safety assessment Method Based on Entropy and Cumulative Prospect Theory. Entropy 2017, 19, 44. [Google Scholar] [CrossRef] [Green Version]
- Song, C.-Y.; Cho, E.-S. A Feature-based Cloud Modeling Method. J. Knowl. Inf. Technol. Syst. 2022, 101–120, 1975–7700. [Google Scholar]
- He, H.; Tian, C.; Jin, G.; An, L. An Improved Uncertainty Measure Theory Based on Game Theory Weighting. Math. Probl. Eng. 2019, 2019, 3893129. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, N.; Liu, X.; Chen, X. Classification Evaluation of Loess Slope Stability Based on the Combination Weight of Game Theory. In Proceedings of the 4th Annual International Workshop on Materials Science and Engineering (IWMSE), Xi’an, China, 18–20 May 2018; p. 381. [Google Scholar]
- Xiao, H.; Xiong, C.; Zhu, F.; Liu, M. Safety assessment for cranes based on ICWGT and grey relational analysis method. J. Shanghai Marit. Univ. 2020, 41, 117–122. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).