Abstract
Advances in next-generation sequencing have provided high-dimensional RNA-seq datasets, allowing the stratification of some tumor patients based on their transcriptomic profiles. Machine learning methods have been used to reduce and cluster high-dimensional data. Recently, uniform manifold approximation and projection (UMAP) was applied to project genomic datasets in low-dimensional Euclidean latent space. Here, we evaluated how different representations of the UMAP embedding can impact the analysis of breast cancer (BC) stratification. We projected BC RNA-seq data on Euclidean, spherical, and hyperbolic spaces, and stratified BC patients via clustering algorithms. We also proposed a pipeline to yield more reproducible clustering outputs. The results show how the selection of the latent space can affect downstream stratification results and suggest that the exploration of different geometrical representations is recommended to explore data structure and samples’ relationships.
1. Introduction
Due to heterogeneity in different cancer types, the stratification of cancer patients is a major clinical challenge. It is also a key goal of precision medicine because it would facilitate targeted therapies [1]. Breast cancer (BC) is the world’s most diagnosed female tumor, with a high incidence ( of female cancer cases) and mortality ( of total female deaths) worldwide in 2020 [2]. Moreover, incidence is estimated to increase to around 3,000,000 cases in 2040 [3]. Tumor stratification for breast carcinoma will therefore become increasingly important in clinical management, clinical trials, and epidemiological and functional studies [4].
Recent advances in next-generation sequencing (NGS) have created massive datasets for genomic big data [5]. NGS has enabled the fast, accurate, and cost-effective analysis of DNA and RNA samples, allowing patients to be stratified by their transcriptomic profiles [6,7,8].
As with all high-dimensional data, RNA-seq datasets suffer from the curse of dimensionality [9]. Thus, several machine learning (ML) methods have been proposed to extract relevant features and information [10,11].
Of these, uniform manifold approximation and projection (UMAP) [12] has been widely used in several tumor stratification and RNA-seq analyses [13,14,15,16].
Unlike other popular dimensionality reduction methods, such as principal component analysis (PCA) [17], UMAP is nonlinear and emphasizes local data structures well. It is therefore used in a preprocessing step to reduce the dimensionality of a genomic dataset, either before implementing a full ML model [18] or before visualizing complex expression profiling data [19]. A recent comparative study [20] showed how UMAP can also considerably improve the performances of clustering algorithms.
In general, users tune the number of neighbors, i.e., the main UMAP hyperparameters, to project local data structures in a low-dimensional Euclidean space. Nevertheless, several other tuning parameters can be specified. In particular, users can choose the embedding metric onto which UMAP projects the data. By default (https://umap-learn.readthedocs.io/en/latest/parameters.html, accessed on 20 April 2022), it is a Euclidean distance. Basically, the more the geometry of the latent space matches the structure of the input data, the more important the quality of the embedding representation [21]; therefore, different metric spaces (onto which to project the data) might reveal different sample relationships and structures. Recently, Ref. [22] proposed a deep generative model to embed cells into low-dimensional hyperspherical or hyperbolic spaces, providing excellent visualization for data exploration. In another study, Ref. [23] demonstrated how a hyperbolic embedding can reveal meaningful hierarchies among samples starting from pairwise similarity information.
Hence, when we cannot know the geometry of the latent space a priori, different types of metrics should be explored. To the best of our knowledge, the literature contains no reports on investigating different curvatures of the UMAP embedding space.
Given the above, here we evaluated how non-Euclidean UMAP embeddings can impact the results of a breast cancer stratification analysis. We used UMAP on RNA-seq data with three different output metrics: Euclidean, spherical, and hyperbolic. Then, we stratified the samples via clustering algorithms applied on each UMAP embedding. We then compared the results in terms of clustering accuracy.
For the present study, we used the RNA-seq breast cancer data downloaded from The Cancer Genome Atlas (TCGA) website. Details of the dataset are presented in the Methods section.
Furthermore, UMAP reproducibility is not exact (https://umap-learn.readthedocs.io/en/latest/reproducibility.html, accessed on 20 April 2022) because it is a stochastic algorithm. Thus, downstream results might differ between runs. To overcome this, we propose a pipeline to combine the clustering outputs obtained from different embeddings into one final robust result.
Our results highlight how a different latent space, onto which practitioners project high-dimensional data, can affect the final results, suggesting that the choice of the embedding geometry is meaningful for tumor stratification. Specifically, our simulations show similar performances between Euclidean and hyperbolic metrics, while the spherical one performs worse than other metrics on three out of four tested algorithms.
2. Materials and Methods
2.1. Data
Because BC is the most commonly diagnosed female tumor [2] and similarly to [24], we used the RNA-seq dataset and the clinical variables related to BC, profiled by The Cancer Genome Atlas (TCGA) [25] (for more details on BC RNA-seq data, see the Data Availability Statement section of the manuscript). We filtered out the male and metastatic samples, then merged the data with the BC subtypes that include 192 basal-like, 563 luminal-A, 207 luminal-B, 82 HER2-enriched, and 40 normal-like samples. The final dataset comprises 20,530 gene expressions per 1084 samples.
2.2. UMAP
To reduce the dimensionality of the RNA-seq data, we used UMAP (umap-learn 0.4.0 package in Python: https://umap-learn.readthedocs.io/en/latest/release_notes.html, accessed on 20 April 2022), an unsupervised algorithm for nonlinear neighbor graph-based dimensionality reduction [12], which is popular in various fields [16,26,27]. This was the first step in a cluster analysis to address the “curse of dimensionality” [9], a common problem for clustering algorithms.
Briefly, UMAP computes a high-dimensional weighted graph of the data, with edge strength quantifying how a vertex (sample) is connected to another. Then, UMAP embeds the data points into a low-dimensional space, minimizing the fuzzy-set cross-entropy between the high- and low-dimensional graphs.
Several parameters must be specified to apply UMAP. First, the number of nearest neighbors (NNs) is required to construct the initial graph. To select the best NN, we embedded the data several times with different NN values, ranging from 10 to 100 (in steps of five), and chose the one that improved the clustering performance in terms of adjusted rand index (ARI) [28] and homogeneity score [29]. Second, to better visualize the projected data, UMAP allows one to define a minimum distance (MD) between nearest neighbors in low-dimensional space. Since a low MD value is more appropriate [30] for downstream clustering analysis, we set MD equal to zero. Finally, two metrics can be defined: one metric to compute the distance between the input data points, and the other to compute distances in the final embedding, i.e., the output metric. Common choices fall within Euclidean distance for both metrics, but there is no reason to assume that the best topological representation of the input data lies in a low-dimensional Euclidean space. Correspondence between the structure of the input data and the geometry of latent space can improve embedding representation and downstream analysis such as clustering and classification [31]. Therefore, setting the input metric as Euclidean, we projected the 20,530 gene expressions not only onto 3-dimensional (we chose 3 dimensions for the Euclidean space as it is viewable and more informative than the 2-dimensional representation) Euclidean space but also onto 2-dimensional spherical and hyperbolic surfaces, in order to visualize and evaluate how a different topology of the latent space can affect the final results in terms of clustering performance.
2.3. Clustering Algorithms
Tumor stratification from transcriptomic data aims to identify groups of samples with common characteristics (i.e., tumor subtype). This task is commonly addressed with clustering techniques. In this study, we tested four clustering algorithms, comparing their outputs: hierarchical density-based spatial clustering of applications with noise (HDBSCAN), density-based spatial clustering of applications with noise (DBSCAN), ordering points to identify the clustering structure (OPTICS), and agglomerative clustering. We chose these algorithms as they do not rely upon centroid computation which is a non trivial operation for non-Euclidean metrics.
HDBSCAN is a density-based hierarchical method developed by Campello et al. [32]. By creating a series of nested sample groups, it allows one to perform hierarchical clustering and so to explore tumor stratification on RNA-seq data in greater detail.
The algorithm does not assign lower density points to any cluster, marking them as Noise. In this work, we referred to them as Not Clusterable (NC) points. Moreover, the algorithm requires two main hyperparameters to be defined. The first hyperparameter, Min Cluster Size (MCS), is the minimum number of elements required to build a group. The second hyperparameter, Min Samples (MS), is related to the extent of NC points. In our analysis, the MCS value was set to 30, while the MS was optimized based on the value of ARI, with testing values ranging from 1 to 100.
The DBSCAN algorithm, proposed in 1996 [33], is the precursor of HDBSCAN. Its main hyperparameters are the maximum distance between two samples (EPS) and MS. The first was optimized by testing values from 0.05 to 10, and the second one was optimized as for HDBSCAN.
Moreover, the OPTICS algorithm [34] is closely related to DBSCAN and its main hyperparameter is MS.
Finally, the agglomerative clustering [35] was the last one we tested. It recursively merges pairs of clusters of sample data and it requires the number of clusters to be defined; we fixed that value at 4.
The evaluation of clustering quality and the hyperparameter optimization were based on two scores. The first score is ARI, a popular score for evaluating the quality of clustering [36,37]. Ranging from to 1, it computes the similarity between the partitions generated by the algorithm and the one we expect, according to a specific clinical variable (in our analysis, the BC subtype). A value of 1 indicates that the algorithm is able, in an unsupervised manner, to aggregate the samples as defined in the clinical variable. The second score is the homogeneity [29], ranging from 0 to 1, where 1 corresponds to a perfectly homogeneous partition. A clustering result is homogeneous if all of its clusters contain only data points that are members of a single class.
We considered it to be a good stratification result if we obtained simultaneously high scores for ARI and homogeneity. In particular, a high ARI score means that the algorithm found similar tumor subtypes to those we expected, while a high homogeneity score indicates that tumor clusters comprise samples of the same BC subtype.
2.4. Reproducibility
Due to use of stochasticity for optimization, the UMAP reproducibility is not exact (https://umap-learn.readthedocs.io/en/latest/reproducibility.html, accessed on 20 April 2022). This means that, for some datasets such as RNA-seq data, where the tumor subgroups are a complex function of the transcriptomic profiles, applying a clustering algorithm on two different runs of UMAP might return two different outputs. We showed that, although relatively stable, the results have a minimum of variability in terms of the number of estimated clusters, or samples belonging to the same or different group. When it is important to identify the correct number of clusters, as in tumor stratification, it is crucial to rely on algorithms that reproduce the same output over several runs, in order to have reliable results.
Therefore, for each NN, to obtain a robust clustering result and to quantify how frequently a sample was paired to another sample set, we propose a new pipeline of analysis that applies a clustering algorithm to T different UMAP embeddings, where T is the number of runs, and compacts all the HDBSCAN tumor groups into one final reproducible output. Specifically, we defined the binary proximity matrix , which indicates if two samples belong to the same cluster. Then, after T iterations, we computed the affinity matrix P as:
The square matrix P quantifies how frequently a pair of samples was clustered together, ranging from 0 (never) to 1 (always). Hence, from P we know the strength with which two individuals belong to the same group, but to obtain a final stratification we must apply a clustering algorithm to P. Spectral clustering (SC) is the most straightforward way to perform clustering, starting from the affinity matrix [38,39,40]. However, the SC algorithm requires the number of clusters k to be returned as a hyperparameter. We set k equal to the mode of the number of partitions observed during the T runs, since it is the favorite solution proposed over the T runs. In the Supplementary Material, we demonstrate via simulations how our method yields a more reproducible clustering output than the implementation of a clustering algorithm on a single UMAP run.
Nevertheless, result reproducibility came at the cost of losing latent space visualization, since the final clusters were no longer computed on one specific embedding, but rather were estimated from several embeddings. However, to visualize the UMAP data projection in a way that best represents the final clustering labels, from T embeddings we selected the one with the most similar clustering result in terms of ARI. This is just a visual approximation, merely useful for results presentation; nevertheless, we were interested here in the reproducibility of the tumor stratification results, that is, in having tumor subgroups that are well-identifiable even if the entire analysis is run many times. Finally, once we had reproducible cluster outputs coming from different geometrical representations, we chose the one with the highest ARI.
Our methodological workflow is depicted in Figure 1.
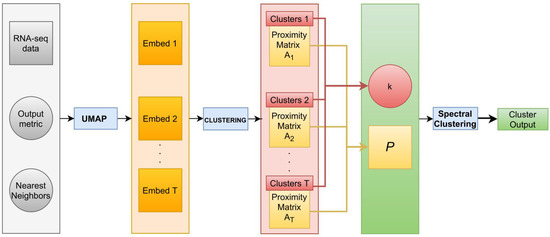
Figure 1.
Methodological workflow of our pipeline. Starting from RNA-seq data, on the left, given an output metric and number of NN (our hyperparameters), we generated T UMAP embeddings, onto which we applied a clustering algorithm. Then, we set k equal to the mode of the number of clusters identified by the clustering technique on T embeddings and we computed the affinity matrix P by summing all T proximity matrices related to each clustering result. Finally, we applied spectral clustering on P with k groups to obtain one final reproducible cluster.
Hyperparameters of the pipeline (Algorithm 1) are: the output metric M, the NN, the number of runs T, and the clustering algorithm. The pipeline can be summarized with the following steps
| Algorithm 1 Pseudocode of the pipeline |
for in {HDBSCAN, DBSCAN, OPTICS, agglomerative clustering} do for M in {Euclidean, Spherical, Hyperbolic} do for NN in do for t in do generate UMAP embedding E with output metric equal to M and number of near neighbors equal to NN; apply on E and save the proximity matrix , where the element of matrix is equal to 1 if the i-th and j-th sample were assigned to the same cluster, 0 otherwise, for , with n the sample size; end for set ; set k equal to the mode of the number of clusters identified over the T clustering results; implement spectral clustering with k groups and P as affinity matrix. end for end for end for among the M UMAP embeddings with different NN, select, within the various , the cluster output with the highest ARI. |
The code was implemented in R 4.1.3 (https://www.r-project.org/, accessed on 20 April 2022) and Python 3.8.10 (https://www.python.org/, accessed on 20 April 2022). The figures were created using the Plotly R package and Matplotlib 3.3.4 Python package. The entire pipeline run on the high-performance computing (HPC) cluster at the data center of Engineering D.HUB in Pont-Saint-Martin, which is equipped with CPU and GPU computational nodes. The code to run the entire pipeline is available at: https://bitbucket.org/jordy_bollon/jordy-bollon/src/master/, accessed on 20 April 2022.
3. Results
3.1. UMAP
We reduced the high dimensionality of RNA-seq data from 20,530 gene expressions to two (spherical and hyperbolic surface) or three (Euclidean space) latent dimensions. For clarity and to give a visual example of the latent spaces, for each metric, we only visualized one UMAP embedding with an NN that returns the best ARI, after HDBSCAN implementation (see Figure 2).
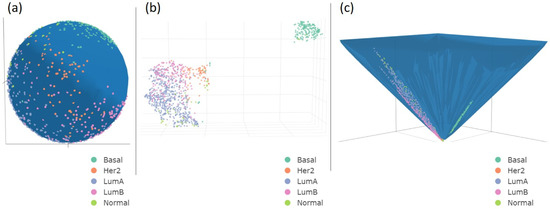
Figure 2.
A 3D visualization of UMAP projection (NN = 65). The pictures show 1084 samples grouped by five BC subtypes on a spherical surface (a), Euclidean space (b), and hyperboloid (c). The input RNA-seq data comprised 20,530 genes. We reduced it to three dimensions for Euclidean space and two dimensions for spherical and hyperbolic embedding.
3.2. Clustering
3.2.1. Irreproducibility Issues
As described in the Reproducibility section, for each output metric and NN, we implemented the UMAP + clustering algorithm pipeline times to highlight how independent runs of UMAP + clustering yield inconsistent outputs in terms of variability of the Nc and ARI. In Figure 3, for each clustering technique, we report the absolute frequency of the estimated Nc over the T iterations for each NN. The Euclidean metric shows the least variability in estimating Nc over the T runs for each NN: the mode of Nc is equal to 2 for HDBSCAN, 4 for DBSCAN, and 3 for OPTICS. The hyperbolic space is slightly more variable than the Euclidean one: the mode of Nc is equal to 2 for HDBSCAN, except for NN equal to 10 and 20, 4 for DBSCAN, and it varies between 3 and 4 for OPTICS. On the contrary, the spherical surface has the highest variability in estimating Nc: the mode of Nc varies between 3 and 4 for HDBSCAN, it ranges from 2 to 5 for DBSCAN, and it is equal to 3 for OPTICS.
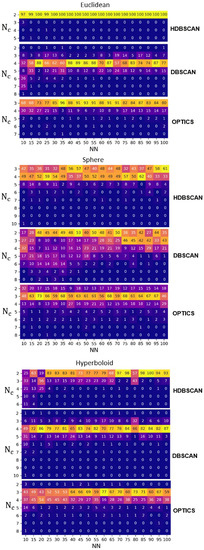
Figure 3.
Variability of the number of clusters (Nc) estimation. Absolute frequency of the Nc obtained from implementing HDBSCAN, DBSCAN, OPTICS in 100 iterations on UMAP embeddings. NN ranging from 10 to 100, for Euclidean, spherical, and hyperbolic space. A lighter color (yellow) indicates a higher frequency value, while a darker color (blue) indicates a lower, tending to zero, frequency value. We did not report Nc of the agglomerative clustering since it is fixed a priori.
The inconsistency in results arises even when considering the clustering quality, which is quantified by means of the ARI score, as described in the Methods section. To assess its irreproducibility, we evaluated the interquantile range of the ARI returned by each implementation of the clustering method applied on T embeddings. Looking at Figure 4, except for HDBSCAN and OPTICS applied on Euclidean and hyperbolic spaces, the interquartile range of the ARI is quite large for each NN. Despite this high variability, if we consider the median of the ARI value, the Euclidean and hyperbolic metrics have higher performances than the spherical one on three (DBSCAN, OPTICS, and agglomerative clustering) clustering algorithms out of four.
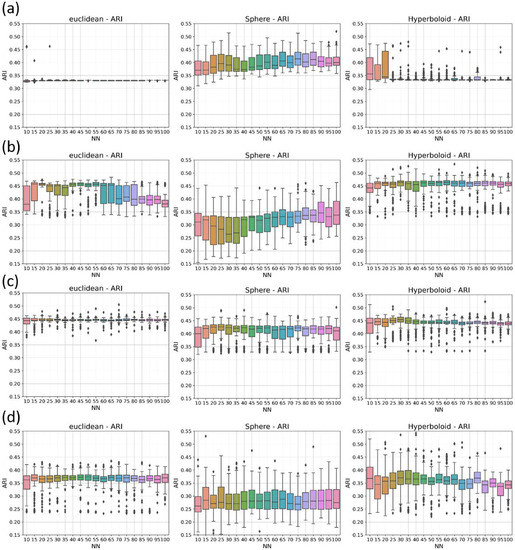
Figure 4.
Variability of clustering performances. Quantitative results of HDBSCAN (a), DBSCAN (b), OPTICS (c), and agglomerative clustering (d) applied to UMAP embeddings, in terms of ARI for each NN. From left to right, panels correspond, respectively, to Euclidean, spherical, and hyperbolic space. Each boxplot represents the distribution of the ARI values, along the T iterations for each specific NN.
3.2.2. Reproducible Results
To compare the clustering performances with reproducible output, as described in the Methods section, from 100 clustering outputs, we computed a final and reproducible clustering result for each NN. Of these, we selected the one with an NN that maximizes the ARI. As shown in supplementary results (Table A2 and Table A3), the best reproducible results are:
- N and ARI equal to 0.47 (spherical metric), N and ARI equal to 0.33 (Euclidean metric), and N and ARI equal to 0.46 (hyperbolic metric), for HDBSCAN;
- N and ARI equal to 0.39 (spherical metric), N and ARI equal to 0.45 (Euclidean metric), and N and ARI equal to 0.46 (hyperbolic metric), for DBSCAN;
- N and ARI equal to 0.28 (spherical metric), N and ARI equal to 0.38 (Euclidean metric), and N and ARI equal to 0.38 (hyperbolic metric), for agglomerative clustering;
- N and ARI equal to 0.41 (spherical metric), N and ARI equal to 0.44 (Euclidean metric), and N and ARI equal to 0.44 (hyperbolic metric), for OPTICS.
Even with our reproducible pipeline, in terms of ARI the Euclidean and hyperbolic metrics have identical performances, higher than the spherical one on three (DBSCAN, OPTICS, and agglomerative clustering) clustering algorithms out of four. Only with HDBSCAN does the Euclidean metric perform worse than spherical and hyperbolic metrics which have similar best ARI values: 0.47 and 0.46, respectively. Overall, we observed the best performance with spherical embedding coupled with HDBSCAN: an ARI index of 0.47, a homogeneity score of 0.43, and four clusters. However, as explained in the Reproducibility section, we cannot have a truthful latent space visualization. We therefore plotted our best final clustering labels on the more representative UMAP embedding (Figure 5b).
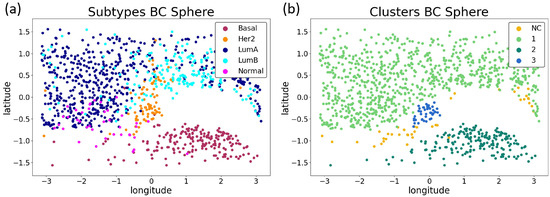
Figure 5.
Visualization of the best UMAP embedding. Two-dimensional spherical surface mapped by UMAP with NN equal to 65 (see Table A2 in Appendix A). The points correspond to the BC samples. In (a) on the left, the color indicates the tumor subtype, whose acronym is shown by labels, for a total of 5 BC types. In (b), the colors refer to the different clusters identified by our method for HDBSCAN, for a total of 4 groups. Latitude and longitude are the commonly used coordinates to identify a point (i.e., a sample) on the spherical surface, expressed in radians. NC stands for the cluster constituted by Not Clusterable points (see Methods section).
3.2.3. Biological Interpretation
At a glance, by comparing Figure 5a with Figure 5b, some of the identified clusters can be directly associated with the different subtypes in the BC dataset. In particular, as we expected (https://www.breastcancer.org/symptoms/types/molecular-subtypes, accessed on 20 April 2022), the basal samples are detached well from the others, and form a separate cluster (cluster 2 in Figure 5). However, as reported in the literature [41], the normal, luminal-A, and luminal-B samples are more similar to each other. Unsurprisingly, they are grouped together in cluster 1, while cluster 3 consists entirely of Her2 points.
This comparison between subtypes and cluster groups is quantified in Figure 6, which reports the relative and absolute frequency of BC subtypes for each estimated cluster. It is clear that clusters 1, 2, and 3 represent three BC subtypes: luminal, basal, and Her2, respectively. In contrast, the NC cluster is a mixture of all subtypes. However, we computed how frequently these samples were assigned to the NC group and we discovered that all 41 points were clustered as such in more than of the iterations performed.
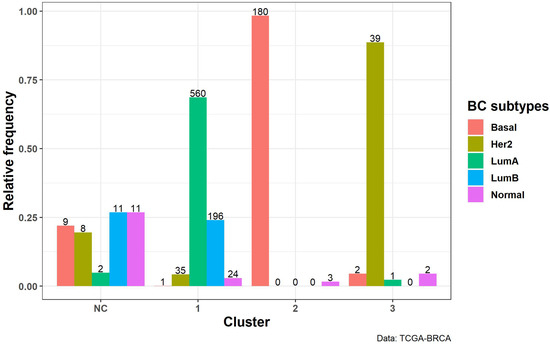
Figure 6.
BC subtype distribution over estimated clusters. Relative (vertical axis) and absolute (top of the bars) frequency of BC subtypes within each cluster, identified on spherical UMAP embedding with NN . On the horizontal axis, we report the cluster labels. NC stands for Not Clusterable (see Methods section).
Although Figure 5b is not the authentic representation of the cluster labels, we can see that the NC points (yellow) are those at the border of the luminal groups.
4. Discussion
Using the UMAP algorithm, here we projected 20,530 gene expression data onto three different latent metric spaces in order to evaluate how different curvatures of the UMAP embedding could affect breast cancer stratification. The evaluation focused on clustering performances in terms of ARI, homogeneity, and number of estimated clusters returned by HDBSCAN, DBSCAN, agglomerative clustering, and OPTICS. We also addressed UMAP reproducibility by proposing an iterative approach to yield more stable clustering outputs.
UMAP has been widely implemented for transcriptomic analyses [13,14,42,43]. In particular, starting from single-cell RNA-seq data, Bao et al. [42] and Landry et al. [43] visualized tumor cell heterogeneity in triple-negative breast cancer and glioblastoma, respectively. Yang et al. [13] and Lebedev et al. [14] performed transcriptomic analyses, applying the HDBSCAN algorithm to UMAP Euclidean embedding. Moreover, Yang et al. [13] also addressed how the choice of the input metric in UMAP (i.e., how we measure the distance between samples in high-dimensional input data) could influence the visualization of clustering structures.
Nevertheless, none of the above approaches raised concerns about the reproducibility and the geometry of the UMAP embedding and, to the best of our knowledge, no study has addressed these issues.
Our work focused on the choice of the output metric in UMAP, showing that the selection of the latent space can affect downstream clustering results. However, by exploring different metric spaces, we encountered UMAP reproducibility issues: some pairwise points were inconsistently projected onto latent spaces and so were not always clustered together over several runs, leading to unstable clustering results (see Figure 3 and Figure 4). Since this work was the first attempt to investigate different curvatures of UMAP embedding, this reproducibility issue spurred us to propose a reproducible pipeline that returns consistent results, regardless of the selected output metrics.
As reported in the Appendix (Table A2 and Table A3), clustering performances were improved by applying HDBSCAN to spherical and hyperbolic metric spaces. On non-Euclidean embedding, the ARI score increased by 14 percentage points (from to ) with respect to the Euclidean latent space. Hence, in this analysis the Euclidean output metric, when applied on HDBSCAN, performs poorly compared to the other metrics. On the contrary, Euclidean and hyperbolic latent spaces showed similar ARI scores that were higher than the spherical one for three clustering algorithms out of four.
The above results are dataset-dependent. Therefore, to validate the generalizability of our approach and the potentiality of our proposed pipeline, more datasets (single-cell RNA-seq, multi-omics, methylation data) should be tested.
5. Conclusions
We consider our results a warning for future UMAP implementations applied upstream of other analyses, such as clustering. For the case study of tumor stratification, we showed that, with HDBSCAN, keeping default UMAP parameters, i.e., Euclidean output metric, would have impoverished the downstream results. Furthermore, we observed high variability in estimating the number of clusters and in clustering performances. For datasets with well-separated groups, it might not be necessary to worry about the UMAP reproducibility issue and investigate various topological UMAP embeddings. However, for more complex data such as RNA-seq, different geometries of output spaces should be explored if one cannot be assumed a priori.
UMAP has mostly been implemented with a Euclidean metric. We hope our work will encourage further research on non-Euclidean embeddings for the analysis of clustering or tumor stratification, even with other metric spaces to investigate further samples’ relationships. Future works should validate different UMAP output metrics on several datasets, analogous to Yang et al. [13] who evaluated the importance of the UMAP input metric. Moreover, as suggested by [44], supervised or semi-supervised dimensionality reduction can provide more informative latent space representations. Therefore, future efforts can integrate our pipeline with a supervised version of UMAP. Finally, even multi-omics data should be exploited [45] within our approach to enhance medical and biological interpretation of the final clustering results.
Author Contributions
J.B. and M.A. conducted data analysis and drafted the first version of the paper. J.B., M.A., A.C. (Andrea Cina), S.M., M.C., C.B.S. and J.M.C. participated in the development. The overall work was supervised by S.G. and A.C. (Andrea Cavalli). All the authors performed a critical review and approved the final version. All authors have read and agreed to the published version of the manuscript.
Funding
The research center CMP3VdA and the Project 5000genomi@VdA are co-founded by “Fondo Europeo di Sviluppo Regionale (FESR) Programma Investimenti per la crescita e l’occupazione 2014/20” (European Social Fund, ESF, and European Regional Development Fund, ERDF), the Autonomous Region of the Aosta Valley, and the Italian Ministry of Labour and Social Policy (CUP B68H19005520007). J.B., M.A., A.C. (Andrea Cina) and S.M. have carried out this work supported by a grant of the EU-ESF, the Autonomous Region of the Aosta Valley, and the Italian Ministry of Labour and Social Policy. The Astronomical Observatory of the Autonomous Region of the Aosta Valley (OAVdA) is managed by the Fondazione Clément Fillietroz-ONLUS, which is supported by the Regional Government of the Aosta Valley, the Town Municipality of Nus, and the “Unité des Communes valdôtaines Mont-Émilius”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The breast cancer RNA-seq dataset (Illumina HiSeq 2000 RNA Sequencing platform, level 3 transcription, log2(x + 1) transformed RSEM-normalized count) and the related clinical variables were downloaded from the University of California Santa Cruz (UCSC) cancer browser website (https://xenabrowser.net/datapages, accessed on 20 April 2022). The breast cancer subtypes are available in a GitHub repository: https://github.com/yxchspring/GOEGCN_BRCA_Subtypes, accessed on 20 April 2022.
Acknowledgments
The Project 5000genomi@VdA (https://5000genomivda.it/en/, accessed on 20 April 2022) is a scientific project that has enabled the creation of a new research center dedicated to personalized, preventive, and predictive medicine (CMP3VdA) for neurodevelopmental, neurodegenerative, and oncological diseases. The Project 5000genomi@VdA is carried out by a research consortium led by Istituto Italiano di Tecnologia (ITT, Italian Institute of Technology), comprising Università della Valle d’Aosta, Città della Salute e della Scienza di Torino, Fondazione Clément Fillietroz-ONLUS Osservatorio Astronomico della Regione Autonoma Valle d’Aosta, and Engineering D.HUB.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Reproducibility
To demonstrate the reproducibility of our pipeline, we carried out the following steps:
- (1)
- comparison in terms of ARI of two clustering outputs generated by HDBSCAN applied to two separate runs of UMAP (NN ; spherical embedding);
- (2)
- for each , comparison in terms of ARI of two clustering outputs generated by two independent runs of our proposed pipeline.
After our simulations, with two independent runs of UMAP, we obtained an ARI of about 0.37 (see Figure A1). In contrast, our approach was more reproducible, with the ARI between these two clustering outputs converging to 0.99.
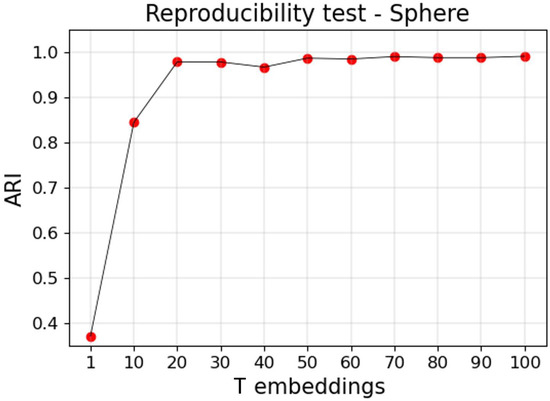
Figure A1.
Reproducibility test. ARI scores between cluster labels obtained from two separate runs of T UMAP embeddings. With , the figure reports the ARI between two clustering outputs generated by HDBSCAN applied to two independent runs of UMAP. With , the ARI indicates the concordance between two clustering outputs generated by two separate runs of our proposed procedure.
To better quantify the difference between an ARI of 0.37 and 0.99, Table A1 reports the number of BC subtype points assigned to each cluster. Looking at Table A1A,B, HDBSCAN applied to two runs of UMAP returned quite different cluster results. In the first run, luminal-A points were stratified into one major group with a size of 553. In the second run, the same points were assigned to two main groups of 339 and 215 elements. Similarly, the luminal-B samples were first divided into one major group and then into two groups.
In contrast, in Table A1C,D, the cluster distributions across the subtypes are consistent, since we obtained almost identical results for both runs.

Table A1.
Joint frequencies of cluster outputs and BC subtypes related to two separate UMAP runs (top tables: A and B), and two independent runs of our proposed procedure with (bottom tables: C and D).
Table A1.
Joint frequencies of cluster outputs and BC subtypes related to two separate UMAP runs (top tables: A and B), and two independent runs of our proposed procedure with (bottom tables: C and D).
| (A) | 1 Embedding Iter1 | (B) | 1 Embedding Iter2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Clusters | Clusters | ||||||||||
| NC | 1 | 2 | 3 | NC | 1 | 2 | 3 | ||||
| Basal | 1 | 1 | 184 | 6 | Basal | 8 | 0 | 179 | 5 | ||
| Her2 | 0 | 31 | 4 | 47 | Her2 | 5 | 41 | 0 | 36 | ||
| LumA | 1 | 553 | 8 | 1 | LumA | 9 | 339 | 0 | 215 | ||
| LumB | 2 | 200 | 1 | 4 | LumB | 9 | 132 | 0 | 66 | ||
| Normal | 1 | 24 | 12 | 3 | Normal | 12 | 21 | 3 | 4 | ||
| (C) | 100 Embeddings Iter1 | (D) | 100 Embeddings Iter2 | ||||||||
| Clusters | Clusters | ||||||||||
| NC | 1 | 2 | 3 | NC | 1 | 2 | 3 | ||||
| Basal | 9 | 1 | 180 | 2 | Basal | 9 | 1 | 180 | 2 | ||
| Her2 | 8 | 35 | 0 | 39 | Her2 | 7 | 35 | 0 | 40 | ||
| LumA | 2 | 560 | 0 | 1 | LumA | 3 | 559 | 0 | 1 | ||
| LumB | 11 | 196 | 0 | 0 | LumB | 9 | 198 | 0 | 0 | ||
| Normal | 11 | 24 | 3 | 2 | Normal | 10 | 24 | 3 | 3 | ||
Appendix A.2. Clustering Results

Table A2.
Comparison of clustering performances. Nc, ARI, and homogeneity score estimated for each NN and latent space (spherical, Euclidean, hyperbolic) for HDBSCAN and DBSCAN clustering methods.
Table A2.
Comparison of clustering performances. Nc, ARI, and homogeneity score estimated for each NN and latent space (spherical, Euclidean, hyperbolic) for HDBSCAN and DBSCAN clustering methods.
| HDBSCAN | Euclidean | Sphere | Hyperboloid | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NN | Nclust | Ari | Homog | Nclust | Ari | Homog | Nclust | Ari | Homog |
| 10 | 2 | 0.33 | 0.31 | 4 | 0.45 | 0.43 | 3 | 0.46 | 0.42 |
| 15 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.44 | 2 | 0.33 | 0.32 |
| 20 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.44 | 3 | 0.45 | 0.42 |
| 25 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.44 | 2 | 0.33 | 0.32 |
| 30 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.44 | 2 | 0.33 | 0.32 |
| 35 | 2 | 0.33 | 0.32 | 4 | 0.45 | 0.43 | 2 | 0.33 | 0.32 |
| 40 | 2 | 0.33 | 0.32 | 3 | 0.37 | 0.35 | 2 | 0.33 | 0.32 |
| 45 | 2 | 0.33 | 0.32 | 3 | 0.37 | 0.35 | 2 | 0.33 | 0.32 |
| 50 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 | 2 | 0.33 | 0.32 |
| 55 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 | 2 | 0.33 | 0.32 |
| 60 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 | 2 | 0.33 | 0.32 |
| 65 | 2 | 0.33 | 0.32 | 4 | 0.47 | 0.43 | 2 | 0.33 | 0.32 |
| 70 | 2 | 0.33 | 0.32 | 4 | 0.47 | 0.43 | 2 | 0.33 | 0.32 |
| 75 | 2 | 0.33 | 0.32 | 4 | 0.47 | 0.43 | 2 | 0.33 | 0.32 |
| 80 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 | 2 | 0.33 | 0.32 |
| 85 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 | 2 | 0.33 | 0.32 |
| 90 | 2 | 0.33 | 0.32 | 3 | 0.45 | 0.4 | 2 | 0.33 | 0.32 |
| 95 | 2 | 0.33 | 0.32 | 3 | 0.45 | 0.39 | 2 | 0.33 | 0.32 |
| 100 | 2 | 0.33 | 0.32 | 3 | 0.46 | 0.4 | 2 | 0.33 | 0.32 |
| 10 | 4 | 0.39 | 0.42 | 4 | 0.28 | 0.39 | 4 | 0.45 | 0.43 |
| 15 | 4 | 0.45 | 0.42 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 |
| 20 | 4 | 0.45 | 0.43 | 2 | 0.33 | 0.32 | 4 | 0.45 | 0.42 |
| 25 | 4 | 0.45 | 0.43 | 2 | 0.33 | 0.32 | 4 | 0.46 | 0.43 |
| 30 | 4 | 0.45 | 0.43 | 2 | 0.32 | 0.31 | 4 | 0.45 | 0.43 |
| 35 | 4 | 0.45 | 0.42 | 2 | 0.31 | 0.3 | 4 | 0.45 | 0.43 |
| 40 | 4 | 0.45 | 0.42 | 2 | 0.32 | 0.3 | 4 | 0.45 | 0.43 |
| 45 | 4 | 0.45 | 0.42 | 2 | 0.32 | 0.3 | 4 | 0.45 | 0.43 |
| 50 | 4 | 0.44 | 0.42 | 2 | 0.32 | 0.31 | 4 | 0.45 | 0.43 |
| 55 | 4 | 0.43 | 0.4 | 2 | 0.29 | 0.28 | 4 | 0.45 | 0.43 |
| 60 | 4 | 0.45 | 0.42 | 2 | 0.31 | 0.29 | 4 | 0.45 | 0.43 |
| 65 | 4 | 0.45 | 0.42 | 2 | 0.32 | 0.31 | 4 | 0.45 | 0.43 |
| 70 | 4 | 0.36 | 0.38 | 2 | 0.32 | 0.3 | 4 | 0.45 | 0.43 |
| 75 | 4 | 0.39 | 0.38 | 3 | 0.37 | 0.38 | 4 | 0.45 | 0.43 |
| 80 | 4 | 0.37 | 0.36 | 3 | 0.38 | 0.38 | 4 | 0.45 | 0.43 |
| 85 | 4 | 0.37 | 0.36 | 2 | 0.32 | 0.31 | 4 | 0.44 | 0.43 |
| 90 | 4 | 0.38 | 0.37 | 3 | 0.4 | 0.39 | 4 | 0.45 | 0.43 |
| 95 | 4 | 0.37 | 0.36 | 2 | 0.32 | 0.31 | 4 | 0.45 | 0.43 |
| 100 | 4 | 0.36 | 0.36 | 3 | 0.39 | 0.38 | 4 | 0.44 | 0.42 |

Table A3.
Comparison of clustering performances. Nc, ARI, and homogeneity score estimated for each NN and latent space (spherical, Euclidean, hyperbolic) for OPTICS and agglomerative clustering (Agg.).
Table A3.
Comparison of clustering performances. Nc, ARI, and homogeneity score estimated for each NN and latent space (spherical, Euclidean, hyperbolic) for OPTICS and agglomerative clustering (Agg.).
| OPTICS | Euclidean | Sphere | Hyperboloid | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NN | Nclust | Ari | Homog | Nclust | Ari | Homog | Nclust | Ari | Homog |
| 10 | 3 | 0.42 | 0.39 | 3 | 0.4 | 0.38 | 3 | 0.43 | 0.4 |
| 15 | 3 | 0.43 | 0.4 | 3 | 0.41 | 0.38 | 3 | 0.44 | 0.41 |
| 20 | 3 | 0.44 | 0.41 | 3 | 0.41 | 0.39 | 4 | 0.36 | 0.41 |
| 25 | 3 | 0.44 | 0.41 | 3 | 0.41 | 0.39 | 3 | 0.44 | 0.41 |
| 30 | 3 | 0.44 | 0.41 | 3 | 0.41 | 0.39 | 3 | 0.44 | 0.41 |
| 35 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.43 | 0.41 |
| 40 | 3 | 0.44 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.44 | 0.41 |
| 45 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.44 | 0.41 |
| 50 | 3 | 0.44 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.44 | 0.41 |
| 55 | 3 | 0.44 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.44 | 0.41 |
| 60 | 3 | 0.44 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.44 | 0.41 |
| 65 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.43 | 0.41 |
| 70 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.42 | 0.4 |
| 75 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.43 | 0.4 |
| 80 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.43 | 0.41 |
| 85 | 3 | 0.43 | 0.4 | 3 | 0.41 | 0.39 | 3 | 0.43 | 0.4 |
| 90 | 3 | 0.43 | 0.41 | 3 | 0.4 | 0.38 | 3 | 0.43 | 0.4 |
| 95 | 3 | 0.43 | 0.4 | 3 | 0.4 | 0.38 | 3 | 0.42 | 0.4 |
| 100 | 3 | 0.43 | 0.41 | 3 | 0.39 | 0.37 | 3 | 0.42 | 0.4 |
| 10 | 4 | 0.37 | 0.48 | 4 | 0.28 | 0.42 | 4 | 0.38 | 0.49 |
| 15 | 4 | 0.37 | 0.48 | 4 | 0.28 | 0.42 | 4 | 0.38 | 0.49 |
| 20 | 4 | 0.36 | 0.48 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.49 |
| 25 | 4 | 0.36 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.37 | 0.47 |
| 30 | 4 | 0.37 | 0.48 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.47 |
| 35 | 4 | 0.37 | 0.48 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.47 |
| 40 | 4 | 0.37 | 0.49 | 4 | 0.24 | 0.41 | 4 | 0.36 | 0.47 |
| 45 | 4 | 0.38 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.47 |
| 50 | 4 | 0.38 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.35 | 0.47 |
| 55 | 4 | 0.38 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.35 | 0.47 |
| 60 | 4 | 0.37 | 0.49 | 4 | 0.24 | 0.41 | 4 | 0.35 | 0.47 |
| 65 | 4 | 0.37 | 0.48 | 4 | 0.24 | 0.41 | 4 | 0.35 | 0.47 |
| 70 | 4 | 0.38 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.48 |
| 75 | 4 | 0.37 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.48 |
| 80 | 4 | 0.37 | 0.48 | 4 | 0.24 | 0.4 | 4 | 0.35 | 0.48 |
| 85 | 4 | 0.37 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.36 | 0.48 |
| 90 | 4 | 0.38 | 0.49 | 4 | 0.24 | 0.4 | 4 | 0.35 | 0.48 |
| 95 | 4 | 0.37 | 0.48 | 4 | 0.24 | 0.39 | 4 | 0.34 | 0.47 |
| 100 | 4 | 0.38 | 0.49 | 4 | 0.24 | 0.41 | 4 | 0.34 | 0.47 |
References
- Baptiste, M.; Moinuddeen, S.S.; Soliz, C.L.; Ehsan, H.; Kaneko, G. Making sense of genetic information: The promising evolution of clinical stratification and precision oncology using machine learning. Genes 2021, 12, 722. [Google Scholar] [CrossRef]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: Globocan estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. Available online: https://acsjournals.onlinelibrary.wiley.com/doi/pdf/10.3322/caac.21660 (accessed on 20 April 2022). [CrossRef] [PubMed]
- Oze, I.; Ito, H.; Kasugai, Y.; Yamaji, T.; Kijima, Y.; Ugai, T.; Kasuga, Y.; Ouellette, T.K.; Taniyama, Y.; Koyanagi, Y.N.; et al. A personal breast cancer risk stratification model using common variants and environmental risk factors in japanese females. Cancers 2021, 13, 3796. [Google Scholar] [CrossRef] [PubMed]
- Russnes, H.G.; Lingjærde, O.C.; Børresen-Dale, A.-L.; Caldas, C. Breast cancer molecular stratification: From intrinsic subtypes to integrative clusters. Am. J. Pathol. 2017, 187, 2152–2162. [Google Scholar] [CrossRef]
- Wordsworth, S.; Doble, B.; Payne, K.; Buchanan, J.; Marshall, D.A.; McCabe, C.; Regier, D.A. Using “big data” in the cost-effectiveness analysis of next-generation sequencing technologies: Challenges and potential solutions. Value Health 2018, 21, 1048–1053. [Google Scholar] [CrossRef] [Green Version]
- Arakelyan, A.; Melkonyan, A.; Hakobyan, S.; Boyarskih, U.; Simonyan, A.; Nersisyan, L.; Nikoghosyan, M.; Filipenko, M.; Binder, H. Transcriptome patterns of brca1-and brca2-mutated breast and ovarian cancers. Int. J. Mol. Sci. 2021, 22, 1266. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Klevebring, D.; Lindberg, J.; Czene, K.; Grönberg, H.; Rantalainen, M. Determining breast cancer histological grade from rna-sequencing data. Breast Cancer Res. 2016, 18, 48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hao, Y.; He, L.; Zhou, Y.; Zhao, Y.; Li, M.; Jing, R.; Wen, Z. Improving model performance on the stratification of breast cancer patients by integrating multiscale genomic features. BioMed Res. Int. 2020, 2020, 1475368. [Google Scholar] [CrossRef]
- Altman, N.; Krzywinski, M. The curse(s) of dimensionality. Nat. Methods 2018, 15, 399–400. [Google Scholar] [CrossRef] [PubMed]
- Townes, F.W.; Hicks, S.C.; Aryee, M.J.; Irizarry, R.A. Feature selection and dimension reduction for single-cell rna-seq based on a multinomial model. Genome Biol. 2019, 20, 295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, X.; Liu, Y.; An, L. Ensemble dimensionality reduction and feature gene extraction for single-cell rna-seq data. Nat. Commun. 2020, 11, 5853. [Google Scholar] [CrossRef] [PubMed]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Yang, Y.; Sun, H.; Zhang, Y.; Zhang, T.; Gong, J.; Wei, Y.; Duan, Y.-G.; Shu, M.; Yang, Y.; Wu, D.; et al. Dimensionality reduction by umap reinforces sample heterogeneity analysis in bulk transcriptomic data. Cell Rep. 2021, 36, 109442. [Google Scholar] [CrossRef] [PubMed]
- Lebedev, T.; Vagapova, E.; Spirin, P.; Rubtsov, P.; Astashkova, O.; Mikheeva, A.; Sorokin, M.; Vladimirova, U.; Suntsova, M.; Konovalov, D.; et al. Growth factor signaling predicts therapy resistance mechanisms and defines neuroblastoma subtypes. Oncogene 2021, 40, 6258–6272. [Google Scholar] [CrossRef]
- Dorrity, M.W.; Saunders, L.M.; Queitsch, C.; Fields, S.; Trapnell, C. Dimensionality reduction by umap to visualize physical and genetic interactions. Nat. Commun. 2020, 11, 1537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, J.; Spielmann, M.; Qiu, X.; Huang, X.; Ibrahim, D.M.; Hill, A.J.; Zhang, F.; Mundlos, S.; Christiansen, L.; Steemers, F.J. The single-cell transcriptional landscape of mammalian organogenesis. Nature 2019, 566, 496–502. [Google Scholar] [CrossRef] [PubMed]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (pca). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Leelatian, N.; Sinnaeve, J.; Mistry, A.M.; Barone, S.M.; Brockman, A.A.; Diggins, K.E.; Greenplate, A.R.; Weaver, K.D.; Thompson, R.C.; Chambless, L.B. Unsupervised machine learning reveals risk stratifying glioblastoma tumor cells. eLife 2020, 9, e56879. [Google Scholar] [CrossRef]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.-A.; Kwok, I.W.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using umap. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Allaoui, M.; Kherfi, M.L.; Cheriet, A. Considerably improving clustering algorithms using umap dimensionality reduction technique: A comparative study. In International Conference on Image and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 317–325. [Google Scholar]
- Gu, A.; Sala, F.; Gunel, B.; Ré, C. Learning mixed-curvature representations in product spaces. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ding, J.; Regev, A. Deep generative model embedding of single-cell RNA-Seq profiles on hyperspheres and hyperbolic spaces. Nat. Commun. 2019, 12, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Nickel, M.; Kiela, D. Learning continuous hierarchies in the lorentz model of hyperbolic geometry. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 3779–3788. [Google Scholar]
- He, Z.; Zhang, J.; Yuan, X.; Xi, J.; Liu, Z.; Zhang, Y. Stratification of breast cancer by integrating gene expression data and clinical variables. Molecules 2019, 24, 631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Lichtenberg, T.; Hoadley, K.A.; Poisson, L.M.; Lazar, A.J.; Cherniack, A.D.; Kovatich, A.J.; Benz, C.C.; Levine, D.A.; Lee, A.V. An integrated tcga pan-cancer clinical data resource to drive high-quality survival outcome analytics. Cell 2018, 173, 400–416. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.; Jones, M.W.; Xie, X.; Williams, M. Timecluster: Dimension reduction applied to temporal data for visual analytics. Vis. Comput. 2019, 35, 1013–1026. [Google Scholar] [CrossRef] [Green Version]
- Pealat, C.; Bouleux, G.; Cheutet, V. Improved time-series clustering with umap dimension reduction method. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 5658–5665. [Google Scholar]
- Rand, W.M. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Rosenberg, A.; Hirschberg, J. V-measure: A conditional entropy-based external cluster evaluation measure. In Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28–30 June 2007; pp. 410–420. [Google Scholar]
- Diaz-Papkovich, A.; Anderson-Trocmé, L.; Gravel, S. A review of umap in population genetics. J. Hum. Genet. 2021, 66, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Aalto, M.; Verma, N. Metric learning on manifolds. arXiv 2019, arXiv:1902.01738. [Google Scholar]
- Campello, R.J.; Moulavi, D.; Sander, J. Density-based clustering based on hierarchical density estimates. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Kuntze, D.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Day, W.H.; Edelsbrunner, H. Efficient algorithms for agglomerative hierarchical clustering methods. J. Classif. 1984, 1, 7–24. [Google Scholar] [CrossRef]
- Jamail, I.; Moussa, A. Current state-of-the-art of clustering methods for gene expression data with rna-seq. In Pattern Recognition; IntechOpen: London, UK, 2020. [Google Scholar]
- Santos, J.M.; Embrechts, M. On the use of the adjusted rand index as a metric for evaluating supervised classification. In Proceedings of the International Conference on Artificial Neural Networks, Limassol, Cyprus, 14–17 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 175–184. [Google Scholar]
- Higham, D.J.; Kalna, G.; Kibble, M. Spectral clustering and its use in bioinformatics. J. Comput. Appl. Math. 2007, 204, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Gaynor, S.M.; Lin, X.; Quackenbush, J. Spectral clustering in regression-based biological networks. bioRxiv 2019, 651950. [Google Scholar] [CrossRef]
- Huang, G.T.; Cunningham, K.I.; Benos, P.V.; Chennubhotla, C.S. Spectral clustering strategies for heterogeneous disease expression data. In Biocomputing 2013; World Scientific: Singapore, 2013; pp. 212–223. [Google Scholar]
- Larsen, M.J.; Kruse, T.A.; Tan, Q.; Laenkholm, A.-V.; Bak, M.; Lykkesfeldt, A.E.; Sørensen, K.P.; Hansen, T.v.O.; Ejlertsen, B.; Gerdes, A.-M. Classifications within molecular subtypes enables identification of brca1/brca2 mutation carriers by rna tumor profiling. PLoS ONE 2013, 8, e64268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bao, X.; Shi, R.; Zhao, T.; Wang, Y.; Anastasov, N.; Rosemann, M.; Fang, W. Integrated analysis of single-cell rna-seq and bulk rna-seq unravels tumour heterogeneity plus m2-like tumour-associated macrophage infiltration and aggressiveness in tnbc. Cancer Immunol. Immunother. 2021, 70, 189–202. [Google Scholar] [CrossRef]
- Landry, A.P.; Balas, M.; Alli, S.; Spears, J.; Zador, Z. Distinct regional ontogeny and activation of tumor associated macrophages in human glioblastoma. Sci. Rep. 2020, 10, 19542. [Google Scholar] [CrossRef] [PubMed]
- Chari, T.; Banerjee, J.; Pachter, L. The specious art of single-cell genomics. bioRxiv 2021. [Google Scholar] [CrossRef]
- Ektefaie, Y.; Yuan, W.; Dillon, D.A.; Lin, N.U.; Golden, J.A.; Kohane, I.S.; Yu, K.H. Integrative multiomics-histopathology analysis for breast cancer classification. NPJ Breast Cancer 2021, 7, 147. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).