1. Introduction
The ladder sleeper, which is a type of longitudinal sleeper with long beams in the longitudinal direction of the rail, was developed for the maintenance-labor saving of ballast tracks [
1,
2]. The ladder sleeper’s main components are two prestressed concrete (PC) beams, steel pipes, and post-tension PC end beams, and its structure differs significantly from that of a conventional prestressed concrete sleeper (PC sleeper) that is orthogonal to the rail. Since the ladder sleepers come into contact with the ballast on a continuous surface in the rail direction, they are superior in load distribution performance compared to PC sleepers that are in contact with the ballast discretely in the rail direction. As a result, the vibration transmission to the ballast caused by the train running can be reduced. As a result, the ladder sleeper is an effective track member not only for reducing structural vibration [
3,
4,
5] and ground vibration [
6], but also for improving the track’s buckling stability [
7,
8,
9]. So far, it has been laid mainly on conventional lines, subways, and light rail transit in Japan, China, Europe, etc. In addition, although the shape is significantly different from that of Japanese and Chinese ladder sleepers, it is also applied to light rail transit in Europe [
10]. In recent years, research on the vibration mitigation characteristics of the ballasted ladder track with elastic elements (under-sleeper pad) has also been conducted [
11].
The ladder sleepers in Japan were researched and developed with the primary purpose of maintenance-labor saving for the ballast track, for which the regular track maintenance based on ballast compaction was indispensable and were put into practical use in 1999. In recent years, it has become increasingly common to apply it not only to general sections of ballast tracks, but also to structural boundaries that require frequent maintenance work, such as rail joints and expansion joints where impact loads are likely to occur, and level crossings where the support condition of the track changes, and so on. Structural boundaries between embankments, abutments, and bridge girders, as well as open culverts that cross railroad tracks, on the other hand, are frequent maintenance points. Even in such places, if a ballasted ladder track is laid, maintenance-labor saving is expected. However, in recent years, the number of installations in such places has tended to increase, but the reality is that there are few public data that quantitatively show the effect of labor saving in maintenance.
It should be noted that the use of an under-sleeper pad (USP) and under-ballast mat (UBM) also can reduce the value of loads transmitted to the ballast [
11,
12,
13,
14], but in this study, we only focus on the ladder sleeper without USP or UBM.
In this study, we decided to verify the longitudinal level irregularity suppression effect at the structural boundary by the ladder sleepers. The three following points are focused on:
To quantify the load distribution effect of ladder sleepers, full-scale model tests are conducted.
Carry out numerical experiments with a three-dimensional numerical analysis model, comparing ladder sleepers and conventional PC sleepers in terms of the pressure on the sleeper bottom plane.
Ladder sleepers are laid on the commercial line and long-term measurement of longitudinal level irregularity are carried out to verify the effect of suppressing the longitudinal level irregularity of the ballasted ladder tracks.
2. Outline of the Ladder Sleeper
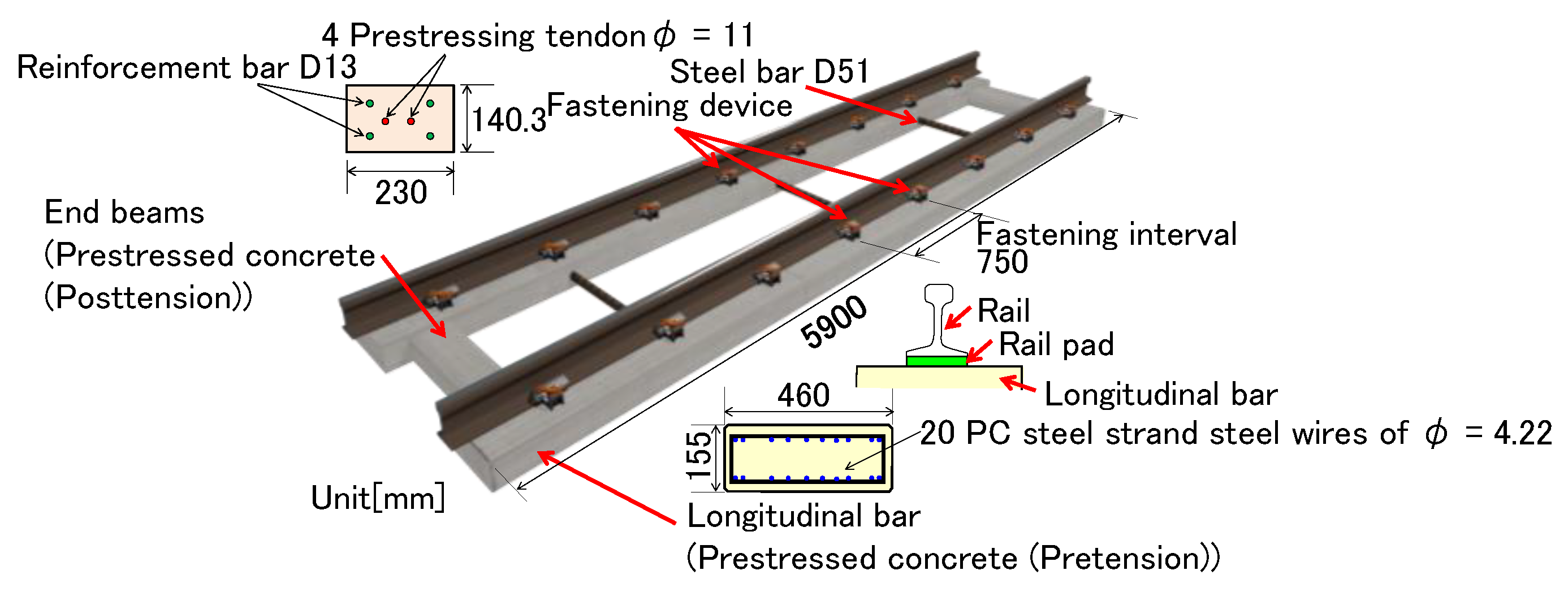
Figure 1 shows the outline of the ladder sleeper. The length of the ladder sleepers is 5900 mm, the longitudinal beam is a rectangular cross-section with a width of 460 mm and a height of 155 mm, and 20 PC steel strand wires of φ = 4.22 mm are arranged in the cross-section. The concrete design standard strength is 50 N/mm
2, which is equivalent to the strength of standard Japanese PC sleepers. The distance between rail fastenings is 750 mm. The ladder sleepers were designed in the same method as traditional Japanese PC sleepers [
15]. Specifically, in the verification of the serviceability limit state [
16], the cross-section of the longitudinal beam was designed using the design response value considering the impact factor (variable wheel-load coefficient) 2 for the static wheel load of 80 kN [
17] and the design limit value of the decompression moment. The cross-section of the longitudinal beam was designed for the ultimate limit state [
16] verification using the design response value considering the impact factor (variable wheel-load coefficient) 4 for the static wheel load of 80 kN and the design limit value of the ultimate moment when the steel material yields or the concrete fractures.
3. Full-Scale Model Test
3.1. Test Method
3.1.1. Outline of the Full-Scale Model Test
Figure 2 shows the outline of the full-scale models. The tests were conducted not only on the ballasted ladder tracks but also on the PC sleeper tracks for comparison. JIS E1201 [
18] specifies the target PC sleepers for straight lines (product type: 3PR). In Japan, this PC sleeper is the most used. The laying interval of the PC sleepers was set to 0.61 m, which is a standard laying interval in Japan.
Figure 3 shows the situation of the tests. In the impulse hammer test, a hammer (Toyo Technica 086C05) was used to vibrate the top surface of the rail in the center of the ladder sleepers. In the weight-falling test, a weight of approximately 80 kg was freely dropped from the maximum height of 2 m that the test frame in the figure can set and the top surface of the rail in the center of the ladder sleeper was vibrated.
Figure 4 shows the sensor installation methods. The accelerometers (RION PV85) were installed on the upper surface of the ladder sleeper in the center of the longitudinal direction of the ladder sleeper and the ballast. The accelerometers were attached to the sleepers by screwing them to an insulation plate that was adhered to the sleepers with adhesive. The accelerometer in the ballast was protected by an iron container, screwed to an insulation plate, and embedded about 200 mm from the sleeper’s bottom. The accelerometer was embedded before the rails and sleepers were laid. The sampling frequency was 10 kHz and the time step is 0.1 ms. Note that the accelerations described below are all vertical accelerations.
3.1.2. Evaluation Method of Response Characteristics
In the impulse hammer tests, the time-history waveform of the excitation force by the impulse hammer and the acceleration measured by the accelerometer embedded in the ballast was frequency analyzed and evaluated by accelerants (ratio of acceleration to excitation force). In addition, the results of the multipoint hammer excitation were used to determine the natural frequency and vibration mode of the ladder sleepers. The ratio of the acceleration of the sleeper measured by the accelerometer installed on the upper surface of the sleeper to the acceleration measured by the embedded accelerometer in the ballast (response magnification) was evaluated in the weight-falling tests.
3.2. Test Results
3.2.1. Impulse Hammer Test
Figure 5 shows the example of the time-history waveform of the excitation force and the vertical acceleration measured by the accelerometer embedded in the ballast. The vibration was attenuated after it was excited to the ballast by the hammer, and it converged in about 0.05 s. The waveform was disordered and not a typical free vibration waveform. This was thought to be because the damping of the ballast itself was larger than that of concrete or steel members and that the ballast was a discrete body rather than a vibration of a continuous body such as a beam [
19].
Figure 6 shows the comparison of the accelerance. From the figure, the ballasted ladder track had smaller acceleration in a wide-frequency band except for around 80 to 100 Hz. The influence of the bending vibration mode of the ladder sleepers described later was the reason why the reduction effect of the ballasted ladder track was not seen at 80 to 100 Hz.
Figure 7 shows the identification results of the natural frequency and vibration mode shape of ladder sleepers. In these vibration mode types, accelerometers were arranged at multiple points and acquired by modal analysis. The natural frequency of the ladder sleepers’ bending first mode was 79 Hz, the second mode was 151 Hz, the third mode was 293 Hz, the fourth mode was 480 Hz, and the fifth mode was 748 Hz. The figure also depicts the natural frequencies obtained by the numerical analysis model described later. From the figure, the natural frequency could be represented with an error of about 10% or less. According to previous research [
19], the natural frequency of the bending first vibration mode of the PC sleepers compared this time is 158 Hz, the second mode is 440 Hz, and the third mode is 850 Hz. It was found that the vibration characteristics of the sleepers differed greatly.
3.2.2. Weight-Falling Test
Figure 8 shows an example of the time-history waveform of the vertical acceleration on the ladder sleepers and the acceleration in the ballast when the weight was fallen. The sleeper acceleration lasted about 0.1 s, while the ballast acceleration converged in about 0.05 s, which was nearly the same as the vibration caused by the impulse hammer. The vibration characteristics of the ladder sleepers and the PC sleepers were compared by the response magnifications of the sleeper acceleration and the acceleration in the ballast as shown in
Figure 9.
From
Figure 9, it was found that the response magnification of the ladder sleepers was smaller than that of the PC sleepers in the frequency bands other than 100 Hz, 580 Hz, and 810 Hz, which was almost the same as the case of the vibration caused by the impulse hammer. The response magnification was determined by dividing the acceleration in the ballast by the acceleration on the sleepers.
From these experimental results, it was confirmed that the ladder sleeper has the effect of reducing vibration transmission in a wider frequency band than the PC sleepers.
4. Numerical Experiment
4.1. Numerical Analysis Method
For the numerical experiment, the three-dimensional numerical analysis model, the Dynamic Interaction Analysis for Shinkansen Train and Railway Structures, was used [
20,
21].
4.1.1. Dynamic Model of the Vehicle
Figure 10 shows the dynamic model of the vehicle assuming that the body, bogies, and wheelsets are rigid. These three-dimensional rigid elements are linked by springs
KN and dampers
CN (N is a suffix of number in
Figure 10) according to their respective characteristics. Each car on the train had 31 degrees of freedom. The train was made up of several vehicle models that were linked together by springs
KC and dampers
CC attached to the ends of the vehicles. Assuming that the train runs at a constant speed, the equation of three-dimensional motion of the train with N vehicles is written in a matrix form [
22] as:
where superscripts
V and
B indicate the vehicle and the structure (i.e., track), respectively;
XV is a displacement vector of the vehicle;
MV,
CV, and
KV are the mass, damping, and stiffness matrices of the vehicle, respectively;
represents the load vectors;
is the interaction force between the rail and the vehicle; and
represents the load vectors of the nonlinear spring force in the car. The vehicles in this study were modeled as a commuter train with a static wheel load of approximately 53 kN, corresponding to full crew/passenger capacity. The train consisted three vehicles of a general Japanese conventional line (wheel load = 40 kN, wheelbase = 2.1 m, vehicle length = 20 m) in recent years, and the train speed was 90 km/h.
4.1.2. Dynamic Model of the Track
Figure 11 shows the dynamic model of the track. The track and structure were modeled using the finite element method. Assembling all elements in the model, the equation of motion of the track and structure was obtained in a standard matrix form as:
where
XB is a displacement vector of the track and structure;
MB,
CB, and
KB are the mass, damping, and stiffness matrices, respectively;
represents the load vectors;
is the interaction force between the rail and the car; and
represents the load vectors of the nonlinear spring force in the structure.
In this study, as shown in
Figure 11, not only was the ballasted ladder track analysis model but also the conventional PC sleeper track analysis model was constructed for comparison. The only difference between the models is the shape of the sleeper; all other conditions are the same.
The rails were represented by beam elements, the rail pads by spring elements, the sleepers by solid elements, and the roadbed by spring elements. In the section adjacent to the ladder sleepers, the rails were modeled with beam elements, rail pads, ballast, and the roadbed with composite springs. In this study, we mainly focus on the transmission of forces and vibrations in the vertical direction, so the degrees of freedom in the Y direction of the analysis model and the degrees of freedom in the X direction of the end in the longitudinal direction of the model are constrained. Furthermore, the degree of freedom of rotation around the Z-axis was constrained.
The space between rails and sleepers was divided into five elements for rails and sleepers, and the entire ballast layer was divided into five layers for ballast. If the actual phenomenon is to be accurately reproduced, a nonlinear element or the like should be provided at the boundary between the sleeper and the ballast to reproduce the contact state and the noncontact state of the sleeper and the ballast. However, because this is not the main point of this study, the nonlinear element is not included in this analysis model, and the sleepers and ballast are connected by a rigid spring. The total number of nodes in the ballasted ladder track analysis model was 5430, and the total number of elements was 5728. The total number of nodes in the PC sleeper track analysis model was 5310, and the total number of elements was 5584.
4.1.3. Numerical Analysis Method
In the previous section, the equation of motion of the vehicle and that of the track and structure were derived in the vehicle’s coordinate system and the global coordinate system, respectively. The coupling of the vehicle’s equations of motion and those of the track and structure was accomplished by applying compatibility and equilibrium conditions to the subregion where the two systems were connected.
To carry out efficient numerical analysis, the equations of motion concerning the vehicle and those of the track and structure, expressed as Equations (1) and (2), respectively, were modally converted. The Newmark method was used to solve the resulting equation of motion on the modal coordinate system of the vehicle, track, and structure in time increments of Δt. The mode order that can reproduce vibrations of up to around 10 kHz was used in modal analysis, and the analysis was run at 0.1 msec intervals. An attenuation constant of 0.1 was used to ensure consistency with time-history response analysis [
19].
4.1.4. Material Constants
Table 1 shows the material constants used in the numerical analysis. Those constants were based on the Design Standards for Railway Structures and Commentary [
16,
23] and nominal values. The ground reaction-force coefficient was determined based on the results of the FWD (falling-weight deflectometer, made by Tokyo Measuring Instruments Laboratory Co., Ltd., Tokyo, Japan) [
24] test conducted in the field and the static loading test described later. The PC sleepers used for the comparison of the ladder sleepers were for the straight line specified in JIS E1201 (product type: 3PR).
4.1.5. Analysis Cases
Table 2 shows the analysis cases. For the test case, the support condition and the exciting method were set as analysis parameters. In addition to the case in which the ladder sleepers are uniformly supported by the ballast, two cases, Support A and Support B, are defined assuming that the ladder sleepers are laid at the structural boundary described in Chapter 1. In this study, the structural boundaries were assumed to be the boundary between the embankment, abutment, and the girder and the open culvert that crosses the track. Support A, as shown in
Figure 12, is a case in which ladder sleepers are laid in front of the structural boundary, whereas Support B is a case in which a ladder sleeper is laid across the structural boundary. The exciting method of the analysis model was static load and train running. The train’s running directions were “step-up”, in which the vehicle was transferred from the ballast section to the rigid support section, and “step-down”, in which the vehicle was transferred from the rigid support section to the ballast section. The rigid support section was modeled by multiplying Young’s modulus of the ballast and the ground reaction force coefficient of the roadbed shown in
Table 1 by 1000.
The stiffness ratio between the ballast section and the rigid support section is an important parameter. However, since the main purpose of this study is to clarify the difference in the pressure on the sleeper bottom plane caused by the structural difference between the ladder sleeper and the PC sleeper, the stiffness ratio is not a parameter and is simply one case. The assumed structure boundary is the one between the ballast section and a concrete structure section such as the concrete abutment with sufficiently high rigidity compared to ballast. Verification of the rigidity ratio on the boundary will be an issue for the future.
4.1.6. Validity Verification Test and Evaluation Method of the Analytical Model
To verify the validity of the analytical model, we compared the results of the full-scale model test conducted in Chapter 3 with the results of the numerical analysis. Previous studies were used to evaluate the analysis results. We concentrated on the pressure on the bottom plane of the sleeper, which is known to have a significant impact on track settlement progress [
26,
27]. As shown in
Figure 13, the evaluation position was the vertical stress of the solid element at the same position as the ladder sleepers and PC sleepers. In this analysis, the ballast is modeled with solid elements, and the stress and vibration of the ballast particles themselves cannot be accurately reproduced.
4.2. Verification of the Validity of the Analysis Model
Figure 14 shows the comparison between the static loading test results and the analysis results. The evaluation position is the center of the ballasted ladder track analysis model shown in
Figure 11a. For loads up to 160 kN, the rails settled by about 1.5 mm and the ladder sleepers settled by about 0.8 mm in the test. The analysis results can accurately reproduce these results. When the analysis results of the ballasted ladder track and the PC sleeper track are compared, the rail displacement of the PC sleeper is 0.07 mm greater than the ladder sleeper, and the ballasted ladder track has a higher track-support rigidity.
As already described in
Figure 7, the natural frequency of the ladder sleepers obtained by numerical analysis could be reproduced with an error of about 10%. Based on the results, it was demonstrated that the ballasted ladder track analysis model developed in this study can reproduce the actual phenomena related to the track’s support rigidity and the vibration characteristics of the ladder sleepers. The results of numerical experiments on the load-distribution performance of ladder sleepers will be shown in the following sections using this analysis model.
4.3. Numerical Analysis Results
4.3.1. Static Load (CASE1)
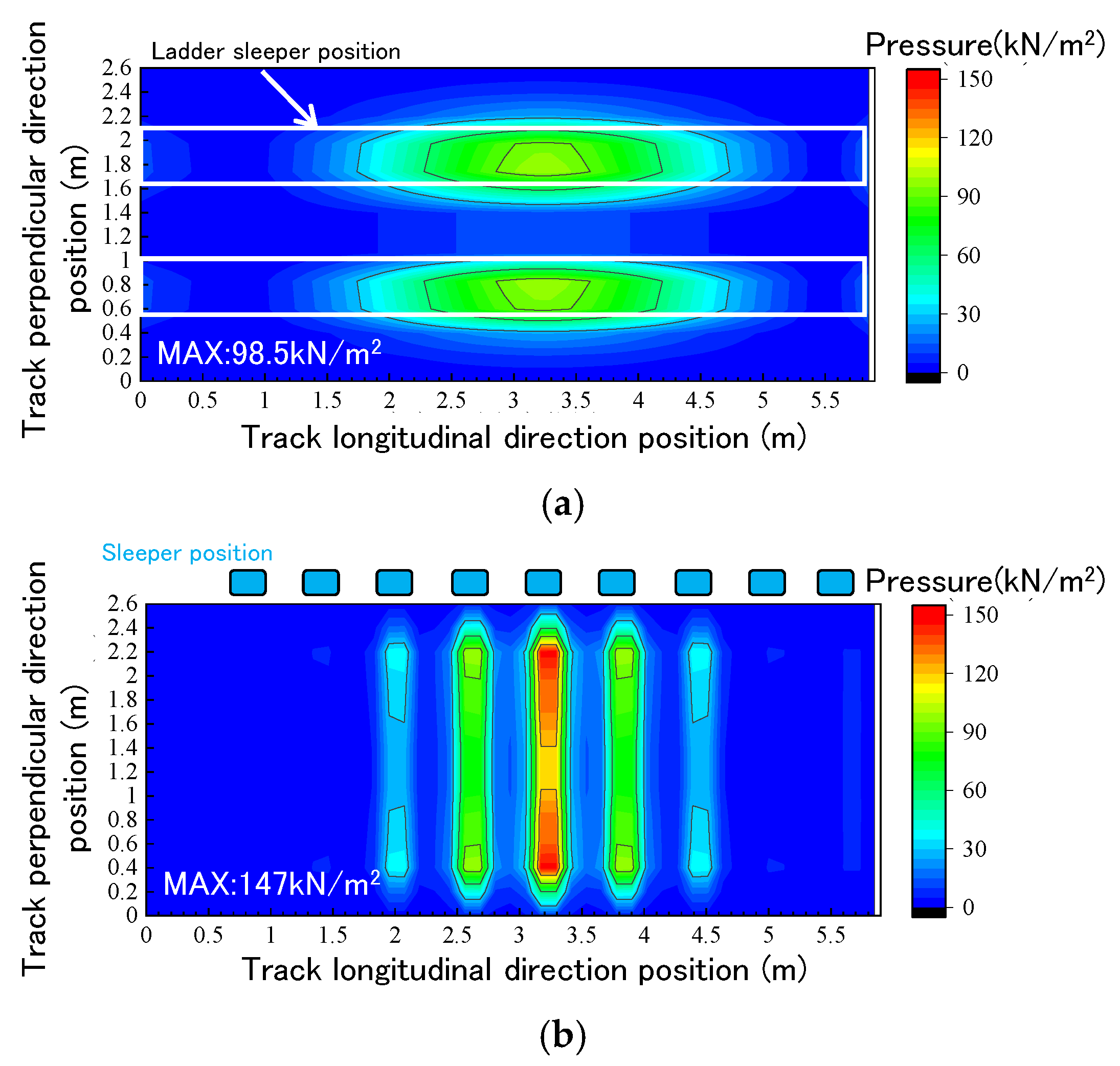
Figure 15 shows the pressure on the sleeper bottom plane when a static load of 80 kN was loaded. According to the figure, the maximum pressure on the sleeper bottom plane was 98.5 kN/m
2 for the ballasted ladder track and 147 kN/m
2 for the PC sleeper track. The pressure on the ballasted ladder track’s sleeper bottom plane was reduced to approximately 67% of that of the PC sleeper track. In addition, the range of load distribution was five sleepers on the PC sleeper track. On the other hand, in the ladder sleeper, the range was about seven sleepers.
4.3.2. Train Running (CASE2)
Figure 16 shows the time-history waveform and frequency characteristics of the pressure on the sleeper bottom plane under the condition that the track was uniformly supported (CASE2). Th e response of the PC sleeper track shows the peak of the response for each wheel axis on the time-history waveform, whereas the response of the ballasted ladder track shows the peak of the response for each bogie. This is due to the ladder sleeper’s load distribution effect. Due to this effect, the component that is due to the vibration frequency 11.2 Hz (≈1/{2.1 m/[90 km/h/3.6]}) for each wheel axis became smaller, as shown in
Figure 16b. The ballasted ladder track has a reduced component of about 10 Hz compared to the PC sleeper track.
Figure 17 shows the distribution of the pressure on the sleeper bottom plane when the vehicle is running under the condition that the track is uniformly supported (CASE2). In the ballasted ladder track, the maximum value of the pressure on the sleeper bottom plane was 55.4 kN/m
2. In the PC sleeper track, the maximum value of the pressure on the sleeper bottom plane was 83.7 kN/m
2. In the ballasted ladder track, the pressure on the sleeper bottom plane was reduced to about 66% compared to the PC sleeper track.
4.3.3. Train Running in Support A and Support B (CASE3, CASE4)
Figure 18 shows the distribution of the pressure on the sleeper bottom plane under the condition of stepping up from the ballast section to the rigid support section (CASE3). The maximum value of the pressure on the sleeper bottom plane at the end of sleepers in the PC sleeper track adjacent to the structural boundary shown in
Figure 18c was 58.6 kN/m
2. However, the maximum pressure on the sleeper bottom plane at the end of the ladder sleeper shown in Support A in
Figure 18a was 31.9 kN/m
2. The pressure on the sleeper bottom plane of the PC sleepers at the same position was reduced to about 54%. For Support B in
Figure 18b, the maximum value of the pressure on the sleeper bottom plane at the end of the ladder sleeper was 11.9 kN/m
2, which was reduced to about 20% of the pressure on the sleeper bottom plane of the PC sleeper at the same position.
Figure 19 shows the distribution of the pressure on the sleeper bottom plane under the condition of running down a step from the rigid support section to the ballast section (CASE4). The magnitude of the pressure on the bottom plane of the ladder and PC sleepers adjacent to the structural boundary was nearly identical to the condition of stepping up from the ballast section to the rigid support section shown in
Figure 18 (CASE3). Specifically, the pressure on the sleeper bottom plane of the PC sleepers was 57.9 kN/m
2, while the Support A of the ladder sleepers was 31.4 kN/m
2 and the Support B was 11.1 kN/m
2. Support A was reduced to 55% and Support B was reduced to 19% to the pressure on the sleeper bottom plane of the PC sleepers.
According to the results of the above numerical experiments, when laying the ladder sleepers near the structural boundary, they were laid across the structural boundary rather than in front of the structural boundary, as shown in
Figure 20. It was shown that this may be more effective for reducing the pressure on the sleeper bottom plane in the ballast section adjacent to the structural boundary.
5. Verification of the Effect of Suppressing the Longitudinal Level Irregularity of the Ballasted Ladder Tracks in the Commercial Line
5.1. Verification Method
Figure 21 shows the situation of the ladder sleepers on the commercial line. The laying method was “Support A” shown in
Table 2, and it was laid in front of the structural boundary. The inspection data of the PC sleepers laid in the same position as before the laying of the ladder sleepers was evaluated for the PC sleepers. After track maintenance was performed four times after the ballast replacement, the ladder sleepers used the inspection data to evaluate the longitudinal level irregularity. Furthermore, the PC sleepers evaluated the longitudinal level irregularity using inspection data after the track maintenance was performed six times following ballast replacement. Since it was not possible to measure data at the time of the initial subsidence of the PC sleeper, it was decided to make a comparison in the gradual subsidence process after the initial subsidence had converged. The progress of the longitudinal level irregularity is expressed by Equation (3) from previous studies [
28]:
where
α is the initial settlement coefficient,
β is the settlement progress coefficient,
γ is the coefficient that is due to the track condition,
Y is the longitudinal level irregularity, and
X is the passing tonnage.
5.2. Verification Results
Figure 22 shows a comparison of the longitudinal level irregularity of the ballasted ladder track and PC sleeper track. Although the ballasted ladder track requires one-third the amount of track maintenance as the PC sleeper track, the longitudinal level irregularity of the ballasted ladder track was about 3.4 mm at a passing tonnage of about 6.5 million tons. The longitudinal level irregularity of the PC sleeper track, on the other hand, was approximately 11.9 mm, and the ballasted ladder track was reduced by approximately 30% when compared to the PC sleeper track. Comparing the subsidence progress coefficient
β, it was 0.00178 for the ballasted ladder track and 0.00990 for the PC sleeper track, and the progress of the longitudinal level irregularity was significantly slower for the ballasted ladder track than for the PC sleeper track. The above results confirmed and demonstrated that laying the ballasted ladder track even at the structural boundary suppressed the progression of the longitudinal level irregularity and resulted in a maintenance-labor-saving effect when compared to the PC sleeper track.
6. Conclusions
In this study, to verify and demonstrate the longitudinal level irregularity suppression effect of the ladder sleepers at the structural boundary, full-scale model tests, numerical experiments, and the laying of the ladder sleepers on the commercial line were conducted. The findings obtained are as follows:
Full-scale model test was conducted to quantify the load distribution effect of the ladder sleepers.
- (a)
The natural frequency of the ladder sleeper was identified. The first mode is 75 Hz, the second mode is 151 Hz, the third mode is 293 Hz, the fourth mode is 480 Hz, and the fifth mode is 748 Hz, and the characteristics were clearly different from the PC sleepers.
- (b)
Full-scale model tests verified and demonstrated that the ladder sleeper had the effect of reducing the transmission of vibration to the ballast compared to the PC sleeper track, except for the natural frequency of the ladder sleeper.
Numerical experiments were conducted using a three-dimensional numerical analysis model, and a comparison was made between the ballasted ladder track and the conventional PC sleeper track regarding the pressure on the sleeper bottom plane.
- (a)
As a result of static loading analysis, the pressure on the sleeper bottom plane of the ladder sleepers was reduced to about 67% in the ballasted ladder track compared to the PC sleeper track. In addition, the range of load distribution was five sleepers on the PC sleeper track. On the other hand, in the ladder sleeper, the range was about seven sleepers.
- (b)
As a result of train-running analysis, the ballasted ladder track was able to reduce the pressure on the sleeper bottom plane to about 66% compared to the PC sleeper track.
- (c)
Tracks that simulate the structural boundary were modeled, which consists of a ballast section and a rigid support section. There was a “step-up” running analysis and a “step-down” running analysis. As a result, it was revealed that laying across the structural boundary may be more effective than laying in front of the structural boundary for reducing pressure on the sleeper bottom plane in the ballast section adjacent to the structural boundary.
Ladder sleepers laid on the commercial line and long-term measurement of longitudinal level irregularity was carried out to verify the effect of suppressing the longitudinal level irregularity. The subsidence progress coefficient β was 0.00178 for the ballasted ladder track and 0.00990 for the PC sleeper track, and the longitudinal level irregularity progressed significantly slower for the ballasted ladder track than for the PC sleeper track.
In the future, we would like to increase the number of ballasted ladder tracks laid at the structural boundary and quantify the longitudinal level irregularity suppression effect under various conditions. In this way, we would like to propose a standard ladder sleeper structure according to the laying conditions.
Author Contributions
Conceptualization, T.W.; methodology, T.W., K.G. and K.M.; software, T.W. and K.G.; validation, T.W., K.M. and S.M.; formal analysis, T.W.; investigation, T.W.; resources, T.W.; data curation, T.W.; writing—original draft preparation, T.W.; writing—review and editing, T.W.; visualization, T.W.; supervision, T.W.; project administration, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the East Japan Railway Company for the significant cooperation in some field measurements of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wakui, H.; Matsumoto, N.; Inoue, H. Ladder sleeper and new track structures development. Q. Rep. Railw. Tech. Res. Inst. 1996, 37, 110–111. [Google Scholar]
- Wakui, H.; Matsumoto, N.; Asanuma, K.; David, M.R.; Kenneth, J.L. Performance of ballasted ladder track under heavy axle loads at TTCI. In Proceedings of the 7th International Heavy Haul Conference, Brisbane, Australia, 10–14 June 2001; pp. 209–216. [Google Scholar]
- Okuda, H.; Sogabe, M.; Matsumoto, N.; Wakui, H. Environmental performance improvement of railway structural system using ladder track. In Proceedings of the IABSE Symposium, Antwerp, Belgium, 27 August 2003; pp. 1–10. [Google Scholar]
- Watanabe, T.; Sogabe, M.; Asanuma, K.; Wakui, H. Estimation of structure-borne noise reduction effect of steel railway bridge equipped with floating ladder track and floating reinforced concrete deck. J. Mech. Syst. Transp. Logist. 2010, 3, 83–91. [Google Scholar] [CrossRef][Green Version]
- Xia, H.; Chen, J.G.; Xia, C.Y.; Inoue, H.; Zenda, Y.; Qi, L. An experimental study of train-induced structural and environmental vibrations of a rail transit elevated bridge with ladder tracks. Proc. Inst. Mech. Eng. Part F 2010, 224, 115–124. [Google Scholar] [CrossRef]
- Meng, M.; Weining, L.; Yulu, L.; Weifeng, L. An experimental study of vibration reduction of a ballasted ladder track. Proc. Inst. Mech. Eng. Part F 2017, 231, 1035–1047. [Google Scholar]
- Kiyoshi, A.; Okuda, H.; Matsumoto, N.; Wakui, H.; Tomita, K. Buckling safety analyses of ballasted ladder track under thermal and vehicle loads. Railw. Tech. Res. Inst. Rep. 2006, 20, 41–46. (In Japanese) [Google Scholar]
- Asanuma, K.; Sogabe, M.; Watanabe, T.; Okayama, J.; Wakui, H. Development of ballasted ladder track equipped with a vehicle guide device. Q. Rep. Railw. Tech. Res. Inst. 2009, 50, 233–240. [Google Scholar] [CrossRef]
- Guoqing, J.; Peyman, A. Review of the lateral resistance of ballasted tracks. Proc. Inst. Mech. Eng. Part F 2020, 234, 807–820. [Google Scholar]
- SATEBA. Available online: https://sateba.com/solutions/light-speed-rail/ (accessed on 8 March 2022).
- Xiangyu, Q.; Meng, M.; Minghang, L.; Yanmei, C.; Weining, L. Analysis of the Vibration Mitigation Characteristics of the Ballasted Ladder Track with Elastic Elements. Sustainability 2019, 11, 6780. [Google Scholar]
- Indraratna, B.; Nimbalkar, S.; Navaratnarajah, S.K.; Rujikiatkamjorn, C.; Neville, T. Use of shock mats for mitigating degradation of railroad ballast. Sri Lankan Geotech. J. Spec. Issue Ground Improv. 2014, 6, 32–41. [Google Scholar]
- Artur, Z.; Cezary, K.; Anna Al, S.; Jan Pnski Sławomir, D. A Novel Approach to the Analysis of Under Sleeper Pads (USP) Applied in the Ballasted Track Structures. Materials 2020, 13, 2438. [Google Scholar]
- Cezary, K.; Artur, Z.; Kacper, W.; Anna Al, S. Laboratory Tests and Analyses of the Level of Vibration Suppression of Prototype under Ballast Mats (UBM) in the Ballasted Track Systems. Materials 2021, 14, 313. [Google Scholar]
- Wakui, H.; Okuda, H. A study on limit state design method for prestressed concrete sleepers. Concr. Libr. JSCE 1999, 33, 1–25. [Google Scholar] [CrossRef][Green Version]
- Railway Technical Research Institute. Design Standards for Railway Structures and Commentary (Track Structures); Railway Technical Research Institute and Maruzen Co., Ltd.: Tokyo, Japan, 2012. [Google Scholar]
- Watanabe, T.; Goto, K.; Matsuoka, K.; Minoura, S. Validation of a dynamic wheel load factor and the influence of various track irregularities on the dynamic response of prestressed concrete sleepers. Proc. Inst. Mech. Eng. Part F 2020, 234, 1275–1284. [Google Scholar] [CrossRef]
- Japanese Industrial Standards Committee. Prestressed Concrete Sleepers—Pretensioning Type; Japanese Standards Association: Tokyo, Japan, 1997; p. 1201. [Google Scholar]
- Kodai, M.; Tsutomu, W. Application of a Frequency Based Detection Method for Evaluating Damaged Concrete Sleepers. In Advances in Structural Health Monitoring; IntechOpen: London, UK, 2018; Available online: https://www.intechopen.com/books/advances-in-structural-health-monitoring/applicationof-a-frequency-based-detection-method-for-evaluatingdamaged-concrete-sleepers (accessed on 5 December 2019).
- Hajime, W.; Nobuyuki, M.; Makoto, T. A study on dynamic interaction analysis for railway vehicle and structures. Q. Rep. Railw. Techn. Res. Inst. 1994, 35, 96–104. [Google Scholar]
- Makoto, T.; Nobuyuki, M.; Hajime, W.; Sogabe, M. Simulation of a Shinkansen train on the railway structure during an earthquake. Jpn. J. Ind. Appl. Math. 2011, 28, 223–236. [Google Scholar]
- Makoto, T.; Satoshi, K.; Hajime, W.; Nobuyuki, M.; Masamichi, S. Simulation and visualization of high-speed Shinkansen train on the railway structure. Jpn. J. Ind. Appl. Math. 2000, 17, 309–320. [Google Scholar]
- Railway Technical Research Institute. Design Standards for Railway Structures and Commentary (Concrete Structures); Railway Technical Research Institute and Maruzen Co., Ltd.: Tokyo, Japan, 2007. [Google Scholar]
- Tokyo Measuring Instruments Lab. Available online: https://tml.jp/e/product/special_ins/fwd-light2.html (accessed on 8 March 2022).
- Japanese Industrial Standards Committee. Flat Bottom Railway Rails and Special Rails for Switches and Crossings of Non-Treated Steel; ISO: Geneva, Switzerland, 2001; p. 1101. [Google Scholar]
- Ishida, M.; Namura, A.; Suzuki, T. Track settlement measurements and dynamic prediction model based on settlement laws. In Proceedings of the World Congress on Railway Research, Edinburgh, Scotland, UK, 28 September–1 October 2003; pp. 1–9. [Google Scholar]
- Suzuki, T.; Ishida, M.; Abe, K.; Koro, K. Measurement on dynamic behavior of track near rail joints and prediction of track settlement. Q. Rep. Railw. Techn. Res. Inst. 2005, 46, 124–129. [Google Scholar]
- Sekine, E.; Kohata, Y. Strength and deformation characteristics of railroad ballst in abrasion process of ballast particles. In Proceedings of the 12th Asian Regional Conference on Soil Mechanics & Geotechnical Engineering, Singapore, 4–8 August 2003; World Scientific Publishing: Singapore, 2003. [Google Scholar]
Figure 1.
Outline of the ladder sleeper.
Figure 1.
Outline of the ladder sleeper.
Figure 2.
Outline of full-scale models: (a) ladder track; (b) PC sleeper track.
Figure 2.
Outline of full-scale models: (a) ladder track; (b) PC sleeper track.
Figure 3.
Situation of tests: (a) impulse hammer test; (b) weight-falling test.
Figure 3.
Situation of tests: (a) impulse hammer test; (b) weight-falling test.
Figure 4.
Sensor installation methods: (a) upper surface of the ladder sleeper; (b) in the ballast.
Figure 4.
Sensor installation methods: (a) upper surface of the ladder sleeper; (b) in the ballast.
Figure 5.
Example of the time-history waveform of the excitation force and the acceleration in the ballast (ballasted ladder track): (a) excitation force; (b) vertical acceleration measured in the ballast.
Figure 5.
Example of the time-history waveform of the excitation force and the acceleration in the ballast (ballasted ladder track): (a) excitation force; (b) vertical acceleration measured in the ballast.
Figure 6.
Comparison of the accelerance.
Figure 6.
Comparison of the accelerance.
Figure 7.
Identification results of natural frequency and vibration mode shape of ladder sleepers.
Figure 7.
Identification results of natural frequency and vibration mode shape of ladder sleepers.
Figure 8.
Example of the time-history waveform of the vertical acceleration on the ladder sleepers and in the ballast.
Figure 8.
Example of the time-history waveform of the vertical acceleration on the ladder sleepers and in the ballast.
Figure 9.
Comparison of the response magnification of the ladder sleeper and PC sleeper.
Figure 9.
Comparison of the response magnification of the ladder sleeper and PC sleeper.
Figure 10.
Dynamic model of the vehicle.
Figure 10.
Dynamic model of the vehicle.
Figure 11.
Dynamic model of the track: (a) ballasted ladder track; (b) PC sleeper track.
Figure 11.
Dynamic model of the track: (a) ballasted ladder track; (b) PC sleeper track.
Figure 12.
Outline of support condition: (a) uniformly supported by ballast; (b) Support A (laying ladder sleeper in front of the structural boundary); (c) Support B (laying ladder sleeper across structural boundaries).
Figure 12.
Outline of support condition: (a) uniformly supported by ballast; (b) Support A (laying ladder sleeper in front of the structural boundary); (c) Support B (laying ladder sleeper across structural boundaries).
Figure 13.
Outline of evaluation point.
Figure 13.
Outline of evaluation point.
Figure 14.
Comparison between the static loading test results and the analysis results: (a) rail; (b) sleeper.
Figure 14.
Comparison between the static loading test results and the analysis results: (a) rail; (b) sleeper.
Figure 15.
Pressure on sleeper bottom plane (CASE1): (a) ladder track; (b) PC sleeper.
Figure 15.
Pressure on sleeper bottom plane (CASE1): (a) ladder track; (b) PC sleeper.
Figure 16.
Analysis results of train running (CASE2): (a) time-history waveform of pressure on sleeper bottom plane of each sleeper; (b) frequency characteristics of pressure on sleeper bottom plane of each sleeper.
Figure 16.
Analysis results of train running (CASE2): (a) time-history waveform of pressure on sleeper bottom plane of each sleeper; (b) frequency characteristics of pressure on sleeper bottom plane of each sleeper.
Figure 17.
Distribution of the pressure on the sleeper bottom plane (CASE2): (a) ladder track; (b) PC sleeper track.
Figure 17.
Distribution of the pressure on the sleeper bottom plane (CASE2): (a) ladder track; (b) PC sleeper track.
Figure 18.
Distribution of the pressure on the sleeper bottom plane with “step-up” running (CASE3): (a) ladder track (Support A); (b) ladder track (Support B); (c) PC sleeper track.
Figure 18.
Distribution of the pressure on the sleeper bottom plane with “step-up” running (CASE3): (a) ladder track (Support A); (b) ladder track (Support B); (c) PC sleeper track.
Figure 19.
Distribution of the pressure on the sleeper bottom plane with “step-down” running (CASE4): (a) ladder track (Support A); (b) ladder track (Support B); (c) PC sleeper track.
Figure 19.
Distribution of the pressure on the sleeper bottom plane with “step-down” running (CASE4): (a) ladder track (Support A); (b) ladder track (Support B); (c) PC sleeper track.
Figure 20.
Recommendation of the way of ladder sleeper at the structural boundary.
Figure 20.
Recommendation of the way of ladder sleeper at the structural boundary.
Figure 21.
Situation of the ladder sleepers on the commercial line (Support A).
Figure 21.
Situation of the ladder sleepers on the commercial line (Support A).
Figure 22.
Comparison of the longitudinal level irregularity of the ballasted ladder track and PC sleeper track.
Figure 22.
Comparison of the longitudinal level irregularity of the ballasted ladder track and PC sleeper track.
Table 1.
Material constants used in the numerical analysis.
Table 1.
Material constants used in the numerical analysis.
| Rail | ”50 kgN” specified by JIS E 1101 [25]
Young’s modulus ES = 200 GPa, Track gauge = 1067 mm |
| Rail Pad | Spring constant DP = 120 MN/m (nominal value = 60 MN/m) |
| Ladder Sleeper | PC steel strand φ = 4.22 mm N = 18
Length LL = 5900 mm, Width BL = 460 mm
Height HL = 155 mm
Young’s modulus EC = 33 GPa |
PC Sleeper
(3PR) | 3PR (JIS E 1201), PC steel strand φ = 2.9 mm N = 12
Length LP = 2000 mm, Bottom width BP = 240 mm
Height HP = 170 mm (Rail seat section), 150 mm (Center section)
Young’s modulus EC = 33 GPa |
| Ballast | Ballast thickness h = 250 mm
Young’s modulus EB = 0.088 GPa |
| Roadbed | Ground reaction coefficient K30 = 50 MN/m3 (Measured value)
Support spring constant DG = 22 MN/m |
Table 2.
Analysis cases.
| CASE | Support Condition | Exciting Method | Note |
|---|
| 1 | Uniformly supported | Static load | Loading from 0 to 80 kN |
| 2 | Uniformly supported | Train running | General Japanese conventional vehicles run |
| 3–1 | Support A | Train running | “step-up” running
Laying ladder sleeper in front of the structural boundary |
| 3–2 | Support B | Train running | “step-up” running
Laying ladder sleeper across structural boundaries |
| 4–1 | Support A | Train running | “step-down” running
Laying ladder sleeper in front of the structural boundary |
| 4–2 | Support B | Train running | “step-down” running
Laying ladder sleeper across structural boundaries |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).