Stock Portfolio Management in the Presence of Downtrends Using Computational Intelligence
Abstract
1. Introduction
2. Background
2.1. Fundamental Analysis
2.2. Artificial Neural Networks
2.3. Multi-Objective Optimization Problem
2.4. Evolutionary Multi-Objective Optimization
3. Literature Review
3.1. Portfolio Management: Price Forecasting, Stock Selection and Portfolio Optimization
3.2. Exploiting Uptrends and Downtrends in Strategies for Stock Investment
4. Methods and Materials
4.1. An Artificial Neural Network to Estimate Future Prices
- Close price. Last transacted price of the stock before the market officially closes.
- Open Price. First price of the stock at which it was traded at the open of the period’s trading.
- High. Highest price of the stock in the period’s trading.
- Low. Lowest price of the stock in the period’s trading.
- Average Price. Average price of the stock in the period’s trading.
- Market Capitalization. Price per share multiplied by the number of outstanding shares of a publicly held company.
- Return Rate. Profit on an investment over a period, expressed as a proportion of the original investment.
- Volume. Number of shares traded (or their equivalent in money) of a stock in a given period.
- Total asset turnover. Net sales over the average value of total assets on the company’s balance sheet between the beginning and the end of the period.
- Fixed asset turnover. Net sales over the average value of fixed assets.
- Volatility. Standard deviation of prices.
- General Capital. Number of preferred and common shares that a company is authorized to issue.
- Price to Earnings. Market value per share over earnings per share.
- Price to Book. Market price per share over book value per share.
- Price to Sales. Market price per share over revenue per share.
- Price to Cash Flow. Market price per share over operating cash flow per share.
4.2. Evolutionary Algorithms to Select Stocks
| Algorithm 1 Differential evolution used to address Problem (3). |
|
- Forecasted return: Output of the ANN.
- Return on equity: Net income over average shareholder’s equity.
- Return on asset: Net income over total assets.
- Operating income margin: Operating earnings over revenue.
- Net income margin: Total liabilities over total shareholder’s equity.
- Levered free cash flow: Amount of money the company left over after paying its financial debts.
- Current ratio: Current assets over current liabilities.
- Quick ratio: (Cash and equivalents + marketable securities + accounts receivable) over current liabilities.
- Inventory turnover ratio: Net sales over ending inventory.
- Receivable turnover ratio: Net credit sales over average accounts receivable.
- Operating income growth rate: (Operating income in the current quarter − operating income at the previous quarter) over operating income in the previous quarter.
- Net income growth rate: (Net income after tax in the current quarter − net income after tax at the previous quarter) over net income after tax in the previous quarter.
4.3. Optimizing Stock Portfolios
5. Experiments
5.1. Experimental Design
5.2. Benchmarks
5.3. Parameter Setting
5.4. Results
6. Conclusions
- I
- A deeper study of the forecasting stage to test the performance of several AI methods by employing more data or different financial variables;
- II
- A deeper study on the selection stage to evaluate the performance of the system by employing different financial variables to build the stock portfolio;
- III
- A deeper study of the performance of the system by modifying different parameters in the optimization stage and comparing the results with other approaches;
- IV
- New experiments to show the robustness of the approach regarding (i) the number and type of alternatives in the universe of stocks, (ii) the number of selected stocks and (iii) the parameter values.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, H.; Long, M. Intelligent Portfolio Theory and Application in Stock Investment with Multi-Factor Models and Trend Following Trading Strategies. Procedia Comput. Sci. 2021, 187, 414–419. [Google Scholar] [CrossRef]
- Jiang, X.; Peterburgsky, S. Investment performance of shorted leveraged ETF pairs. Appl. Econ. 2017, 49, 4410–4427. [Google Scholar] [CrossRef]
- Hurlin, C.; Iseli, G.; Pérignon, C.; Yeung, S. The counterparty risk exposure of ETF investors. J. Bank. Financ. 2019, 102, 215–230. [Google Scholar] [CrossRef]
- Holzhauer, H.M.; Lu, X.; McLeod, R.W.; Mehran, J. Bad news bears: Effects of expected market volatility on daily tracking error of leveraged bull and bear ETFs. Manag. Financ. 2013, 39, 1169–1187. [Google Scholar]
- Gregory-Allen, R.B.; Smith, D.M.; Werman, M. Chapter 30—Short Selling by Portfolio Managers: Performance and Risk Effects across Investment Styles. In Handbook of Short Selling; Gregoriou, G.N., Ed.; Academic Press: San Diego, CA, USA, 2012; pp. 437–451. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Li, X.; Xie, H.; Wang, R.; Cai, Y.; Cao, J.; Wang, F.; Min, H.; Deng, X. Empirical analysis: Stock market prediction via extreme learning machine. Neural Comput. Appl. 2016, 27, 67–78. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Rao, Q.; Li, K.; Zhang, H. Exploring mutual information-based sentimental analysis with kernel-based extreme learning machine for stock prediction. Soft Comput. 2017, 21, 3193–3205. [Google Scholar] [CrossRef]
- Das, S.P.; Padhy, S. Unsupervised extreme learning machine and support vector regression hybrid model for predicting energy commodity futures index. Memetic Comput. 2017, 9, 333–346. [Google Scholar] [CrossRef]
- Yang, F.; Chen, Z.; Li, J.; Tang, L. A novel hybrid stock selection method with stock prediction. Appl. Soft Comput. 2019, 80, 820–831. [Google Scholar] [CrossRef]
- Fernandez, E.; Navarro, J.; Solares, E.; Coello, C.C. A novel approach to select the best portfolio considering the preferences of the decision maker. Swarm Evol. Comput. 2019, 46, 140–153. [Google Scholar] [CrossRef]
- Solares, E.; Coello, C.A.C.; Fernandez, E.; Navarro, J. Handling uncertainty through confidence intervals in portfolio optimization. Swarm Evol. Comput. 2019, 44, 774–787. [Google Scholar] [CrossRef]
- Xidonas, P.; Mavrotas, G.; Psarras, J. A multicriteria methodology for equity selection using financial analysis. Comput. Oper. Res. 2009, 36, 3187–3203. [Google Scholar] [CrossRef]
- Marasović, B.; Poklepović, T.; Aljinović, Z. MArkowitz’model with fundamental and technical analysis–complementary methods or not. Croat. Oper. Res. Rev. 2011, 2, 122–132. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Sumathi, S.; Paneerselvam, S. Computational Intelligence Paradigms: Theory & Applications Using MATLAB; CRC Press: New York, NY, USA, 2010. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin, Germany, 2007; Volume 5. [Google Scholar]
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef]
- Pławiak, P. Novel genetic ensembles of classifiers applied to myocardium dysfunction recognition based on ECG signals. Swarm Evol. Comput. 2018, 39, 192–208. [Google Scholar] [CrossRef]
- Pławiak, P. Novel methodology of cardiac health recognition based on ECG signals and evolutionary-neural system. Expert Syst. Appl. 2018, 92, 334–349. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Krink, T.; Paterlini, S. Multiobjective optimization using differential evolution for real-world portfolio optimization. Comput. Manag. Sci. 2011, 8, 157–179. [Google Scholar] [CrossRef]
- Krink, T.; Mittnik, S.; Paterlini, S. Differential evolution and combinatorial search for constrained index-tracking. Ann. Oper. Res. 2009, 172, 153. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Sharma, D.K.; Hota, H.; Brown, K.; Handa, R. Integration of genetic algorithm with artificial neural network for stock market forecasting. Int. J. Syst. Assur. Eng. Manag. 2021, 1–14. [Google Scholar] [CrossRef]
- Ferreira, F.; Gandomi, A.H.; Cardoso, R.T.N. Artificial Intelligence Applied to Stock Market Trading: A Review. IEEE Access 2021, 9, 30898–30917. [Google Scholar] [CrossRef]
- Chopra, R.; Sharma, G.D. Application of Artificial Intelligence in Stock Market Forecasting: A Critique, Review, and Research Agenda. J. Risk Financ. Manag. 2021, 14, 526. [Google Scholar] [CrossRef]
- Ma, Y.L.; Han, R.Z.; Wang, W.Z. Prediction-Based Portfolio Optimization Models Using Deep Neural Networks. IEEE Access 2020, 8, 115393–115405. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Long, W.; Lu, Z.; Cui, L. Deep learning-based feature engineering for stock price movement prediction. Knowl.-Based Syst. 2019, 164, 163–173. [Google Scholar] [CrossRef]
- Zhong, X.; Enke, D. Predicting the daily return direction of the stock market using hybrid machine learning algorithms. Financ. Innov. 2019, 5, 1–20. [Google Scholar] [CrossRef]
- Kaczmarek, T.; Perez, K. Building portfolios based on machine learning predictions. Econ. Res.-Ekon. Istraz. 2021, 1–19. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock and stock price index movement using Trend Deterministic Data Preparation and machine learning techniques. Expert Syst. Appl. 2015, 42, 259–268. [Google Scholar] [CrossRef]
- Chong, E.; Han, C.; Park, F.C. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef]
- Huang, G.B.; Siew, C.K. Extreme learning machine: RBF network case. In Proceedings of the 2004 8th International Conference on Control, Automation, Robotics and Vision (ICARCV) ICARCV 2004, Kunming, China, 6–9 December 2004; Volume 2, pp. 1029–1036. [Google Scholar] [CrossRef]
- Peykani, P.; Mohammadi, E.; Jabbarzadeh, A.; Rostamy-Malkhalifeh, M.; Pishvaee, M.S. A novel two-phase robust portfolio selection and optimization approach under uncertainty: A case study of Tehran stock exchange. PLoS ONE 2020, 15, e239810. [Google Scholar] [CrossRef] [PubMed]
- Mussafi, N.S.M.; Ismail, Z. Optimum Risk-Adjusted Islamic Stock Portfolio Using the Quadratic Programming Model: An Empirical Study in Indonesia. J. Asian Financ. Econ. Bus. 2021, 8, 839–850. [Google Scholar] [CrossRef]
- Lim, S.; Kim, M.J.; Ahn, C.W. A Genetic Algorithm (GA) Approach to the Portfolio Design Based on Market Movements and Asset Valuations. IEEE Access 2020, 8, 140234–140249. [Google Scholar] [CrossRef]
- Wang, W.Y.; Li, W.Z.; Zhang, N.; Liu, K.C. Portfolio formation with preselection using deep learning from long-term financial data. Expert Syst. Appl. 2020, 143, 113042. [Google Scholar] [CrossRef]
- Zhang, C.; Liang, S.; Lyu, F.; Fang, L. Stock-index tracking optimization using auto-encoders. Front. Phys. 2020, 8, 388. [Google Scholar] [CrossRef]
- Paiva, F.D.; Cardoso, R.T.N.; Hanaoka, G.P.; Duarte, W.M. Decision-making for financial trading: A fusion approach of machine learning and portfolio selection. Expert Syst. Appl. 2019, 115, 635–655. [Google Scholar] [CrossRef]
- Galankashi, M.R.; Rafiei, F.M.; Ghezelbash, M. Portfolio selection: A fuzzy-ANP approach. Financ. Innov. 2020, 6, 34. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Kalayci, C.B.; Ertenlice, O.; Akbay, M.A. A comprehensive review of deterministic models and applications for mean-variance portfolio optimization. Expert Syst. Appl. 2019, 125, 345–368. [Google Scholar] [CrossRef]
- Rockafellar, R.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2002, 2, 21–41. [Google Scholar] [CrossRef]
- Rockafellar, R.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]
- Sehgal, R.; Mehra, A. Robust reward–risk ratio portfolio optimization. Int. Trans. Oper. Res. 2021, 28, 2169–2190. [Google Scholar] [CrossRef]
- Hu, Y.; Lindquist, W.B.; Rachev, S.T. Portfolio Optimization Constrained by Performance Attribution. J. Risk Financ. Manag. 2021, 14, 201. [Google Scholar] [CrossRef]
- Dai, Z.; Wen, F. Some improved sparse and stable portfolio optimization problems. Financ. Res. Lett. 2018, 27, 46–52. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Yunusoglu, M.G.; Özsoydan, F.B. A GRASP based solution approach to solve cardinality constrained portfolio optimization problems. Comput. Ind. Eng. 2015, 90, 339–351. [Google Scholar] [CrossRef]
- Mayambala, F.; Rönnberg, E.; Larsson, T. Eigendecomposition of the Mean-Variance Portfolio Optimization Model. In Optimization, Control, and Applications in the Information Age; Migdalas, A., Karakitsiou, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 209–232. [Google Scholar]
- Kocadağli, O.; Keskin, R. A novel portfolio selection model based on fuzzy goal programming with different importance and priorities. Expert Syst. Appl. 2015, 42, 6898–6912. [Google Scholar] [CrossRef]
- He, F.; Qu, R. Hybridising Local Search With Branch-And-Bound For Constrained Portfolio Selection Problems. In Proceedings of the 30th European Council for Modeling and Simulation, Regensburg, Germany, 31 May–3 June 2016; Claus, T., Herrmann, F., Manitz, M., Rose, O., Eds.; Digital Library of the European Council for Modelling and Simulation: Regensburg, Germany, 2016; pp. 1–7. [Google Scholar]
- Ruiz-Torrubiano, R.; Suárez, A. A memetic algorithm for cardinality-constrained portfolio optimization with transaction costs. Appl. Soft Comput. 2015, 36, 125–142. [Google Scholar] [CrossRef]
- Soleymani, F.; Paquet, E. Financial portfolio optimization with online deep reinforcement learning and restricted stacked autoencoder—DeepBreath. Expert Syst. Appl. 2020, 156, 113456. [Google Scholar] [CrossRef]
- García, F.; Guijarro, F.; Oliver, J. Index tracking optimization with cardinality constraint: A performance comparison of genetic algorithms and tabu search heuristics. Neural Comput. Appl. 2018, 30, 2625–2641. [Google Scholar] [CrossRef]
- Hadi, A.S.; Naggar, A.A.E.; Bary, M.N.A. New model and method for portfolios selection. Appl. Math. Sci. 2016, 10, 263–288. [Google Scholar] [CrossRef]
- Liagkouras, K.; Metaxiotis, K. A new efficiently encoded multiobjective algorithm for the solution of the cardinality constrained portfolio optimization problem. Ann. Oper. Res. 2018, 267, 281–319. [Google Scholar] [CrossRef]
- Macedo, L.L.; Godinho, P.; Alves, M.J. Mean-semivariance portfolio optimization with multiobjective evolutionary algorithms and technical analysis rules. Expert Syst. Appl. 2017, 79, 33–43. [Google Scholar] [CrossRef]
- Lwin, K.T.; Qu, R.; MacCarthy, B.L. Mean-VaR portfolio optimization: A nonparametric approach. Eur. J. Oper. Res. 2017, 260, 751–766. [Google Scholar] [CrossRef]
- Ban, G.Y.; Karoui, N.E.; Lim, A.E.B. Machine Learning and Portfolio Optimization. Manag. Sci. 2016, 64, 1136–1154. [Google Scholar] [CrossRef]
- Kizys, R.; Juan, A.; Sawik, B.; Calvet, L. A Biased-Randomized Iterated Local Search Algorithm for Rich Portfolio Optimization. Appl. Sci. 2019, 9, 3509. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Ertenlice, O.; Akyer, H.; Aygoren, H. An artificial bee colony algorithm with feasibility enforcement and infeasibility toleration procedures for cardinality constrained portfolio optimization. Expert Syst. Appl. 2017, 85, 61–75. [Google Scholar] [CrossRef]
- Mendonça, G.H.; Ferreira, F.G.; Cardoso, R.T.; Martins, F.V. Multi-attribute decision making applied to financial portfolio optimization problem. Expert Syst. Appl. 2020, 158, 113527. [Google Scholar] [CrossRef]
- Fernández, E.; Figueira, J.R.; Navarro, J. An interval extension of the outranking approach and its application to multiple-criteria ordinal classification. Omega 2019, 84, 189–198. [Google Scholar] [CrossRef]
- Sunaga, T. Theory of an Interval Algebra and Its Applications to Numerical Analysis. RAAG Memoirs 1958, 2, 29–46. [Google Scholar] [CrossRef]
- Moore, R.E. Interval Arithmetic And Automatic Error Analysis in Digital Computing; Stanford University: Stanford, CA, USA, 1963. [Google Scholar]
- Hui, E.C.; Chan, K.K.K. Alternative trading strategies to beat “buy-and-hold”. Phys. A Stat. Mech. Its Appl. 2019, 534, 120800. [Google Scholar] [CrossRef]
- Hui, E.C.; Chan, K.K.K. A new time-dependent trading strategy for securitized real estate and equity indices. Int. J. Strateg. Prop. Manag. 2018, 22, 64–79. [Google Scholar] [CrossRef]
- Allen, D.E.; Powell, R.J.; Singh, A.K. Chapter 32—Machine Learning and Short Positions in Stock Trading Strategies. In Handbook of Short Selling; Gregoriou, G.N., Ed.; Academic Press: San Diego, CA, USA, 2012; pp. 467–478. [Google Scholar] [CrossRef]
- Baumann, M.H.; Grüne, L. Simultaneously long-short trading in discrete and continuous time. Syst. Control. Lett. 2017, 99, 85–89. [Google Scholar] [CrossRef][Green Version]
- Primbs, J.A.; Barmish, B.R. On Robustness of Simultaneous Long-Short Stock Trading Control with Time-Varying Price Dynamics. IFAC-PapersOnLine 2017, 50, 12267–12272. [Google Scholar] [CrossRef]
- O’Brien, J.D.; Burke, M.E.; Burke, K. A Generalized Framework for Simultaneous Long-Short Feedback Trading. IEEE Trans. Autom. Control. 2021, 66, 2652–2663. [Google Scholar] [CrossRef]
- Deshpande, A.; Gubner, J.A.; Barmish, B.R. On Simultaneous Long-Short Stock Trading Controllers with Cross-Coupling. IFAC PapersOnLine 2020, 53, 16989–16995. [Google Scholar] [CrossRef]
- Fu, X.; Du, J.; Guo, Y.; Liu, M.; Dong, T.; Duan, X. A machine learning framework for stock selection. arXiv 2018, arXiv:1806.01743. [Google Scholar]
- Zhang, R.; Lin, Z.; Chen, S.; Lin, Z.; Liang, X. Multi-factor Stock Selection Model Based on Kernel Support Vector Machine. J. Math. Res 2018, 10, 9. [Google Scholar] [CrossRef]
- Becker, Y.L.; Fei, P.; Lester, A.M. Stock selection: An innovative application of genetic programming methodology. In Genetic Programming Theory and Practice IV; Springer: Berlin, Germany, 2007; pp. 315–334. [Google Scholar]
- Levin, A. Stock selection via nonlinear multi-factor models. Adv. Neural Inf. Process. Syst. 1995, 8, 966–972. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Sengupta, A.; Pal, T.K. On comparing interval numbers. Eur. J. Oper. Res. 2000, 127, 28–43. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Tanaka, H. Multiobjective programming in optimization of the interval objective function. Eur. J. Oper. Res. 1990, 48, 219–225. [Google Scholar] [CrossRef]
- Shi, J.R.; Liu, S.Y.; Xiong, W.T. A new solution for interval number linear programming. Syst. Eng.-Theory Pract. 2005, 2, 16. [Google Scholar]
- Solares, E.; Fernandez, E.; Navarro, J. A generalization of the outranking approach by incorporating uncertainty as interval numbers. Investig. Oper. 2019, 39, 501–514. [Google Scholar]
- Li, G.-D.; Yamaguchi, D.; Nagai, M. A grey-based decision-making approach to the supplier selection problem. Math. Comput. Model. 2007, 46, 573–581. [Google Scholar] [CrossRef]
- Bhattacharyya, R. A grey theory based multiple attribute approach for r&d project portfolio selection. Fuzzy Inf. Eng. 2015, 7, 211–225. [Google Scholar]
- Fernández, E.; Navarro, J.; Solares, E. A hierarchical interval outranking approach with interacting criteria. Eur. J. Oper. Res. 2022, 298, 293–307. [Google Scholar] [CrossRef]
- Ivkovic, N.; Jakobovic, D.; Golub, M. Measuring Performance of Optimization Algorithms in Evolutionary Computation. Int. J. Mach. Learn. Comput. 2016, 6, 167–171. [Google Scholar] [CrossRef]
- McKenna, B. Why NVIDIA Stock Plunged 31% in 2018; Motley Fool: Alexandria, VA, USA, 2019. [Google Scholar]
- Li, X.; Xie, H.; Chen, L.; Wang, J.; Deng, X. News impact on stock price return via sentiment analysis. Knowl.-Based Syst. 2014, 69, 14–23. [Google Scholar] [CrossRef]
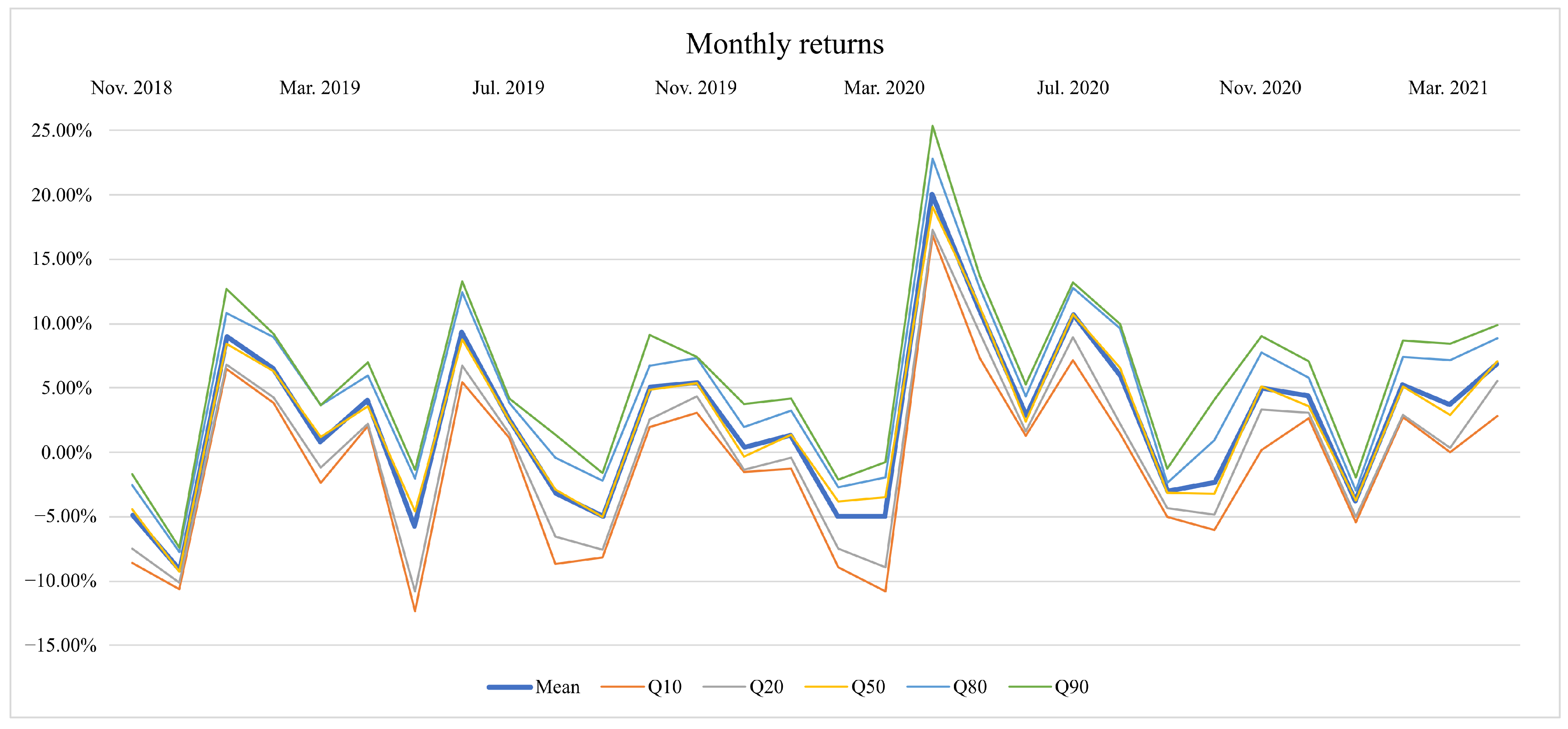
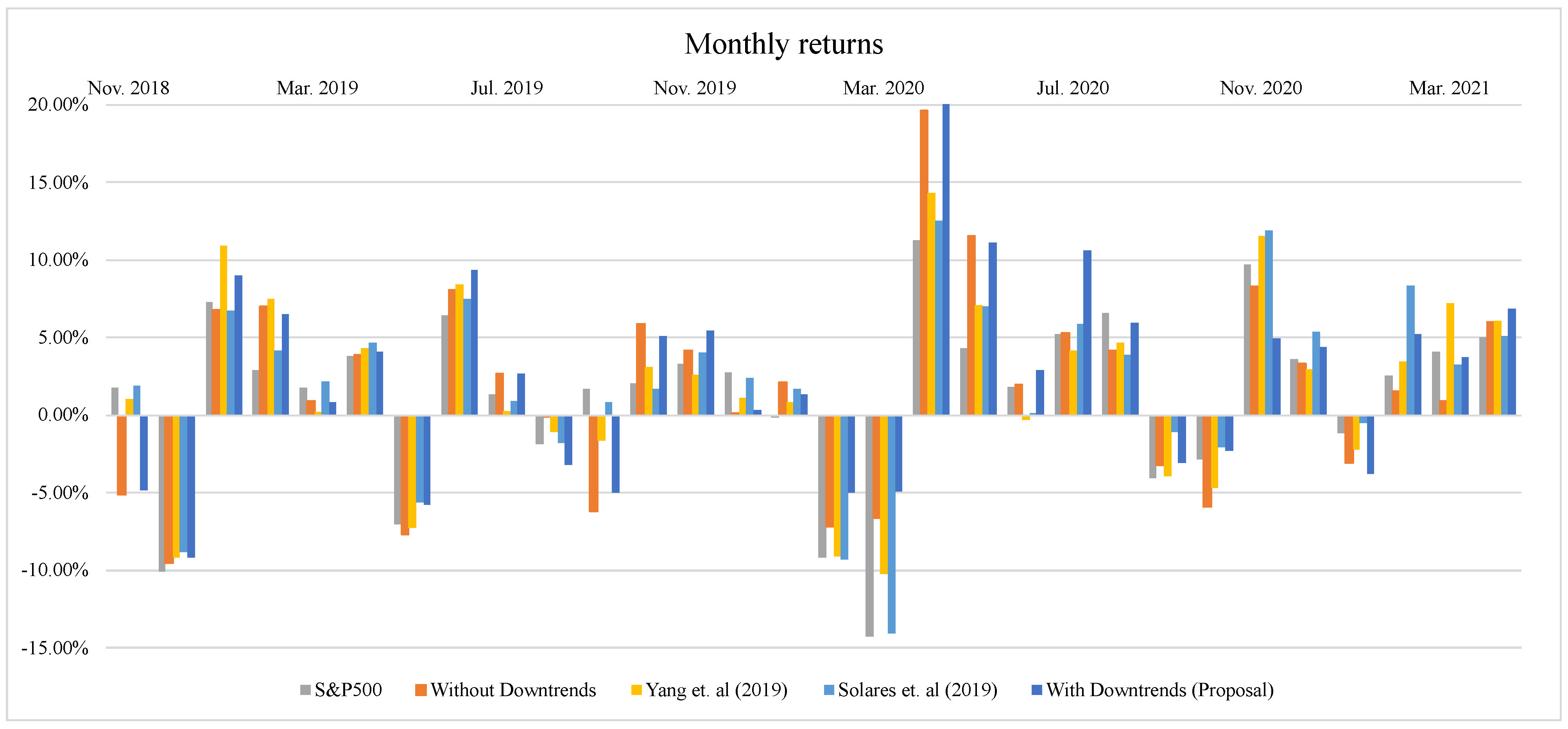
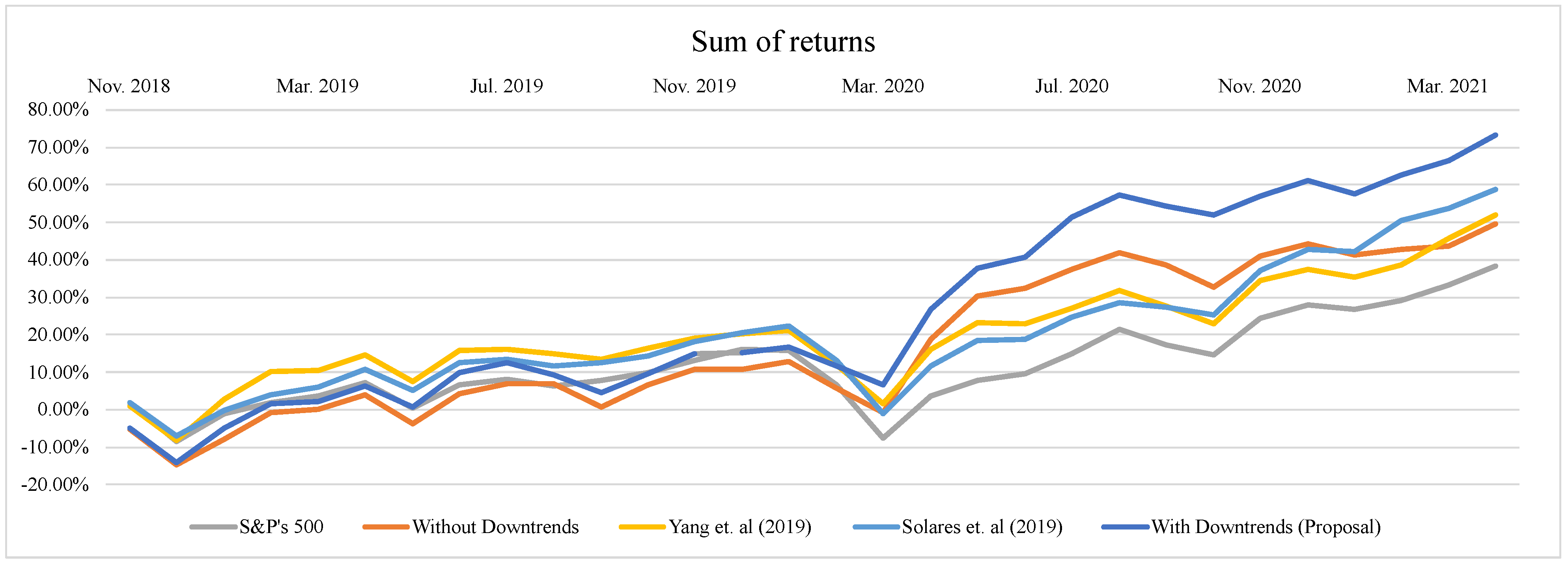
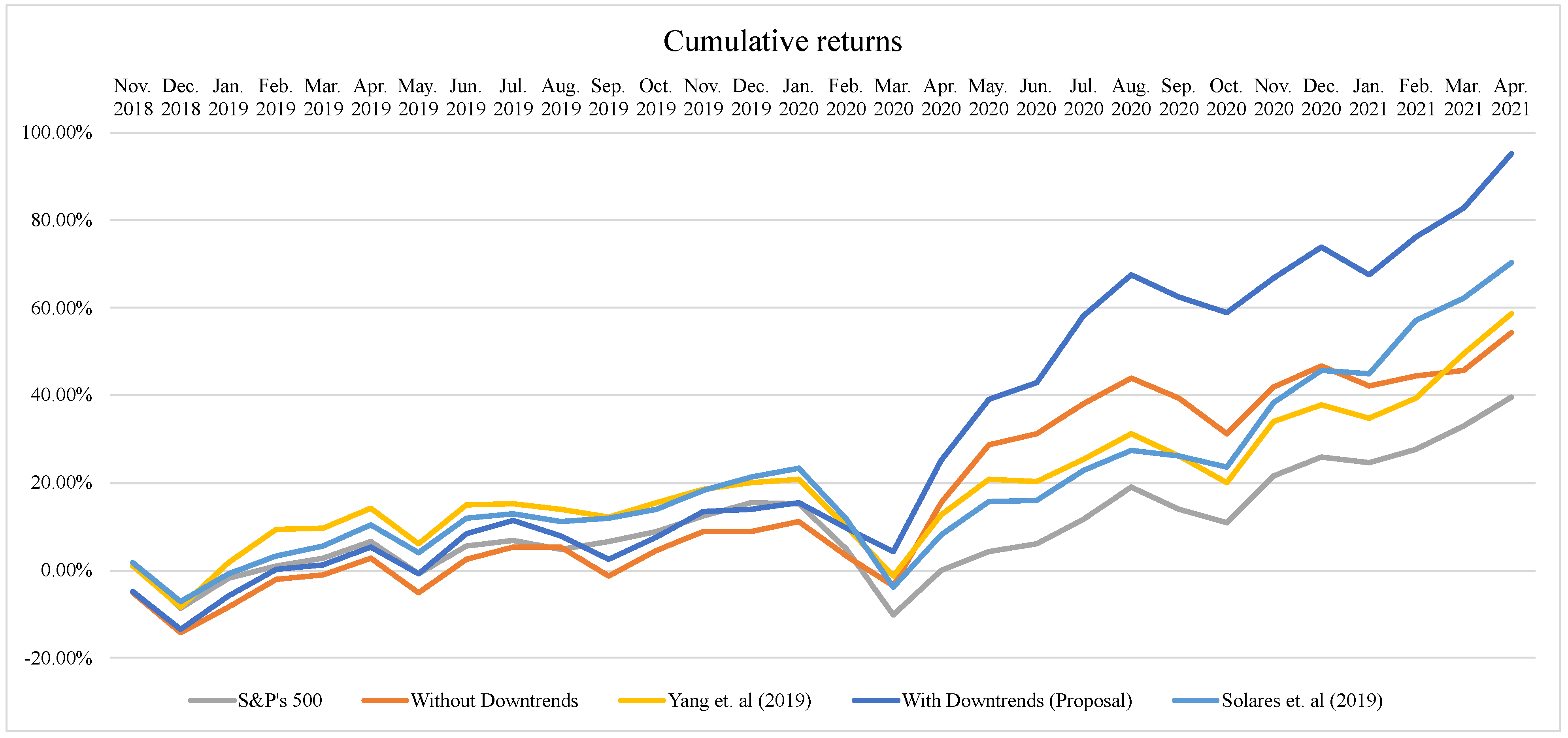
| S&P500 Index | Yang et al. (2019) | Solares et al. (2019) | Without Negative Trends | With Negative Trends | |
|---|---|---|---|---|---|
| Nov. 2018 | 1.75% | 1.01% | 1.87% | −5.11% | −4.87% |
| Dec. 2018 | −10.11% | −9.18% | −8.81% | −9.56% | −9.14% |
| Jan. 2019 | 7.29% | 10.88% | 6.71% | 6.77% | 9.00% |
| Feb. 2019 | 2.89% | 7.47% | 4.19% | 7.00% | 6.52% |
| Mar. 2019 | 1.76% | 0.20% | 2.17% | 0.89% | 0.81% |
| Apr. 2019 | 3.78% | 4.29% | 4.65% | 3.88% | 4.06% |
| May. 2019 | −7.04% | −7.22% | −5.65% | −7.66% | −5.77% |
| Jun. 2019 | 6.45% | 8.45% | 7.53% | 8.06% | 9.33% |
| Jul. 2019 | 1.30% | 0.25% | 0.92% | 2.66% | 2.64% |
| Aug. 2019 | −1.84% | −1.08% | −1.78% | −0.03% | −3.19% |
| Sep. 2019 | 1.69% | −1.63% | 0.83% | −6.20% | −4.96% |
| Oct. 2019 | 2.00% | 3.12% | 1.67% | 5.85% | 5.09% |
| Nov. 2019 | 3.29% | 2.58% | 4.00% | 4.17% | 5.43% |
| Dec. 2019 | 2.78% | 1.13% | 2.39% | 0.13% | 0.36% |
| Jan. 2020 | −0.16% | 0.81% | 1.67% | 2.13% | 1.29% |
| Feb. 2020 | −9.18% | −9.09% | −9.28% | −7.22% | −4.96% |
| Mar. 2020 | −14.30% | −10.27% | −14.03% | −6.59% | −4.94% |
| Apr. 2020 | 11.26% | 14.33% | 12.53% | 19.64% | 20.02% |
| May. 2020 | 4.33% | 7.09% | 7.02% | 11.54% | 11.11% |
| Jun. 2020 | 1.81% | −0.29% | 0.15% | 1.95% | 2.88% |
| Jul. 2020 | 5.22% | 4.18% | 5.87% | 5.28% | 10.65% |
| Aug. 2020 | 6.55% | 4.68% | 3.90% | 4.18% | 5.94% |
| Sep. 2020 | −4.08% | −3.95% | −1.10% | −3.20% | −3.04% |
| Oct. 2020 | −2.85% | −4.74% | −2.05% | −5.88% | −2.31% |
| Nov. 2020 | 9.71% | 11.50% | 11.91% | 8.28% | 4.97% |
| Dec. 2020 | 3.58% | 2.95% | 5.39% | 3.33% | 4.37% |
| Jan. 2021 | −1.13% | −2.23% | −0.53% | −3.06% | −3.76% |
| Feb. 2021 | 2.54% | 3.43% | 8.35% | 1.51% | 5.23% |
| Mar. 2021 | 4.07% | 7.22% | 3.23% | 0.88% | 3.75% |
| Apr. 2021 | 4.98% | 6.05% | 5.09% | 6.00% | 6.84% |
| Average | 1.28% | 1.73% | 1.96% | 1.65% | 2.45% |
| Std desv. | 5.61% | 6.06% | 5.76% | 6.35% | 6.27% |
| Sum of Returns | Cumulative Returns | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S&P500 Index | Yang et al. (2019) | Solares et al. (2019) | Without Down- Trends | With Down- Trends | S&P500 Index | Yang et al. (2019) | Solares et al. (2019) | Without Down- Trends | With Down- Trends | |
| Nov. 2018 | 1.75% | 1.01% | 1.87% | −5.11% | −4.87% | 1.75% | 1.01% | 1.87% | −5.11% | −4.87% |
| Dec. 2018 | −8.35% | −8.17% | −6.94% | −14.67% | −14.01% | −8.53% | −8.27% | −7.11% | −14.18% | −13.56% |
| Jan. 2019 | −1.06% | 2.70% | −0.24% | −7.89% | −5.01% | −1.86% | 1.71% | −0.88% | −8.37% | −5.79% |
| Feb. 2019 | 1.83% | 10.17% | 3.95% | −0.89% | 1.51% | 0.98% | 9.31% | 3.28% | −1.95% | 0.36% |
| Mar. 2019 | 3.59% | 10.37% | 6.12% | 0.00% | 2.32% | 2.76% | 9.53% | 5.52% | −1.08% | 1.17% |
| Apr. 2019 | 7.37% | 14.66% | 10.77% | 3.88% | 6.38% | 6.64% | 14.23% | 10.42% | 2.76% | 5.28% |
| May. 2019 | 0.33% | 7.44% | 5.12% | −3.78% | 0.61% | −0.87% | 5.98% | 4.18% | −5.11% | −0.80% |
| Jun. 2019 | 6.78% | 15.89% | 12.65% | 4.28% | 9.94% | 5.53% | 14.93% | 12.03% | 2.54% | 8.46% |
| Jul. 2019 | 8.08% | 16.14% | 13.58% | 6.94% | 12.58% | 6.89% | 15.22% | 13.07% | 5.27% | 11.32% |
| Aug. 2019 | 6.24% | 15.06% | 11.80% | 6.91% | 9.39% | 4.93% | 13.97% | 11.05% | 5.23% | 7.77% |
| Sep. 2019 | 7.92% | 13.43% | 12.63% | 0.70% | 4.43% | 6.70% | 12.11% | 11.98% | −1.29% | 2.43% |
| Oct. 2019 | 9.93% | 16.54% | 14.30% | 6.56% | 9.52% | 8.83% | 15.61% | 13.85% | 4.48% | 7.64% |
| Nov. 2019 | 13.22% | 19.12% | 18.30% | 10.72% | 14.95% | 12.42% | 18.59% | 18.40% | 8.84% | 13.48% |
| Dec. 2019 | 16.00% | 20.25% | 20.68% | 10.85% | 15.31% | 15.54% | 19.93% | 21.22% | 8.97% | 13.89% |
| Jan. 2020 | 15.84% | 21.06% | 22.36% | 12.98% | 16.60% | 15.35% | 20.90% | 23.25% | 11.30% | 15.36% |
| Feb. 2020 | 6.65% | 11.98% | 13.07% | 5.76% | 11.64% | 4.76% | 9.92% | 11.81% | 3.26% | 9.64% |
| Mar. 2020 | −7.65% | 1.71% | −0.96% | −0.83% | 6.70% | −10.22% | −1.37% | −3.88% | −3.54% | 4.23% |
| Apr. 2020 | 3.61% | 16.04% | 11.57% | 18.81% | 26.73% | −0.12% | 12.77% | 8.16% | 15.40% | 25.10% |
| May. 2020 | 7.94% | 23.13% | 18.58% | 30.36% | 37.84% | 4.21% | 20.76% | 15.75% | 28.72% | 38.99% |
| Jun. 2020 | 9.75% | 22.84% | 18.73% | 32.31% | 40.72% | 6.09% | 20.41% | 15.91% | 31.24% | 43.00% |
| Jul. 2020 | 14.97% | 27.01% | 24.60% | 37.59% | 51.37% | 11.63% | 25.43% | 22.72% | 38.16% | 58.23% |
| Aug. 2020 | 21.52% | 31.69% | 28.51% | 41.77% | 57.31% | 18.94% | 31.30% | 27.51% | 43.94% | 67.63% |
| Sep. 2020 | 17.43% | 27.74% | 27.41% | 38.57% | 54.28% | 14.09% | 26.12% | 26.11% | 39.33% | 62.54% |
| Oct. 2020 | 14.59% | 23.01% | 25.36% | 32.68% | 51.97% | 10.84% | 20.14% | 23.53% | 31.13% | 58.80% |
| Nov. 2020 | 24.30% | 34.51% | 37.27% | 40.97% | 56.94% | 21.60% | 33.97% | 38.24% | 41.99% | 66.69% |
| Dec. 2020 | 27.88% | 37.47% | 42.66% | 44.30% | 61.31% | 25.96% | 37.92% | 45.70% | 46.73% | 73.97% |
| Jan. 2021 | 26.75% | 35.23% | 42.14% | 41.24% | 57.55% | 24.54% | 34.85% | 44.93% | 42.24% | 67.43% |
| Feb. 2021 | 29.29% | 38.66% | 50.48% | 42.75% | 62.78% | 27.70% | 39.47% | 57.03% | 44.39% | 76.18% |
| Mar. 2021 | 33.36% | 45.88% | 53.71% | 43.63% | 66.52% | 32.90% | 49.54% | 62.10% | 45.66% | 82.78% |
| Apr. 2021 | 38.35% | 51.93% | 58.80% | 49.64% | 73.36% | 39.52% | 58.59% | 70.35% | 54.41% | 95.28% |
| Sharpe Ratio | Sortino Ratio | |
|---|---|---|
| S&P’s 500 | 0.1831 | 0.2529 |
| Yang et al. (2019) | 0.2445 | 0.4072 |
| Solares et al. (2019) | 0.2966 | 0.4551 |
| Without downtrends | 0.2213 | 0.3884 |
| With downtrends | 0.3502 | 0.7223 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz, R.; Solares, E.; de-León-Gómez, V.; Salas, F.G. Stock Portfolio Management in the Presence of Downtrends Using Computational Intelligence. Appl. Sci. 2022, 12, 4067. https://doi.org/10.3390/app12084067
Díaz R, Solares E, de-León-Gómez V, Salas FG. Stock Portfolio Management in the Presence of Downtrends Using Computational Intelligence. Applied Sciences. 2022; 12(8):4067. https://doi.org/10.3390/app12084067
Chicago/Turabian StyleDíaz, Raymundo, Efrain Solares, Victor de-León-Gómez, and Francisco G. Salas. 2022. "Stock Portfolio Management in the Presence of Downtrends Using Computational Intelligence" Applied Sciences 12, no. 8: 4067. https://doi.org/10.3390/app12084067
APA StyleDíaz, R., Solares, E., de-León-Gómez, V., & Salas, F. G. (2022). Stock Portfolio Management in the Presence of Downtrends Using Computational Intelligence. Applied Sciences, 12(8), 4067. https://doi.org/10.3390/app12084067






