Abstract
The multi-scale, high-resolution and accurate structural modeling of rocks is a powerful means to reveal the complex failure mechanisms of rocks and evaluate rock engineering safety. Due to the non-uniformity and opacity of rocks, describing their internal microstructure, mesostructure and macro joints accurately, and how to model their progressive fracture process, is a significant challenge. This paper aims to build a numerical method that can take into account real spatial structures of rocks and be applied to the study of crack propagation and failure in different scales of rocks. By combining the failure process analysis (RFPA) simulator with digital image processing technology, large-scale finite element models of multi-scale rocks, considering microstructure, mesostructure, and macro joints, were created to study mechanical and fracture behaviors on a cloud computing platform. The Windows-Linux interactive method was used for digital image processing and parallel computing. The simulation results show that the combination of a parallel RFPA solver and digital image modeling technology can achieve high-resolution structural modeling and high-efficiency calculation. In microscopic simulations, the influence of shale fractures and mineral spatial distribution on the fracture formation process can be revealed. In the mesostructure simulation, it can be seen that the spatial distribution of minerals has an impact on the splitting mode of the Brazilian splitting model. In the simulation of a joined rock mass, the progressive failure process can be effectively simulated. According to the results, it seems that the finite element parallel computing simulation method based on digital images can simulate the multi-scale failure process of brittle materials from micro to macro scales. Primarily, efficient parallel computing based on a cloud platform allows for the multi-scale, high-resolution and realistic modeling and analysis of rock materials.
1. Introduction
The mechanical properties and structural safety of rocks are relevant to many fields, including mining engineering, civil engineering and petroleum engineering. Many accidents occur due to the strength of rocks exceeding their ultimate bearing capacity, and rocks’ instantaneous failure often leads to catastrophic consequences. Due to the heterogeneity and opacity of brittle materials, it is difficult to accurately visualize their internal structure and characterize the fracture process [1,2,3].
Traditional fracture mechanism research mainly focuses on macro-mechanical tests, such as the uniaxial/triaxial compression test [4,5,6,7,8] and indoor fracturing model experiments [9,10,11,12]. However, in these studies, it is impossible to predict or determine which components of the sample will interact with the cracks before testing. Numerical methods have been widely used [13,14] to solve the above problem. However, in most cases, to simplify the numerical calculation, the inhomogeneity of the material is ignored, which will cause a deviation between the simulated crack morphology and the actual crack morphology [15]. Therefore, to consider the influence of heterogeneity in the model, many scholars have adopted different statistical methods to incorporate heterogeneity into the numerical model, and to assign different mechanical properties to the units in the numerical model [16,17,18,19]. For example, heterogeneity was introduced into materialhrough the Weibull statistical model [14].
The above methods are used to characterize the heterogeneity of rock materials; they are random-level models that cannot entirely reflect the actual geometric changes taking place in the microstructures of the materials [20]. Additionally, few documents describe how the virtual structure generated by this method reflects the natural structure of the rocks [21]. The internal microstructure and composition determine the macroscopic mechanical properties of rocks, and the contours of different components determine their macroscopic fracture mechanisms [22]. Therefore, the actual internal structure of rocks should be considered as much as possible in mechanical analysis and fracture research [23].
Reconstructing digital models based on digital images has been applied in fields such as petroleum engineering [15,24]. Previous studies have shown that digital image data, such as mineral and fracture data, can be used to characterize the heterogeneity of materials quantitatively [25]. Digital image processing (DIP) technology can accurately introduce the heterogeneity of materials into numerical models, and depict the physical qualities and microstructures of actual materials more accurately [26,27,28]. These investigations have shown that models that take into account real microscopic heterogeneity may better predict materials’ mechanical behavior and fracture reactions. However, these studies are limited to the establishment and research of two-dimensional (2D) numerical models.
The accuracy and efficiency of numerical simulation research depend on the computing performance of numerical codes. This method has reduced advantages in three-dimensional (3D) numerical research due to the limitations of computational performance. The coarse mesh of the 3D dimensional model fails to characterize the actual structure of rocks, so this method is not widely used in mechanical and fracture behaviors research. For instance, Yu et al. [28] reconstructed a 3D finite element (FE) numerical model of a jointed rock mass based on X-ray microcomputed tomography (micro-CT), and studied its mechanical behavior. The pixel size of the micro-CT image is 30 μm, and the element size of the reconstructed finite element numerical model is 2/3 mm × 2/3 mm × 2/3 mm. The element size of the reconstructed finite element model is about 22 times larger than the pixel size of the original image, which affects the accuracy of the reconstructed finite element model. Ref. [2] used the same method to reconstruct the numerical model of volcanic rock, and studied the failure behavior of volcanic rock through uniaxial compression and Brazilian splitting numerical experiments. The numerical model replicated the pore microstructure of natural volcanic rock. Some mechanical parameters, such as the strength and elastic modulus of the constituent minerals, are not reflected in the numerical simulation because of the limitations of calculation scale and model accuracy. Therefore, it is necessary to develop a more effective method to eliminate these problems, and to improve the 3D numerical model’s calculation scale and efficiency.
In this paper, multi-scale three-dimensional (3D) finite element numerical models characterizing the actual structures of rocks were reconstructed based on digital image processing techniques and high-performance computing methods to study their mechanical behavior and failure processes. First, different scanning techniques were used to obtain digital images characterizing the actual structures of rocks at different scales. Microscale digital images were obtained from FIB-SEM (Focused Ion Beam Scanning Electron Microscopes), mesoscale digital images were obtained via the micro-CT scanning technique, and macro-scale digital images were obtained from a video camera. A numerical code Parallel Rock Failure Process Analysis (RFPA3D) simulator was used to reconstruct multiple-resolution 3D numerical models considering natural structure, such as microscopic shale models, mesoscale models, and CJRM (Columnar jointed rock mass) models, using the digital images. Finally, the numerical models were simulated and analyzed for their failure processes under external loadings.
2. Methodology
2.1. Brief Description of RFPA3D
Through continuum mechanics, RFPA3D is programmed to simulate discontinuous mechanical problems by reducing parameters after element failure. This code reproduces nonlinear deformation characteristics by introducing the heterogeneity of material properties into the model and assuming that the mechanical parameters conform to the distribution statistics (Weibull distribution function, distribution function, or normal distribution function). This paper assumes that the strength and elastic modulus follow the Weibull distribution function [14,19,29,30], as:
where is the mean value of the elements (such as strength or elastic modulus) put into the numerical simulation program, and is the mechanical parameter of the element. In addition, the parameter m describes the shape of the distribution function and reflects the degree of homogeneity of the material; it is called the homogeneity index.
It is initially linearly elastic until the specified damage threshold is reached. This study has calculated the damage thresholds using the maximum tensile strain criterion and the Mohr–Coulomb criterion. As expressed in Equation (2), the maximum tensile strain criterion primarily determines whether a crack has been initiated. The second damage threshold, defined in Equation (3), is the Mohr–Coulomb criterion, which determines whether an element is damaged in the shear mode in the absence of tensile damage.
The maximum tensile strain criterion is:
The Mohr–Coulomb criterion is:
Until the element stress satisfies the above criteria, the elastic modulus remains constant and the same as before loading. According to the strain equivalence assumption, the elastic modulus of an element degrades gradually with damage progress, as follows:
It is characterized by an elastic–brittle damage constitutive relation, with a given residual strength (illustrated in Figure 1). As shown in the negative half of the axis of Figure 1, there are three kinds of elements determined by the damage variable, namely, elastic elements (), damaged elements (), and complete failure elements Under multiaxial stress states, we can express the parameter of an element as [31,32,33]:
where is the equivalent principal strain. It is defined as follows:
where , , and are the three principal strains and is a function defined as follows:
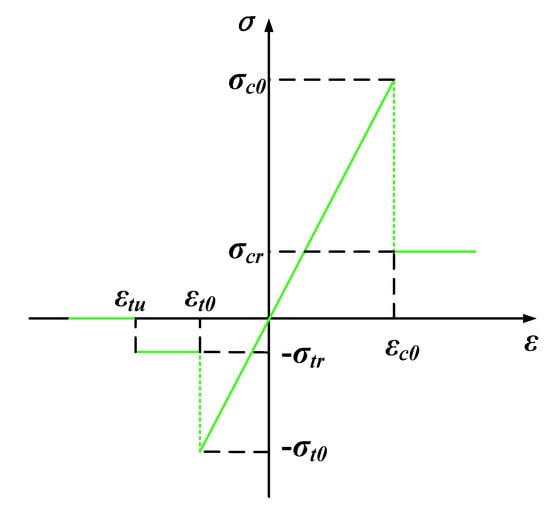
Figure 1.
Elastic–brittle damage constitutive law of elements.
As shown in the positive half of the axis in Figure 1, for a shear mode element under multiaxial stress states, the damage variable can be described as follows [31,32,33]:
According to the constitutive law of elastic damage, the element gradually deteriorates. It is important to emphasize that the finite element analysis will fail if the modulus equals zero. Therefore, the limit of the elastic modulus is specified as a relatively small number, i.e., 10−5.
2.2. Parallelization Strategy
The RFPA3D system consists of pre-processing, elastic stress analysis, failure analysis, and post-processing. The RFPA3D procedures are completed with coordinated processing on an interactive Windows-Linux platform. The linear elastic stress analysis module is implemented on the Linux operating system cluster, and the other modules are completed on the Windows platform. After the data of the Windows platform are prepared, they are completely transferred to the Linux cluster, and the finite element parallel computing program on the Linux cluster is automatically started to complete the parallel computing. After the parallel calculation, it sends the results back to windows to view the results in real-time. A Hybrid OpenMP/MPI (message passing interface) parallel programming model is used to solve the finite element problem [34]. First, the whole domain is separated into local data sets scattered across the domain. A processing node is given to each partition, and MPI is used to communicate between processors and interconnect computing nodes between distributed memories. It is the most time-consuming process in the entire analysis process. It is also the core of the numerical realization, because each loading step requires a stiffness calculation and the resolving of the system equation. Parallelism and coarse-grained domain decomposition can improve the computational scale and speed of the master–slave solution.
This parallel computing structure uses a master–slave programming model, dividing the computational process into several slave processes (see Figure 2). It is a control program that does not participate in calculations, but is responsible for obtaining global machine numbers, initializing data, and processing data before receiving it. The data include unit information, node information, and material properties. According to the domain decomposition algorithm (See Figure 3, where the grid nodes in the I partition are divided into two types: internal nodes and boundary nodes. When solving the physical quantity of the partition boundary node, it is also necessary to exchange information with the adjacent area of the I partition to obtain the information of the node connected to the boundary of the I partition, that is, the information of the external node. The internal nodes and boundary nodes are the nodes to be solved in the I partition. When solving the boundary nodes, the external nodes are auxiliary nodes that provide boundary information), the program automatically decomposes the entire solution region into relatively independent sub-regions, and distributes the sub-region data into the corresponding processors. When the calculation of each slave process is completed, the master process retrieves the results of each sub-region from each slave process. It outputs the results of the entire solution region. Each slave process is a calculation program responsible for completing subtask calculations. Each slave process receives the master process data and individually completes the unit stiffness matrix, the total stiffness matrix synthesis, and the load vector assembly of each sub-region. The sub-region system equations are solved iteratively using the Krylov subspace preconditioner biconjugate gradient stabilized method. It is necessary to exchange data with adjacent sub-regions to update the data during solving. The sub-area solution is completed via the slave process, and the physical quantities of the stress and strain waiting to be solved are output into the master process.
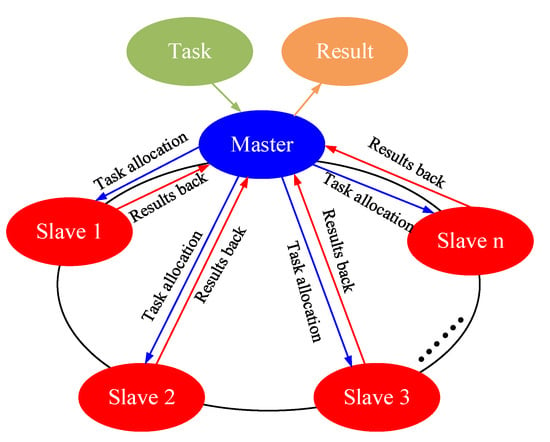
Figure 2.
Flowchart of the parallel FEM solver.
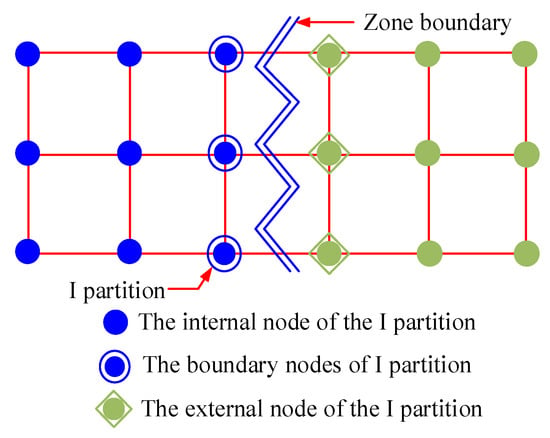
Figure 3.
Example of the partitioning of a finite element grid.
The calculations in this study are completed on the Int Cloud computing platform, which integrates the resources of nearly 20 mainstream cloud service providers and supercomputing centers in China as the infrastructure, which can provide parallel computing for 10,000-core clusters. At present, a single cloud workstation node can provide more than 100 core Xeon platinum processors (Intel Xeon platinum 8260 series, main frequency 3.1 Ghz, L3 cache 36 MB), 8 Tesla V100 computing cards, 40,960 core CUDA (Compute Unified Device Architecture) computing cores, 736 GB memory, 256 GB video memory, 10 Gbps internal network bandwidth and 100 Mbps public network bandwidth for each user. The current comprehensive theoretical calculation peak of the platform exceeds 500 TFlps, and the storage capacity exceeds 100 PB. The underlying server virtualization system is the KVM (Keyboard Video Mouse) architecture. The platform uses the CentOS (Community Enterprise Operating System) system. The user cloud operating system is Windows Server 2016 Datacenter version.
2.3. Three-Dimensional Numerical Model Reconstruction by Digital Image Processing
Using the DIP technology, the actual microstructure of heterogeneous rocks could be precisely extracted from images and incorporated into numerical models. Pixels make up a digital image on a computer. Each pixel consists of the intersection area on either side of horizontal and vertical scan lines of equal width, resulting in a square element with a width of w. Each pixel is represented by three primary colors, namely, red (R), green (G), and blue (B). The reconstruction of 3D numerical samples was divided into four steps based on the digital image. As a first step, we collected high-resolution pictures of the research object, which provided information about its microstructure—numerical models of different scales with different image sources. The shale images at the microscale in Section 3.1 were obtained using Focused Ion Beam Scanning Electron Microscopes technology (Figure 4a). Mesoscale shale images were obtained using the micro-CT scanning technique in Section 3.2. The columnar jointed rock mass image of Section 3.3 was obtained using a video camera [35]. Second, the image vectorization processing used DIP technology to convert the image into vectorized data that could be recognized by numeric codes. In order to construct a 3D model, the extracted digital microstructures were stacked layer by layer in a particular sequence and at specific intervals based on variation within a certain thickness t (Figure 4c,d). The 3D FE meshes were simultaneously established (Figure 4c). A pixel’s size determines the dimensions of the elements, which were all hexahedral quads. The thickness of each element was equal to the distance between layers. That is, the length and width of each element mesh are w, and the height is h. Third, we determined the segmentation threshold to distinguish and segment the constructed 3D microstructure of the finite element model, with microcracks, cracks, voids, and mineral particles. Finally, the DIP method was applied to assign the corresponding mechanical properties to the elements of the components (Figure 4d). In the following section, we describe the third step in detail.
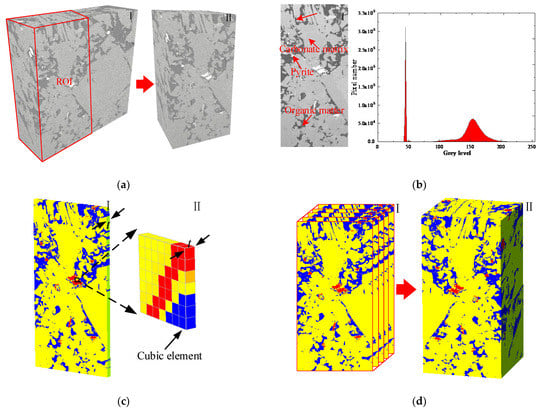
Figure 4.
Reconstruction of 3D numerical models by digital image processing. (a) Getting the picture of the study model. (b) Determination of segmentation threshold. (c) A layer generated with a vertical extension of a slice image (Vectorization). (d) The 3D image stacking and numerical reconstruction model of shale specimens.
In order to accurately characterize the microscopic and macroscopic structures of the models, the image processing methods and segmentation thresholding methods were slightly different for each model. The following briefly introduces the method of determining the segmentation threshold, taking the microscale shale in Section 3.1 as an example. The gray histogram threshold method was adopted to segment microstructural segmentation [2] from the solid matrix to determine the segmentation threshold. Figure 4b shows a microscopic image of the shale and the corresponding grayscale histograms of the I values. I represents the average of R, G, and B, while the X-axis represents the level of grey and the Y-axis represents the pixel count. The gray level is similar in the same material, but there are significant differences among different materials. The peaks reflect this difference in the histogram. Therefore, the different rock components can be classified by identifying the grayscale at the start and end of each peak. That is, the gray value at the location of each trough is the segmentation threshold. After this, we artificially adjusted the repeated segmentation threshold until the derived model could accurately reflect the reality of the microstructural and mineral distribution inside the shale. The final segmentation thresholds of this model are 25, 75, and 225. Here, the I value in the range of 0–25 corresponds to fractures, the I value in the range of 25–75 corresponds to organic matters, the I value in the range of 75–225 corresponds to the carbonate mineral matrix dominated by calcite, and the I value in the range of 225–255 corresponds to pyrite.
3. Multi-Scale Numerical Modeling of Rock Failure Process under Compression
3.1. Microscale Simulation
Shale is a natural composite material composed of various inorganic minerals and organic matter [36,37], and its macro-mechanical behavior depends on its microstructure and mineral composition [2,38]. During the fracturing process, the microstructure of shale will affect fracture propagation and fracture morphology, resulting in more tortuous and complex fractures [12,39]. Therefore, it is vital to study the mechanical properties and crack propagations of shale at the microscale. However, it is difficult to directly or indirectly observe and record the interaction between fractures and different mineral components of shale, and describe the crack propagation path, at the microscopic scale. Understanding of the shale failure mechanism on the microscale is not complete as yet [40]. Numerical experimental methods provide an effective way to solve the above problems. While the heterogeneity index can introduce the heterogeneity of the rock matrix, along with the statistical distribution, it cannot accurately represent the heterogeneity of the actual material [20]. The actual spatial distribution of the microscopic heterogeneity and some mechanical parameters of the mineral composition of the shale should be considered during numerical modeling [2].
3.1.1. Microscale Numerical Model
FIB-SEM has been widely used to characterize shale’s nanoscale structural features [41,42]. Based on the images obtained by FIB-SEM, this section reconstructed an actual 3D multi-mineral component shale numerical model to study the influence of mineral distribution on the shale fracture process at the microscopic scale. In this way, the interaction between cracks and different mineral components can be observed, and the propagation process of cracks at the microscopic scale can be presented. The shale samples in this section were collected from the Yanchang Formation in the Ordos Basin, Gansu, China. The experimental equipment used in this section was the FIB-SEM HELIOS NANOLAB650 from the Research Institute of Petroleum Exploration and Development of China, and the acquisition pixel was about 10 nm.
Figure 4a shows shale sample 3D FIB-SEM images, and the single image resolution is 1500 pixels by 1500 pixels, with a pixel size of 10 nm × 10 nm. The interval of longitudinal cutting was 10 nm for each layer, and 750 layers were cut. Therefore, the size of the 3D FIB-SEM image of the shale sample obtained was about 15 × 15 × 7.5 μm (Figure 4a(I)). In our research, the FIB-SEM image analysis results show that the white particles are pyrite, the light gray minerals are silicate minerals, the dark gray minerals are carbonate minerals, the gray-black minerals are organic matter, and the black is fractures (Figure 4a,b).
The objective of this section (Figure 4a(II)) was to select the region of interest from Figure 4a(I)), the size of which was about 15 × 7.5 × 7.5 μm. In an attempt to increase the calculation speed without affecting the calculation accuracy of the model, when constructing the numerical model, the pixels of the image were reduced five-fold, and one image was taken at intervals (the size of the element is 50 × 50 × 50 nm). The method introduced in Section 2.3 reconstructs the three-dimensional numerical model of shale at the microscopic scale, as shown in Figure 5c,d ((c) front view, (d) back view), represented by the elastic modulus diagram. Comparing Figure 5a,b and Figure 5c,d, it can be found that the reconstructed numerical model (Figure 5c,d) reproduces the real microstructure of the shale well, and the introduction of inhomogeneous coefficients characterizes the inhomogeneity of single minerals more realistically, which makes the reconstructed numerical model more natural and realistic. The total number of finite element elements in the specimen section is 6.75 million. The blue mineral is pyrite, the yellow mineral is the carbonate matrix dominated by calcite, and the red mineral is organic matter.
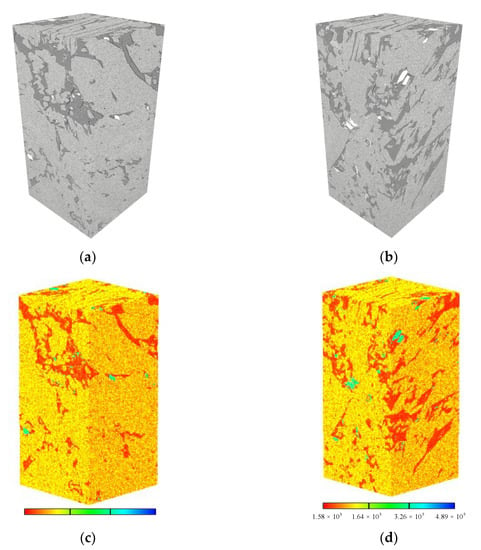
Figure 5.
Shale microscopic model. (a,b) Original FIB-SEM 3D model: (a) is a front view, and (b) is a back view. (c,d) Finite element numerical model, expressed by elastic modulus: (c) is a front view, and (d) is a back view. (  organic matter,
organic matter,  carbonate minerals,
carbonate minerals,  pyrites).
pyrites).
 organic matter,
organic matter,  carbonate minerals,
carbonate minerals,  pyrites).
pyrites).
In contrast, the transparent mineral is fractured, with contents of 1.09, 8.54, 18.18, and 0.19%. The shale numerical specimen was then built using the mechanical input parameters in Table 1 [43,44,45]. The uniaxial compressive simulation was carried out with an external displacement at a constant rate of 2.25 × 10−4 μm/step in the vertical direction.

Table 1.
Material properties of the shale FE model.
3.1.2. Microscale Numerical Modeling Results
The spatial distribution of shale minerals at the microscopic scale affects the crack initiation position, propagation path, and final failure pattern. Despite the small amount of pyrite, cracks tend to begin in the organic matter around pyrite. Pyrite has a decisive effect on where cracks emerge. The crack propagates easily along the organic lamina, and the distribution of the organic lamina also determines the failure pattern. The simulation system can reproduce the typical characteristics of the failure process of microscale multi-mineral rock, and the failure characteristics obtained by the numerical simulation are in reasonable agreement with the physical test results [46].
Figure 6a–f shows the dynamic failure process of microscale organic laminar shale. Referring to the mineral distribution of the sample in Figure 5, it can be seen that at the initial stage of loading (point A), obvious stress concentration occurs at the organic matter lamina and the organic matter around pyrite (Figure 6a). In stages A–B, with the increase in load, the crack first initiates in the organic matter around pyrite (Figure 6b). Before peak point C (including the peak point), there is an obvious displacement discontinuity at the organic lamina (Figure 6c), and a small number of acoustic emission events occur, but there is no obvious macro crack. In stages C–E, with the continuous increase in load, a large number of acoustic emission events are generated, the stress–strain curve decreases in a stepwise pattern, and a small platform appears at point D. The results may be due to the fact that the fracture extension meets the primary fracture, resulting in a sudden increase in strain. In addition, the fracture gradually expands along the organic matter lamina (Figure 6d,e), and the displacement discontinuity gradually increases. Finally, a macro shear plane along the organic matter lamina is formed, and multiple macro cracks are formed along the organic matter lamina. It can be seen that the organic matter lamina plays a decisive role in the final shape of the crack. The macroscopic fracture surface is formed after the peak point, which is also consistent with our general understanding. In E–F, a small number of acoustic emission events occur, the stress–strain curve slowly decreases, and the displacement discontinuity is more pronounced at the main crack (Figure 6f). The strength and modulus of elasticity of the shale were 78.40 MPa and 60,700 MPa, respectively (Figure 6g). Figure 6h depicts the spatial distribution of acoustic emission events in the final damage. A sphere with a specific diameter and color represents an acoustic emission event. The diameter represents the relative magnitude of the released acoustic emission energy. The color represents the type of element failure. Red and blue indicate tensile damage and shear damage, respectively. It can be seen that most of the AE events are caused by tensile damage (red spheres), while only a small number of AE events are caused by sheer damage (blue spheres). Tensile failure is the main cause of rock failure, which is consistent with our general understanding [47]. In addition, through the acoustic emission diagram, we can see that the complex spatial morphology of the main crack and the spatial distribution of the organic matter lamina play decisive roles in the spatial morphology of the crack.
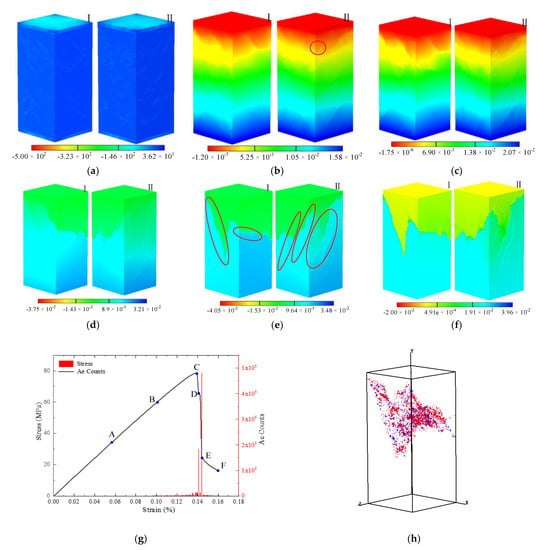
Figure 6.
Numerical simulation of the shale sample at the microscale. (a) Minimum principal stress. (b–f) Vertical displacement contours at different loading stages, (a–f) correspond to points A–F in (g), respectively. (I) front view, and (II) back view. (g) The spatial distribution of acoustic emission (AE) events. (h) The stress–strain curve associated with AE counts for shale. The unit of stress in (a) is the MPa, and the unit of displacement in (b–f) is the millimeter.
Figure 7 shows the internal failure process of six slices under different strain levels, in which dark blue represents the damage element, and black represents the failure element. The positions of the six slices (i.e., Slice#1, Slice#2, Slice#3, Slice#4, Slice#5, and Slice#6) are located at distances of +Z 7.5, 6.0, 4.5, 3.0, 1.5 and 0 μm. Figure 7a–f correspond to points A–F on the stress–strain curve in Figure 6g, respectively. As can be seen, at point A (Figure 7a), all slices have only damage elements in the organic laminar, and no failure elements appear. Note that the black elements shown on the slice at this point are all primary pores and fissures, rather than new ones under the action of external forces. In stages A–D, with the increase in load, the number of damaged elements increases continuously, and they are distributed in three-phase minerals (Figure 7a–d). More failure elements appear in the vicinity of the pre-existing fracture, and new failure elements gradually conjoin the main fracture and the pre-existing fracture (slice#1). In addition, some of the fractures expand along with the pre-existing fractures and gradually form macroscopic cracks (slice#5). Hard mineral grains (pyrite), on the other hand, are susceptible to global failure, influenced by their own mechanical properties and those of the surrounding minerals (slice#4). In stages D–E, as the load continues to increase, the cracks continue to expand, mainly along the narrower organic laminae, forming shear cracks (Figure 7d,e). Nevertheless, the fracture distribution of each slice differs, primarily due to the heterogeneity of mineral distributions, and especially due to the influence of organic matter lamina distributions. In stages E–F, almost no new cracks are generated, and the work done by the external force is mainly used for crack width expansion (Figure 7e,f). In summary, it can be seen that the differences in mineral distribution lead to significant differences in cracks in different slices at the same strain. The spatial distribution of minerals, especially the spatial distribution of organic laminae, greatly influences the fracture process of cracks. This is consistent with the results of the study [22], which indicate that the heterogeneous mineral distribution controls the fracture occurrence and damage pattern of the samples.
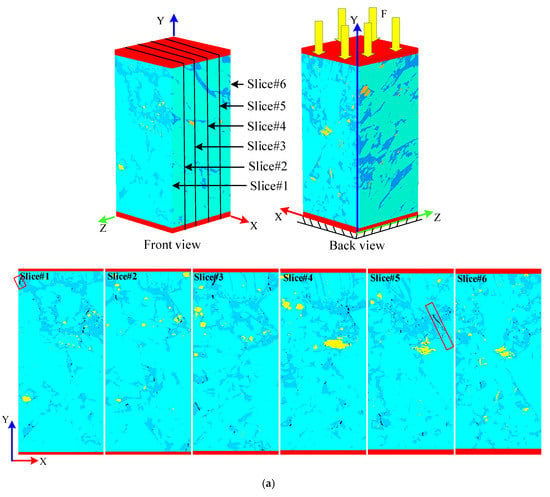
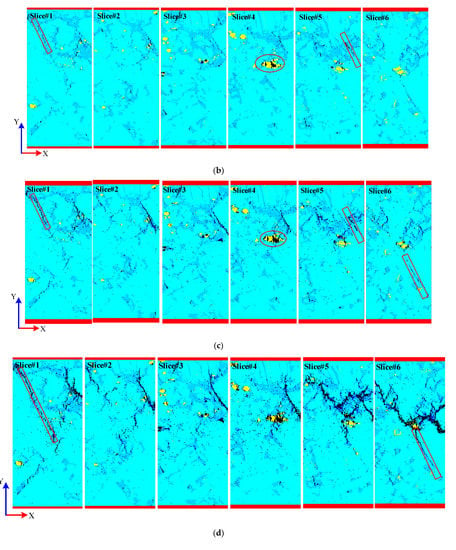
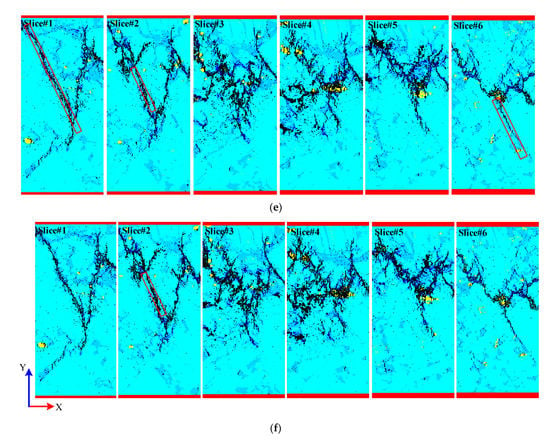
Figure 7.
Internal fracture evolution in micro shale sample sliced along different Z planes. (a–f) The slices at different loading stages, corresponding to points A–F in Figure 6g, respectively. (  organic matter,
organic matter,  carbonate minerals,
carbonate minerals,  pyrites,
pyrites,  damage elements,
damage elements,  fractures).
fractures).
 organic matter,
organic matter,  carbonate minerals,
carbonate minerals,  pyrites,
pyrites,  damage elements,
damage elements,  fractures).
fractures).
3.2. Mesoscale Simulation
Different scales of study objects can lead to significant differences in the spatial structures of identifiable rock materials [48]. Micro-CT can be widely used to characterize the spatial distribution of microstructures such as pores and fractures in shale reservoirs [49]. Therefore, the three-dimensional X-ray scanning of shale specimens can be used to obtain high-resolution three-dimensional images without loss, and effectively characterize the natural three-dimensional spatial structure of shale. In this section, a micro-CT 3D finite element numerical model characterizing the actual structure of shale was developed by combining the micro-CT scanning technique and the RFPA parallel computing method. The dynamic splitting process and mechanical properties of mesoscale shale were studied via a Brazilian splitting experiment.
The samples for the experiments in this section were selected from a shale oil and gas reservoir in a block of Qijiagulong Sag, Songliao Basin, with a burial depth of 2350 m. The sample was machined into a cylinder with a diameter of 4 mm and a height of 10 mm along the laminar direction. The CT scan experiment was completed at the Research Institute of Petroleum Exploration and Development, CNPC, Beijing. The experimental equipment was an Xradia 510 Versa high-resolution 3D X-ray microscope from Carl Zeiss Company, Oberkohen, Germany. The voltage was 80 kV, the single exposure time was 1 s, and the scanning resolution was 4 µm.
3.2.1. Mesoscale Numerical Model
Figure 8 shows the CT images of the shale samples. The resolution of a single CT image is 1000 pixels × 1000 pixels, and the pixel size is about 4 μm × 4 μm (Figure 8b). The scan spacing is about 8 μm, and a total of 1250 layers were scanned. Therefore, the diameter of the original 3D micro-CT cylinder of the shale sample obtained was 4 mm and the height was 10 mm (Figure 8a). In our study, the results of the micro-CT image analysis show that the white mineral grains are calcite-dominated carbonates, the gray minerals are clay minerals, and the dark gray minerals are organic matter. The objective of this section is to select the region of interest from Figure 8a, with a diameter of 4 mm and a thickness of 2 mm. As a result of the need to increase computational speed without compromising the computational accuracy of the model, the pixels were reduced 4-fold when constructing the numerical model, and images were taken once at each interval (16 × 16 × 16 μm), for a total of 125 images. Due to the principle of CT imaging, circular artifacts (images that are bright in the middle and dark around) are inevitable in CT images. Therefore, in order to ensure the authenticity of the model and improve threshold segmentation accuracy, this subsection refers to the improved threshold segmentation method proposed by [50] regarding CT images, and the processing results are shown in Figure 8c. Next, the three-dimensional numerical model of Brazilian shale was reconstructed on the mesoscale based on the method introduced in Section 2.3, as shown in Figure 9 ((a) front view, (b) back view), which is represented by the elastic modulus diagram. By comparing Figure 9 with Figure 8a, we can see that the reconstructed numerical model reproduces the mesostructure of the shale, and that the addition of the inhomogeneity coefficient makes the reconstructed numerical model more natural. There are approximately 7.81 million finite elements in the Brazilian disc model. It consists of organic matter, calcite-based carbonate particles, and clay matrix, at 2.98%, 92.88%, and 4.14%, respectively. The Brazilian disc model exhibits a highly inhomogeneous structure, with X-type organic matter and large calcite-dominated carbonate particles distributed on the front side. However, only a few small grains of calcite-dominated carbonates are distributed on the backside of the model. Afterward, the mechanical input parameters from Table 1 are used to establish the meso shale Brazilian disk numerical sample. In the vertical direction, load is applied at a constant rate of 4.8 × 10−5 mm/step.

Figure 8.
Mesoscale shale CT image. (a) Three-dimensional CT model. (b) Single CT image. (c) CT image after threshold segmentation (  organic matter,
organic matter,  clay minerals,
clay minerals,  carbonate minerals).
carbonate minerals).
 organic matter,
organic matter,  clay minerals,
clay minerals,  carbonate minerals).
carbonate minerals).
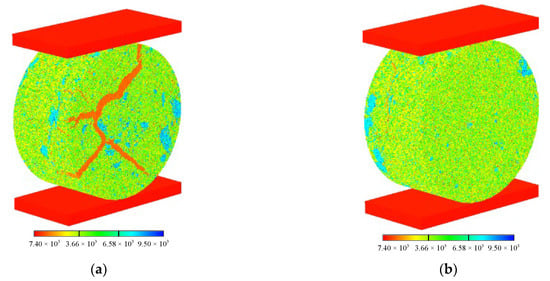
Figure 9.
A three-dimensional numerical model of the Brazilian disc at the mesoscale, expressed by elastic modulus. (a) is the front view, and (b) is the back view (  organic matter,
organic matter,  clay minerals,
clay minerals,  carbonate minerals).
carbonate minerals).
 organic matter,
organic matter,  clay minerals,
clay minerals,  carbonate minerals).
carbonate minerals).
3.2.2. Mesoscale Numerical Modeling Results
The spatial distribution of shale minerals affects the stress state, the location of crack initiation, the expansion path, and the final failure mode of the meso Brazilian disk model. Although the organic matter is only distributed on the front side of the model and the content is only 2.98%, it plays a decisive role in the initiation and expansion of cracks, and the final failure morphology and mechanical behavior.
The dynamic failure process is depicted in Figure 10a–f for the Brazilian disk model of calciteitic shale on the mesoscale. Figure 10a(I) shows that obvious stress concentration occurs in the organic matter at the initial stage of loading; displacement discontinuities are generated as the load increases. Organic matter distribution largely determines the frontal displacement discontinuity of the Brazilian disk, whereas cracks emerge at the frontal displacement discontinuity (Figure 10b). In addition, the back displacement discontinuity is consistent with the splitting experiments of typical Brazilian discs. At point C, the Brazilian disk displacement discontinuity becomes more and more significant. There is a large difference between the displacement discontinuity on the front and the back sides of the Brazilian disk model at point C (Figure 10b). As the load increases in the C–F stages, the cracks continue to grow along with the organic matter of the Brazilian disk, until they eventually form macroscopic cracks. On the back side of the Brazilian disc, no macroscopic cracks are formed. Only a few small cracks form at the intersection of the specimen and the loading plate (Figure 10d–f). Due to the effect of organic matter, the acoustic emission events increase slowly during the numerical experiments, but almost no new acoustic emission events occur after the F point. Likewise, the load–displacement curves show no obvious decrease in brittleness.
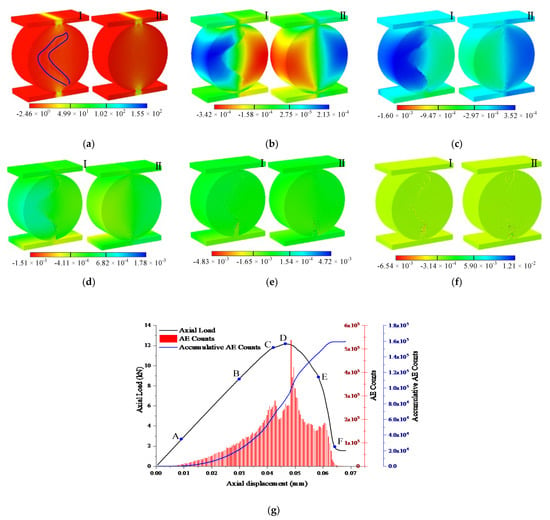
Figure 10.
Numerical simulation of the shale sample at the mesoscale. (a) Maximum principal stress. (b–f) Vertical displacement contours at different loading stages, (a–f) correspond to points A–F in (g), respectively. (I) front view, and (II) back view. (g) The stress–strain curve associated with AE counts for shale. The unit of stress in (a) is the MPa, and the unit of displacement in (b–f) is the millimeter.
Figure 11 shows the internal failure processes of meso Brazilian disk models at different loading stages. Dark blue represents damage elements and black represents failure elements. The six slices (Slice#1, Slice#2, Slice#3, Slice#4, Slice#5, and Slice#6) are located at distances of +Z 2.0, 1.6, 1.2, 0.8, 0.4 and 0 mm. Figure 11a–f correspond to points A–F on the load–displacement curve in Figure 10g, respectively. By observing slice#1 and silce#2, it can be seen that the damage occurs near the center of the Brazilian disc. However, the initial fractures begin on the central axis near the upper and lower loading plates of the Brazilian disk, and continue to expand in the direction of organic matter until they merge into one main fracture. In the lower parts of the Brazilian disc, the fracture no longer propagates along with the organic matter because it is farther away from the central axis, and therefore it turns towards the central axis. The initial stages of loading are not damaged, as can be seen in slices #3–6. In response to the increased external load, some elements are damaged or fail at the central axis, but no macroscopic cracks appear. It is not until after the peak point that cracks are formed near the upper and lower loading plates, respectively. Although the cracks rarely extend, they only remain near the loading plate until the specimen is a mode of completely unstable failure.
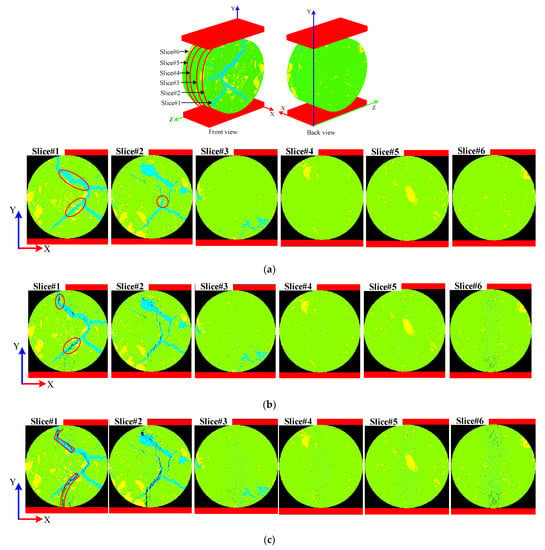
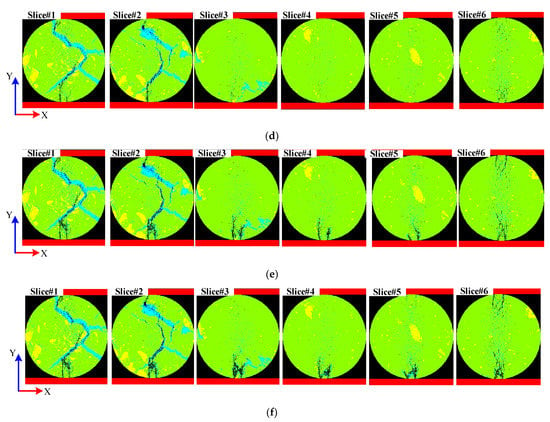
Figure 11.
Internal fracture evolution in a shale meso sample sliced along different Z planes. (a–f) The slices are at different loading stages, corresponding to points A–F in Figure 10g, respectively. (  organic matter,
organic matter,  clay minerals,
clay minerals,  carbonate minerals,
carbonate minerals,  damage elements, fractures).
damage elements, fractures).
 organic matter,
organic matter,  clay minerals,
clay minerals,  carbonate minerals,
carbonate minerals,  damage elements, fractures).
damage elements, fractures).
In summary, differences in mineral distribution at the mesoscale lead to significant differences in cracking in different slices of the Brazilian disc model under the same strain. The inhomogeneous distribution of minerals leads to large differences in the crack distribution in different slices of the disc model. The spatial distribution of minerals greatly affects the fracture process of cracks, especially for minerals with low mechanical properties or minerals with high mechanical properties, which may not be highly present in the model, but play a decisive role in the mechanical behavior, fracture process, and fracture pattern of the model, which is consistent with the findings of [51].
3.3. Macroscale Simulation
It is usually the cooling process of the lava flow that forms the columnar jointed structures in igneous basalt [52]. The lava flow usually cuts the basalt into regular (quadrilateral or pentagonal) or irregular prismatic prisms. Several hydropower stations around the world have the same geologic structure of columnar joints. Previously, the formation mechanism and controlling factors of CJRM have been investigated [53,54,55]. In recent years, the construction and application of many large-scale CJRM projects have led to an increase in the interest of engineering geologists in the mechanical properties of CJRMs. The main techniques used to study the structural characteristics of CJRM are in situ tests, laboratory tests, indoor tests, and numerical simulations [52,56,57]. Those resulting from laboratory tests of small-scale rock mass differ significantly from those obtained under field conditions, so there is no advantage to considering rough columnar joint networks on-site. While large-scale rock masses cannot be conveniently sampled on-site, experimental results are often scattered. The numerical simulation method has advantages when it comes to studying the mechanical properties of a rock mass. The model is often simplified in practice, and it is hard to determine whether the joints are distributed accurately. The CJRM reconstructed according to field conditions is essential to studies of the mechanical behavior of this geological structure.
3.3.1. Macroscale Numerical Model of Columnar Jointed Rock Mass
In this section, combined with geological features of the Baihetan hydropower station and based on the CJRM Window images obtained through the sampling window method, a CJRM reflecting the real structure is constructed. Figure 12a,b is the transverse section information image of the CJRM obtained from the selected window on the right slope of the steep-descent basin of the Baihetan hydropower station [35]. Different colors represent different shapes of column-shaped joints, which cut the basalt into columns. In the columnar block cross-sections, the triangular, quadrangular, pentagonal, and hexagonal polygon frequencies are 39.9%, 45.3%, 9.9%, and 4.9%, respectively. Based on the image in Figure 12b, the finite numerical model of CJRM is constructed according to the method and principle introduced in Section 4, as shown in Figure 12c, which is represented by the elastic modulus diagram. Figure 12d depicts the spatial distribution of joints in the model, and the critical information of the numerical model is consistent with that of the digital image. The size of the model is 2.75 m × 2.75 m × 2.75 m; the number of image pixels in each layer is 275 × 275 (the number of single-layer finite element grids is 75,625). A total of 275 layers of images are copied, so the size of the unit is 1 cm × 1 cm × 1 cm, and the total number of model units is about 20 million. The mechanical parameters are derived from [58], as shown in Table 2. The loading method is displacement loading, and the loading rate is 0.1 mm/step.

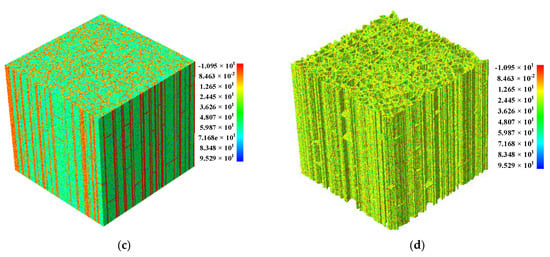
Figure 12.
Configurations of columnar jointed basalt. (a,b) Structural descriptions of columnar jointed basalt in transverse sections [35]. (c) A numerical model for the columnar jointed basalt. (d) The spatial shape of the joints is characterized.

Table 2.
Material properties of the CJRM FE model [58].
3.3.2. Macroscale Numerical Simulation Results
The three-dimensional CJRM reconstructed by digital image processing can actually reflect the spatial distribution of the joints on the engineering site (Figure 12). The spatial distribution of the joints greatly influences the fracture process and the final failure pattern of CJRM. Due to the low strength of the joints, they generate a tensile stress area around the joints in the initial stage of loading (Figure 13), causing the joints to fracture under a relatively small external load. The failure characteristics of the three-dimensional numerical simulation and the in-situ tests are very similar. Most of the failure occurs along the joint planes due to their lower tensile strength. Most longitudinal joints suffer from tensile failure, and the low-angle horizontal joints suffer from compression shear failure (Figure 14). The method proposed provides a useful reference for research into irregular CJRM.
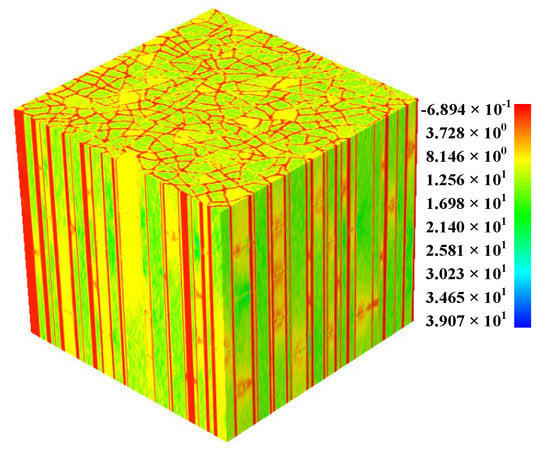
Figure 13.
The maximum principal stress distribution; the unit is MPa.
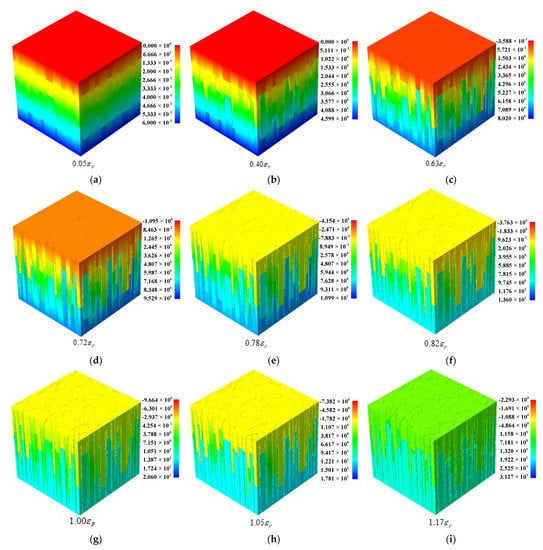
Figure 14.
Numerical uniaxial compression test of columnar jointed basalt at the macroscale. (a–i) Vertical displacement contours at different loading stages, (a–i) correspond to points A–F in Figure 15. The unit of displacement in (a–i) is the millimeter.
The stress–strain curves of CJRM are different from those of intact rock samples, and the brittle characteristics of intact rocks are significantly higher than those of CJRM. The stress–strain curve and the AE count for CJRM are shown in Figure 15. There is a stepwise increase when the curve rises to the DE stage before the peak strength. The strain increases from 0.36% to 0.46% at this stage, an increase of 27.8%. The stress increases from 131.2 MPa to 137.5 MPa, a rise of 4.8%. This may be due to the crushed low-angle horizontal joints and the longitudinal blocks being squeezed. After the peak strength, the stress–strain curve of the complete rock sample under uniaxial compression generally decreases sharply. The stress–strain curve of CJRM decreases gradually, without prominent brittle failure characteristics. It can be seen from the changing trend of AE events that AE events occur at low stress levels, and AE events maintain a relatively stable level before peak point E. Due to the low strength of the joints, the joints fracture at low stress levels, and AE events occur. AE events in the A–D interval are mainly caused by longitudinal joint failure, while AE events in the D–E interval are mainly caused by low-angle horizontal joint failure. After the peak point E, the acoustic emission events are mainly concentrated in the E–F interval, and the fracture of the basalt column leads to a large number of AE events. At this stage, the AE events account for about 50% of the total AE events in the fracture process.
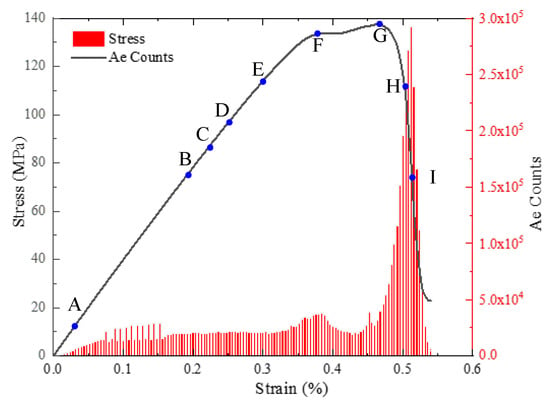
Figure 15.
The stress–strain curve associated with AE counts for CJRM.
The mechanical responses of joints and intact rock vary with the same external displacement (e.g., mismatch stress). Figure 13 shows the maximum principal stress distribution at 0.1 mm displacement. Even under compression, tensile stresses (in red) can be observed in the surroundings of joints. Figure 14 illustrates the vertical displacement field during fracture. Due to the existence of joints when the strain level is 0.40 εP (Figure 14b), there are obvious cracks in the longitudinal joints in the middle of the CJRM. With the increase in external displacement, cracks propagate upward and downward along the direction of longitudinal joints simultaneously, and the color of the vertical displacement field is different (Figure 14b–i). The low-level joint is at the junction of the color change, indicating that the displacement is not continuous. At peak point E, macro cracks are apparent along the joint plane on the surface of the CJRM (Figure 14g). Figure 16 describes the damage evolution process of CJRM. The symbols (i.e., A, B, C, D, E, and F) plotted on the stress–strain curve in Figure 8 indicate the strain levels of 0.05, 0.14, 0.40, 0.83, 1.00 and 1.15 εP. Figure 16a shows the initial damage pattern, with a strain of 0.05 εP. Multiple points of damage co-occur at the longitudinal joint. This shows that the joint strength is low, and the damage occurs at a low-stress level. With the load increase, the number of damage points increases and accumulates in longitudinal joints. Damage points also appear at low and horizontal angles (Figure 16b–e). Finally, multiple macroscopic damage zones are formed.

Figure 16.
Damage evolution in columnar jointed basalt, where the yellow spots represent the damage occurrence and transparent means that the element is completely damaged, (a–f) correspond to points A–F in Figure 15.
Figure 17 compares the damage characteristics of CJRM between the numerical test and the in-situ test. It can be seen from Figure 17a–c that the failure characteristics of the three-dimensional numerical sample are very similar to those of the field test, and the failure mode is also consistent. Figure 17d describes the spatial distribution of AE events when the numerical model finally fails. A sphere with a specific diameter and color represents an acoustic emission event. The diameter represents the relative magnitude of the released acoustic emission energy. The color represents the type of element failure. Red and blue indicate tensile damage and shear damage, respectively. It can be seen that most AE events occur at joint locations. Most AE events at low-angle horizontal joints are caused by compression tensile damage (red sphere), while most AE events at longitudinal joints are caused by shear damage (blue sphere).

Figure 17.
Comparisons of CJRM failure modes between the numerical specimen and the in-situ specimen. (a,b) The fracture mode of the in-situ specimen; (a) is the top view, and (b) is the front view [7]. (c) The fracture mode of the numerical specimen. (d) The spatial distribution of acoustic emission (AE) events.
4. Discussion
The statistical damage mechanical approach has been used to effectively predict rock failure issues [59,60]. Furthermore, it is possible to create realistic numerical rock samples using digital image processing methods. Our study was based on the study of [14,59,60], which considered the non-homogeneity of the structure through digital image techniques, and the non-homogeneity of single minerals through Weibull distributions [50]. That is, the dual inhomogeneity of structure and material is considered simultaneously. Therefore, the multi-scale numerical models we developed were all more realistic in reflecting the spatial rock structure compared with previous studies [34]. Meanwhile, the constructs of the numerical models were integrated into the RFPA3D parallel computing simulator, which simulates with high efficiency the progressive damage process and mechanical property behavior of the high-resolution multi-scale rock models with the help of a cloud computing platform [34]. Consequently, complex, heterogeneous rocks can be modeled successfully with this integration approach.
It is crucial to acquire digital images of rocks at different scales using suitable scanning techniques before constructing numerical models based on digital images of rocks. There are currently a variety of techniques available for obtaining 3D digital images of rocks on the micro-, meso-, and macroscales [41,49,61,62,63]. Even so, the three-dimensional structural characteristics of engineering-scale rocks are often difficult to determine, particularly for rock reservoirs that are deep underground, such as shale oil and gas reservoirs. In future research, we should integrate multiple technologies, including geological exploration, to construct more realistic engineering-scale numerical models, i.e., digital rock masses. Furthermore, although a modeling and simulation study, from digital cores to digital rock masses, was completed in this paper, the microscopic to macroscopic linkage has not been addressed. Therefore, establishing an effective macroscopic linkage is also the focus of our future research.
5. Conclusions
The statistical meso-damage mechanical model has been applied to study the failure of rocks. However, it is difficult for numerical models to characterize the actual sample structure due to the limitations of modeling methods. Additionally, the bottleneck of element number and calculation efficiency limits numerical modeling. The DIP technology in this paper is used to extract the structural characteristics of samples obtained by micro-CT, FIB-SEM, or sample window methods, reconstruct the 3D models, and then combine the models into a 3D numerical model using a vectorizing method. The 3D finite element numerical model was integrated into the RFPA parallel simulator. The finite element parallel computing system based on the digital image was built, which effectively solved the above problems. By incorporating the intrinsic shale geometric features, i.e., the spatial distribution of mineral composition, the 3D numerical simulations can reasonably predict the mechanical and fracture properties of the shale sample. The calculation system can also help us monitor and analyze the stress, strain, and displacement fields of the sample from any angle. This method is superior to some traditional methods, such as acoustic emission monitoring, in-situ CT scanning monitoring, and the 3DP method, which struggle to accurately and quantitatively monitor the initiation and evolution of micro cracks in real-time. Meanwhile, the results show that the finite element numerical models we constructed from the microscopic digital core to the macroscopic digital rock mass can effectively simulate mechanical behavior. In addition, they can reproduce dynamic fracture processes. That is, the numerical simulation system proposed in this paper is a useful tool for simulating the multi-scale rock model failure process. It has significant potential for use in studying the mechanical properties of rocks at multiple scales and high resolutions. The research basis of this paper is the RFPA numerical code, which has been successfully applied to the study of many brittle rock materials. Therefore, the method proposed in this paper can be used to study brittle rock. However, because the essence of this method is based on digital image modeling, the accuracy of the numerical model constructed in this paper is seriously limited by the accuracy of the digital images.
Author Contributions
Conceptualization and methodology, X.L.; investigation, Z.L., S.M., C.T. and J.T.; formal analysis, writing—original draft preparation, X.L.; writing—review and editing, X.L. and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Grant Nos. 52009016, 51779031), National Key R&D Program of China (2018YFE0196000), and China Postdoctoral Science Foundation (2019M663502).
Conflicts of Interest
The authors declare no conflict of interest.
List of Symbols
| Symbol | Property | Unite |
| Damage variable | - | |
| Elastic modulus of the damaged elements | MPa | |
| Mean elastic modulus of element | MPa | |
| Elastic modulus | MPa | |
| Elastic modulus of the undamaged elements | MPa | |
| Mean axial compressive strength of element | MPa | |
| Axial compressive strength | MPa | |
| Ratio of tensile to compressive strength | - | |
| Distribution density | MPa−1 | |
| Homogeneity index | - | |
| Numerical output strength of element | MPa | |
| Material parameters of the element (such as Young’s modulus and strength) obtained from experiments | MPa | |
| The mean value of elements put into the numerical simulation program | MPa | |
| Strain tensor | - | |
| Equivalent principal strain | - | |
| Maximum principal strain | - | |
| Middle principal strain | - | |
| Minimum principal strain | - | |
| Critical strain under peak compressive | - | |
| Ultimate compression strain | - | |
| Threshold strain | - | |
| Ultimate tensile strain | - | |
| Strain under peak compressive strength | - | |
| Ultimate tensile stress factor | - | |
| Poisson ratio | - | |
| Stress tensor | MPa | |
| Maximum principal stress | MPa | |
| Minimum principal stress | MPa | |
| Fracture closure pressure | MPa | |
| Uniaxial compressive strength | MPa | |
| Residual tensile stress | MPa | |
| Residual compressive stress | MPa | |
| Uniaxial tensile strength | MPa | |
| Friction angle | ° | |
| Initial gray value of the pixel (X, Y) | - | |
| Gray value of the pixel (X, Y) after binarization | - | |
| Segmentation threshold | - |
References
- Ju, Y.; Liu, P.; Chen, J.; Yang, Y.; Ranjith, P.G. CDEM-based analysis of the 3D initiation and propagation of hydrofracturing cracks in heterogeneous glutenites. J. Nat. Gas Sci. Eng. 2016, 35, 614–623. [Google Scholar] [CrossRef]
- Zhu, J.B.; Zhou, T.; Liao, Z.Y.; Sun, L.; Li, X.B.; Chen, R. Replication of internal defects and investigation of mechanical and fracture behaviour of rock using 3D printing and 3D numerical methods in combination with X-ray computerized tomography. Int. J. Rock Mech. Min. Sci. 2018, 106, 198–212. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, L.; Xie, H.; Ma, G.; Mao, L.; Zheng, Z.; Lu, J. Visualization of the three-dimensional structure and stress field of aggregated concrete materials through 3D printing and frozen-stress techniques. Constr. Build. Mater. 2017, 143, 121–137. [Google Scholar] [CrossRef]
- Belda, R.; Palomar, M.; Peris-Serra, J.L.; Vercher-Martínez, A.; Giner, E. Compression failure characterization of cancellous bone combining experimental testing, digital image correlation and finite element modeling. Int. J. Mech. Sci. 2020, 165, 105213. [Google Scholar] [CrossRef]
- Amann, F.; Kaiser, P.; Button, E.A. Experimental Study of Brittle Behavior of Clay Shale in Rapid Triaxial Compression. Rock Mech. Rock Eng. 2011, 45, 21–33. [Google Scholar] [CrossRef] [Green Version]
- Daigle, H.; Hayman, N.W.; Kelly, E.D.; Milliken, K.L.; Jiang, H. Fracture capture of organic pores in shales. Geophys. Res. Lett. 2017, 44, 2167–2176. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, C.; Zhou, H.; Hou, J.; Su, G.; Gao, Y.; Liu, N.; Singh, H.K. Mechanical behavior of structurally reconstructed irregular columnar jointed rock mass using 3D printing. Eng. Geol. 2020, 268, 105509. [Google Scholar] [CrossRef]
- Yang, B.; Xue, L.; Zhang, K. X-ray micro-computed tomography study of the propagation of cracks in shale during uniaxial compression. Environ. Earth Sci. 2018, 77, 652. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, M.; Jin, Y.; Zhang, G.-Q. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2008, 45, 1143–1152. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, S.; Qu, Z.; Zhou, T.; Xiao, Y.; Gao, J. Experimental study of hydraulic fracturing for shale by stimulated reservoir volume. Fuel 2014, 128, 373–380. [Google Scholar] [CrossRef]
- Tang, J.; Li, J.; Tang, M.; Du, X.; Yin, J.; Guo, X.; Wu, K.; Xiao, L. Investigation of multiple hydraulic fractures evolution and well performance in lacustrine shale oil reservoirs considering stress heterogeneity. Eng. Fract. Mech. 2019, 218, 218. [Google Scholar] [CrossRef]
- Peng, T.; Yan, J.; Bing, H.; Yingcao, Z.; Ruxin, Z.; Zhi, C.; Meng, F. Laboratory investigation of shale rock to identify fracture propagation in vertical direction to bedding. J. Geophys. Eng. 2018, 15, 696–706. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.Y.; Pater, C.J.D. Numerical implementation of displacement discontinuity method and its application in hydraulic fracturing. Comput. Methods Appl. Mech. Eng. 2001, 191, 745–760. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Xing, H.; Wang, S.Y.; Williams, D.J.; Tang, C.A. A three-dimensional numerical investigation of the fracture of rock specimens containing a pre-existing surface flaw. Comput. Geotech. 2012, 45, 19–33. [Google Scholar] [CrossRef]
- Li, Z.; Li, L.; Huang, B.; Zhang, L.; Li, M.; Zuo, J.; Li, A.; Yu, Q. Numerical investigation on the propagation behavior of hydraulic fractures in shale reservoir based on the DIP technique. J. Pet. Sci. Eng. 2017, 154, 302–314. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J. Development of a local degradation approach to the modelling of brittle fracture in heterogeneous rocks. Int. J. Rock Mech. Min. Sci. 2002, 39, 443–457. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Fatahi, H.; Hossain, M.; Fallahzadeh, S.H.; Mostofi, M. Numerical simulation for the determination of hydraulic fracture initiation and breakdown pressure using distinct element method. J. Nat. Gas Sci. Eng. 2016, 33, 1219–1232. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.A.; Xu, T.; Yang, T.H.; Liang, Z.Z. Numerical investigation of the mechanical behavior of rock under confining pressure and pore pressure. Int. J. Rock Mech. Min. Sci. 2004, 41, 336–341. [Google Scholar] [CrossRef]
- Yue, Z.Q.; Chen, S.; Tham, L.G. Finite element modeling of geomaterials using digital image processing. Comput. Geotech. 2003, 30, 375–397. [Google Scholar] [CrossRef]
- Li, Q.; Xing, H.; Liu, J.; Liu, X. A review on hydraulic fracturing of unconventional reservoir. Petroleum 2015, 1, 8–15. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Yue, Z.Q.; Tham, L.G. Digital Image Based Approach for Three-Dimensional Mechanical Analysis of Heterogeneous Rocks. Rock Mech. Rock Eng. 2006, 40, 145–168. [Google Scholar] [CrossRef]
- Zhu, W.C.; Liu, J.H.; Yang, T.C.; Sheng, J.; Elsworth, D. Effects of local rock heterogeneities on the hydromechanics of fractured rocks using a digital-image-based technique. Int. J. Rock Mech. Min. Sci. 2006, 43, 1182–1199. [Google Scholar] [CrossRef]
- Hambli, R. Micro-CT finite element model and experimental validation of trabecular bone damage and fracture. Bone 2013, 56, 363–374. [Google Scholar] [CrossRef] [PubMed]
- Ruggieri, S.; Cardellicchio, A.; Leggieri, V.; Uva, G. Machine-learning based vulnerability analysis of existing buildings. Autom. Constr. 2021, 132, 103936. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Randall, N.X.; Zong, Z.; Grasselli, G. A novel approach for micro-scale characterization and modeling of geomaterials incorporating actual material heterogeneity. Geophys. Res. Lett. 2012, 39, L01303. [Google Scholar] [CrossRef]
- Wu, M.Y.; Zhang, D.M.; Wang, W.S.; Li, M.H.; Liu, S.M.; Lu, J.; Gao, H. Numerical simulation of hydraulic fracturing based on two-dimensional surface fracture morphology reconstruction and combined finite-discrete element method. J. Nat. Gas Sci. Eng. 2020, 82, 103479. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, S.; Ranjith, P.G.; Zhu, W.; Yang, T. Numerical Modeling of Jointed Rock Under Compressive Loading Using X-ray Computerized Tomography. Rock Mech. Rock Eng. 2016, 49, 877–891. [Google Scholar] [CrossRef]
- Tang, C.A.; Webb, A.A.G.; Moore, W.B.; Wang, Y.Y.; Ma, T.H.; Chen, T.T. Breaking Earth’s shell into a global plate network. Nat. Commun. 2020, 11, 3621. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sloan, S.W.; Tang, C.A. Three-Dimensional Numerical Investigations of the Failure Mechanism of a Rock Disc with a Central or Eccentric Hole. Rock Mech. Rock Eng. 2013, 47, 2117–2137. [Google Scholar] [CrossRef]
- Li, T.; Li, L.; Tang, C.; Zhang, Z.; Li, M.; Zhang, L.; Li, A. A coupled hydraulic-mechanical-damage geotechnical model for simulation of fracture propagation in geological media during hydraulic fracturing. J. Pet. Sci. Eng. 2019, 173, 1390–1416. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, N.; Li, Y.; Li, H.; Li, W. Numerical Study on Anisotropy of the Representative Elementary Volume of Strength and Deformability of Jointed Rock Masses. Rock Mech. Rock Eng. 2019, 52, 4387–4402. [Google Scholar] [CrossRef]
- Wu, N.; Liang, Z.-Z.; Li, Y.-C.; Li, H.; Li, W.-R.; Zhang, M.-L. Stress-dependent anisotropy index of strength and deformability of jointed rock mass: Insights from a numerical study. Bull. Eng. Geol. Environ. 2019, 78, 5905–5917. [Google Scholar] [CrossRef]
- Li, G.; Tang, C.-A.; Liang, Z.-Z. Development of a parallel FE simulator for modeling the whole trans-scale failure process of rock from meso- to engineering-scale. Comput. Geosci. 2017, 98, 73–86. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, C.; Zhou, H.; Chen, J.; Gao, Y.; Liu, N.; Chen, P. Structural characteristics of columnar jointed basalt in drainage tunnel of Baihetan hydropower station and its influence on the behavior of P-wave anisotropy. Eng. Geol. 2020, 264, 105304. [Google Scholar] [CrossRef]
- Wang, G.; Carr, T.R. Methodology of organic-rich shale lithofacies identification and prediction: A case study from Marcellus Shale in the Appalachian basin. Comput. Geosci. 2012, 49, 151–163. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, Y.; Wang, H.; Liu, H.; Wei, W.; Fang, J. Shale gas reservoir characterisation: A typical case in the southern Sichuan Basin of China. Energy 2011, 36, 6609–6616. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 2: Ductile creep, brittle strength, and their relation to the elastic modulus. Geophysics 2013, 78, D393–D402. [Google Scholar] [CrossRef]
- Ouchi, H.; Agrawal, S.; Foster, J.T.; Sharma, M.M. Effect of Small Scale Heterogeneity on the Growth of Hydraulic Fractures. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017. [Google Scholar]
- Zhao, J.; Zhang, D. Dynamic microscale crack propagation in shale. Eng. Fract. Mech. 2020, 228, 106906. [Google Scholar] [CrossRef]
- Tang, X.; Jiang, Z.; Jiang, S.; Li, Z. Heterogeneous nanoporosity of the Silurian Longmaxi Formation shale gas reservoir in the Sichuan Basin using the QEMSCAN, FIB-SEM, and nano-CT methods. Mar. Pet. Geol. 2016, 78, 99–109. [Google Scholar] [CrossRef]
- Gu, X.; Cole, D.R.; Rother, G.; Mildner, D.F.R.; Brantley, S.L. Pores in Marcellus Shale: A Neutron Scattering and FIB-SEM Study. Energy Fuels 2015, 29, 1295–1308. [Google Scholar] [CrossRef]
- Kumar, V.; Sondergeld, C.; Rai, C.S. Effect of mineralogy and organic matter on mechanical properties of shale. Interpretation 2015, 3, SV9–SV15. [Google Scholar] [CrossRef]
- Veytskin, Y.B.; Tammina, V.K.; Bobko, C.P.; Hartley, P.G.; Clennell, M.B.; Dewhurst, D.N.; Dagastine, R.R. Micromechanical characterization of shales through nanoindentation and energy dispersive x-ray spectrometry. Géoméch. Energy Environ. 2017, 9, 21–35. [Google Scholar] [CrossRef]
- Li, C.; Ostadhassan, M.; Kong, L.; Bubach, B. Multi-scale assessment of mechanical properties of organic-rich shales: A coupled nanoindentation, deconvolution analysis, and homogenization method. J. Pet. Sci. Eng. 2019, 174, 80–91. [Google Scholar] [CrossRef]
- Voltolini, M.; Ajo-Franklin, J. Evolution of propped fractures in shales: The microscale controlling factors as revealed by in situ X-Ray microtomography. J. Pet. Sci. Eng. 2020, 188, 106861. [Google Scholar] [CrossRef]
- Healy, D.; Jones, R.R.; Holdsworth, R.E. Three-dimensional brittle shear fracturing by tensile crack interaction. Nature 2006, 439, 64–67. [Google Scholar] [CrossRef]
- Gou, Q.; Xu, S.; Hao, F.; Yang, F.; Zhang, B.; Shu, Z.; Zhang, A.; Wang, Y.; Lu, Y.; Cheng, X.; et al. Full-scale pores and micro-fractures characterization using FE-SEM, gas adsorption, nano-CT and micro-CT: A case study of the Silurian Longmaxi Formation shale in the Fuling area, Sichuan Basin, China. Fuel 2019, 253, 167–179. [Google Scholar] [CrossRef]
- Ma, Y.; Pan, Z.; Zhong, N.; Connell, L.D.; Down, D.I.; Lin, W.; Zhang, Y. Experimental study of anisotropic gas permeability and its relationship with fracture structure of Longmaxi Shales, Sichuan Basin, China. Fuel 2016, 180, 106–115. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, H.; Yang, T.; Liu, H. 3D numerical study on fracture process of concrete with different ITZ properties using X-ray computerized tomography. Int. J. Solids Struct. 2018, 147, 204–222. [Google Scholar] [CrossRef]
- Xu, H.; Wang, G.; Fan, C.; Liu, X.; Wu, M. Grain-scale reconstruction and simulation of coal mechanical deformation and failure behaviors using combined SEM Digital Rock data and DEM simulator. Powder Technol. 2020, 360, 1305–1320. [Google Scholar] [CrossRef]
- Goehring, L. On the Scaling and Ordering of Columnar Joints; University of Toronto: Toronto, ON, Canada, 2008. [Google Scholar]
- Goehring, L.; Morris, S.W. Order and disorder in columnar joints. Eur. Lett. 2005, 69, 739–745. [Google Scholar] [CrossRef]
- Chavdarian, G.V.; Sumner, D.Y. Origin and evolution of polygonal cracks in hydrous sulphate sands, White Sands National Monument, New Mexico. Sedimentology 2011, 58, 407–423. [Google Scholar] [CrossRef]
- Hetényi, G.; Taisne, B.; Garel, F.; Médard, É.; Bosshard, S.; Mattsson, H.B. Scales of columnar jointing in igneous rocks: Field measurements and controlling factors. Bull. Volcanol. 2011, 74, 457–482. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, W.; Wang, H.; Zhang, J.; Wei, W.; Wang, R.; Ji, H. Anisotropic characteristic of irregular columnar-jointed rock mass based on physical model test. KSCE J. Civ. Eng. 2017, 21, 1728–1734. [Google Scholar] [CrossRef]
- Jin, C.; Yang, C.; Fang, D.; Xu, S. Study on the Failure Mechanism of Basalts with Columnar Joints in the Unloading Process on the Basis of an Experimental Cavity. Rock Mech. Rock Eng. 2015, 48, 1275–1288. [Google Scholar] [CrossRef]
- Meng, Q.-X.; Wang, H.-L.; Xu, W.-Y.; Chen, Y.-L. Numerical homogenization study on the effects of columnar jointed structure on the mechanical properties of rock mass. Int. J. Rock Mech. Min. Sci. 2019, 124, 104127. [Google Scholar] [CrossRef]
- Tang, C.; Liu, H.; Lee, P.; Tsui, Y.; Tham, L. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part I: Effect of heterogeneity. Int. J. Rock Mech. Min. Sci. 2000, 37, 555–569. [Google Scholar] [CrossRef]
- Tang, C.; Tham, L.; Lee, P.; Tsui, Y.; Liu, H. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part II: Constraint, slenderness and size effect. Int. J. Rock Mech. Min. Sci. 2000, 37, 571–583. [Google Scholar] [CrossRef]
- Cao, D.; Hou, Z.; Liu, Q.; Fu, F. Reconstruction of three-dimension digital rock guided by prior information with a combination of InfoGAN and style-based GAN. J. Pet. Sci. Eng. 2021, 208, 109590. [Google Scholar] [CrossRef]
- Han, J.; Han, S.; Kang, D.H.; Kim, Y.; Lee, J.; Lee, Y. Application of digital rock physics using X-ray CT for study on alteration of macropore properties by CO2 EOR in a carbonate oil reservoir. J. Pet. Sci. Eng. 2020, 189, 107009. [Google Scholar] [CrossRef]
- Kelly, S.; El-Sobky, H.; Torres-Verdín, C.; Balhoff, M.T. Assessing the utility of FIB-SEM images for shale digital rock physics. Adv. Water Resour. 2016, 95, 302–316. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).