Gradient-Guided and Multi-Scale Feature Network for Image Super-Resolution
Abstract
:1. Introduction
- We propose a gradient-guided and multi-scale feature network for image super-resolution (GFSR), including a trunk branch and a gradient branch, and extensive experiments demonstrate that our GFSR outperforms state-of-the-art methods for comparison in terms of both visual quality and quantitative metrics.
- The gradient feature map is extracted from the input image and used as structural prior to guide the image reconstruction process.
- Two effective multi-scale feature extraction modules with parallel structure (i.e., RRIB and RRRFB) are proposed to extract more abundant features at different scales.
- An adaptive weighted residual feature fusion block (RFFB) is proposed to exploit the dependency of image contextual feature information to generate more discriminative representations.
2. Related Works
2.1. CNN-Based SR Models
2.2. Residual Network
2.3. Attention Mechanism
2.4. Gradient Feature
3. Proposed Network
3.1. Network Structure
3.2. Gradient Branch
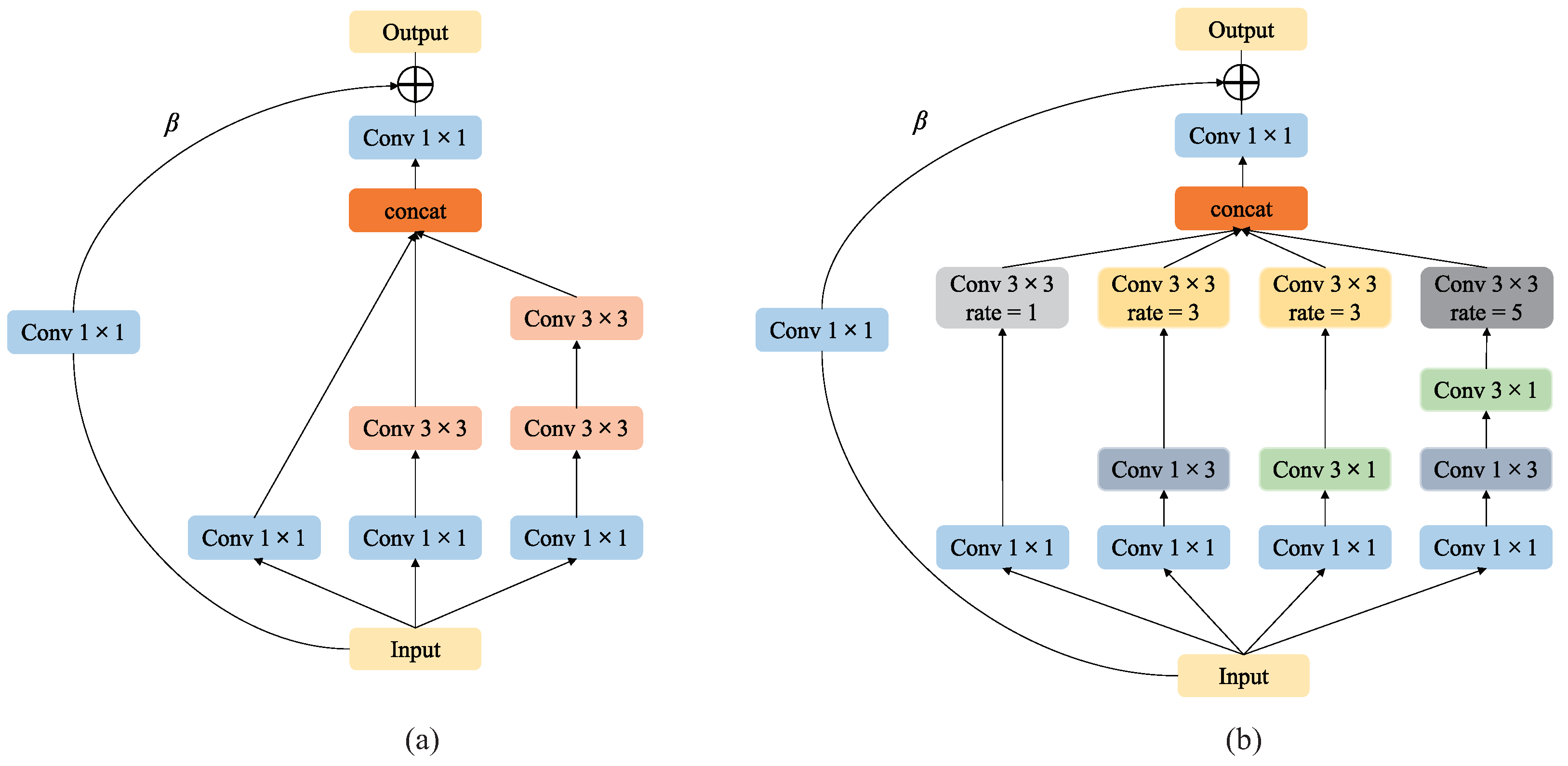
3.3. Multi-Scale Convolution Unit
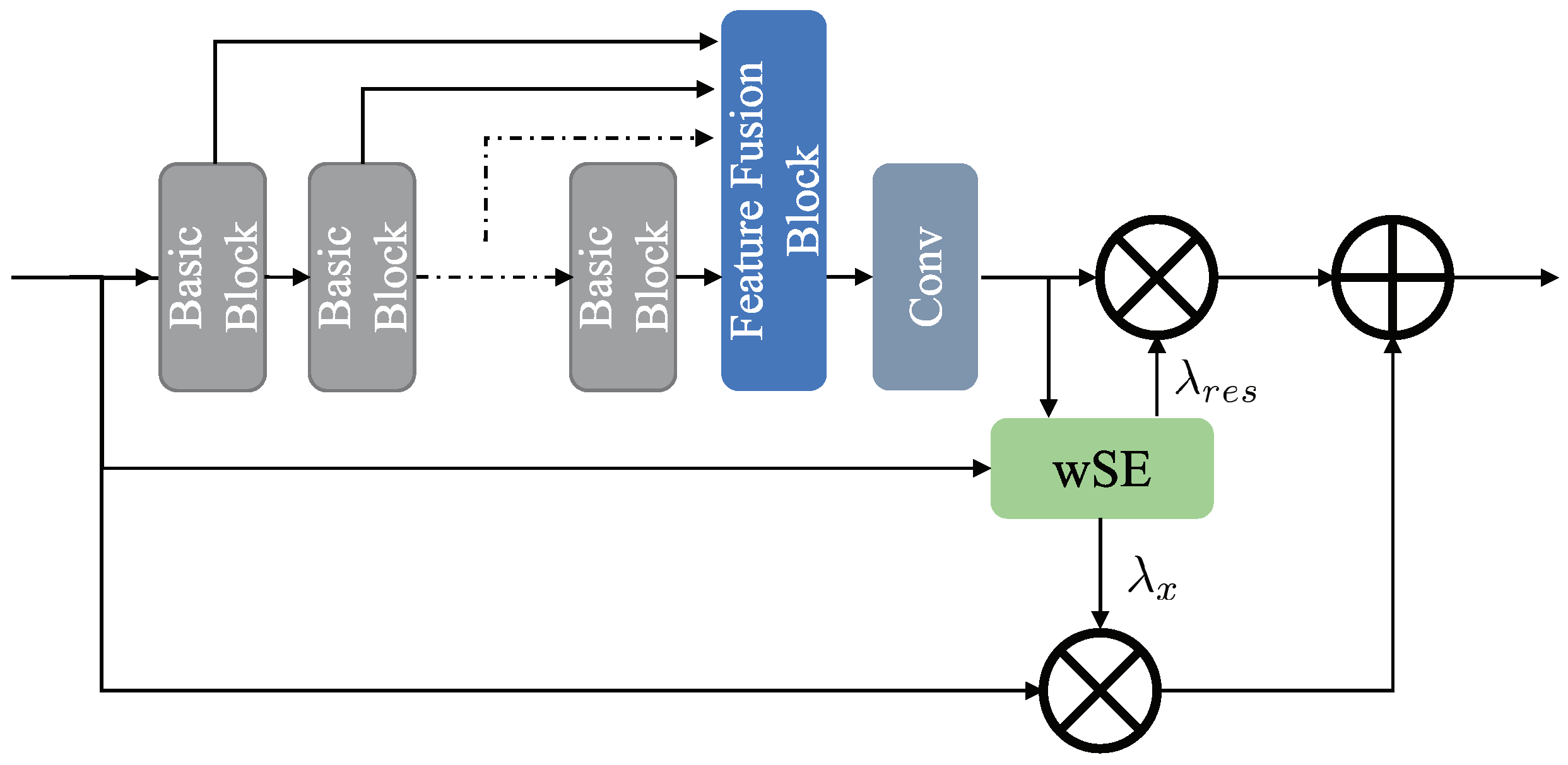
3.4. Residual Feature Fusion Block
3.5. Adaptive Channel Attention Block
4. Experimental and Analysis
4.1. Datasets and Metrics
4.2. Experimental Details
4.3. Ablation Experiment
4.3.1. Verification of the Effectiveness of Multi-Scale Feature Extraction Unit
4.3.2. Verification of the Effectiveness of Structure Prior
4.3.3. Verification of the Effectiveness of Adaptive Weight Residual Unit
4.3.4. Verification of the Effectiveness of the Remaining Modules
4.3.5. Selection of Related Hyperparameters
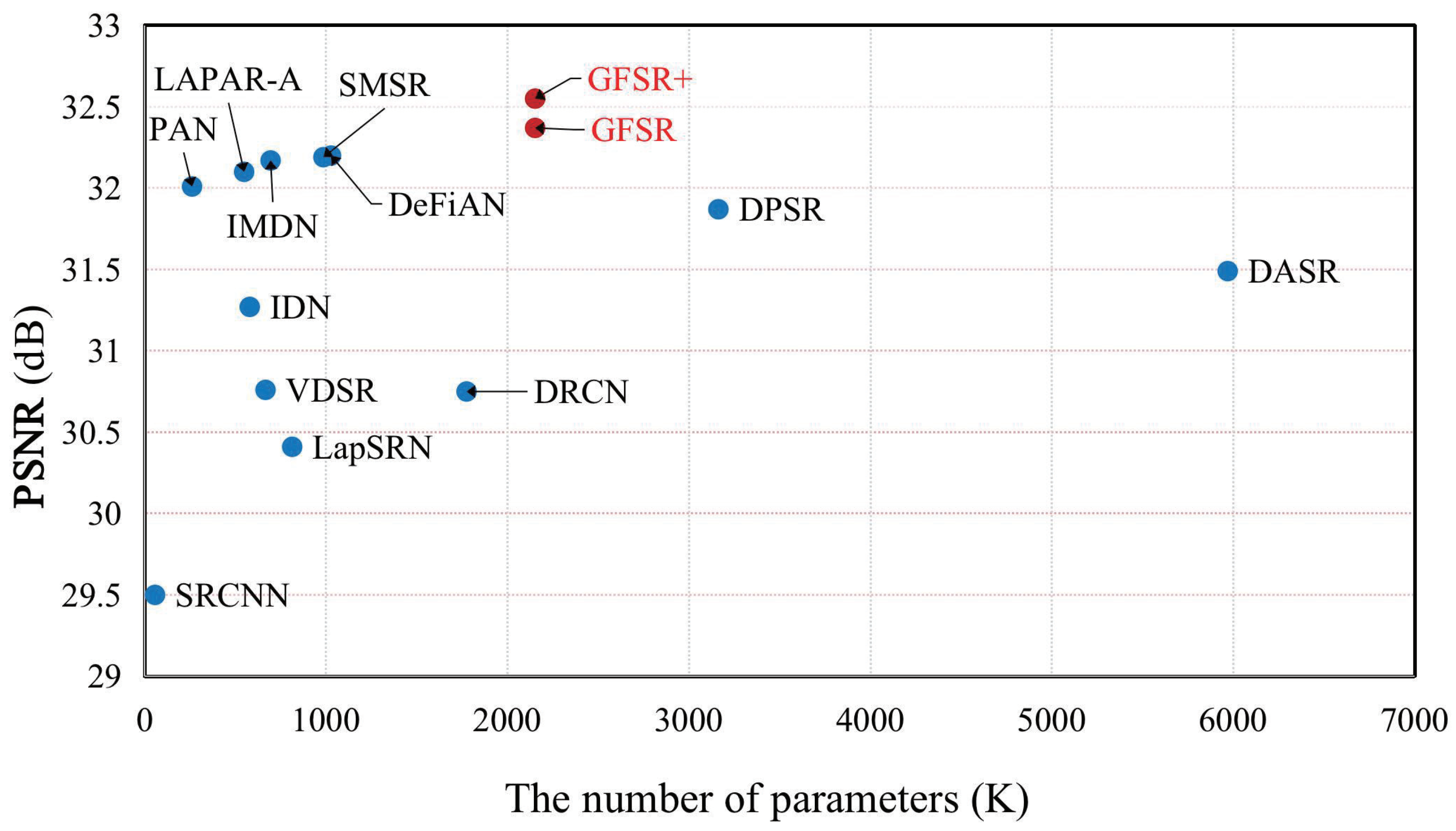
4.4. Comparison with State-of-the-Art Methods
4.5. Analysis of the Number of Parameters of the Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhou, Y.; Zhang, Y.; Xie, X.; Kung, S.Y. Image super-resolution based on dense convolutional auto-encoder blocks. Neurocomputing 2021, 423, 98–109. [Google Scholar] [CrossRef]
- Huang, Y.; Shao, L.; Frangi, A.F. Simultaneous Super-Resolution and Cross-Modality Synthesis of 3D Medical Images Using Weakly-Supervised Joint Convolutional Sparse Coding. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5787–5796. [Google Scholar] [CrossRef] [Green Version]
- Rasti, P.; Uiboupin, T.; Escalera, S.; Anbarjafari, G. Convolutional Neural Network Super Resolution for Face Recognition in Surveillance Monitoring. In Proceedings of the Articulated Motion and Deformable Objects, Palma de Mallorca, Spain, 13–15 July 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 175–184. [Google Scholar] [CrossRef]
- Mhatre, H.; Bhosale, V. Super resolution of astronomical objects using back propagation algorithm. In Proceedings of the 2016 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; Volume 2, pp. 1–6. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, J.; Zhang, T.; Lin, Y. Residual scale attention network for arbitrary scale image super-resolution. Neurocomputing 2021, 427, 201–211. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef] [Green Version]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef] [Green Version]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar] [CrossRef] [Green Version]
- Ahn, N.; Kang, B.; Sohn, K.A. Fast, Accurate, and Lightweight Super-Resolution with Cascading Residual Network. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 256–272. [Google Scholar] [CrossRef] [Green Version]
- Tai, Y.; Yang, J.; Liu, X. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar] [CrossRef]
- Li, J.; Fang, F.; Mei, K.; Zhang, G. Multi-scale Residual Network for Image Super-Resolution. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 527–542. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhang, W.; Tang, Y.; Tang, J.; Wu, G. Residual Feature Aggregation Network for Image Super-Resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 2356–2365. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 294–310. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Rao, Y.; Cheng, Y.; Chen, C.; Lu, J.; Zhou, J. Structure-Preserving Super Resolution with Gradient Guidance. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 7766–7775. [Google Scholar] [CrossRef]
- Shang, T.; Dai, Q.; Zhu, S.; Yang, T.; Guo, Y. Perceptual Extreme Super Resolution Network with Receptive Field Block. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 1778–1787. [Google Scholar] [CrossRef]
- Wei, P.; Xie, Z.; Lu, H.; Zhan, Z.; Ye, Q.; Zuo, W.; Lin, L. Component Divide-and-Conquer for Real-World Image Super-Resolution. In Proceedings of the Computer Vision—ECCV 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 101–117. [Google Scholar] [CrossRef]
- Liu, S.; Huang, D.; Wang, Y. Receptive Field Block Net for Accurate and Fast Object Detection. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 404–419. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11531–11539. [Google Scholar] [CrossRef]
- Lai, W.; Huang, J.; Ahuja, N.; Yang, M. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zuo, W.; Zhang, L. Deep Plug-And-Play Super-Resolution for Arbitrary Blur Kernels. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1671–1681. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Li, J.; Gao, X.; Hu, Y.; Lu, W. Interpretable Detail-Fidelity Attention Network for Single Image Super-Resolution. IEEE Trans. Image Process. 2021, 30, 2325–2339. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Y.; Dong, X.; Xu, Q.; Yang, J.; An, W.; Guo, Y. Unsupervised Degradation Representation Learning for Blind Super-Resolution. In Proceedings of the 2021 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 10576–10585. [Google Scholar] [CrossRef]
- Hui, Z.; Wang, X.; Gao, X. Fast and Accurate Single Image Super-Resolution via Information Distillation Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 723–731. [Google Scholar] [CrossRef] [Green Version]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight Image Super-Resolution with Information Multi-Distillation Network. In Proceedings of the 27th ACM International Conference on Multimedia—MM 2019, Nice, France, 21–25 October 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2024–2032. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhou, K.; Qi, L.; Jiang, N.; Lu, J.; Jia, J. LAPAR: Linearly-Assembled Pixel-Adaptive Regression Network for Single Image Super-resolution and Beyond. Adv. Neural Inf. Process. Syst. 2020, 33, 20343–20355. [Google Scholar]
- Wang, L.; Dong, X.; Wang, Y.; Ying, X.; Lin, Z.; An, W.; Guo, Y. Exploring Sparsity in Image Super-Resolution for Efficient Inference. In Proceedings of the 2021 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 4915–4924. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Zhou, Y.; Jiang, Z.; Guo, X.; Yang, Z. Channel Attention and Multi-level Features Fusion for Single Image Super-Resolution. In Proceedings of the 2018 IEEE Visual Communications and Image Processing (VCIP), Taichung, Taiwan, 9–12 December 2018; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.; Zhang, L. Second-Order Attention Network for Single Image Super-Resolution. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 11057–11066. [Google Scholar] [CrossRef]
- Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single Image Super-Resolution via a Holistic Attention Network. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 191–207. [Google Scholar] [CrossRef]
- Zhao, H.; Kong, X.; He, J.; Qiao, Y.; Dong, C. Efficient Image Super-Resolution Using Pixel Attention. In Proceedings of the Computer Vision—ECCV 2020 Workshops; Springer International Publishing: Cham, Switzerland, 2020; pp. 56–72. [Google Scholar] [CrossRef]
- Xie, J.; Feris, R.S.; Sun, M.T. Edge-Guided Single Depth Image Super Resolution. IEEE Trans. Image Process. 2016, 25, 428–438. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Sun, J.; Xu, Z.; Shum, H.Y. Gradient Profile Prior and Its Applications in Image Super-Resolution and Enhancement. IEEE Trans. Image Process. 2011, 20, 1529–1542. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Xu, Y.; Yang, X.; Nguyen, T.Q. Single Image Superresolution Based on Gradient Profile Sharpness. IEEE Trans. Image Process. 2015, 24, 3187–3202. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Feng, J.; Yang, J.; Zhao, F.; Liu, J.; Guo, Z.; Yan, S. Deep Edge Guided Recurrent Residual Learning for Image Super-Resolution. IEEE Trans. Image Process. 2017, 26, 5895–5907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-Enhanced GAN for Remote Sensing Image Superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Wu, Y.; Wang, Z.; Wang, G. MDCN: Multi-Scale, Deep Inception Convolutional Neural Networks for Efficient Object Detection. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2510–2515. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Guo, Y.; Ding, G.; Han, J. ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 1911–1920. [Google Scholar] [CrossRef] [Green Version]
- Wandell, B.A.; Winawer, J. Computational neuroimaging and population receptive fields. Trends Cogn. Sci. 2015, 19, 349–357. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A Persistent Memory Network for Image Restoration. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.; Lee, R.; Lee, S.H.; Hwang, W. Active weighted mapping-based residual convolutional neural network for image classification. Multimed. Tools Appl. 2021, 80, 33139–33153. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1122–1131. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi Morel, M.L. Low-Complexity Single-Image Super-Resolution based on Nonnegative Neighbor Embedding. In Proceedings of the British Machine Vision Conference; BMVA Press: Guildford, UK, 2012; pp. 135.1–135.10. [Google Scholar] [CrossRef] [Green Version]
- Zeyde, R.; Elad, M.; Protter, M. On Single Image Scale-Up Using Sparse-Representations. In Proceedings of the Curves and Surfaces; Springer: Berlin/Heidelberg, Germany, 2012; pp. 711–730. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Lu, Y.; Fu, Y.; Jiang, Q. Image quality evaluation based on image weighted separating block peak signal to noise ratio. In Proceedings of the International Conference on Neural Networks and Signal Processing, Nanjing, China, 14–17 December 2003; Volume 2, pp. 994–997. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Timofte, R.; Rothe, R.; Van Gool, L. Seven Ways to Improve Example-Based Single Image Super Resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1865–1873. [Google Scholar] [CrossRef] [Green Version]
- Ketkar, N.; Moolayil, J. Automatic Differentiation in Deep Learning. In Deep Learning with Python: Learn Best Practices of Deep Learning Models with PyTorch; Apress: Berkeley, CA, USA, 2021; pp. 133–145. [Google Scholar] [CrossRef]









| Single Scale Convolution | Multi-Scale Convolution w/o RRFB | Multi-Scale Convolution | |
|---|---|---|---|
| PSNR | 32.97 | 33.00 | 33.02 |
| Adaptive | ||||
|---|---|---|---|---|
| PSNR | 33.12 | 33.07 | 33.17 | 33.24 |
| Base | ||||||||
|---|---|---|---|---|---|---|---|---|
| ACAB | ✓ | ✓ | ✓ | ✓ | ||||
| RFFB | ✓ | ✓ | ✓ | ✓ | ||||
| GB | ✓ | ✓ | ✓ | ✓ | ||||
| PSNR | 33.02 | 33.07 | 33.12 | 33.15 | 33.11 | 33.18 | 33.19 | 33.24 |
| 1:1 | 2:1 | 3:1 | |
|---|---|---|---|
| PSNR | 32.83 | 33.24 | 32.97 |
| Param. | 2018 K | 2152 K | 2220 K |
| 2 | 3 | 4 | 5 | |
|---|---|---|---|---|
| PSNR | 32.58 | 33.07 | 33.24 | 33.30 |
| Param. | 1931 K | 2042 K | 2152 K | 2264 K |
| Method | Scale | Set5 | Set14 | B100 | Urban100 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Factor | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| SRCNN | 2 | 36.66 | 0.9542 | 32.45 | 0.9067 | 31.36 | 0.8879 | 29.50 | 0.8946 |
| VDSR | 37.53 | 0.9587 | 33.03 | 0.9124 | 31.90 | 0.8960 | 30.76 | 0.9140 | |
| LapSRN | 37.52 | 0.959 | 33.08 | 0.913 | 31.80 | 0.8950 | 30.41 | 0.9100 | |
| DRCN | 37.63 | 0.9588 | 33.04 | 0.9118 | 31.85 | 0.8942 | 30.75 | 0.9133 | |
| IDN | 37.83 | 0.96 | 33.30 | 0.9148 | 32.08 | 0.8985 | 31.27 | 0.9196 | |
| DPSR | 37.77 | 0.9591 | 33.48 | 0.9164 | 32.12 | 0.8984 | 31.87 | 0.9256 | |
| IMDN | 38.00 | 0.9605 | 33.63 | 0.9177 | 32.19 | 0.8996 | 32.17 | 0.9283 | |
| PAN | 38.00 | 0.9605 | 33.59 | 0.9181 | 32.18 | 0.8997 | 32.01 | 0.9273 | |
| LAPAR-A | 38.01 | 0.9605 | 33.62 | 0.9183 | 32.19 | 0.8999 | 32.10 | 0.9283 | |
| SMSR | 38.00 | 0.9601 | 33.64 | 0.9179 | 32.17 | 0.8990 | 32.19 | 0.9284 | |
| DASR | 37.87 | 0.9599 | 33.34 | 0.9160 | 32.03 | 0.8986 | 31.49 | 0.9227 | |
| DeFiAN | 38.03 | 0.9605 | 33.62 | 0.9181 | 32.20 | 0.8999 | 32.20 | 0.9286 | |
| GFSR | 38.08 | 0.9612 | 33.74 | 0.9193 | 32.20 | 0.9002 | 32.37 | 0.9302 | |
| GFSR+ | 38.12 | 0.9614 | 33.84 | 0.9203 | 32.24 | 0.9007 | 32.55 | 0.9317 | |
| SRCNN | 3 | 32.75 | 0.9090 | 29.30 | 0.8215 | 28.41 | 0.7863 | 26.24 | 0.7989 |
| VDSR | 33.66 | 0.9213 | 29.77 | 0.8314 | 28.82 | 0.7976 | 27.14 | 0.8279 | |
| DRCN | 33.82 | 0.9226 | 29.76 | 0.8311 | 28.80 | 0.7963 | 27.15 | 0.8276 | |
| IDN | 34.11 | 0.9253 | 29.99 | 0.8354 | 28.95 | 0.8013 | 27.42 | 0.8359 | |
| DPSR | 34.32 | 0.9259 | 30.25 | 0.8410 | 29.08 | 0.8044 | 28.07 | 0.8504 | |
| IMDN | 34.36 | 0.9270 | 30.32 | 0.8417 | 29.09 | 0.8046 | 28.17 | 0.8519 | |
| PAN | 34.40 | 0.9271 | 30.36 | 0.8423 | 29.11 | 0.8050 | 28.11 | 0.8511 | |
| LAPAR-A | 34.36 | 0.9267 | 30.34 | 0.8421 | 29.11 | 0.8054 | 28.15 | 0.8523 | |
| SMSR | 34.40 | 0.9270 | 30.33 | 0.8412 | 29.10 | 0.8050 | 28.25 | 0.8536 | |
| DASR | 34.11 | 0.9254 | 30.13 | 0.8408 | 28.96 | 0.8015 | 27.65 | 0.8450 | |
| DeFiAN | 34.42 | 0.9273 | 30.34 | 0.8410 | 29.10 | 0.8053 | 28.20 | 0.8528 | |
| GFSR | 34.49 | 0.9282 | 30.41 | 0.8437 | 29.14 | 0.8066 | 28.40 | 0.8562 | |
| GFSR+ | 34.56 | 0.9287 | 30.47 | 0.8446 | 29.18 | 0.8073 | 28.52 | 0.8579 | |
| SRCNN | 4 | 30.48 | 0.8628 | 27.50 | 0.7513 | 26.90 | 0.7101 | 24.52 | 0.7221 |
| VDSR | 31.35 | 0.8838 | 28.01 | 0.7674 | 27.29 | 0.7251 | 25.18 | 0.7524 | |
| LapSRN | 31.54 | 0.8850 | 28.19 | 0.7720 | 27.32 | 0.7280 | 25.21 | 0.7560 | |
| DRCN | 31.53 | 0.8854 | 28.02 | 0.7670 | 27.23 | 0.7233 | 25.14 | 0.7510 | |
| IDN | 31.82 | 0.8903 | 28.25 | 0.7730 | 27.41 | 0.7297 | 25.41 | 0.7632 | |
| DPSR | 32.19 | 0.8945 | 28.65 | 0.7829 | 27.58 | 0.7354 | 26.15 | 0.7864 | |
| IMDN | 32.21 | 0.8946 | 28.58 | 0.7811 | 27.56 | 0.7353 | 26.04 | 0.7838 | |
| PAN | 32.13 | 0.8948 | 28.61 | 0.7822 | 27.59 | 0.7363 | 26.11 | 0.7854 | |
| LAPAR-A | 32.15 | 0.8944 | 28.61 | 0.7818 | 27.61 | 0.7366 | 26.14 | 0.7871 | |
| SMSR | 32.12 | 0.8932 | 28.55 | 0.7808 | 27.55 | 0.7351 | 26.11 | 0.7868 | |
| DASR | 31.99 | 0.8923 | 28.50 | 0.7799 | 27.51 | 0.7346 | 25.82 | 0.7742 | |
| DeFiAN | 32.16 | 0.8942 | 28.62 | 0.7810 | 27.57 | 0.7363 | 26.10 | 0.7862 | |
| GFSR | 32.33 | 0.8969 | 28.69 | 0.7839 | 27.62 | 0.7373 | 26.19 | 0.7886 | |
| GFSR+ | 32.45 | 0.8980 | 28.73 | 0.7847 | 27.65 | 0.7382 | 26.29 | 0.7906 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Huang, D.; Zhu, X.; Chen, F. Gradient-Guided and Multi-Scale Feature Network for Image Super-Resolution. Appl. Sci. 2022, 12, 2935. https://doi.org/10.3390/app12062935
Chen J, Huang D, Zhu X, Chen F. Gradient-Guided and Multi-Scale Feature Network for Image Super-Resolution. Applied Sciences. 2022; 12(6):2935. https://doi.org/10.3390/app12062935
Chicago/Turabian StyleChen, Jian, Detian Huang, Xiancheng Zhu, and Feiyang Chen. 2022. "Gradient-Guided and Multi-Scale Feature Network for Image Super-Resolution" Applied Sciences 12, no. 6: 2935. https://doi.org/10.3390/app12062935
APA StyleChen, J., Huang, D., Zhu, X., & Chen, F. (2022). Gradient-Guided and Multi-Scale Feature Network for Image Super-Resolution. Applied Sciences, 12(6), 2935. https://doi.org/10.3390/app12062935






