Abstract
The use of compressive sensing in several applications has allowed to capture impressive results, especially in various applications such as image and video processing and it has become a promising direction of scientific research. It provides extensive application value in optimizing video surveillance networks. In this paper, we introduce recent state-of-the-art video compressive sensing methods based on neural networks and categorize them into different categories. We compare these approaches by analyzing the networks architectures. Then, we present their pros and cons. The general conclusion of the paper identify open research challenges and point out future research directions. The goal of this paper is to overview the current approaches in image and video compressive sensing and demonstrate their powerful impact in computer vision when using well designed compressive sensing algorithms.
1. Introduction
Wireless sensor network (WSN) technology has been identified as one of the key components in designing future internet of things platforms [1]. It has been gaining a lot of attention since smart sensors have become an important part in our daily lives. However, in real life, these devices are resource-constrained: the storage resources, the energy capacity and the computing performances are all limited. That is why the processing of huge data especially video data is becoming very challenging. In order to shift the computation burdens from the sensor level to the decoder in WSN, compressive sensing is used as an effective way to reduce the complexity of the encoder, which means that by optimizing the way the acquire and transmit data over wireless channels, we optimize the computational resources of the devices and enhance their performances. In fact, the compressive sensing technique significantly enhances the coding efficiency of the wireless devices (considered as encoders) by reducing the sampling rate (in comparison with the well-known Shannon–Nyquist) and synchronizing the data sampling process. Another problem can be detected from a macro perspective in WSN platforms: the sporadic (infrequent) transmission rate. Indeed, not all wireless sensors send their data simultaneously to the central server, which means that the WSN architecture sparsity should be exploited to reach high data reliability with a limited number of sensors. In addition, IoT platforms can easily integrate compressive sensing into their several applications because many real-world datasets can be well approximated by sparse signals using an appropriate transform (e.g., DCT, DWT… to represent images, videos…). So, in many applications related to WSN, energy consumption is a principal concern because sensors have to send regularly their sensing data to the coordinator node. Data transmission being considered as a principal factor of energy consumption, many research efforts are focusing on reducing the amount of data acquired at the sensor level. In order to reduce the amount of transmission data, we have to compress them inside the network. As a result, compressive sensing (CS) algorithms have led to new ways of designing energy efficient WSN with low cost data acquisition [2].
Compressive sensing is a technique exploited today in several applications such as medical imaging, remote sensing and wireless sensor networks. In fact, CS is a theory which can efficiently acquire and reconstruct sparse signals [3]. CS theory suggests that the sampling rate necessary to acquire and reconstruct the signal can be significantly lower than the minimal rate required by the Nyquist-Shannon sampling theorem. This lower sampling rate can reduce the processing and energy requirement at the sensor nodes which can lead to revolutionary results for embedded video sensors.
In fact, the video signal in general is sparse so it contains a significant amount of redundancy in both spatial and temporal domains and therefore video compression is one of the most important fields where CS can be applied.
The advent of CS has led to the emergence of new image devices such as Single Pixel Cameras [4]. CS techniques are commonly used to deal with high transmission throughput and large storage spaces.
Indeed, an impressive progress has been made in Video Compressive Sensing (VCS) with the appearance of single pixel cameras where the video is represented in the Fourier domain [5] or the Wavelet domain [6]. Then, video CS cameras tried to integrate temporal compression into the systems with the arrival of the optical flow based algorithms for video reconstruction [7]. In addition, Total Variation (TV) [8] and Dictionary Learning [9] were among the popular approaches used for VCS. TV methods suppose the sparsity of the gradient of each video frame and try to minimize the norm of the gradient frames. However, dictionary-based approaches consider the video patches as a sparse linear extension in the dictionary elements.
Another challenge of VCS, especially for the video reconstruction process is the complexity of the mathematical formulations handled by the reconstruction system. For the sake of simplicity, video recovery techniques can be classified into two main categories: Optimization based algorithms, categorized also into convex and greedy algorithms, and Deep Learning methods. Section 2 and Section 4 introduces the main approaches used to reconstruct the main video scenes from the compressed measurements.
On the one hand, we clearly notice that iterative based approaches have high complexity (from few seconds to few minutes to recover an image). However, these techniques are not applicable for real-time applications. On the other hand, Neural Networks (NN) are applied in our topic of interest: the optimization of the transmission and reconstruction of video signals in wireless sensor networks.
Neural networks have shown excellent performances in terms of quality of image reconstruction and reconstruction processing time (in the order of milliseconds). This makes the NN approach a good candidate for real-time applications of video-monitoring in a smart city context. Thus, this paper aims at better characterizing and comparing existing state of the art NN reconstruction based methods.
The remaining of the paper is organized as follows: Section 2 presents an overview of the principles of compressive sensing. In Section 3 we present different image compressive sensing architectures, whilst Section 4 discusses different video compressive sensing sampling and reconstruction architectures while classifying them based on their sampling strategy. In Section 5 we classify recent deep learning-based video compressive sensing algorithms according to their modulation strategy. In Section 6, we provide recent research results with an experimental study on several VCS approaches to compare their performances in terms of the quality of their output and the testing time. Section 7 discusses the future research challenges and opportunities of compressive sensing. Section 8 eventually concludes the paper by identifying open research challenges and pointing out future research directions.
2. Compressive Sensing
Conventional sensors are based on the sampling theorem of Shannon–Nyquist which is based on the following principle: the minimum sampling frequency of a signal that not distorts its underlying information, should be the double of its highest frequency component. However, this theorem which imposes an unnecessary high sampling rate is becoming outdated for applications that require a large amount of data. Thus, the Compressive Sensing paradigm seeks to decrease the rate of the Shannon–Nyquist principle and meets the expectations of the Massive data-intensive applications. To keep it simple, for our application case, a CS camera takes a number of measurements coded from the scene much smaller than the number of reconstructed pixels. In fact, CS is an approach that facilitates the efficient acquisition of the sparse signals where detection and compression are performed at the same time.
2.1. Mathematical Introduction
To understand the mathematics behind the CS technique we recall here some basis principles: Instead of acquiring N samples of a signal , M random measures are acquired with (CS theory states that the number of measurement sufficient to reconstruct the signal x is such that:
where is the known compressed measurement vector and is the sensing matrix that will be discussed in the next section. To recover the signal x given y and , x must be sparse in a given base :
where s is K-sparse which means that s has at most K non-zero elements. From (1) and (2):
where . Figure 1 shows the compressed sensing framework.
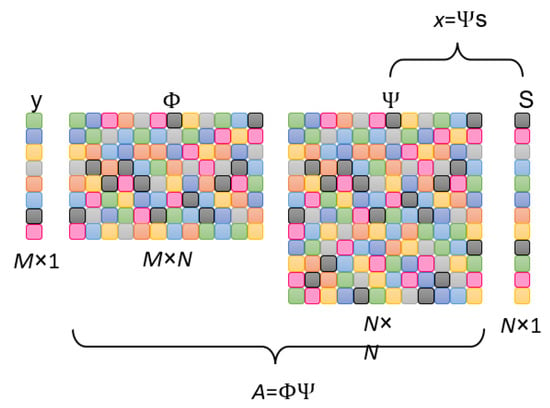
Figure 1.
Compressive sensing framework.
However, the reconstruction of x or s from y is not possible. Therefore, an approximate solution can be obtained by solving the following minimization problem [3,10]:
To reconstruct s from y, CS algorithms use different reconstruction approaches. Then x can be reconstructed from .
Since there is only one measurement vector, the above problem is generally referred to as a Single Measurement Vector (SMV) problem in the compressive sensing. However, when the input becomes a 3D signal (video) instead of 1D signal, the SMV problem becomes a Multiple Measurement Vector (MMV) problem. The sparse vector s becomes in this case a set of vectors which must be recovered jointly from a set of measurement vectors [11].
The set of the known measurement vectors can correspond to different frames of the video signal. In fact, the video could be cut into series of images and then each image obtained could be associated to a measurement vector and then it is possible to apply MMV model on the video. Therefore, the common approach used to deal with sequence data is Recurrent neural networks (RNN). However, RNN work well when we are dealing with short-term dependencies. In other words, these neural networks remember things for short periods of time and if a lot of information has been entered, it suffers from important losses. This problem could be solved by applying a modified version of the RNN: LSTM (Long Short Term Memory) [12]. The advantage of LSTM is that it avoids the problem of long term dependency i.e., it allows to remember information for a long period of time.
As a result, and in agreement with CS properties, CS has a great potential to be applied to images and videos because of their huge spatial and temporal redundancies which allow to have sparse representations to enable their reconstruction.
Nevertheless, RNNs are not the only Deep Learning approach experimented in video compressive sensing recovery phase. Indeed, many methods will be discussed in the following sections.
2.2. Sensing Matrix
One of the most interesting research directions in compressive sensing is the construction of the sensing matrices. Indeed, the sensing matrix must satisfy some constraints. Firstly, it should be coherent with the sparsifying matrix to capture the salient information of the initial signal with the minimum number of projections. Secondly, it may satisfy the restricted isometry property (RIP) to preserve the original signal main information in the compression process. However, it has been proved in [13] that RIP property is not always required to hold neither the sparsity level in a CS context, nor the random model of a signal. In addition, for real-time applications and low power requirements, we should design low complexity and hardware friendly sensing matrices. In most works, especially for those who are focusing on the reconstruction stage, the problem of the sampling matrix is not discussed since it is chosen as a random matrix such as Gaussian or Bernoulli matrix which meets the restricted isometry property (RIP) of CS. Although random matrices are easy to implement and can ensure better reconstruction results, they have many disadvantages. In fact, they require a large storage resources and the recovery process may be difficult when dealing with large signal dimensions [14]. It can also be chosen as circulant sensing matrix [15]. However, other researchers use some features of the original input to design these matrices which is known as data-driven sampling matrix design. Other works are oriented to binary and bipolar sampling matrices that can be easily implemented on hardware devices and they do not require large computation resources.
2.3. Reconstruction Algorithms
The reconstruction process is the key to efficiently incorporate compressive sensing in real-world applications. Therefore, designing and implementing new optimization algorithms is the major concern of CS researchers. These algorithms can be categorized into several categories. In this section, we will cover the main two types of the recovery algorithms in CS: convex optimization algorithms and greedy algorithms.
2.3.1. Convex Optimization
To reconstruct the original signal x, the trivial approach is to solve the minimization problem:
Since, minimization is an NP-hard problem fro large scale matrices, in our case is computationally complex, minimization process is proposed to overcome the limitations of . In this case, the minimization problem, known as basis pursuit (BP) [16], becomes:
Another approach called basis pursuit denoising (BPDN) [17] is adapted when dealing with noisy systems. In addition, Least Absolute Shrinkage and Selection Operator (LASSO) [18] can be used when we have no prior knowledge about the noise level. The minimization process of some variational problems can also practically be solved using fast iterative thresholding algorithm (FISTA) [19], forward-backward splitting (FBS) [20] or approximation message passing (AMP) [21].
2.3.2. Greedy Algorithms
Greedy algorithms are commonly used in CS applications because of their low complexity and their fast reconstruction. Currently, the most exploited greedy algorithms are classified into sequential and parallel greedy pursuit techniques. Sequential methods count gradient pursuit [22], matching pursuit (MP) [23,24], orthogonal matching pursuits (OMP) [25], regularized OMP (ROMP) and stagewise OMP (StOMP) [26,27,28]. Although OMP allows a faster signal reconstruction than convex relaxation approaches, it deteriorates the recovery quality for signals with low sparsity. Therefore, improved versions of OMP have been proposed to avoid these drawbacks such as compressive sampling matching pursuit (CoSaMP) [29], subspace pursuit (SP) [30], Regularized OMP [27], Stagewise OMP [26], and orthogonal multiple matching pursuit [31]. Those techniques are considered as parallel greedy pursuit methods.
Obviously, the performance of the reconstitution algorithms depends on the applications and there is no obvious metric to determine the best reconstruction algorithm. However, for some algorithms, we can compare their complexity and the minimum measurements required for the CS recovery.
3. Image Compressive Sensing
Recently, deep learning is used in various computer vision tasks and it shows high performance results in several applications such as CS reconstruction algorithms. Since many computer vision algorithms applied on 2D signals (e.g., [32] in which ISTA-Net is applied in a video CS context) are extended to be applied on 3D signals (e.g., videos), we introduce in this section recent image CS algorithms.
Among the reconstruction methods, various block-by-block methods are already proposed such as stacked denoising autoencoder (SDA) [33], non iterative reconstruction using CNN (ReconNet) [34] and DR2-Net [35] which are deep learning based end to end reconstruction networks. However, the outputs of these algorithms suffer generally from blocky artifacts. Therefore, the use of a BM3D algorithm, as a post processed procedure, is compulsory to eliminate the blocky artifacts in reconstructions. Among the well mentioned algorithms in image reconstruction, we have the iterative shrinkage thresholding algorithm based network (ISTA-Net) [36] that integrates the traditional ISTA into a neural network to achieve superior reconstructed quality, its enhanced version ISTA-NET+, trainable ISTA for sparse signal recovery (TISTA) [37] and ADMM-Net [38] which is proposed by adapting ADMM method for CS magnetic resonance imaging (CS-MRI) using neural networks. Experimental results in various research works prove that deep learning networks can successfully solve the two main issues of compressive sensing: the design of proper sampling matrices and the reconstruction process. The performances are significantly increased and lower computation complexity is obtained than traditional methods. Shi et al. [39] and T.N. Canh et al. [40] proposed CNN-based methods for 2D image reconstruction that split the reconstruction process into two stages. Firstly, the initial reconstruction which aims to recover the images from the patches. Secondly, a better quality reconstruction is obtained from the enhancement of the initial reconstruction. In [39], deep networks are used in the reconstruction phase by imitating the traditional CS image recovery and the training of the sampling matrix through a CNN network. These two theoretically separated networks are considered as an encoder-decoder approach to generate the CS measurements and to reconstruct the 2D images.
Deep compressive sensing was extended to multi-scale schemes [40,41,42] utilizing image decomposition. In [41], a multiphase reconstruction process is proposed. The first phase is dedicated to a multi-scale sampling and an initial reconstruction that are jointly trained. Then, the quality of the initial image is enhanced with convolution layers and ReLU activation function. The third phase, used in the experimental comparison because of its better performances, is enhanced with Multilevel Wavelet Convolution (MWCNN).
4. Video Compressive Sensing
Obviously, the main function of video compressive sensing systems is to capture video data with low-dimensional detectors and then use the optimized based algorithms, as explained above in Section 2.3, to solve the ill-posed reconstruction problem. These two systems: the hardware encoder and the software recovery system enable to optimize encoders resources, especially in the transmission process. However, their long running time prevents them from being exploited in real-time applications. So, thanks to recent advances in deep learning, we expand the variety of algorithms used in the reconstruction phase. Deep learning-based approaches enable a fast end-to-end recovery of video scenes with better quality performances despite the long training time. Indeed, The basic framework of video compressive sensing is composed of two main systems: the hardware encoder and the software decoder, and a channel to transmit video data over it. This is the main digital video delivery system employed by communication systems that rely on compressive sensing to acquire, transmit and reconstruct data. In fact, the encoder uses special cameras (low-speed cameras such as single pixel cameras) to capture and process high speed videos. Then, it generates fewer compressive measurements that could be easily transmitted or stored. Finally, a reconstruction algorithm will be applied in order to reconstruct the received video at the receiver device (e.g., server). Figure 2 illustrates the basic video compressive sensing framework.
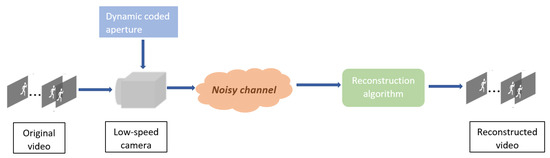
Figure 2.
Basic model of video compressive sensing.
Video CS algorithms have used various models and architectures to sample and reconstruct the signals. According to the way the video signals are sampled, we review these works in the following three categories: Temporal VCS, Spatial VCS and Spatio-temporal VCS.
4.1. Temporal VCS
The sampling phase of the Temporal VCS (TVCS) relies on the 2D measurements obtained from the sampling across the temporal axis which means that the compression is done in the temporal domain.
The non neural networks approaches exploit the sparsity of the video scenes and the variety of the existing algorithms for optimization problems. In [43], J. Yang et al. propose a Gaussian mixture model (GMM) based algorithm to reconstruct spatio-temporal video patches from temporally compressed measurements. This robust algorithm is less-dependent on the offline training dataset which enable to be extended to real-time applications. X. Yuan et al. [44] solved the compressive sensing problem by exploiting the Generalized Alternating Projection (GAP) to solve the Total Variation (TV) minimization mathematical problem.
Another approach to deal with TVCS, Deep learning has become one of the CS community promising trends. In [45], the authors present a deep fully connected network and non-iterative algorithm to recover the frames already sampled using a 3D Bernoulli sensing matrix to measure consecutive frames simultaneously. This article represents the first deep learning architecture for temporal compressive sensing reconstruction. The work of this article concerns temporal CS where the multiplexing is done through the temporal dimensions and its architecture is based on Multi-layer Perceptrons (MLP) as shown in Figure 3 Indeed, the MLP architecture is used to learn the f non-linear function which maps a measured frame patch via multiple layers to a video block .
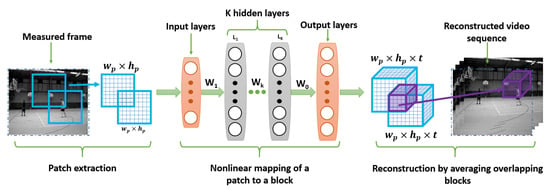
Figure 3.
Video Compressive Sensing Architecture based on an MLP Network.
Each hidden layer is defined by:
where is the k-hidden layer, is the bias vector and is the weight matrix. The non-linear activation function used in this model is the rectified linear unit (ReLU) defined as . In this model, the 1st fully connected layer must provide a 3D signal from the 2D compressed measurements. The other layers are considered as 3D layers. The size of the video blocks used is and increasing the block size would considerably increase the network complexity. This algorithm is tested by changing either the number of MLP layers (4 or 7) or the size of the learning database. The metrics used are the PSNR and SSIM [46]. In fact, increasing the number of layers for small datasets (not for large datasets) improves the metrics because several parameters are trained. However, increasing the number of layers will inevitably lead to an increase of the complexity of the network.
Compressive sensing allows signals to be detected with far fewer measurements than those of Shannon–Nyquist. It entails lower costs for IOT projects and a reduction in the acquisition time. In this context, many papers have proposed architectures such as Single Pixel Cameras (SPC) providing a framework which seems to be effective for images in terms of acquisition using a reduced number of coded measurements with low-cost sensors. In [47], the authors were able to extend the CS imaging model beyond the images to work with the video. In the article quoted above, which talks about single-pixel cameras, it is a demonstration of the Deep Learning application with a convolutional auto-encoder network to retrieve a 128 × 128 real-time video pixels at 30 frames/s from a sampling of single-pixel cameras with a compression ratio of 2%. Thus, the proposed architecture is a Deep Convolutional Autoencoder Network (DCAN) architecture which represents a powerful and efficient computation pipeline to solve inverse problems with good quality and in real time. In this research work, deep neural networks have been exploited to produce an algorithm to reconstruct a video signal in real time from a single-pixel camera consisting of a Digital Micromirror Device (DMD) as a spatial modulator.
It is obvious from the DCAN architecture, represented in Figure 4, that it is a calculation model which includes coding and decoding layers. The main goal of these layers is to reconstruct an image or an input scene. The input of this network is measured by M () binary filters and reconstructed using fully connected layers and 3 convolutional blocks. After the fully connected layers, each convolution operation is followed by ReLU activation and batch normalization. The optimization of the filter weights is done using the gradient descent stochastic algorithm while respecting the minimization of the standard cost function in measuring the Euclidean distance between the observed and desired output. In order to test the performance of this algorithm, three metrics were used: peak-signal-to-noise ratio (PSNR), structural similartity index (SSIM) and standard deviation (SD). Thus, since authors can change the input resolution size and compression ratio, the best results in terms of PSNR and SSIM were obtained with a resolution size of and a compression ratio of 98%.
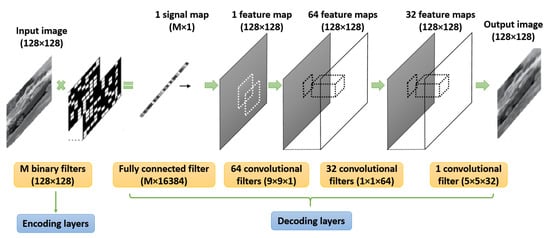
Figure 4.
DCAN Architecture.
Thanks to the evolution in the field of deep learning, another compressive sensing system has been proposed in [48]. This system allows an instantaneous reconstruction by estimating the output from the input measurements. This approach requires a design based on a network model of neurons, a computing capability linked to the machine used to run the model designed and a large database of learning and validation data.
However, models based on neural networks are less flexible than iterative models because they are based on the learning process and subsequently work only on systems with parameters already determined during the learning phase such as image size and compression rate. The model proposed in [48] is a Snapshot Compressive Imaging (SCI) system which refers to compressive sensing systems where multiple frames are mapped into a single measurement frame. It is based on a DMD, an end-to-end CNN algorithm (E2E-CNN) and a plug-and-play (PnP) environment to solve the reverse problem related to the video compressive sensing.
This model is inspired from video CS and is shown in Figure 5. The video is considered to be a dynamic scene that is represented as a sequence of images with different chrono-dating . The coded frames are then integrated over time on a camera forming a measurement compressed to a single image. In accordance with the measurement and coding models, the iterative algorithms or pre-formed neural networks are used to reconstruct the video.
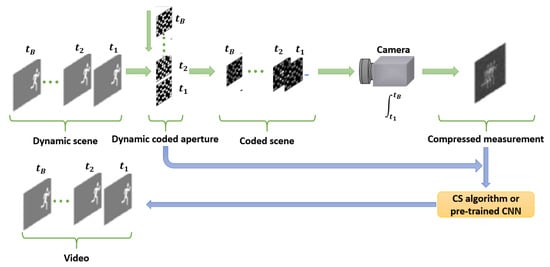
Figure 5.
Video SCI.
The principle of SCI video is based on binary spatial coding. Unlike to traditional image processing approaches where signals are acquired directly, in computational imaging, the captured measurement may not be visually explainable but includes the original images. After reconstruction of the video with the model described in this article, the authors compare these performances with those of the best known algorithms in the field of SCI video such as TwIST [49], GAP-TV [44], GMM [43] and DeSCI.
Indeed, the advancement in the field of Deep Learning applied to images have inspired researchers to expand their work on the CS video. Among them, we have Deep fully connected neural network for video CS, Deep tensor ADMM-Net for video SCI problem or E2E-CNN [48].
The learning of this model is done by applying a residual learning for the encoder-decoder in order to speed up the video CS. It is important to know that this deployment is based on an optical system using a high-speed DMD spatial modulator, because the idea behind this model was to apply a spatial modulation to the image sequences at high speed.
To understand this model, we will detail the mathematical approach behind this video CS model:
Let f represent the dynamic scene that has and t as the spatial and temporal variables of the video. Let also , and be the coordinates of spatial and temporal measurements. Then the measurement formed on the detector plane is given by the function g:
where T is the time modulation introduced by the DMD, the pixel pitch, the camera integration time, and the spatial dimensions space, the temporal dimension, p and the functions of spatial and temporal pixel sampling.
The sampling of the pixel is discrete and follows the following equation:
where B is the number of pixels, X is the high speed frames, C is the coding patterns, G represents the noise and ∘ is the Hadamard product.
Let the position of the pixel and thus the above equation becomes:
We define: where . We have for .
It is obvious that our problem is a compressive sensing problem:
where is the detection matrix (which is only dense when ), the signal and the noise vector. The matrix consists of diagonal matrices.
It is now clear that the goal of this problem is to reconstruct the signal x from the measurements y. As a result, the E2E-CNN model has been proposed. However, this model needs a large database and huge execution time. In addition, if we change the matrix , the neural network must execute another learning process which needs another temporal data. To cope with this, PnP framework is needed to use pre-trained data in an optimization framework in order to establish an equilibrium between the flexibility of the algorithm and its running time.
E2E-CNN architecture, represented in Figure 6, is based on convolutional encoder-decoder architecture. It consists of 5 residual blocks for the encoder and 5 other blocks for the decoder and the two stuctures are connected by 2 convolutional layers. Each convolution is followed by ReLU activation function and a batch normalization. In addition, the output of a residual block of the decoder is added to the input of the residual block of the mapped decoder. In this architecture, the authors did not use pooling layers nor the oversampling in order not to lose the details of the images.
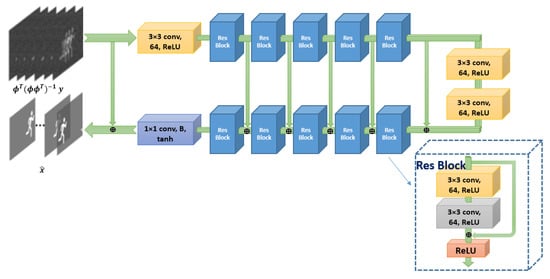
Figure 6.
E2E-CNN Architecture.
The loss function of this model is:
where MS.SSIM is multiscale structural similarity index between the output of the network. The actual values of x, and are predetermined.
It has been said before that E2E-CNN suffers from a problem of flexibility (for different tasks and different compression ratios) which means that when we change the measurement matrix , we are forced to retrain our model which requires other databases and more execution time. This problem will be corrected by the PnP algorithm that allows to reconstruct x from y and :
where is an equilibrium parameter between the norm and the deep denoising prior used to solve the minimization problem without re-training the model which enables the flexibility of the algorithm.
To solve Equation (13), the ADMM technique could be applied [48]. In addition, a denoising problem could be faced and then FFDNet algorithm is needed to solve it. The only drawback with the FFDNet is the undesirable artifacts produced with high compression ratios. This is due to the fact that learning with the FFDNet is made with a Gaussian noise for video compressive sensing: for each iteration, the noise is different. To conclude this approach, ref. [48] proposes an implementation of a video compressive sensing algorithm that uses a DMD as a dynamic modulator and an E2E-CNN and PnP algorithms with FFDNet for the video reconstruction.
The most recent research in temporal VCS is presented in [50]. It uses 3D CNN from temporal compressive imaging and the residual network concept to exploit temporal and spatial correlation among successive object frames. The idea of measurement calibration algorithm in this approach has improved its final performances on both simulation experiments and optical ones. Another recent work is proposed by Zheng et al. [51]. It consists of an encoder-decoder flexible and concise architecture to reconstruct video frames in a CS framework. The reconstruction process is based on deep unfolding structure that uses 2 stages. This reconstruction algorithm outperforms recent deep learning-based algorithms as illustrated in Section 6 in terms of quality performances.
4.2. Spatial VCS
The compression approach in spatial video compressive sensing (SVCS) is based only on the spatial domain which means that the sampling step is processed on the scene video frame by frame. In the reconstruction phase, the frames are recovered independently. Then, the reconstruction algorithm integrate an estimation process to predict the motions of the preliminary recovered frames.
One of the most known conventional (non neural networks) SVCS methods used is [52]. C. Zhao et al. propose an initial recovery of each frame independently using the spatial correlation. Then, they optimize the output using the inter-frame correlation.
As in TVCS, Deep leaning is used to solve SVCS problems. In [53], K. Xu et al. propose a robust algorithm to sample the different frames in the spatial domain. Then, they use CNN and RNN to reconstruct the original video and enhance the recovery quality, respectively. The video compressive sensing model was proposed to overcome the limitations of CS cameras. CSVideoNet was inspired from CNN [54], that is a type of deep networks in which filters and pooling operations are applied alternatingly on the input images to extract their main features, and RNN architectures in order to improve the trade-off between compression ratio and spatial-temporal resolution of reconstructed videos. High-speed cameras can capture videos with frame rates that arrive up to 100 frames/s. This model allows to improve the compression ratio and enhance the quality of the video.
Currently, two types of CS cameras are in use: the spatial multiplexing cameras (SMC) and the temporal multiplexing (TMC) cameras. Since SMC cameras take fewer measurements than the number of pixels, they suffer from low spatial resolution. However, TMC cameras have low frame rate sensors in spite of their high spatial resolution. Thus, in [53], a new model has been proposed in order to overcome the problem of spatial resolution using SMC cameras. This model, represented in Figure 7, consists of 3 parts: a static encoder, a CNN network dedicated for the extraction of spatial features for each frame of the compressed data and an LSTM network for motion estimation and video reconstruction.
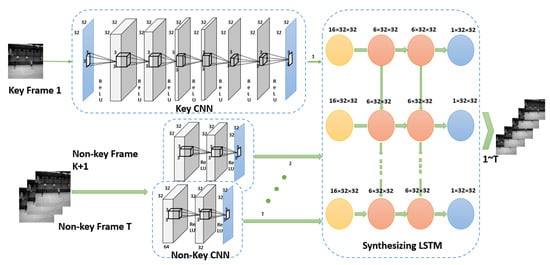
Figure 7.
CSVideoNet Architecture.
In the proposed architecture, the design of the encoder is inspired from the CNN’s architecture because the main goal does not only consist in extracting visual features but also in preserving the details of the dynamic scenes. For this reason, the authors eliminated the pooling layer which causes an information loss. In fact, the pooling layer allows to progressively decrease the spatial dimensions to reduce the number of parameters and as a result the complexity of the network. In addition, all feature maps have the same dimensions as the reconstructed videos. The first fully connected layer enables to convert the m-dimensional video data into 2D feature maps. The size of the video block in this model is 32 × 32. All convolutional layers are followed by the ReLU activation function except for the last layer. The CNN layers are divided into 2 types: 8 CNN Key layers and 3 non-key CNN layers.
The CNN key layers are compressed with a low compression ratio and non-key CNN layers with a high compression ratio. The weight of the non-key CNN layers are shared to reduce storage requirements. The Key frame that represents the input of the CNN key layer is the key image of the video sequence and contains more information than the non-key frames of the non-key CNN layers. In the implementation of the CSVideoNet solution, for every 10 frames of the video, the 1st one is defined as the key frame.
The LSTM decoder is designed to improve the spatial-temporal resolution. In fact, LSTM is used to extract the movement features that are essential to improve the temporal resolution of the CNN output. In addition, it allows to reduce the size of the model and therefore to obtain a faster speed of reconstruction. For this network, increasing the size of the CNN has been tested, but it does not provide any improvement for the reconstruction because the CNN network is unable to capture temporal features. So, the LSTM network is important to improve the PSNR, which shows that the temporal resolution is processed at this level. This proves the importance of LSTM for video reconstruction. Thus, CSVideoNet is a non-iterative algorithm for real-time applications. The main goal of CSVideoNet is to improve the reconstruction quality and the compression ratio.
In addition to the SVCS models already mentioned, two famous studies, based on stacked denoising autoencoders [33] or CNN [34] have been proposed for spatial CS to extremely fast reconstruct the frames from the compressively sensed measurements.
In conclusion, it is important to say that the SVCS is originally based on single pixel cameras (SPC) to execute spatial multiplexing and enable video reconstruction by accelerating the acquisition process. However, there have been many extensions to the SPC. One of the famous extensions aims to parallelize the SPC architecture by applying many sensors to separately sample spatial areas of the moving scene [55,56]. These prototypes are better than traditional SPC not only in terms of the manufacturing cost but also in terms of the measurement rate and the quality of the captured frames.
4.3. Spatio-Temporal VCS
Video compressive sensing approaches are mostly based on either temporal or spatial domain. These approaches consider one single domain to compress data which is not optimal. However, spatio-temporal data can convey more features that can be used to optimize the sensing and the recovery processes. In fact, the spatio-temporal approach consists in sampling both the temporal and spatial information simultaneously. In this case, the sensing matrix becomes a sensing cube that encode the video i nits 3rd dimension. In [57], T. Xiong et al. implemented a hardware-friendly algorithm for video compressive sensing where the sensing cube, that is composed of either 1 or 0, is used to encode the video signal into a single coded image. Then, the recovery phase is processed using dictionary and simple sparse recovery. However, the computational cost of the recovery process used in [57] remains one the major limitations of this spatiotempral VCS algorithm. In [58], the same research team improved their previous work, by adding a CNN layer to extract key features from the frames to enhance the recovery process and improve the sensing quality. D. Lam et al. [59] propose a video sampling process divided into 2 steps. Firstly, the 3D image volume is decomposed by a 3D Wavelet transform. Then, a second measurement is obtained by a Noiselet transform. Using this sampling paradigm, the CS reconstruction, with Total Variation, performs successfully.
Motivated by the success of convolutional neural network(CNN) in image processing, 3D CNN are commonly used for decades to extract useful features from video signals. In [60], the authors apply a 3D CNN network to extract spatial and temporal features for action recognition. This architecture is used later in [61] to design a 3D video compressive sensing algorithm. One other similar approach is proposed in [62] which proposes a 3D Convolutional network that is more suitable to extract spatiotemporal features compared to 2D ConvNets by exploring the effect of different depths and filter sizes.
In the later work of Weil et al. [63], an improved version of ISTA-Net+ is proposed which learns an adaptive sampling matrix by simultaneously optimizing the sampling and reconstruction procedures. A two-phase joint deep reconstruction is adopted to selectively exploit spatial-temporal information, consisting of a temporal alignment with a learnable occlusion mask and a multiple frames fusion with spatial temporal feature weighting (see Figure 8). The separated frames (key and non-key) reconstructions are based on the attention mechanism that applies an adaptive shrinkage-thresholding for discriminative transform coefficients suppression. A specific measure loss is also proposed to ease the network optimization by reducing the inverse mapping space. Accordingly, the reconstruction network is able to adaptively exploit spatial-temporal correlations to recover the full video from few 3D samples of the original video tensor.
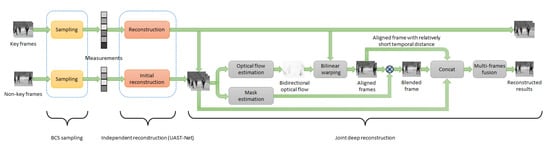
Figure 8.
Overall architecture of STEM-Net.
5. Video Single-Pixel Imaging and Video Snapshot Compressive Imaging
According to the modulation, video compressive sensing approaches can be categorized into two main groups: Single-Pixel Imaging systems and Video Snapshot Compressive Imaging (SCI).
5.1. Single Pixel Imaging
Single-Pixel Imaging (SPI) is a novel paradigm that enables a device, equipped only with a single point detector called single pixel camera (SPC), to produce high-quality images. The general implementation of the SPI can be schematized as in Figure 9.
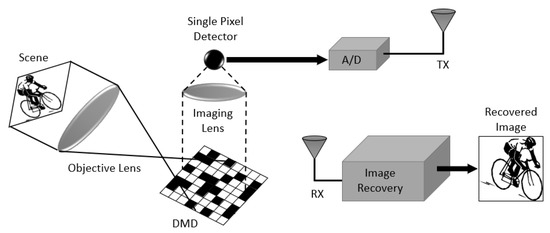
Figure 9.
Single Pixel Camera diagram.
Technically, the single-pixel camera essentially detects the inner product of the video and a set of patterns [4]. Then, need to solve an inverse problem to reconstruct the original scene from the raw measurement.
Mathematically, let , where is the t-th frame of the detected video. The SPC enables the access to the measurement vector , then the acquisition step can be modeled by:
where is a dense matrix that encode the list of patterns (one row represents one pattern of the modulator) and defines the integration time for each pattern. At each time step, is a matrix containing a set of M patterns. Generally, it is an orthogonal basis (e.g., Fourier, Wavelet, Hadamard). Indeed, using these structural matrices enables to accelerate the computational process because random matrices require huge storage resources which affect the computational mechanism (Figure 10).
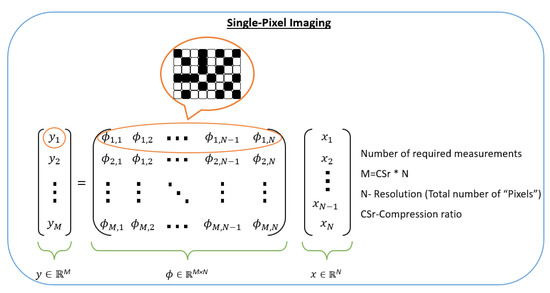
Figure 10.
Model of Single Pixel Imaging.
The most challenging part åin single pixel imaging is the reconstruction paradigm. Therefore, many approaches were proposed in the last decade. These reconstruction approaches can be categorized into two groups: traditional approaches and deep learning based model.
In traditional strategies we find -regularized approaches [64] and -regularized approaches [4,65] called also Total-variation approaches. Each approach has its advantages and drawbacks. For -regularized approaches: they are faster but they lead to decreased frame quality. However, -regularized approaches are much slower but they lead to better image quality.
Recently, deep neural networks have been used successfully in signal pixel imaging reconstruction problems. In [66], A. l. Mur et al. have exploited the spatio-temporal features of video and proposed a Convolutional Gated Recurrent Units (ConvGRU) based algorithm to reconstruct video frames already captured by a single pixel camera. N. Ducros et al. [67] defined a generic convolutional network to recover the original video. In addition, in [47], an auto-encoder network is proposed for SPI reconstruction purposes. However, this approach does not exploit the temporal features of video scenes since it enables to reconstruct the video frames independently.
5.2. Video Snapshot Compressive Imaging
Compressing high-speed videos is already possible due to the huge research work done in video snapshot compressive imaging (SCI). The video SCI system is composed of two main networks: the hardware encoder and the software reconstruction (decoder) network [68]. The hardware decoder represents the optical imaging framework and the software decoder denotes the reconstruction algorithm. The hardware decoder aims to compress the 3D video signal into a 2D measurement and the compression is done across the third dimension (the temporal dimension in this case). This compression aims to avoid huge memory storage and transmission bandwidth. The optical system is called the coded aperture compressive temporal imaging (CACTI) [69] system. In this system ad during one exposure time, the video scene is gathered by an objective lens and then coded by a temporal-variant mask (shifting physical mask [69,70] or different patterns on a Digital Micromirror Device (DMD) [7,71]). Then, the output is detected by a Charge Coupled Device (CCD) and then integrated into one single measurement frame.
From a mathematical perspective, a video SCI system captures a dynamic scene of B frames (h and w are the height and the weight of the frame, respectively) is modulated by B masks before being integrated into one single measurement frame by a camera sensor in one exposure time (B frame). This operation is expressed as follows:
where ∘ and denote the Hadamard product and noise, respectively. Then, we define and . Correspondingly, we define as:
The measurement y can then be expressed as:
where , for . We have in this case a matrix that is highly structured and sparse. Depending on the theoretical study in [72], the original video can be reconstructed from the single measurement frame y (Figure 11).
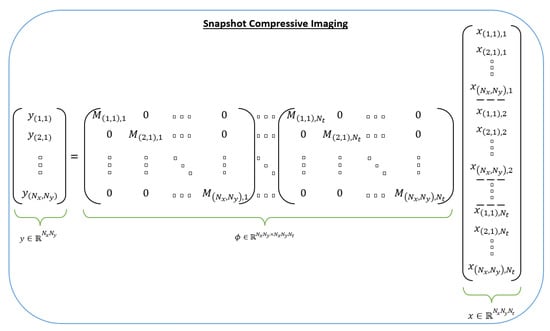
Figure 11.
Model of Snapshot Compressive Imaging.
The second important part of video SCI is the reconstruction process which aim to recover the original video from the 2D measurement frames and the masks. This process is crucial to have a practical and efficient video SCI system. In the literature, the reconstruction algorithms could be categorized into two categories: optimization based methods and Deep Learning based algorithms. The optmization based algorithms, such as GAP-TV [44], GMM [43], DeSCI [73], and PnP-FFDNet [74], require huge computational resources and large reconstruction time. For instance, DeSCI, that has led recently the state-of-the-art optimization based approaches, takes hours to generate a video from one single measurement frame). However, GAP-TV is a fast algorithm but it can not provide a good reconstruction. In general, to use an algorithm in a real world application, we need a PSNR ⩾ 30 which is not the case for GAP-TV [74].
In Deep Learning based methods [34,45,48,53,75,76,77,78,79], these problems have been ameliorated.
Indeed, Z. Cheng et al. [75] proposed a bidirectional neural network based method to reconstruct the video frames from the measurement matrix and the masks by exploiting the correlation of sequential frames. The idea behind this approach, illustrated in Figure 12, is based on two main sub-networks: A deep convolutional neural network (CNN) with ResBlock [80] and a self attention module [81] in order to reconstruct the first frame (reference frame), and a bidirectional neural network to reconstruct the rest of the frames. To improve the quality of the reconstruction, an adversarial training is defined with the Mean Square Error (MSE) loss. However, the main drawback of BIRNAT is its impractical computational time in the training phase (weeks to train a model of size [82]) and its huge GPU memory consumption that make it unsuitable for large-scale SCI applications especially with the high-resolution videos used in real life.
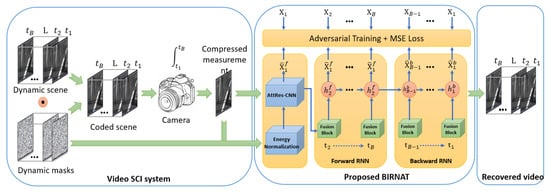
Figure 12.
BIRNAT Architecture.
The GPU memory storage problem in the training phase is ameliorated in RevSCI-net [82] by introducing a reversible CNN network to free the memory from the middle activation generated by each layer of the network. This technique enables to redue the memory cost from to (where N is the number of layers). RevSCI-Net rely on an end-to-end CNN model exploring the temporal and spatial correlations of the original video.
In addition to the speed issue, some deep learning based reconstruction algorithms, such as BIRNAT, suffer from flexibility and adaptability problems which affect their performances. Therefore, Z. Wang et al. [83] introduced a Meta Modulated Convolutional Network (MetaSCI) as a new scalable and adaptive reconstruction model. MetaSCI is a fully CNN approach that exploits the fast adaption encoding paradigm in order to efficiently reconstruct the video frames in terms of memory consumption.
Recently, an ensemble learning based algorithm is proposed in [84], originally exploited in inverse problems, to enhance the scalability of video SCI reconstruction approaches. Zongliang et al. [85] still work on combining iterative algorithms and deep neural networks. An online Plug-and-play algorithm is proposed to adaptively update the model’s parameters using the PnP iteration, which enhance the network’s noise resistance. The second part of the paper focus on color SCI videos. The authors present an ADMM optimization and deep neural network to improve the output quality. Finally, a deep equilibrium-based model is proposed in [86] that combines data-driven regularization and stable convergence to deal with the problems of memory requirement and unstable reconstruction in some exiting approaches.
Obviously, both categories have their advantages and drawbacks, which make this research direction challenging and very promising for the future if we aim to come up with a memory friendly model that consume less computational cost for our daily life applications.
6. Comparative Study
6.1. Optimization-Based VCS Algorithms
Table 1 presents the complexity of optimization-based sparse recovery algorithms as well as the minimum measurement requirement. It shows also some challenging issues considered as crucial when designing CS reconstruction algorithms: Sparsity information, Noise resistance and hardware feasibility:

Table 1.
Complexity, minimum measurement requirement and crucial properties of CS recovery algorithms.
- The sparsity information: it may not be provided for the reconstruction process
- Noise resistance: It is important to design a recovery algorithm where the measurements are not affected by measurement noise
- Hardware feasibility: low-complexity algorithms can usually be implemented on hardware devices for real-world applications
6.2. Deep Learning-Based VCS Algorithms
6.2.1. Quantitative Comparison
Training Details
It is important to mention that video compressive sensing algorithms (acquisition and reconstruction) does not have a particular training dataset and can be applied on any scene. Indeed, all experiments are trained on Densely Annotated VIdeo Segmentation (DAVIS2017) [87] dataset. DAVIS2017 is an object segmentation dataset that contains 90 different videos with a resolution of . To efficiently train the state-of-the-art algorithms, 6516 videos of size are generated from DAVIS2017 to learn different parameters on the same compression ratio . Then, all algorithms are tested on 6 simulation datasets: Aerial, Drop, Kobe, Runner, Traffic, Vehicle to evaluate their performances. All experiments are tested on the RTX 2080 GPU and Intel® Core™ i7-9700K CPU (3.6 GHz, 32 GB memory).
Comparison Metrics
The following three metrics are employed to compare different approaches:
- Peak Signal to Noise Ratio (PSNR) [46]: Quality metric
- Structural Similarity Index (SSIM) [46]: Quality metric
- Reconstruction Time: this metric is used to prove whether the algorithm can be applied in real-time applications at the testing step
Benchmark Results
We present a quantitative comparison to compare the quality performances of the following VCS algorithms: GAP-TV [44], DeSCI [73], PnP-FFDNet [74], Pnp-FastDVDNet [88], GAP-FastDVDNet(online) [85], DE-RNN [86], DE-GAP-FFDnet [86], E2E-CNN [48], BIRNAT [75], MetaSCI [83], RevSCI [82], DeepUnfold-VCS [51], GAP-Unet-S12 [76], ELP-Unfolding [84].
Table 2 summarizes the comparison of several VCS algorithms on PSNR, SSIM and the reconstruction time. From this table, different performance results are plotted in Figure 13, Figure 14, Figure 15 and Figure 16 for visualization purposes. From Figure 13 and Figure 14, we notice that iterative algorithms (GAP-TV, DeSCI, PnP-FFDnet and PnP-FastDVDnet) provide inferior quality performance results (both in terms of PSNR and SSIM) with low recovery speed (from one second to even hours) which threaten their hardware implementation for real-time applications. However, the other deep learning-based algorithms outperforms these iterative approaches in terms of quality performances with faster reconstruction time (<1 s). These performances can prove the potential usability of deep learning-based approaches in real-time applications. From Figure 15 and Figure 16, we notice that DeSCI, the iterative algorithm, provide little improvement over some deep learning-based algorithms on the Kobe, Runner and Drop (e.g., PSNR: and over BIRNAT, and over MetaSCI on Drop, Kobe and Runner, respectively). Indeed, these datasets are characterized by high-speed motions of some objects. However, we infrequently find these features in DAVIS2017 dataset, which explain these results. As a result, high-speed motions datasets are recommended while training these deep learning-based algorithms to enhance their quality performances. In addition, we note that the recent ensemble learning-based algorithm (ELP-Unfolding) is proposed to enhance the performance of the previous algorithms by strategically generate and combine multiple models which confirm the fact to consider this technique as a promising research topic in video reconstruction. In addition, we notice from Figure 15 and Figure 16, that DeepUnfold-VCS outperforms the rest of the proposed algorithms in terms of quality performances (PSNR and SSIM) on almost all experiments. In fact, the authors propose an algorithm that combines iterative strategy and deep learning. In addition, they used a deep unfolding approach and exploit its interpretability to reconstruct the video scene. In the other hand, GAP-net-Unet-S12 is the fastest VCS reconstruction approach with good quality performances since it proposes also to combine ADMM-net and neural networks. However, in contrast to DeepUnfold-VCS, it proposes a CNN-based network which much faster than recurrent neural nets. It can be used in real-time applications that require prompt capture and reconstruction time. GAP-net-Unet-S12 can acquire and reconstruct up to 250 measurement per second. To conclude, recent deep learning-based approaches proposed for VCS purposes present good quality performances and research in this field becomes very competitive and very challenging to come up with the fastest algorithm.

Table 2.
Quantitative comparison of different approaches for video compressive sensing system. The average results of PSNR in dB, SSIM and reconstruction time (seconds) per measurement. GAP-TV and DeSCI are tested on CPU while other approaches are on GPU.
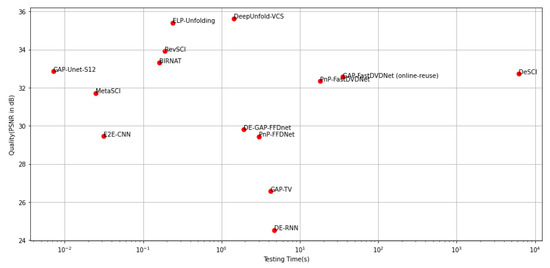
Figure 13.
Trade-off between quality (in PSNR) and testing time of several VCS reconstruction algorithms.
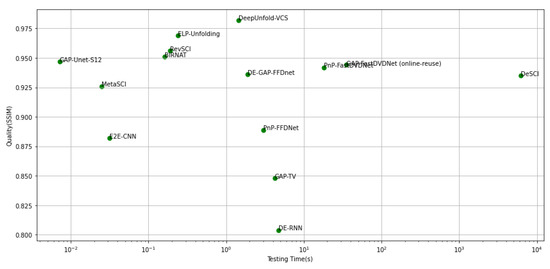
Figure 14.
Trade-off between quality (in SSIM) and testing time of several VCS reconstruction algorithms.
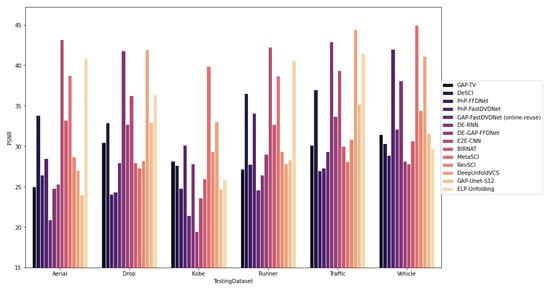
Figure 15.
Performance comparison based on PSNR obtained by several VCS reconstruction algorithms on 6 grayscale benchmark datasets.
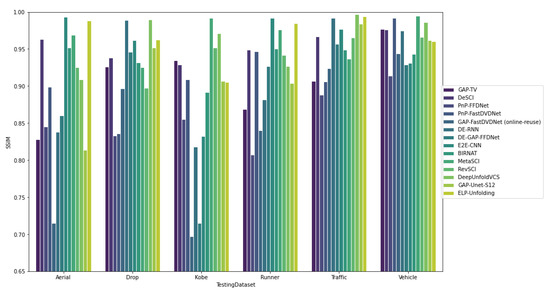
Figure 16.
Performance comparison based on SSIM obtained by several VCS reconstruction algorithms on 6 grayscale benchmark datasets.
6.2.2. Qualitative Comparison
Different VCS approaches, together with their specific advantages and limitations, are summarized in Table 3 and Table 4 to compare their qualitative performances that should be taken into consideration while implementing the network for a particular application.

Table 3.
Different algorithms for video compressive sensing (Part 1).

Table 4.
Different algorithms for video compressive sensing (Part 2).
7. Compressive Sensing: Research Challenges and Opportunities
Data today is generated at exponentially growing rates which creates unbearable demands on the sensing, storage and processing devices. Indeed, thousands of data centers are built worldwide to store this huge amount of data which leads to extremely high power that is consumed on acquiring and processing. As long as we generate more data there is an urgent need for novel data acquisition and processing concepts such as compressive sensing.
Obviously, there is a tremendous intellectual progress in compressive sensing and sparse representation systems. Therefore, many mathematical concepts such as probability theory, convex optimization and reconstruction algorithms become an essential toolbox for many researchers and engineers to design and develop real-world applications.
Hence, in the future, we are going to talk about designing hybrid systems that integrate hardware and software, where these two systems are implemented simultaneously from the beginning using the mathematical concepts described above.
Also, a new research direction has appeared with deploying a video compressive sensing system with edge computing to optimize the memory storage and bandwidth [89]. In addition, theoretical studies on detection algorithms directly from the snapshot compressed measurement have already started [90]. Finally, we can say that compressive sensing allows us to think about data, complexity, algorithms and hardware at the same time. In a nutshell, the answer will be an algorithm with better flexibility, accuracy and speed.
8. Conclusions
In this review, after reformulating the compressive sensing paradigm, we have closely reviewed the fundamentals of image and video compresssive sensing. In addition, we analyzed the backbone deep learning based architectures for image and video CS in order to provide the CS community the essential background knowledge. Indeed, we classified different concepts of compressive sensing in general and image and video compressive sensing in particular into categories to facilitate their understanding. The methods have been analyzed in this review from different angles: network architecture, contribution, complexity and performance results. In the end, we have discussed the future research challenges of compressive sensing. In conclusion, compressing sensing is a promising research direction in order to optimize data gathering and processing. Although there have been great achievements in this field, there is still room for improvement in image and video compressive sensing using neural networks.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing original draft preparation and visualization: W.S.; writing review and editing: W.S. and F.C.; supervision, project administration and funding acquisition: D.H., F.C., J.-P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the sensors generation project of Nouvelle Aquitaine region (2018-1R50214).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar]
- Amarlingam, M.; Mishra, P.K.; Rajalakshmi, P.; Giluka, M.K.; Tamma, B.R. Energy efficient wireless sensor networks utilizing adaptive dictionary in compressed sensing. In Proceedings of the 2018 IEEE 4th World Forum on Internet of Things (WF-IoT), Singapore, 5–8 February 2018; pp. 383–388. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Veeraraghavan, A.; Reddy, D.; Raskar, R. Coded Strobing Photography: Compressive Sensing of High Speed Periodic Videos. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 671–686. [Google Scholar] [CrossRef]
- Wakin, M.; Laska, J.N.; Duarte, M.F.; Baron, D.; Sarvotham, S.; Takhar, D.; Kelly, K.F.; Baraniuk, R.G. Compressive imaging for video representation and coding. In Proceedings of the Picture Coding Symposium, Beijing, China, 24–26 April 2006; pp. 1–6. [Google Scholar]
- Reddy, D.; Veeraraghavan, A.; Chellappa, R. P2C2: Programmable pixel compressive camera for high speed imaging. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 329–336. [Google Scholar]
- Kittle, D.; Choi, K.; Wagadarikar, A.; Brady, D.J. Multiframe image estimation for coded aperture snapshot spectral imagers. Appl. Opt. 2010, 49, 6824–6833. [Google Scholar] [CrossRef]
- Hitomi, Y.; Gu, J.; Gupta, M.; Mitsunaga, T.; Nayar, S.K. Video from a single coded exposure photograph using a learned over-complete dictionary. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 287–294. [Google Scholar]
- Candés, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef] [Green Version]
- Palangi, H.; Ward, R.; Deng, L. Distributed Compressive Sensing: A Deep Learning Approach. IEEE Trans. Signal Process. 2016, 64, 4504–4518. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Candes, E.J.; Plan, Y. A Probabilistic and RIPless Theory of Compressed Sensing. IEEE Trans. Inf. Theory 2011, 57, 7235–7254. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.L.; Shin, Y. Deterministic sensing matrices in compressive sensing: A survey. Sci. World J. 2013, 2013, 192795. [Google Scholar] [CrossRef] [Green Version]
- Rousseau, S.; Helbert, D. Compressive Color Pattern Detection Using Partial Orthogonal Circulant Sensing Matrix. IEEE Trans. Image Process. 2020, 29, 670–678. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 1998, 20, 33–61. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. The Dantzig selector: Statistical estimation when p is much larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [Green Version]
- Combettes, P.L.; Pesquet, J.-C. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Springer: New York, NY, USA, 2011; pp. 185–212. [Google Scholar]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef] [Green Version]
- Figueiredo, M.A.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Krstulovic, S.; Gribonval, R. MPTK: Matching pursuit made tractable. In Proceedings of the 2006 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toulouse, France, 14–19 May 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 3, p. III. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.-L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comp. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Tropp, J. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef] [Green Version]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef] [Green Version]
- Liu, E.; Temlyakov, V.N. The orthogonal super greedy algorithm and applications in compressed sensing. IEEE Trans. Inf. Theory 2012, 58, 2040–2047. [Google Scholar] [CrossRef]
- Xuan, Y.; Yang, C. 2Ser-Vgsr-Net: A Two-Stage Enhancement Reconstruction Based On Video Group Sparse Representation Network For Compressed Video Sensing. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Mousavi, A.; Patel, A.B.; Baraniuk, R.G. A deep learning approach to structured signal recovery. In Proceedings of the 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–2 October 2015; pp. 1336–1343. [Google Scholar] [CrossRef] [Green Version]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. ReconNet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Yao, H.T.; Dai, F.; Zhang, S.L.; Zhang, Y.D.; Tian, Q.; Xu, C.S. DR2 -Net: Deep residual reconstruction network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1828–1837. [Google Scholar]
- Ito, D.; Takabe, S.; Wadayama, T. Trainable ISTA for Sparse Signal Recovery. IEEE Trans. Signal Process. 2019, 67, 3113–3125. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Bao, Q.; Chen, Z. ADMM–Net: A Deep Learning Approach for Parameter Estimation of Chirp Signals under Sub-Nyquist Sampling. IEEE Access 2020, 8, 75714–75727. [Google Scholar] [CrossRef]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Image Compressed Sensing Using Convolutional Neural Network. IEEE Trans. Image Process. 2020, 29, 375–388. [Google Scholar] [CrossRef]
- Canh, T.N.; Jeon, B. Multi-Scale Deep Compressive Sensing Network. In Proceedings of the 2018 IEEE Visual Communications and Image Processing (VCIP), Taichung, Taiwan, 9–12 December 2018; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Canh, T.N.; Jeon, B. Difference of Convolution for Deep Compressive Sensing. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 2105–2109. [Google Scholar] [CrossRef]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Scalable Convolutional Neural Network for Image Compressed Sensing. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12282–12291. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, X.; Liao, X.; Llull, P.; Brady, D.J.; Sapiro, G.; Carin, L. Video compressive sensing using Gaussian mixture models. IEEE Trans. Image Process. 2014, 23, 4863–4878. [Google Scholar] [CrossRef]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2539–2543. [Google Scholar]
- Iliadis, M.; Spinoulas, L.; Katsaggelos, A.K. Deep fully-connected networks for video compressive sensing. Digit. Signal Process. 2018, 72, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Higham, C.F.; Murray-Smith, R.; Padgett, M.J.; Edgar, M.P. Deep learning for realtime single-pixel video. Sci. Rep. 2018, 8, 2369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiao, M.; Meng, Z.; Ma, J.; Yuan, X. Deep learning for video compressive sensing. APL Photonics 2020, 5, 030801. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for Image Restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Lam, E.Y.; Ke, J. Temporal compressive imaging reconstruction based on a 3D-CNN network. Opt. Express 2022, 30, 3577–3591. [Google Scholar] [CrossRef]
- Zheng, S.; Yang, X.; Yuan, X. Two-Stage is Enough: A Concise Deep Unfolding Reconstruction Network for Flexible Video Compressive Sensing. arXiv 2022, arXiv:2201.05810. [Google Scholar]
- Zhao, C.; Ma, S.; Zhang, J.; Xiong, R.; Gao, W. Video compressive sensing reconstruction via reweighted residual sparsity. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 1182–1195. [Google Scholar] [CrossRef]
- Xu, K.; Ren, F. CSVideoNet: A real-time end-to-end learning framework for high-frame-rate video compressive sensing. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1680–1688. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, H.; Salman Asif, M.; Sankaranarayanan, A.C.; Veeraraghavan, A. FPA-CS: Focal plane array-based compressive imaging in short-wave infrared. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2358–2366. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Gupta, M.; Sankaranarayanan, A.C. LiSens—A Scalable Architecture for Video Compressive Sensing. In Proceedings of the 2015 IEEE International Conference on Computational Photography (ICCP), Houston, TX, USA, 24–26 April 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Xiong, T.; Rattray, J.; Zhang, J.; Thakur, C.S.; Chin, S.; Tran, T.D.; Etienne-Cummings, R. Spatiotemporal compressed sensing for video compression. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017. [Google Scholar]
- Wang, X.; Zhang, J.; Xiong, T.; Tran, T.D.; Chin, S.P.; Etienne-Cummings, R. Using deep learning to extract scenery information in real time spatiotemporal compressed sensing. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar]
- Lam, D.; Wunsch, D. Video compressive sensing with 3-D wavelet and 3-D noiselet. In Proceedings of the 19th IEEE International Conference on Image Processing (ICIP ’12), Orlando, FL, USA, 30 September–3 October 2012. [Google Scholar] [CrossRef]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Xie, X.; Liu, W.; Pan, Q. A hybrid-3D convolutional network for video compressive sensing. IEEE Access 2020, 8, 20503–20513. [Google Scholar] [CrossRef]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3D convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4489–4497. [Google Scholar]
- Wei, Z.; Yang, C.; Xuan, Y. Efficient Video Compressed Sensing Reconstruction via Exploiting Spatial-Temporal Correlation with Measurement Constraint. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar]
- Rousset, F.; Ducros, N.; Farina, A.; Valentini, G.; D’Andrea, C.; Peyrin, F. Adaptive Basis Scan by Wavelet Prediction for Single-pixel Imaging. IEEE Trans. Comput. Imaging 2016, 3, 36–46. [Google Scholar] [CrossRef] [Green Version]
- Baraniuk, R.G.; Goldstein, T.; Sankaranarayanan, A.C.; Studer, C.; Veeraraghavan, A.; Wakin, M.B. Compressive video sensing: Algorithms, architectures, and applications. IEEE Signal Process. Mag. 2017, 34, 52–66. [Google Scholar] [CrossRef]
- Mur, A.L.; Peyrin, F.; Ducros, N. Recurrent Neural Networks for Compressive Video Reconstruction. In Proceedings of the IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 1651–1654. [Google Scholar]
- Ducros, N.; Lorente Mur, A.; Peyrin, F. A completion network for reconstruction from compressed acquisition. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 619–623. [Google Scholar]
- Yuan, X.; Brady, D.; Katsaggelos, A.K. Snapshot compressive imaging: Theory, algorithms and applications. IEEE Signal Process. Mag. 2020, 38, 65–88. [Google Scholar] [CrossRef]
- Llull, P.; Liao, X.; Yuan, X.; Yang, J.; Kittle, D.; Carin, L.; Sapiro, G.; Brady, D.J. Coded aperture compressive temporal imaging. Opt. Express 2013, 21, 10526–10545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koller, R.; Schmid, L.; Matsuda, N.; Niederberger, T.; Spinoulas, L.; Cossairt, O.; Schuster, G.; Katsaggelos, A.K. High spatio-temporal resolution video with compressed sensing. Opt. Express 2015, 23, 15992–16007. [Google Scholar] [CrossRef]
- Sun, Y.; Yuan, X.; Pang, S. Compressive high-speed stereo imaging. Opt. Express 2017, 25, 18182–18190. [Google Scholar] [CrossRef]
- Jalali, S.; Yuan, X. Snapshot compressed sensing: Performance bounds and algorithms. IEEE Trans. Inf. Theory 2019, 65, 8005–8024. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yuan, X.; Suo, J.; Brady, D.J.; Dai, Q. Rank Minimization for Snapshot Compressive Imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2990–3006. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Liu, Y.; Suo, J.; Dai, Q. Plug-and-Play Algorithms for Large-Scale Snapshot Compressive Imaging. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1444–1454. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, R.; Wang, Z.; Zhang, H.; Chen, B.; Meng, Z.; Yuan, X. BIRNAT: Bidirectional recurrent neural networks with adversarial training for video snapshot compressive imaging. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Meng, Z.; Jalali, S.; Yuan, X. Gap-net for snapshot compressive imaging. arXiv 2020, arXiv:2012.08364. [Google Scholar]
- Yuan, X.; Pu, Y. Parallel lensless compressive imaging via deep convolutional neural networks. Opt. Express 2018, 26, 1962–1977. [Google Scholar] [CrossRef]
- Ma, J.; Liu, X.; Shou, Z.; Yuan, X. Deep tensor admm-net for snapshot compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Iliadis, M.; Spinoulas, L.; Katsaggelos, A.K. Deepbinarymask: Learning a binary mask for video compressive sensing. Digit. Signal Process. 2020, 96, 102591. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Cheng, Z.; Chen, B.; Liu, G.; Zhang, H.; Lu, R.; Wang, Z.; Yuan, X. Memory-efficient network for large-scale video compressive sensing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Wang, Z.; Zhang, H.; Cheng, Z.; Chen, B.; Yuan, X. Metasci: Scalable and adaptive reconstruction for video compressive sensing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Yang, C.; Zhang, S.; Yuan, X. Ensemble learning priors unfolding for scalable Snapshot Compressive Sensing. arXiv 2022, arXiv:2201.10419. [Google Scholar]
- Wu, Z.; Yang, C.; Su, X.; Yuan, X. Adaptive Deep PnP Algorithm for Video Snapshot Compressive Imaging. arXiv 2022, arXiv:2201.05483. [Google Scholar]
- Zhao, Y.; Zheng, S.; Yuan, X. Deep Equilibrium Models for Video Snapshot Compressive Imaging. arXiv 2022, arXiv:2201.06931. [Google Scholar]
- Pont-Tuset, J.; Perazzi, F.; Caelles, S.; Arbelaez, P.; Sorkine-Hornung, A.; Gool, L.V. The 2017 DAVIS challenge on video object segmenta tion. arXiv 2017, arXiv:1704.00675. [Google Scholar]
- Yuan, X.; Liu, Y.; Suo, J.; Durand, F.; Dai, Q. Plug-and-play algorithms for video snapshot compressive imaging. arXiv 2021, arXiv:2101.04822. [Google Scholar]
- Liu, S.; Liu, L.; Tang, J.; Yu, B.; Wang, Y.; Shi, W. Edge computing for autonomous driving: Opportunities and challenges. Proc. IEEE 2019, 107, 1697–1716. [Google Scholar] [CrossRef]
- Lu, S.; Yuan, X.; Shi, W. An integrated framework for compressive imaging processing on CAVs. In Proceedings of the ACM/IEEE Symposium on Edge Computing (SEC), San Jose, CA, USA, 12–14 November 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).