Searching Strategies with Low Computational Costs for Multiple-Vehicle Bike Sharing System Routing Problem

Abstract

We have already proposed a multiple-vehicle bike sharing system routing problem (mBSSRP) to adjust the number of bicycles at each port using multiple vehicles in short time. However, there are many strict constraints in the mBSSRP, thus it is difficult to obtain feasible solutions of the mBSSRP for some instances. To obtain feasible solutions of the mBSSRP, we have proposed a mBSSRP with soft constraints (mBSSRP-S) that removes some constraints from mBSSRP and appends violations to an objective function as penalties, and a searching strategy that explores both the feasible and infeasible solution spaces. Numerical experiments indicated that solving mBSSRP-S to obtain feasible solutions of mBSSRP results in better performance than solving mBSSRP directly. However, mBSSRP-S includes infeasible solutions of mBSSRP, thus the neighborhood solutions and computational costs increase. In this study, we propose search strategies with low computational costs while maintaining performance. In particular, we propose two search strategies: the first one is to reduce neighborhood solutions to obtain a feasible solution in a short time before finding a feasible solution of the mBSSRP, and the second one is to change the problem to be solved (mBSSRP or mBSSRP-S) after a feasible solution is obtained and to search good near-optimal solutions in a short time. As the first search strategy, we propose two search methods for reducing the number of neighborhood solutions in the Or-opt and the CROSS-exchange and compare their performance with our previous results. From numerical experiments, we confirmed that a feasible solution can be obtained within a short time by exploring only the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange as the neighborhood solutions. Next, as the second search strategy after a feasible solution of mBSSRP is obtained, we propose four search methods and compare their performance with our previous results. Numerical experiments show that the search method that only searches for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange with hard constraints after obtaining a feasible solution can obtain short tours within a short time.

1. Introduction

Bicycle sharing systems (BSSs) have been introduced in many cities around the world as a new public transportation system. Currently, more than 1,700 programs of BSSs are operating in the world [1], for instance, BIXI in Montréal [2], Velib’ in Paris [3], docomo bike share in Tokyo [4], citybike in Vienna [5], Citi Bike in New York [6], Capital bikeshare in Washington D.C. [7], BULEbikes in Boston [8] and Bicing in Barcelona [9].

A BSS consists of many distributed automatic rental ports and many rental bicycles. A registered user can rent a bicycle at a port, use it for a short trip and return it to a different port. A BSS is not only a convenient service, but also it can reduce greenhouse gas and traffic congestion issues. For example, Zhang et al. (2018) [10] have estimated that the introduction of a BSS at Shanghai saved 8358 tonnes of petrol, and reduced CO${}_2$ and ${\mathrm{NO}}_{\mathrm{x}}$ emissions 25,240, and 64 tonnes, respectively in 2016.

In a BSS, almost all ports are in either an empty or full state after a while. An empty bicycle port implies that a user cannot rent a bicycle, whereas a full bicycle port implies that a user cannot return a bicycle. Thus, full or empty states lead to dissatisfaction of users. In addition, broken bicycles are left unattended. Consequently, users’ frustration is further increased. To address these issues, several capacitated vehicles need to relocate bicycles among ports so that sufficient bicycles are available at each port. If operators can execute repositioning works efficiently, users will not have experience that they cannot rent or return bicycles and BSS companies can reduce labor costs and carbon emissions of vehicles. Thus, both users and BSS companies benefit.

Recently, many studies have been conducted on repositioning bicycles of a BSS. The repositioning of BSS can be divided into two cases.

The first one is a static case. In the static case problem, the number of bicycles does not change at each port while the bicycles are restored by the vehicle, because the system assumes that the bicycles are not moving much at midnight or after operation hours. As for the static case problem, Dell’Amico et al. (2014) [11] proposed a bike sharing rebalancing problem (BRP) and formulated BRP as a mixed integer linear programming problem, and they solved BRP using the branch-and-cut algorithm for the 22 real world instances collected from the web sites. Then, they proposed a destroy and repair algorithm for the BRP, and tested their algorithm on benchmark instances [12]. Although these studies [11,12] are interesting, they did not consider a time limit constraint: vehicles must return to a depot within a given time limit. Then, it is not guaranteed that all operations will be finished within the working hour in BRP.

On the other hand, Rainer-Harbach et al. (2013) [13] proposed a general variable neighborhood search (VNS) with an embedded variable neighborhood descent for finding efficient vehicle tours of a balancing bicycle sharing system (BBSS). In the BBSS, they considered the time limit constraint, and that a vehicle can visit a port multiple times. Then, they tested their algorithm on benchmark instances of real-world data provided by Citybike in Vienna with up to 90 ports, and the result of numerical experiments showed that their algorithm obtained good solutions in a reasonable time. In addition, Raidl et al. (2013) [14] proposed efficiently determining optimal loading operation of VNS method for finding efficient vehicle tours of the BBSS. They tested the same instances with Rainer-Harbach et al. (2013), and they reported that their method showed better performance than the original VNS. Moreover, Papazek et al. (2013) [15] also address the BBSS, and they proposed two GRASP (Greedy Randomized Adaptive Search Procedure) heuristic approaches and conducted numerical experiments by varying sizes of instances that ranged from 30 to 700. The numerical experiments show that combined PILOT (Preferred Iterative Look Ahead Technique) and GRASP method obtained good performance than VNS for large size instances. In the BBSS, when vehicles start and come back to a depot, the vehicles must be empty. However, if broken bicycles are found in the process of rebalancing operation, they must be repaired at the depot after the rebalancing operation, because the depot has many spare bicycles. Thus, the constraint that vehicles must be empty when vehicles start and come back to the depot is not realistic [13,14,15].

The second one of the repositioning of the bicycle sharing system is a dynamic case. In the dynamic case problem, the number of bicycles is changed at each port while the bicycles are restored by the vehicle. Kloimüllner et al. (2014) [16] extended the BBSS to a dynamic case problem, and proposed a model of a dynamic balancing bicycle sharing system (DBBSS). Then, they applied their previous approach to the DBBSS. The numerical experiments showed that their approach was also effective to DBBSS. Chiariotti et al. (2018) [17] also addressed the dynamic case problem. Then, they tested instances with 280 ports generated by New York City’s CitiBike, and the result of numerical experiments showed that their dynamic strategy obtained better performance than static approach. In the numerical experiments for the dynamic repositioning of BSS, Kloimüllner et al. (2014) and Chiariotti et al. (2018) used Vienna and New York City’s data, respectively. However, it is not clear whether their approaches can be applied to other cities. 

Table 1. Summary of the related literatures.

Paper	Static or Dynamic	Maximum Number of Port Size
Rainer-Harbach et al. (2013)	static	90
Raidl et al. (2013)	static	90
Papazek et al. (2013)	static	700
Kloimüllner et al. (2014)	dynamic	90
Dell’Amico et al. (2014)	static	116
Dell’Amico et al. (2016)	static	564
Chiariotti et al. (2018)	dynamic	280
This study	static	100

summarizes the related literatures.

In our previous study, we formulated a new bicycle sharing system routing problem as “multiple-vehicle bike sharing system routing problem (mBSSRP).” The mBSSRP finds tours within the shortest travel time when multiple vehicles load and unload bicycles at each port. In the mBSSRP, we consider the time limit constraint, and vehicles can start and finish at the depot with bicycles. Although we treated the static case problems, the mBSSRP is close to a real-life situation. As a result of solving the mBSSRP using a mixed-integer linear programming (MIP) solver [18], an optimal solution is obtained for small-size instances. However, we cannot obtain an optimal solution for large-size instances within a reasonable time frame. Thus, we proposed local search methods to obtain approximate solutions of mBSSRP within a short time [19]. Nevertheless, owing to some strict constraints of mBSSRP, the proposed methods could not obtain feasible solutions for some instances. Therefore, we proposed a “multiple-vehicle bike sharing system routing problem with soft constraints (mBSSRP-S) ” that removes some constraints from the mBSSRP and appends violations of the mBSSRP to the objective function as penalties [20]. In Ref. [20], we also proposed a method that controls the execution of the Or-opt [21] and the CROSS-exchange [22] with the tabu search method [23,24,25] for solving mBSSRP and mBSSRP-S. Numerical experiments show that solving mBSSRP-S to obtain feasible solutions of mBSSRP achieves good performance when compared to solving directly mBSSRP [20]. However, computational costs increase because neighborhood solutions increase as a result of including infeasible solutions of mBSSRP. Thus, it is necessary to reduce the computational costs while maintaining the performance.

Regarding the reduction in computational costs, there are several discussions for the combinatorial optimization problems. For example, Hasegawa et al. (2002) [26] and Matsuura et al. (2008) [27] introduced a method of limiting the search space to short paths when they solved the TSP (Traveling Salesman Problem). In particular, Hasegawa et al. (2002) used only the 10% nearest neighbors of the cities. Then, Matsuura et al. (2008) used only the near neighbors of the cities. This is because most good TSP solutions have short paths. Motohashi et al. (2008) [28] used a neighborhood list to efficiently solve the TSP. Moreover, Motohashi et al. (2009) [29] used two different candidate lists, that is, the nearest neighbors and quadrant neighbors to solve a large scale TSP. Finally, Taillard et al. (2019) [30] showed that the computational costs of heuristic methods can be significantly reduced by constructing a set of edges that are considered to be included in the optimal solution at first.

Regarding the BSS, Pal et al. (2016) [31] used a candidate list based on nearest neighbors to efficiently solve the static complete rebalancing problem. Then, Dell’Amico et al. (2016) [12] used some formulations to determine whether constraints are satisfied or not to speed up the computation of bike sharing rebalancing problem. Thus, it is important to reduce the computational costs for finding a good rebalancing tour of the BSS, because a BSS has hundreds of ports and it is not practical to wait for hours to find a rebalancing tour of the BSS. Then, the goal of this study is to propose efficient search strategies with low computational costs while maintaining the performance of the mBSSRP.

To reduce computational costs in this study, we focused on the search process and investigated the rate of the Or-opt and the CROSS-exchange executions. The execution rate of the Or-opt that inserts ports in the normal order was 66%, that of the CROSS-exchange that exchanges ports in the normal order was 20%, and the reverse orders of insertion of the Or-opt and exchange of the CROSS-exchange were rarely executed. In addition, we found that once a feasible solution of the mBSSRP is obtained, our conventional method [20] searches for the feasible solutions successively.

From these results of the investigation, in this paper, we propose two search strategies: the first one is to reduce neighborhood solutions to obtain a feasible solution in a short time before finding a feasible solution of the mBSSRP from the mBSSRP-S, and the second one is to change the problem to be solved (mBSSRP or mBSSRP-S) after a feasible solution is obtained and to search good near-optimal solutions in a short time. As the first search strategy, we propose two search methods for reducing the number of neighborhood solutions in the Or-opt and the CROSS-exchange, and compare their performance with our previous results. The results of the numerical experiments indicate that by limiting the neighborhood solutions to the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange, we obtained feasible solutions within a short time while maintaining the performance.

Next, as the second search strategy after obtaining a feasible solution, we proposed four methods in which the searching space is further reduced. The problem to be solved is changed from mBSSRP-S to mBSSRP to explore only feasible solutions. The results of the numerical experiments show that by reducing the number of the neighborhood solution, only searching for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange with hard constraints after obtaining a feasible solution can obtain short tours within a short time. From these numerical experiments, we have succeeded in reducing the computational time while maintaining the performances. Furthermore, we found that after finding a feasible solution, we could find short tours within a short time by solving the hard constraint problem instead of the soft constraint problem.

This paper is structured as follows. In Section 2, we describe the mBSSRP and mBSSRP-S. In Section 3, we present the heuristic method. Then, Section 4 presents the computational costs reduction method. Numerical experiments are reported in Section 5. Finally, conclusions and future works are provided in Section 6.

2. Problem Description

To determine tours that efficiently relocate bicycles using multiple vehicles, we have already proposed mBSSRP and mBSSRP-S [20]. In mBSSRP, the search is executed with satisfying hard constraints of the time and capacity of the vehicles. In mBSSRP-S, these constraints are removed and violations of these constraints are added to the objective function as penalties.

In mBSSRP and mBSSRP-S, given are one depot, n ports and m vehicles. Each port is classified into two types: pickup and delivery ports. In the pickup ports, the number of bicycles is excess and bicycles must be loaded on the vehicle. In the delivery ports, the number of bicycles is lack and bicycles must be delivered. In mBSSRP and mBSSRP-S, vehicles relocate the bicycles from the pickup port to the delivery port. The rules of mBSSRP and mBSSRP-S as follows:

(1)

The vehicles can load bicycles at the depot, because the depot has spare bicycles available.

(2)

All vehicles must leave the depot and return to the depot.

(3)

The number of bicycles does not change during the repositioning process.

(4)

Each port can be visited only once by one vehicle.

Under these rules, reposition of bicycles is executed using vehicles. For details, we refer to Tsushima et al. [20].

2.1. Multiple-Vehicle Bike Sharing System Routing Problem (mBSSRP)

In addition to the rules, the solution of the mBSSRP must satisfy the following two constraints:

(i)

time limit constraint: vehicles must return to the depot within the time limit.

(ii)

capacity constraint: vehicles cannot load more bicycles than their capacity, and the capacity of a vehicle cannot be less than zero.

The purpose of the mBSSRP is to find the tour that minimizes the total travel time of the vehicles among the routes that satisfy the rules (1) to (3) and the constraints of (i) and (ii).

2.2. Multiple-Vehicle Bike Sharing System Routing Problem with Soft Constraints (mBSSRP-S)

In the mBSSRP-S, the hard constraints (i) and (ii) are removed from mBSSRP and these constraints are added to the objective function as penalties if they are violated. Then, the objective function of mBSSRP-S is defined as follows:

$$\begin{array}{ccc}\hfill \mathrm{minimize}& \hfill & \hfill T+\alpha \times P_T+\beta \times (P_{B+}+P_{B-})\end{array}$$

(1)

where T denotes the total travel time and is the objective function of mBSSRP, $P_T$ denotes the time that vehicles worked over the time limit, $P_{B+}$ and $P_{B-}$ are the number of bicycles that could not be loaded or supplied, and $\alpha$ and $\beta$ are the weight coefficients of the penalty. If $P_T$, $P_{B+}$ and $P_{B-}$ are equal to zero, the solution is a feasible solution for mBSSRP.

3. Heuristic Methods

To obtain good approximation solutions of mBSSRP, we proposed a method using the tabu search method [23,24,25]. In the proposed method [20], first, we generate an initial solution by the construction method based on the farthest insertion method. Second, we improve the initial solution by the local searches: the inserting method and the swapping method. Finally, good approximate solutions are searched by the tabu search method, which is one of the metaheuristic methods. The neighborhood solution of the tabu search is constructed by the Or-opt and the CROSS-exchange. Figure 1 represents the flow of the proposed method.

3.1. Construction Method for Generating an Initial Solution

First, to generate an initial solution, we use the construction method based on the farthest insertion method. It is often used as one of the construction methods for the combinatorial optimization problem. The procedure of the construction method is described as follows:

• We randomly select p ports, where p denotes the number of available vehicles.
• Each vehicle constructs a subtour with the depot and one of the selected p ports.
• An unvisited port k, which is the farthest from the depot, is selected.
• The port k is inserted between ports i and j in the subtour where ${\mathrm{\Delta }}_{ikj}=t_{ik}+t_{kj}-t_{ij}$ is minimized.
• Steps 3 and 4 are repeated until all ports are visited once by one vehicle.

When we solve mBSSRP, we continue this operation while the constraints of mBSSRP are satisfied. On the other hand, when we solve mBSSRP-S, we consider only the travel time between ports i and j.

3.2. Local Search Methods for Improving the Initial Solution

To improve the initial solutions, we use the following two local search methods: the inserting method and the swapping method. The inserting and the swapping methods improve a single tour. The inserting and the swapping methods are used after constructing an initial tour and after improving the tour by the tabu search.

In the inserting method, a partial tour $i-j$, whose length covers a maximum of three ports in a tour is inserted into an edge ($k,l$) in the same tour (Figure 2). Then, there are two types of insertion operations as follows: the normal order (Figure 2b) and the reverse order (Figure 2c).

The swapping method swaps a partial tour $i-j$ for a partial tour $k-l$ (Figure 3). Then, there are four types of swapping operations: both partial tours $i-j$ and $k-l$ are exchanged with the normal order (Figure 3b), only the tour $i-j$ is the reverse order (Figure 3c), only the tour $k-l$ is the reverse order (Figure 3d), and both partial tours $i-j$ and $j-k$ are exchanged with the reverse order (Figure 3e).

3.3. Method by Using the Tabu Search

In the local search methods, a solution moves to only good solutions that are better than the current solution. Thus, the solutions get stuck at local optimal solutions. To escape from the local optimal solutions, we use the tabu search method in this study as well as in our previous study [20]. Namely, we used the tabu search to propose search strategies with low computational costs while maintaining the performance for the mBSSRP in this study. The tabu search is one of the powerful meta-heuristic strategies for solving the combinatorial optimization problem. The tabu search is successively used for the vehicle routing problem, which is a similar combinatorial optimization problem to mBSSRP. Moreover, the tabu search also has some advantages, because it has few parameters, leads to easy implementation and has low computational costs. To avoid repetitive operations, a tabu list is used in the tabu search. The tabu list records the previous search history. Thereafter, the solution in the tabu list cannot be selected for a certain temporal duration. This duration is known as a tabu tenure.

In this study, a current solution moves to the best neighborhood solution generated by the Or-opt and the CROSS-exchange. The Or-opt and the CROSS-exchange methods improve the total length of the tours using two different tours. The Or-opt inserts a partial tour $i-j$ of a tour in an edge ($k,l$) in another tour (Figure 4). There are two types of insertions: the normal order (Figure 4b) and the reverse order (Figure 4c). The CROSS-exchange replaces a partial tour $i-j$ in one tour with a partial tour $j-l$ in the other tour (Figure 5). There are four types for swap operations: both partial tours $i-j$ and $k-l$ are exchanged in the normal order (Figure 5b); the partial tour $i-j$ is in the normal order, and the partial tour $k-l$ is in the reverse order (Figure 5c); the partial tour $i-j$ is in the reverse order, and the partial tour $k-l$ is in the normal order (Figure 5d); and both partial tours $i-j$ and $k-l$ are exchanged with the reverse order (Figure 5e). If a neighborhood solution of the CROSS-exchange that exchanges the partial tours $i-j$ and $k-l$ is selected, the combination i and k is memorized in the tabu list. If a neighborhood solution of the Or-opt is selected that inserts the partial $i-j$ into the edge ($k,l$) is selected, the combination i and k is memorized. Thus, the selection of the neighborhood solution that connects port i and port k is prohibited during a certain temporal iteration.

If a feasible solution of mBSSRP is found, the 2-opt method is executed to obtain better solutions than the current one. The 2-opt method replaces two edges by two other edges (Figure 6). If we have never obtained a feasible solution of mBSSRP at once in the tabu search process, the 2-opt method is not executed.

3.4. Dynamically Changing Weight of Penalties

To move good solutions of mBSSRP from the solution of the mBSSRP-S, we must set appropriate values of the weight parameters $\alpha$ and $\beta$ in the objective function (Equation (1)) of the mBSSRP-S. If we set the parameters to small values, we cannot obtain feasible solutions owing to the small values of the parameters. Because the penalty becomes weak even when the solution has many constraint violations. Meanwhile, if we set the parameters to large values, the power of the parameters will be excessively strong, which is the same situation for solving mBSSRP. Thus, we dynamically change the parameters $\alpha$ and $\beta$ according to the solution state.

To adjust the weight parameters $\alpha$ and $\beta$ dynamically, the objective function of the mBSSRP-S was modified as follows:

$$\begin{array}{ccc}\hfill \mathrm{minimize}& \hfill & \hfill T\left(t\right)+\alpha \left(t\right)\times P_T\left(t\right)+\beta \left(t\right)\times (P_{B+}\left(t\right)+P_{B-}\left(t\right))\end{array}$$

(2)

where $\alpha \left(t\right)$ and $\beta \left(t\right)$ represent weight parameters for the time limit, loading and supplying constraints at the tth iteration, $T\left(t\right)$ denotes the total travel time at the tth iteration, $P_T\left(t\right)$ denotes the excess working time beyond the time limit at the tth iteration, $P_{B+}\left(t\right)$ denotes the loading violation of the bicycles at the tth iteration and $P_{B-}\left(t\right)$ denotes the supplying violation of the bicycles at the tth iteration.

The adjustment of the parameters is determined by comparing $\alpha \left(t\right)\times P_T\left(t\right)$ and $\beta \left(t\right)\times (P_{B+}\left(t\right)+P_{B-}\left(t\right))$ at the tth iteration. If the penalty of the time limit $\alpha \left(t\right)\times P_T\left(t\right)$ is larger than the sum of penalties loading and supplying constraints $\beta \left(t\right)\times (P_{B+}\left(t\right)+P_{B-}\left(t\right))$, $\alpha \left(t\right)$ is increased and $\beta \left(t\right)$ is decreased. If the penalty $\beta \left(t\right)\times (P_{B+}\left(t\right)+P_{B-}\left(t\right))$ is larger than $\alpha \left(t\right)\times P_T\left(t\right)$, $\alpha \left(t\right)$ is decreased and $\beta \left(t\right)$ is increased. If $P_T\left(t\right)=0$ or $P_{B+}\left(t\right)+P_{B-}\left(t\right)=0$, a corresponding weight $\alpha \left(t\right)$ or $\beta \left(t\right)$ is not updated. Then, the followings are used for adjusting the parameters:

$\mathrm{if}{p}_{\mathrm{T}}\left(t\right)=0,$

$$\begin{array}{ccc}\hfill \alpha (t+1)& =& \alpha \left(t\right),\hfill \end{array}$$

(3)

otherwise

$$\begin{array}{ccc}\hfill \alpha (t+1)& =& \left\{\begin{array}{cc}\alpha \left(t\right)\hfill & \mathrm{if}\alpha \left(t\right)p_{\mathrm{T}}\left(t\right)=\beta \left(t\right)(p_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)),\hfill \\ \lambda \alpha \left(t\right),\hfill & \mathrm{if}\alpha \left(t\right)p_{\mathrm{T}}\left(t\right)>\beta \left(t\right)(p_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)),\hfill \\ \mu \alpha \left(t\right),\hfill & \mathrm{if}\alpha \left(t\right)p_{\mathrm{T}}\left(t\right)<\beta \left(t\right)(p_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)),\hfill \end{array}\right.\hfill \end{array}$$

(4)

and $\mathrm{if}{p}_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)=0,$

$$\begin{array}{ccc}\hfill \beta (t+1)& =& \beta \left(t\right),\hfill \end{array}$$

(5)

otherwise

$$\begin{array}{ccc}\hfill \beta (t+1)& =& \left\{\begin{array}{cc}\beta \left(t\right),\hfill & \mathrm{if}\alpha \left(t\right)p_{\mathrm{T}}\left(t\right)=\beta \left(t\right)(p_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)),\hfill \\ \lambda \beta \left(t\right),\hfill & \mathrm{if}\alpha \left(t\right)p_{\mathrm{T}}\left(t\right)<\beta \left(t\right)(p_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)),\hfill \\ \mu \beta \left(t\right),\hfill & \mathrm{if}\alpha \left(t\right)p_{\mathrm{T}}\left(t\right)>\beta \left(t\right)(p_{\mathrm{q}+}\left(t\right)+p_{\mathrm{q}-}\left(t\right)),\hfill \end{array}\right.\hfill \end{array}$$

(6)

where $\lambda$ is an increasing parameter ($\lambda >1$) and $\mu$ is a decreasing parameter ($0<\mu <1$). If the value of the weights is less than 1.0, the weights are set to unity ($\alpha (t+1)=1$ or $\beta (t+1)=1$).

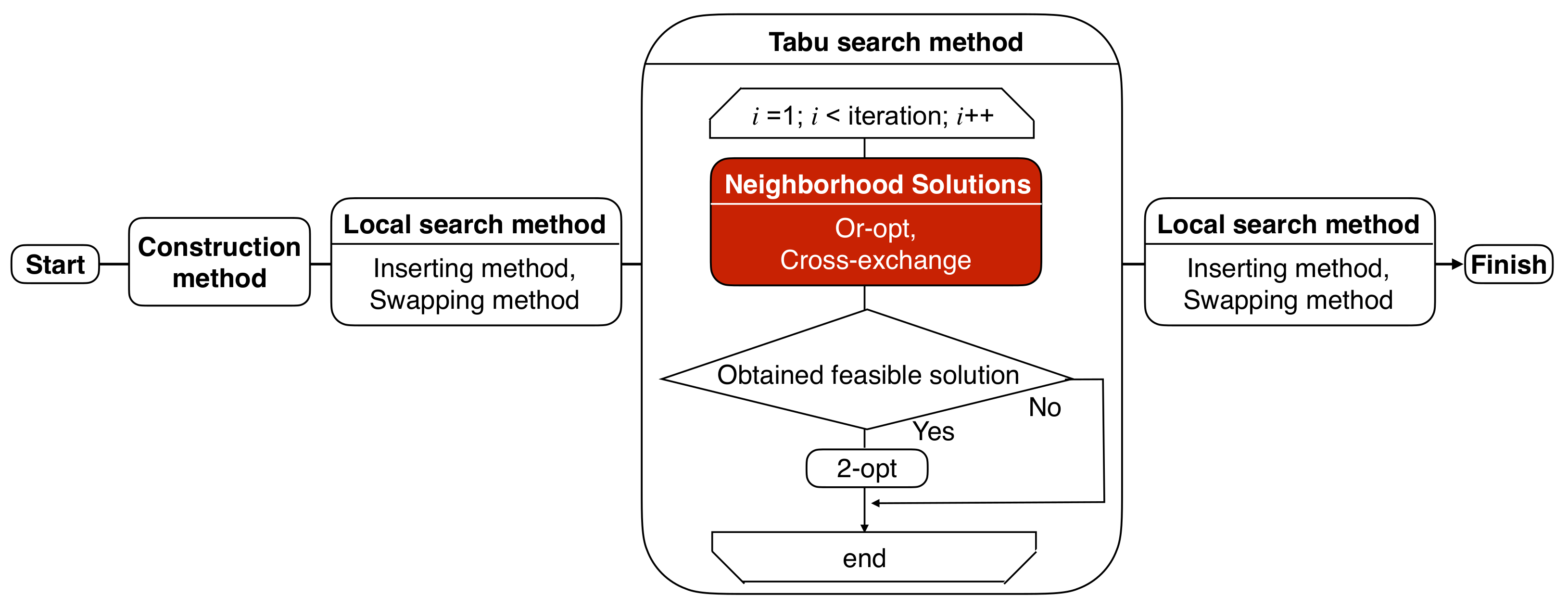
4. Computational Cost Reduction Method

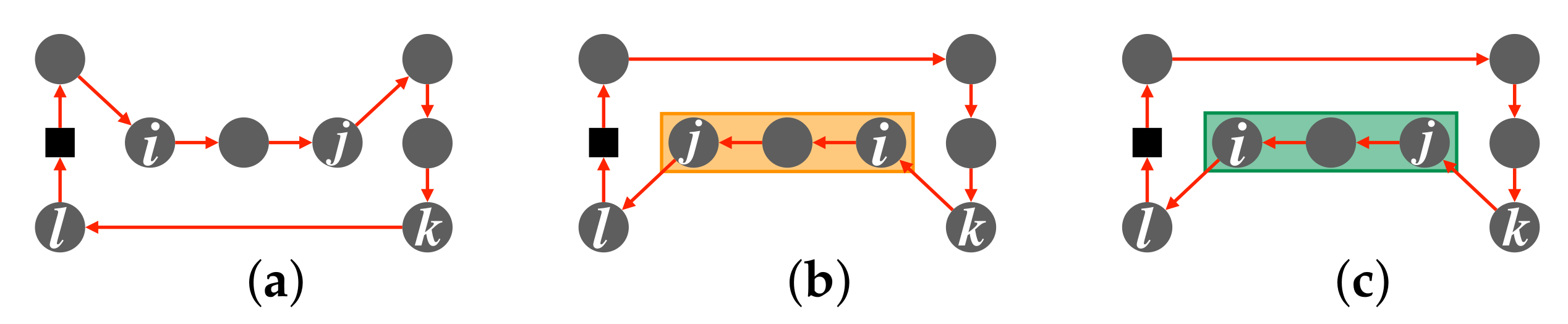
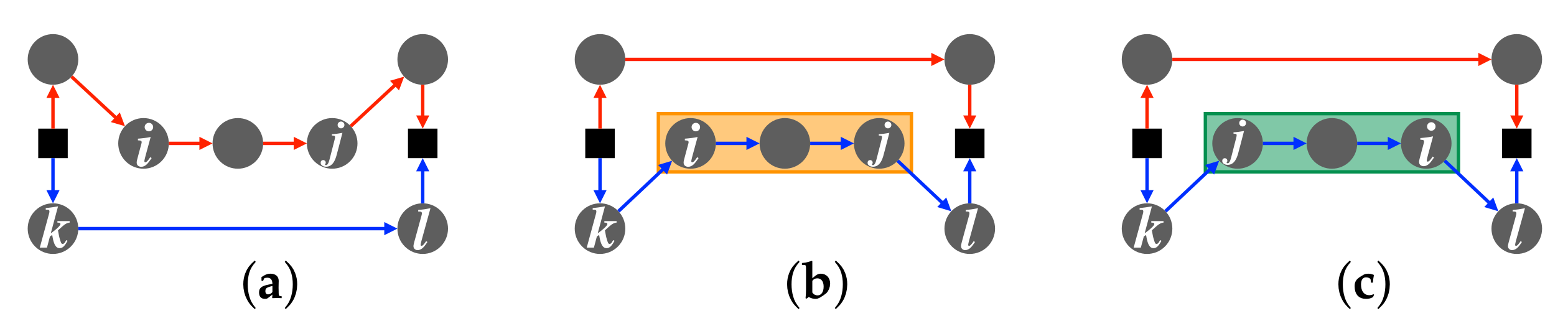
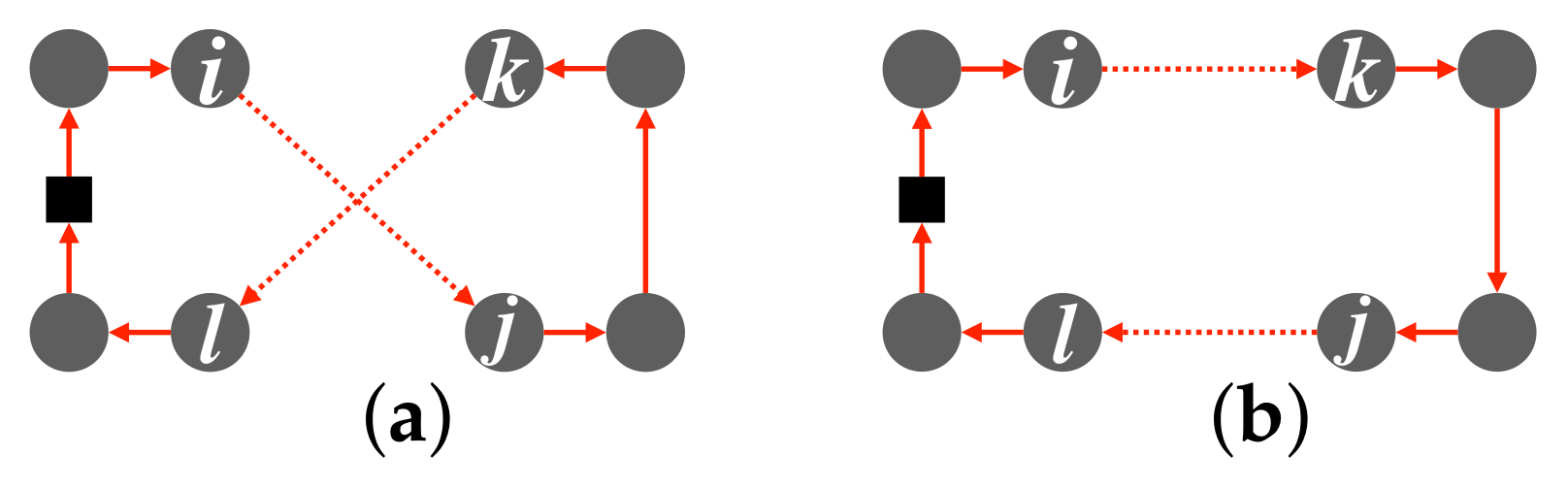
To reduce neighborhood solution and computational costs, we investigate the percentage of the Or-opt and the CROSS-exchange executions used in the tabu search part. The feasible neighborhood solutions of the mBSSRP-S include the infeasible neighborhood solutions of the mBSSRP. Therefore, when we solve the mBSSRP-S, it takes more time to determine the next solution than in the case of mBSSRP. To reduce the computational cost of solving mBSSRP-S, we need to remove unnecessary neighborhood solutions. The percentage of the insertion and exchange operations performed by the proposed method was approximately 66% for the Or-opt, which inserts ports in the normal order (Figure 4b), and approximately 20% for the CROSS-exchange, which exchanges ports in the normal order (Figure 5b), implying that the reverse order of insertion and exchange was rarely executed. Thus, we did not search for less frequently performed reverse order operations to reduce the computational costs. In our previous study, we have shown that once a feasible solution of the mBSSRP is obtained, the proposed method searches for the feasible solutions successively [20]. Next, to find a good feasible solution of the mBSSRP, we examine whether we should change the problem to be solved (mBSSRP or mBSSRP-S) before and after a feasible solution is obtained.

Table 2. Search strategy before finding a feasible solution of the mBSSRP. The first column shows local search names, the second column shows the types of the Or-opt or the CROSS-exchange operations, the third to fifth columns show the name of the search method and the sixth column shows the percentage of local search methods that are executed.

Local Search	Type	1A-S	1B-S	1C-S	Executed Rate (One Decimal Point Omitted)
Or-opt	Normal	✓	✓	✓	66%
	Reverse	✓			4%
CROSS-exchange	Normal	✓		✓	20%
	One-sided reverse	✓			2%
	One-sided reverse	✓			3%
	Reverse	✓			4%

summarizes the search strategy before obtaining a feasible solution of the mBSSRP. We propose two search methods (1B-S and 1C-S) in this case. In Table 2, the first search method 1A-S searches for all neighborhood solutions of the Or-opt and the CROSS-exchange. Thus, this search method is the same as the conventional search method [20]. The second search method 1B-S only explores insertion of the normal order of the Or-opt which is the most executed (Figure 4b). The third search method 1C-S searches for the insertion of the normal order of the Or-opt and exchange of the normal order of the CROSS-exchange (Figure 4b and Figure 5b). The goal of the search methods before obtaining a feasible solution is to find a feasible solution within a short time for all trials.

In addition, to further reduce the computational costs the search strategy is changed after a feasible solution of mBSSRP is obtained. In this paper, we propose four new search methods (2B-S, 2B-H, 2C-S and 2C-H).

Table 3. Search strategy after finding a feasible solution of the mBSSRP. The first column represents local search names, the second column shows the types of the Or-opt or the CROSS-exchange operations, the third to the eighth columns show the name of the search method and the bottom line indicates whether instances were solved with hard or soft constraints.

Local Search	Type	2A-S	2A-H	2B-S	2B-H	2C-S	2C-H
Or-opt	Normal	✓	✓	✓	✓	✓	✓
	Reverse	✓	✓
CROSS-exchange	Normal	✓	✓			✓	✓
	One-sided reverse	✓	✓
	One-sided reverse	✓	✓
	Reverse	✓	✓
Constraint		Soft	Hard	Soft	Hard	Soft	Hard

shows the search strategy after finding a feasible solution of the mBSSRP. In Table 3, the first search method 2A-S involves to searching for all neighborhood solutions of the Or-opt and the CROSS-exchange with soft constraints. The second search method 2A-H involves searching for all neighborhood solutions of the Or-opt and the CROSS-exchange with hard constraints. The difference between the search methods 2A-S and 2A-H is whether the instances are solved with hard or soft constraints. The reason why we introduced both soft and hard constraints is that we found that once a feasible solution of the mBSSRP is obtained, our conventional method [20] searches for the feasible solutions successively. Then, 2A-S and 2A-H are the same as the conventional search method [20]. The third search method 2B-S only searches for insertion in the normal order of the Or-opt with soft constraints. The fourth search method 2B-H only searches for insertion in the normal order of the Or-opt with hard constraints. The fifth search method 2C-S explores the insertion of the normal order of the Or-opt and the exchange of the normal order of the CROSS-exchange with soft constraints. Finally, the sixth search method 2C-H explores the insertion of the normal order of the Or-opt and the exchange of the normal order of the CROSS-exchange with hard constraints.

5. Numerical Experiments

To evaluate the performance of the computational cost reduction methods, we generated benchmark instances. Figure 7 shows an example of these instances. We distributed 100 ports and a depot uniformly in a region measuring 10 ${\mathrm{km}}^2$. The number of bicycles at each port was set to a random number between $-5$ and $+5$ at intervals of 1. A negative value (“−”) represents the delivery port, and a positive value (“+”) represents the pickup ports. The capacity of the vehicles was 10, the average moving speed of the vehicles was 30 [km/h], the loading or unloading time of a bicycle was 2 [min] and the time limit (all vehicles start from the depot and return to it) was 180 [min]. Thereafter, the tabu tenure was set to 50 and the initial values of weights were set to $\alpha \left(0\right)$ = 1 and $\beta \left(0\right)$ = 1. The increasing $\lambda$ and decreasing parameter $\mu$ were set to 1.07 and 0.3, respectively.

For the search methods 1A-S, 1B-S and 1C-S (before a feasible solution was obtained), we performed 50 trials per instance and performed 200 [s] of computation for trials. Meanwhile, for the search methods 2A-S, 2A-H, 2B-S, 2B-H, 2C-S and 2C-H (after a feasible solution was obtained), we started the calculation from 50 feasible solutions per instance and performed 200 [s] of computation for each solution. These numerical experiments were performed on a Mac mini with a 3-GHz 6-Core Intel Core i5 processor and 32 GB RAM.

5.1. Results of Search Strategy before Obtaining a Feasible Solution

Results of the numerical experiments for the search strategy before obtaining a feasible solution are shown in

Table 4. Results of search methods before obtaining a feasible solution. (a) Search method 1A-S (search for all neighborhood solutions of the Or-opt and the CROSS-exchange). (b) Search method 1B-S (search only normal order insertion of the Or-opt). (c) Search method 1C-S (search for normal order insertion of the Or-opt and normal order exchange of the CROSS-exchange).

(a)
No.	Avg. [min]	Best [min]	Worst [min]	# of Feasible Solution
1	243.76	230.85	259.07	50
2	238.16	230.87	252.95	50
3	228.47	218.98	237.25	50
4	242.56	232.38	252.36	50
5	249.06	240.95	260.69	50
6	270.81	260.50	284.04	31
7	238.52	225.12	252.72	34
8	213.15	207.43	226.01	50
9	241.64	231.13	255.18	49
10	243.28	234.40	252.54	45
Avg.	240.94	231.26	253.28	45.9
(b)
No.	Avg. [min]	Best [min]	Worst [min]	# of Feasible Solution
1	245.46	234.80	258.63	40
2	242.59	228.66	260.92	50
3	234.57	222.44	249.94	50
4	246.81	236.23	268.79	49
5	254.91	241.88	269.26	42
6	268.45	260.94	276.57	16
7	238.02	222.71	247.85	10
8	213.98	207.79	237.93	49
9	245.18	233.40	260.38	44
10	244.20	236.92	257.74	29
Avg.	243.42	232.58	258.80	37.9
(c)
No.	Avg. [min]	Best [min]	Worst [min]	# of Feasible Solution
1	241.63	233.74	251.90	50
2	236.61	227.33	246.43	50
3	228.31	217.29	242.36	50
4	242.15	233.15	254.30	50
5	249.59	241.04	259.27	50
6	269.55	256.99	284.94	32
7	236.17	225.00	252.39	30
8	213.14	205.85	224.93	50
9	239.44	228.72	252.01	50
10	239.80	229.91	253.65	44
Avg.	239.64	229.90	252.22	45.6

. In Table 4a–c, the first column lists the instance numbers, the second to the fourth columns present the average, the best and the worst objective function values [min] for each instance, and the fifth column indicates the number of obtained feasible solutions for each trial. We performed 50 trials; thus, the maximum value was 50. Table 4a summarizes the result that searches for all neighborhood solutions of the Or-opt and the CROSS-exchange (the search method 1A-S). From Table 4a, feasible solutions of the mBSSRP were obtained for almost all trials. From Table 4b, the search method that searches for only normal order of the Or-opt (the search method 1B-S) cannot obtain several feasible solutions compared to Table 4a. By contrast, the search method 1C-S (Table 4c) obtained almost the same number of feasible solutions and the average objective function values [min] as the search method 1A-S (Table 4a).

To compare the performance of the search methods 1A-S and 1C-S by statistical analysis, we used the t-test.

Table 5. Results of the t-test to evaluate the difference of the average objective function values [min] between the search methods 1A-S and 1C-S.

	1A-S		1C-S
No.	Avg. [min]	SD	Avg. [min]	SD	p
1	243.76	5.72	241.63	4.51	0.041
2	238.16	5.08	236.61	4.34	0.104
3	228.47	4.36	228.31	6.42	0.886
4	242.56	4.92	242.15	4.54	0.668
5	249.06	4.64	249.59	4.38	0.558
6	270.81	6.42	269.55	7.13	0.464
7	238.52	6.27	236.17	6.96	0.163
8	213.15	3.39	213.14	4.00	0.985
9	241.64	6.19	239.44	5.25	0.061
10	243.28	4.62	239.80	5.14	0.001
Avg.	240.94	5.16	239.64	5.27	0.393

shows the results of the t-test. In Table 5, the first column lists the instance numbers, the second and the fourth columns present the average objective function values [min] for each instance, the third and the fifth columns show the standard deviations and the sixth column presents the results of the t-test. In the numerical experiment, the level of significance was 5%. Thus, if p ≥ 0.05, there is no significant difference between the performance of the search methods 1A-S and 1C-S. By contrast, if the results show that p < 0.05, there is a significant difference between the performance of the search methods 1A-S and 1C-S. From Table 5, only for instance No.1 and No.10, the p-values are smaller than 0.05. However, for instance No.2∼No.9 (Table 5), the p-values are larger than 0.05. These results indicate that we cannot say that there is a significant difference between the performance of the search methods 1A-S and 1C-S.

Next, to clarify the difference between the search methods 1A-S and 1C-S, we evaluated the relationship between the time [s] until a feasible solution was obtained and the number of obtained feasible solutions (Figure 8). Figure 8a shows the result of the search method 1A-S (search for all neighborhood solutions of the Or-opt and the CROSS-exchange), and Figure 8b shows the result of the search method 1C-S (search for normal order insertion of the Or-opt and normal order exchange of the CROSS-exchange). The horizontal axis shows time [s] and the vertical axis indicates the number of obtained feasible solutions. We can see that the highest value of the number of obtained feasible solutions takes approximately 70 [s] from Figure 8a. Meanwhile, the highest value of the number of obtained feasible solutions takes approximately 40 [s] from Figure 8b. Thus, although the number of obtained feasible solutions and the average objective function values [min] for the search methods 1A-S and 1C-S were almost the same as shown in Table 4, the search method 1C-S finds a feasible solution approximately 30 [s] faster than the search method 1A-S (Figure 8).

To investigate whether there is a significant difference in the average time [s] until a feasible solution was obtained between the search methods 1A-S and 1C-S, we also conducted a statistical analysis by the t-test.

Table 6. Results of the t-test to evaluate the difference time [s] until a feasible solution was obtained between the search methods 1A-S and 1C-S.

	1A-S		1C-S
No.	Avg. [s]	SD	Avg. [s]	SD	p
1	78.76	24.84	44.67	16.83	0.000
2	72.83	16.30	32.84	5.60	0.000
3	66.37	10.68	30.22	5.79	0.000
4	75.37	13.50	36.85	9.72	0.000
5	72.86	10.15	42.23	15.70	0.000
6	123.70	41.62	109.59	45.82	0.205
7	115.36	37.28	89.80	45.26	0.018
8	68.81	19.88	32.74	8.61	0.000
9	75.99	16.51	42.16	16.41	0.000
10	102.82	39.51	84.23	42.42	0.035
Avg.	85.29	23.03	54.53	21.22	0026

shows the results of the t-test. In Table 6, the first column lists the instance numbers, the second and the fourth columns present the average time [s] until a feasible solution was obtained for each instance, the third and the fifth columns show the standard deviations and the sixth column presents the results of the t-test. From the results, the p-values are smaller than 0.05 except for instance No.6. Thus, we could find a significant difference between the search methods 1A-S and 1C-S for almost all instances from the viewpoint of a searching speed.

To summarize the results, there is no difference in the performance between the search methods 1A-S and 1C-S (Table 4 and Table 5). On the other hand, as for the search speed, the search method 1C-S (54.53 [s]) can find feasible solutions with shorter time (approximately 30 [s]) than the search method 1A-S (85.29 [s]), which means that by using the search method 1C-S, we can reduce the computation time by $(85.29-54.53)/85.29\times 100=36.1\%$. Therefore, we concluded that the search method 1C-S (the search for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange) is the best search method before finding a feasible solution.

5.2. Results of Search Strategy after Obtaining a Feasible Solution

Results of the numerical experiments using the six search methods after obtaining the feasible solution are shown in

Table 7. Results of search methods after obtaining a feasible solution. (a) Search method 2A-S (search for all neighborhood solutions of the Or-opt and the CROSS-exchange with soft constraints). (b) Search method 2A-H (search for all neighborhood solutions of the Or-opt and the CROSS-exchange with hard constraints). (c) Search method 2B-S (search for only normal order insertion of the Or-opt with soft constraints). (d) Search method 2B-H (search for only normal order insertion of the Or-opt with hard constraints). (e) Search method 2C-S (search for normal order insertion of the Or-opt and normal order exchange of the CROSS-exchange with soft constraints). (f) Search method 2C-H (search for normal order insertion of the Or-opt and normal order exchange of the CROSS-exchange with hard constraints).

(a)
No.	Avg. [min]	Best [min]	Worst [min]
1	241.81	232.13	254.94
2	238.45	227.14	245.73
3	228.09	218.60	244.40
4	241.43	231.95	251.71
5	247.58	240.39	256.60
6	266.76	257.19	281.07
7	234.84	222.53	251.80
8	212.02	205.77	220.14
9	240.48	232.09	251.94
10	241.65	230.99	256.75
Avg.	239.31	229.88	251.51
(b)
No.	Avg. [min]	Best [min]	Worst [min]
1	242.53	235.06	251.29
2	237.70	229.25	247.47
3	227.98	219.98	237.32
4	241.36	231.52	250.18
5	248.68	241.96	258.93
6	268.91	253.71	286.59
7	235.25	222.83	255.66
8	211.91	205.99	218.02
9	239.90	227.68	253.67
10	239.90	231.80	252.12
Avg.	239.41	229.98	251.13
(c)
No.	Avg. [min]	Best [min]	Worst [min]
1	244.20	232.75	259.46
2	239.29	228.66	249.19
3	227.79	217.16	238.15
4	242.41	234.88	254.57
5	251.11	242.17	264.62
6	270.60	253.39	284.24
7	236.22	226.03	251.93
8	211.75	206.02	223.83
9	243.22	231.37	258.92
10	241.93	230.33	258.83
Avg.	240.85	230.28	254.37
(d)
No.	Avg. [min]	Best [min]	Worst [min]
1	248.89	236.91	270.39
2	241.65	228.40	258.26
3	230.96	221.46	244.89
4	246.12	230.94	263.21
5	252.34	240.32	267.20
6	275.42	263.31	286.62
7	242.98	225.28	262.27
8	212.27	206.68	222.78
9	243.85	233.61	259.85
10	249.20	231.04	266.57
Avg.	244.37	231.79	260.20
(e)
No.	Avg. [min]	Best [min]	Worst [min]
1	240.88	232.42	254.18
2	235.86	228.96	243.84
3	226.88	216.81	235.18
4	240.18	231.96	254.29
5	246.75	241.68	254.52
6	264.58	255.89	276.92
7	234.09	222.51	254.30
8	211.11	205.87	216.95
9	237.62	227.48	249.52
10	238.92	230.84	249.83
Avg.	237.69	229.44	248.95
(f)
No.	Avg. [min]	Best [min]	Worst [min]
1	241.36	232.87	255.56
2	236.58	227.65	249.19
3	225.96	216.81	233.52
4	239.99	231.78	247.36
5	247.18	240.11	255.19
6	267.60	254.18	281.03
7	235.12	222.29	255.66
8	210.42	206.12	215.98
9	238.72	230.49	247.28
10	237.86	230.42	253.19
Avg.	238.08	229.27	249.40

. In Table 7a–f, the first column lists the instance numbers, the second to the fourth columns present the average, the best and the worst objective function values [min] in 200 [s] of each trial, when we started the calculation from a feasible solution. From Table 7e,f, the search methods of reducing neighborhood solutions were also effective when the search was started from feasible solutions. The performance showed no significant differences between soft (Table 7e) and hard constraints (Table 7f). In particular, the difference of the average objective function values [min] of the search method 2C-S and the search method 2C-H is only 0.39 [min].

To investigate whether there is a significant difference in performance, the t-test was used on the average objective function values [min].

Table 8. Results of the t-test to evaluate the difference of performance between methods 2C-S and 2C-H.

	2C-S		2C-H
No.	Avg. [min]	SD	Avg. [min]	SD	p
1	240.88	4.20	241.36	4.41	0.572
2	235.86	3.89	236.58	5.18	0.432
3	226.88	4.64	225.96	4.39	0.309
4	240.18	4.74	239.99	3.66	0.833
5	246.75	3.26	247.18	3.92	0.550
6	264.58	5.27	267.60	6.45	0.016
7	234.09	7.27	235.12	8.14	0.518
8	211.11	2.86	210.42	2.54	0.209
9	237.62	5.09	238.72	4.64	0.262
10	238.92	3.91	237.86	4.27	0.203
Avg.	237.69	4.51	238.08	4.76	0.390

shows the results of the t-test. In Table 8, the first column lists the instance numbers, the second and the fourth columns present the average objective function values [min] for each instance, the third and the fifth columns show the standard deviations, and the sixth column presents the results of the t-test. From Table 8, except for instance No.6, the p-values are larger than 0.05. Thus, we could not find any significant difference between the performance of the search methods 2C-S and 2C-H from the viewpoint of the statistical analysis.

Next, to investigate whether there is a difference in searching process between the two search methods 2C-S and 2C-H, we evaluated the transition of the most feasible solutions when solving soft and hard constraints. The results of instance No.1 are shown in Figure 9. From Figure 9, we can find that there is a difference between these two search methods 2C-S and 2C-H. From Figure 9a, it takes a long time (38.82 [s]) to update the better solution for solving the mBSSRP-S. The reason is that to realize an effective search, the weight values of penalty in Equations (3)–(6) must be adjusted to appropriate values. The average transition time to a better solution for other instances is shown in

Table 9. Results of the average transition time to a feasible solution for the search method 2C-S.

No.	Avg. [s]
1	38.82
2	31.54
3	31.71
4	36.01
5	34.17
6	77.78
7	68.04
8	29.10
9	35.56
10	59.94
Avg.	44.27

. In Table 9, the first column lists instance numbers and the second column shows the average transition time [s] to a better solution. From Table 9, the search method 2C-S takes about 30∼80 [s] to find a better feasible solution. Meanwhile, from Figure 9b, a solution of the search method 2C-H moves to a better solution as soon as a search is started because it cannot search for an infeasible solution.

The results of the t-test of the average objective function values of the search methods 2C-S and 2C-H showed that there was no significant difference in performance (Tables Figure 7 and Figure 8). However, from Figure 9 and Table 9, the search method 2C-H can find a better feasible solution in a shorter time (approximately 30∼80 [s]) than the search method 2C-S. Therefore, as for the search strategy after finding a feasible solution, we concluded that the search method 2C-H (the search for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange with hard constraints) is the best search method.

6. Conclusions

In this study, we proposed two search strategies with low computational costs while maintaining the performance of the mBSSRP: the first one is to reduce neighborhood solutions to obtain a feasible solution in a short time before finding a feasible solution of the mBSSRP, and the second one is to change the problem to be solved (mBSSRP or mBSSRP-S) after a feasible solution is obtained and to search good near-optimal solutions in a short time.

As the first search strategy before obtaining a feasible solution, we propose two search methods (the search methods 1B-S and 1C-S) and compare their performance with our previous method (the search method 1A-S) [20]. The search method 1A-S searches for all neighborhood solutions of the Or-opt and the CROSS-exchange [20]. The search method 1B-S searches only the normal order insertion of the Or-opt. The search method 1C-S searches for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange. The results of the numerical experiments showed that the search method 1C-S that only searches for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange is the best search method, because the search method 1C-S obtained many feasible solutions within a short time.

Next, as the second search strategy after a feasible solution of mBSSRP is obtained, we propose four search methods (2B-S, 2B-H, 2C-S and 2C-H) and compare their performance with our previous methods (2A-S and 2A-H) [20]. The search method 2A-S searches for all neighborhood solutions of the Or-opt and the CROSS-exchange with soft constraints. The search method 2A-H searches for all neighborhood solutions of the Or-opt and the CROSS-exchange with hard constraints. The search method 2B-S searches for insertion in the normal order of the Or-opt with soft constraints. The search method 2B-H searches for insertion in the normal order of the Or-opt with hard constraints. The search method 2C-S searches for the insertion of the normal order of the Or-opt and the exchange of the normal order of the CROSS-exchange with soft constraints. Finally, the search method 2C-H searches for the insertion of the normal order of the Or-opt and the exchange of the normal order of the CROSS-exchange with hard constraints. The results of the numerical experiments showed that the search method 2C-H that searches for the normal order insertion of the Or-opt and the normal order exchange of the CROSS-exchange with hard constraints is the best search method, because the search method 2C-H obtained short tours within a short time. These results indicate that the search method 1C-S reduces the neighborhood solutions in the Or-opt and the CROSS-exchange and that the search space was shifted from soft constraints to hard constraints after a feasible solution is obtained is effective.

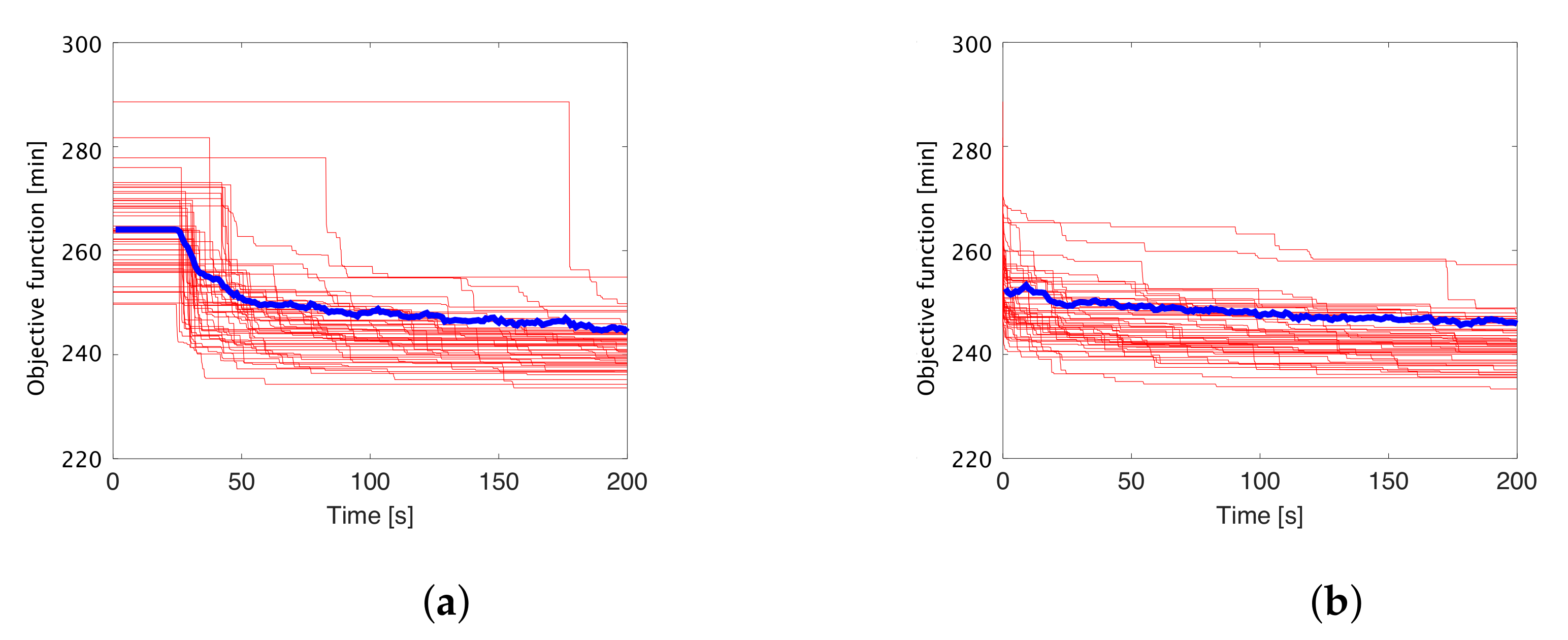
In this study, we used a dynamically changing method for weight parameters ($\alpha$ and $\beta$) to find good solutions of mBSSRP from the solution of the mBSSRP-S. To adjust these weight parameters $\alpha$ and $\beta$, we used an adjustment method (Equations (3)–(6)). Then, from the results of numerical experiments (Figure 9a), it takes a long time to update the better solution for solving the mBSSRP-S (for example, 38.82 [s] for instance No. 1). The results of other instances are shown in Table 9. From Table 9, the search method 2C-S takes about 30∼80 [s] to find better feasible solutions. In this temporal duration of 30∼80 [s], the weight values $\alpha$ and $\beta$ must be adjusted to appropriate values by Equations (3)–(6). If we can set optimal parameters for an initial state, the search method 2C-S can find a better solution more efficiently and quickly than the search method 2C-H. Thus, one of the future works is to determine the parameters by using a parameter optimization approach.

In the numerical experiment, we used randomly distributed ports. However, some bicycle sharing repositioning studies have used real BSS data. For instance, Rainer-Harbach et al. (2013) [13], Raidl et al. (2013) [14] and Papazek et al. (2013) [15] use data from Vienna, and Chiariotti et al. (2018) [17] use data from New York. Thus, it is an important work to use real BSS data in a future study.

Moreover, we need to address the dynamic cases because the number of bicycles in each port changes while restoring bicycles in the real BSS. The studies of static BSS (Rainer-Harbach et al. (2013) [13], Raidl et al. (2013) [14] and Papazek et al. (2013) [15]) have been extended to dynamic BSS by Kloimüllner et al. (2014) [16]. Thus, we also aim to extend this study to a dynamic case. The completion of the dynamic case would have a great impact on solving an issue inherent in BSS: users cannot rent or return a bicycle at an empty or a full port. A solution to this issue would lead to the development of BSS in the future, and it is expected that BSS will be used for a wide range of purposes such as commuting to work, daily life, and even in times of disaster. It will also have an effect to promote the spread of the next generation system called MaaS (Mobility as a Service), which has been attracting attention recently: all public transportation systems are connected by IT technology. To address the dynamic case, we have to consider forecasting future demands of bicycles from actual data and repositioning them based on the forecast data by investigating statistical characteristics of real data of BSSs [32].

In our previous study [20], we proposed a heuristic method by using the tabu search. Then, in this paper, we also used the tabu search to propose search strategies with low computational costs while maintaining the performance of the mBSSRP. However, it is important to use not only the tabu search but also the other approaches (for example, simulated annealing) and compare these approaches. In addition, we only focus on the operation of the rebalancing bicycles [19,20] and statistical analysis of BSS usage history [32]. However, Kabak et al. (2018) [33] focus on the location of bicycle ports. It is an important idea to evaluate the existing BSS ports and suggest alternative places for additional BSS ports.