Design of a Dead-Time Compensator Robust H∞ State Feedback Temperature Controller for a Precalciner of a Cement Rotary Kiln
Abstract
1. Introduction
2. Materials and Methods
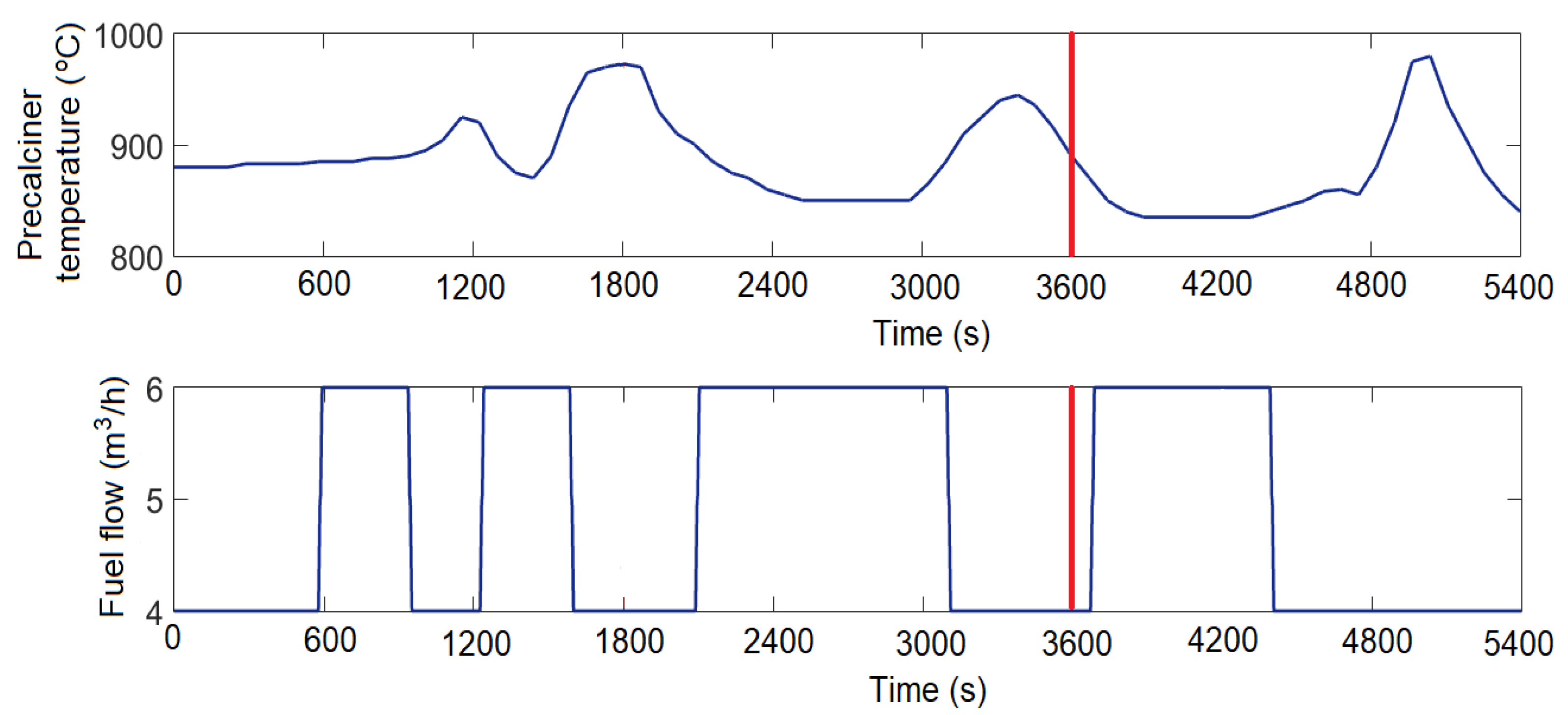
2.1. Identification of the Temperature Dynamic Behaviour in a Precalciner
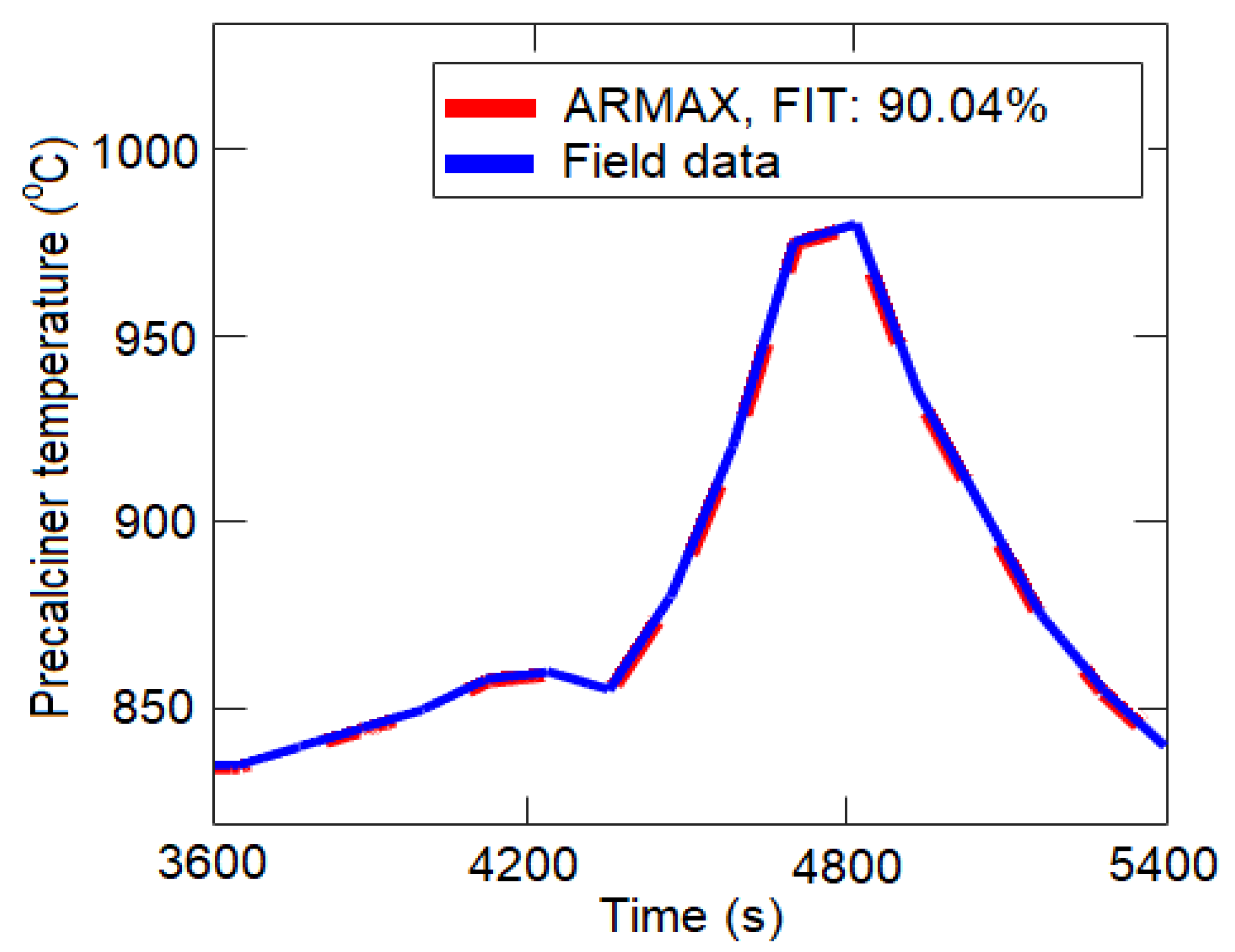
2.2. Model Validation
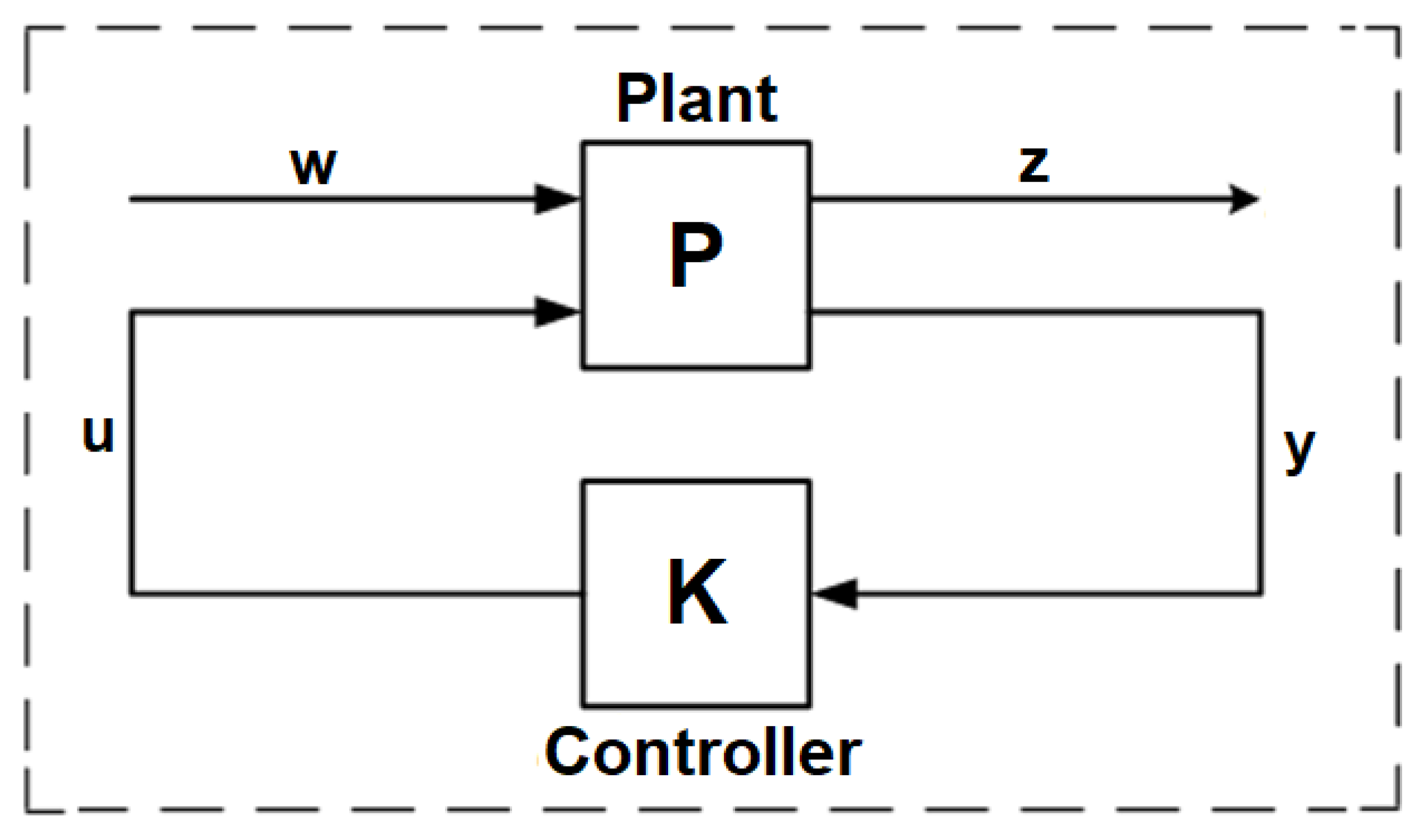
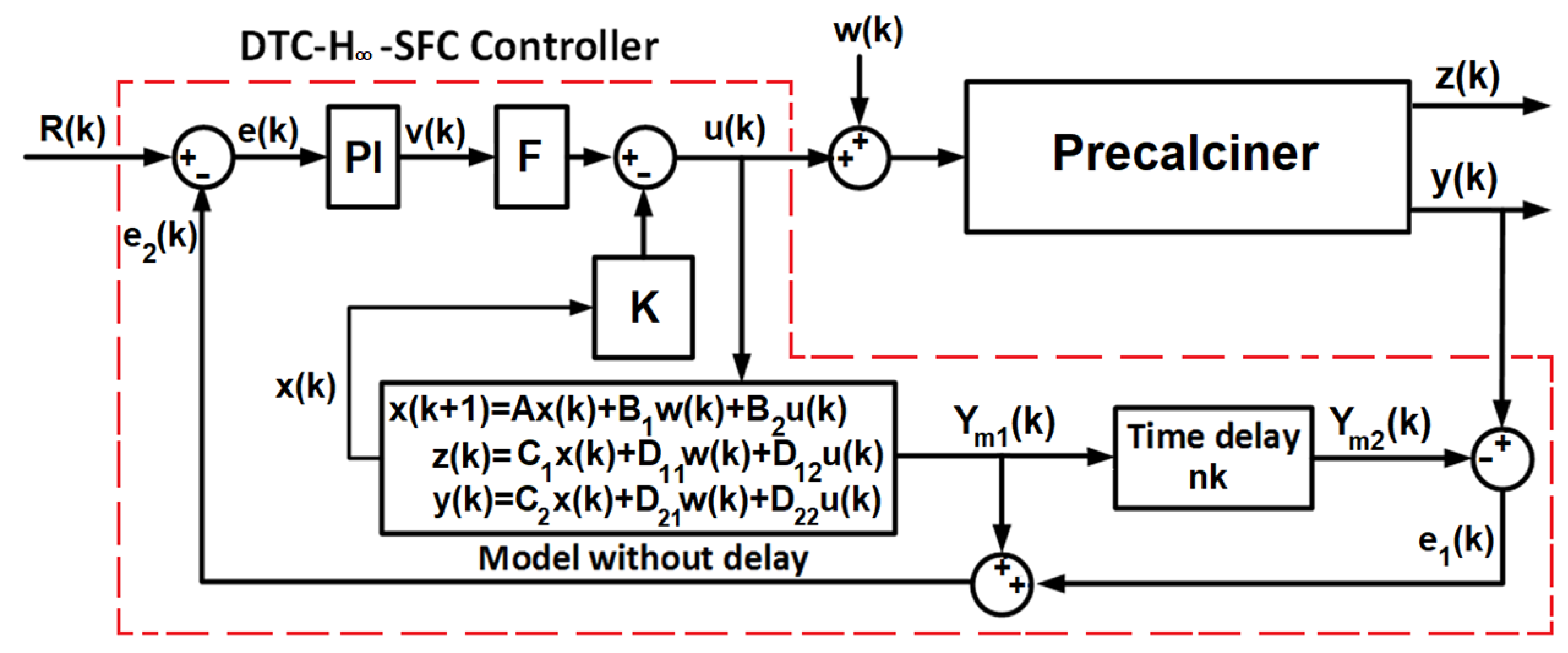
2.3. Design of a DTC-H∞-SFC Controller
- (i)
- is stabilizable and is detectable;
- (ii)
- is stabilizable and is detectable.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Udugu, A.A.; Khare, A. Automation of cement industries. Int. J. Res. Eng. Adv. Technol. 2014, 1, 1–5. [Google Scholar]
- Samanta, A.; Chowdhury, A.; Dutta, A. Process automation of cement plant. Int. J. Inform. Technol. Control Automat. 2012, 2, 63–72. [Google Scholar] [CrossRef]
- Rodrigues, F.A.; Joekes, I. Cement industry: Sustainability, challenges and perspectives. Environ. Chem. Lett. 2011, 9, 151–166. [Google Scholar] [CrossRef]
- Poudyal, L.; Adhikari, K. Environmental sustainability in cement industry: An integrated approach for green and economical cement production. Resour. Environ. Sustain. 2021, 4, 100024. [Google Scholar] [CrossRef]
- Deolalkar, S.P. Handbook for Designing Cement Plants; BS Publications: Hyderabad, India, 2021. [Google Scholar]
- Alsop, P.A. The Cement Plant Operations Handbook, 6th ed.; Tradership Publication LTD.: Surrey, UK, 2014. [Google Scholar]
- Millera, S.A.; John, V.M.; Paccac, S.A.; Horvath, A. Carbon dioxide reduction potential in the global cement industry by 2050. Cem. Concr. Res. 2018, 114, 115–124. [Google Scholar] [CrossRef]
- Atmaca, A.; Yumrutas, R. Analysis of the parameters affecting energy consumption of a rotary kiln in cement industry. Appl. Therm. Eng. 2014, 66, 435–444. [Google Scholar] [CrossRef]
- Schneider, M. The cement industry on the way to a low-carbon future. Cem. Concr. Res. 2019, 124, 105792. [Google Scholar] [CrossRef]
- Boateng, A.A. Rotary Kilns Transport Phenomena and Transport Processes; Butterworth-Heinemann: Oxford, UK, 2008. [Google Scholar]
- Peray, K.E. The Rotary Cement Kiln, 2nd ed.; Chemical Publishing Co. Inc.: New York, NY, USA, 1986. [Google Scholar]
- Goshayeshi, H.R.; Poo, F.K. Modeling of rotary kiln in cement industry. J. Energy Power Eng. 2016, 8, 23–33. [Google Scholar] [CrossRef][Green Version]
- Salcedo Hernández, J.; Rivas-Perez, R.; Sotomayor Moriano, J.J. Design of a generalized predictive controller for temperature control in a cement rotary kiln. IEEE Lat. Am. Trans. 2018, 16, 1015–1021. [Google Scholar] [CrossRef]
- Stadler, K.S.; Poland, J.; Gallestey, E. Model predictive control of a rotary cement kiln. Control Eng. Pract. 2011, 19, 1–9. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Rivas-Perez, R. Design of a robust fractional order controller for burning zone temperature control in an industrial cement rotary kiln. IFAC-PapersOnLine 2020, 53, 3657–3662. [Google Scholar] [CrossRef]
- Teja, R.; Sridhar, P.; Guruprasath, M. Control and optimization of a triple string rotary cement kiln using model predictive control. IFAC-PapersOnLine 2016, 49, 748–753. [Google Scholar] [CrossRef]
- Salcedo Hernández, J.; Rivas-Perez, R.; Sotomayor Moriano, J.J. Model reference adaptive temperature control of a rotary cement kiln. In Proceedings of the 2018 IEEE PES Transmission & Distribution Conference and Exhibition—Latin America, Lima, Peru, 18–21 September 2018; pp. 1–4. [Google Scholar]
- King, R. Intelligent control in the cement industry. IFAC Proc. Vol. 1988, 21, 303–307. [Google Scholar] [CrossRef]
- Salcedo Hernández, J.; Rivas-Perez, R. Model based predictive control of temperature in a cement rotatory kiln. Electro-Electrónica 2010, 34, 52–60. [Google Scholar]
- Koumboulis, F.N.; Kouvakas, N.D. Indirect adaptive neural control for precalcination in cement plants. Math. Comput. Simul. 2002, 60, 325–334. [Google Scholar] [CrossRef]
- Griparis, M.K.; Koumboulis, F.N.; Machos, N.S.; Marinos, J. Precalcination in cement plants (system descriptions and control trends). IFAC Proc. Vol. 2000, 33, 273–278. [Google Scholar] [CrossRef]
- Camdali, U.; Erisen, A.; Celen, F. Energy and exergy analyses in a rotary kiln with pre-calcinations in cement production. Energy Convers. Manag. 2004, 45, 3017e3031. [Google Scholar] [CrossRef]
- Li, S.; Ge, Y.; Wei, X. Experiment on NOx reduction by advanced reburning in cement precalciner. Fuel 2018, 224, 235–240. [Google Scholar] [CrossRef]
- Stadler, K.S.; Wolf, B.; Gallestey, E. Precalciner control in the cement production process using MPC. IFAC Proc. Vol. 2007, 40, 201–206. [Google Scholar] [CrossRef]
- Salcedo Hernández, J.; Feliu Battle, V.; Rivas-Perez, R. State feedback temperature control based on a Smith predictor in a precalciner of a cement kiln. IEEE Lat. Am. Trans. 2021, 19, 138–146. [Google Scholar]
- Yang, B.; Cao, D. Action-dependent adaptive critic design based neurocontroller for cement precalciner kiln. Int. J. Comput. Netw. Inf. Secur. 2009, 1, 60–67. [Google Scholar] [CrossRef][Green Version]
- Stadler, K.S.; Wolf, B.; Gallestey, E. Model predictive control of the calciner at Holcim’s Lägerdorf plant. ZKG Int. 2007, 60, 60–67. [Google Scholar]
- Valarmathi, R.; Guruprasath, M.; Ramkumar, K. Design and implementation of evolutionary algorithm based controller for calciner process. Int. J. Pure Appl. Math 2017, 117, 711–723. [Google Scholar]
- Osmic, J.; Omerdic, E.; Imsirovic, E.; Smajlovic, T.O.; Omerdic, E. Identification and control of precalciner in the cement plant. In Proceedings of the 14th APCA International Conference on Automatic Control and Soft Computing, Bragança, Portugal, 1–3 July 2020; pp. 126–135. [Google Scholar]
- Tsamatsoulis, D.C.; Zlatev, G. PID parameterization of cement kiln precalciner based on simplified modeling. Int. J. Neural Netw. Adv. Appl. 2016, 3, 41–45. [Google Scholar]
- Mohankrishna, P.B.; Vigneshwaran, S.; Padmadarshan, M.B.; Brijet, Z. Fuzzy based PID for calciner temperature control. Int. J. Pure Appl. Math. 2018, 119, 14563–14570. [Google Scholar]
- Normey-Rico, J.E.; Camacho, E.F. Control of Dead-Time Processes; Springer: London, UK, 2007. [Google Scholar]
- Kao, T.G.; Nguen, M.; Rivas-Perez, R. Adaptive control of a delay plant by using a nonsearching self-adjusting systems with a model. Avtom. Telemekh. 1988, 12, 106–116. [Google Scholar]
- Wang, Z.; Yuan, M.; Wang, B.; Wang, H.; Wang, T. Dynamic model of cement precalcination process. In Proceedings of the 27th IASTED International Conference on Modeling, Identification, and Control, Innsbruck, Austria, 11–13 February 2008; pp. 352–357. [Google Scholar]
- Tsamatsoulis, D.C. Simplified modeling of cement kiln precalciner. Int. J. Mater. 2016, 3, 69–73. [Google Scholar]
- Fellaou, S.; Harnoune, A.; Seghra, M.A.; Bounahmidi, T. Statistical modeling and optimization of the combustion efficiency in cement kiln precalciner. Energy 2018, 155, 351–359. [Google Scholar] [CrossRef]
- Fidaros, D.K.; Baxevanou, C.A.; Dritselis, C.D.; Vlachos, N.S. Numerical modelling of flow and transport processes in a calciner for cement production. Powder Technol. 2007, 171, 81–85. [Google Scholar] [CrossRef]
- Kovalienko, P.I.; Matzeliuk, E.M.; Rivas-Perez, R. Adaptive control of water distribution in main irrigation canals with variable time delay. Sci. Res. Hydrotech. Land Reclam. 1990, 32–40. [Google Scholar]
- Acedo Sánchez, J. Control Avanzado de Procesos, Teoría y Práctica; Ediciones Díaz de Santos, S.A.: Madrid, España, 2009. [Google Scholar]
- Rivas-Perez, R. Technological Process Control in Main Canals of Irrigation Systems, with Application to Irrigation Systems of Cuba. Ph.D. Thesis, Scientific Research Institute on Land Reclamation and Hydraulic Engineering of Ukrainian Academy of Agricultural Sciences (UkrNIIGIM), Kiev, Ukraine, 1984. [Google Scholar]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Calderon Mendoza, E.M.; Rivas-Perez, R.; Sotomayor-Moriano, J.J. Design of neuro-fuzzy controller for control of water distribution in an irrigation main canal. IEEE Lat. Am. Trans. 2016, 14, 471–476. [Google Scholar] [CrossRef]
- Astrom, K.; Hagglund, T. Advanced PID Control; Pearson Education, S.A.: Madrid, Spain, 2009. [Google Scholar]
- Fridman, E. Introduction to Time-Delay Systems Analysis and Control; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Sanz, R.; García, P.; Albertos, P. A generalized Smith predictor for unstable time-delay SISO systems. ISA Trans. 2018, 72, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Rivas-Perez, R. Synthesis of optimal stationary automatic control systems of water distribution in main irrigation canals by means of time delay compensation. Land Reclam. Water Manag. 1991, 74, 77–82. [Google Scholar]
- Richter, H. Advanced Control of Turbofan Engines; Springer: Cleveland, OH, USA, 2012. [Google Scholar]
- Rodriguez Vasquez, J.R.; Rivas-Perez, R.; Sotomayor-Moriano, J.J.; Peran-González, J.R. Advanced control system of the steam pressure in a fire-tube boiler. IFAC Proc. Vol. 2008, 41, 11028–11033. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J. Essentials of Robust Control; Pearson Education: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Gu, D.W.; Petko, H.P.; Konstantinov, M.M. Robust Control Design with MATLAB®, 2nd ed.; Springer: London, UK, 2013. [Google Scholar]
- Sánchez-Peña, R.; Sznaier, M. Robust Systems Theory and Applications; Wiley-Interscience: New York, NY, USA, 2008. [Google Scholar]
- Normey-Rico, J.E.; Camacho, E.F. Dead-time compensators: A survey. Control Eng. Pract. 2008, 16, 407–428. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Rivas-Perez, R. Control of the temperature in a petroleum refinery heating furnace based on a robust modified Smith predictor. ISA Trans. 2021, 12, 251–270. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.; Glover, K. Robust and Optimal Control; Prentice Hall: New Jersey, NJ, USA, 1996. [Google Scholar]
- Feliu-Batlle, V.; Rivas-Perez, R.; Sanchez-Rodriguez, L.; Castillo-García, F.J.; Linarez Saez, A. Robust fractional order PI controller for a main irrigation canal pool. IFAC Proc. Vol. 2008, 41, 15535–15540. [Google Scholar] [CrossRef]
- Stoorvogel, A. The H∞ Control Problem: A State–Space Approach; Prentice Hall: New Jersey, NJ, USA, 1992. [Google Scholar]
- Morari, M.; Zafirou, E. Robust Process Control; Prentice Hall: New Jersey, NJ, USA, 1989. [Google Scholar]
- Benitez, I.O.; Rivas, R.; Feliu, V.; Castillo, F.J. Temperature control based on a modified Smith predictor for injectable drug formulations. IEEE Lat. Am. Trans. 2015, 13, 1041–1047. [Google Scholar] [CrossRef]
- Fridman, L.; Poznyak, A.; Bejarano, F.J. Robust Output LQ Optimal Control via Integral Sliding Modes; Springer: New York, NY, USA, 2014. [Google Scholar]
- Salcedo-Hernández, J.; Rivas-Perez, R.; Sotomayor-Moriano, J. Design of a robust H2 state feedback temperature controller for a steel slab reheating furnace. Appl. Sci. 2020, 10, 1731. [Google Scholar] [CrossRef]
- Dolly Mary, A.; Mathew, A.T.; Jacob, J. Robust H-infinity (H∞) stabilization of uncertain wheeled mobile robots. Glob. J. Res. Eng. Electric. Electron. Eng. 2012, 12, 090602. [Google Scholar]
- Ljung, L. System Identification. In Theory for the User; Prentice-Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Inoue, M.; Wada, T.; Ikeda, M.; Uezato, E. State-space H∞ controller design for descriptor systems. Automatica 2015, 59, 164–170. [Google Scholar] [CrossRef]
- Xu, S.; Chen, T. Robust H∞ control for uncertain discrete-time systems with time-varying delays via exponential output feedback controllers. Systems Control Lett. 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Kailath, T. Linear Systems; Prentice Hall: New Jersey, NJ, USA, 1980. [Google Scholar]
- Rivas-Perez, R.; Cao, T.H.; Pichuguin, E.D.; Nguen, V.D. State space reconstruction in multivariable plants with time-delay. Control Cibernética Y Autom. 1989, 22, 30–35. [Google Scholar]
- Ogata, K. Discrete-Time Control System, 2nd ed.; Prentice-Hall International Inc.: New Jersey, NJ, USA, 1995. [Google Scholar]

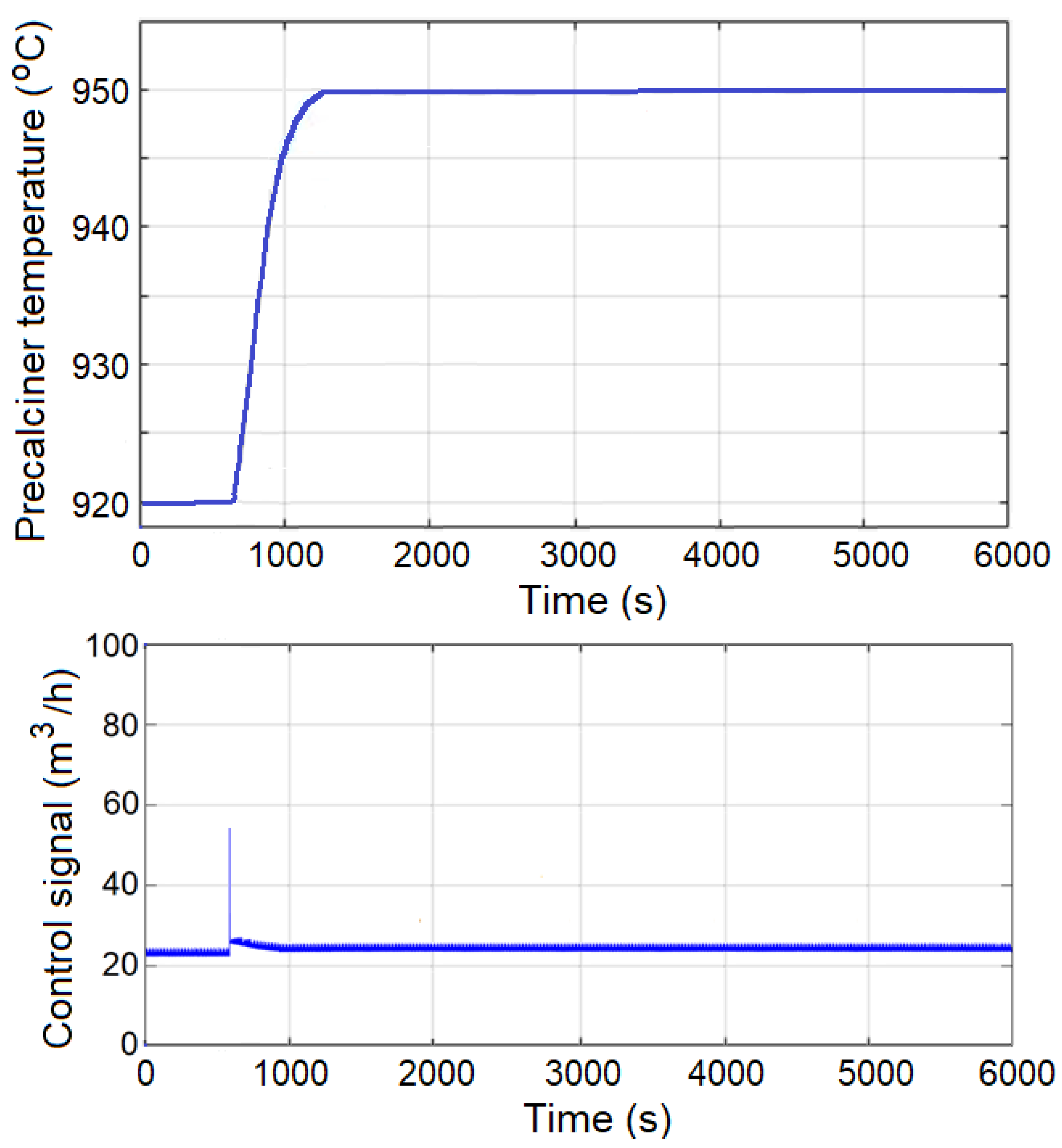
| Model Structure | Model Order | Performance Index(FIT) | |||||
|---|---|---|---|---|---|---|---|
| na | nb | nc | nd | nf | nk | ||
| ARMAX | 4 | 4 | 4 | - | - | 10 | 90.04% |
| BJ | - | 4 | 4 | 4 | 4 | 9 | 86.72% |
| ARX | 4 | 4 | - | - | - | 10 | 84.25% |
| OE | - | 2 | - | - | 2 | 11 | 85.45% |
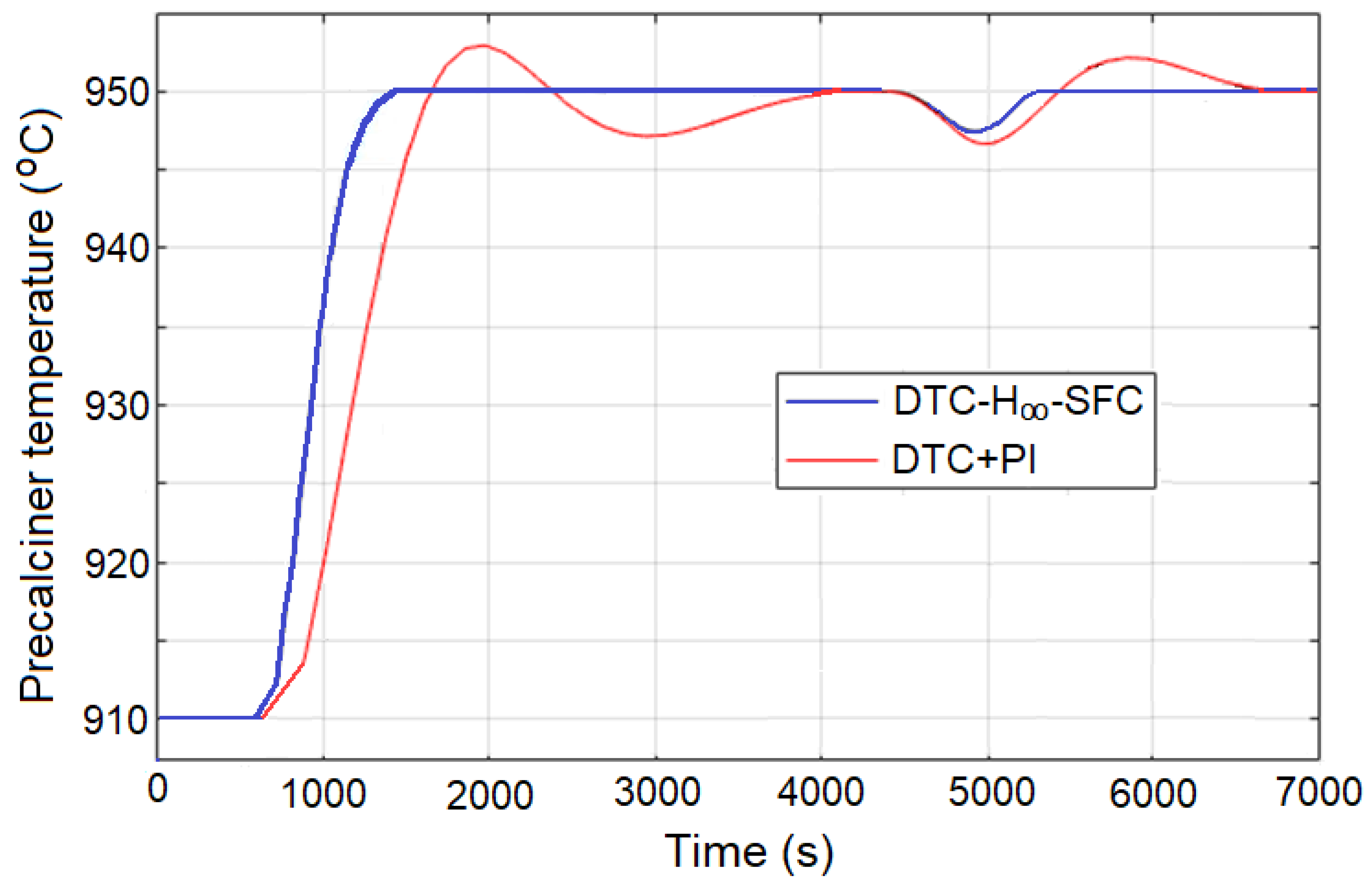
| ISE | ISE | |
|---|---|---|
| (NOMINAL) | (DISTURBANCE) | |
| DTC+PI | 14,149 | 140 |
| DTC-H∞-SFC | 13,230 | 45 |
| IAE | IAE | |
|---|---|---|
| (NOMINAL) | (DISTURBANCE) | |
| DTC+PI | 302 | 42 |
| DTC-H∞-SFC | 277 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salcedo-Hernández, J.; Rivas-Perez, R.; Sotomayor-Moriano, J. Design of a Dead-Time Compensator Robust H∞ State Feedback Temperature Controller for a Precalciner of a Cement Rotary Kiln. Appl. Sci. 2022, 12, 2594. https://doi.org/10.3390/app12052594
Salcedo-Hernández J, Rivas-Perez R, Sotomayor-Moriano J. Design of a Dead-Time Compensator Robust H∞ State Feedback Temperature Controller for a Precalciner of a Cement Rotary Kiln. Applied Sciences. 2022; 12(5):2594. https://doi.org/10.3390/app12052594
Chicago/Turabian StyleSalcedo-Hernández, José, Raul Rivas-Perez, and Javier Sotomayor-Moriano. 2022. "Design of a Dead-Time Compensator Robust H∞ State Feedback Temperature Controller for a Precalciner of a Cement Rotary Kiln" Applied Sciences 12, no. 5: 2594. https://doi.org/10.3390/app12052594
APA StyleSalcedo-Hernández, J., Rivas-Perez, R., & Sotomayor-Moriano, J. (2022). Design of a Dead-Time Compensator Robust H∞ State Feedback Temperature Controller for a Precalciner of a Cement Rotary Kiln. Applied Sciences, 12(5), 2594. https://doi.org/10.3390/app12052594








