Unique Features of Nonlocally Nonlinear Systems with Oscillatory Responses
Abstract
:1. Introduction
2. Nonlocality-Controllable Kerr Nonlinearities
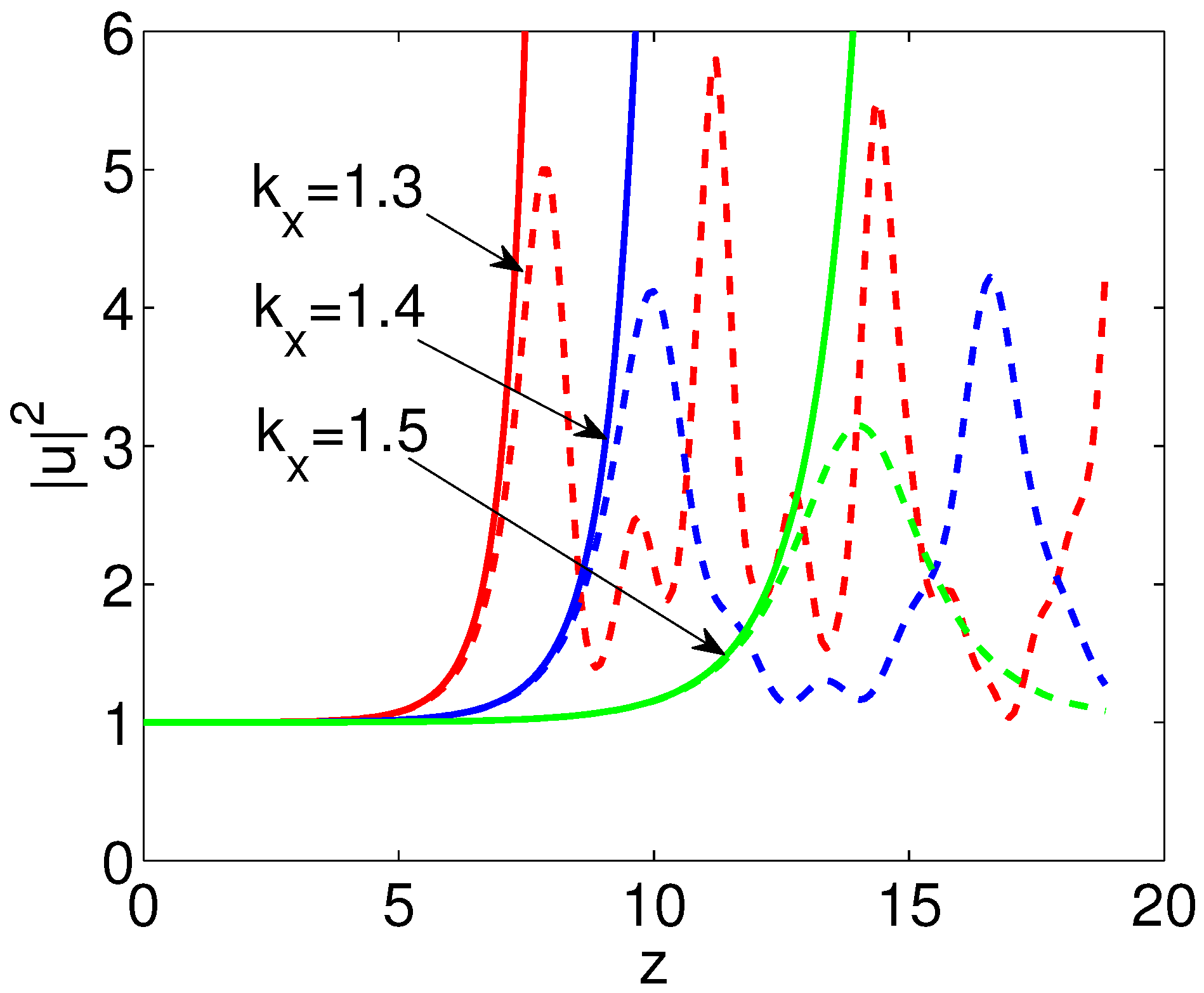
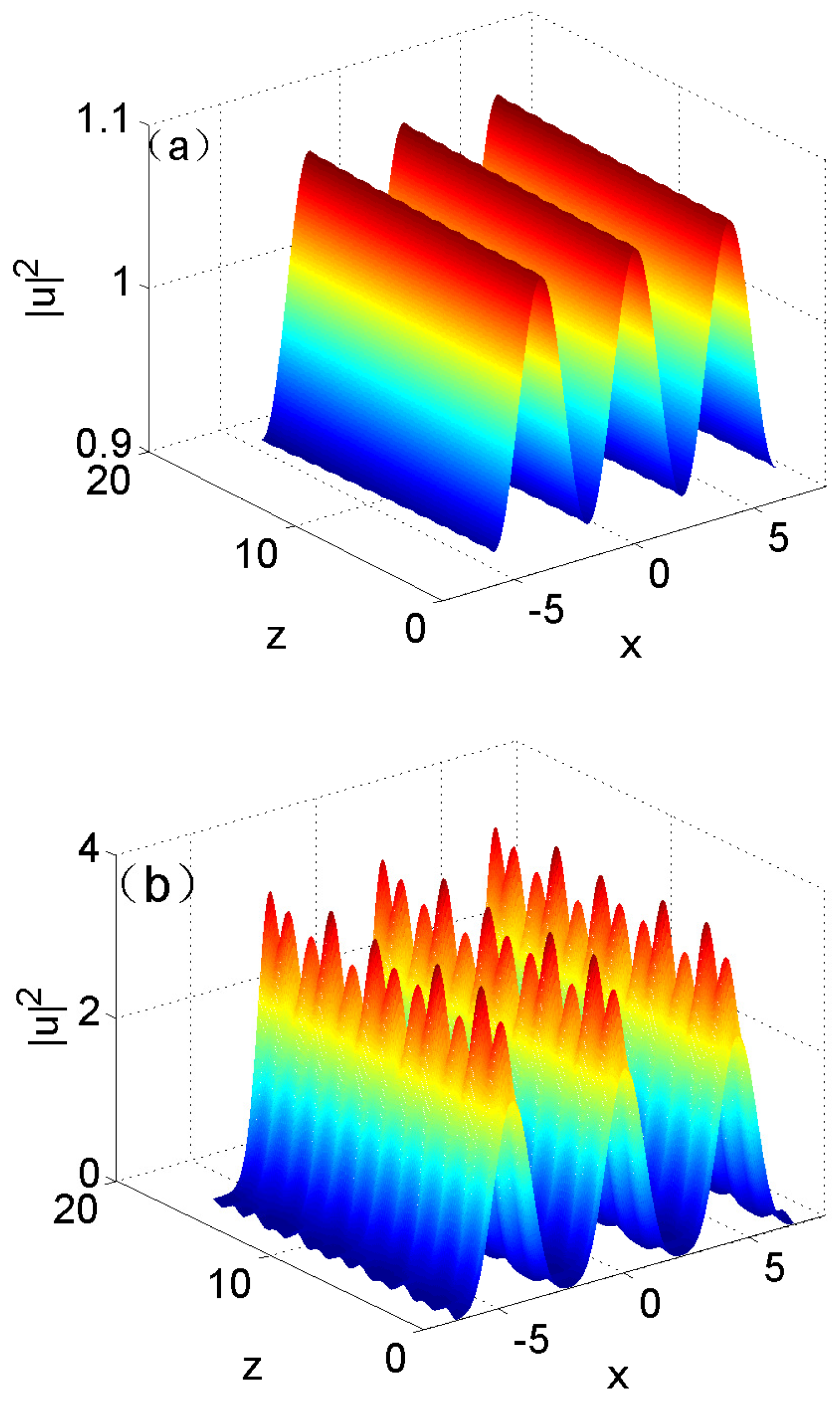
3. Unique Modulational Instability
3.1. Short-Term Evolution of MI
3.2. Long-Term Evolution of MI
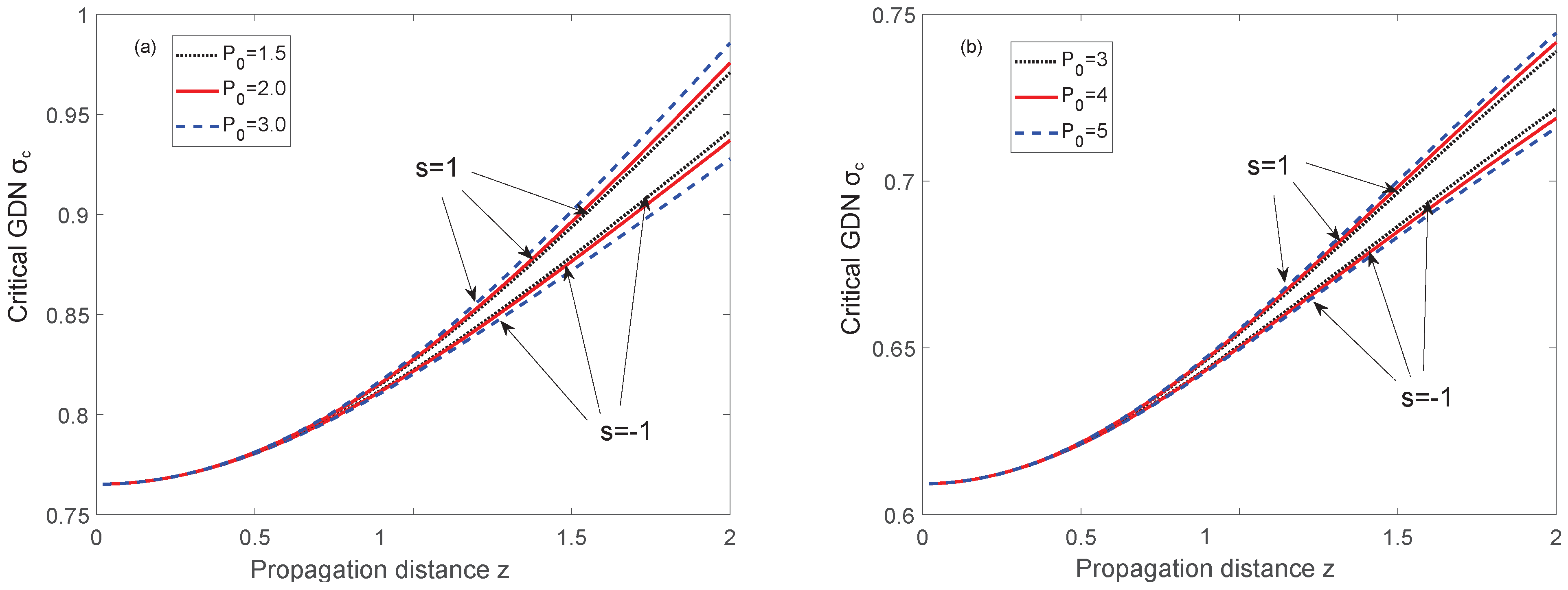
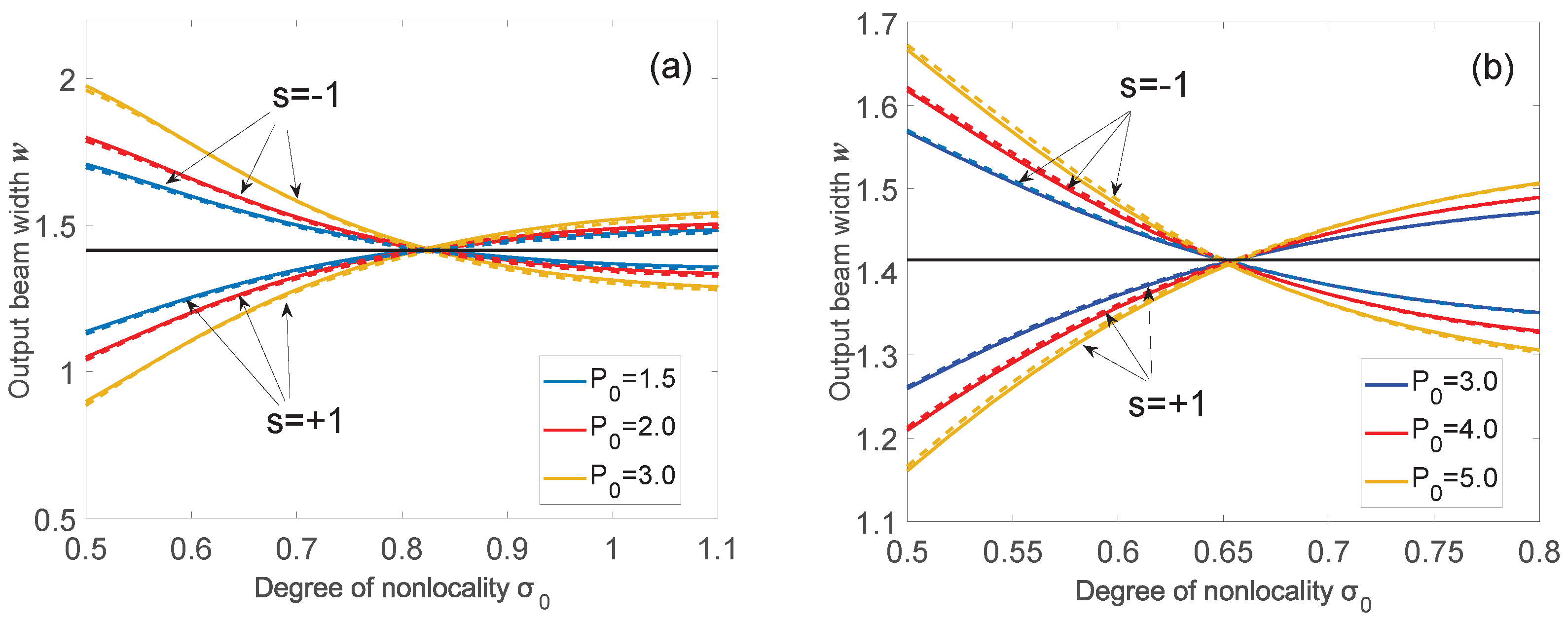
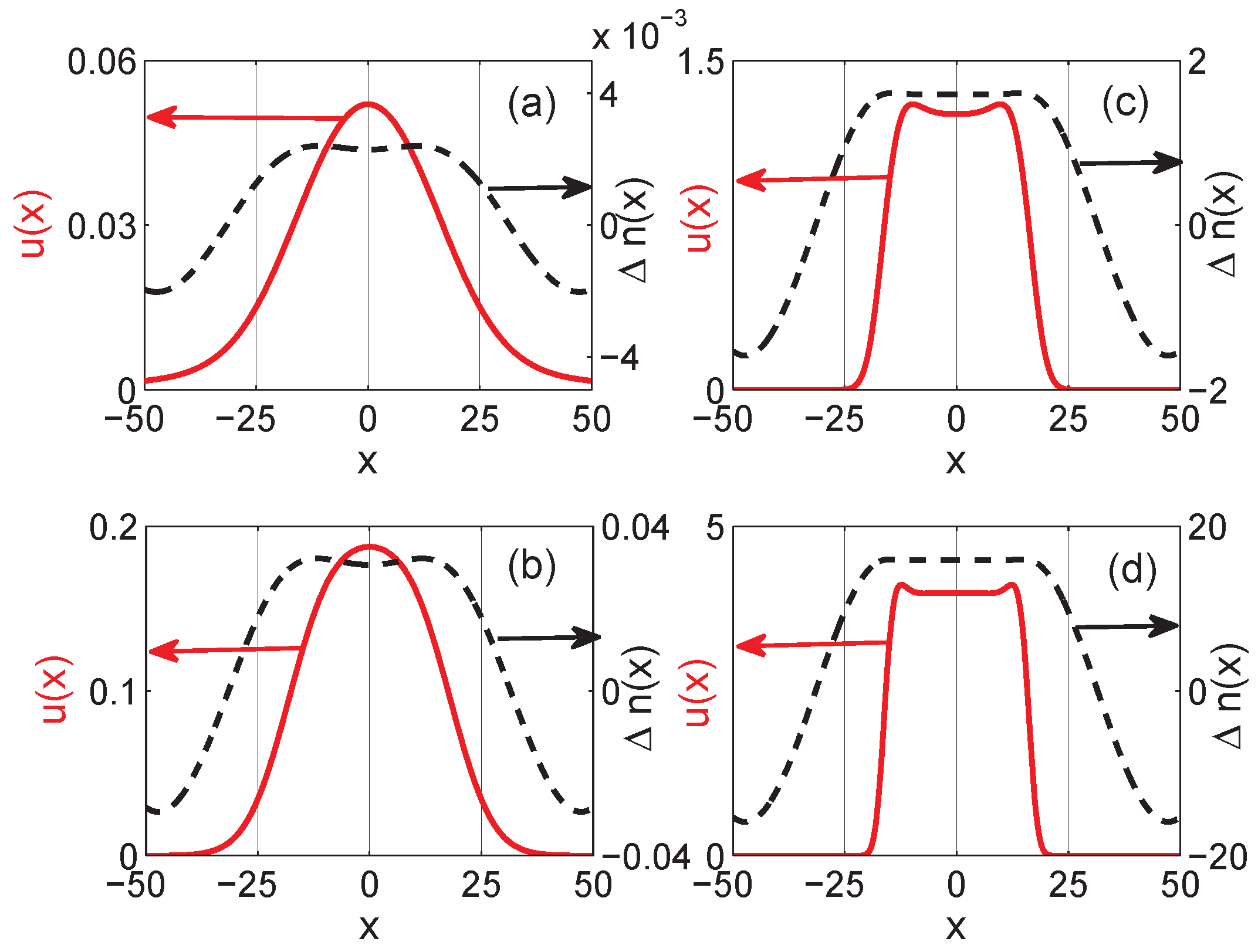
4. Characteristics of Solitons
4.1. Fundamental Solitons
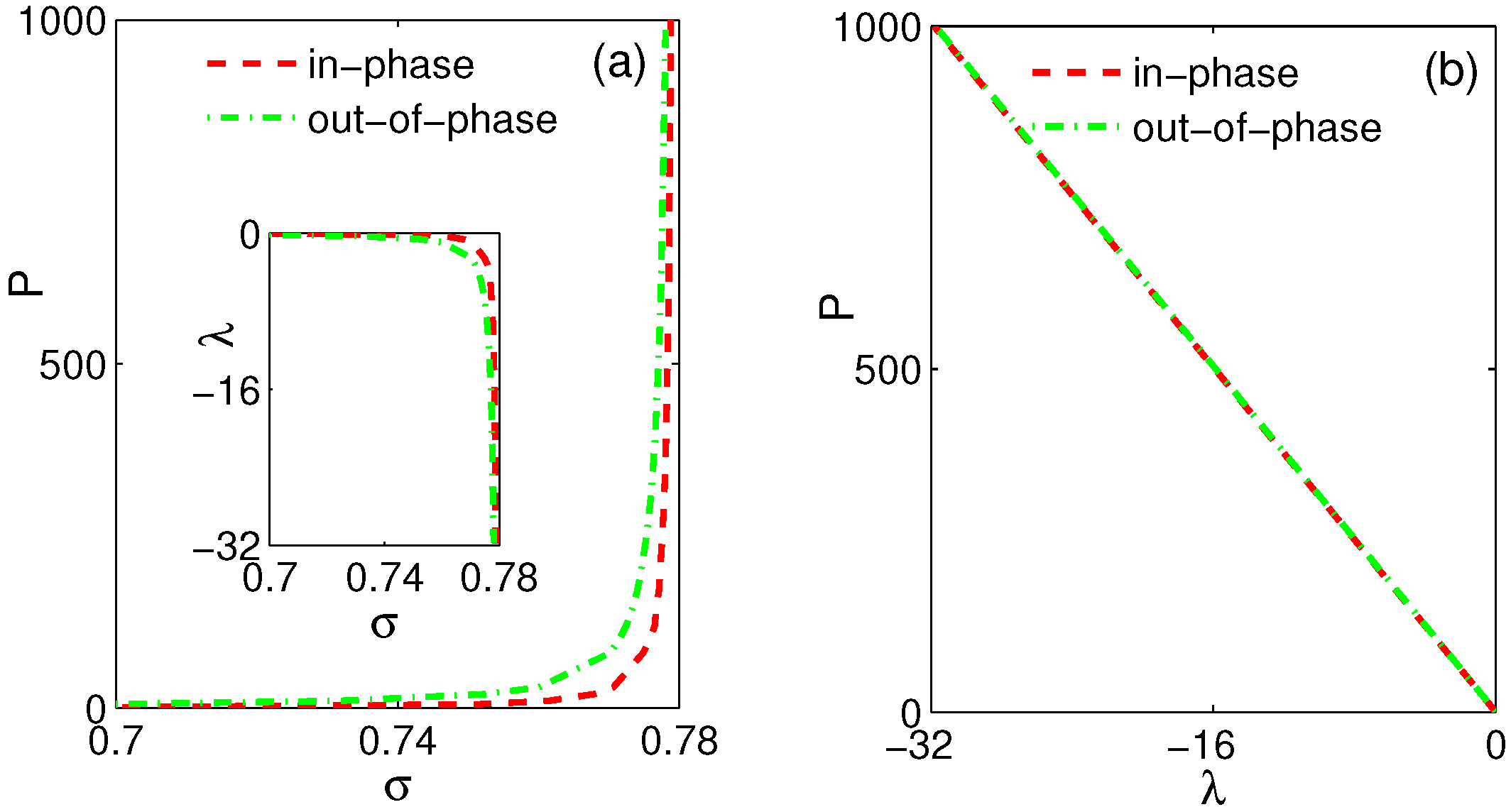
4.2. In-Phase and Out-of-Phase Bound-State Solitons
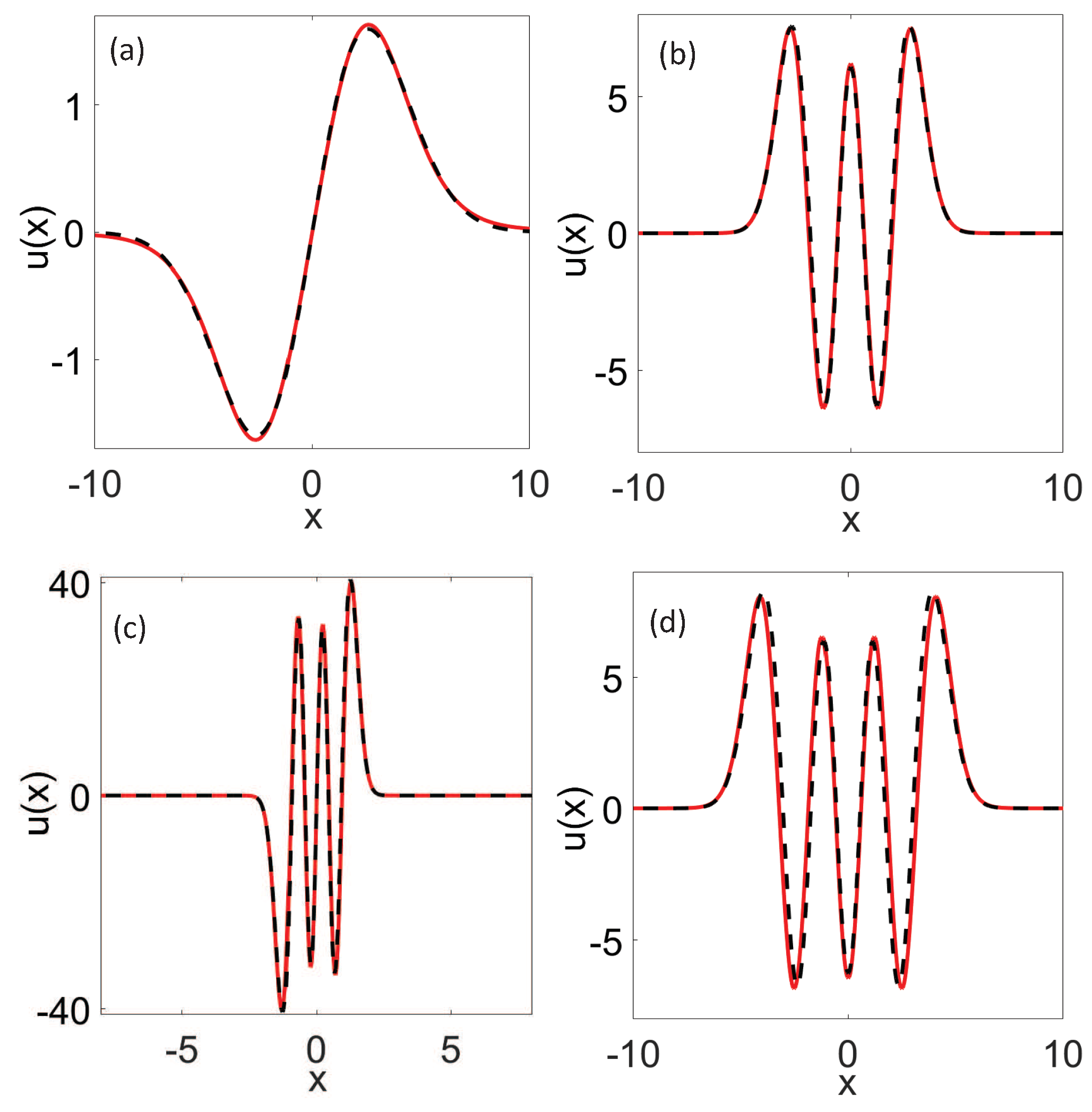
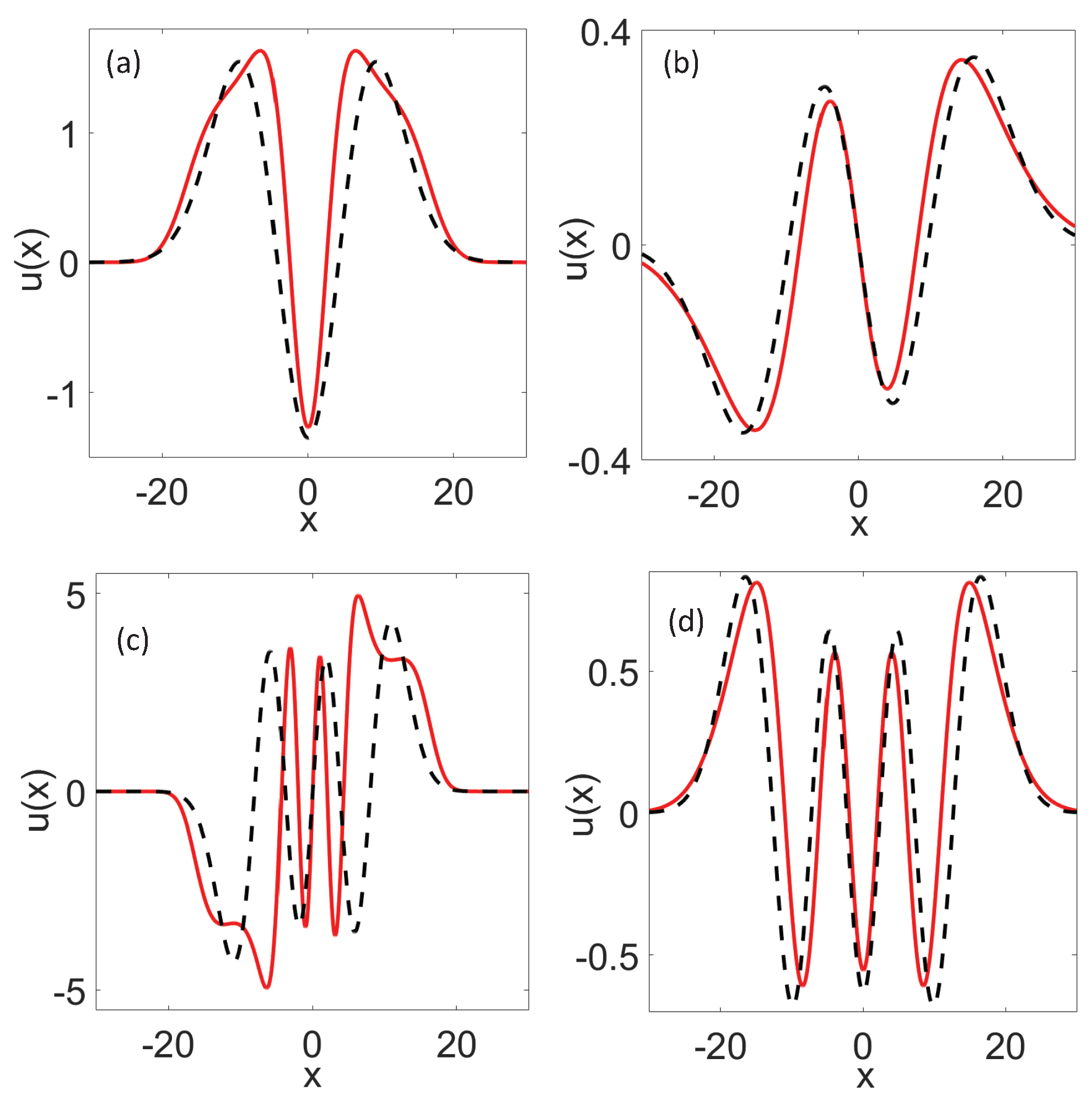
4.3. Multi-Peak Solitons
5. Perturbation-Iteration Method
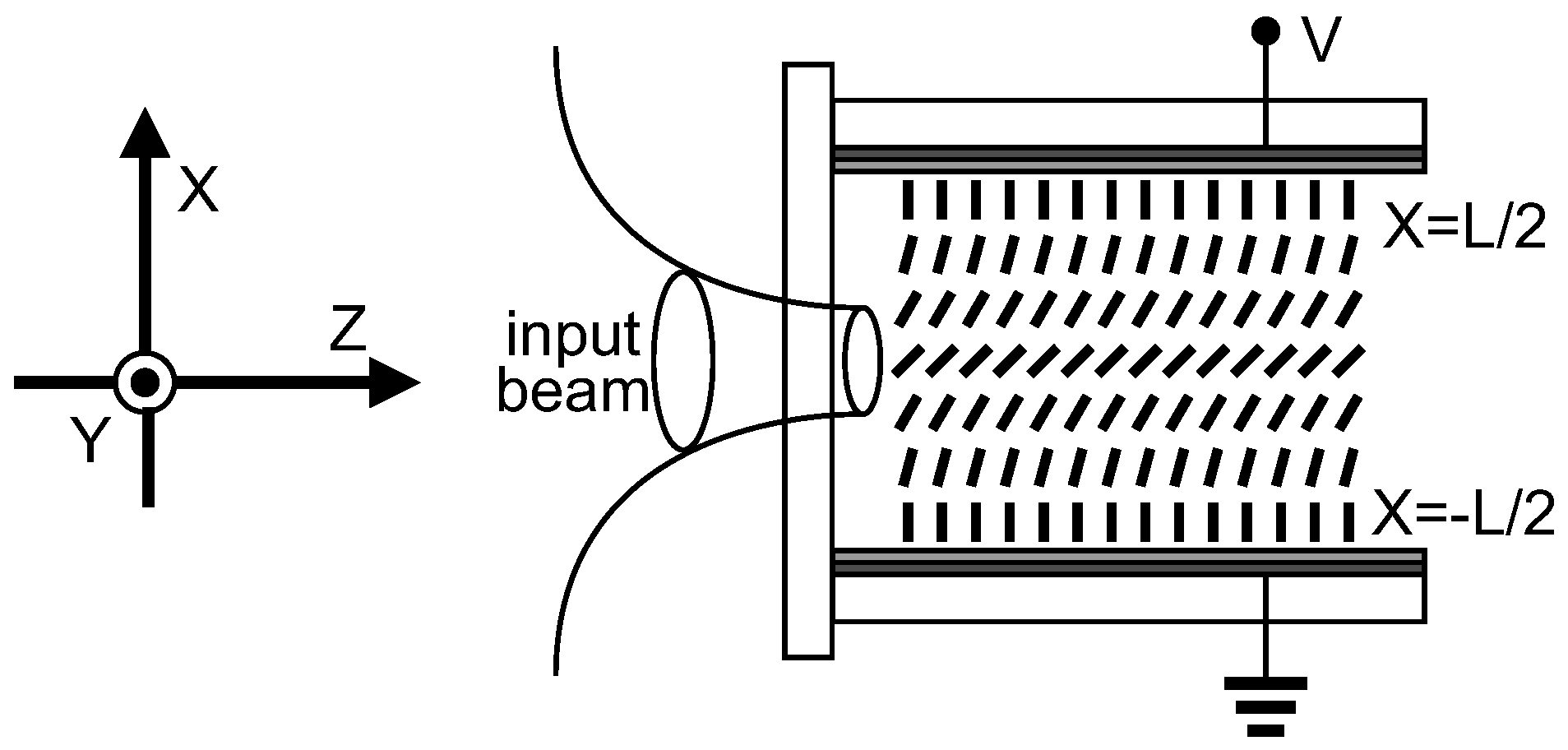
6. Optical Beams in NLC with Negative Dielectric Anisotropy
6.1. Evolution Equation for Optical Beams in NLC
6.2. Optical Nonlinearities of NLC with Negative Dielectric Anisotropy
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, Y.R. Principles of Nonlinear Optics; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Assanto, G. Nematicons: Spatial Optical Solitons in Nematic Liquid Crystals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Snyder, A.W.; Mitchell, D.J. Accessible Solitons. Science 1997, 276, 1538. [Google Scholar] [CrossRef]
- Guo, Q.; Lu, D.; Deng, D. Nonlocal spatial optical solitons. In Advances in Nonlinear Optics; Chen, X., Zhang, G., Zeng, H., Guo, Q., Shen, W., Eds.; De Gruyter: Berlin, Germany, 2015; Chapter 4; pp. 227–305. [Google Scholar]
- Peccianti, M.; Assanto, G. Nematicons. Phys. Rep. 2012, 516, 147. [Google Scholar] [CrossRef]
- Królikowski, W.; Bang, O.; Nikolov, N.I.; Neshev, D.; Wyller, J.; Rasmussen, J.J.; Edmundson, D. Modulational instablity, solitons and beam propagation in spatially nonlocal nonlinear media. J. Opt. B Quantum Semiclass. Opt. 2004, 6, S288. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q. Nonlocal spatial solitons and their interactions. In Optical Transmission, Switching, and Subsystems; SPIE: Bellingham, WA, USA, 2004; Volume 5281, pp. 581–594. [Google Scholar]
- Królikowski, W.; Bang, O.; Briedis, D.; Dreischuh, A.; Edmundson, D.; Luther-Davies, B.; Neshev, D.; Nikolov, N.; Petersen, D.E.; Rasmussen, J.J. Nonlocal solitons. In Nonlinear Optics Applications; SPIE: Warsaw, Poland, 2005; Volume 5949, pp. 76–85. [Google Scholar]
- Conti, C.; Peccianti, M.; Assanto, G. Route to nonlocality and observation of accessible solitons. Phys. Rev. Lett. 2003, 91, 073901. [Google Scholar] [CrossRef] [Green Version]
- Conti, C.; Peccianti, M.; Assanto, G. Observation of optical spatial solitons in a highly nonlocal medium. Phys. Rev. Lett. 2004, 92, 113902. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Buchnev, O.; Kaczmarek, M.; Khoo, I.C.; Assanto, G. Frequency-controlled deflection of spatial solitons in nematic liquid crystals. Appl. Phys. Lett. 2012, 101, 081112. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Buchnev, O.; Kaczmarek, M.; Khoo, I.C.; Assanto, G. Frequency-controlled routing of self-confined beams in nematic liquid crystals. Mol. Cryst. Liq. Cryst. 2013, 573, 26. [Google Scholar] [CrossRef]
- Laudyn, U.; Kwasny, M.; Karpierz, M.; Assanto, G. Electro-optic quenching of nematicon fluctuations. Opt. Lett. 2019, 44, 167. [Google Scholar] [CrossRef]
- Rotschild, C.; Cohen, O.; Manela, O.; Segev, M.; Carmon, T. Solitons in nonlinear media with an infinite range of nonlocality: First observation of coherent elliptic solitons and of vortex-ring solitons. Phys. Rev. Lett. 2005, 95, 213904. [Google Scholar] [CrossRef] [Green Version]
- Suter, D.; Blasberg, T. Stabilization of transverse solitary waves by a nonlocal response of the nonlinear medium. Phys. Rev. A 1993, 48, 4583. [Google Scholar] [CrossRef]
- Segev, M.; Crosignani, B.; Yariv, A.; Fischer, B. Spatial solitons in photorefractive media. Phys. Rev. Lett. 1992, 68, 923. [Google Scholar] [CrossRef] [PubMed]
- Parola, A.; Salasnich, L.; Reatto, L. Structure and stability of bosonic clouds: Alkali-metal atoms with negative scattering length. Phys. Rev. A 1998, 57, R3180. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, P.D.; Bang, O.; Krolikowski, W. Theory of nonlocal soliton interaction in nematic liquid crystals. Phys. Rev. E 2005, 72, 066611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, W.; Zhang, T.; Guo, Q.; Xuan, L.; Lan, S. Nonlocality-controlled interaction of spatial solitons in nematic liquid crystals. Appl. Phys. Lett. 2006, 89, 071111. [Google Scholar] [CrossRef] [Green Version]
- Nikolov, N.I.; Neshev, D.; Bang, O.; Krolikowski, W.Z. Quadratic solitons as nonlocal solitons. Phys. Rev. E 2003, 68, 036614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esbensen, B.K.; Bache, M.; Krolikowski, W.; Bang, O. Quadratic solitons for negative effective second-harmonic diffraction as nonlocal solitons with periodic nonlocal response function. Phys. Rev. A 2012, 86, 023849. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Dong, G.; Malomed, B.A. Hybrid matter-wave-microwave solitons produced by the local-field effect. Phys. Rev. Lett. 2015, 115, 023901. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, Y.; Guo, Q.; Hu, W. Stabilization of nonlocal solitons by boundary conditions. Opt. Lett. 2014, 39, 405. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Z.; Li, Y.; Lu, D.; Guo, Q.; Hu, W. Stable quadratic solitons consisting of fundamental waves and oscillatory second harmonics subject to boundary confinement. Phys. Rev. A 2015, 91, 033801. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, Y.; Wang, J.; Lv, F.; Lu, D.; Hu, W. Bright nonlocal quadratic solitons induced by boundary confinement. Phys. Rev. A 2017, 95, 013808. [Google Scholar] [CrossRef]
- Liang, G.; Hong, W.; Luo, T.; Wang, J.; Li, Y.; Guo, Q.; Hu, W.; Christodoulides, D.N. Transition between self-focusing and self-defocusing in a nonlocally nonlinear system. Phys. Rev. A 2019, 99, 063808. [Google Scholar] [CrossRef] [Green Version]
- Liang, G.; Dang, D.; Li, W.; Li, H.; Guo, Q. Nonlocality-controllable Kerr-nonlinearity in nonlocally nonlinear system with oscillatory responses. New J. Phys. 2020, 22, 073204. [Google Scholar] [CrossRef]
- Liang, G.; Hong, W.; Guo, Q. Spatial solitons with complicated structure in nonlocal nonlinear media. Opt. Express. 2016, 24, 28784. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Dang, D.; Li, W.; Ren, Z.; Guo, Q. Multi-peak solitons in nonlocal nonlinear system with sine-oscillation response. Commun. Nonlinear Sci. 2022, 109, 106322. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Q.; Hong, W.; Hu, W. Modulational instability in nonlocal Kerr media with a sine-oscillatory response. Opt. Commun. 2017, 394, 31. [Google Scholar] [CrossRef] [Green Version]
- Guan, J.; Ren, Z.; Guo, Q. Stable solution of induced modulation instability. Sci. Rep. 2020, 10, 10081. [Google Scholar] [CrossRef]
- Anderson, D. Variational approach to nonlinear pulse propagation in optical fibers. Phys. Rev. A 1983, 27, 3135. [Google Scholar] [CrossRef]
- Guo, Q.; Luo, B.; Chi, S. Optical beams in sub-strongly non-local nonlinear media: A variational solution. Opt. Commun. 2006, 259, 336. [Google Scholar] [CrossRef]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 4th ed.; Academic: San Diego, CA, USA, 2007. [Google Scholar]
- Hu, Y.; Lou, S. Analytical descriptions of dark and gray solitons in nonlocal nonlinear media. Commun. Theor. Phys. 2015, 64, 665. [Google Scholar] [CrossRef]
- Hong, W.; Tian, B.; Li, R.; Guo, Q.; Hu, W. Perturbation-iteration method for multi-peak solitons in nonlocal nonlinear media. J. Opt. Soc. Am. B 2018, 35, 317. [Google Scholar] [CrossRef] [Green Version]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press Inc.: Cambridge, MA, USA, 2003. [Google Scholar]
- Sakaguchi, H.; Malomed, B.A. Solitons in combined linear and nonlinear lattice potentials. Phys. Rev. A 2010, 81, 013624. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Dong, G.; Malomed, B.A. Stable giant vortex annuli in microwave-coupled atomic condensates. Phys. Rev. A 2016, 94, 053611. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Liang, Z.; Malomed, B.A.; Dong, G. Tail-free self-accelerating solitons and vortices. Phys. Rev. A 2019, 99, 023610. [Google Scholar] [CrossRef] [Green Version]
- Buryak, A.V.; Kivshar, Y.S. Solitons due to second harmonic generation. Phys. Lett. A 1995, 197, 407. [Google Scholar] [CrossRef]
- Xu, Z.; Kartashov, Y.V.; Torner, L. Upper threshold for stability of multipole-mode solitons in nonlocal nonlinear media. Opt. Lett. 2005, 30, 3171. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Ye, F. Stability of multipole-mode solitons in thermal nonlinear media. Phys. Rev. A 2010, 81, 013815. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, S.; Guo, Q.; Hu, W. Perturbative analysis of generally nonlocal spatial optical solitons. Phys. Rev. E 2006, 74, 036622. [Google Scholar] [CrossRef] [Green Version]
- Tian, B.; Guo, Q.; Hong, W.; Hu, W. Extension of the perturbation-iteration method to (1 + 2)-dimensional case. Optik 2019, 192, 162909. [Google Scholar] [CrossRef]
- Khoo, I.C. Liquid Crystals: Physical Properties and Nonlinear Optical Phenomena; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Schiekel, M.F.; Fahrenschon, K. Deformation of nematic liquid crystals with vertical orientation in electrical fields. Appl. Phys. Lett. 1971, 19, 391. [Google Scholar] [CrossRef]
- Peccianti, M.; Conti, C.; Assanto, G.; De Luca, A.; Umeton, C. Nonlocal optical propagation in nonlinear nematic liquid crystals. J. Nonlinear Opt. Phys. Mater. 2003, 12, 525. [Google Scholar] [CrossRef]
- Peccianti, M.; Conti, C.; Assanto, G. Interplay between nonlocality and nonlinearity in nematic liquid crystals. Opt. Lett. 2005, 30, 415. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G.; Peccianti, M. Spatial solitons in Nematic liquid crystals. IEEE J. Quantum Electron. 2003, 39, 13. [Google Scholar] [CrossRef]
- Zhang, Y. Numerical Research on Modulation Instability of Nematic Liquid Crystals with Negative Dielectric Anisotropy. Master’s Dissertation, South China Normal University, Guangzhou, China, 2005. (In Chinese). [Google Scholar]
- Krolikowski, W.; Bang, O. Solitons in nonlocal nonlinear media: Exact solutions. Phys. Rev. E 2000, 63, 016610. [Google Scholar] [CrossRef] [Green Version]
- Kong, Q.; Wang, Q.; Bang, O.; Krolikowski, W. Analytical theory of dark nonlocal solitons. Opt. Lett. 2010, 35, 2152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conti, C.; Fratalocchi, A.; Peccianti, M.; Ruocco, G.; Trillo, S. Observation of a gradient catastrophe generating solitons. Phys. Rev. Lett. 2009, 102, 083902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Chen, J.; Liu, J.; Li, Y.; Guo, Q.; Hu, W.; Xuan, L. Nematicons in liquid crystals with negative dielectric anisotropy. arXiv 2018, arXiv:1403.2154v2. [Google Scholar]





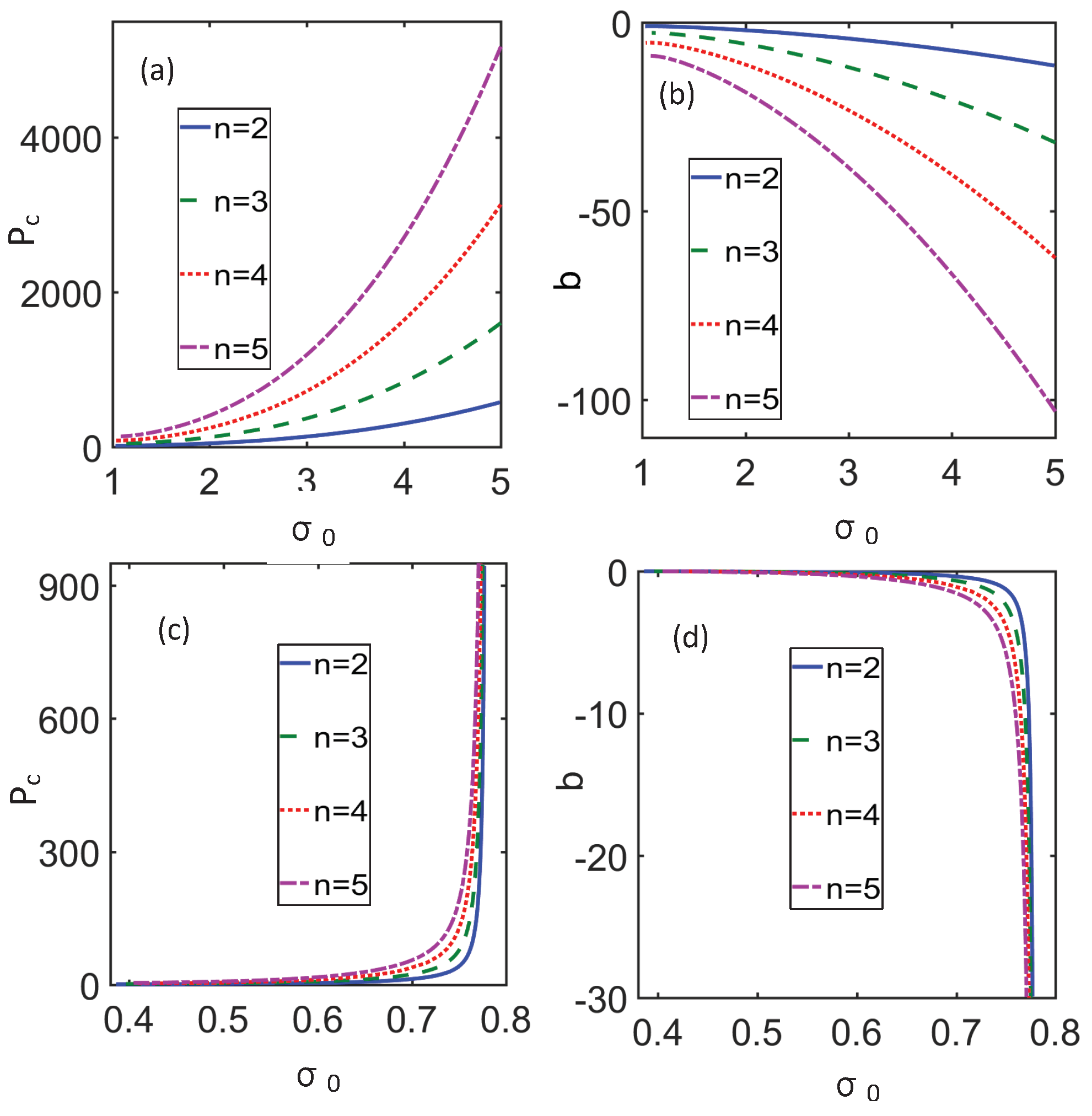
| variational | |||||
| numerical | |||||
| variational | |||||
| numerical |
| no | ||||||
| no | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, G.; Liu, J.; Hu, W.; Guo, Q. Unique Features of Nonlocally Nonlinear Systems with Oscillatory Responses. Appl. Sci. 2022, 12, 2386. https://doi.org/10.3390/app12052386
Liang G, Liu J, Hu W, Guo Q. Unique Features of Nonlocally Nonlinear Systems with Oscillatory Responses. Applied Sciences. 2022; 12(5):2386. https://doi.org/10.3390/app12052386
Chicago/Turabian StyleLiang, Guo, Jinlong Liu, Wei Hu, and Qi Guo. 2022. "Unique Features of Nonlocally Nonlinear Systems with Oscillatory Responses" Applied Sciences 12, no. 5: 2386. https://doi.org/10.3390/app12052386
APA StyleLiang, G., Liu, J., Hu, W., & Guo, Q. (2022). Unique Features of Nonlocally Nonlinear Systems with Oscillatory Responses. Applied Sciences, 12(5), 2386. https://doi.org/10.3390/app12052386







