Design and Application of Secret Codes for Learning Medical Data

Abstract

In distributed learning for data requiring privacy preservation, such as medical data, the distribution of secret information is an important problem. In this paper, we propose a framework for secret codes in application to distributed systems. Then, we provide new methods to construct such codes using the synthesis or decomposition of previously known minimal codes. The numerical results show that new constructions can generate codes with more flexible parameters than original constructions in the sense of the number of possible weights and the range of weights. Thus, the secret codes from new constructions may be applied to more general situations or environments in distributed systems.

1. Introduction

With the fourth Industrial Revolution, the application of artificial intelligence technology is expanding in the medical field [1,2,3,4,5,6]. The biggest obstacle to the collaboration of medical data from distinct institutes has been the protection the private information contained in the distributed system. In particular, federate learning is in the spotlight as a distributed machine learning technique that can simultaneously retain privacy and efficiency [7]. It can produce a similar result to learning all data at once without sharing private data. Since federated learning does not centralize data to a big server, it can protect the private information of each user. Currently, it is being applied to several areas, including health care, smart factories, and finance [8,9,10,11,12,13]. Major companies such as Google and NVIDIA have been conducting research on medical artificial intelligence through the development of their own federated learning algorithms [8,9,10].

Linear block codes have been investigated for applications in several areas of engineering, such as communication systems, cryptography, and security [14]. A minimal code is a block code in which the support of a codeword is not included in that of any other codewords [15]. Using the minimal code, one user’s information is not subordinate to other users’ information. This has been constantly studied as one of the mathematical structures that can be used in secret-sharing schemes [16,17,18,19,20,21,22,23]. Furthermore, a minimal code can be used in federated learning due to its distributed characteristics of secret information. Almost all the known minimal codes so far have been designed based on the structure and characteristics of finite fields [24]. In particular, for binary cases, several design methods have been proposed [16,17,18,19,20]. On the other hand, non-binary minimal code has been investigated recently [21,22,23]. Research on previously known minimal codes has focused only on the weight distribution of the codes. Considering recent applications, further characteristics or structures of minimal codes, such as their error-correction capability and relation to the learning rate, should be investigated.

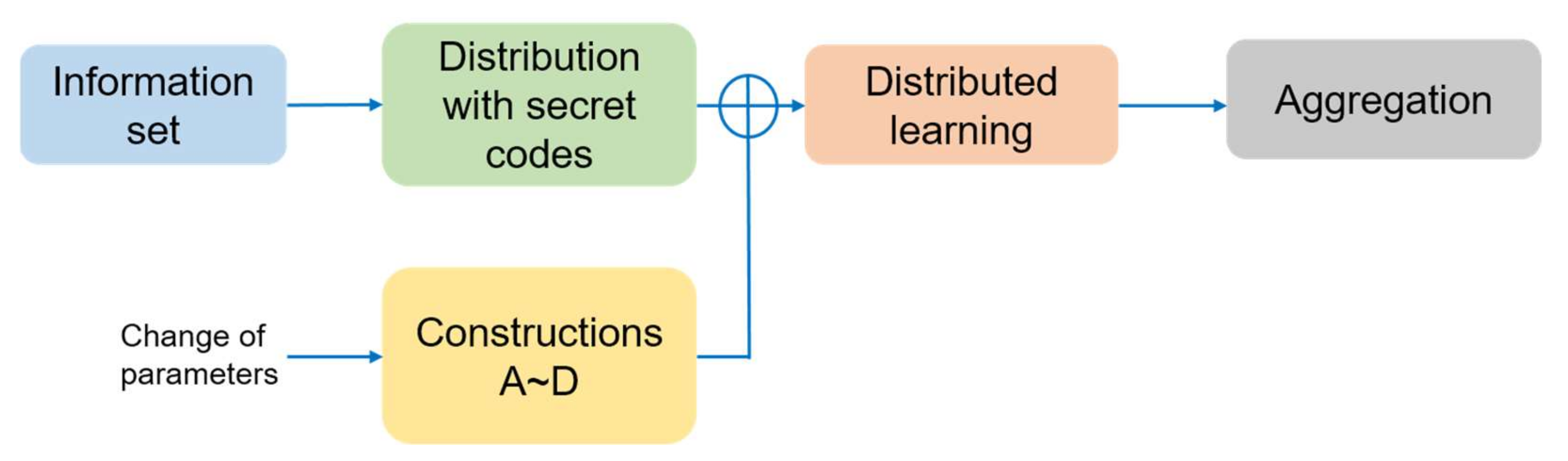
In this paper, we propose a framework for secret codes in application to distributed systems. Then, we provide new methods to construct such codes using the synthesis or decomposition of previously known minimal codes. The numerical results show that new constructions can generate codes with more flexible parameters than original constructions in the sense of the number of possible weights and the range of weights. The secret codes from new constructions may be applied to more general situations or environments in distributed systems.

The remainder of this paper is organized as follows. In Section 2, we present some preliminaries on secret-sharing schemes, finite fields, and minimal codes. We present design methods for secret codes, and propose a framework for the application of designed codes to distributed learning systems in Section 3. We provide the results of our construction in Section 4, and then compare them with the previous researches in Section 5. Finally, we present concluding remarks in Section 6.

2. Preliminaries

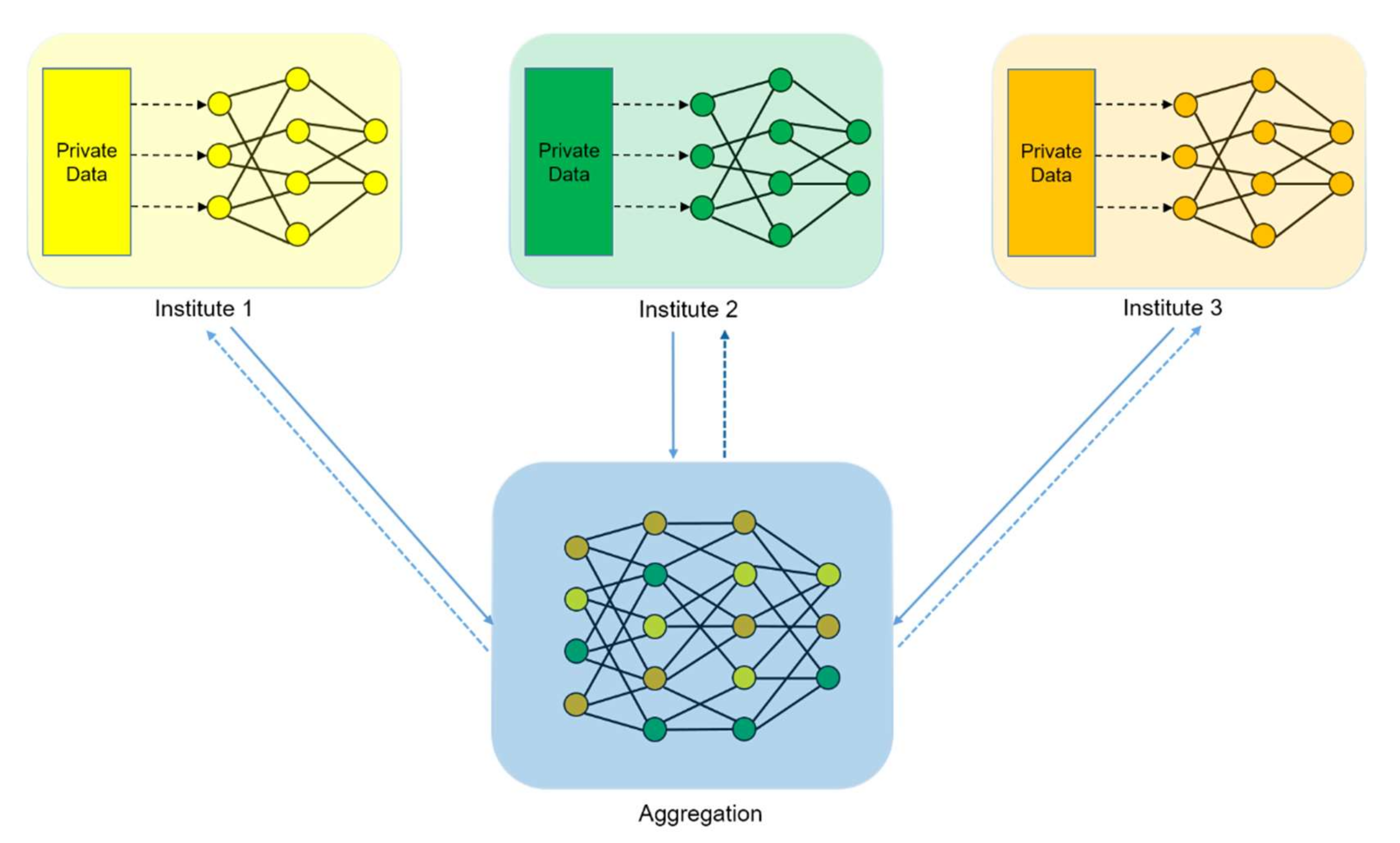
In the distributed learning schemes depicted in Figure 1, the distribution of secret or private information is very important in order to retain secret properties. Linear block codes can be used as a mathematical tool to design such distribution strategies [17,18]. In this section, we present some preliminary knowledge on finite fields and algebraic codes that are used in secret-sharing schemes.

Minimal codes are a class of linear block codes, in which the support of a codeword is not included to that of another codeword. A binary linear block code $\mathrm{C}$ of length $N$ is a subspace of vectors in the space ${\left\{0,1\right\}}^N$. An element of a linear block code is called a codeword. A codeword $x$ of length $N$ in a binary linear block code can be expressed as

$$x=\left\{x\left[n\right] :x\left[n\right]\in \left\{0,1\right\}, n\in Z_N\right\}$$

where $n$ represent the index of each symbol, and $Z_N$ is the set of integers modulo $N$. Because a linear block code is a subspace, the vector addition of any two codewords in a code is included as another codeword in the code. The support of $x$ is a subset of $Z_N$, which is defined as

$$\mathrm{supp}\left(x\right)=\left\{n :x\left[n\right]=1, n\in Z_N\right\}$$

(1)

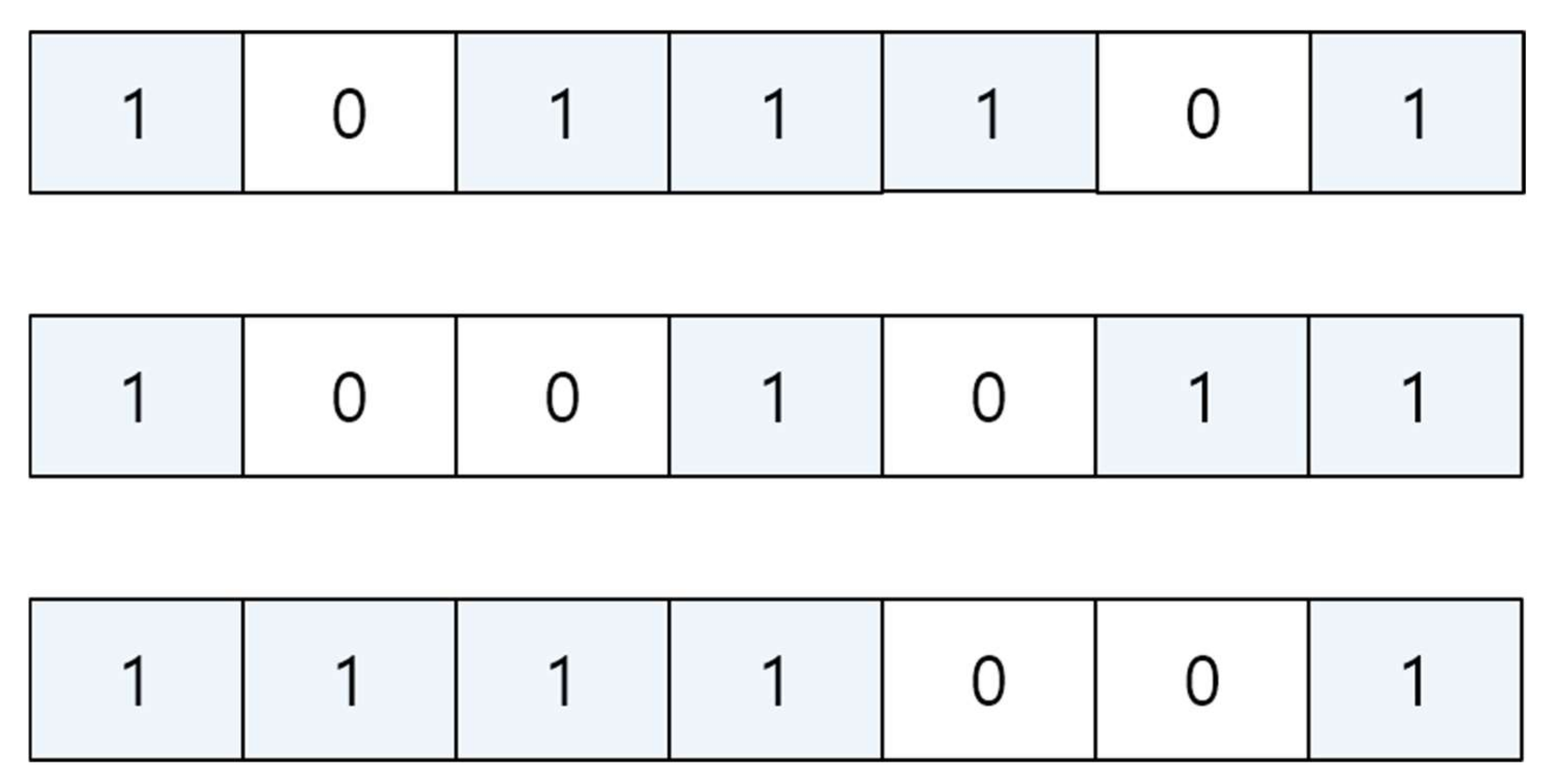
The size of $\mathrm{supp}\left(x\right)$ is called the Hamming weight of $x$. In secret-sharing schemes, a secret codeword is assigned to a user or a device. Information in the codeword should not be subordinate to any other codewords. A minimal code is defined as a linear block code in which the support of a codeword is not a subset of the support of any other codeword, as shown in Figure 2. Using this characteristic, secret information can be distributed to users, and the information of a user is not fully revealed to the other users. Due to this characteristic, minimal codes have been applied to secret-sharing schemes [15,17]. However, in distributed learning, the secret-storing structure is important, as is the weight distribution of a code. Research on analytic approaches to the structure is ongoing.

A secret-sharing scheme is, from a mathematical viewpoint, constructed on a finite field. A finite field is an algebraic structure in which addition, subtraction, multiplication, and division can be freely operated [24]. For a prime $p$ and a positive integer $m$, a finite field $\mathrm{GF}\left(p^m\right)$ consists of the additive identity $0$ and $1={\alpha }^0,{\alpha }^1,{\alpha }^2,\dots , {\alpha }^{p^m-2}$, where $\alpha$ is called a primitive element of $\mathrm{GF}\left(p^m\right)$. The finite field $\mathrm{GF}\left(p^m\right)$ is an Abelian group with respect to the addition modulo $p$, and $\mathrm{GF}\left(p^m\right)\backslash \left\{0\right\}$ is a cyclic group with respect to the multiplication. Any element of a finite field can be represented not only in a multiplicative way using the power of the primitive element, but also in an additive way using vector representation on the basis $\left\{1, {\alpha }^1,{\alpha }^2,\dots ,{\alpha }^{m-1}\right\}$. Note that $\mathrm{GF}\left(p^m\right)$ can be interpreted as a vector space of dimension $m$ over $\mathrm{GF}\left(p\right)$. Most of the well-known error-correction codes and pseudorandom sequences have been constructed based on the properties of finite fields [14]. In this paper, we assume that $p=2$, which corresponds to the cases of binary codes. Because most machine learning algorithms are based on the binary operation, the assumption is appropriate.

In a secret-sharing scheme defined on $\mathrm{GF}\left(p^m\right)$, a secret corresponds to an element of the finite field. Let $U_1,\dots ,U_l$ be users or devices engaged in the scheme. Pieces of the secret are assigned to each user using a secret code. This secret information must be encoded so that the whole information is not synthesized from any proper subset of information of users. Moreover, in a partial group of users, if a user can recover some part of the secret, the other user should also be able to recover the same information. Minimal codes are good mathematical structures to apply to various kinds of secret-sharing schemes due to their linearity and the non-inclusive properties of supports. A minimal code can be parameterized by the length of codewords, the number of codewords, and the weight distribution. The length means the number of information indices, the number of codewords corresponds to the number of users or devices, and the weight distribution is related to the placement of information. In

Table 1. Known classes of binary minimal codes ($p$ is an odd prime).

Reference	Alphabet Size	Length	Number of Distinct Weights	Restricted in (1)
[16]	$2$	$2^m-1$	$3$	Yes
[19]	$2$	$2^m-1$	$3$	Yes
[20]	$2$	$2^m-1$	$4~6$	No
[21]	$p$	$p^m-1$	3	Yes
[22]	$p$	$p^m-1$	$3~4$	No

, some well-known constructions for minimal codes are summarized. Recently, Mesnager et al. presented a generalized construction tool including several existing design methods [23]. Since most of known minimal codes are designed using the structure of $\mathrm{GF}\left(p^m\right)$, their lengths are restricted to $p^m-1$ for a prime $p$.

In [16], Aschkmin and Barg established a sufficient condition on the existence of minimal codes as in the following theorem.

Theorem 1.

[16] A linear code $C$ defined over a finite field of characteristic $p$ becomes a minimal code if

$$\frac{w_{min}}{w_{max}}>\frac{p-1}{p}$$

(2)

where$w_{min}$(resp.$w_{min}$) is the minimum (resp. maximum) value among the Hamming weights of the codewords of$C$.

Note that the ratio between the minimum and the maximum weights refers to the possible range of information throughput or performance of each device that the system can accommodate. Although the inequality (1) provides an efficient guideline for designing a minimal code, it also restricts the range of selection of Hamming weights, which is closely related to the flexibility of information distribution in learning data. Recently, some constructions which are not restricted in (1) have been presented [20,22], as shown in Table 1. These constructions can provide flexibility in the selection of amounts of information according to distinct users.

3. Design of Secret Codes for Distributed Systems

The authors of [12] summarized the federated learning structure for health care systems sharing data. In this section, we consider a framework for a group of users or institutions with secret information. If a group of users or participants in the distributed learning system can regenerate some part of the secret information, any other group including this group should also be able to regenerate the same information. On the other hand, the entire secret should not be generated from one user or a small group of users. Furthermore, to support adaptive amounts of information on each user and flexibility in the number of users, the construction of secret codes supporting various numbers of users and adaptive rates of information is required. Our framework, with secret codes for application in distributed systems, is summarized in Figure 3.

The support of a codeword can be regarded as the position of the secret information on the corresponding user. Let $C=\left\{x_1,x_2,\dots ,x_l\right\}$ be a minimal code of length $N$ and size $l$. For each codeword $x_i$, $1\le i\le l$, we can describe its support as

$$s_i=\mathrm{supp}\left(x_i\right)=\left\{s_{i,j} | s_{i,j}<s_{i,j^{\prime }} \mathrm{if} j<j^{\prime }\right\}.$$

(3)

Furthermore, we define the set of user indices as $L=\left\{1,2,\dots ,l\right\}$.

Construction A.

For a minimal code$C$of length$N$, let $y_{l+1}$be a new vector whose support is given by a union of supports of two codewords as

$$supp\left(y_{l+1}\right)=s_{i_1}\cup s_{i_2}$$

(4)

where$1\le i_1<i_2\le l$and$s_i$is not a subset of$s_{i_1}\cup s_{i_2}$for any$i\in L\backslash \left\{i_1, i_2\right\}.$The new code$C_A$is constructed as the union of$C\backslash \left\{x_{i_1},x_{i_2}\right\}$ and $\left\{y_{l+1}\right\}$. In a recursive way, the supports can be merged into an arbitrary combination of the supports.

Note that the code $C_{\mathrm{A}}$ in Construction A is not linear since the support set is not the direct sum of two supports, but the union of the two sets. However, the distributed property of the secret is preserved by the characteristics of the minimal code. Construction A corresponds to the situation where a user is out of the federated group, and the amount of corresponding information and learning resources can be assigned to another user. The information of a user is not subordinate to that of the other users even after merging the resources. Although Construction A only describes a case where the information on the user who has left is assigned to only one user, we can generalize to a case where it is distributed to multiple users.

Construction B.

For a minimal code$C$of length$N$, let $y_{l+1}, y_{l+2}$be a new vector whose union of two supports make

$$s_i=supp\left(y_{l+1}\right)\cup supp\left(y_{l+2}\right)$$

(5)

where$1\le i\le l$and$supp\left(y_{l+1}\right)$and$supp\left(y_{l+2}\right)$are not a subset of$s_i$for any$i\in L\backslash \left\{i\right\}.$The new code$C_B$is constructed as the union of$C\backslash \left\{x_i\right\}$and$\left\{y_{l+1}, y_{l+2}\right\}$. Applying this construction in a recursive way, the supports can be separated into arbitrary sizes.

Because of the non-inclusive property of the supports in Construction B, the situation can be interpreted as one where a user is out of the federated group, and the amount of corresponding information and learning resources can be assigned to another user. The information of a user is not included to that of the other users even after separating the resources. Construction B describes a case in which the support is separated from only one user, but it can be easily generalized to a case in which the information is extracted from different users.

When we consider merging two disjoint distributed systems with secret codes, it is impossible to preserve the non-inclusive property of supports if the two codes are unified without any additional modification of the structure. The interleaving of blocks is a well-known technique in the design of pseudorandom sequences [25]. We apply the technique to the structure of minimal codes as in the following construction.

Construction C.

For minimal codes$C_1$and$C_2$of odd length$N$and size$l$, where$C_1=\left\{x_{1,1},\dots ,x_{1,l}\right\}$and$C_2=\left\{x_{2,1},\dots ,x_{2,l}\right\}$. Define codewords of length$y_i=\left\{y_i\left[n\right] | y_i\left[n\right]\in \left\{0,1\right\}, 0\le k\le 2N-1\right\}, 1\le i\le l,$as

$$y_i\left[n\right]=\left\{\begin{array}{c}{x}_{1,i}\left[\lfloor \frac{n}{2}\rfloor \right], if n is even;\\ x_{2,i}\left[\lfloor \frac{n}{2}\rfloor \right], if n is odd,\end{array}\right.$$

(6)

where$\lfloor x\rfloor$is the greatest integer less than$x$. Define a new code$C_C$as the set of all combination of$C_1$and$C_2$.

In Construction C, if the index of $y_i\left[n\right]$ is even, the code structure follows $C_1$. Otherwise, it follows $C_2$. Since the non-inclusive properties and linearity are preserved by the structure of the original codes, the new code could be used in merging two disjoint systems. Moreover, the extension can be generalized to the case of merging three or more distinct systems. Therefore, when two or more distributed systems are merged, we do not need to design a new code for the new system. When we have two distinct secret codes of relatively prime lengths, it is possible to enlarge the number of codewords and the length as in the following construction.

Construction D.

For two minimal codes,$C_1=\left\{x_{1,1},\dots ,x_{1,l_1}\right\}$of length$N_1$and size$l_1$, and$C_2=\left\{x_{2,1},\dots ,x_{2,l_2}\right\}$of lengths$N_2$and size$l_2$, assume that$N_1$and$N_2$are relatively prime. Define codewords of length$y_{i,j}=\left\{y_{i,j}\left[n\right] | y_{i,j}\left[n\right]\in \left\{0,1\right\}, 0\le n\le N_1{N}_2-1\right\}, 1\le i\le l_1, 1\le j\le l_2,$as

$$y_{i,j}\left[n\right]=\left\{\begin{array}{cc}1,& if \left(n mod N_1\right)\in supp\left(x_{1,i}\right) and \left(n mod N_2\right)\in supp\left(x_{2,j}\right);\\ 0,& otherwise.\end{array}\right.$$

(7)

where$\left(x mod y\right)$means the remainder of$x$divided by$y$. Define a new code$C_D$as collection of all$y_{i,j}$s for$1\le i\le l_1$and$1\le i\le l_2$.

Figure 4 shows application scenarios for Constructions A and B. The two constructions correspond to a case in which a user or a device leaves or joins the federation, respectively. Construction C can be applied to a situation where two distributed systems are merged into one, as shown in Figure 5. The original codes are embedded into the extended code without a change in the structure in Construction C. Therefore, any new algebraic design of the distribution is not required for that case. It is also easy to generalize to a case in which three or more systems are merged. Note that the three constructions can be combined according to the application scenarios, and several known constructions, including those in Table 1, can be applied to the four constructions.

4. Results

In this section, we present some resultant theory and examples obtained from our constructions. Constructions C and D provide extended codes in the sense of the length and the weight. Moreover, their properties can be shown by combining the properties of the original codes and the construction terminologies, as shown in the following propositions.

Proposition 1.

The code$C_C$in Construction C is a minimal code of length$2N$and size$l$. The weight of each codeword$y_i$is the sum of the weights of$x_{1,i}$and$x_{2,i}$.

Proof .

The length and the size of the code $C_C$ are clear from the definition. The next step is to check the linearity of the new code, that is, whether the equality $y_i+y_j\in C_C$ for any $1\le i,j\le l$ is satisfied or not. Note that the addition is the vector addition modulo 2. Since ${\mathrm{C}}_1$ and ${\mathrm{C}}_2$ are linear codes, it is possible to let $x_{1,i}+x_{1,j}=x_{1,k}$ for some $k$ with $1\le k\le l$. Similarly, we have $x_{2,i}+x_{2,j}=x_{2,k}$. These two equations imply

$$y_i\left[n\right]+y_j\left[n\right]=y_k\left[n\right]=\left\{\begin{array}{c}{x}_{1,k}\left[\lfloor \frac{n}{2}\rfloor \right], if n is even;\\ x_{2,k}\left[\lfloor \frac{n}{2}\rfloor \right], if n is odd,\end{array}\right.$$

(8)

by the definition in Construction C. Thus, for all $1\le i,j\le l$, there exists a $k$ with $1\le k\le l$ such that $y_i+y_j=y_k$, which implies that $C_C$ is linear. Non-inclusive properties of supports can be also shown using the definition. The support $\mathrm{supp}\left(y_i\right)$ can be partitioned into ${\mathrm{supp}}_e\left(y_i\right)\cup {\mathrm{supp}}_o\left(y_i\right)$, where ${\mathrm{supp}}_e\left(y_i\right)$ (resp. ${\mathrm{supp}}_e\left(y_{\mathrm{i}}\right)$) is the subset of $\mathrm{supp}\left(y_i\right)$ with even (resp. odd) indices. It is clear that ${\mathrm{supp}}_e\left(y_i\right)$ is equivalent to multiplying $\mathrm{supp}\left(x_{1,i}\right)$ by two, and ${\mathrm{supp}}_o\left(y_i\right)$ is equivalent to adding one after multiplying $\mathrm{supp}\left(x_{2,i}\right)$ by two. Thus, ${\mathrm{supp}}_e\left(y_i\right)$ and ${\mathrm{supp}}_e\left(y_j\right)$ are not included in one another for any $1\le i\ne j\le l$. Similarly,${\mathrm{supp}}_o\left(y_i\right)$ and ${\mathrm{supp}}_o\left(y_k\right)$ satisfy the same property. Therefore, it is shown that the code $C_C$ satisfies the conditions of minimal codes. □

Example 1 shows a resultant code applying Construction C to a code present in [20]. Additional parameters of codes with more flexible choices of weights can be obtained by simply changing the index of one code. More parameters from numerical simulations are presented in Section 5.

Example 1.

In Example 20 from[20], a minimal code of length$63$ and size $128$ is given. The weight distributions for weights ($0,14,30,32,38$) are given by ($1,1,49,63,14$). Using two codes from two different primitive elements of the finite field GF(63), we can construct a new code of length $126$ whose weight distribution is given by ($0,14,30,32,38$) for weights ($0,28,60,64,76$) when assuming the order of indices of the codewords are according to the order of weights. If we change the order of combinations, several different codes with different weight distributions are generated.

Table 2. Comparison of Construction Methods.

Constructions	Characteristic	Linearity
A	Separated supports	may be broken
B	Merged supports	may be broken
C	Merging two codes	preserved
D	Enhanced parameters	preserved

compares one example of the code of length $126$ with the original code of length $63$.

The properties of codes from Construction D can be formulated in the following proposition.

Proposition 2.

The code$C_D$in Construction D is a minimal code of length$N_1{N}_2$and size$l_1{l}_2$. The weight of each codeword is the product of the weights of two component codewords.

Proof .

By the definition, the length of each codeword is clearly $N_1{N}_2$, and the size of the code is $l_1{l}_2$. For each support of $x_{1,i}$, all the indices of support of $x_{2,j}$ can be combined. Thus, the weight of $y_{i,j}$ is equal to the product of the weights of $x_{1,i}$and $x_{2,j}$. Assume that $x_{1,i_1}+x_{1,i_2}=x_{1,i_3}$ for $1\le i_1, i_2, i_3\le l_1$ and $x_{2,j_1}+x_{2,j_2}=x_{2,j_3}$ for $1\le j_1, j_2, j_3\le l_2$. Then, it is clear that $y_{i_3,j_3}=y_{i_1,j_1}+y_{i_2,j_2}$ for any combination of $1\le i_1, i_2, i_3\le l_1$ and $1\le j_1, j_2, j_3\le l_2$, which implies that $C_D$ is linear. Note that for any $1\le i_1, i_2\le l_1$ and $1\le j_1, j_2\le l_2$, the supports of $y_{i_1,j_1}$ and $y_{i_2,j_2}$ are not included in one another if $i_1\ne i_2$ or $j_1\ne j_2$ due to the properties of $C_1$ and $C_2$. □

Example 2.

Assume that there are two codes:$C_1$of length$31$and$C_2$of length$63$. Furthermore, suppose the weight distribution of$C_1$be given by ($d_1^{},d_2^{},\dots ,d_k^{}$) for weights ($w_1^{},w_2^{},\dots ,w_k^{}$), and the weight distribution of $C_2$ by ($d_1^{\prime },d_2^{\prime },\dots ,d_l^{\prime }$) for weights ($w_1^{\prime },\dots ,w_l^{\prime }$). Then, by Construction D, we can obtain a code of length $1953=31\times 63$. The weight of a codeword is the product of two weights from $C_1$ and $C_2$.

It may be possible to use Construction D in the case that computing resources are enhanced and the number of devices is significantly increased. However, Construction D extends the size and weight from the component codes, cases where $N_1$ and $N_2$ are relatively prime are very rare for previously known constructions. Thus, finding primary constructions for minimal codes for more general parameters should be a future research topic. Furthermore, as shown in Example 2, the parameters of the codes are increased significantly. Therefore, it would be possible to apply Construction D to a case in which the resources are also increased considerably. Table 2 summarizes the characteristics of the resultant codes from Constructions A~D.

5. Discussions

In this section, we discuss the flexibility of resultant codes from Construction C compared with the previously known constructions.

Table 3. An example of the weight distribution of the resultant code from Construction C (code length: 127).

	Original Code in [20]	Construction C
Possible weights	1,14,30,32,38	2,28,60,62,64,68,70,76
Weight Distribution	(1,1,49,63,14)	(1,1,25,38,41,10,6), (1,1,30,32,44,6,6,8), (1,1,35,20,50,8,6,7), ….
Number of distinct information lengths	5	8

, which was obtained by numerical simulation, shows an example of code parameters with more possible numbers of information lengths compared to the previous construction. In this example, we can observe that there are more choices of possible weights in Construction C. This means that the distribution of information becomes more flexible. Note that several additional combinations for weight distribution are possible by exchanging the order of codewords in Construction C.

Table 4. Examples of the ratio between the minimum and the maximum weights from Construction C.

Length	$\frac{{\mathit{w}}_{\mathit{m}\mathit{i}\mathit{n}}}{{\mathit{w}}_{\mathit{m}\mathit{a}\mathit{x}}} \mathbf{in}$ [20]	$\frac{{\mathit{w}}_{\mathit{m}\mathit{i}\mathit{n}}}{{\mathit{w}}_{\mathit{m}\mathit{a}\mathit{x}}} \mathbf{in}\mathbf{Construction}\mathbf{C}$
128	48.15%	24.08%, 27,78%, 29.89%,…, 48.15%
512	48.28%	24.24%, 25.86%, 31.91%,…, 48.28%

, which was obtained by another numerical simulation, compares the ratio between the minimum and the maximum Hamming weights presented in (1) of Theorem 1. The original codes of lengths 128 and 512 from [20] are not restricted in (1), since the ratio $\frac{w_{min}}{w_{max}}$ is less than 1/2. It is possible to obtain a ratio farther from 1/2 using Construction C, as shown in Table 4. Thus, Construction C can provide an extended range of the information ratio among different users.

From the comparisons in Table 2 and Table 3, we can deduce that Construction C provides more flexibility in the distribution of secret information compared to the previous construction. Therefore, the new codes can be not only applied to more general cases but also adapted to the flexible learning conditions.

6. Conclusions

In this paper, we have proposed a design scheme and framework for secret codes which can be applied in flexible situations in distributed learning systems for medical data. The new code from the constructions could be applied to the cases that are not covered by previously known codes. It is shown that secret information can be distributed or merged according to the design of appropriate secret codes based on block codes. According to the parameters of learning resources, we may be able to apply more algebraic constructions or synthesis algorithms for block codes. Learning systems can be implemented under general conditions such as tensorflow; multiple workstations with 8 GB or more RAM, RTX1060, or more; and Mbps networks. The secret codes could be used in the distribution of private or secret information, as well as merging and separating distributed systems. Our future work will focus on the development of more advanced and detailed coding techniques for distributed learning systems, including various kinds of servers and devices. Furthermore, the realization of distributed learning systems with actual parameters from the environments of hospitals will be an interesting topic.