Analysis of Viscoelastic Damping Effect on the Underwater Acoustic Radiation of a Ring-Stiffened Conical Shell
Abstract
:1. Introduction
2. Method of Fluid–Structure Coupling Vibration and Acoustic Radiation
2.1. FEM
2.2. BEM
3. Coupled Modal Analysis of Ring-Stiffened Conical Shell with Bases
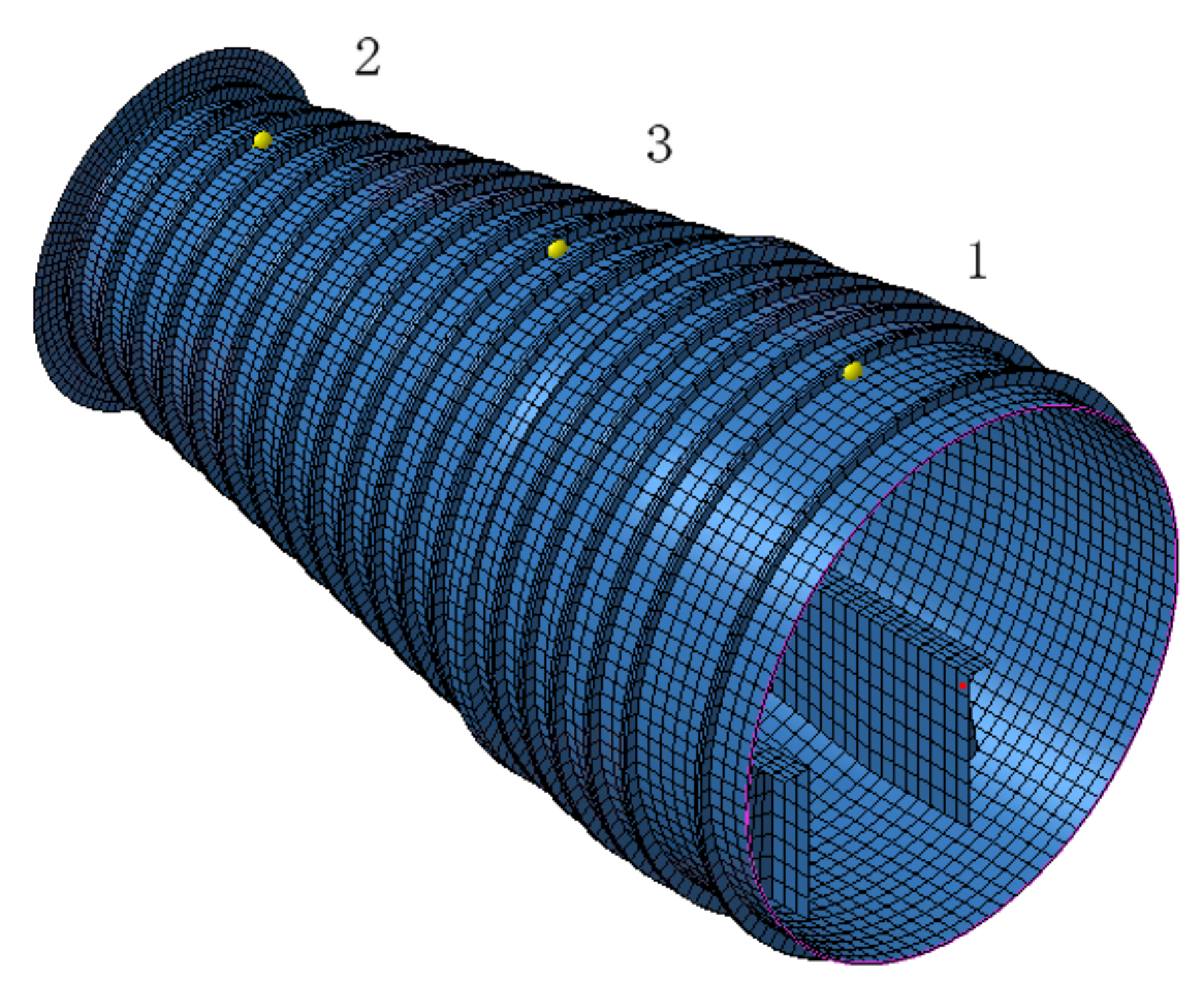
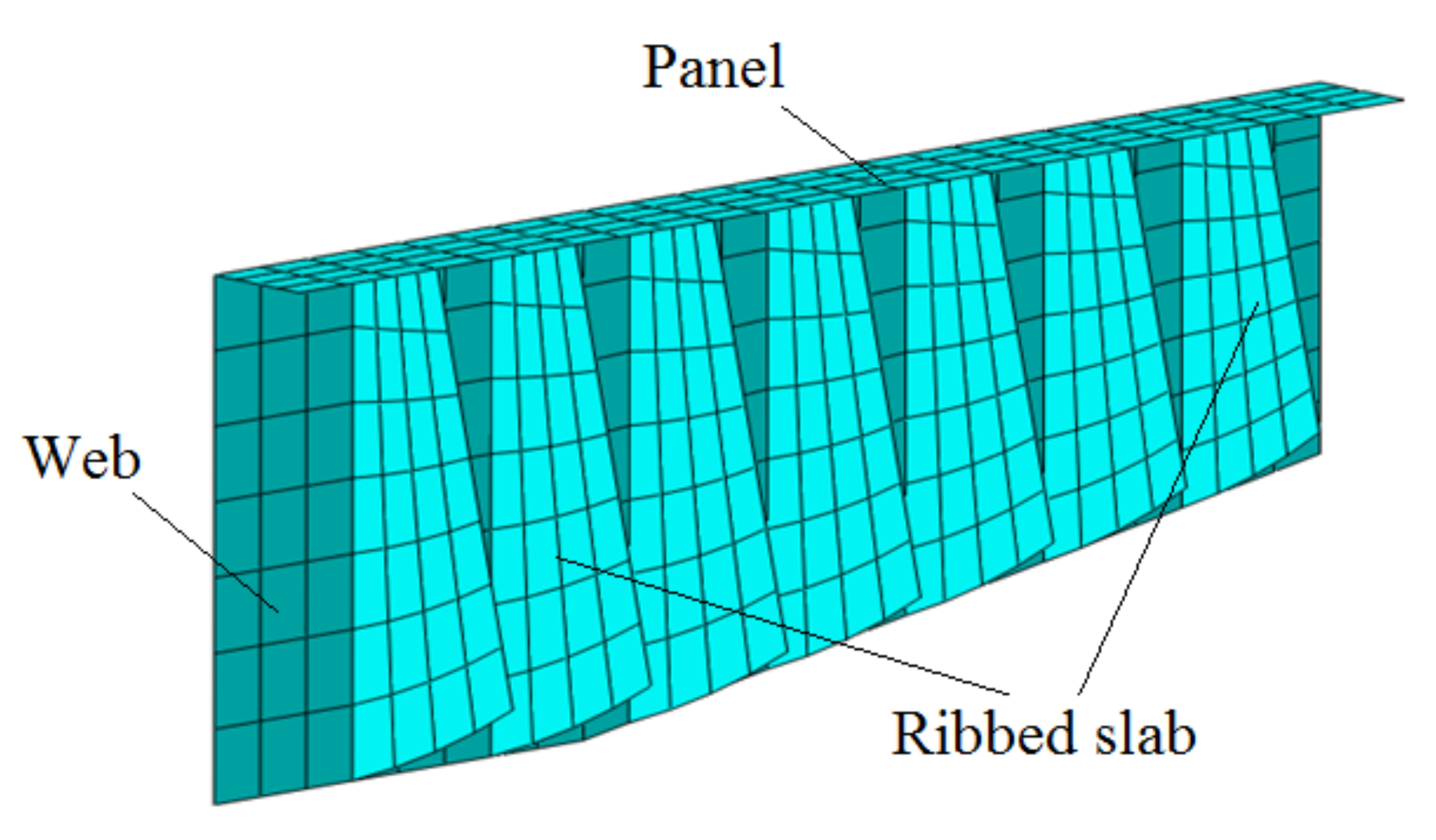
3.1. Establishment of Structural Model
3.2. Coupled Modal Analysis
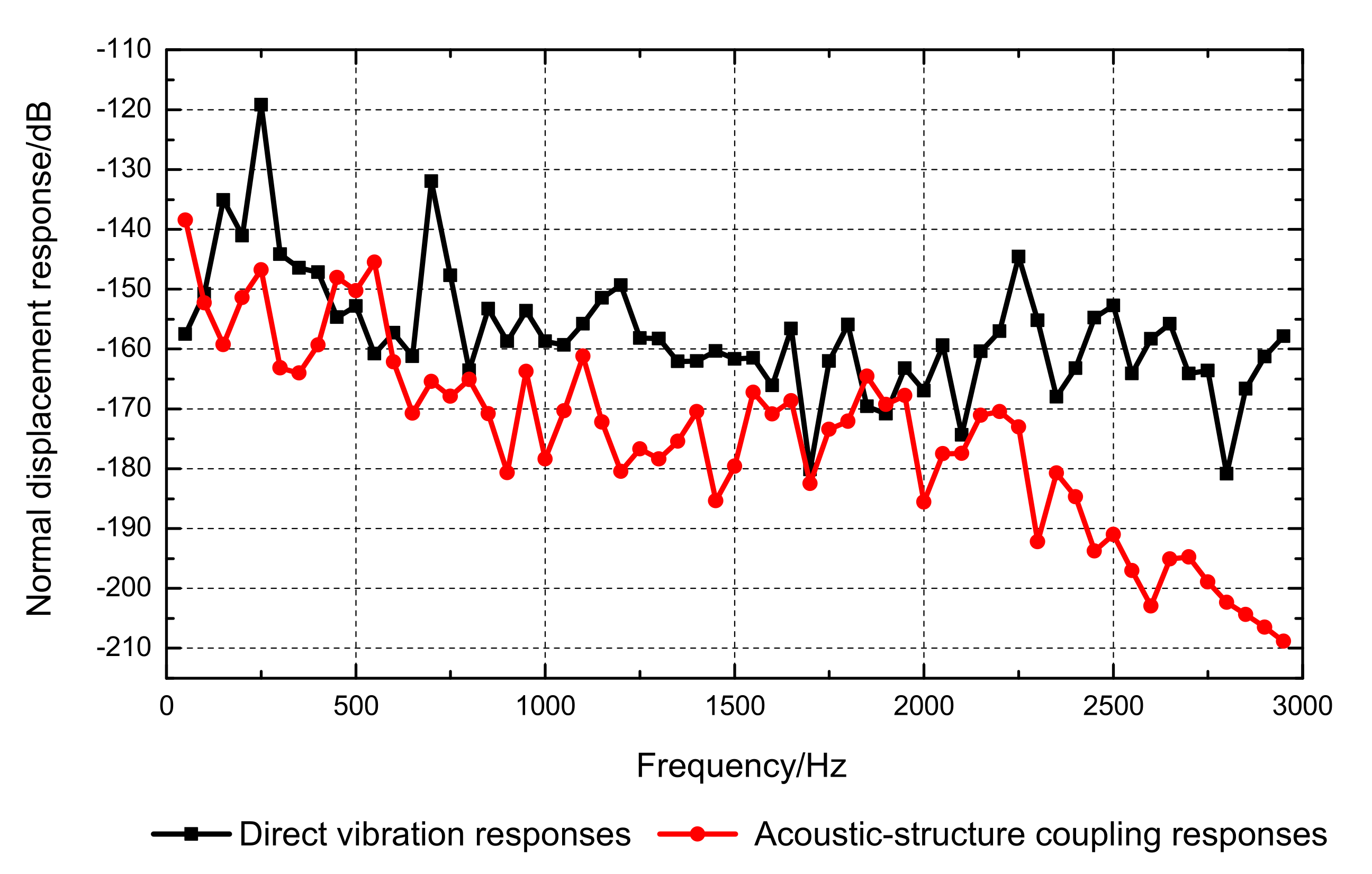
3.2.1. Acoustic–Structure Coupled Modal Analysis
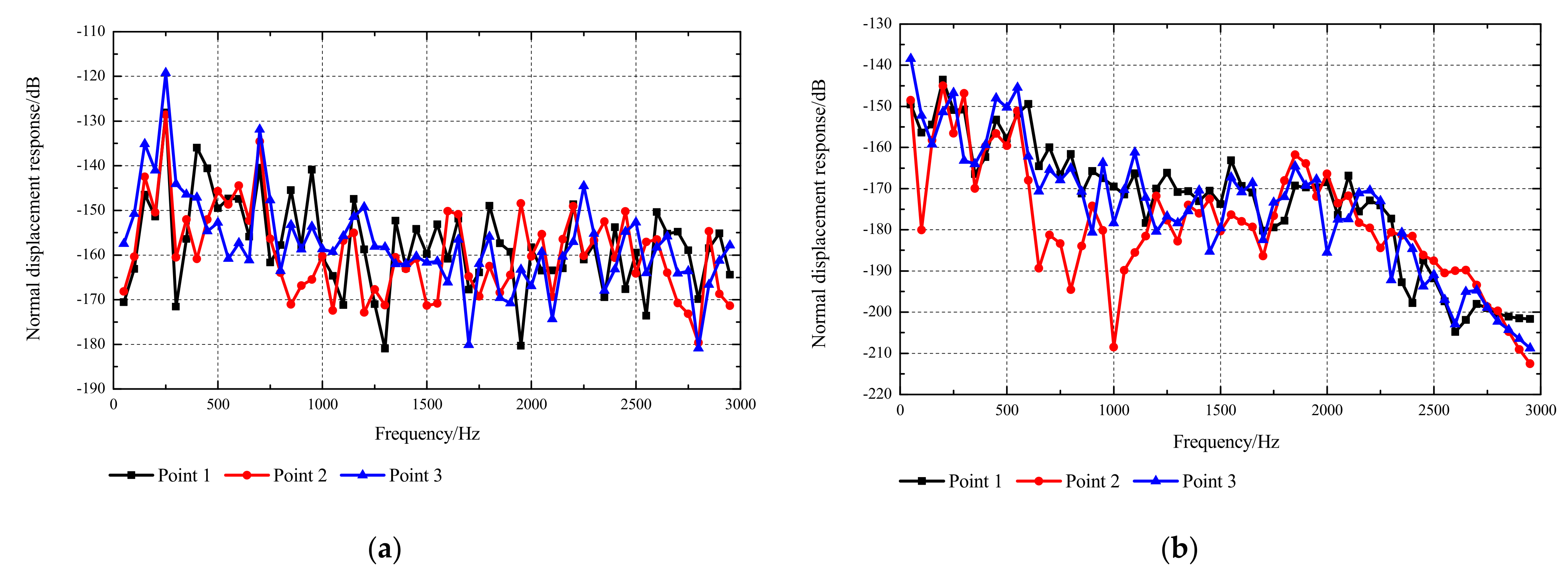
3.2.2. Frequency Response of the Ring-Stiffened Conical Shell
- The modal analysis of the structure is carried out firstly;
- The corresponding node information of the outer surface is obtained and imported into acoustic mesh;
- The structural mesh and acoustic mesh are coupled by means of BEM for the acoustic–structure coupling analysis;
- The acoustic characteristic quantity of the structure is obtained.
4. Effect of Viscoelastic Damping on Underwater Acoustic Radiation
4.1. Numerical Method Validation
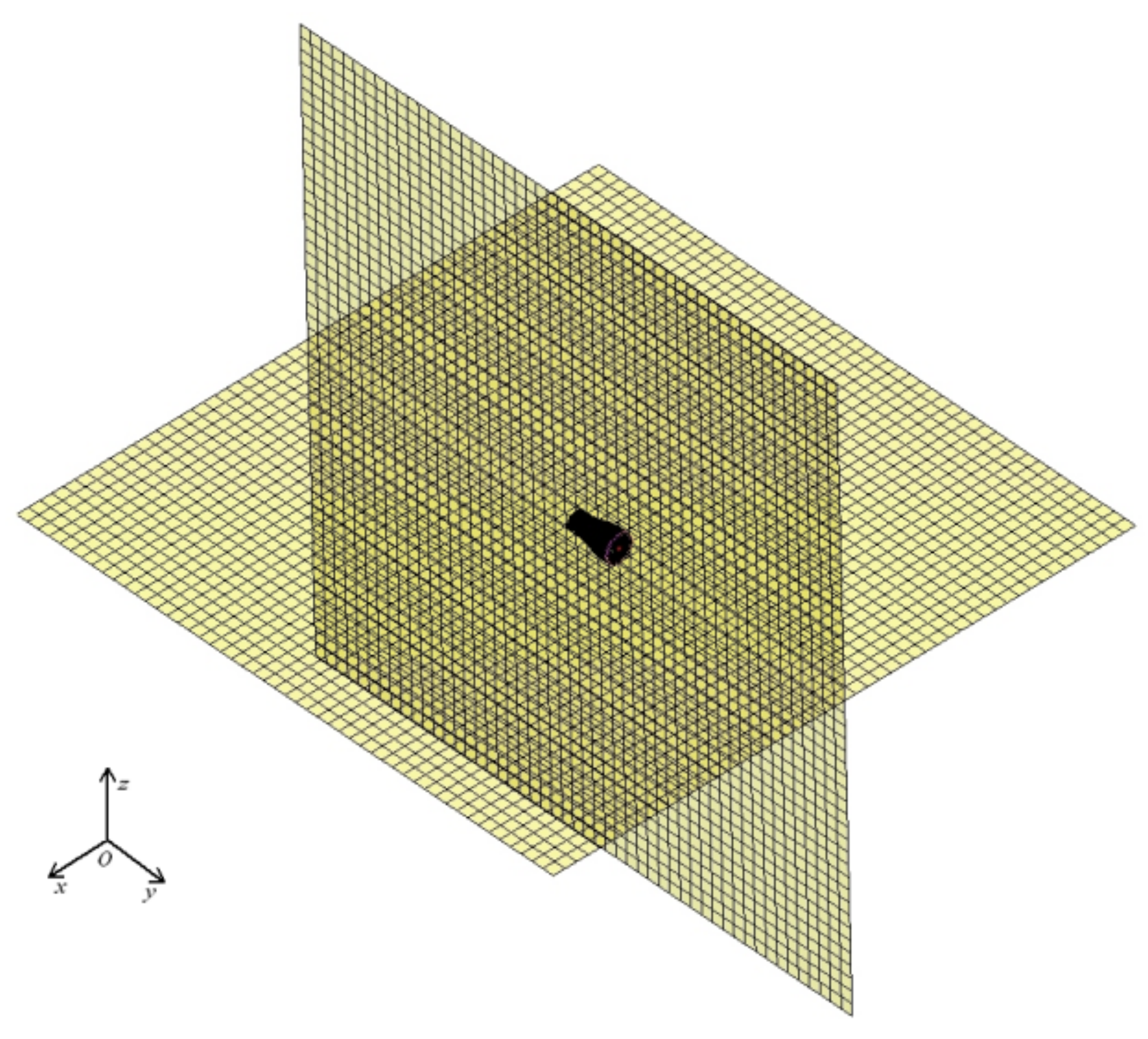
4.2. The Acoustic Field Model and Viscoelastic Damping Material
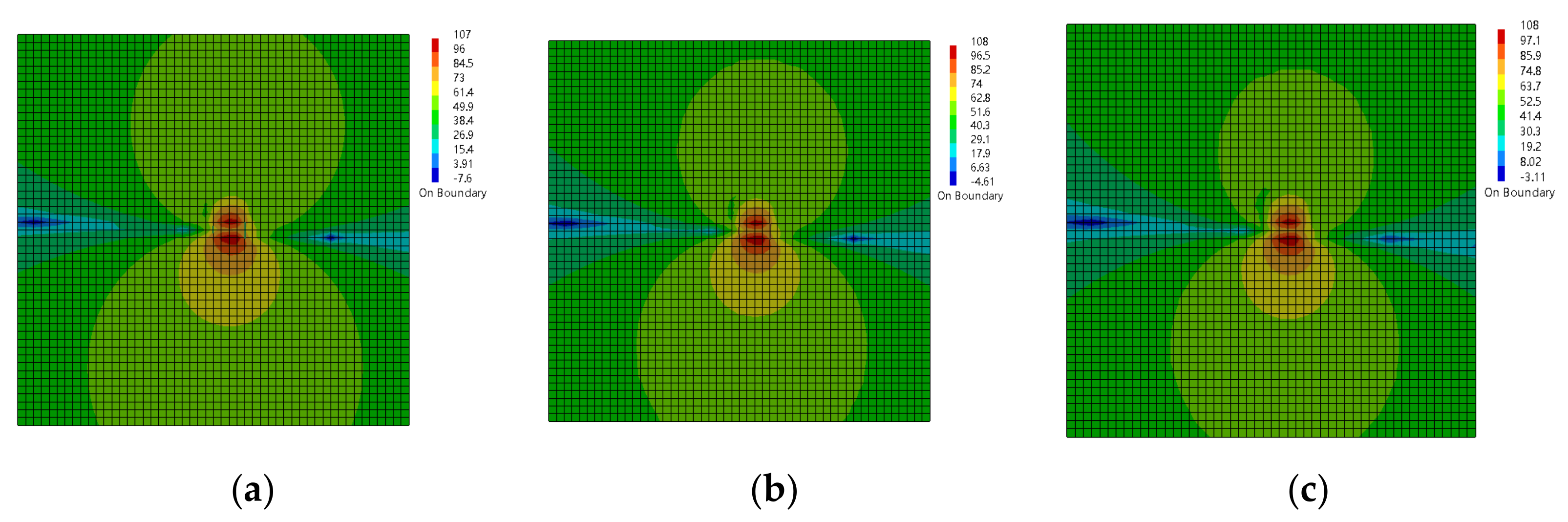
4.3. Damping Thickness
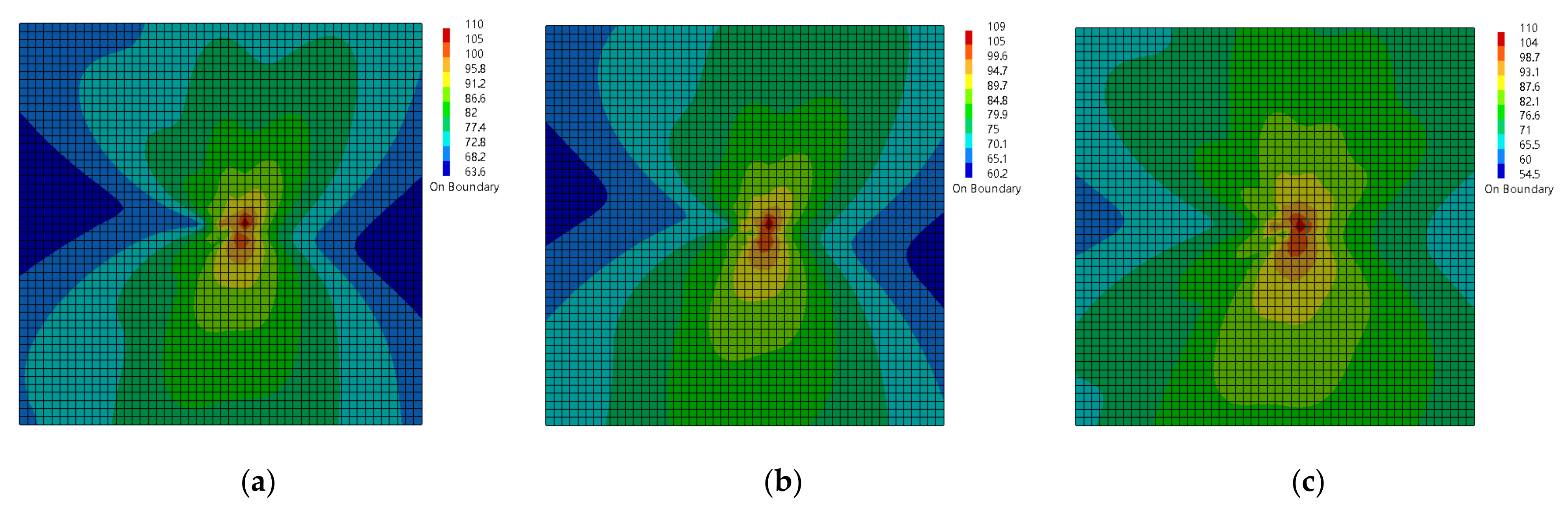
4.4. Location of Damping
5. Conclusions
- (1)
- The water medium can reduce the natural frequency and change the modal shapes. Meanwhile, the effect of suppressing vibration responses at a high frequency is better than that at a low frequency;
- (2)
- The damping effect at a high frequency is better than that at a low frequency. The increase in damping thickness would effectively reduce the amplitude of radiated noise, but does not change the distribution of the acoustic field;
- (3)
- There is a strong correlation between the damping position and the vibration mode of the structure. The damping on the web may achieve the best vibration damping effect, while the damping on the ribbed slab may result in the minimum radiation range.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Laplace operator, | |
| - | Flow field computational domain |
| p(x, y, z) | Sound pressure |
| k | Number of waves per second (m−1), k = ω/c = 2πf/c |
| ω | Angular frequency (rad/s), ω = 2πf |
| f | Frequency (Hz) |
| c | Sound velocity (m/s) |
| Density of medium | |
| q(x, y, z) | Normal velocity |
| j | Imaginary unit, |
| S | Boundary of |
| V | Volume |
| Weight function | |
| [K] | Stiffness matrix |
| [M] | Mass matrix |
| [C] | Damping matrix |
| Sound pressure matrix | |
| {Qi} | Acoustic excitation |
| fn | Natural frequency |
| η | Loss factor |
References
- Liang, S.; Chen, H. The natural vibration of a conical shell with an annular end plate. J. Sound Vib. 2006, 294, 927–943. [Google Scholar] [CrossRef]
- Guo, W.; Li, T.; Zhu, X.; Miao, Y.; Zhang, G. Vibration and acoustic radiation of a finite cylindrical shell submerged at finite depth from the free surface. J. Sound Vib. 2017, 393, 338–352. [Google Scholar] [CrossRef]
- Chen, M.X.; Deng, N.Q.; Zhang, C.; Wei, J.H. Vibration of submerged and ring stiffened conical shells. J. Vib. Shock 2014, 33, 25–32. [Google Scholar]
- Manela, A.; Miloh, T. Forced motion and acoustic radiation of an elastic cylinder in axial flow. J. Sound Vib. 2012, 331, 3544–3557. [Google Scholar] [CrossRef]
- Mitri, F.; Fellah, Z. Acoustic radiation force on coated cylinders in plane progressive waves. J. Sound Vib. 2007, 308, 190–200. [Google Scholar] [CrossRef]
- Dou, S.R. Research on Viscoelastic Damping Control Technique for Vibration and Acoustic Radiation of Shell Structure; Harbin Institute of Technology: Harbin, China, 2015. [Google Scholar]
- Li, F.-M.; Kishimoto, K.; Huang, W.-H. The calculations of natural frequencies and forced vibration responses of conical shell using the Rayleigh–Ritz method. Mech. Res. Commun. 2009, 36, 595–602. [Google Scholar] [CrossRef]
- Wu, C.-P.; Lee, C.-Y. Differential quadrature solution for the free vibration analysis of laminated conical shells with variable stiffness. Int. J. Mech. Sci. 2001, 43, 1853–1869. [Google Scholar] [CrossRef]
- Sweedan, A.; El Damatty, A. Experimental and analytical evaluation of the dynamic characteristics of conical shells. Thin-Walled Struct. 2002, 40, 465–486. [Google Scholar] [CrossRef]
- Sofiyev, A.; Kuruoglu, N.; Halilov, H. The vibration and stability of non-homogeneous orthotropic conical shells with clamped edges subjected to uniform external pressures. Appl. Math. Model. 2010, 34, 1807–1822. [Google Scholar] [CrossRef]
- Desmet, W. A Wave Based Prediction Technique for Coupled Vibro-Acoustic Analysis; Katholieke University Leuven: Leuven, Belguim, 1998. [Google Scholar]
- Pluymers, B.; Desmet, W.; Vandepitte, D.; Sas, P. Application of an efficient wave-based prediction technique for the analysis of vibro-acoustic radiation problems. J. Comput. Appl. Math. 2004, 168, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Bilasse, M.; Azrar, L.; Daya, E. Complex modes based numerical analysis of viscoelastic sandwich plates vibrations. Comput. Struct. 2011, 89, 539–555. [Google Scholar] [CrossRef]
- Daya, E.; Azrar, L.; Potier-Ferry, M. An amplitude equation for the non-linear vibration of viscoelastically damped sandwich beams. J. Sound Vib. 2004, 271, 789–813. [Google Scholar] [CrossRef]
- Galucio, A.; Deu, J.-F.; Ohayon, R. Hybrid Active-passive Damping Treatment of Sandwich Beams in Non-linear Dynamics. J. Vib. Control 2007, 13, 851–881. [Google Scholar] [CrossRef]
- Boutyour, E.H.; Daya, E.M.; Azrar, L.; Potier-Ferry, M. An Approximated Harmonic Balance Method for Nonlinear Vibration of Viscoelastic Structures. J. Eng. Mater. Technol. 2006, 128, 330–334. [Google Scholar] [CrossRef]
- Bilasse, M.; Daya, E.; Azrar, L. Linear and nonlinear vibrations analysis of viscoelastic sandwich beams. J. Sound Vib. 2010, 329, 4950–4969. [Google Scholar] [CrossRef]
- Araújo, A.L.; Martins, P.; Soares, C.M.M.; Herskovits, J. Damping optimization of viscoelastic laminated sandwich composite structures. Struct. Multidiscip. Optim. 2009, 39, 569–579. [Google Scholar] [CrossRef]
- Araújo, A.; Soares, C.M.; Herskovits, J. Optimal design and parameter estimation of frequency dependent viscoelastic laminated sandwich composite plates. Compos. Struct. 2010, 92, 2321–2327. [Google Scholar] [CrossRef]
- Ross, C.T.F.; Richards, W.D. The Vibration of Ring-Stiffened Cones Under External Water Pressure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1994, 208, 177–185. [Google Scholar] [CrossRef]
- Zhou, Q.; Joseph, P. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure. J. Sound Vib. 2005, 283, 853–873. [Google Scholar] [CrossRef]
- Ihlenburg, F. Finite Element Analysis of Acoustic Scattering; Springer Science & Business Media: Hamburg, Germany, 2006. [Google Scholar]
- Vendhan, C.P.; Diwan, G.; Bhattacharya, S. Finite-element modeling of depth and range dependent acoustic propagation in oceanic waveguides. J. Acoust. Soc. Am. 2010, 127, 3319–3326. [Google Scholar] [CrossRef] [PubMed]
- Isakson, M.J.; Goldsberry, B.; Chotiros, N.P. A three-dimensional, longitudinally-invariant finite element model for acoustic propagation in shallow water waveguides. J. Acoust. Soc. Am. 2014, 136, 206–211. [Google Scholar] [CrossRef]
- Seybert, A.F.; Cheng, C.Y.R.; Wu, T.W. The solution of coupled interior/exterior acoustic problems using the boundary element method. J. Acoust. Soc. Am. 1990, 88, 1612–1618. [Google Scholar] [CrossRef]
- Li, S.; Huang, Q. A fast multipole boundary element method based on the improved Burton–Miller formulation for three-dimensional acoustic problems. Eng. Anal. Bound. Elem. 2011, 35, 719–728. [Google Scholar] [CrossRef]
- Zou, M.-S.; Wu, Y.-S.; Liu, S.-X. A three-dimensional sono-elastic method of ships in finite depth water with experimental validation. Ocean Eng. 2018, 164, 238–247. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, C.; Chen, H. FEM/wideband FMBEM coupling for structural-acoustic design sensitivity analysis. Comput. Methods Appl. Mech. Eng. 2014, 276, 1–19. [Google Scholar] [CrossRef]
- Chen, L.; Chen, H.; Zheng, C.; Marburg, S. Structural-acoustic sensitivity analysis of radiated sound power using a finite element/ discontinuous fast multipole boundary element scheme. Int. J. Numer. Methods Fluids 2016, 82, 858–878. [Google Scholar] [CrossRef]
- Zheng, C.J.; Bi, C.X.; Zhang, C.; Gao, H.F.; Chen, H.B. Free vibration analysis of elastic structures submerged in an infinite or semi-infinite fluid domain by means of a coupled FE-BE solver. J. Comput. Phys. 2018, 359, 183–198. [Google Scholar] [CrossRef]
- Zampolli, M.; Tesei, A.; Canepa, G.; Godin, O. Computing the far field scattered or radiated by objects inside layered fluid media using approximate Green’s functions. J. Acoust. Soc. Am. 2008, 123, 4051–4058. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.-W.; Zou, M.-S.; Liu, S.-X.; Huang, H. Calculation method of acoustic radiation for floating bodies in shallow sea considering complex ocean acoustic environments. J. Sound Vib. 2020, 476, 115330. [Google Scholar] [CrossRef]
- Han, G.; Zhang, C.; Shu, L.; Rodrigues, J. Impacts of Deployment Strategies on Localization Performance in Underwater Acoustic Sensor Networks. IEEE Trans. Ind. Electron. 2014, 62, 1725–1733. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, J.; Wan, L.; Fang, X.; Tong, F.; Xu, X. Routing failure prediction and repairing for AUV-assisted underwater acoustic sensor networks in uncertain ocean environments. Appl. Acoust. 2022, 186, 108479. [Google Scholar] [CrossRef]
- Alfouzan, F. Energy-Efficient Collision Avoidance MAC Protocols for Underwater Sensor Networks: Survey and Challenges. J. Mar. Sci. Eng. 2021, 9, 741. [Google Scholar] [CrossRef]
- Li, J.T. Theoretical and Experimental Research on Vibration Properties of Composite Foundations; Shanghai Jiao Tong University: Shanghai, China, 2010. [Google Scholar]
- Bilasse, M.; Charpentier, I.; Daya, E.M.; Koutsawa, Y. A generic approach for the solution of nonlinear residual equations. Part II: Homotopy and complex nonlinear eigenvalue method. Comput. Methods Appl. Mech. Eng. 2009, 198, 3999–4004. [Google Scholar] [CrossRef]
- Baydoun, S.K.; Marburg, S. Investigation of radiation damping in sandwich structures using finite and boundary element methods and a nonlinear eigensolver. J. Acoust. Soc. Am. 2020, 147, 2020–2034. [Google Scholar] [CrossRef] [Green Version]
- Fu, Z.; Xi, Q.; Li, Y.; Huang, H.; Rabczuk, T. Hybrid FEM–SBM solver for structural vibration induced underwater acoustic radiation in shallow marine environment. Comput. Methods Appl. Mech. Eng. 2020, 369, 113236. [Google Scholar] [CrossRef]



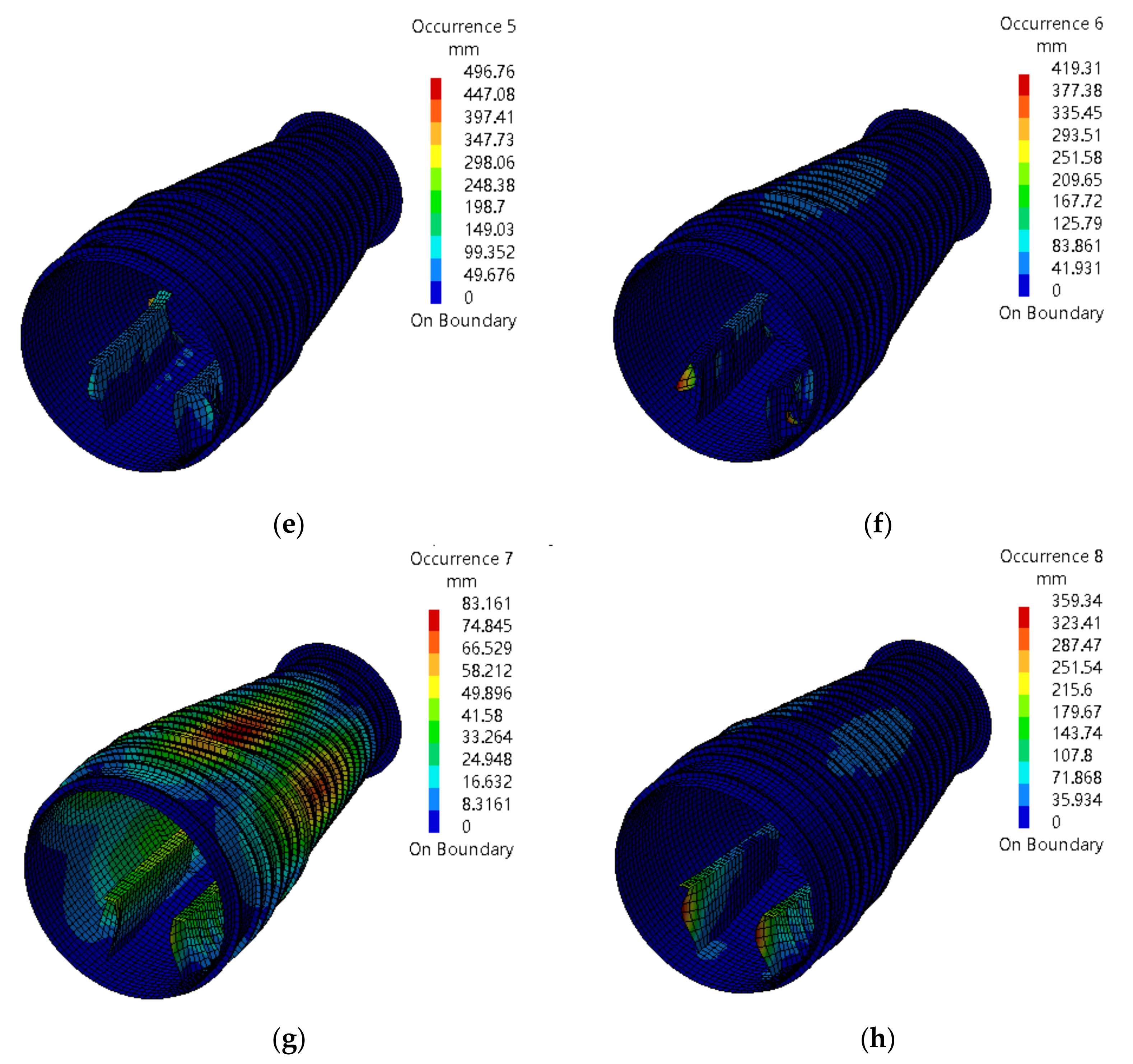


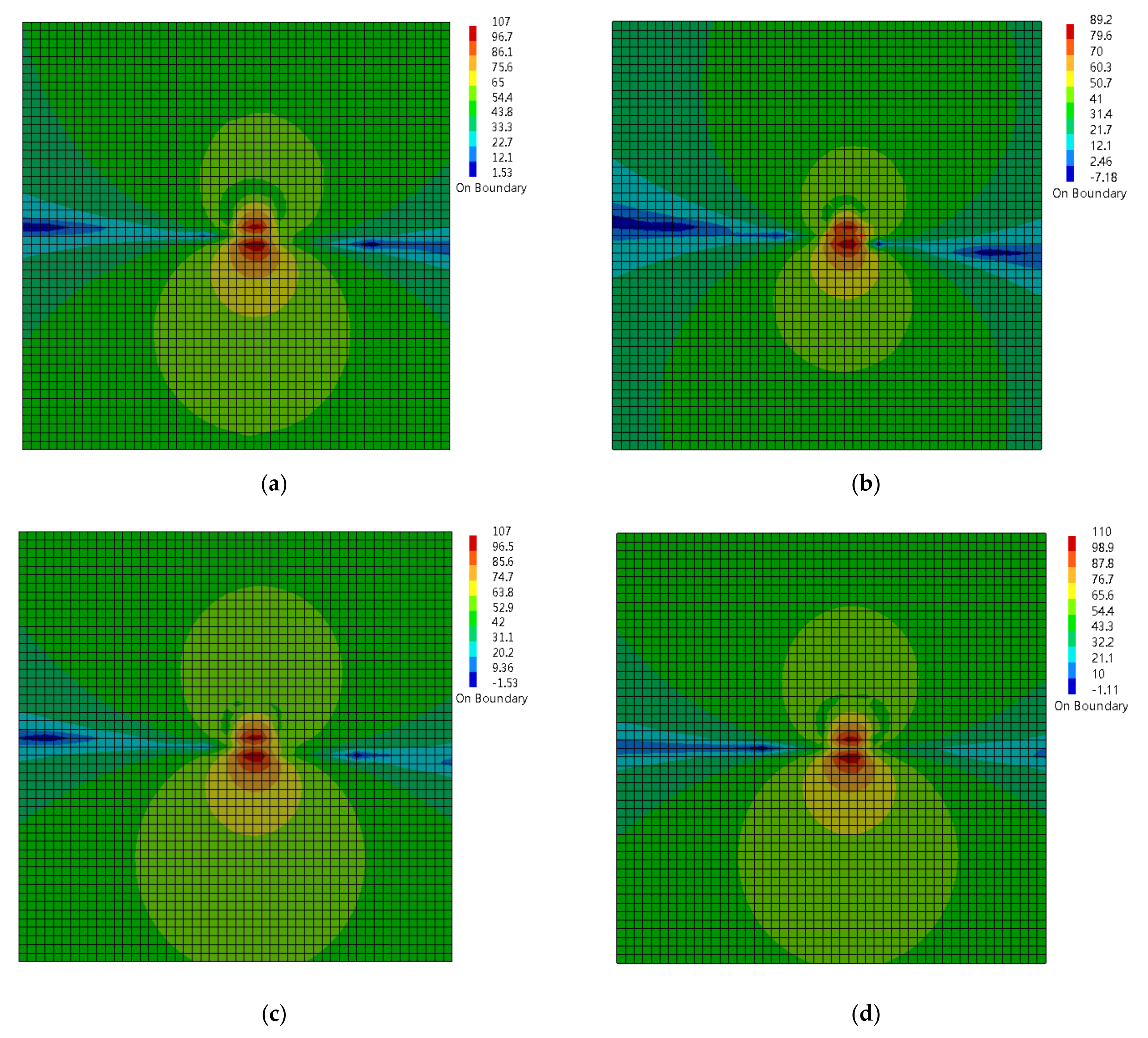

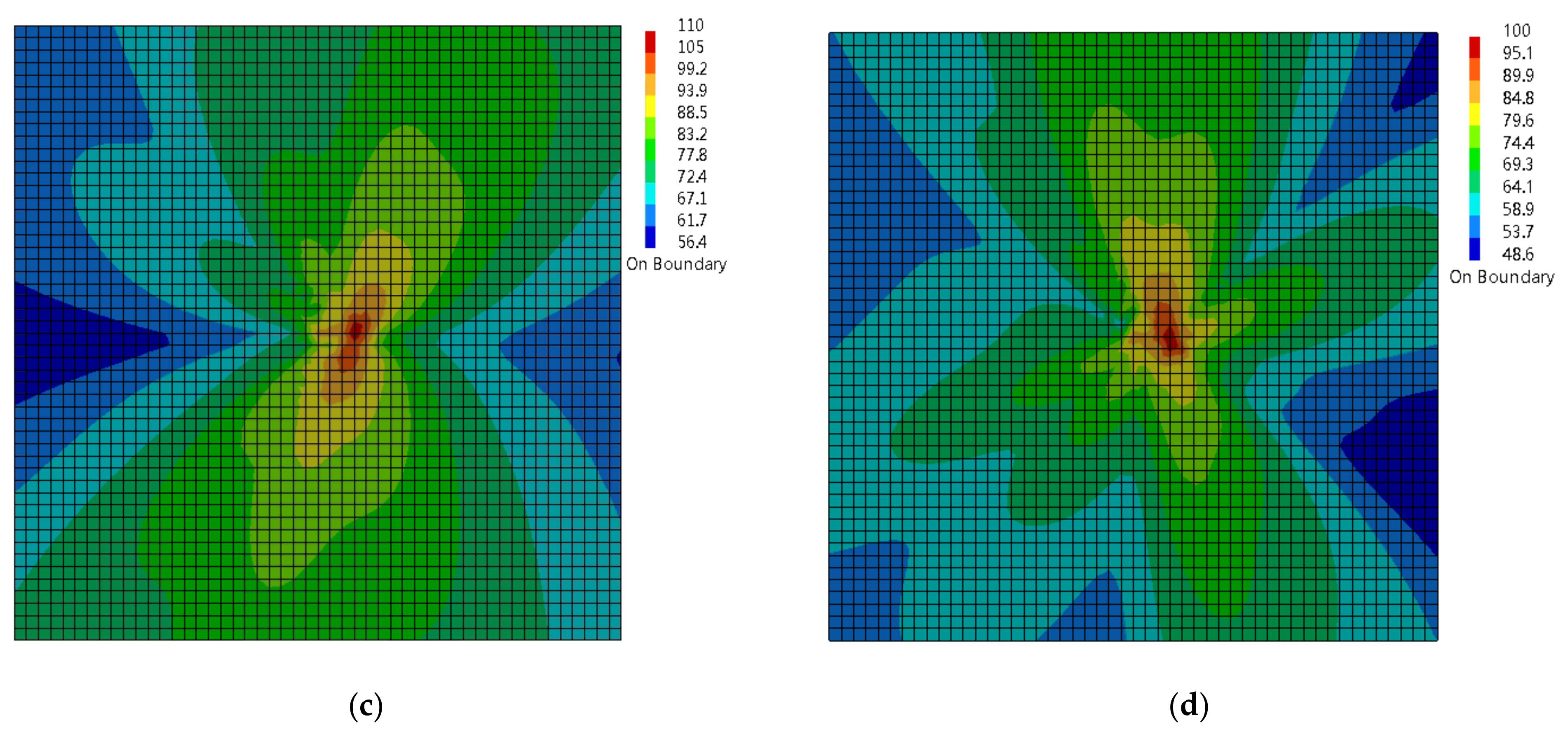
| Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Vacuum | 143.1 | 144.1 | 163.7 | 170.6 | 184.1 | 199.2 | 206.0 | 207.9 | 225.5 | 226.0 |
| Water | 55.4 | 55.6 | 76.0 | 81.1 | 86.1 | 86.6 | 90.0 | 92.5 | 115.6 | 121.4 |
| Order | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Vacuum | 248.0 | 249.0 | 249.2 | 259.0 | 261.8 | 262.3 | 266.3 | 266.4 | 267.3 | 268.0 |
| Water | 128.1 | 130.7 | 135.5 | 136.8 | 138.8 | 141.3 | 144.4 | 144.6 | 150.9 | 151.4 |
| Elastic Faces | Viscoelastic Core | Beam | ||
|---|---|---|---|---|
| Young’s modulus | 6.9 × 1010 N/m−2 | 1.794 × 106 N/m−2 | Length | 177.8 mm |
| Poisson ratio | 0.3 | 0.3 | ||
| Density | 2766 kg/m−3 | 968.1 kg/m−3 | Width | 12.7 mm |
| Thickness | 1.524 mm | 0.127 mm | ||
| Mode | The Present Method | Ref. [37] | ||
|---|---|---|---|---|
| fn (Hz) | η | fn (Hz) | η | |
| 1st | 81.71 | 1.28 × 10−3 | 81.79 | 1.37 × 10−3 |
| 2nd | 494.14 | 6.20 × 10−3 | 504.16 | 5.43 × 10−3 |
| 3rd | 1323.4 | 8.06 × 10−3 | 1380.34 | 9.38 × 10−3 |
| 4th | 2449.8 | 1.19 × 10−2 | 2627.87 | 1.36 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Gong, Q.; Zhao, W.; Gui, H. Analysis of Viscoelastic Damping Effect on the Underwater Acoustic Radiation of a Ring-Stiffened Conical Shell. Appl. Sci. 2022, 12, 1566. https://doi.org/10.3390/app12031566
Chen Z, Gong Q, Zhao W, Gui H. Analysis of Viscoelastic Damping Effect on the Underwater Acoustic Radiation of a Ring-Stiffened Conical Shell. Applied Sciences. 2022; 12(3):1566. https://doi.org/10.3390/app12031566
Chicago/Turabian StyleChen, Zhanyang, Qingtao Gong, Weidong Zhao, and Hongbin Gui. 2022. "Analysis of Viscoelastic Damping Effect on the Underwater Acoustic Radiation of a Ring-Stiffened Conical Shell" Applied Sciences 12, no. 3: 1566. https://doi.org/10.3390/app12031566
APA StyleChen, Z., Gong, Q., Zhao, W., & Gui, H. (2022). Analysis of Viscoelastic Damping Effect on the Underwater Acoustic Radiation of a Ring-Stiffened Conical Shell. Applied Sciences, 12(3), 1566. https://doi.org/10.3390/app12031566






