From Climate Conditions to the Numerical Slope Stability Analysis of Surface Coal Mines
Abstract
Featured Application
Abstract
1. Introduction
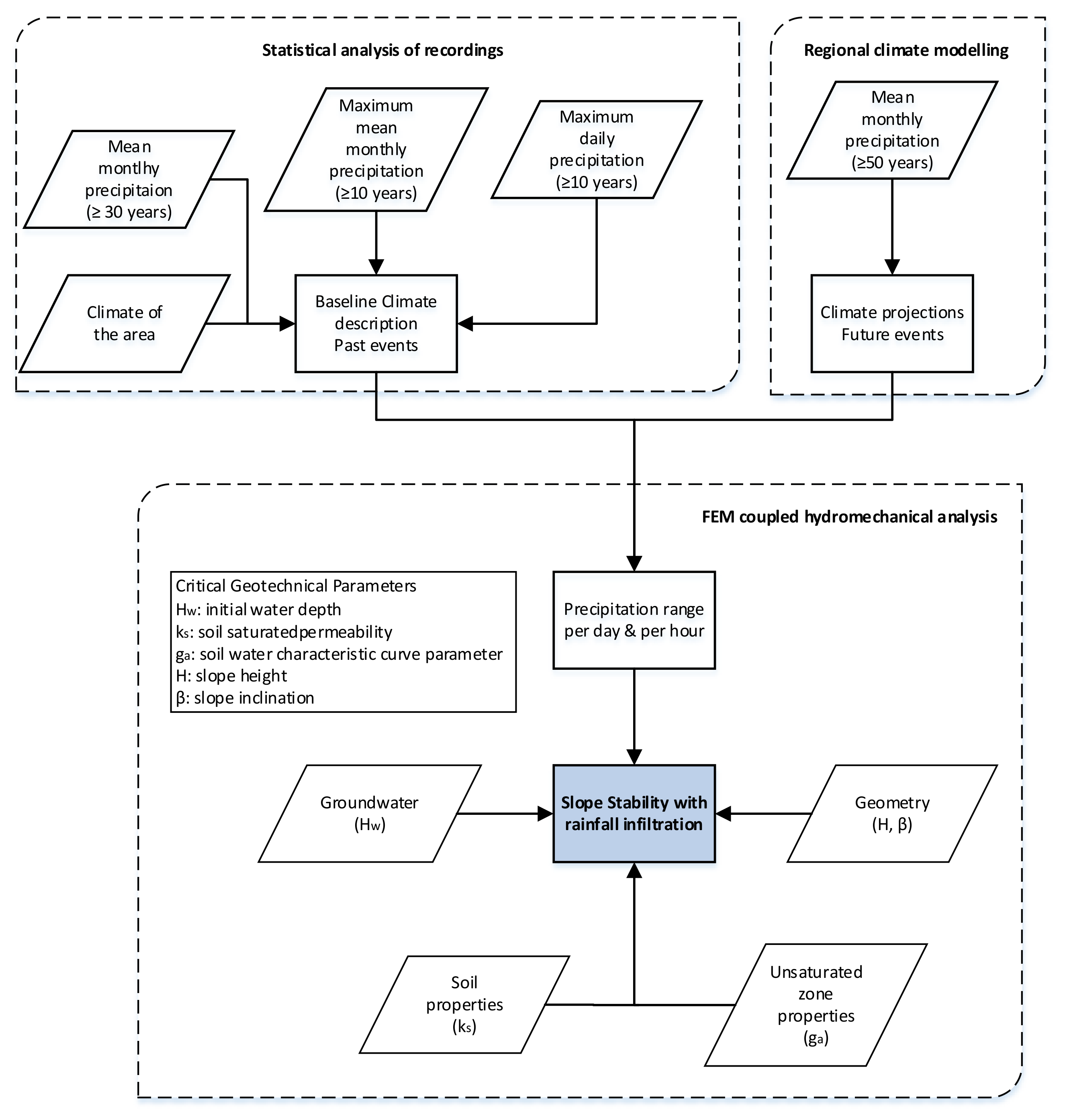
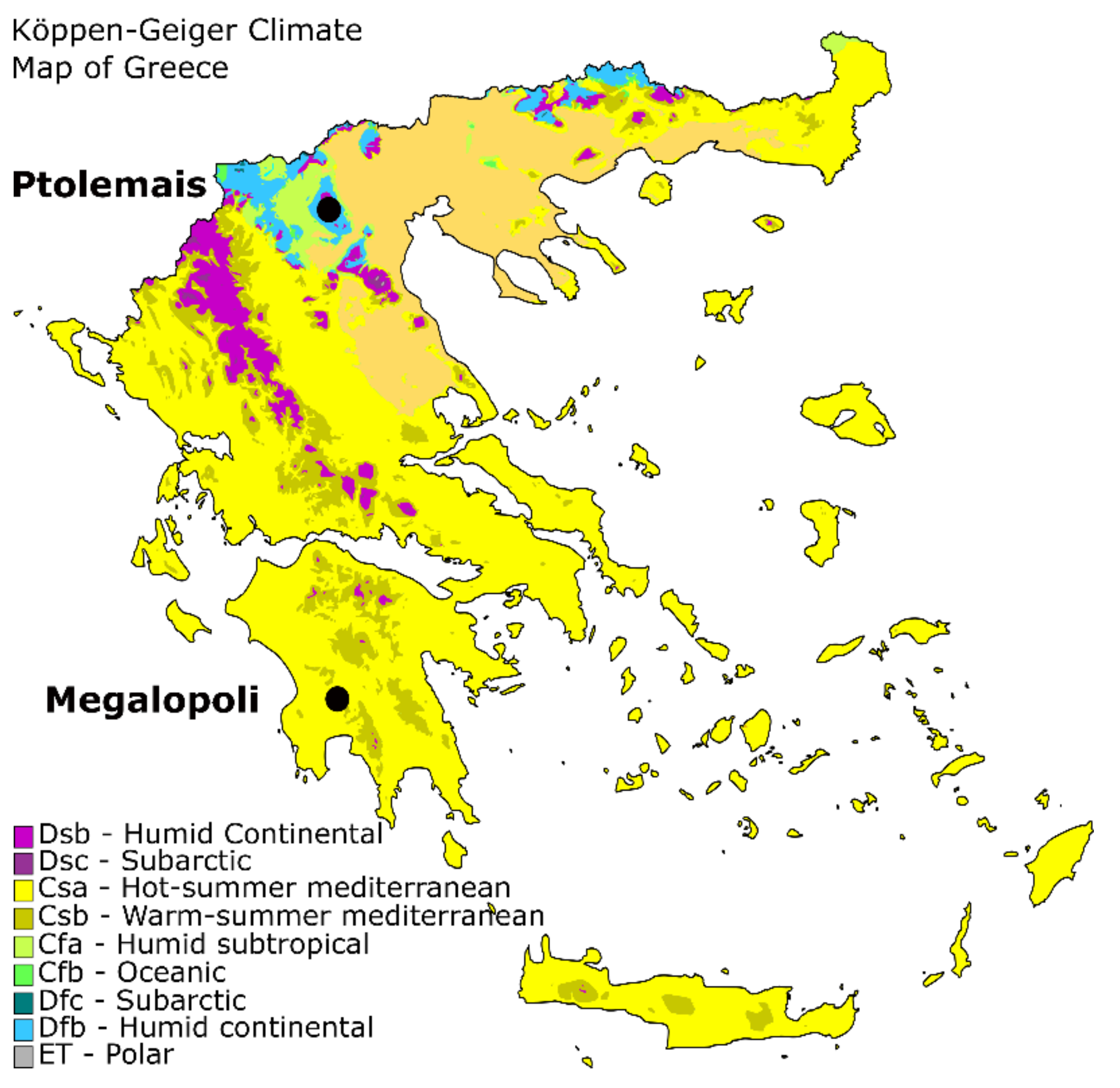
2. The Methodology and the Case Example of Greek Lignite Mines
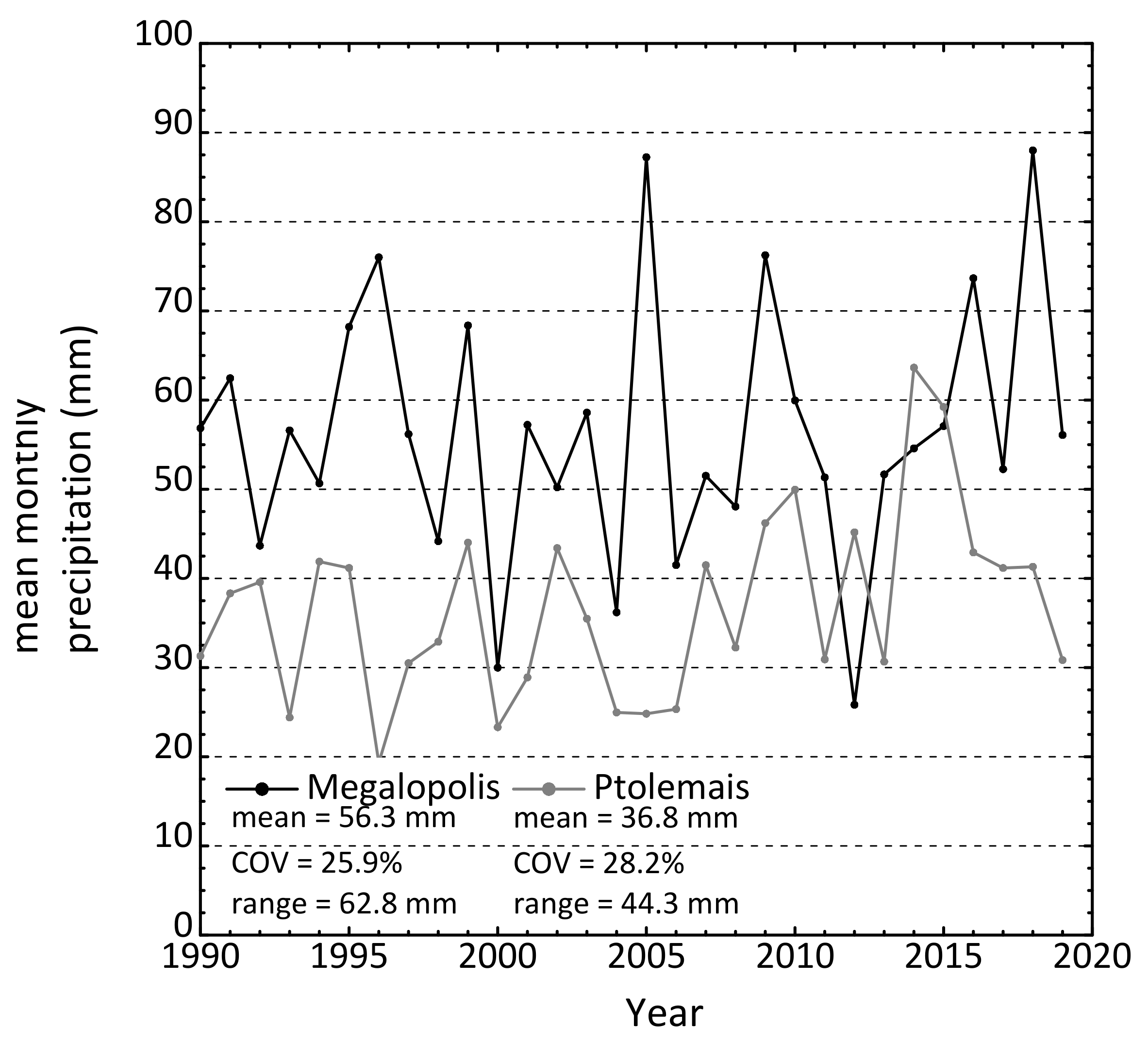
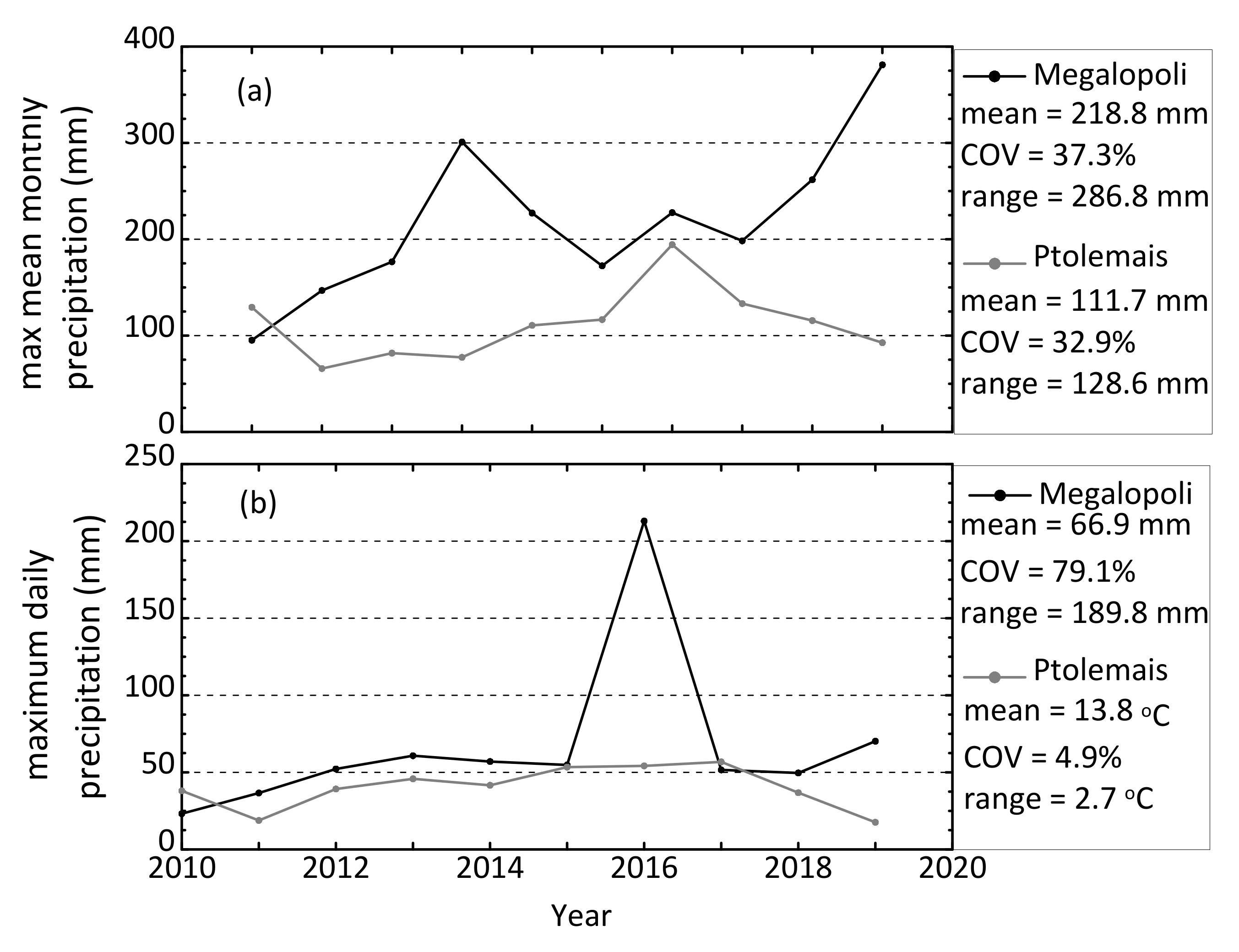
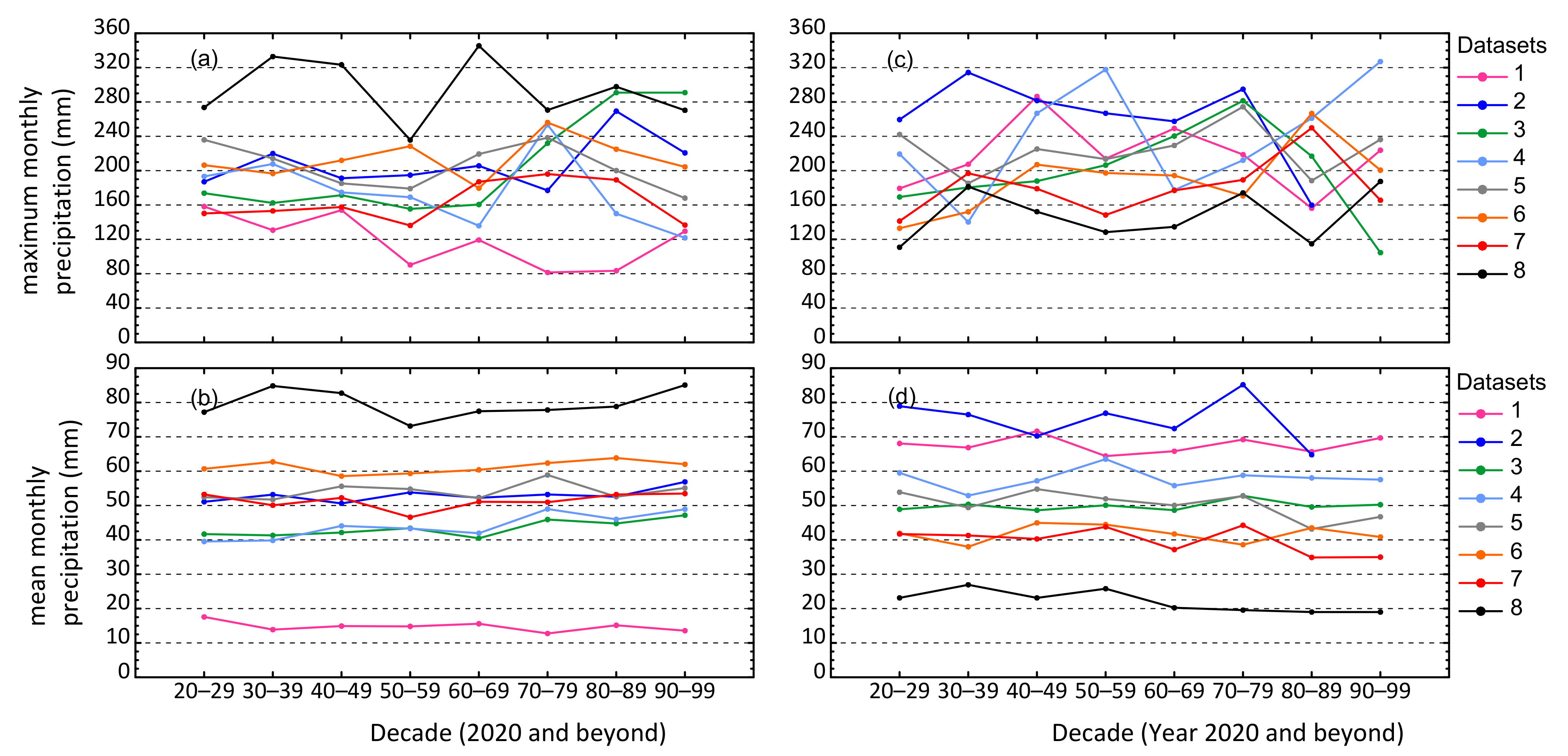
3. Baseline Climate Description—Past Events
4. Climate Projections—Future Events
5. Numerical Analysis of Slope Stability of Lignite Mines under Extreme Rainfall Events
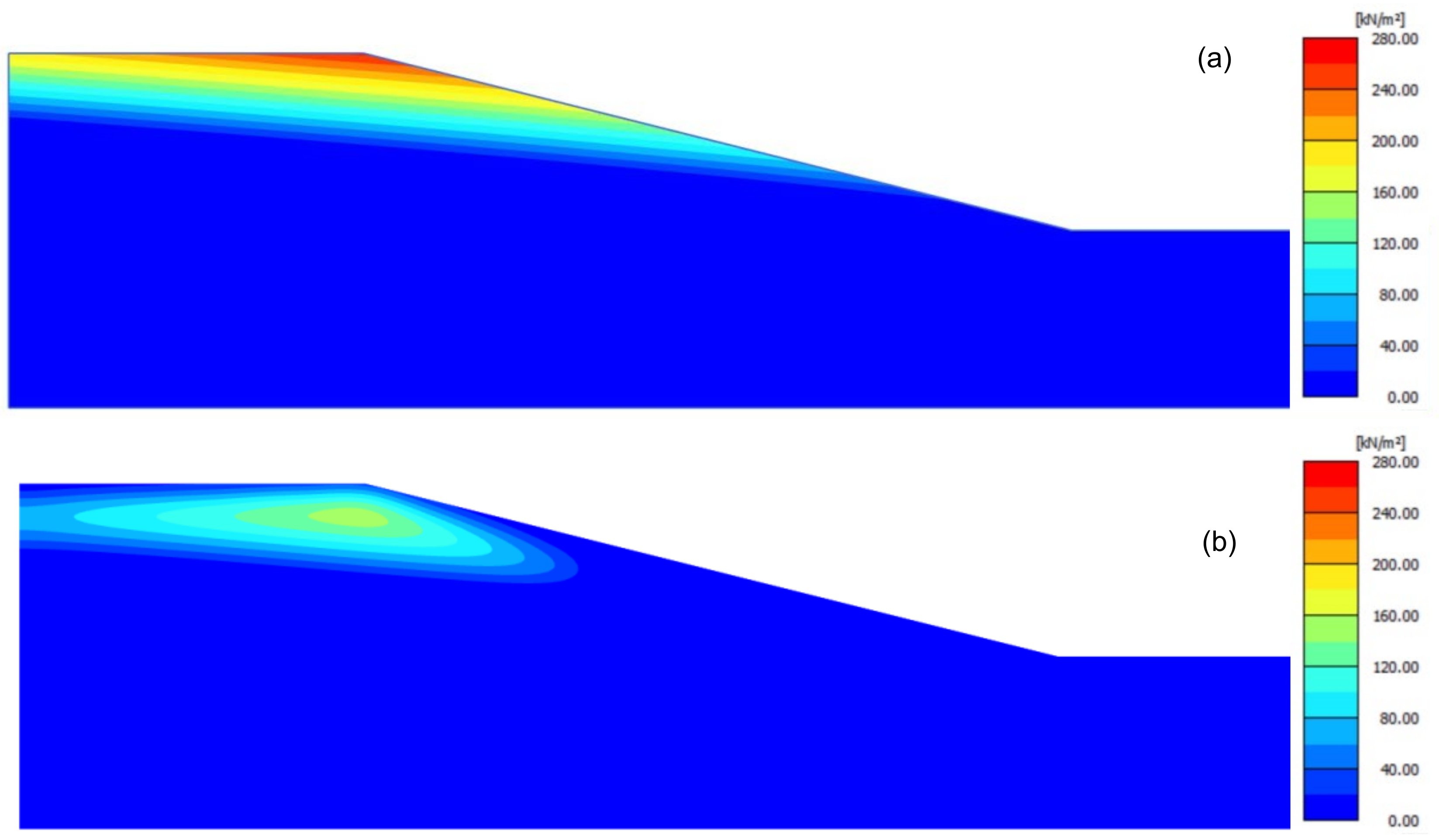
5.1. Numerical Model Overview
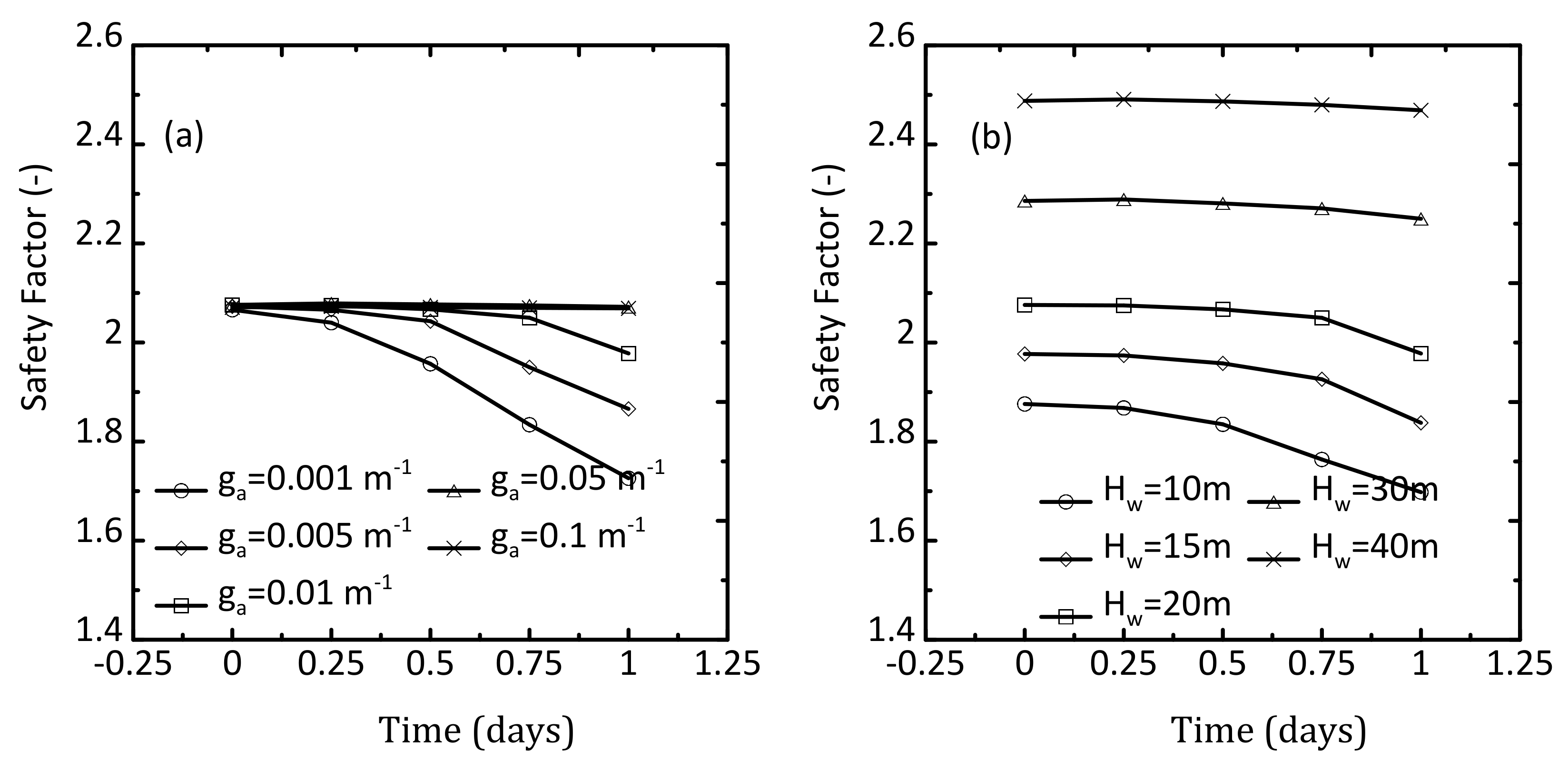
5.2. Effect of Rainfall on Slope Stability
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- BP. BP Statistical Review of World Energy; BP p.l.c: London, UK, 2021. [Google Scholar]
- Cai, F.; Ugai, K. Numerical Analysis of Rainfall Effects on Slope Stability. Int. J. Geomech. 2004, 4, 69–78. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Zhang, L.; Zhou, Y.; Ye, G.; Guo, N. Modelling rainfall-induced landslides from initiation of instability to post-failure. Comput. Geotech. 2021, 129, 103877. [Google Scholar] [CrossRef]
- Robinson, J.D.; Vahedifard, F.; AghaKouchak, A. Rainfall-triggered slope instabilities under a changing climate: Comparative study using historical and projected precipitation extremes. Can. Geotech. J. 2017, 54, 117–127. [Google Scholar] [CrossRef]
- Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C. Factors Controlling Instability of Homogeneous Soil Slopes under Rainfall. J. Geotech. Geoenviron. Eng. 2007, 133, 1532–1543. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lu, N. Unsaturated slope stability analysis with steady infiltration or evaporation using elasto-plastic finite elements. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 249–267. [Google Scholar] [CrossRef]
- De Leon, D.; Garduño, J. Time-variant failure probability of critical slopes under strong rainfall hazard including mitigation effects. Struct. Infrastruct. Eng. 2020, 16, 1481–1492. [Google Scholar] [CrossRef]
- Mahmood, K.; Ryu, J.H.; Kim, J.M. Effect of anisotropic conductivity on suction and reliability index of unsaturated slope exposed to uniform antecedent rainfall. Landslides 2013, 10, 15–22. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effect of hydraulic properties of soil on rainfall-induced slope failure. Eng. Geol. 2010, 114, 135–143. [Google Scholar] [CrossRef]
- Chowdhury, R.; Nguyen, V. Risk updating for rainfall-triggered spoil failures. In Proceedings of the International Symposium on Prediction and Performance in Geotechnical Engineering, Calgary, AB, USA, 17–19 June 1987; pp. 439–444. [Google Scholar]
- Pariseau, W.; Schmelter, S.; Sheik, A. Mine slope stability analysis by coupled finite element modelling. Int. J. Rock Mech. Min. Sci. 1997, 34, 242.e1–242.e17. [Google Scholar] [CrossRef]
- Steiakakis, E.; Kavouridis, K.; Monopolis, D. Large scale failure of the external waste dump at the “South Field” lignite mine, Northern Greece. Eng. Geol. 2009, 104, 269–279. [Google Scholar] [CrossRef]
- Steiakakis, C.; Agioutantis, Z.; Apostolou, E.; Papavgeri, G.; Tripolitsiotis, A. Integrating weather and geotechnical monitoring data for assessing the stability of large scale surface mining operations. Open Geosci. 2016, 8, 694–699. [Google Scholar] [CrossRef][Green Version]
- Lin, H.; Zhong, W. Influence of Rainfall Intensity and Its Pattern on the Stability of Unsaturated Soil Slope. Geotech. Geol. Eng. 2019, 37, 615–623. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Delahaye, C.H. Influence of rainfall on the deformation and stability of a slope in overconsolidated clays: A case study. Hydrogeol. J. 2003, 11, 174–192. [Google Scholar] [CrossRef]
- Rouainia, M.; Helm, P.; Davies, O.; Glendinning, S. Deterioration of an infrastructure cutting subjected to climate change. Acta Geotech. 2020, 15, 2997–3016. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage. Comput. Geotech. 1998, 22, 1–28. [Google Scholar] [CrossRef]
- Tsaparas, I.; Rahardjo, H.; Toll, D.G.; Leong, E.C. Controlling parameters for rainfall-induced landslides. Comput. Geotech. 2002, 29, 1–27. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, S.; Park, S.; Sharma, J. Influence of rainfall-induced wetting on the stability of slopes in weathered soils. Eng. Geol. 2004, 75, 251–262. [Google Scholar] [CrossRef]
- Zhang, L.L.; Fredlund, D.G.; Zhang, L.M.; Tang, W.H. Numerical study of soil conditions under which matric suction can be maintained. Can. Geotech. J. 2004, 41, 569–582. [Google Scholar] [CrossRef]
- Rahardjo, H.; Nio, A.S.; Leong, E.C.; Song, N.Y. Effects of Groundwater Table Position and Soil Properties on Stability of Slope during Rainfall. J. Geotech. Geoenviron. Eng. 2010, 136, 1555–1564. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, S.; Regueiro, R.A. Instability of partially saturated soil slopes due to alteration of rainfall pattern. Eng. Geol. 2012, 147–148, 28–36. [Google Scholar] [CrossRef]
- Hamdhan, I.N.; Schweiger, H.F. Finite Element Method–Based Analysis of an Unsaturated Soil Slope Subjected to Rainfall Infiltration. Int. J. Geomech. 2013, 13, 653–658. [Google Scholar] [CrossRef]
- Qi, S.; Vanapalli, S.K. Hydro-mechanical coupling effect on surficial layer stability of unsaturated expansive soil slopes. Comput. Geotech. 2015, 70, 68–82. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Tsai, Y.-J. Analyzing the Effect of Soil Hydraulic Conductivity Anisotropy on Slope Stability Using a Coupled Hydromechanical Framework. Water 2018, 10, 905. [Google Scholar] [CrossRef]
- Blatz, J.A.; Ferreira, N.J.; Graham, J. Effects of near-surface environmental conditions on instability of an unsaturated soil slope. Can. Geotech. J. 2004, 41, 1111–1126. [Google Scholar] [CrossRef]
- Tommasi, P.; Boldini, D.; Caldarini, G.; Coli, N. Influence of infiltration on the periodic re-activation of slow movements in an overconsolidated clay slope. Can. Geotech. J. 2013, 50, 54–67. [Google Scholar] [CrossRef]
- Leshchinsky, B.; Vahedifard, F.; Koo, H.-B.; Kim, S.-H. Yumokjeong Landslide: An investigation of progressive failure of a hillslope using the finite element method. Landslides 2015, 12, 997–1005. [Google Scholar] [CrossRef]
- Zhang, J.; Little, D.N.; Hariharan, N.; Kim, Y.-R. Prediction of climate specific vertical movement of pavements with expansive soils based on long-term 2D numerical simulation of rainwater infiltration. Comput. Geotech. 2019, 115, 103172. [Google Scholar] [CrossRef]
- Postill, H.; Dixon, N.; Fowmes, G.; El-Hamalawi, A.; Take, W.A. Modelling seasonal ratcheting and progressive failure in clay slopes: A validation. Can. Geotech. J. 2020, 57, 1265–1279. [Google Scholar] [CrossRef]
- Theocharis, A.Ι.; Zevgolis, I.E.; Koukouzas, N.C. A comprehensive geotechnical characterization of overburden material from lignite mine excavations. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 30. [Google Scholar] [CrossRef]
- Kavvadas, M.; Roumpos, C.; Schilizzi, P. Stability of Deep Excavation Slopes in Continuous Surface Lignite Mining Systems. Geotech. Geol. Eng. 2020, 38, 791–812. [Google Scholar] [CrossRef]
- Koukouzas, N. Mineralogy and geochemistry of diatomite associated with lignite seams in the Komnina Lignite Basin, Ptolemais, Northern Greece. Int. J. Coal Geol. 2007, 71, 276–286. [Google Scholar] [CrossRef]
- Zevgolis, I.E.; Deliveris, A.V.; Koukouzas, N.C. Slope failure incidents and other stability concerns in surface lignite mines in Greece. J. Sustain. Min. 2019, 18, 182–197. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future köppen-geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Eleftheriou, D.; Kiachidis, K.; Kalmintzis, G.; Kalea, A.; Bantasis, C.; Koumadoraki, P.; Spathara, M.E.; Tsolaki, A.; Tzampazidou, M.I.; Gemitzi, A. Determination of annual and seasonal daytime and nighttime trends of MODIS LST over Greece-climate change implications. Sci. Total Environ. 2018, 616-617, 937–947. [Google Scholar] [CrossRef]
- Stournaras, G.; Skourtos, M.; Kontogianni, A.; Yoxas, G.; Machleras, A.; Nastos, P. The Environmental, Economic and Social Impacts of Climate Change in Greece; Bank of Greece: Athens, Greece, 2011. [Google Scholar]
- Gofa, F.; Mamara, A.; Anadranistakis, M.; Flocas, H. Developing gridded climate data sets of precipitation for Greece based on homogenized time series. Climate 2019, 7, 68. [Google Scholar] [CrossRef]
- Feidas, H.; Karagiannidis, A.; Keppas, S.; Vaitis, M.; Kontos, T.; Zanis, P.; Melas, D.; Anadranistakis, E. Modeling and mapping temperature and precipitation climate data in Greece using topographical and geographical parameters. Theor. Appl. Climatol. 2014, 118, 133–146. [Google Scholar] [CrossRef]
- Valipour, M.; Bateni, S.M.; Jun, C. Global Surface Temperature: A New Insight. Climate 2021, 9, 81. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing climate information needs at the regional level: The CORDEX framework. World Meteorol. Organ. (WMO) Bull. 2009, 58, 175. [Google Scholar]
- Williams, D.N.; Lawrence, B.N.; Lautenschlager, M.; Middleton, D.; Balaji, V. The earth system grid federation: Delivering globally accessible petascale data for CMIP5. In Proceedings of the 32nd Asia-Pacific Advanced Network Meeting, New Delhi, India, 22–26 August 2011. [Google Scholar]
- Henderson-Sellers, A.; McGuffie, K. The Future of the World’s Climate; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Luhunga, P.; Botai, J.; Kahimba, F. Evaluation of the performance of CORDEX regional climate models in simulating present climate conditions of Tanzania. J. South. Hemisph. Earth Syst. Sci. 2016, 66, 32–54. [Google Scholar] [CrossRef]
- Jacob, D.; Teichmann, C.; Sobolowski, S.; Katragkou, E.; Anders, I.; Belda, M.; Benestad, R.; Boberg, F.; Buonomo, E.; Cardoso, R.M.; et al. Regional climate downscaling over Europe: Perspectives from the EURO-CORDEX community. Reg. Environ. Change 2020, 20, 51. [Google Scholar] [CrossRef]
- European Environment Agency. Climate Change, Impacts and Vulnerability in Europe 2012: An Indicator-Based Report; 9292133462; European Environment Agency: Copenhagen, Denmark, 2012. [Google Scholar]
- Plaxis 2D Finite Element Geotechnical Analysis Software, version 20.3; Bentley: Dublin, Ireland, 2020.
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Géotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Fredlund, D.G. The 1999 R.M. Hardy Lecture: The implementation of unsaturated soil mechanics into geotechnical engineering. Can. Geotech. J. 2000, 37, 963–986. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, M.D.; Fredlund, D.G.; Wilson, G. Prediction of the soil-water characteristic curve from grain-size distribution and volume-mass properties. In Proceedings of the 3rd Brazilian Symposium on Unsaturated Soils, Rio de Janeiro, Brazil, 21–25 April 1997; pp. 13–23. [Google Scholar]
- Lazarou, G.; Loukidis, D.; Bardanis, M. Moisture Migration Under Mat Foundations in Nicosia Marl. Geotech. Geol. Eng. 2019, 37, 1585–1608. [Google Scholar] [CrossRef]
- Sitarenios, P.; Bardanis, M.; Kavvadas, M. Evaluation of Various Soil-Water Characteristic Curve Models for Soils from Greece. In Unsaturated Soils: Research and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 69–76. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.; Huang, S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 533–546. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some Aspects of Effective Stress in Saturated and Partly Saturated Soils. Géotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Plaxis: Bishop’s Effective Stress: Validation & Verification; Bentley: Dublin, Ireland, 2018.



| References | ga (m−1) | φ’ (°) | c’ (kPa) | ks (cm/s) | H (m) | q (mm/h) | Hw (m) | Comments |
|---|---|---|---|---|---|---|---|---|
| Cai and Ugai [2] | 1.06–7.09 | 25 | 8 | 10−4–6 × 10−3 | 10 | 5–50 | * 0 | Cut |
| Zhang, Fredlund, Zhang, and Tang [20] | 0.05–10 | - | - | 10−3 | 20 | 0.036–18 | ** 20 | Cut |
| Griffiths and Lu [6] | 0.05–0.5 | 20–30 | 5–10 | 10−11–10−3 | 10 | 4 × 10−8–10−3 | * 2.5 | Cut |
| Rahardjo, Ong, Rezaur, and Leong [5] | 0.1–10 | 26 | 10 | 10−4–10−2 | 5–40 | 9–900 | * 2.5–15 | Natural |
| Rahimi, Rahardjo, and Leong [9] | 0.01–10.0 | 26 | 10 | 10−5–10−2 | 15 | 0.036–360 | * 2 | Natural |
| Tommasi, Boldini, Caldarini, and Coli [27] | 0.02 | 21 | 18 | 1 × 10−4 | 100 | 0.02–4.2 | - | Natural—Case study |
| Leshchinsky, Vahedifard, Koo, and Kim [28] | 0.20 | 20 | 15 | 5 × 10−3 | 58 | 0.04–10.4 | - | Natural—Case study |
| Qi and Vanapalli [24] | 0.03–1.00 | 17.5 | 5 | 4 × 10−9–6 × 10−7 | 20 | 0.02 | * 8–23 | Cut |
| Robinson, Vahedifard, and AghaKouchak [4] | 1.60 | 30 | 10 | 4 × 10−4 | 10 | 2.1–4.2 | * 2 | Cut |
| Yeh and Tsai [25] | 0.1–1.0 | 26 | 10 | 10−4–10−2 | 10 | 0.8–30 | * 10 | Cut |
| Rouainia, Helm, Davies, and Glendinning [16] | 0.08 | 20 | 7 | 10−7 | 8 | 21–43 | * 1 | Cut |
| Chen, Zhang, Zhang, Zhou, Ye, and Guo [3] | 1.00 | 26 | 30 | 5 10−3 | 125 | 0.1–2.5 | ** 0 | Natural—Case study |
| Current Study | 0.001–0.1 | 25 | 50 | 10−5–10−3 | 50 | 0.8–17.0 | ** 10–40 | Cut |
| Parameter | Symbol | Value |
|---|---|---|
| Young’s modulus | E’ (MPa) | 50 |
| Poisson’s ratio | ν’ (-) | 0.25 |
| Effective cohesion | c’ (kPa) | 50 |
| Effective friction angle | φ’ (ο) | 25 |
| Dilation angle | ψ (ο) | 0 |
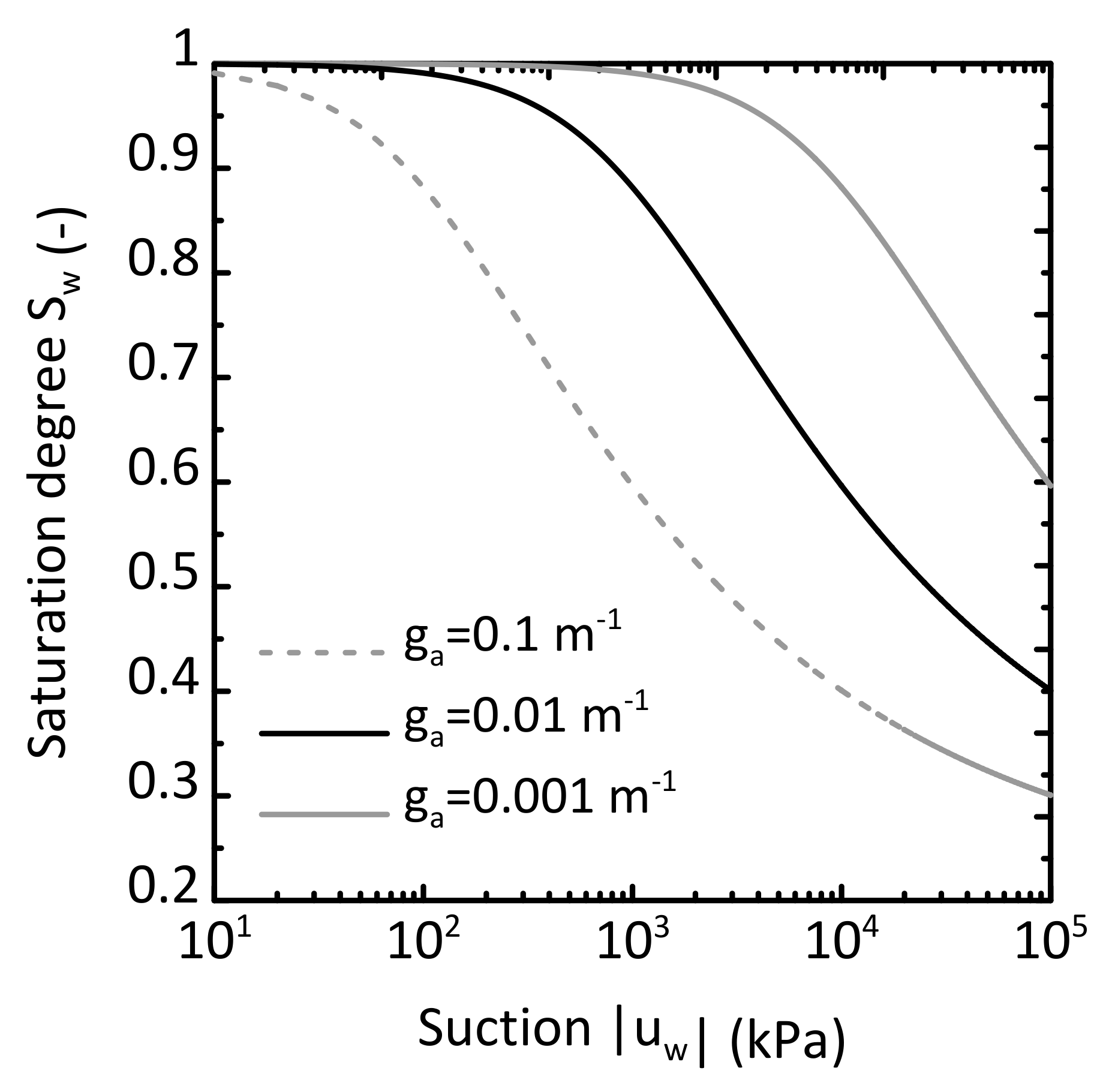
| SWCC parameter | ga (m−1) | 0.01 |
| SWCC parameter | gn (-) | 1.3 |
| SWCC parameter | gl (-) | 0.5 |
| Bulk water unit weight | γw (kN/m3) | 9.81 |
| Unsaturated soil unit weight | γ’ (kN/m3) | 16 |
| Saturated soil unit weight | γs (kN/m3) | 18 |
| Void ratio | eo (-) | 0.8181 |
| Residual saturation degree | Sr (-) | 0.2 |
| Saturated saturation degree | Ss (-) | 1.0 |
| Saturated permeability | ks (cm/s) | 10−4 |
| Geostatic stress coefficient | Ko (-) | 0.3333 |
| SWCC material parameter ga (m−1) | 0.001 | 0.005 | 0.01 | 0.05 | 0.1 |
| Saturated permeability ks (cm/s) | 10−5 | 5 × 10−5 | 10−4 | 5 × 10−4 | 10−3 |
| Initial groundwater head Hw (m) | 10 | 15 | 20 | 30 | 40 |
| Rainfall intensity q (mm/h) | 1.2 | 2.4 | 3.6 | 4.8 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theocharis, A.I.; Zevgolis, I.E.; Deliveris, A.V.; Karametou, R.; Koukouzas, N.C. From Climate Conditions to the Numerical Slope Stability Analysis of Surface Coal Mines. Appl. Sci. 2022, 12, 1538. https://doi.org/10.3390/app12031538
Theocharis AI, Zevgolis IE, Deliveris AV, Karametou R, Koukouzas NC. From Climate Conditions to the Numerical Slope Stability Analysis of Surface Coal Mines. Applied Sciences. 2022; 12(3):1538. https://doi.org/10.3390/app12031538
Chicago/Turabian StyleTheocharis, Alexandros I., Ioannis E. Zevgolis, Alexandros V. Deliveris, Rania Karametou, and Nikolaos C. Koukouzas. 2022. "From Climate Conditions to the Numerical Slope Stability Analysis of Surface Coal Mines" Applied Sciences 12, no. 3: 1538. https://doi.org/10.3390/app12031538
APA StyleTheocharis, A. I., Zevgolis, I. E., Deliveris, A. V., Karametou, R., & Koukouzas, N. C. (2022). From Climate Conditions to the Numerical Slope Stability Analysis of Surface Coal Mines. Applied Sciences, 12(3), 1538. https://doi.org/10.3390/app12031538








