Energy-Aware Multi-Objective Job Shop Scheduling Optimization with Metaheuristics in Manufacturing Industries: A Critical Survey, Results, and Perspectives

Abstract

In recent years, the application of artificial intelligence has been revolutionizing the manufacturing industry, becoming one of the key pillars of what has been called Industry 4.0. In this context, we focus on the job shop scheduling problem (JSP), which aims at productions orders to be carried out, but considering the reduction of energy consumption as a key objective to fulfill. Finding the best combination of machines and jobs to be performed is not a trivial problem and becomes even more involved when several objectives are taken into account. Among them, the improvement of energy savings may conflict with other objectives, such as the minimization of the makespan. In this paper, we provide an in-depth review of the existing literature on multi-objective job shop scheduling optimization with metaheuristics, in which one of the objectives is the minimization of energy consumption. We systematically reviewed and critically analyzed the most relevant features of both problem formulations and algorithms to solve them effectively. The manuscript also informs with empirical results the main findings of our bibliographic critique with a performance comparison among representative multi-objective evolutionary solvers applied to a diversity of synthetic test instances. The ultimate goal of this article is to carry out a critical analysis, finding good practices and opportunities for further improvement that stem from current knowledge in this vibrant research area.

1. Introduction

The new industrial revolution, known as Industry 4.0 [1], is improving manufacturing environments based on nine pillars: Big Data, simulation, additive manufacturing, cybersecurity, cloud computing, the Internet of Things, cyber–physical systems and robotics integration, and augmented reality [2]. A key enabler of the Industry 4.0 paradigm is the use of artificial intelligence (both machine learning and optimization), which can be used to improve the production process by finding complex relationships between process variables and their final quality [3], predictive maintenance [4], the prediction of demand and sales [5], computer vision [6], the optimization of the furnace’s charge [7], parameter optimization [8], industrial simulator optimizations [9], and many more similar use cases.

An important area in production environments is production planning, widely known as the job shop scheduling problem (JSP) [10,11]. In the JSP, multiple jobs are processed on several machines. Each job comprises a sequence of tasks that must be processed in a given order, whereas each task must be processed on a specific machine. The problem is to schedule the tasks on the machines towards minimizing one or several measures of the production efficiency (e.g., the time needed for all the jobs to be completed). The flexible JSP (FJSP) extends the JSP by considering that a task can be processed by any machine from a given set, so that the solution also includes the assignment of tasks to machines. There are a number of practical factors that must be taken into account in order to carry out production planning satisfactorily, such as the machines’ availability, jobs, materials, personnel, or machine depreciation costs. The dimensions of these factors increase in larger factories due to the equally increasing number of installed production assets, the continuous arrival of more production orders, and other aspects that make the underlying production planning processes even more difficult to tackle.

Finding the best combination for production planning is not a trivial task. The number of possible combinations is in the order of ${(n!)}^m$, n being the number of jobs and m the number of machines [12]. For instance, five jobs can be assigned and scheduled in a factory of just five machines in approximately $24.8\times {10}^9$ different combinations. Consequently, the use of exhaustive optimization techniques is not feasible in real-world industrial scenarios, where the number of machines and jobs can be much higher than the aforementioned example. Therefore, non-exact optimization techniques have been proposed as an alternative to cope with the complexity of JSP problems, including metaheuristics, a broad family of optimization techniques that do not guarantee the discovery of optimal solutions, but usually provide near-optimal solutions within reasonable times [13]. Evolutionary computation, which is arguably the most widely known subfamily of metaheuristics, has been applied to the JSP as well over the years [14].

The formulation of a JSP problem may consider more than one conflicting objective to be minimized, such as the makespan (total time to complete a given production plan), total tardiness, and machine changes. Consequently, the JSP can be formulated as a multi-objective optimization problem, wherein the optimum is not a unique solution, but a set of trade-off solutions differently balancing among the established objectives (known as the Pareto set). From an algorithmic perspective, addressing several objectives and approximating the Pareto set that optimally balances them even further increases the complexity of designing an efficient and scalable optimization technique.

In addition to the common production-related goals mentioned previously (e.g., makespan, total tardiness), the reduction of the energy consumption is a crucial aspect of today’s society, due to the effects of climate change and the rising concerns about the long-term sustainability of the planet [15,16]. This objective has been prevalent over the years during which JSP problems have been approached with metaheuristic algorithms, yet it has not been until recently when energy efficiency has become of utmost relevance in the industrial realm, in particular in energy-intensive industries. The growing importance of energy consumption as a key indicator of industrial performance and efficiency has permeated into practical planning processes. Consequently, the interests of the research community working on metaheuristics for JSP problems have progressively steered towards energy efficiency as another objective, giving rise to an upsurge of contributions dealing with energy-aware multi-objective JSP problems for industrial production scheduling.

In light of this rising research trend, this survey aims to provide the readership of this journal with a comprehensive survey of multi-objective meta-heuristic algorithms applied to JSP problems where energy efficiency is considered among the objectives to be optimized. The literature study offered in our work intends to pose itself as a reference material for those interested in pursuing research in this area. To this end, we systematically reviewed and critically analyzed the most relevant features of both problem formulations and algorithms to solve them effectively. To do this, three taxonomies are proposed to arrange the contributions so far as per (1) the JSP problem to be solved (i.e., type and domain, number of objectives and secondary objectives), (2) practical constraints and considerations that affect the formulation of the problem and the feasibility of the solutions, and (3) the technique in use to solve the formulated problem (correspondingly, the adopted algorithm, main parameter settings, etc.). After organizing and describing the contributions noted in this area, we highlight good practices identified in the reviewed corpus of literature, a well as underscore research niches and poor practices that must be overcome to achieve actionable insights and approaches of practical utility.

The manuscript also informs with empirical evidence the main findings of our bibliographic review. To this end, the survey includes an experimental study including representative multi-objective evolutionary solvers applied to a number of synthetic JSP test instances that have appeared in the literature [17]. These instances were augmented with energy costs added in order to be representative of the area surveyed in this study. The ultimate goal of this experimental study was to methodologically prescribe how to perform a comparison among multi-objective metaheuristic solvers for energy-aware JSP problems in a principled way, considering not only the quantitative significance of the performance differences found among the algorithms under comparison, but also pausing on the qualitative implications of such differences in practical settings. In order to promote reproducibility and transparency, the source code of the software generating the discussed results has been made public in a GitHub repository, together with the augmented JSP instances under consideration.

The rest of this manuscript is structured as follows. Section 2 introduces the basic concepts about multi-objective optimization, metaheuristic optimization, and a generic description of the JSP problem. The literature collection methodology, the three proposed taxonomies, and the literature review on multi-objective JSP problems with energy as one of the objectives are provided in Section 3. This section is concluded with the summary of critical points mentioned above, flowing into the experimental setup and results obtained therefrom discussed in Section 4. Finally, conclusions are drawn and research directions are outlined in Section 5, motivating the readership towards investing further research efforts in this exciting research avenue.

2. Background

For the sake of the self-completeness of this survey, this section includes basic concepts about multi-objective optimization (Section 2.1), metaheuristic algorithms (Section 2.2), and the formulation of the JSP problem (Section 2.3). Before proceeding further, we note that the explanations and definitions given in what follows are kept to the minimum required for properly understanding the subsequent examination of the literature and the experimental use case. Supportive references for the interested reader are given in place for further details about any of the exposed concepts.

2.1. Multi-Objective Optimization

Multi-objective optimization is the discipline dealing with problems formulated around two or more objective functions that have to be optimized at the same time [18,19]. These functions are usually in conflict, so improving one of them leads to the degradation of the others. We assumed, without loss of generality, that all objective functions are to be minimized.

Broadly speaking, the goal sought in a multi-objective optimization problem (MOP) is to find a set of solutions that not only satisfy eventually imposed equality and inequality constraints (as per the problem to be solved), but also best balance the trade-off between the established objectives, i.e., solutions for which it is not possible to find any others that improve (minimize) the values of the defined objectives. Mathematically:

Definition 1. 

(MOP) Find a vector ${\overrightarrow{x}}^{*}=\left[x_1^{*},x_2^{*},\dots ,x_n^{*}\right]$ that satisfies m inequality constraints $g_i\left(\overrightarrow{x}\right)\ge 0,i=1,2,\dots ,m$ and p equality constraints $h_i\left(\overrightarrow{x}\right)=0,i=1,2,\dots ,p$ (if any such constraints exists) and minimizes the vector function $\overrightarrow{f}\left(\overrightarrow{x}\right)={\left[f_1\left(\overrightarrow{x}\right),f_2\left(\overrightarrow{x}\right),\dots ,f_k\left(\overrightarrow{x}\right)\right]}^T$, where $\overrightarrow{x}={\left[x_1,x_2,\dots ,x_n\right]}^T$ is the vector of decision variables.

In the above definition, all the values of the vector of decision variables that satisfy the constraints circumscribe the feasible region $\mathsf{\Omega }$, so any point $\overrightarrow{x}\in \mathsf{\Omega }$ can be referred to as a feasible solution.

The conflicting nature of the objectives $\overrightarrow{f}\left(\overrightarrow{x}\right)$ of an MOP implies the need for defining what an optimal solution is. Connecting with the broad explanation of what an MOP pursues that is given above, this leads to the definition of Pareto optimality:

Definition 2. 

(Pareto optimality) A point ${\overrightarrow{x}}^{*}\in \mathsf{\Omega }$ is said to be Pareto optimal if for every $\overrightarrow{x}\in \mathsf{\Omega }$ and $I=\left\{1,2,\dots ,k\right\}$, either ${\forall }_{i\in I}\left(f_i\left(\overrightarrow{x}\right)=f_i\left({\overrightarrow{x}}^{*}\right)\right)$ or there is at least one $i\in I$ such that $f_i\left(\overrightarrow{x}\right)>f_i\left({\overrightarrow{x}}^{*}\right)$.

According to this definition, a vector (point or solution) ${\overrightarrow{x}}^{*}$ is Pareto optimal if no feasible vector $\overrightarrow{x}$ exists that would improve some criteria without causing a simultaneous worsening of at least one other criterion.

Given two vectors corresponding to solutions of a given MOP, comparing them to determine which is better in terms of objective minimization is not as simple as in single-objective optimization. When dealing with a single objective, the vector having the lower associated function value can be declared to be better than the other. By contrast, when there are several objectives involved, the concept of Pareto dominance is introduced to compare among solutions:

Definition 3. 

(Pareto Dominance) A vector $\overrightarrow{u}=\left(u_1,\dots ,u_k\right)$ is said to dominate $\overrightarrow{v}=\left(v_1,\dots ,v_k\right)$ (denoted by $\overrightarrow{u}\preccurlyeq \overrightarrow{v}$) if and only if $\overrightarrow{u}$ is partially less than $\overrightarrow{v}$, i.e., $\forall i\in \left\{1,\dots ,k\right\},u_i\le v_i\wedge \exists i\in \left\{1,\dots ,k\right\}:u_i<v_i.$

By using Pareto dominance, we can determine whether, given two solutions, one dominates the other, or instead, they do not dominate each other. In this last case, they are non-dominated solutions, and therefore, it cannot be said which of them is better in the sense of the trade-off between the objectives of the MOP. Pareto optimality can be thus defined in terms of dominance, as a Pareto-optimal point is one that is not dominated by any other point in $\mathsf{\Omega }$.

Optimizing an MOP can be defined then as the process of finding the set composed of all the Pareto-optimal solutions. This set is referred to as the Pareto-optimal set, or the simply Pareto set, and can be defined as:

Definition 4. 

(Pareto-optimal set) For a given MOP $\overrightarrow{f}\left(\overrightarrow{x}\right)$, the Pareto-optimal set is defined as ${\mathcal{P}}^{*}=\{\overrightarrow{x}\in \mathsf{\Omega }|\neg \exists \overrightarrow{x^{\prime }}\in \mathsf{\Omega },\overrightarrow{f}\left(\overrightarrow{x^{\prime }}\right)\preccurlyeq \overrightarrow{f}\left(\overrightarrow{x}\right)\}$.

Each vector in the Pareto-optimal set has a correspondence in the objective function space, leading to the so-called Pareto front:

Definition 5. 

(Pareto front) For a given MOP $\overrightarrow{f}\left(\overrightarrow{x}\right)$ and its Pareto-optimal set ${\mathcal{P}}^{*}$, the Pareto front is defined as ${\mathcal{PF}}^{*}=\left\{\overrightarrow{f}\left(\overrightarrow{x}\right)\right|\overrightarrow{x}\in {\mathcal{P}}^{*}\}$.

Finding the optimal solutions of an MOP is a first step in the full optimization process, as it is followed by the decision-making step, where an expert in the problem domain has to choose one of them satisfying some criteria [20]. Consequently, the algorithms used for solving MOPs aim at finding an approximation of the Pareto set having a relatively low number of diverse solutions, based on which the user in the application at hand (in our case, the manager of the production plant) can eventually make informed decisions.

2.2. Metaheuristics and Evolutionary Algorithms

Searching for the full Pareto set of a given MOP can be unpractical for two reasons. On the one hand, providing a huge number of the solutions can complicate the decision-making process; in general, the algorithms used for solving MOPs are aimed at obtaining an approximation of the Pareto set having a relatively low number of solutions. On the other hand, MOPs can be characterized by a number of features, making them very difficult to solve, such as the NP-hard complexity, non-linear functions, epistasis, or several objectives or a large number of decision variables, to mention a few [21].

As a consequence, the use of exact optimization techniques is frequently unfeasible in practice. The alternative is to shift to other kinds of algorithms. In this context, metaheuristics appear as a family of non-exact techniques that have gained much popularity since the 1990s. They can be defined as iterative strategies that guide and manage the operations of subordinate heuristics to efficiently find high-quality solutions [13]. Metaheuristics are usually non-deterministic and not problem specific, although they can incorporate domain knowledge by virtue of the flexibility of their algorithmic design.

Sub-classes of metaheuristics include evolutionary algorithms (by far, the most well-known metaheuristic), ant colony optimization, simulated annealing, and particle swarm optimization. In fact, many metaheuristics have been designed, so a number of approaches to classify them have been proposed. The most accepted taxonomy distinguishes between nature-inspired and non-nature-inspired metaheuristics.

Table 1. Classification of metaheuristics in nature-inspired and non-nature-inspired techniques, together with some illustrative examples for each of these categories.

Nature-Inspired	Non-Nature-Inspired
• Simulated annealing (SA)	• Tabu search (TS)
• Swarm Intelligence	• Variable neighborhood search (VNS)
− Particle swarm optimization (PSO)	• Scatter search (SS)
− Ant colony optimization (ACO)	• Iterated local search (ILS)
• Evolutionary computation (EC)	• Guided local search (GLS)
− Genetic algorithm (GA)	• Path relinking (PR)
− Evolution strategy (ES)	• Greedy randomized adaptive
− Genetic programming (GP)	Search procedure (GRASP)
• Artificial immune system (AIS)

contains a list of representative metaheuristic algorithms according to this classification. A more thorough compendium of nature-inspired metaheuristics can be found in any of the taxonomic studies recently contributed by the community (see, e.g., [22] and the references therein).

Among nature-inspired metaheuristics, evolutionary algorithms are techniques inspired by biological evolution, where solutions are termed as individuals and grouped into populations that are refined over the search process. The individuals evolve by the iterative application of selection, reproduction, and replacement operators over the population of individuals, which mimic the evolution of beings in an ecosystem. Within evolutionary computation, we highlight genetic algorithms, which apply recombination and mutation in the reproduction step. As in traditional single-objective optimization, metaheuristics have been widely used to solve MOPs [18,19]. In particular, well-known multi-objective metaheuristics comprise evolutionary computation search operators and concepts at their core, such as NSGA-II [23], MOEA/D [24], and SMS-EMOA [25]. These three exemplified MOP metaheuristics are, respectively, representatives of the three commonly accepted categories of multi-objective metaheuristics: Pareto dominance, decomposition, and indicator-based MOP metaheuristics.

2.3. The JSP Problem

The job shop scheduling problem (JSP or JSSP) [26,27] is an optimization problem focused on assigning production jobs to industrial resources at a particular time. It is one of the main problems in today’s companies’ production planning, as they are dedicating resources in an attempt at efficiently finding optimal plannings. Given the NP-hard complexity of the JSP, in many cases, the assignment of tasks/jobs to resources is performed by humans, which severely limits the possibility of successfully finding global optimum assignments.

Therefore, the main goal of the JSP is to find a production plan taking into account variables and constraints that affect the production in the scenario under consideration. Such aspects can be assorted in their nature, including the availability of machines, the minimum quantities to be produced for each type of product, the quality and availability of materials, the personnel qualifications, the eventual occurrence of breakdowns, etc. An objective that is usually considered across the literature related to the JSP is the minimization of the total production time needed to achieve certain production goals (commit), also referred to as makespan. In general, the makespan can be regarded as the total time needed for all jobs to be completed from the beginning [26]. Several studies presented in the 1980s and 1990s approached the makespan minimization problem using optimization algorithms [14,28,29,30]. However, this seminal JSP formulation still has relevance and continues receiving the interest of the research community working on metaheuristics [31,32].

Besides the continued consideration of the makespan as a core target of the JSP, energy consumption has climbed up the priority ranking in the last few years, due to the global awareness arising around climate change and the sustainability of the industrial value chain [15]. There is a global challenge to curb emissions generated by countries, with high penalties for non-compliers, which is also associated with higher energy costs due to penalties for using energy production methods with a high environmental impact, such as the use of coal.

Mathematically, the JSP (and its FJSP extension) can be formulated departing from a set $\mathcal{J}$ of N independent jobs ${\left\{j_n\right\}}_{n=1}^N$. Each job has its own processing order through M machines available in the production plant, which are denoted as $\mathcal{M}={\left\{m_i\right\}}_{i=1}^M$. Each job $j_n$ comprises a number $O_n$ of ordered tasks $[T_1^n,\dots ,T_{O_n}^n]$, which must be completed for job $j_n$ to be declared as processed. As such, task $T_k^n$ can be assumed to be processed (1) on a predefined machine $m_j\in \mathcal{M}$ (as in the JSP) or (2) on any machine in a given subset of qualified machines ${\mathcal{M}}_j\subseteq \mathcal{M}$. When task $T_k^n$ is assigned to machine $m_j$, a cost $C_{j,n,k}$ is incurred (e.g., processing time or energy consumption). In other words, the naive JSP can be regarded as a sequence optimization problem as the assignment of tasks to machines is established beforehand; the FJSP, however, also seeks an optimal assignment (routing) of each task $T_k^n$ to a machine from the qualified set $M_j$, together with the order of tasks on the machines. The discovery of the optimal assignment and/or task sequence is driven by the minimization of the total cost to produce all N jobs in their entirety, which is driven by the values of the costs $C_{j,n,k}$. While typically, for only one objective (minimization of the makespan, wherein $C_{j,n,k}^{time}$ denotes the processing time of task k of job $j_n$ on machine $m_j$), the search can be driven by several conflicting costs (for instance, besides the makespan, energy consumption, i.e., $C_{j,n,k}^{pow}$, is measured in units of consumed power to produce the task), in this case, the goal of the multi-objective JSP/FJSP is to find a set of different assignment and/or ordering solutions that optimally balance (in the Pareto sense) between the makespan and the total energy required to process the production commit.

In this regard, there can be found several studies considering multiple objectives in a single JSP [33,34]. Our study complements them by performing an extensive review of the literature addressing the JSP as a multi-objective problem with energy as one of its objectives. The examination of the contributions considered in our study and the critical insights extracted from the analysis of this literature are presented in the next section.

3. Literature Survey and Critical Analysis

To conduct the survey on the energy-aware JSP, a thorough literature collection and crosscheck were performed, yielding a selection of more than 60 references related to multi-objective optimization applied to JSP problems with energy as one of their objectives. Even though we tried to encompass a wide and thorough review, it is important to clarify that the aim was not to be comprehensive, but rather to analyze representative studies that showcase the current status of the research area. This being said, other works may not have been included in the study.

The section is divided into three different parts. First, Section 3.1 details the methodological steps followed to compile the related literature and to end up with the selected corpus of contributions considered in the survey. Section 3.2 follows with the analysis of the literature based on three taxonomies: problem features, constraints and considerations, and the multi-objective optimizer in use. Finally, the section ends with a summary of our main findings after the analysis of the literature; as such, Section 3.3 stresses the lessons learned, good and poor practices, and opportunities for further research in the examined area.

3.1. Literature Collection and Filtering Methodology

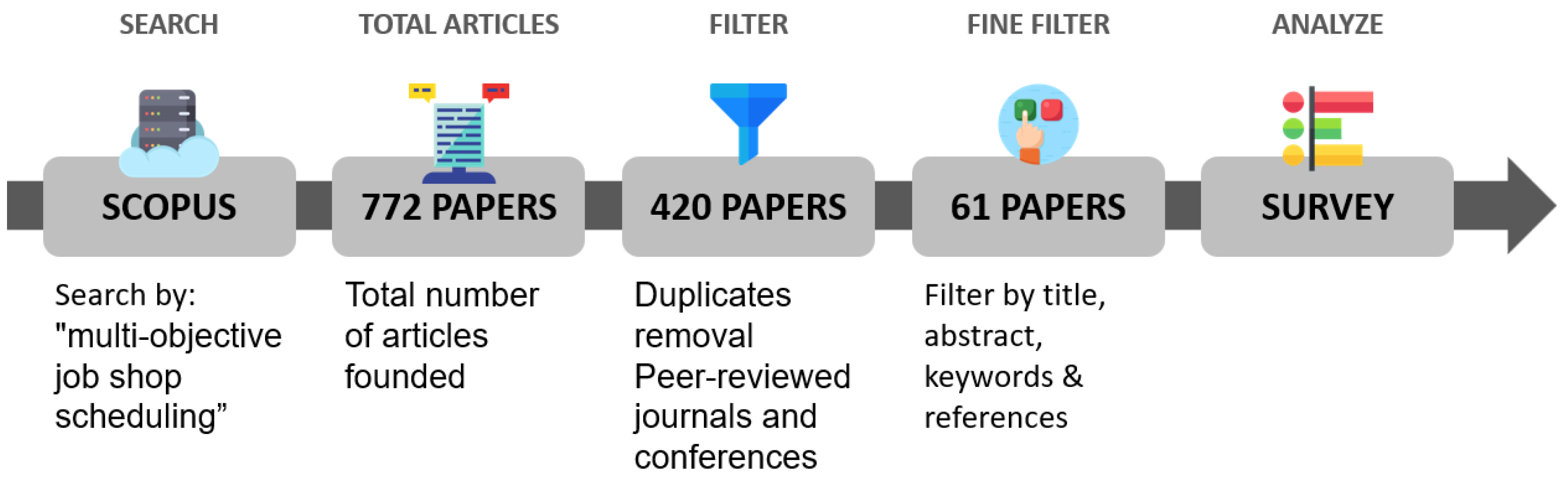
The search process carried out is depicted schematically in Figure 1. The source of the bibliographic search was SCOPUS [35], using as search terms “multi-objective job shop scheduling”, without any type of limitation. The search query using these terms returned a total of 772 results, over which a first filter was applied: duplicated works were removed, as well as those contributions that did not relate at all to industrial and/or manufacturing processes. Likewise, works that were not peer-reviewed were excluded from the search results, so as to retain only journal articles and conference papers. This first filtering exercise reduced the amount of returned documents to 420 results.

A second filter selected those papers that had terms such as job, shop, job shop, flow shop, job-shop, and industry-focused and with at least two objectives, one of them focused on energy. After this filtering, we were left with 61 references.

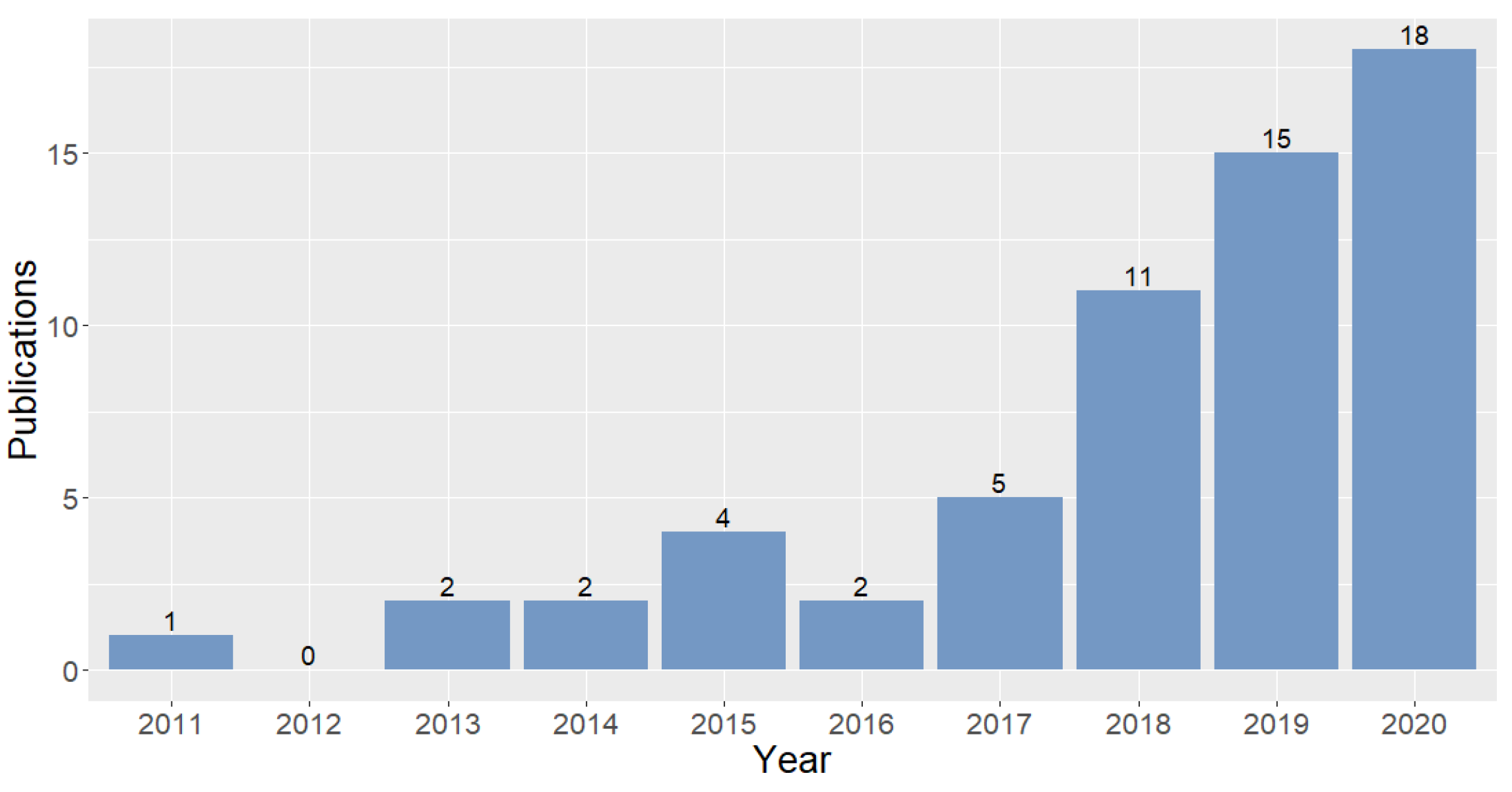
Figure 2 shows the number of papers published per year until 2020. We can observe an almost linear growth since 2017, indicating that the field of multi-target JSPs considering energy has been gaining momentum in recent years. This suggests the need for a reflexive compendium of the research activity reported in these studies, which is the motivation of the literature analysis presented in the subsections following hereafter.

3.2. Taxonomies and Literature Analysis

Once the search and filtering of papers produced a list of the most relevant works, we proceeded to analyze them. To do so, we defined three taxonomies that covered different aspects that deserve to be studied:

• Problem features: type of problem, number of objectives, the energy objective, and secondary objectives;
• Constraints and other considerations that have been taken into account in the analyzed works;
• Multi-objective optimizer, including the algorithm in use, compared algorithms, and values of the main parameters.

The three taxonomies are described in detail and analyzed next.

3.2.1. Taxonomy 1: Problem Features

From the point of view of the features of the problem, four taxonomic features of interest were considered: (1) number of objectives; (2) energy objective; (3) secondary objectives; (4) the type of JSP formulation. The classification of the works according to these taxonomy criteria [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94] is shown in Figure 3.

We started our analysis of the literature through this first taxonomy by analyzing the first of the problem features: the number of objectives. This feature is about the formulation of the optimization problem in terms of the number of objectives. The higher this number is, the more complex the problem can be thought of to be, as the search space grows (the curse of dimensionality) and decision-making becomes harder to handcraft in practice. We can observe in Figure 3 that 75.44% of the reviewed references considered two objectives, more than 22% had the objectives, and only one paper focused on a problem with more than three objectives. As will be later discussed, this predominance of references with two or three references aligns with the characteristics of real-world problems, in which we rarely find JSPs that are governed by more than three conflicting objectives.

We now turn the focus of the analysis to the specific energy objective defined in the formulated JSP. Indeed, the generic objective of reducing energy consumption can be defined by means of different indicators. We considered four criteria: energy consumption, electric power costs, non-processing energy, and idle energy. Based on this criteria, we found that 81.97% of the analyzed works were based on the consumption point of view, expressed in kWh. By contrast, 11.48% of the contributions referred to the cost of energy consumption, which does not necessarily have to be the same as consumption due to the different energy policies applied in each region, such as, for example, hourly discrimination. In this sense, an algorithm could find, for example, that it is better to produce at night at high rates, consequently increasing the energy consumption, but with a low impact on the energy cost, as opposed to producing at lower speeds in the evening (higher consumption, lower cost). The consumption of energy not used in production and the energy consumed in machine waiting times were taken into account in 4.92% and 1.6% of the reviewed literature works, respectively.

Therefore, less than 10% of the works under analysis studied the idle energy consumption when the machine is on standby. As the reduction of the makespan is directly affected by the waiting times, the consumption of machines during waiting times can be of great importance, e.g., in a steel or smelting furnace, where energy consumption during the standby of production assets is critical. Ignoring this part of the behavior can be a great waste of energy.

Since the survey addressed works dealing with multi-objective formulations of the JSP where energy consumption is minimized jointly with other secondary objectives, we continued our examination of the first taxonomy by evaluating which other objectives not related to energy have been in use. The secondary objective that appeared most frequently was, as expected (as the research has been performed in industrial environments), makespan, with 70.5% of the reviewed articles. This objective gauges the total amount of time that is necessary to produce and complete a set of scheduled jobs (production commit). The lower the makespan is, the more production efficient or the higher the production capacity of a plant is. Therefore, makespan is an objective to be minimized. This objective can conflict with the energy objective, since a shorter production time may require higher production speeds or the use of more machines, thereby consuming more energy. This is the most addressed case, although it is possible to find a global optimum that guarantees the minimum makespan and the minimum energy, wherever waiting times between operations are the only aspect of the plant that allows energy to be minimized. However, this is not generally the norm, paving the way for the adoption of multi-objective optimization solvers.

The next most important secondary objective is the total tardiness, which was accounted for in 14.76% of the works organized in the taxonomy. Total tardiness refers to the delay time and is critical for production, as it can incur serious production cost overruns due to late deliveries. This objective is related to the makespan, and if we consider both together, around 90% of the papers included production efficiency in one form or another as a secondary objective. The total workload appeared as the next-most-addressed secondary objective, appearing in 4.92% of the jobs. Finally, the remaining 22.96% included other key performance metrics not necessarily related to production efficiency, such as noise, worker costs, and product quality (among others), which have less impact on production when searching for an optimal scheduling plan.

We end the analysis of our first proposed taxonomy by pausing on the type of JSP formulated in every work. In most contributions, the authors defined each use case by mapping it to a specific type of problem. Although all of them were related to JSP problems, in many cases, they showed problem types that were too specific to be generalized to other practical use cases. This implies that many reported cases described by the authors are only applicable under the conditions of the particular setup they considered in their work. This could be observed in 57.38% of the papers reviewed, in which the type of problem was unique for that study and defined under acronyms that do not provide any relevant information to the reader. The next largest group referred to the flexible JSP (FJSP), which was described in 21.32% of the contributions. Similarly, 16.40% of the cases referred to the hybrid flow shop scheduling problem (HFSP), whereas 4.92% were about a naive JSP problem, without any further formulation specifics whatsoever.

3.2.2. Taxonomy 2: Constraints and Considerations

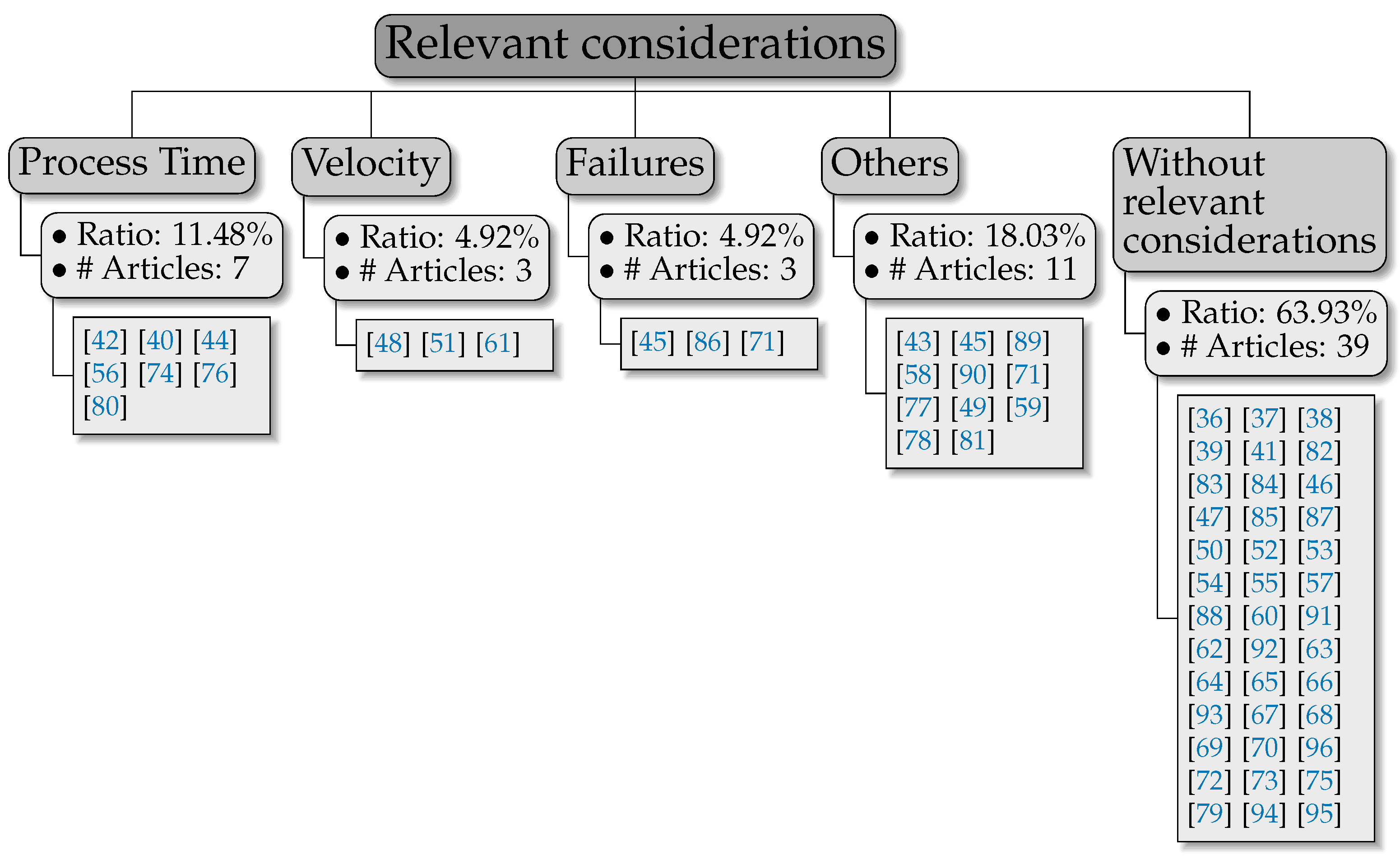
We continued our examination of the literature by analyzing contributions through the lenses of the constraints and practical aspects considered in the underlying MOP, beyond the objectives themselves. The variability of constraints and aspects is high, so it is difficult to arrange them in a coherent fashion. Nevertheless, several patterns and trends [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95] were identified, which are shown in Figure 4 and discussed in the rest of this subsection.

To begin with, most of the reviewed papers considered similar constraints that are posed to tell when a good solution as per the objectives defined for the JSP at hand is feasible. These constraints that are in common over most studied literature include:

• A job can only be assigned to one machine;
• The number of jobs assigned to a machine cannot exceed the net production capacity of the machine;
• The processing time of a batch is equal to the longest time of the jobs on the machine;
• A job cannot start before the previous job is finished on the machine;
• No machine can do more than one job at a time;
• Each operator can only operate one machine at a time;
• Jobs are independent of each other.

However, there are other constraints and considerations that pose a difference in the way in which the authors approached the problem. In this way, some works assumed overly idealistic production environments, inserting several constraints that can be considered far from being realistic. These are shown in Figure 4 include:

• Machines are always available from the start: this first assumption does not hold in many practical circumstances, because not always are all machine available in real environments. This may occur for a manifold of reasons. For example, a machine can be broken, under maintenance, or can be blocked to produce only one type of unit. Surprisingly, all the reviewed papers assumed this start point;
• Once a job is started at a machine, the job cannot be stopped: this second assumption is not always possible either due to breakdowns, production priorities arising during the production cycle, and other assorted reasons. Therefore, in some cases (especially when there are many sub-processes flowing inside the same machine), the production of a unit has to be stopped and does not necessarily resume in the same unit. Possible issues derived from these circumstances during the manufacturing process were considered in [71];
• Each operation should begin immediately after the previous one has been completed: this third assumption is not always the best practice due to production bottlenecks: if a machine has a cycle time higher than other assets, it is a good practice to start the next/previous machine before the other ends. All the papers reviewed made this assumption;
• The production buffer between machines is unlimited: this assumption may hold sometimes, but it is not always true. Now that lean manufacturing is becoming a revolution in factories and that one of its pillars is based on producing only what is indispensable by reducing the length of the batches, assuming unlimited buffers will violate this principle [43];
• Transportation time within the plant and production chain is negligible: this is not always feasible, as the time needed to transport from one part to another one of the productive process can be even higher than that of the productive process itself. Lean manufacturing strives to reduce waste, so improving the product routing inside the factory is important. This constraint will be opposite the route and transport optimization, and its influence in the makespan is mostly considered as negligible. Nevertheless, some works have stepped aside this trend and considered this aspect in the problem formulation [55];
• The change time is negligible: this sixth constraint can be mainly assumed in the production of large batches, but currently, most factories are required to manufacture small batches of products. This entails that tooling changes happen more frequently, so their aggregate impact on production makespans can no longer be neglected [53,55,56,57].

Another important aspect that is not always taken into account is the impact on energy consumption of idle and standby time. Idle time is a period of time in which an asset (machine or employee) is ready and available, but is not doing anything productive. Standby time is the time during which a part of the process is waiting for a previous operation to finish. The energy consumption of these states of industrial assets is relevant and has been considered in several works [40,42,44,56,74,76,80].

Finally, we pause on an important and relevant root cause of energy consumption: the processing velocity of machines endowed with the capability to produce at different rates. Higher production speeds usually imply a higher energy consumption. Since this capacity of machines is specific to the industrial sector and type of product, only a few works have paid attention to this matter [48,51,61].

3.2.3. Taxonomy 3: Multi-Objective Optimizer

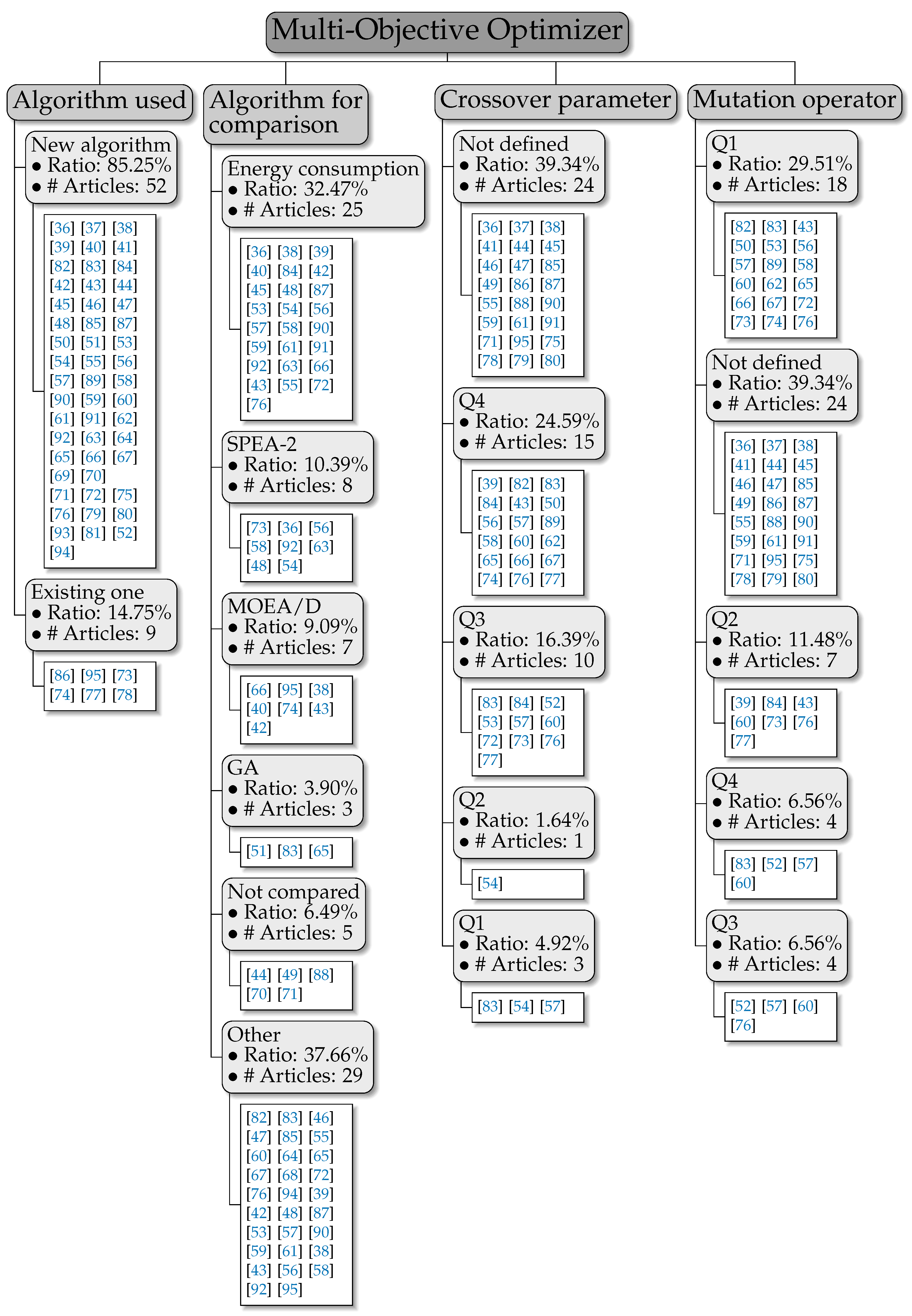
The analysis of the literature arrives at the third criterion followed to perform optimization in a principled manner: the algorithmic procedure by which every JSP under consideration has been optimized. In this regard, we used four criteria [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95] to orchestrate the literature in the taxonomy shown in Figure 5: (1) specific algorithm utilized; (2) the algorithm(s) to which the proposal has been compared; (3) crossover parameters; (4) mutation parameters. In what follows, we discuss the general design and methodological patterns stemming from this third systematic analysis.

We begin the discussion by considering the specific multi-objective algorithm used in every contribution. This classification is focused on the multi-objective algorithm used to optimize the problem. A priori, here, we expected to find widely known multi-objective evolutionary algorithms, such as NSGA-II, MOEA/D, or SPEA-2. However, after carrying out the review, most of the papers analyzed referred to new optimization techniques that attempt to improve the performance of the aforementioned algorithms. This is why this feature does not account for the specific algorithm in use, but rather ascertains whether a new algorithm has been developed for the study or not. Surprisingly, we found that 88.5% of the articles included in the review developed new algorithms or improvements of existing ones, whereas only in 9.8% of the cases, no new algorithm was proposed. This fact links to one of the critical points elaborated later in Section 3.3.

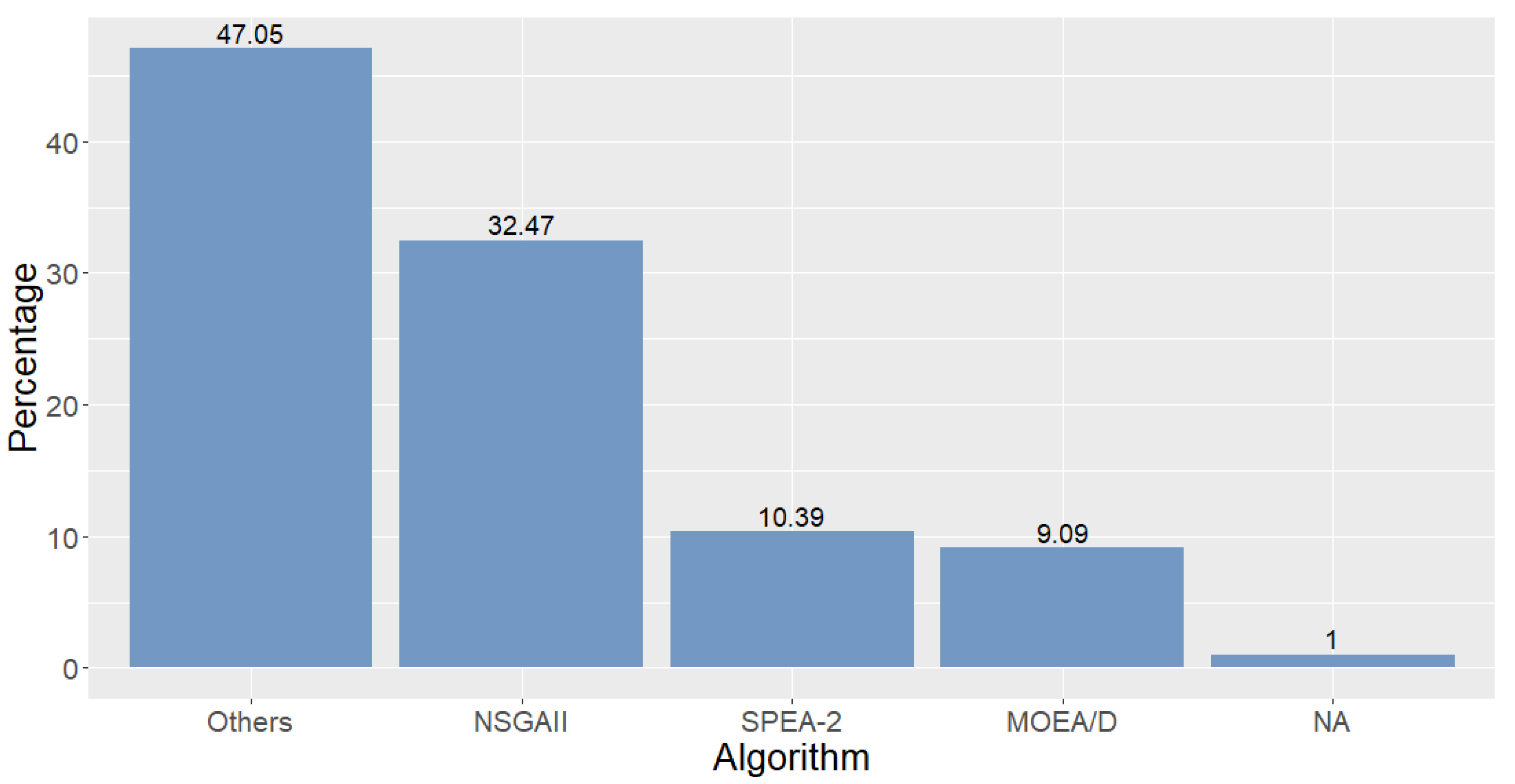
We turn the scope of the discussion to the algorithm for comparison included in benchmarks. For this criterion, we considered those techniques that the authors of every contribution used to compare their performance to that elicited by their own proposed algorithms. As expected, NSGA-II prevailed in the area as a comparison counterpart, with 32.47% of the papers featuring it in their benchmarks. This multi-objective evolutionary algorithm is followed by SPEA-2, which was used in 10.39% of the cases. MOEA/D, another popular multi-objective evolutionary algorithm, appeared in 9.09% of the analyzed literature, while the remainder included comparisons with other algorithms such as NSGA-III, MOGWO, SPEAR, etc.

Another fact to take into account in this category is that commercial software for optimization such as CPLEX is quite frequently employed in this area. This statement is buttressed by Figure 6, where we can observe that the three aforementioned algorithms predominated over the rest.

Table 2. Algorithms found in the analyzed papers.

Year	Reference	Algorithm Used	Initial Algorithm	Algorithms Used for Comparisons
2011	[94]	SPNE	Dynamic game theory	AL+CGA; PSO+TS; HSISAT
2013	[36]	MOACO	ACO	NSGA-II; SPEA-2
	[70]	IGSAA	SA	-
2014	[82]	BVNSGA-II	NSGA-II	-
	[86]	NSGA-II	NSGA-II	-
2015	[41]	SAA	GA	-
	[69]	Continuous-time MILP	-	-
	[67]	GD-MOCDE	MOCDE, Gradient descent (DC),	MODE;
	[68]	ABC	ABC	IGAMU; CSO; SAGA
2016	[37]	MILMO	-	-
	[39]	GAEJP	NSGA-II	NSGA-II; LEKING
2017	[84]	MOGA	Simplex lattice design	NSGA-II;
	[89]	GA-based	GA	-
	[66]	HMOBSA	MOEAs	NSGA-II; MOEA/D;
	[89]	Enhanced GA	Standard GA	-
	[94]	SPNE	DGT	AL+CGA; PSO+TS; HSISAT
2018	[38]	EA-MOA	-	NSGA-II; MOEA/D; DBEA; EADD
	[44]	IGALL	IG	-
	[46]	SFLA	SFLA	BVNSGA-II
	[50]	MCEAs	-	NSGA;
	[57]	Multi-objective DE	-	NSGA-II; AMGA
	[88]	Bee Colony	Artificial bee colony (ABC)	-
	[92]	HMOGWO	GWO; GA	NSGA-II; SPEA2; MOGWO; MOGWO1; MOGWO2
	[63]	TEPSO	PSO; TABOO	NSGA-II; SPEA2
	[64]	NBI	Normal boundary intersection	-
	[65]	TTLBO	-	IGSA; GA
	[95]	NSGA-III	NSGA-III	NSGA-III-NIG; EFR-RR; crEA
2019	[40]	MOBSO	Basic BSO	NSGA-II; MOEA/D
	[42]	MDABC	MOEA	NSGAII; EAMOA; CMFOA; MOEA/D; iMOEA/D
	[43]	EOMO	(MOEA/D).	SPGA-II; NSGA-II; MOEA/D
	[45]	MOHPIOSA	PIO	NSGA-II
	[85]	IMOMVO		MOMVO; MOPSO; MOALO; NSGA-II
	[71]	MOGSA	MOGA	-
	[93]	DCRO	CRO	-
	[56]	MOCGWO	MOG	NSGA-II; NSGA-II + NDM; SPEA2; SPEA2 + NDM; MOCGWO
	[55]	iMOEA/D	MOEA/d	HMOBSA; NSGA-II
	[56]	MOCGWO	GWO and CA	NSGA-II; SPEA2; MOCGWO
	[58]	MOWSA	Whale swarm algorithm	NSGA-II; SPEA2; PAES
	[61]	COA		NSGA-II; IMEA/D
	[91]	ILS	ILS	NSGA-II
	[54]	New MOGA	MOGA	-
	[80]	MOGA-LS	ILS; VILS	-
2020	[83]	PH-MOEAD	MOEAD	EMBO; GA; GAR; DPSO; DABC
	[47]	DEMO	-	MODWWO; MPVNS; MOMBO
	[48]	MHACO	-	NSGA-II; MODEA; SPEA-II
	[49]	CPLEX (not provided)	-	-
	[87]	EMA		NSGA-II; NNIA; NSGA-III
	[51]	EDA		GA
	[52]	Own algorithm	-	-
	[53]	2-echelon iMOEA/D	MOEA/D	NSGA-II; MOGLS
	[90]	HEA	-	NSGA-II; NNIA
	[59]	iIMOALO	ALO	NSGA-II; MOPSO
	[60]	NMA	MA	MA
	[73]	NSGA-II	NSGA-II	SPEA2
	[74]	NSGA-II	NSGA-II	-
	[75]	EE-VBIH; EE-IG; IG-ALL
	[76]	MDSS-MOGA-DE		MOABC; MOACO; MOCS
	[77]	NSGA-II; SPEA-2	NSGA-II; SPEA-II	NSGA-II; SPEA-2
	[78]	NSGA-II	NSGA-II
	[81]	PSO_SWS; PSO_LWR	PSO	PSO_SWS; PSO_LWR; PSO
2021	[72]	HPSO	PSO i	NSGA-II; HPSO-LS

provides a complete list, ordered by publication year, of the algorithms used, the algorithm taken as a starting point to develop the newly proposed approach, and the algorithms against which it was compared. We can clearly observe that most of the papers focused their efforts on developing their own algorithm. It is also worth noting that none of the newly developed metaheuristics over the years makes a comparison with previously defined solvers in the table. This indicates that research works reported in this area mainly attempted beating generic algorithms (e.g., NSGA-II, ILS, MOGA) and did not include in the comparison algorithms specifically designed to solve JSP instances.

Since most of the metaheuristics used to solve multi-objective formulations of the JSP are genetic algorithms (i.e., evolutionary algorithms using crossover and mutation operators in the variation step), we now analyze the crossover operators in use and, in particular, the value of the crossover probability parameter (see again Figure 5). In the experimental phase, the authors of the papers carried out different experiments varying the crossover and mutation values, so that in many cases, more than one value was provided for these operators. Therefore, we decided to group them by quartiles, with the first quartile Q1 being the probability of crossover set between [0, 0.25), Q2 between [0.25, 0.5), Q3 between [0.5, 0.75), and Q4 between [0.75 and 1].

The crossover operator was not always given, sometimes because the algorithm does not make any use of it (as in, e.g., PSO-based proposals). However, when used, there were a high number of papers that did not provide detailed information: in 39.34% of cases, the crossover operator was not specified; in 24.59% of the cases, the crossover probability was high, belonging to Q4; in 16.39% of the cases, the crossover parameters were in the third quartile; 1.6% and 4.92% had crossover probabilities belonging to the second quartile and the first quartile, respectively.

It is remarkable that a large number of papers did not provide the crossover parameter settings, so they cannot be reproduced in new studies. This practice detracts from the scientific value of the publications because the statements and findings cannot be validated by the community. A well-conducted study should transparently inform about the operators and algorithms in use, so that interested researchers can replicate and advance the general knowledge in the field. Moreover, it is striking that this type of information did not appear when, in many cases, the studied problem was synthetic and there was no commitment to confidentiality. Apart from that, the probability values used more were the higher ones (i.e., in the Q4 range), as expected.

We end the analysis of the literature through the third taxonomy by assessing the mutation operator adopted by the selected contributions. To analyze the mutation operator, we defined, as in the crossover operator, quartiles, with the first quartile Q1 being the probability of mutation set between [0, 0.25), Q2 between [0.25, 0.5), Q3 between [0.5, 0.75), and Q4 between [0.75 and 1]. In general, the mutation probabilities were low, as can be told from the most-used quartile for this parameter (34.2% in the first quartile and 15.8% in the second one). Similar to the crossover, a significant fraction of the papers (39.34%) did not clearly indicate the mutation parameters chosen for the experimental part of the study, which aggravates even further the reproducibility problems exposed previously.

3.3. Summary of Critical Points Identified in the Literature Analysis

Now that the literature falling in the intersection between energy-aware production scheduling and multi-objective metaheuristics has been described, we now summarize the main observations that emerged from the critical analysis of such works. Before proceeding further, we claim that with this critique, we did not aim to discourage the readership from performing research at these crossroads, but rather (1) to underscore realistic aspects and assumptions that are tightly coupled to real-world settings, (2) to pinpoint poor practices that should be avoided in prospective studies, and (3) to call for research efforts in directions of inherent value for the field. Such observations are exposed in what follows:

• The first taxonomy given in Section 3.2.1 uncovered that most JSPs solved in the analyzed literature corpus addressed two or three objectives. This conforms to real-world settings, where production scheduling is often driven by a few key performance indicators. Nevertheless, we emphasize that the potential of multi-objective meta-heuristics to seamlessly cope with problems comprising several objectives should be propelled by a real-world need for taking them into consideration. In this regard, most cases reported in the literature posed sophisticated mathematical problem statements without giving an explicit rationale connecting the problem statement itself to real-world circumstances, KPIs, and constraints. This not only hinders the generalization of the studies, but also questions whether the research is truly motivated by real-world problems.
• The formulation of the JSP is based mainly on energy consumption and makespan. This is not an issue, but rather a consequence of the fact that in most practical settings, scheduling in industrial plants is governed mainly by production efficiency, i.e., the production of as much product as possible. The relatively low number of scientific works related to energy-aware production scheduling (slightly above 60 references) is also symptomatic of the fact that it has not been until recently when energy efficiency has become a concerning issue in real-world industries. Several reasons for this growing concern can be speculated around the sharply increasing energy costs, particularly noticeable in certain countries [96]. This fact is encouraging and should catalyze efforts brought to the area surveyed in this work;
• On the negative side, and repeating previous claims, we encountered that most types of JSPs tackled in the analyzed studies were largely specific for the use case under target in the paper, leading to a loose generalization of the results to new real-world setups. Again, this should not be considered an issue if the work at hand confined the conclusions of its experiments to the JSP variant under consideration. However, this was not the case in a subset of the references examined, wherein the novelty of the JSP problem was entangled with the proposal of a novel metaheuristic algorithm without any solid reason. This echoes the longstanding controversy about the role of the metaphor in the design of nature-inspired metaheuristics. We also noted this practice in several works resorting to new biologically inspired solvers over ad hoc JSP formulations, avoiding (1) the inclusion of well-established multi-objective algorithms in the comparisons and (2) the reproducibility of the results of the benchmark leading to the claims about the performance of the new solver. Principled and thorough performance studies should be performed in prospective works to clarify whether the performance of such solvers corresponds to a truly better search capability of their bio-inspired operators;
• When it comes to the realism of the formulated problem, very few papers took into account aspects that are prevalent across the production plants of a diversity of industries, such as waiting times, maintenance cycles, machine downtimes, and other aspects that impact the overall computation of the makespan. The intensity by which the makespan can be affected by not considering these aspects is subject to the use case under consideration. However, the growing capability of modern manufacturing execution systems (MESs) to integrate and handle all sources of information related to the production process should entail more realistic JSP formulations, showing that the makespan computation and the set of imposed constraints can harness the availability of external sources of information. Furthermore, new opportunities for dynamic production scheduling could arise, depending on the rate at which information is updated in the MES;
• Performance comparisons between algorithms should be made incremental. When new algorithms are proposed, they should be evaluated over synthetic JSP instances (i.e., leaving aside conditions/constraints imposed by real settings), so that advances can be validated by the community and improved upon. Our literature analysis revealed that reproducing an article dealing with a real-world scenario with a JSP at its core is hard to achieve. Key information is not provided (in some cases, due to confidentiality clauses), and source codes are not made available. Therefore, one can easily question whether new algorithms are developed ex professo for the use case under analysis, showing off a superior performance over a very scarcely comparableJSP. This could be the reason why Table 2 evinces that almost no multi-objective algorithm that falls out of the metaheuristic mainstream was used in studies published after it was first presented. We definitely envision that the community should report a fair and methodologically principled performance comparison between well-known algorithms over diverse, yet synthetically generated energy-aware JSP problem instances. This study could inform whether there is any value in the set of modern metaheuristic approaches that lie within the boundaries of the aforementioned controversy. Most importantly, by including customized/memetic/hybrid algorithm in the benchmark, such a study would evince whether the customization of metaheuristic algorithms provides any further value beyond solving better specific formulations of the energy-aware JSP.

Emboldened by the deficiencies discussed above, we complement the literature analysis conducted in this section with a rigorous experimental study, following the methodology that is commonly used in comparative studies of multi-objective metaheuristics when applied to a particular set of problems. The study not only included the use of quality indicators and statistical test to assess whether the differences of the results provided by the algorithms are significant or not; to foster its reproducibility, we provide also the source codes of the algorithms and the problems, which will be included in jMetal [97], a Java-based framework for multi-objective optimization with metaheuristics, which is widely used in the field, thus ensuring that they are available to the community.

4. Experimental Study

As commented in the closing paragraph of the previous section, we carried out an experimental study to solve instances of a multi-objective formulation of the JSP, which considers energy and makespan as the objectives to be simultaneously minimized. As our purpose here was to illustrate how a comparative study should be conducted, we were not interested in proposing a new algorithm. Instead, our overarching goal was to assess the performance of three multi-objective metaheuristic solvers that are representative of the state-of-the-art and compare them with established methodological tools. To ensure reproducibility, all source code producing the results reported in this section and the energy-aware JSP instances in use are available at: https://github.com/jMetal/JSP (accessed on 22 December 2021).

4.1. Problem Statement

One of the conclusions of the analysis of the taxonomies is that the problems were mainly focused on two objectives: from the energy point of view, energy consumption was a priority, and from the operational point of view, makespan was key. Therefore, we propose to solve a bi-objective problem that tries to find the optimal solution for these two objectives. Makespan is the total time needed to achieve the production needs, so it can be calculated as the elapsed time between the beginning and the end of the production process. Energy can be considered as the energy consumption of the machines that are needed to achieve the production plan. In this case, we took into account the times and consumption of the machines, the times and consumption of starting and stopping the machines, and their speed. Makespan is expressed in units of time and energy in units of energy.

We generated a number of JSP instances based on existing ones [17], but they were enriched with information related to energy. The data defining a given JSP instance were stored in a file with the following format (the numbers are example values):

5 3

0 19 9 33 ...

9 11 10 22 ...

...

The first row indicates the number of jobs and the number of machines (5 and 3 in the example), and the next ones contain pairs including the machine and time needed to execute that part of the job. In this case, for example, the first job runs on 0 machines during 19 units of time. As mentioned above, we enriched these data with extra information about energy, taking into account time stops, idle times, and machine velocities. To this end, new fields associated with energy were included:

• Energy consumption per time unit:

  –

  machineWorkingEnergy: Total energy consumption by unit time while a machine is working;

  –

  machineIdleEnergy: Total energy consumption by time unit while a machine is in the idle state;

  –

  machineWorkingToStopEnergy: Total energy consumption by time unit while a machine stops from working;

  –

  machineWorkingToIdleEnergy: Total energy consumption by time unit while a machine changes from working to the idle state;

• Machine velocity variables:

  –

  numberOfVelocities: Array of the velocities that a machine can have;

• Velocity energy penalization:

  –

  velocityPenalty: Energy consumption penalization by different velocities;

• Unit time variables:

  –

  machineTimeToIdle: Units of time that a machine needs to change from the idle state to start or from start to idle;

  –

  machineTimeToStop: Units of time that a machine needs to change from the working state to stop or vice versa.

With these new variables, we can define how much energy and time will be consumed by a machine for a given job that runs in x number of time units. It is worth noting that the user can configure different machine speeds and machine waiting times, allowing making decisions such as leaving a machine in the idle state until the next operation or turning it off and starting it again, depending on the energy consumption.

With all the considerations described above, we used these JSP instances:

• la04 [98], 5 machines and 10 jobs;
• la10 [98], 5 machines and 15 jobs;
• ft06 [99], 6 machines and 6 jobs;
• orb01 [98], 10 machines and 10 jobs;
• abz5 [100], 10 machines and 10 jobs;
• swv20 [101], 10 machines and 50 jobs;
• ta12 [102], 15 machines and 20 jobs;
• dmu11 [103], 15 machines and 30 jobs;
• yn03 [104], 20 machines and 20 jobs;
• dmu40 [103], 20 machines and 50 jobs;
• ta77 [17], 20 machines and 100 jobs.

The criterion to select these problem instances was to cover at least one dataset of each publications that has appeared in the analyzed literature, but trying to choose a sufficient variety of instances, regarding the number of machines and the number of jobs, with the gradual increase in the complexity of the problem, from lower to higher.

4.2. Benchmark and Comparison Methodology

To optimize a given multi-objective problem, it is necessary to implement it, which implies making decisions about the problem encoding (i.e., how the solutions are represented) and, in the case of deciding to use evolutionary algorithms to solve it, defining the variation operators (crossover and mutation; the plan was to use genetic algorithms). We implemented our JSP in jMetal [97], so we could make use of algorithms already existing in the framework.

In order to carry out a comparative study of the problem, we needed to select a representative set of instances and choose which algorithms would be used to try to find which one was the most promising one to solve the problem effectively. Once the algorithms were selected, their control parameters were set, paying attention that they were configured to ensure a fair comparison; thus, the size of the population, as well as the stopping condition must be the same.

The next step was to define the number of independent runs per configuration (i.e., pair <algorithm, problem instance>), the indicators to measure the quality of the obtained Pareto fronts applied, the statistical tests needed to analyze the results, and providing tables and figures to support the analysis.

4.2.1. Encoding Strategy

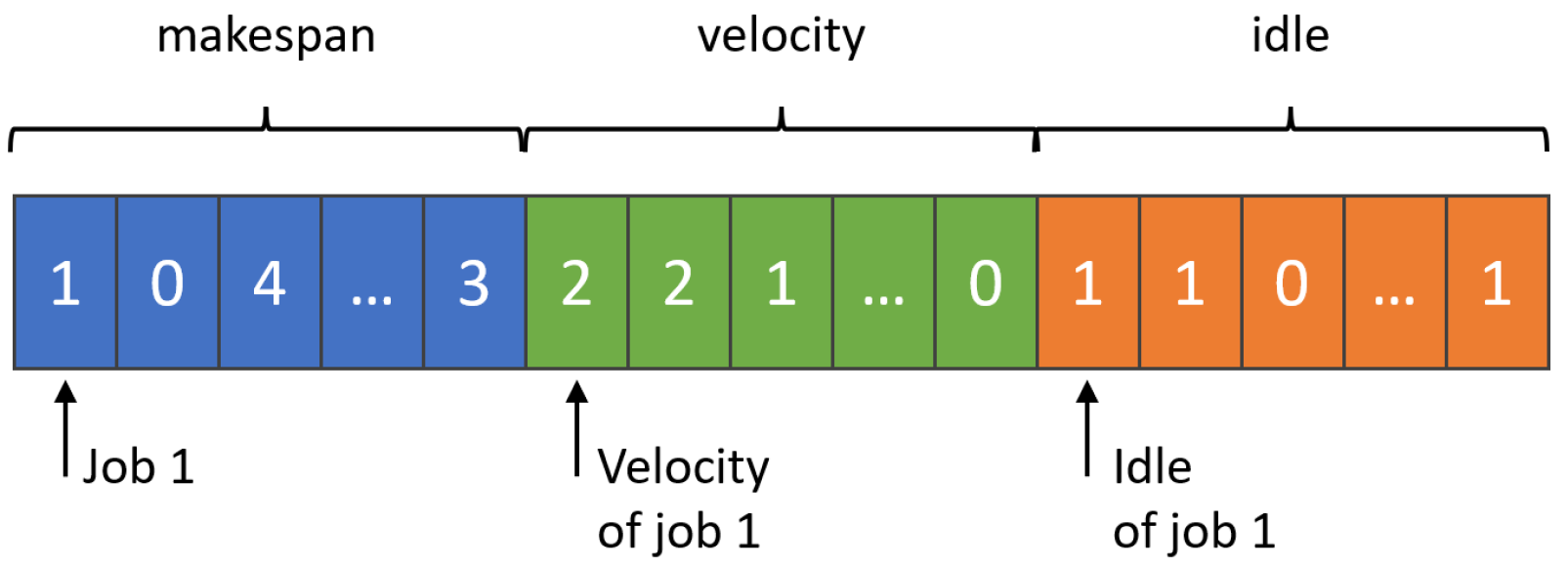
The encoding of the problem regarding the makespan was based on an array of integers of length equal to the number of jobs multiplied by the number of machines. To include the machine velocity per job execution, we added another array of the same length as the makespan one. Finally, a third array was used to include if the machine for a job must be stopped or remain idle. Therefore, the encoding of the problem was the union of these 3 arrays (makespan, velocity, and idle), with a length of three times the number of jobs per number of machines. The three arrays were initialized as follows:

• Makespan array: To fill this array, random integer numbers between one and the total number of available jobs were pushed to it, with the condition that a job number cannot appear more times than the total number of machines to which the the job has been assigned;
• Velocity array: This array contains random integer numbers between one and the number of available velocities;
• Idle array: The contents of this array are random binary numbers.

Figure 7 illustrates the solution encoding strategy adopted in our experiments for the sake of its better understanding by the reader.

4.2.2. Multi-Objective Algorithms

To perform this experimental study, we selected three well-known algorithms that are representative of the three categories of multi-objective evolutionary algorithms: NSGA-II [23] (Pareto-based), MOEA/D [24] (decomposition-based), and SMS-EMOA [25] (indicator-based). We remark that the purpose of this experimental study was to expose how to properly conduct it using representative techniques, not to try find the best algorithm, nor the most accurate configuration of the three we selected.

All of them were configured with a population size of 50 individuals and a stopping condition of computing 300,000 function evaluations. They shared the same crossover and mutation operators (see

Table 3. Summary of the operators and parameter values set in the multi-objective algorithms considered in our experiments.

NSGA-II			MOEA/D			SMS-EMOA
Parameter	Value		Parameter	Value		Parameter	Value
Selection	Binary tournament		Neighbor selection probability	0.9		Selection	Random
			Neighbor size	20
			Maximum number of replaced solutions	2
			Aggregation scheme	Tschebyscheff
Common Parameters:
Population size: 50 individuals
Number of function evaluations: $3\times {10}^5$
Crossover: 2-parent position exchange in uniformly selected array of the chromosome
Crossover probability: 0.9
Mutation: random exchange in uniformly selected array of the chromosome
Mutation probability: 1.0

below). MOEA/D was set with a neighbor selection probability of 0.9, a neighbor size of 20, a maximum number of replaced solutions of 2, and a Tschebyscheff aggregation scheme.

We implemented a crossover operator for integer encoding that works as follows: After selecting two parent solutions, an array of the solution (makespan, velocity, idle) is chosen randomly. After that, two random positions are selected again randomly, and they are interchanged between the two parents, leading to two children. The crossover probability was set to 90%.

The mutation operator works as follows: first, as in the crossover, a random selection is performed between one of the three arrays composing the encoded solution (makespan, velocity and idle); second, a random interchange position is performed between two positions. The mutation probability was set to 100% (i.e., we always applied the mutation operator).

Should the goal of the experimental study be the determination of which algorithm performs best for every problem instance, these parameter values should be tuned by resorting to any of the parameter tuning strategies known in the field of metaheuristics (e.g., Bayesian optimization, extensive search over a grid of values, and other similar techniques [105]). However, since the purpose of this experimental study was to exemplify how to develop a principled performance comparison conforming to standards and good practices, such parameters were left to their default values set in the reference implementation of every algorithm in jMetal. Table 3 summarizes the values of the parameters for every algorithm.

4.2.3. Constraints and Considerations

We applied no constraints to present a simplified model, but there are some considerations that must be taken into account:

• Machines can be in the idle state, with an associated idle energy consumption;
• Machines can be switched off, with power off and power on energy consumption considered;
• Machines can run at different velocities.

4.2.4. Solution Evaluation

Evaluating a solution means calculating its total makespan and energy consumption. As the makespan is the total time that elapses between the start and the end of all the jobs for a given machine, the total makespan will be the maximum of all the makespans of every machine. Energy consumption is the sum of all the unit times that the machines are running multiplied by the energy consumption per unit time, added to the idle energy consumption and the power on/off consumption. To calculate the unit times that a job needs to run in a machine, the velocity and the velocity energy consumption penalization were taken into account.

4.2.5. Quality Indicators

To measure the quality of the Pareto front approximation yielded by multi-objective metaheuristics, two aspects are usually taken into account: Minimizing the distance of the obtained front to the Pareto front of the problem (convergence) and maximizing the extension of solutions on the front so that the distribution is as uniform as possible (diversity). There are different ways to measure these properties, so quality indicators have been defined for that purpose. In our experimental study, we used the additive epsilon (EP) [106], the normalized hypervolume (NHV) [107], and the inverted generational distance plus (IGD+) [108]. The EP measures convergence, while the NHV and IGD+ give a measure of both convergence and diversity; in all of them, the lower the indicator value, the better it is. They are briefly described next:

• The EP is a measure of the absolute deviation needed to translate each solution in a Pareto front approximation in such a way that it weakly dominates the front used as a reference (it can be the true Pareto front or a subset of it);
• The NHV is computed as 1.0 minus the ratio between the hypervolume of the front to be evaluated and the hypervolume of the reference front. The hypervolume metric calculates the volume (in the space of objectives) covered by members of a given set of non-dominated solutions with respect to a reference point;
• The IGD+ evaluates the convergence performance and the distribution performance of the algorithm by calculating the sum of the minimum distances between each point (individual) on the reference front and the front of solutions obtained by the algorithm.

Computing the quality indicators requires obtaining a reference front. As the Pareto front of the considered problems is unknown, we constructed, for each problem, a reference front by taking the non-dominated solutions of all the runs of all the algorithms per problem.

4.3. Results and Discussion

We report the median and interquartile range (IQR) of the indicator values corresponding to the 20 independent runs per configuration in

Table 4. EP median and interquartile range. Dark and light grey background cells highlight the best and second best results, respectively.

	SMSEMOA	NSGAII	MOEAD
la10	$2.34e-{01}_{2.2e-01}$	$1.68e-{01}_{7.1e-02}$	$9.01e-{01}_{1.6e-01}$
ft06	$3.00e-{01}_{0.0e+00}$	$3.00e-{01}_{0.0e+00}$	$1.20e+{00}_{5.0e-01}$
orb01	$3.38e-{01}_{3.5e-01}$	$2.32e-{01}_{9.9e-02}$	$1.15e+{00}_{4.1e-01}$
swv20	$7.26e-{01}_{4.1e-01}$	$4.83e-{01}_{4.2e-01}$	$7.09e-{01}_{8.5e-01}$
ta12	$1.59e-{01}_{7.2e-02}$	$1.02e-{01}_{8.0e-02}$	$3.79e-{01}_{1.8e-01}$
dmu11	$3.71e-{01}_{1.4e-01}$	$1.78e-{01}_{1.4e-01}$	$4.14e-{01}_{3.2e-01}$
yn03	$5.35e-{01}_{2.9e-01}$	$1.97e-{01}_{2.0e-01}$	$8.66e-{01}_{3.4e-01}$
dmu40	$9.59e+{00}_{7.1e+00}$	$5.85e+{00}_{3.6e+00}$	$6.97e+{00}_{8.5e+00}$
ta77	$2.64e+{01}_{9.4e+00}$	$2.23e+{01}_{7.7e+00}$	$1.93e+{00}_{1.4e+00}$

,

Table 5. NHV median and interquartile range. Dark and light grey background cells highlight the best and second best results, respectively.

	SMSEMOA	NSGAII	MOEAD
la10	$3.14e-{01}_{2.0e-01}$	$2.03e-{01}_{1.3e-01}$	$8.88e-{01}_{2.2e-01}$
ft06	$1.66e-{01}_{5.7e-02}$	$1.06e-{01}_{5.4e-02}$	$1.00e+{00}_{0.0e+00}$
orb01	$5.05e-{01}_{3.2e-01}$	$2.76e-{01}_{5.9e-02}$	$1.00e+{00}_{1.0e-01}$
swv20	$7.64e-{01}_{3.9e-01}$	$4.60e-{01}_{4.4e-01}$	$7.02e-{01}_{6.2e-01}$
ta12	$1.45e-{01}_{7.0e-02}$	$7.96e-{02}_{3.5e-02}$	$3.67e-{01}_{1.8e-01}$
dmu11	$3.79e-{01}_{1.4e-01}$	$1.41e-{01}_{1.8e-01}$	$4.03e-{01}_{3.2e-01}$
yn03	$5.21e-{01}_{3.9e-01}$	$1.62e-{01}_{2.1e-01}$	$8.62e-{01}_{3.2e-01}$
dmu40	$1.00e+{00}_{0.0e+00}$	$1.00e+{00}_{0.0e+00}$	$1.00e+{00}_{0.0e+00}$
ta77	$1.00e+{00}_{0.0e+00}$	$1.00e+{00}_{0.0e+00}$	$1.00e+{00}_{0.0e+00}$

and

Table 6. GD+ median and interquartile range. Dark and light grey background cells highlight the best and second best results, respectively.

	SMSEMOA	NSGAII	MOEAD
la10	$1.78e-{01}_{1.3e-01}$	$9.89e-{02}_{6.1e-02}$	$5.54e-{01}_{1.4e-01}$
ft06	$1.03e-{01}_{2.3e-02}$	$7.72e-{02}_{2.7e-02}$	$6.89e-{01}_{5.0e-01}$
orb01	$2.90e-{01}_{2.2e-01}$	$1.56e-{01}_{6.2e-02}$	$8.27e-{01}_{4.1e-01}$
swv20	$4.97e-{01}_{2.6e-01}$	$2.78e-{01}_{3.1e-01}$	$4.44e-{01}_{7.6e-01}$
ta12	$6.01e-{02}_{3.5e-02}$	$3.45e-{02}_{2.4e-02}$	$2.08e-{01}_{1.4e-01}$
dmu11	$2.82e-{01}_{1.1e-01}$	$1.02e-{01}_{1.2e-01}$	$3.01e-{01}_{2.5e-01}$
yn03	$2.71e-{01}_{3.2e-01}$	$6.61e-{02}_{1.3e-01}$	$5.54e-{01}_{3.2e-01}$
dmu40	$9.11e+{00}_{7.1e+00}$	$5.34e+{00}_{3.5e+00}$	$6.47e+{00}_{8.5e+00}$
ta77	$2.68e+{01}_{9.3e+00}$	$2.27e+{01}_{7.8e+00}$	$1.58e+{00}_{1.8e+00}$

. The best and second-best results are highlighted with a dark and light grey background, respectively. We applied the Wilkinson rank-sum test [109] (at a 5% level of significance) to determine whether the differences were statistically significant. The results of the test are shown in

Table 7. Wilcoxon rank-sum test results (quality indicator: EP).

	NSGAII									MOEAD
SMSEMOA	▽	–	▽	▽	–	▽	▽	▽	–	▲	▲	▲	–	▲	–	▲	–	▽
NSGAII										▲	▲	▲	▲	▲	▲	▲	–	▽

,

Table 8. Wilcoxon rank-sum test results (quality indicator: NHV).

	NSGAII									MOEAD
SMSEMOA	▽	▽	▽	▽	▽	▽	▽	–	–	▲	▲	▲	–	▲	–	▲	–	–
NSGAII										▲	▲	▲	–	▲	▲	▲	–	–

and

Table 9. Wilcoxon rank-sum test results (quality indicator: IGD+).

	NSGAII									MOEAD
SMSEMOA	▽	▽	▽	▽	–	▽	▽	▽	–	▲	▲	▲	–	▲	–	▲	–	▽
NSGAII										▲	▲	▲	–	▲	▲	▲	–	▽

. In each table, each symbol in the cells represent a problem instance, and there are different symbols: a dark up triangle means that the algorithm in the row performed better than the one in the column with confidence; a white down triangle stands for the opposite; a “-” symbol means that no significant differences were found.

From the results of the tables, we can observe that NSGA-II was the best-performing algorithm, achieving the lowest indicator values in most of the cases. According to the EP indicator (Table 4), which measures the diversity of the Pareto front approximations found by the solvers, NSGA-II achieved the best values in seven out of nine benchmark problems, while SMS-EMOA and MOEA/D yielded the fronts with the highest degree of convergence in one instance. The Wilcoxon rank-sum test (Table 7) showed that the differences between NSGA-II and SMS-EMOA and between NSGA-II and MOEA/D were statistically significant in six problems and eight problems, respectively.

The data reported in Table 5 show that NSGA-II obtained the lowest NHV values in seven instances. Here, we must note that values of 1.0 in the NHV indicator mean that the evaluated fronts were dominated by the reference point, and consequently, their HV was 0.0. This occurred, in particular, in all the algorithms when solving the dmu40 and ta77 problems. As these are the most complex JSP instances, it is clear that the algorithms would need more than 300,000 function evaluations as their stopping condition to find more accurate Pareto front approximations. The Wilcoxon rank-sum test (Table 8) confirmed that the differences in these two problems were not significant between the solvers in the comparison.

Finally, the results of the IGD+ quality indicator, included in Table 6, confirmed again the best performance of NSGA-II against the other two algorithms in the conducted study with statistical confidence in most of the cases (see Table 9). We can observe that MOEA/D achieved the best IGD+ value in instance ta77, so this algorithm performed the best, with confidence, when solving the most complex JSP instance; this is coherent with its EP values (see Table 4 and Table 7).

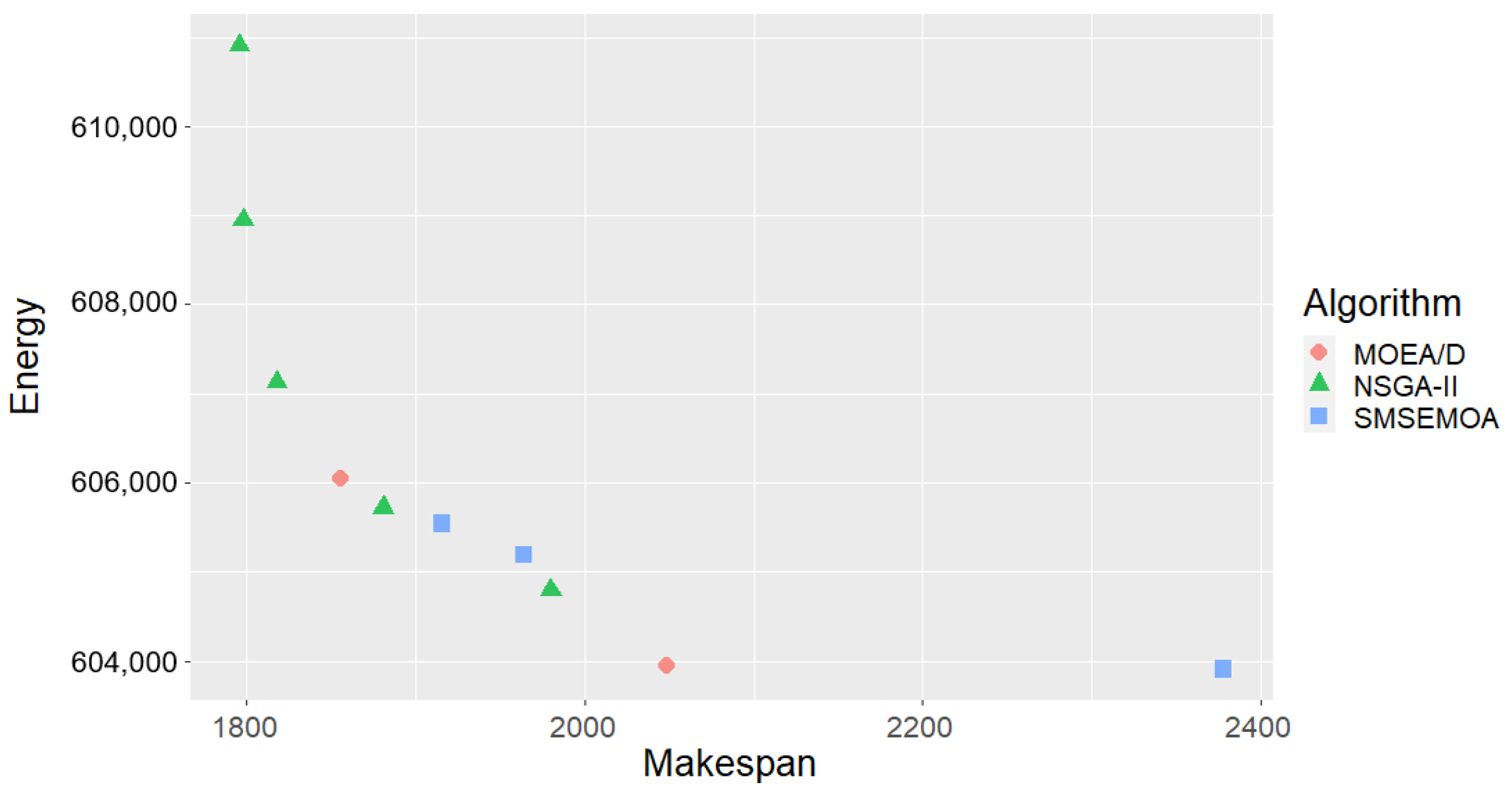
To illustrate the fronts that were obtained, we selected the ta12 instance, consisting of 15 machines and 20 jobs. The reference front is shown in Figure 8, where we used different symbols to represent the points contributed by each algorithm: triangles (NSGA-II), circles (MOEA/D), and squares (SMS-EMOA). It can be seen how the best energy solution was obtained by SMS-EMOA, while the best makespan solution corresponded to NSGA-II. This brings an interesting observation: the quality indicators revealed that NSGA-II obtained the best values, but in the particular case of ta12, if a decision maker is interested in the energy, then SMS-EMOA could be the best choice.

If we choose the extreme points of this reference front, we obtain a solution with the lowest energy consumption, but highest makespan and another one with the opposite. Figure 9 shows these two extreme solutions: the one with the best (minimum) energy consumption, above in the figure, with an energy of 603,908 units of energy and a makespan of 2378 units of time, and below the solution with 610,910 units of energy and a makespan of 1796 units of time.

Including machine velocity and idle/stop energy consumption to the usual makespan problems has a big impact in the makespan and the energy consumption. There is a trade-off between energy consumption and total production time that allows production plants to gain flexibility in choosing, depending on the production needs, which job scheduling plan must be applied.

5. Conclusions and Prospective

Multi-objective optimization with metaheuristics has become a hot research topic over the last decades, as it has been proven to be an easy and effective approach for solving real-world optimization problems. The survey carried out in this paper confirms this fact when applied to energy-aware JSP problems in manufacturing industries. Our main purpose was to provide the audience with a comprehensive review of relevant papers related to the application of multi-objective metaheuristics to such problems, as a useful source of information about the most salient studies in this area.

5.1. Summary of Critical Insights Drawn from the Literature Review

From the analyzed information, a summary of issues and best practices in the JSP problem was given. From the point of view of the type of problem, most of the papers reviewed described their own type of JSP problem, which in essence reduces to a particular variant of a more general type of JSP. This can create a problem because, as in the case of searching for a particular problem, it can be more complex to find other approaches because it does not fit the particularities of the cases presented. On the other hand, it is worth noting that the majority of the papers reviewed had two or at most three objectives, which is helpful for decision making (the selection of the solution in the estimated Pareto front). As for the non-energy objectives, the makespan was the main objective, which conforms to real-world evidence since the makespan—or any other measure of production efficiency—still remains as the primary concern for the manufacturing industry.

From the point of view of the constraints and considerations, some of them repeatedly appeared in the reviewed articles, such as the assumption that machines must be available at the beginning, the machine does not start the next job until it has finished the previous one, and the existence of infinite buffers. However, it is striking how considerations such as waiting times, machine speeds, or possible machine shutdowns have not been taken into account in the vast majority of the articles reviewed.

For the optimization features, the usually crossover and mutation operators were in the usual values: high probability of crossover and low for mutation. However, this information was not always provided, which jeopardizes the reproducibility of many of the studies. It is also surprising to notice that many authors opted to generate new algorithms to find solutions to the multi-objective problem for energy and makespan, but they omitted considerations of energy consumption in real environments such as those produced by waiting times. To test the performance of these algorithms, a benchmark was made against existing algorithms, where the best-known ones, such as NSGA-II, MOEA/D, SPEA-2, etc., were usually found. Furthermore, the authors focused their efforts on developing new algorithms that were not used again in studies contributed thereafter. This may be due to the low reproducibility that existed in the articles: undefined operators, source code not present in public repositories, etc.

5.2. Summary of Conclusions from the Experimental Results

The limitations observed in this study stimulated an experimental analysis of the classical JSP problem, which was augmented by taking into account the energy consumption during waiting times or machine shutdowns, as well as different machine speed configurations. After performing a study with nine augmented JSP instances and three types of algorithms (namely, NSGA-II, SMS-EMOA, MOEAD), we concluded that the best results were obtained by NSGA-II.A more thorough experimental study would require tuning the parameters of the algorithms under comparison. Nevertheless, an important conclusion can be drawn from the results obtained in our benchmark: the inclusion of machine velocity and idle/stop energy consumption data to the usual makespan minimization considered in naive JSP formulations may have a high impact on the schedule, costs, and sustainability of real-world manufacturing industries.

5.3. Research Directions and Perspectives

Several research directions were identified through the critical analysis of our reviewed literature. Among them, we highlight (1) the lack of rationale for the real-world applicability of certain energy-aware JSP formulations, (2) the impact of exogenous factors on the energy consumed during production (which could render solutions produced for the production scheduling of no practical use), and (3) the opportunities unleashed by manufacturing execution systems gathering information from several data sources over the plant.

More specifically, planned research efforts stimulated by this work will replicate this study over a wider number and diversity of energy-aware JSP instances, including a larger number of algorithms and searching for their optimal hyperparameter values. Furthermore, we aim to develop a methodology to translate the performance gaps observed among multi-objective metaheuristics to real-world KPIs. In many practical use cases requiring solving a JSP, there is no guarantee that the observed superior performance of a given algorithm in terms of multi-objective quality indicators translates directly to operational gains of real impact. Elaborating on this crucial aspect of the real-world application of metaheuristic algorithms [110] will be among our research priorities in the near future.