A Fuzzy Method for Joint Resource Allocation and Stable Pairing in D2D Communications
Abstract
:1. Introduction and Related Works
1.1. Pairing in D2D Communications
1.2. Fuzzy Mathematics
- ,
- ,
- .
- , (Lukasiewicz t-conorm);
- , (Maximum t-conorm);
- , (Probabilistic sum).
1.3. Contributions
- A joint resource allocation and pairing scenario in D2D communications is investigated. A number of D2D receivers are considered for the reuse of cellular network resources. For each D2D receiver, there exists a number of potential D2D transmitters, and a stable fuzzy pairing criteria is proposed for the selection of the best transmitter.
- The set of transmitters is considered as a fuzzy set in such a way that a fuzzy degree is assigned to each node, concerning the data rates and battery levels in connection with their potential receiver. We claim that this fuzzy membership function can be considered as a measure of the stability of the connections.
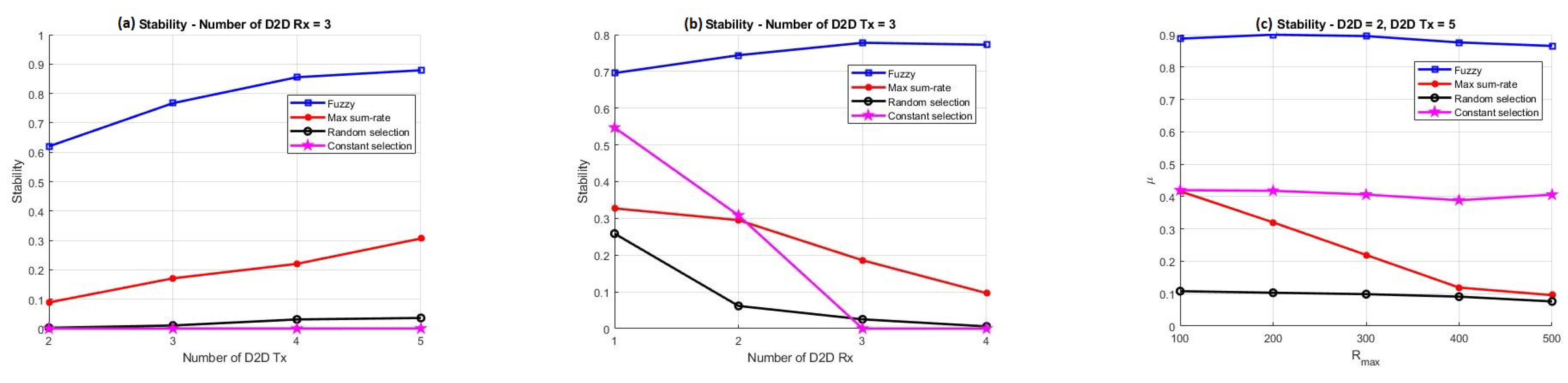
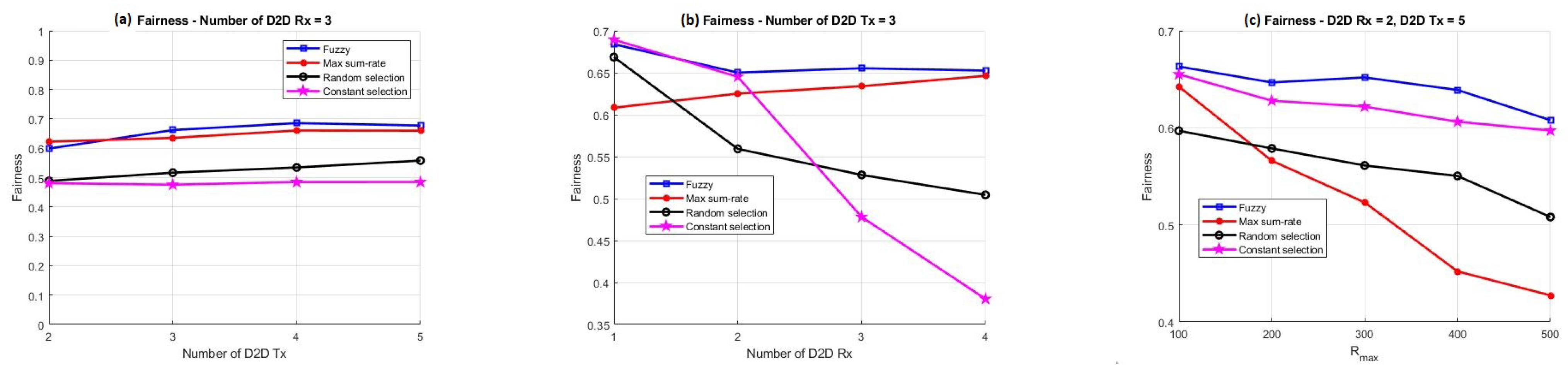
- To examine the proposed method, this method is compared with three other pairing methods, so that the three parameters of stability, fairness, and sum rate in different modes such as changing the D2D search radius and increasing the number of D2D transmitters and receivers for all four methods are investigated.
- The proposed method for D2D pairing, in addition to reducing the traffic load of the cellular network, leads to more stable connections with a higher quality of service. One of the significant applications of this method is that bulky content can be transferred more reliably.
2. System Model
2.1. Communication Models
- and are the direct channel and distance between the cellular user and evolved node base station (eNB), respectively.
- and are the channel and distance between the D2D transmitter and the D2D receiver , respectively where , , and .
- and are the interference channel and distance between the D2D transmitter and eNB, respectively.
- and are the interference channel and distance between the cellular user and D2D receiver , respectively.
2.2. Construing the Fuzzy Membership Function
3. Simulation Results
- Fuzzy-based pairing (FP) method;
- Max-sum-rate pairing (MSP) method;
- Random pairing (RP) method;
- Constant pairing (CP) method.
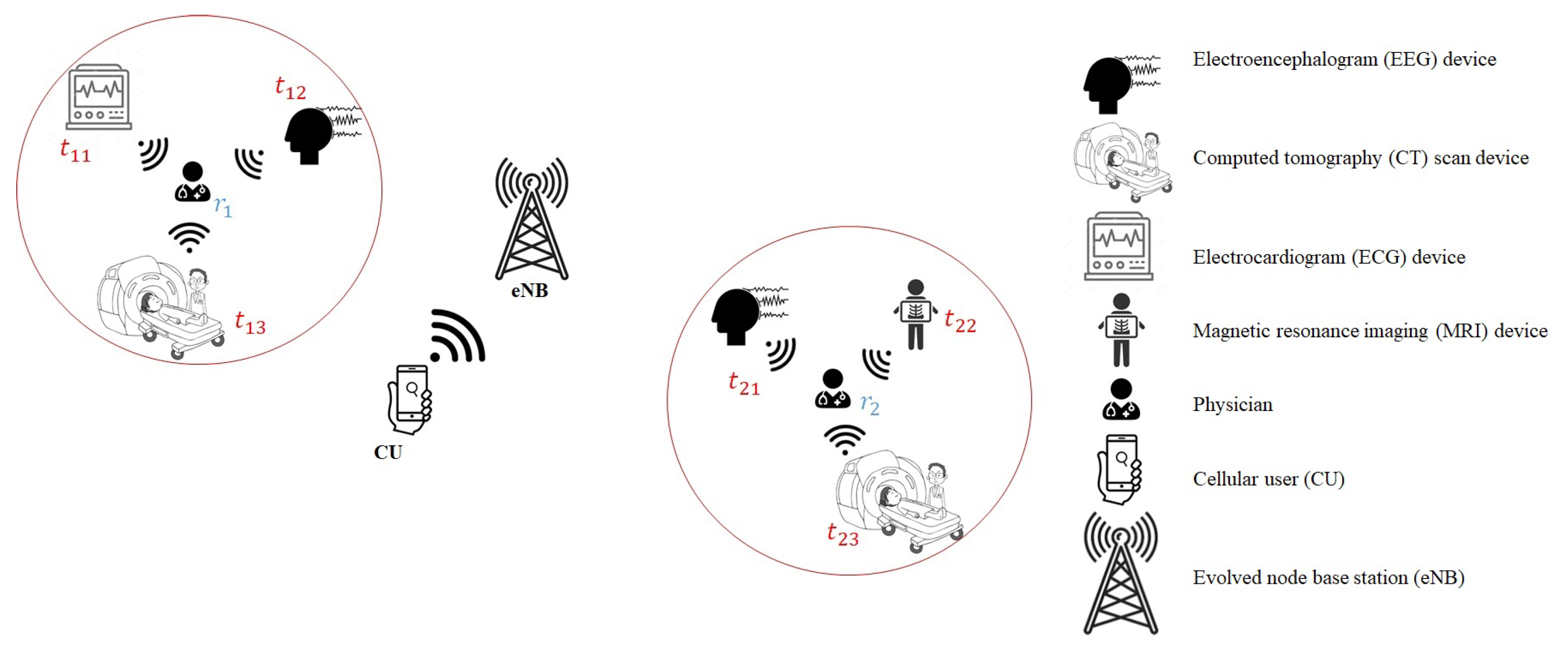
4. Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mach, P.; Becvar, Z.; Vanek, T. In-band device-to-device communication in OFDMA cellular networks: A survey and challenges. IEEE Commun. Surv. Tutor. 2015, 17, 1885–1922. [Google Scholar] [CrossRef]
- Jameel, F.; Hamid, Z.; Jabeen, F.; Zeadally, S.; Javed, M.A. A survey of device-to-device communications: Research issues and challenges. IEEE Commun. Surv. Tutor. 2018, 20, 2133–2168. [Google Scholar] [CrossRef]
- Wei, G.; Zhao, X. Induced hesitant interval-valued fuzzy Einstein aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2013, 24, 789–803. [Google Scholar] [CrossRef]
- Wang, L.; Wu, H. Fast pairing of device-to-device link underlay for spectrum sharing with cellular users. IEEE Commun. Lett. 2014, 18, 1803–1806. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, Y.; Pan, M.; Han, Z. Cheating in matching of device to device pairs in cellular networks. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014. [Google Scholar]
- Wang, L.; Stuber, G.L. Pairing for resource sharing in cellular device-to-device underlays. IEEE Netw. 2016, 30, 122–128. [Google Scholar] [CrossRef]
- Li, Y.; Song, C.; Jin, D.; Chen, S. A dynamic graph optimization framework for multihop device-to-device communication underlaying cellular networks. IEEE Wirel. Commun. 2014, 21, 52–61. [Google Scholar] [CrossRef] [Green Version]
- Choi, K.W.; Han, Z. Device-to-device discovery for proximity-based service in LTE-advanced system. IEEE J. Sel. Areas Commun. 2014, 33, 55–66. [Google Scholar] [CrossRef]
- Xu, C.; Gao, C.; Zhou, Z.; Chang, Z.; Jia, Y. Social network-based content delivery in device-to-device underlay cellular networks using matching theory. IEEE Access 2016, 5, 924–937. [Google Scholar] [CrossRef]
- Miao, L.; Bai, B.; Chen, W. 4-DMWM approach for caching based optimal D2D pairing and channel allocation: Centralized and distributed algorithm design. IEEE Access 2016, 4, 9213–9224. [Google Scholar] [CrossRef]
- Pourmoslemi, A.; Rajabi, S.; Salimi, M. Selecting the Best Transmitter in Wireless Device-to-Device Communications Using a Fuzzy Decision-Making Method. In Proceedings of the International Online Conference on Intelligent Decision Science, Istanbul, Turkey, 7–8 August 2020; Springer: Berlin/Heidelberg, Germany. [Google Scholar]
- Rajabi, S.; Ghorashi, S.A.; Shah-Mansouri, V. Impact of connecting to the nth nearest node in dedicated device-to-device communications. Electron. Lett. 2018, 54, 535–537. [Google Scholar] [CrossRef]
- Rashed, S.K.; Asvadi, R.; Rajabi, S.; Ghorashi, S.A.; Martini, M.G. Power allocation for D2D communications using max-min message-passing algorithm. IEEE Trans. Veh. Technol. 2020, 69, 8443–8458. [Google Scholar] [CrossRef]
- Zhou, Z.; Kaoru, O.; Dong, M.; Chen, X. Energy-efficient matching for resource allocation in D2D enabled cellular networks. IEEE Trans. Veh. Technol. 2020, 66, 5256–5268. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Yang, T.; Hu, Y.; Feng, H.; Hu, B. Two-Timescale Resource Allocation for Cooperative D2D Communication: A Matching Game Approach. IEEE Trans. Veh. Technol. 2020, 70, 543–557. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, G.; Dong, M.; Ota, K.; Xu, C.; Jia, Y. Iterative energy-efficient stable matching approach for context-aware resource allocation in D2D communications. IEEE Access 2016, 4, 6181–6196. [Google Scholar] [CrossRef]
- Ma, R.; Chang, Y.J.; Chen, H.H.; Chiu, C.Y. On relay selection schemes for relay-assisted D2D communications in LTE–A systems. IEEE Trans. Veh. Technol. 2017, 66, 8303–8314. [Google Scholar] [CrossRef]
- Gandotra, P.; Jha, R.K. Zonal-based GrEEn algorithm for augmenting the battery life in spectrum shared networks via D2D communication. IEEE Trans. Veh. Technol. 2018, 68, 405–419. [Google Scholar] [CrossRef]
- Chaudhari, A.; Gandikota, J.; Sen, A.; Narayan, S. A Realistic Approach to Enhance the Battery Performance of Device-to-Device (D2D) Relay UEs. In Proceedings of the 17th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.J.; Rassias, T.M.; Saadati, R. Fuzzy Operator Theory in Mathematical Analysis; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bellman, R.; Kalaba, R.; Zadeh, L. Abstraction and pattern classification. J. Math. Anal. Appl. 1966, 13, 1–7. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, B-141. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets and their application to pattern classification and clustering analysis. In Classification and Clustering; Elsevier: Amsterdam, The Netherlands, 1977; pp. 251–299. [Google Scholar]
- Bezdek, J.C. Fuzzy Mathematics in Pattern Classification. Ph.D. Thesis, Applied Mathematics, Cornell University, Ithaca, NY, USA, 1973. [Google Scholar]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Kosko, B. Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to Machine Intelligence; Prentice Hall: Hoboken, NJ, USA, 1992. [Google Scholar]
- Ahvar, E.; Pourmoslemi, A.; Piran, M.J. FEAR: A fuzzy-based energy-aware routing protocol for wireless sensor networks. Int. J. Grid Comput. Appl. 2011, 7. [Google Scholar] [CrossRef]
- Bělohlávek, R.; Dauben, J.W.; Klir, G.J. Fuzzy Logic and Mathematics: A Historical Perspective; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Wei, W.; Li, Z.; Li, Z.; Sha, X. Fuzzy logic power control of device to device communication underlay td-lte-a system. In Proceedings of the 3rd International Conference on Consumer Electronics, Communications and Networks, Xianning, China, 20–22 November 2013. [Google Scholar]
- Li, H.; Chen, X.; Zhang, Y.; Wang, P.; Qiang, W.; Liu, N. Fuzzy mathematics and game theory based D2D multicast network construction. J. Syst. Eng. Electron. 2019, 30, 13–21. [Google Scholar]
- Liu, M.; Liu, Y.; Zhou, Y.; Zhang, W.; Yu, Y. Research on D2D resource allocation algorithm based on improved fuzzy clustering. In Proceedings of the Tenth International Conference on Digital Image Processing (ICDIP 2018), Shanghai, China, 11–14 May 2018. [Google Scholar]
- Chen, P.; Xue, J.; Chen, Y.; Wei, S.; Ji, Y. Resource allocation algorithm based on Fuzzy cluster grouping for device-to-device communication. In Bio-Inspired Computing-Theories and Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Subramani, M.; Kumaravelu, V.B. A quality-aware fuzzy-logic-based vertical handover decision algorithm for device-to-device communication. Arab. J. Sci. Eng. 2019, 44, 2413–2425. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Morms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Schweizer, B. Associative funcrions and statistical triangle inequalities. Puble. Math. Debr. 1961, 8, 169–186. [Google Scholar]
- Munir, M.; Kalsoom, H.; Ullah, K.; Mahmood, T.; Chu, Y.-M. T-spherical fuzzy Einstein hybrid aggregation operators and their applications in multi-attribute decision making problems. Symmetry 2020, 12, 365. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Wei, G. Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowl.-Based Syst. 2013, 37, 472–479. [Google Scholar] [CrossRef]
- Lin, X.; Andrews, J.G.; Ghosh, A. Spectrum sharing for device-to-device communication in cellular networks. IEEE Trans. Wirel. Commun. 2014, 13, 6727–6740. [Google Scholar] [CrossRef]
- Muhammad, G.; Alqahtani, S.; Alelaiwi, A. Pandemic Management for Diseases Similar to COVID-19 Using Deep Learning and 5G Communications. IEEE Netw. 2021, 35, 21–26. [Google Scholar] [CrossRef]
- Siriwardhana, Y.; De Alwis, C.; Gür, G.; Ylianttila, M.; Liyanage, M. The fight against the COVID-19 pandemic with 5G technologies. IEEE Eng. Manag. Rev. 2020, 48, 72–84. [Google Scholar] [CrossRef]
- Patzold, M. The Role of 5G in Limiting the Impact of the COVID-19 Pandemic [Mobile Radio]. IEEE Veh. Technol. Mag. 2020, 15, 6–12. [Google Scholar] [CrossRef]
- Ye, B.; Yuan, X.; Cai, Z.; Lan, T. Severity Assessment of COVID-19 Based on Feature Extraction and V-Descriptors. IEEE Trans. Ind. Inform. 2021, 17, 7456–7467. [Google Scholar] [CrossRef]
- Lin, J.C. Telecommunications health and safety: The Covid-19 pandemic and 5G cellular telecommunication systems. URSI Radio Sci. Bull. 2020, 372, 56–59. [Google Scholar] [CrossRef]
- Ren, H.; Shen, J.; Tang, X.; Feng, T. 5G Healthcare Applications In COVID-19 Prevention And Control. In Proceedings of the 2020 ITU Kaleidoscope: Industry-Driven Digital Transformation (ITU K), Ha Noi, Vietnam, 7–11 December 2020; pp. 1–4. [Google Scholar]
- Wang, P.; Zhao, Y. Research on the Development of 5G under the Background of the COVID-19 Epidemic. In Proceedings of the 2021 2nd International Conference on E-Commerce and Internet Technology (ECIT), Hangzhou, China, 5–7 March 2021; pp. 34–137. [Google Scholar]
- Chamola, V.; Hassija, V.; Gupta, V.; Guizani, M. A comprehensive review of the COVID-19 pandemic and the role of IoT, drones, AI, blockchain, and 5G in managing its impact. IEEE Access 2020, 8, 90225–90265. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| D2D receiver | |
| Potential D2D transmitter for D2D receiver | |
| N | The maximum number of co-channel D2D receivers |
| K | The number of D2D transmitters around each receiver |
| The maximum search radius of D2D receivers | |
| The direct channel between the cellular user and eNB | |
| The distance between the cellular user and eNB | |
| The channel between the D2D transmitter and the D2D receiver | |
| The distance between the D2D transmitter and the D2D receiver | |
| The interference channel between the D2D transmitter and eNB | |
| The distance between the D2D transmitter and eNB | |
| The interference channel between the cellular user and D2D receiver | |
| The distance between the cellular user and D2D receiver | |
| The cellular link SINR | |
| The cellular link data rate | |
| The D2D link (consists of transmitter and receiver ) SINR | |
| The D2D link (consists of transmitter and receiver ) data rate | |
| Cellular user’s power | |
| D2D transmitters’ power | |
| Path loss exponent | |
| The received noise power | |
| The battery level of transmitter | |
| The battery level threshold | |
| The date-rate threshold |
| Parameter | Value |
|---|---|
| (Cellular radius) | 500 m |
| (D2D search radius) | 200 m |
| N (The number of D2D receivers for each cellular users) | 1–4 |
| K (The number of D2D transmitters for each receiver) | 1–4 |
| (Cellular user’s power) | 23 dBm |
| (D2D transmitters’ power) | 15 dBm |
| (Path loss exponent) | 3.5 |
| (Data-rate threshold) | 0.3 |
| (Battery-level threshold) | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourmoslemi, A.; Rajabi, S.; Salimi, M.; Ferrara, M. A Fuzzy Method for Joint Resource Allocation and Stable Pairing in D2D Communications. Appl. Sci. 2022, 12, 1343. https://doi.org/10.3390/app12031343
Pourmoslemi A, Rajabi S, Salimi M, Ferrara M. A Fuzzy Method for Joint Resource Allocation and Stable Pairing in D2D Communications. Applied Sciences. 2022; 12(3):1343. https://doi.org/10.3390/app12031343
Chicago/Turabian StylePourmoslemi, Alireza, Siavash Rajabi, Mehdi Salimi, and Massimiliano Ferrara. 2022. "A Fuzzy Method for Joint Resource Allocation and Stable Pairing in D2D Communications" Applied Sciences 12, no. 3: 1343. https://doi.org/10.3390/app12031343
APA StylePourmoslemi, A., Rajabi, S., Salimi, M., & Ferrara, M. (2022). A Fuzzy Method for Joint Resource Allocation and Stable Pairing in D2D Communications. Applied Sciences, 12(3), 1343. https://doi.org/10.3390/app12031343









