Lower Bound Limit Analysis of Non-Persistent Jointed Rock Masses Using Mixed Numerical Discretization
Abstract
1. Introduction
2. Fundamental Theory and General Assumptions
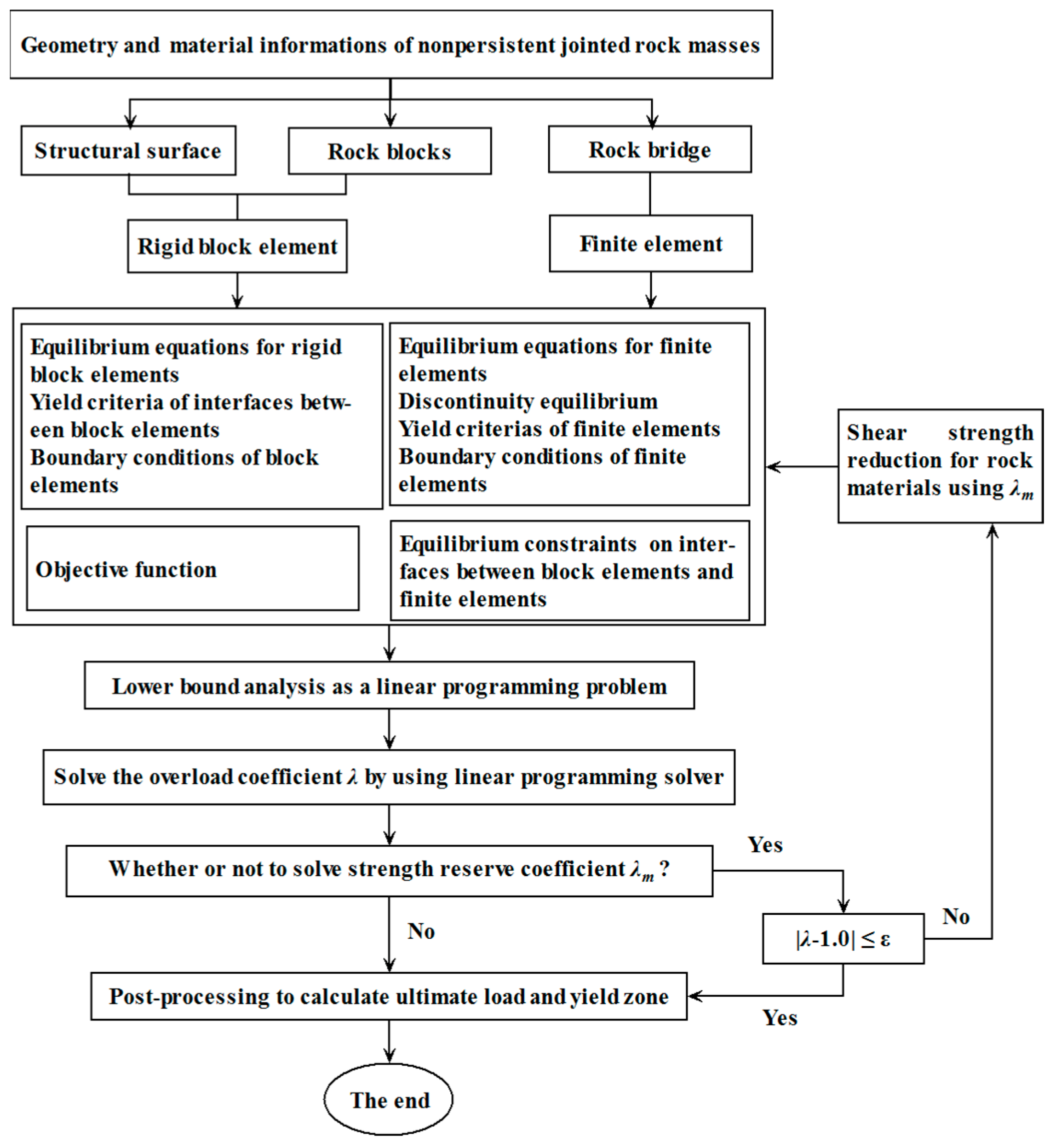
3. Mixed Numerical Discretization
4. Mixed Formulation of Lower Bound Limit Analysis
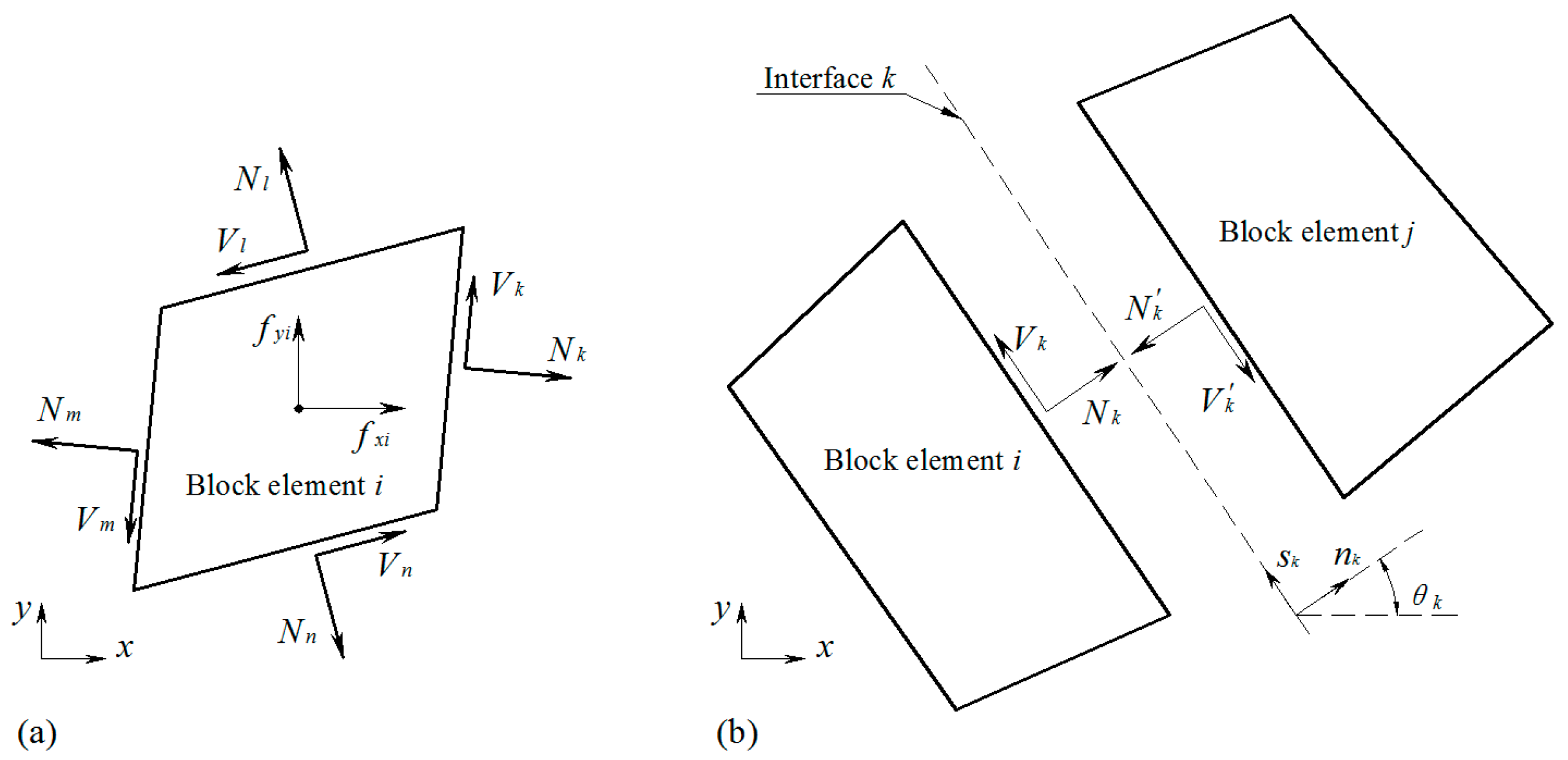
4.1. Constraints of Lower Bound Method for Rock Block Elements
4.1.1. Equilibrium Equations of Rigid Block Element
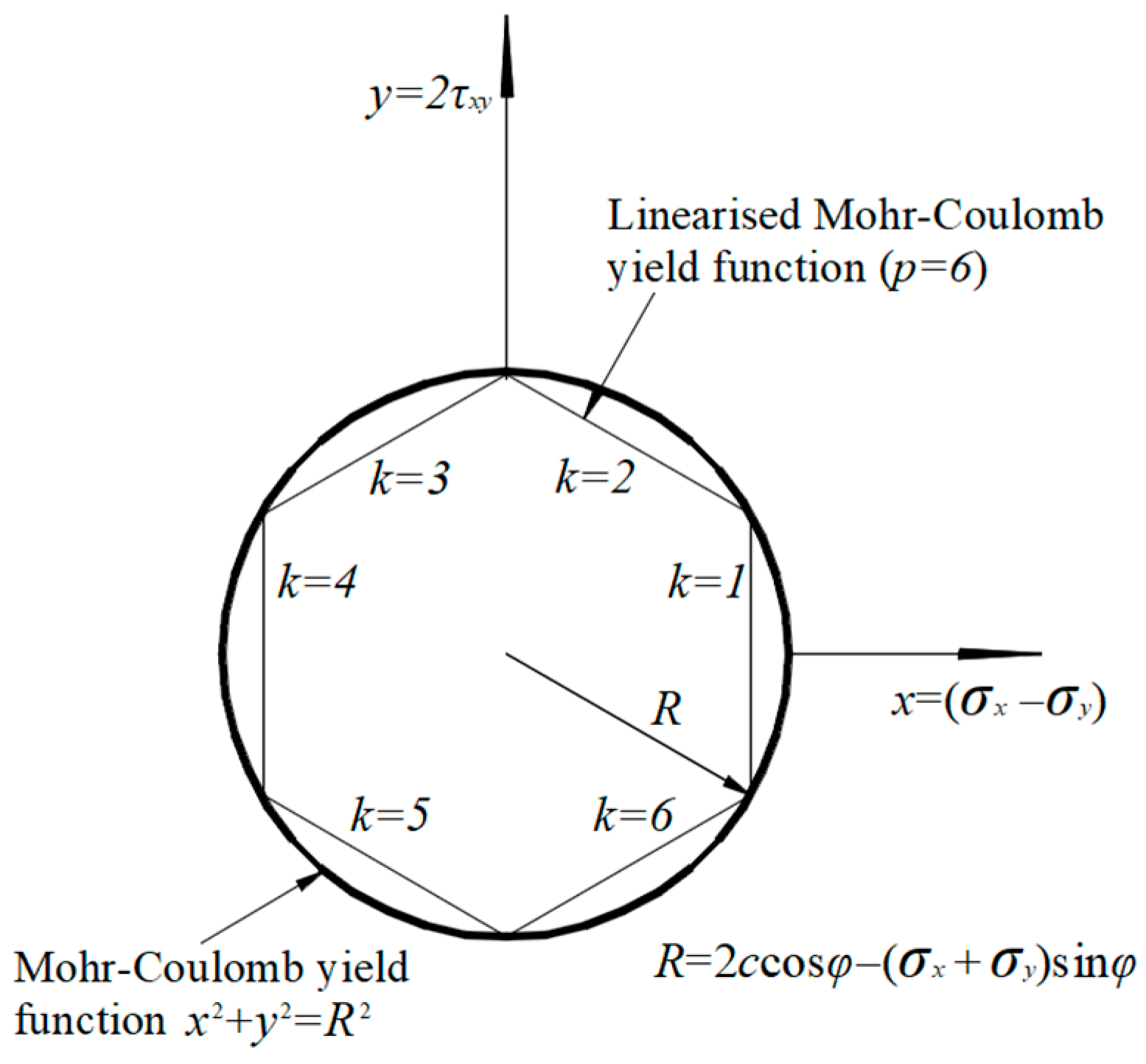
4.1.2. Yield Criteria of the Interfaces between Two Rigid Block Elements
4.1.3. Boundary Condition of Rigid Block Elements
4.2. Constraints of Lower Bound Method for Finite Elements
4.2.1. Equilibrium Equations of the Finite Element Method
4.2.2. Discontinuity Equilibrium of Finite Elements of Rock Bridge
4.2.3. Yield Criteria of Finite Element
4.2.4. Stress Boundary Conditions of Finite Element
4.3. Equilibrium Constraint on the Interface between Block Elements and Finite Elements
4.4. The Objective Function
4.5. Linear Programming and Solution Strategy for Lower Bound Analysis
5. Calibration and Application
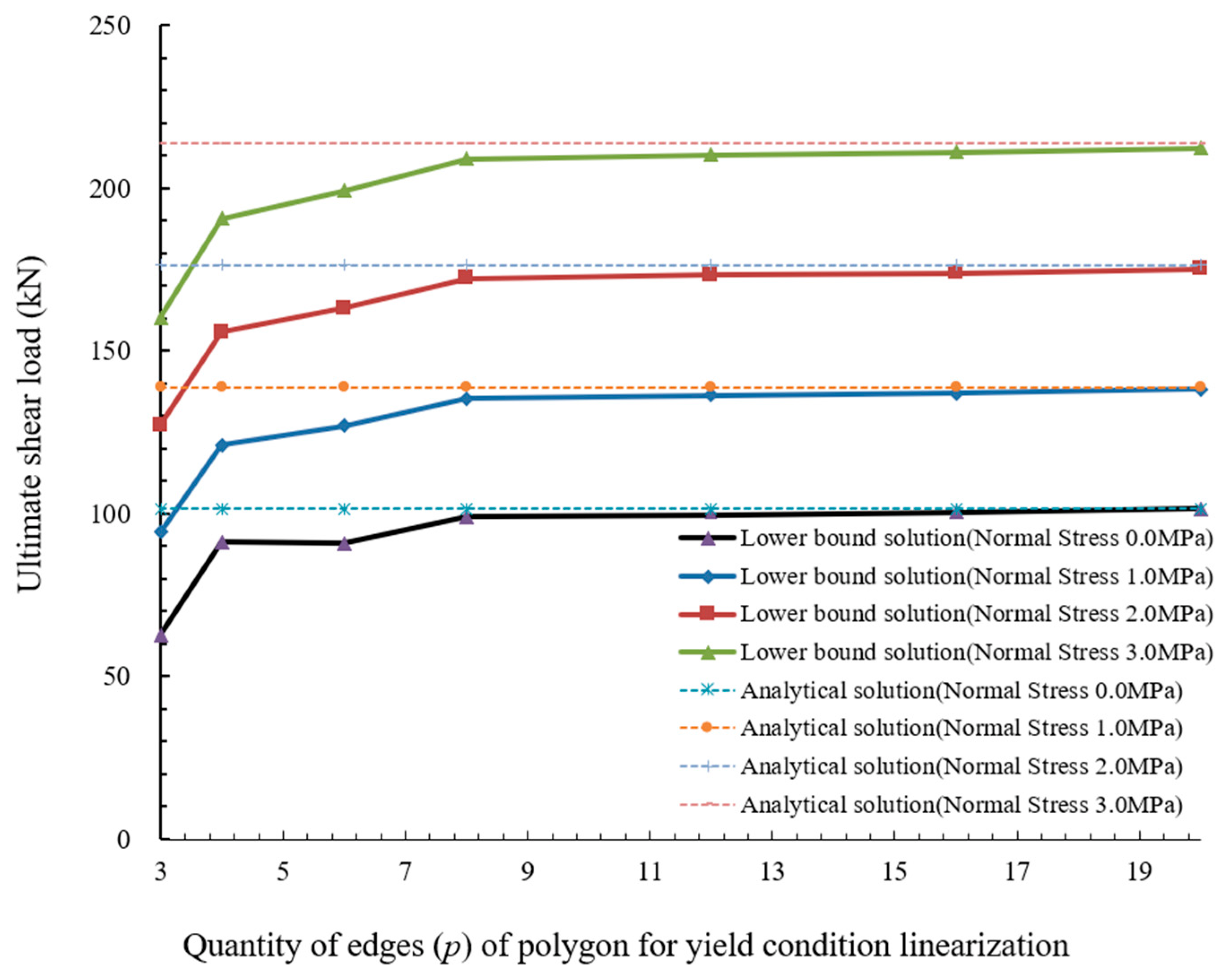
5.1. Ultimate Shear Load of Direct Shear Specimen with Coplanar Intermittent Joints
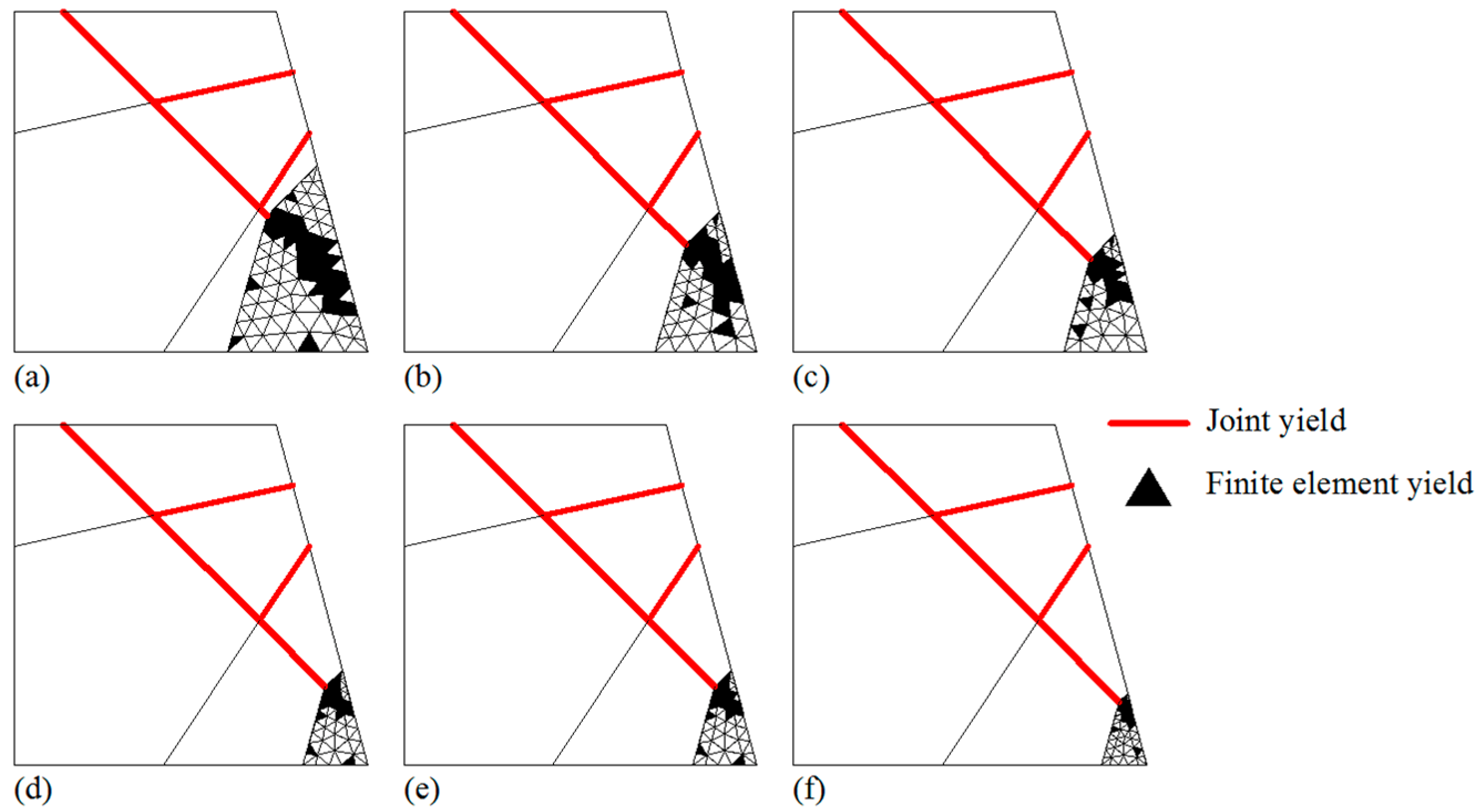
5.2. Stability of a Rock Slope with Three Joints and a Rock Bridge
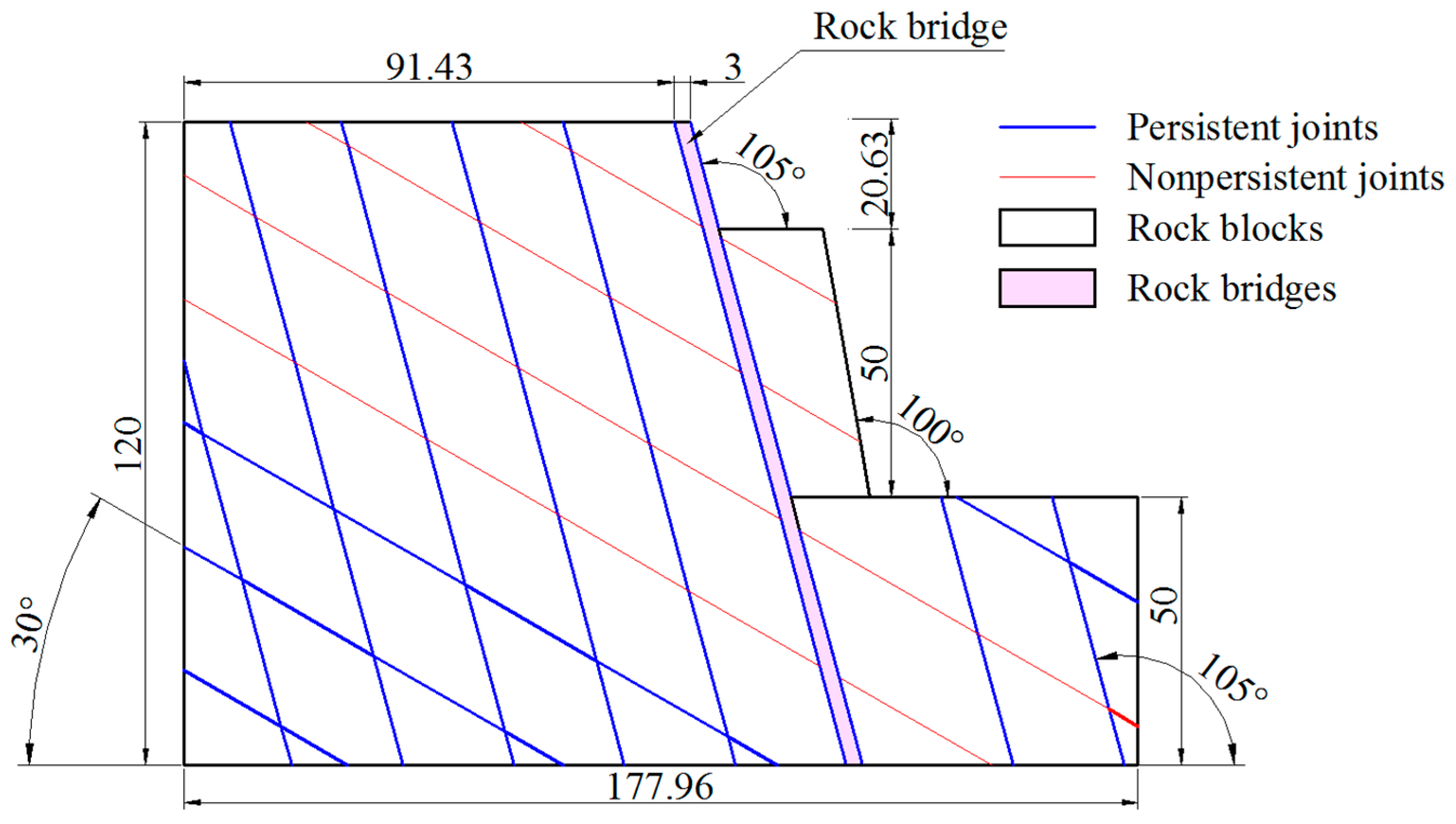
5.3. Stability of Rock Slope with Two Joint Sets and a Rock Bridge
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| area of triangular finite element e (m2); | |
| boundary condition matrix for all boundary edges of finite elements; | |
| equilibrium matrix of all finite elements; | |
| discontinuity equilibrium matrix of all discontinuities for all finite elements; | |
| yield matrix for all nodes of finite elements; | |
| coefficient vector of all boundary edges of finite elements; | |
| load vector of all finite element equilibriums; | |
| coefficient vector of yield conditions for all finite elements; | |
| equilibrium matrix for all block elements; | |
| global external force vector for all block elements; | |
| length of interface between rigid block element and finite elements (m); | |
| normal force of the interface k between two adjacent block elements in the direction; | |
| normal force in the direction of rigid block element applied on the interface between rigid block element and finite elements; | |
| force vector at the boundary surfaces of block elements; | |
| known force vector applied to the boundary surfaces of block elements; | |
| global internal force vector for all block elements; | |
| shear force in the direction of the interface k between the two adjacent block elements; | |
| shear force in the direction of rigid block element applied on the interface between rigid block element and finite elements; | |
| shape function coefficients of the linear triangular finite element ; | |
| cohesion of initial and final strength reduction, respectively (Pa); | |
| cohesion of the rock bridge at nodes of eth finite element; | |
| shape function coefficients of the linear triangular finite element ; | |
| cohesion of the kth interface (Pa); | |
| x component of force acting on the center of block element i; | |
| y component of force acting on the center of block element i; | |
| length of the interface between finite element and the rigid block element (m); | |
| length of the interface k (m); | |
| number of interfaces in block element i; | |
| number of all block elements; | |
| surfaces number on known boundary; | |
| number of finite element stress discontinuities in the rock bridges; | |
| number of all triangular finite elements in rock bridges; | |
| interface number between the rock blocks and finite elements in the entire rock slope; | |
| number of triangular finite elements on interface ; | |
| number of all interfaces in all rock block elements; | |
| number of nodes of all finite elements; | |
| number of sides of interior polygon for linearizing Mohr–Coulomb yield function; | |
| inclination angle of -axis with respect to x-axis measured anticlockwise (°); | |
| friction angles of initial and final strength reduction, respectively (°); | |
| friction angle of the rock bridge at ith node of finite element (°); | |
| friction angle of the kth interface (°); | |
| unit weight of finite element (N/m3); | |
| load multiplier of rock mass; | |
| strength reserve coefficient; | |
| inclination angle of the discontinuity d measured anticlockwise with respect to x-axis (°); | |
| inclination angle of the interface measured anticlockwise with respect to x-axis (°); | |
| stress vector of all nodes for all finite elements; | |
| stress vector of nodes of finite elements on the interface ; | |
| normal stress acting on the node i of the discontinuity d between two adjacent finite elements, ; | |
| normal stress of the finite element j on the interface between rigid block element and finite elements; | |
| normal stress of node 1 and node 2 of finite element on the interface in the direction; | |
| x component of normal stress acting on node i of finite element; | |
| x component of normal stress of node 1 and node 2 of finite element on the interface ; | |
| y component of normal stress acting on node i of finite element; | |
| y component of normal stress of node 1 and node 2 of finite element on the interface ; | |
| shear stress of node 1 and node 2 of finite element on the interface in the direction; | |
| tangential shear stress acting on node i of the discontinuity d between two adjacent finite elements, ; | |
| normal stress of the finite element j on the interface between rigid block element and finite elements in the direction; | |
| shear stress acting on node i of finite element; | |
| shear stress of node 1 and node 2 of finite element on the interface . |
References
- Lei, Q.; Wang, X.; Min, K.B.; Rutqvist, J. Interactive roles of geometrical distribution and geomechanical deformation of fracture networks in fluid flow through fractured geological media. J. Rock Mech. Geotech. Eng. 2020, 12, 780–792. [Google Scholar] [CrossRef]
- Gao, K.; Lei, Q.; Bozorgzadeh, N.; Chau, V.T. Can we estimate far-field stress using the mean of local stresses? an examination based on numerical simulations. Comput. Geotech. 2019, 116, 103188. [Google Scholar] [CrossRef]
- Bishop, A. The use of the slip in the stability analysis of earth slopes. Geotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Janbu, N. Application of composite slip surfaces for stability analysis. In Proceedings of the European Conference on Stability of Earth Slopes, Stockholm, Sweden, 20–25 September 1954; Volume 3, pp. 43–49. [Google Scholar]
- Morgenstern, N.; Price, V.E. The analysis of the stability of general slip surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Sarma, S. Stability analysis of embankments and slopes. Geotechnique 1973, 23, 423–433. [Google Scholar] [CrossRef]
- Griffiths, D.; Lane, P. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Cai, M.; Horii, H. A constitutive model and fem analysis of jointed rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 351–359. [Google Scholar] [CrossRef]
- Kim, D.; Jeong, S. Estimation of the excavation damage zone in TBM tunnel using large deformation FE analysis. Geomech. Eng. 2021, 24, 323–335. [Google Scholar] [CrossRef]
- Sitharam, T.; Maji, V.; Verma, A. Practical equivalent continuum model for simulation of jointed rock mass using flac3d. Int. J. Geomech. 2007, 7, 389–395. [Google Scholar] [CrossRef]
- Shi, G.-H. Discontinuous deformation analysis: A new numerical model for the statics and dynamics of deformable block structures. Eng. Comput. 1992, 9, 157–168. [Google Scholar] [CrossRef]
- Jing, L. Formulation of discontinuous deformation analysis (DDA)—An implicit discrete element model for block systems. Eng. Geol. 1998, 49, 371–381. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, Y. A novel random discrete element analysis of rock fragmentation. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1386–1395. [Google Scholar] [CrossRef]
- Goodman, R.E.; Shi, G.-H. Block Theory and Its Application to Rock Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Li, Z.; Hu, Z.; Zhang, X.Y.; Du, S.G.; Guo, Y.K.; Wang, J. Reliability analysis of a rock slope based on plastic limit analysis theory with multiple failure modes. Comput. Geotech. 2019, 110, 132–147. [Google Scholar] [CrossRef]
- Chen, G.H.; Zou, J.F.; Zhan, R. Stability analysis of rock slopes using strength reduction adaptive finite element limit analysis. Struct. Eng. Mech. 2021, 79, 487–498. [Google Scholar] [CrossRef]
- Chen, S. A general formulation of elastic viscoplastic block theory of rock masses. J. Hydraul. Eng. 1996, 1, 78–84. [Google Scholar]
- Drucker, D.; Prager, W.; Greenberg, H. Extended limit design theorems for continuous media. Q. Appl. Math. 1952, 9, 381–389. [Google Scholar] [CrossRef]
- Chen, J.; Yin, J.-H.; Lee, C. Upper bound limit analysis of slope stability using rigid finite elements and nonlinear programming. Can. Geotech. J. 2003, 40, 742–752. [Google Scholar] [CrossRef]
- Lysmer, J. Limit analysis of plane problems in soil mechanics. J. Soil Mech. Found. Div. 1970, 96, 1311–1334. [Google Scholar] [CrossRef]
- Sloan, S. Lower bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1988, 12, 61–77. [Google Scholar] [CrossRef]
- Ukritchon, B.; Whittle, A.J.; Sloan, S.W. Undrained limit analyses for combined loading of strip footings on clay. J. Geotech. Geoenviron. Eng. 1998, 124, 265–276. [Google Scholar] [CrossRef]
- Lyamin, A.; Sloan, S. Lower bound limit analysis using non-linear programming. Int. J. Numer. Methods Eng. 2002, 55, 573–611. [Google Scholar] [CrossRef]
- Yu, H.; Salgado, R.; Sloan, S.; Kim, J. Limit analysis versus limit equilibrium for slope stability. J. Geotech. Geoenviron. Eng. 1998, 124, 1–11. [Google Scholar] [CrossRef]
- Kim, J.; Salgado, R.; Yu, H. Limit analysis of soil slopes subjected to pore-water pressures. J. Geotech. Geoenviron. Eng. 1999, 125, 49–58. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, J. Limit analysis of slope stability by rigid finite-element method and linear programming considering rotational failure. Int. J. Geomech. 2012, 13, 827–839. [Google Scholar] [CrossRef]
- Sutcliffe, D.; Yu, H.; Sloan, S. Lower bound solutions for bearing capacity of jointed rock. Comput. Geotech. 2004, 31, 23–36. [Google Scholar] [CrossRef]
- Durand, A.F.; Vargas, E.A., Jr.; Vaz, L.E. Applications of numerical limit analysis (NLA) to stability problems of rock and soil masses. Int. J. Rock Mech. Min. Sci. 2006, 43, 408–425. [Google Scholar] [CrossRef]
- Chakraborty, M.; Kumar, J. Bearing capacity of circular footings over rock mass by using axisymmetric quasi lower bound finite element limit analysis. Comput. Geotech. 2015, 70, 138–149. [Google Scholar] [CrossRef]
- Wang, X.G.; Lin, X.C. Limit analysis method for slope stability based on discretization of rigid blocks. Chin. J. Geotech. Eng. 2022, 44, 1587–1597. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Q.; Wang, J. Rigid block based lower bound limit analysis method for stability analysis of fractured rock mass considering rock bridge effects. Comput. Geotech. 2017, 86, 173–180. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, J. Lower bound limit analysis of wedge stability using block element method. Comput. Geotech. 2017, 86, 120–128. [Google Scholar] [CrossRef]
- Li, G.; Shen, Z. Application of lower bound method of finite element method to geotechnical problems. Chin. J. Geotech. Eng. 1997, 19, 84–89. [Google Scholar]
- Mehrotra, S. On the implementation of a primal-dual interior point method. SIAM J. Optim. 1992, 2, 575–601. [Google Scholar] [CrossRef]
- Jiang, M.; Jiang, T.; Crosta, G.B.; Shi, Z.; Chen, H.; Zhang, N. Modeling failure of jointed rock slope with two main joint sets using a novel DEM bond contact model. Eng. Geol. 2015, 193, 79–96. [Google Scholar] [CrossRef]






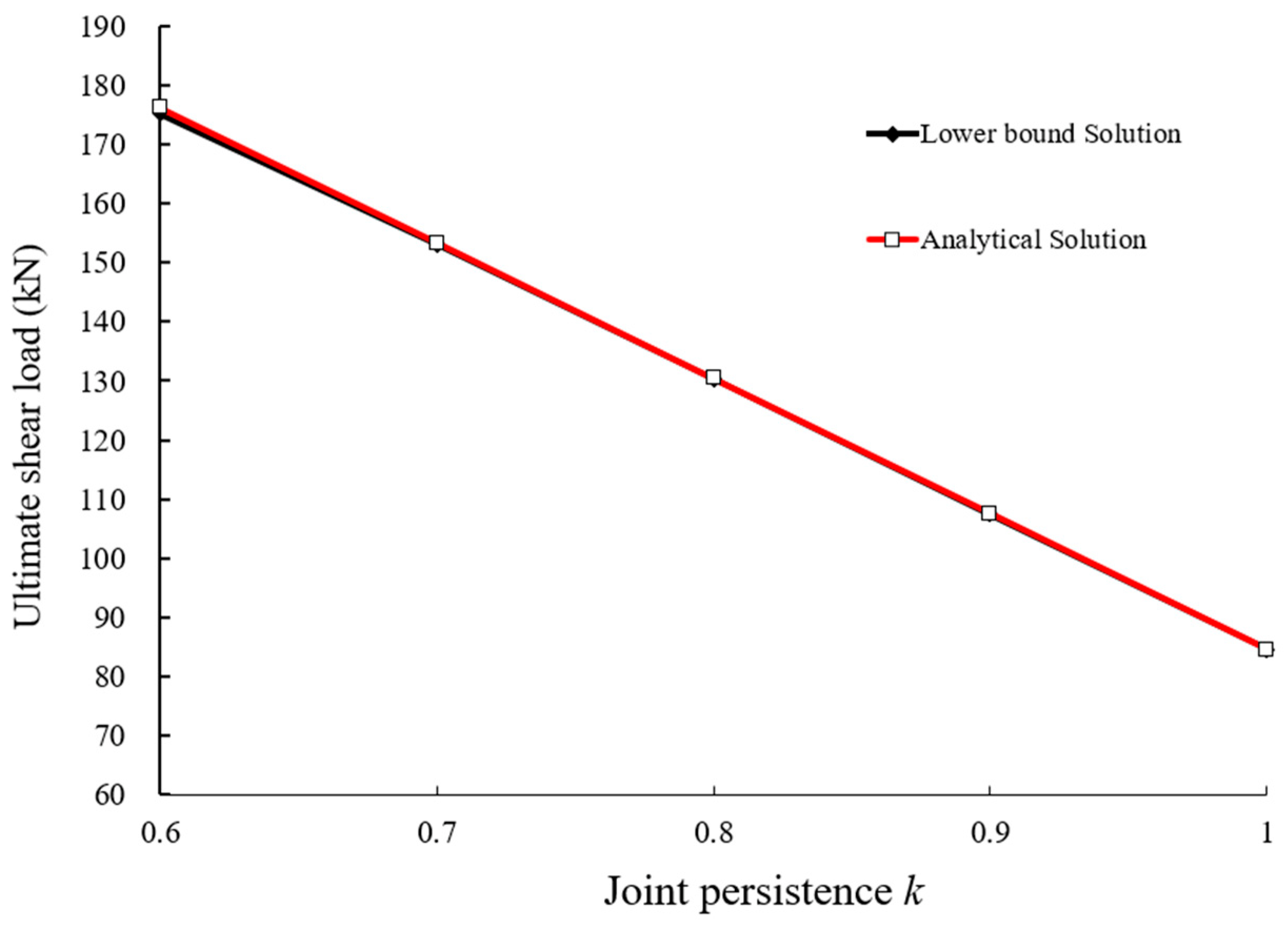
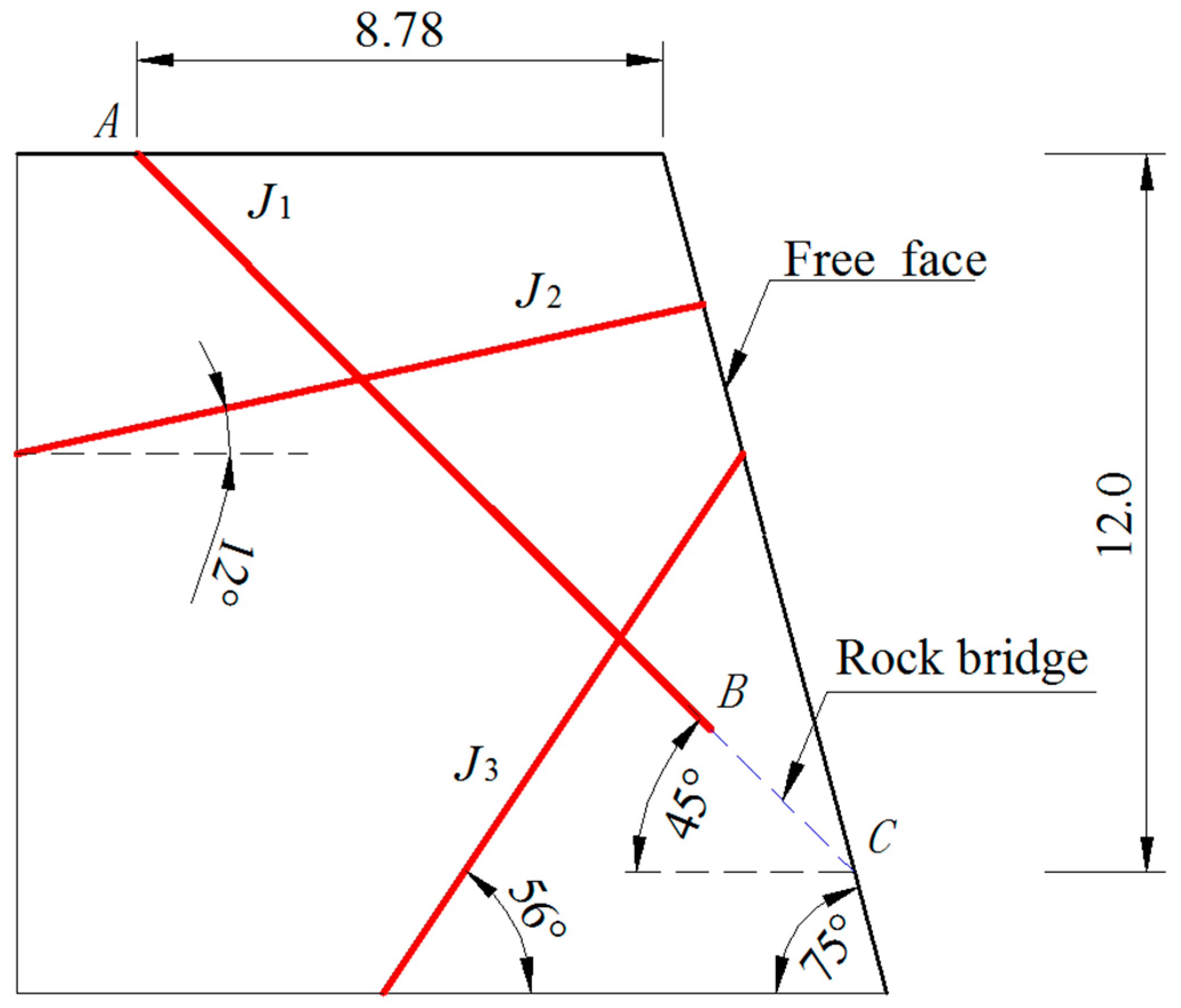
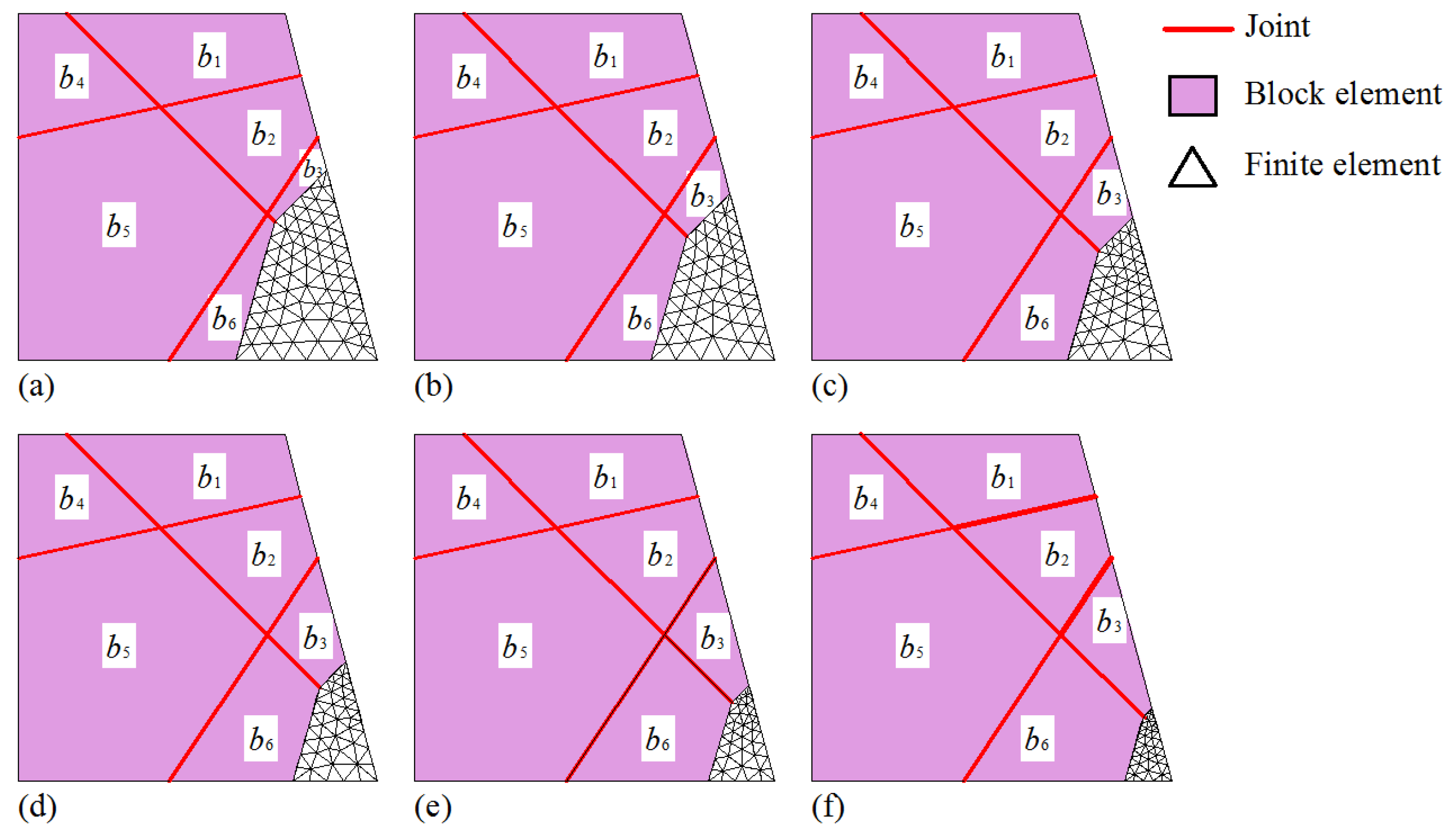
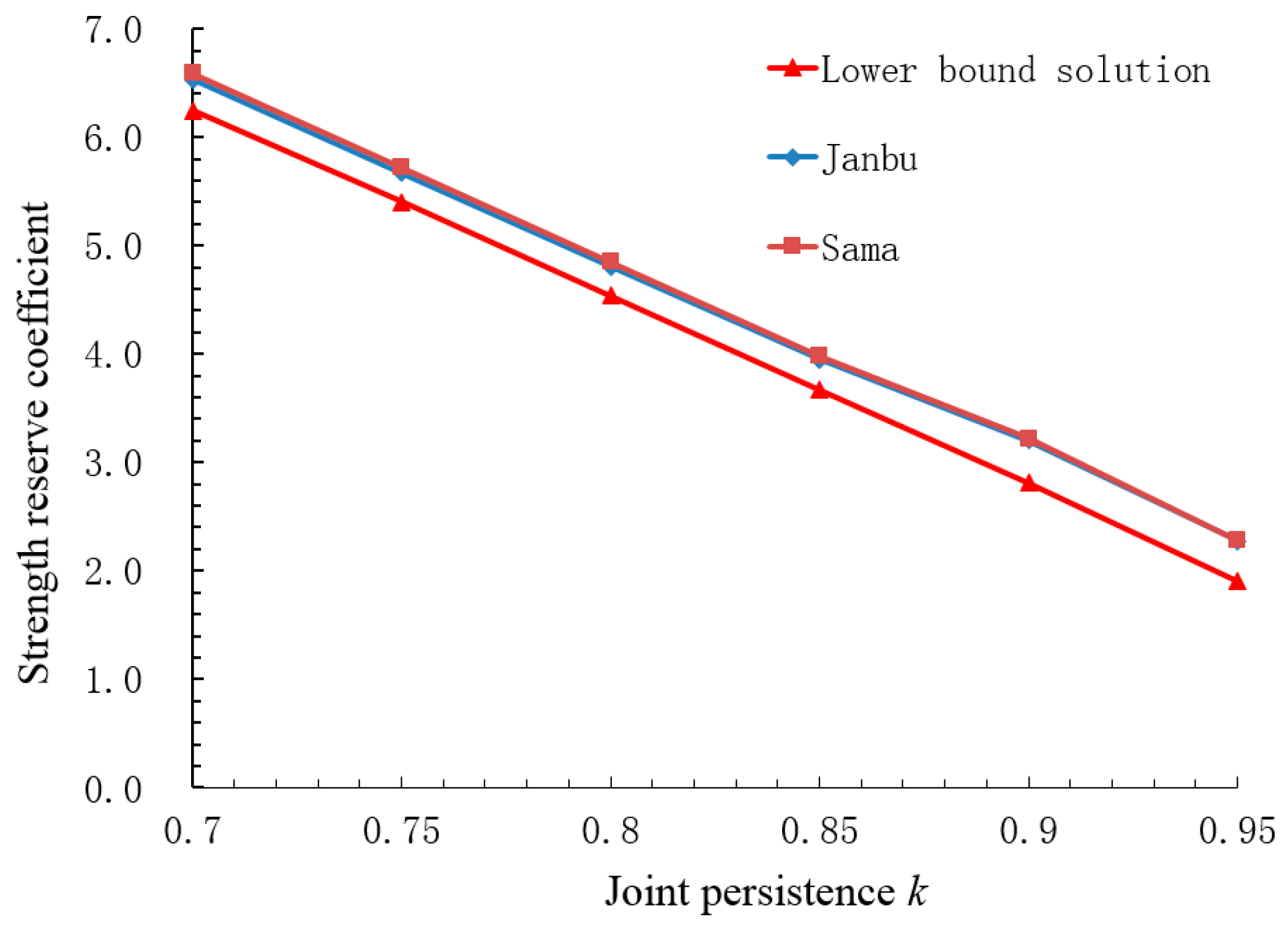


| Material Name | Unit Weight (kN/m3) | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|
| Rock mass | 15.00 | 4230.00 | 26.55 |
| Jointed plane | / | 0.00 | 35.20 |
| Joint Persistence k (%) | |
|---|---|
| 90 | 2.0 |
| 80 | 2.0 |
| 70 | 2.0 |
| 60 | 0.0 |
| 60 | 1.0 |
| 60 | 2.0 |
| 60 | 3.0 |
| Material Name | Unit Weight (kN/m3) | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|
| Intact rock mass | 25.50 | 1000.00 | 36.00 |
| Rock bridge | 25.50 | 1000.00 | 36.00 |
| Jointed plane | / | 0.05 | 30.00 |
| Material Name | Unit Weight (kN/m3) | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|
| Intact rock mass | 25.00 | 500.00 | 30.00 |
| Rock bridge | 25.00 | 500.00 | 30.00 |
| Jointed plane | / | 120.00 | 24.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Xu, H.; Sui, S.; Li, Z.; Zhang, X.; Peng, P. Lower Bound Limit Analysis of Non-Persistent Jointed Rock Masses Using Mixed Numerical Discretization. Appl. Sci. 2022, 12, 12945. https://doi.org/10.3390/app122412945
Liu W, Xu H, Sui S, Li Z, Zhang X, Peng P. Lower Bound Limit Analysis of Non-Persistent Jointed Rock Masses Using Mixed Numerical Discretization. Applied Sciences. 2022; 12(24):12945. https://doi.org/10.3390/app122412945
Chicago/Turabian StyleLiu, Wenlian, Hanhua Xu, Sugang Sui, Ze Li, Xiaoyan Zhang, and Pu Peng. 2022. "Lower Bound Limit Analysis of Non-Persistent Jointed Rock Masses Using Mixed Numerical Discretization" Applied Sciences 12, no. 24: 12945. https://doi.org/10.3390/app122412945
APA StyleLiu, W., Xu, H., Sui, S., Li, Z., Zhang, X., & Peng, P. (2022). Lower Bound Limit Analysis of Non-Persistent Jointed Rock Masses Using Mixed Numerical Discretization. Applied Sciences, 12(24), 12945. https://doi.org/10.3390/app122412945







