Abstract
In the automatic shoveling operation of wheel loaders, the shovel trajectory has a significant influence on the operation’s performance. In order to obtain a suitable shovel trajectory and optimize the automatic shovel performance of the loader, we developed a test platform for the operational performance of loaders. Nine parallel shoveling trajectories of different depths were designed according to the coordination shoveling method. The formula for calculating the operational performance is established. The automatic shoveling test is performed according to the designed trajectory to obtain the real-time shoveling parameters, which are then combined with the calculation formula to calculate the operating parameters of the loader. Finally, the actual range of operational performance parameters is calculated by the normal distribution. The test results show that the trajectory with a shovel depth of 400 mm is the optimal trajectory. It was also verified by comparing manually controlled shoveling with it. With only a 1% difference in the full bucket rate, the operation time of automatic shoveling was 15.3% less than manually controlled shoveling, fuel consumption was 4.7% less, the energy consumption of practical work performed was 10.7% more, and maximum operation resistance was 20.5% lower. Therefore, the operational performance of the loader following this trajectory for shoveling meets the actual requirements.
1. Introduction
The automated operation of loaders [1] can reduce labor and increase the safety of people working in harsh environments, which plays a crucial role in modern construction [2]. Thus, the automatic shoveling operation performance of loaders has received much attention. Wheel loaders have many operational performances [3], such as full bucket rate [4], operational resistance [5], fuel consumption [6,7], etc. These are essential criteria to evaluate the loader in the automatic shoveling operation process. Many factors affect the operational performance of the loader, such as material type, trajectory, the resting angle of the pile, etc., of which the operational trajectory has a more significant impact. Since the whole process of automatic shoveling of the loader depends on the operation trajectory of the import controller [8], it is a critical technology for the loader to achieve automatic shoveling operation. Therefore, it is urgent to investigate the influence of shovel trajectory on the operational performance of wheel loaders.
At present, the research on the automatic shoveling of loaders has achieved fruitful results. Liu et al. [9] found four solutions to fuel consumption that can be applied to wheel loaders from HMPST, then found the optimal fuel-saving solution from the four solutions, and finally built a simulation model of the loader power system to verify the effectiveness of the solution. Osumi et al. [10] studied the buck’s forces at various stages of the loader shoveling process, modeled the forces acting on the bucket, and experimentally validated the model. Frank et al. [11] developed a general and reproducible efficiency test method for the reproducible evaluation of the fuel and handling performance of wheel loaders, which can be tested for acceleration, and resting angle-induced drag by physical models and by developing a real-time test program. Huang et al. [12] proposed a reinforcement learning method to improve a loader’s automatic shoveling performance, built a statistical model to simulate the natural environment, and then trained the proposed algorithm on the statistical model. The final results proved that the algorithm has good adaptability and fuel consumption performance. Gottschalk et al. [13] developed a method for repeated evaluation of the fuel performance and handling performance of various wheel loaders to measure the loader’s overall efficiency. Other scholars have also optimized these aspects by reducing operating resistance, improving practical work performed by structural optimization, and simplifying the loader operation process. Since most of them still use methods such as modeling [14], simulation design [15], and prediction [16], it is evident that the final result is also only a theoretical optimization. There are still considerable differences from the actual, and it is also difficult to have a practical improvement in the optimization of loader-shovel operation performance.
Others have used machine learning [17,18,19] methods to improve the operational performance of loaders. Backman et al. [20] studied reinforcement learning control of loaders in a simulated environment using a deep neural network approach. At the start of shoveling, one agent selects the digging position via the depth camera, and another agent is responsible for filling the bucket with the material. The agent can continuously learn strategies for efficient shoveling during the shoveling process and shovel up to approximately 75% of the maximum capacity. However, the method cannot cope with situations that are significantly distinct from those included in the training. Dadhich et al. [21] proposed a neural network reinforcement learning method to enhance the shovel weight of a loader. The shovel weight could be improved by 5–10% after automatic shoveling testing and reinforcement learning of the loader using this method. Nevertheless, the method was only validated on one material, leading to the fact that this method is only sometimes applied to other materials. Bhola et al. [22] used a machine learning approach to develop 2-DOF and 3-DOF energy management controllers for closed-circuit hydrostatic transmission of front-end loader machines. The engine’s fuel consumption in the 3-degree-of-freedom control system was 34% lower than in the 2-degree-of-freedom system through tests. The drive efficiency was relatively improved by 20–30%. Since this controller takes fewer factors into account, it is challenging to face more complex working conditions. Dadhich et al. [23] proposed a supervised machine learning method to improve the effect of material-filled buckets, which can predict the lifting action of the operator with an excellent shoveling effect. The root mean square error of the prediction results was below 0.2. The method lacks corresponding experimental validation and is only theoretically analyzed for feasibility. According to the above analysis, machine learning also has some limitations, and it has a narrow range of applications, poor generalization ability, and high requirements for mechanical equipment.
In response to the above problems, we conducted tests on our self-developed test platform and obtained the basic parameters such as shovel weight, resistance, and fuel consumption for different trajectories. Then the theoretical approach and experimental parameter analysis are combined to optimize the automatic shoveling performance of the loader.
2. Test Platform and Test Process Analysis
2.1. Analysis of Comprehensive Performance Test Platform for Wheel Loader Operation Process
In order to obtain the primary data of the loader operation process and to optimize the shoveling performance, this paper conducts repeatability tests on wheel loaders based on the developed comprehensive performance test platform for the loader operation process. The platform is based on test methods of full bucket rate, fuel consumption, practical work, and resistance. Additionally, then built based on the loader power system with test sensors and self-developed measurement devices. It is mainly composed of an operation parameter measurement system, test dolly power system, automatic shoveling control system, operation material preparation device, data processing system, and other parts. As shown in Figure 1, the operational parameter measurement system mainly consists of pressure sensors, flow sensors, displacement sensors, etc. The sensors are used to monitor real-time resistance, fuel consumption, and other performance parameters. The test dolly power system mainly consists of a wheel loader with a shoveling capacity of 5 tons as test dolly because the vehicle has the advantages of fast operation, high efficiency, and easy operation, which is one of the main types of machines for earthwork sites. As shown in Figure 2, it consists of a working device, frame, hydraulic system, transmission system, double-variable system, drive axle, and engine subsystem. The automatic shoveling control system mainly controls the loader to carry out automatic shoveling according to the designed shoveling trajectory, which avoids the error of human operation and improves the repeatability and versatility of the test. It also increases the manual shoveling mode, and the control system has the function of "manual operation priority" to protect the safety of people and loaders. The operational material preparation device is to return the shoveled material to its previous state, thus ensuring the same shoveling conditions and improving the consistency of test data. The data processing system mainly collects, analyzes, and stores the shoveling data collected by the sensors of the test platform.

Figure 1.
The composition of the operational parameter measurement system.
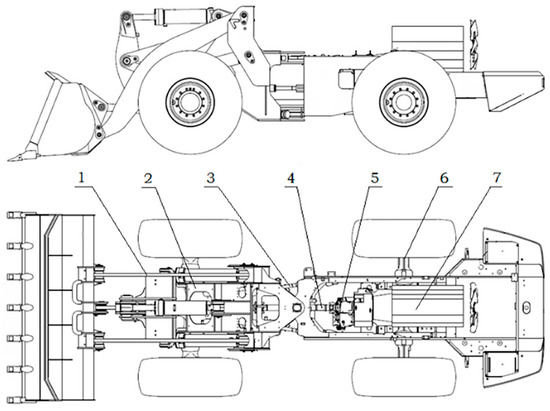
Figure 2.
The composition of the test dolly power system: 1. working device, 2. Frame, 3. hydraulic system, 4. transmission system, 5. double-variable system, 6. drive axle, 7. engine.
Based on the above analysis, the loader operation process comprehensive performance test platform for automatic shoveling test has versatility and repeatability, which can also improve the accuracy of test data and maintain a high degree of consistency.
2.2. Analysis of Automatic Shoveling Operation Process
Before the test, the onboard PC, the five-wheel instrument, the data acquisition instrument, the rear drive shaft torque signal receiver, the front drive shaft torque signal receiver, and other test instruments should be checked to ensure they can work well. The above experimental apparatus is installed in the driver’s compartment, and its installation position is shown in Figure 3. At the same time, attention should be paid to not having excess material on the shoveled path to avoid errors in the data measured by the measuring device of real-time displacement. The measuring device for real-time displacement is installed at the rear of the loader to measure the real-time displacement and speed of the loader. As shown in Figure 4, the driven wheel follows the real-time rotation of the loader, the gear plate on the rotating shaft follows the real-time rotation of the driven wheel, and the rotational speed sensor on the gear plate can measure the real-time displacement and speed of the driven wheel. Due to the real-time rotation of the driven wheel following the loader, the real-time displacement and velocity of the whole vehicle are equal to the real-time displacement and velocity of the driven wheel.

Figure 3.
Installation position of test instruments: a. onboard PC, b. five-wheel instrument, c. data acquisition instrument, d. rear driveshaft torque signal receiver, e. front driveshaft torque signal receiver.

Figure 4.
The measuring device of real-time displacement: f. driven wheel, g. gear plate, h. rotational speed sensor, i. rotating shaft.
After doing the above work, then can start the test. The process of the automatic shoveling test is shown in Figure 5.
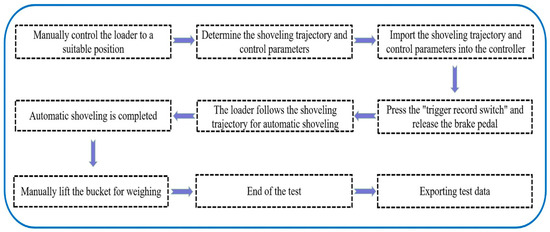
Figure 5.
The process of the automatic shoveling test.
3. Wheel Loader Shoveling Trajectory Planning
The task of shoveling trajectory planning is to plan a feasible operating trajectory for the loader working mechanism. The automatic shoveling control system will track the operating trajectory to realize the autonomous operation of the loader. Therefore, the purpose of shoveling trajectory planning is to find the trajectory that can achieve low energy consumption and better operation performance, which has essential engineering significance for the loader to achieve energy saving and emission reduction, improve work efficiency, and adapt to an extreme working environment.
3.1. Parallel Shoveling Trajectory Planning
There are many methods of shoveling materials by loaders, the most commonly used of which are the one-step shoveling method, the step-by-step shoveling method, the excavation method, and the coordination shoveling method of these four shoveling methods. Due to the minimal resistance to shoveling by the loader according to the coordination shoveling trajectory, the shoveling process is smooth, the shoveling range is more extensive, and the high full bucket rate can be ensured, so the coordination shoveling method was chosen as the automatic shoveling of the loader in this test experiment [24]. The trajectory planned according to the coordination shoveling method is further divided into the straight trajectory and the curved trajectory, as shown in Figure 6.
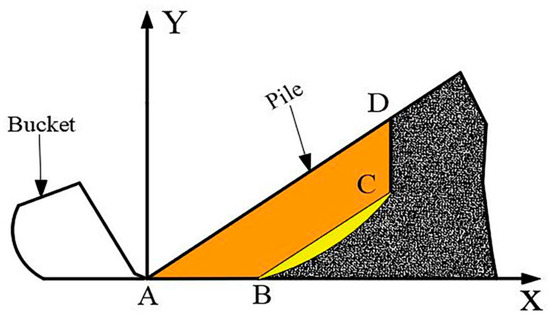
Figure 6.
Coordination shoveling trajectory.
AB is the horizontal shoveling stage; BC is the shoveling stage; CD is the bucket lifting stage; AD is the surface of the pile.
In the loader shoveling process, the bucket is first inserted horizontally into the pile from point A to point B. then it starts to cooperate with shoveling from point B to point C. Finally, the bucket is lifted from point C to point D, and the automatic shoveling ends. In the BC section, it can be a straight trajectory or a curved trajectory. However, on the premise of meeting the same shoveling volume, the loader requires less energy to shovel according to the straight trajectory than the curved trajectory [25], so the straight trajectory is more suitable for this shoveling test to reduce carbon emissions and improve efficiency.
The loader shovels the material according to the straight-line trajectory. If the inclination angle of the straight trajectory is greater than the resting angle of the material pile will produce Coulomb passive earth pressure and affect the full bucket rate. If the straight trajectory inclination angle is less than the resting angle of the pile, the shoveling resistance in the shovel excavation phase will increase [26]. Therefore, as shown in Figure 7, the inclination angle β of the straight shoveling trajectory is equal to the angle α of the pile, and such a straight shoveling trajectory is called parallel shoveling trajectory. The shoveling cross-section of the parallel shoveling trajectory is shown in Figure 6, and the bucket tooth tip trajectory formed by the bucket shoveling according to the parallel shoveling trajectory is shown in Figure 8.
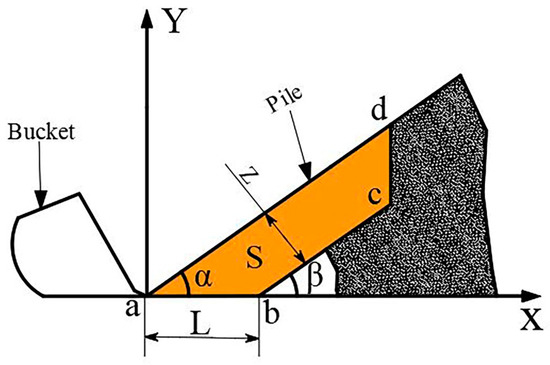
Figure 7.
Shoveling cross-section.
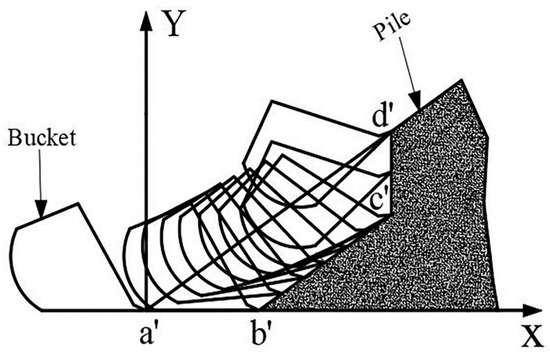
Figure 8.
Trajectory of the bucket tooth tip.
Where Z is the vertical distance between the linear shoveling trajectory and the pile surface; also known as parallel shoveling depth; α is the pile rest angle; S is the cross-sectional area.
As shown in Figure 7, the parallel shoveling trajectory has three phases, the ab interval is the horizontal insertion phase, the bc interval is the shovel digging phase, and the cd interval is the lifting phase. The shoveling cross-section S consists of the surface profile of the stockpile and the bucket tip curve. According to our previous deduction inside the literature [27], The curve equation of the bucket tip can be defined as:
where G is the rated shovel weight of the test vehicle; B is the width of the bucket; ρ is the density of the material; N is the porosity of the material.
According to Equation (1), the bucket tip position is only a function of Z, provided that the material density, porosity, rest angle of the pile, bucket width, and rated shoveling weight are known. Then different Z values are selected and brought into Equation (1) to obtain the corresponding bucket tip trajectory.
3.2. Trajectory Parameters
The test vehicle has a rated shovel weight of G = 5000 kg, a rated bucket volume of V2 = 3 m3, and a bucket width of B = 2.9 m. It is also necessary to analyze and investigate the material characteristics to determine the bucket tip trajectory of the flat bucket and to calculate the relevant essential test data later.
The material object of this shoveling test is gravel, so the characteristics of gravel are analyzed. The main objects of analysis are the diameter, rest angle, porosity, and density of gravel, as shown in Table 1.

Table 1.
Analysis of gravel characteristics.
Since the bucket tooth trajectory curve is a function of Z, the trajectory for this shoveling test was planned by changing the parallel shovel depth Z and keeping the cross-sectional area S formed by the bucket in the shoveled material constant. In other words, the automatic shoveling performance of the loader at different shoveling depths is investigated by maintaining a specific full bucket rate. The Z values of the trajectory planning are shown in Table 2.

Table 2.
Values of Z.
The Z values of Table 2 are brought into Equation (1) to calculate the shoveling trajectory for different Z values, and the shoveling trajectory diagram is shown in Figure 9. Since the bucket is lifted and turned while shoveling, the bucket is set to be evenly turned during the shoveling stage, with a total turning angle of 47.3° and a shovel cross-sectional area of 1.05 m2.
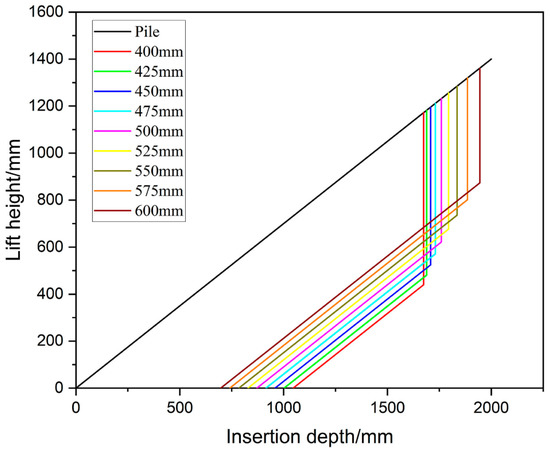
Figure 9.
Parallel shoveling trajectory.
4. Loader Automatic Shoveling Operation Performance Analysis
This test experiment mainly analyzes the five operational performances of full bucket rate, resistance, practical work performed, fuel consumption, and operating time during the automatic shoveling operation of the loader. However, since the data from the sensor test is the essential raw data and cannot be directly analyzed, it is necessary to establish the calculation formula of operational performance by combining the test method and theoretical analysis and then calculate the performance parameters according to the calculation formula and raw data.
4.1. Full Bucket Rate Analysis
The full bucket rate is one of the most critical evaluation standards for the automatic shoveling performance of wheel loaders. Any other work is futile if the full bucket rate is not up to standard. The shoveling method of manual control can only rely on the operator’s experience to meet the full bucket rate. However, frequent operations and long working hours make it difficult to ensure that the full bucket rate can reach the standard. In the case of meeting the full bucket rate, other shoveling performances may not always meet the requirements. It is not easy to achieve consistency in shoveling performance parameters each time. Therefore, the automatic shoveling of the loader is very important, which can eliminate the dilemma of manual operation shoveling and avoid some human errors.
Since this test was carried out according to the independently planned trajectory, other parameters and the test conditions were consistent, so the calculation of the full bucket rate only needed to be calculated according to the relevant parameters of the shoveling trajectory. The formula for calculating the full bucket rate is as follows:
where E is the full bucket rate; V1 is the volume of material in the bucket; and V2 is the rated volume of the bucket.
Since the rated bucket volume and the bucket’s width in Equation (2) are known, the bucket is shown in Figure 10. Therefore, the full bucket rate can be obtained by finding V1. According to the planning principle of the operating trajectory, the volume of material in the bucket is equal to the volume of material between the stockpile’s surface and the shoveling trajectory. Thus, the theoretical volume of material in the bucket is:
where V1′ is theoretically the volume of the material in the bucket; B is the bucket width; S is the shovel cross-sectional area.
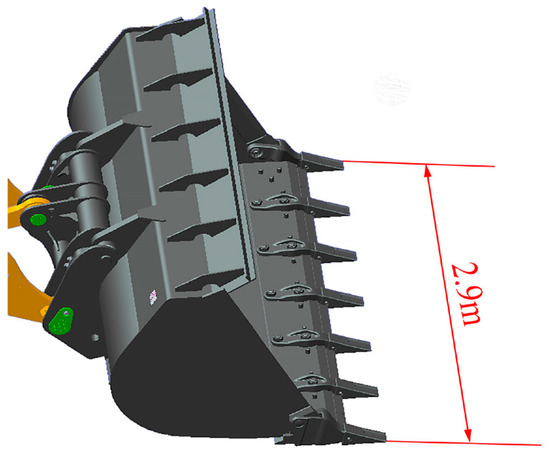
Figure 10.
Bucket.
The theoretical full bucket rate calculated from the shoveling trajectory is:
In general, it is impossible to achieve a 100% full bucket rate due to operating resistance, material particle size, and the loader’s performance, which means that the true V1 is not equal to the BS, so the specific shoveled volume in the bucket is calculated based on the porosity, the density, and the specific shoveled weight in the bucket.
Therefore, the full bucket rate is:
where V1″ is the real volume of the material in the bucket; N is the porosity of the gravel; G is the weight of the material in the bucket; and ρ is the density of the material.
4.2. Analysis of Operational Resistance
Excessive resistance of the loader’s automatic shoveling will lead to excessive energy consumption, skidding of tires, and reduction in the full bucket rate, which seriously affects the loader’s shoveling performance. There are many reasons for excessive shoveling resistance, such as material bulk, particle size, dense nucleus, etc., among which the influence of dense nuclei is greater. In the horizontal shoveling stage, as the bucket is inserted deeper, because of the characteristics of the gravel, it will squeeze the powdered gravel produced by the contact into a dense nucleus when the concentrated stress between the bucket and the gravel contact reaches the limit value. Once the dense nucleus is formed, the resistance to the bucket will sharply increase in a short period of time and reach its peak, which hinders the loader from inserting the material [28].
As shown in Figure 11, in order to study the resistance variation of the loader, pin-axis sensors were installed at connection points B1, B2, and C of the bucket to the lift arm and the connecting rod of the test vehicle. The pin sensors at points B1 and C are subjected to the same force direction in the X and Y directions, and the pin sensor at point B2 is subjected to the opposite force direction in the X direction and the same force direction in the Y direction as B1 and C. The pin sensor at point B2 is subjected to the same force direction as B1 and C. The pin-axis sensor can measure the change in horizontal resistance in the X direction and vertical resistance in the Y direction at the point of connection in real-time. Since the pin-axis sensor rotates with the bucket during the shoveling process, the measured horizontal resistance and vertical resistance also change in the same direction with the bucket. Therefore, it is necessary to calculate the horizontal force and vertical force of the bucket according to the real-time turning angle of the bucket, and the calculation formula is:
where FX is the horizontal resistance of the bucket; FY is the vertical resistance of the bucket; Fx is the real-time horizontal resistance of the bucket; Fy is the real-time vertical resistance of the bucket; and θ is the real-time bucket flip angle.
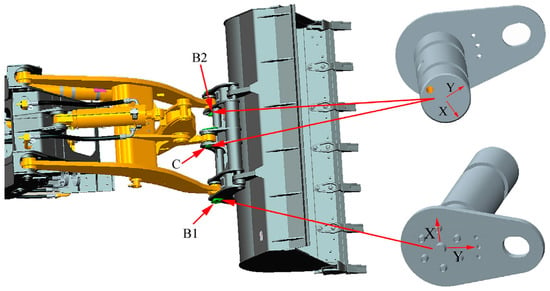
Figure 11.
Installation position and force direction of the pin-axis sensor.
4.3. Analysis of Energy Consumption of Practical Work Performed
Loaders are large, high-energy, high-emission construction machinery. In the shoveling process, in addition to the fan, heat dissipation, exhaust, transmission losses, and other aspects will produce energy consumption. The most important thing that a loader uses to do work is the energy consumption of the whole vehicle and the energy consumption of the cylinders. The whole vehicle’s energy consumption is generated by the loader’s wheels to overcome ground friction to move. The energy consumption of the cylinder is generated by the life arm cylinder and the tilt cylinder of the loader to control the bucket when shoveling the material and overcome the material’s resistance to the bucket.
Since the energy of the loader’s wheels to overcome the work of friction is transferred through the front and rear drive shafts, the energy consumption of the whole vehicle is equal to the product of the drive shaft’s torque and the variable box’s output speed. The front and rear drive shaft torques are measured by the drive shaft torque sensor, as shown in Figure 12a, and the variable box output speed is measured by the rotational speed sensor, as shown in Figure 12b. The energy consumption of the whole vehicle is calculated by the formula:
where M1 is the front drive shaft torque; M2 is the rear drive shaft torque; W is the transmission output speed.
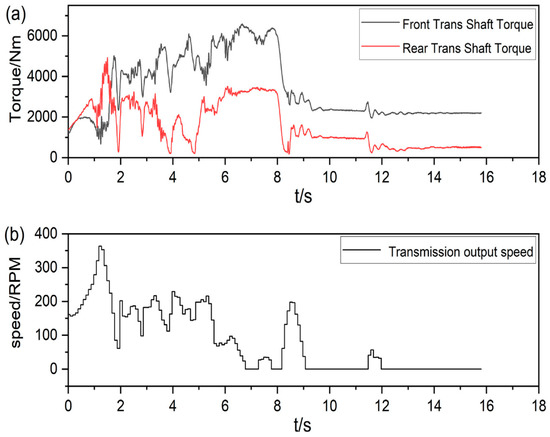
Figure 12.
(a) Torque of the front drive shaft and torque of the rear drive shaft; (b) transmission output speed.
The energy consumption of the oil cylinder is generated by the work performed by the cylinder’s expansion and contraction. It is equal to the product of the extension length of the cylinder and the force on the cylinder. The cylinder displacement is measured by the pressure sensor, as shown in Figure 13, and the cylinder pressure is measured by the pressure sensor, as shown in Figure 14. The calculation formula for the energy consumption of the lift cylinder is:
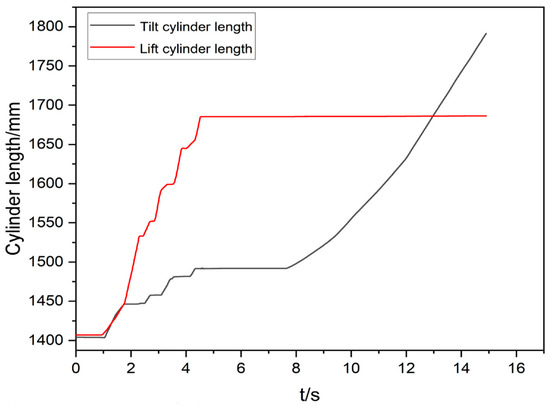
Figure 13.
Displacement of cylinder.
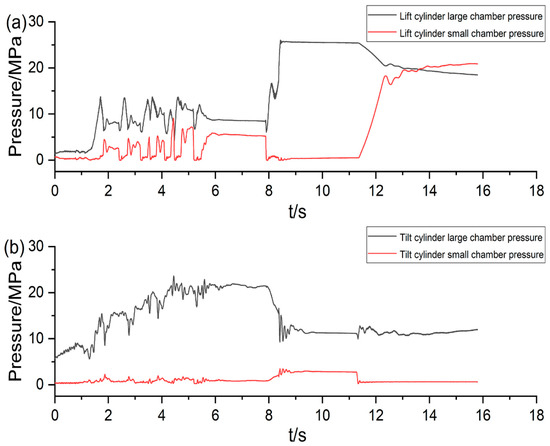
Figure 14.
(a) Pressure of the lift cylinder; (b) pressure of the tilt cylinder.
The calculation formula for the energy consumption of the tilt cylinder is
where P1 is the big chamber pressure of the lift cylinder; P2 is the pressure of the small chamber of the lift cylinder; P3 is the pressure of the big chamber of the tilt cylinder; P4 is the pressure of the small chamber of the tilt cylinder; R1 is the radius of the large chamber of the lift cylinder; R2 is the radius of the small chamber of the lift cylinder; R3 is the radius of the big chamber of the tilt cylinder; R4 is the radius of the small chamber of the tilt cylinder; l1 is the extension of the lift cylinder; l2 is the elongation of the tilt cylinder.
The loader has two lift cylinders and one rotary tilt cylinder, so the energy consumption of the cylinders is:
The total sum of energy consumption of the cylinder and the whole vehicle is:
4.4. Analysis of Operating Time and Fuel Consumption
The operating time of the loader determines the efficiency of shoveling, and the longer the working time, the higher the fuel consumption and cost will be. Therefore, in a shorter time, the full bucket rate achieves the requirement, and the fuel consumption is less, which is a more reasonable way of shoveling.
In this test, to improve the accuracy and continuity of the collected parameters, the collection frequency of the data acquisition system is 50 Hz, and a set of data is recorded every 0.002 s. This entire process is recorded, from the loader running to the first point of the track to the end of the weighing. The time and fuel consumption required for the process, from the bucket insertion into the pile to the weighing end, are called the operating time and operating fuel consumption.
5. Experimental Data Analysis
This test obtained a large number of essential performance parameters, such as full bucket rate, resistance, energy consumption, fuel consumption, and operating time, through the performance test platform of the loader. Additionally, detailed calculations and consistency analysis of these parameters were conducted to optimize the automatic shoveling process of the loader.
5.1. Analysis Method
In order to obtain an accurate range of operational performance parameters for the loader. In this paper, the 95% confidence interval of the confidence level of the operational performance parameters for each trajectory is calculated using a normal distribution. The normal distribution is shown in Figure 15.
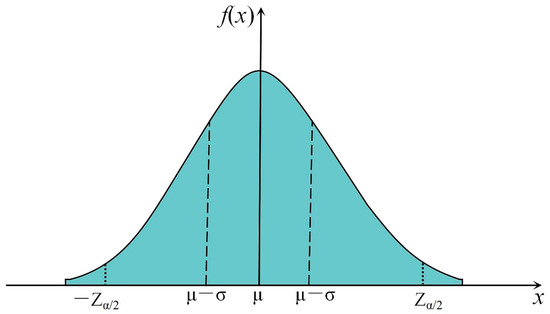
Figure 15.
Normal distribution.
µ is the expected value of the normal distribution; σ is the variance of the normal distribution; Zα/2 is the corresponding standard score.
Since the confidence level is 95% and the significance level α is 0.05, it can be concluded that:
It is known that Zα/2 = 0.96, so the two-sided confidence interval with 95% confidence is:
Therefore, by substituting the automatic operating performance parameters of each parallel shoveling trajectory into Equation (16), a parameter with 95% confidence can be statistically obtained, which means that there is a 95% probability that the actual value of the loader operating performance parameter is in the interval.
5.2. Analysis of Wheel Loader Shoveling Performance
Substituting the measured shoveling weight, the density of gravel, and the porosity into Equation (6), the full bucket rate of the wheel loader for automatic shoveling according to nine shovel trajectories is shown in Figure 16, except for the trajectory with a parallel shoveling depth of 600 mm, which has the lowest full bucket rate of 70.6% and cannot meet the actual operation requirements. The full bucket rate of the rest of the shovel trajectory was between 80% and 90%, which met the actual requirements. Among them, the full bucket rate of the trajectory with a parallel shovel depth of 400 mm is the highest, with a full bucket rate of 88.4%.
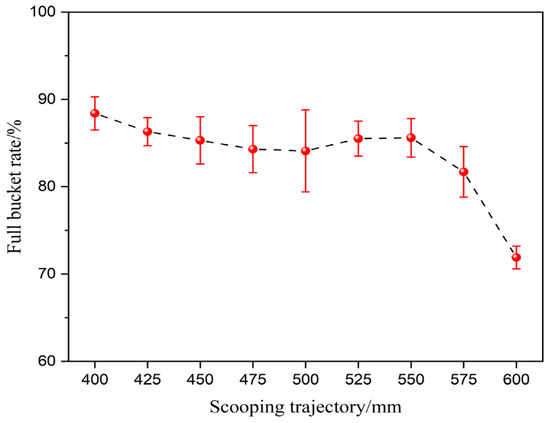
Figure 16.
Full bucket rate.
The automatic shoveling working time of the loader is shown in Figure 17. The trajectory with a parallel shovel depth of 600 mm had the lowest operating time of 12.8 s. Since the full bucket rate could not reach the requirement, the operation time of the remaining trajectories was between 16.1 and 21.3 s after excluding the trajectory with a parallel shoveling depth of 600 mm. The working time of the trajectory with parallel shoveling depths of 400 mm and 500 mm is 16.1 s and 16.5 s. The working time of the trajectory with parallel shoveling depths of 425 mm and 450 mm is higher, all reaching more than 20 s, and the working time of the rest of the trajectory is between 17 s and 20 s.
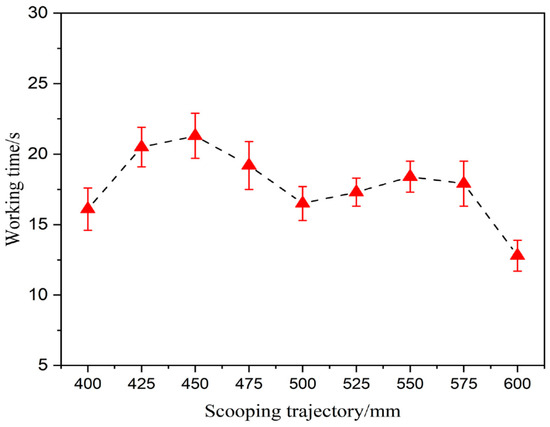
Figure 17.
Working time.
The operating fuel consumption is shown in Figure 18. After excluding the trajectory with a parallel shoveling depth of 600 mm, the operating fuel consumption of the trajectories with parallel shoveling depths of 425 mm, 450 mm, and 475 mm is higher, the highest reaches 180.4 mL, the lowest is 115.5 mL for the trajectory with a parallel shoveling depth of 400 mm, and the operating fuel consumption of the other trajectories is 130–134 mL.
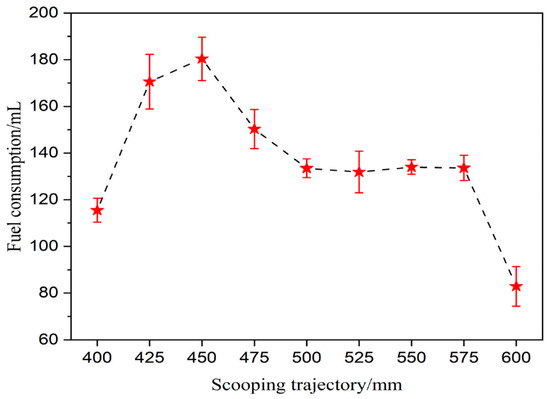
Figure 18.
Fuel consumption.
The measured front and rear drive shaft torque and engine output speed are brought into Equation (8), and the displacement, pressure, and radius of the bucket cylinder and moving arm cylinder are brought into Equations (9) and (10). The energy consumption of work performed by the cylinder and the energy consumption of work performed by the whole vehicle are obtained, respectively. As shown in Figure 19a, except for the trajectory with a parallel shoveling depth of 600 mm, the energy consumption of the work performed by the cylinder is between 288.9 kJ and 345 kJ, and the energy consumption of work performed by the whole vehicle is between 312 kJ and 388.5 kJ. The energy consumption of the work performed by the whole vehicle for each shoveling trajectory is higher than that of the work performed by the cylinder. Figure 19b shows the total energy consumption of the sum of the energy consumption of the work performed by the whole vehicle and the energy consumption of the work performed by the cylinder. The highest total energy consumption for the work was 713.5 kJ for the trajectory with a shovel depth of 400 mm. The total energy consumption for the work was also higher for shovel depths of 425 mm, 450 mm, and 500 mm, ranging from 693.7 kJ to 698.3 kJ. The operating energy consumption of the remaining trajectories is lower, except for the trajectory of the shovel depth of 600 mm; the total energy consumption of the remaining trajectories is between 600.8 kJ and 658 kJ.
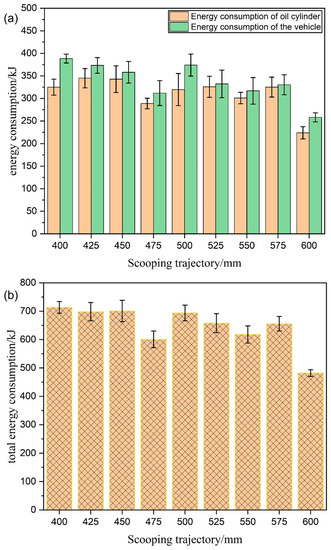
Figure 19.
(a) Energy consumption of work performed by the oil cylinder and the whole vehicle; (b) the total energy consumption of the sum of the energy consumption of the work performed by the whole vehicle and the energy consumption of the work performed by the cylinder.
The operating resistance curve of the bucket in the horizontal phase is shown in Figure 20a. The bucket starts to insert the pile from point O, and the operating resistance starts to increase. Due to the compression of the material and its lumpiness, a dense nucleus is formed in the front area of the bucket teeth, which leads to a rapid increase in the operating resistance to peak point A. The resistance at point A is the maximum operating resistance of the bucket in the horizontal shoveling phase.
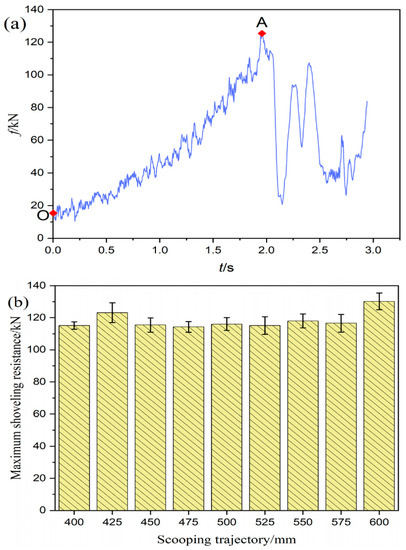
Figure 20.
(a) The operating resistance curve of the bucket in the horizontal shoveling phase; (b) the maximum operational resistance of the loader during the horizontal shoveling phase.
The maximum operating resistance of the loader in the horizontal shoveling phase is shown in Figure 20b. It can be seen that the maximum operating resistance of the nine trajectories is between 114.3 kN and 130.2 kN, and the maximum operating resistance of the trajectory with a parallel shovel depth of 600 mm is 130.2 kN, which is the largest among the nine parallel shovel trajectories. The maximum operating resistance of the trajectory with parallel shoveling depths of 400 mm and 475 mm is 115.1 kN and 114.3 kN. The maximum operating resistance of the other trajectories is between 115.5 kN and 123.1 kN.
In summary, each trajectory’s range of performance parameters was analyzed using the statistical method of normal distribution. The performance parameters of each trajectory were compared. In the case of excluding the trajectory with a parallel shovel depth of 600 mm, the trajectory with a parallel shovel depth of 400 mm has the highest full bucket rate, the lowest operating time, the lowest fuel consumption, and the highest total energy consumption for practical work performed, and the lowest maximum operating resistance. Therefore, the shoveling performance of the trajectory with a parallel shoveling depth of 400 mm is optimal compared with other trajectories in terms of all aspects of performance.
Where Point O is the operating resistance of the bucket at the beginning of its insertion into the pile. Point A is the maximum operating resistance of the bucket during the horizontal shoveling phase.
5.3. Comparison of Automatic Shoveling and Manually Controlled Shoveling
The test platform has the function of automatic shoveling and manual control of shoveling. Therefore, to verify whether the performance of the trajectory with a parallel shoveling depth of 400 mm could meet the standard construction requirements, the test platform was changed to a manually controlled shoveling mode, and the experienced driver controlled the loader to test the gravel. To ensure the consistency of the test environment, the manually controlled shoveling still used the same test equipment and materials as the automatic shoveling, and the sensors in each part of the loader could still obtain real-time shoveling data from the loader. Manually controlled shoveling only needs to control the loader to move the material a certain distance and keep the bucket close to the ground. The driver can control the loader to shovel and lift the bucket to the body 2/3 height, measure the weight of the material in the bucket, and the test is over.
The performance parameters of various aspects of automatic shoveling and manually controlled shoveling are shown in Figure 21a,b. The full bucket rate of the trajectory with a parallel shoveling depth of 400 mm is only 1% less than the manually controlled one. However, the operating time of the whole shoveling process is 15.3% less than the manually controlled shoveling; the fuel consumption is 4.9% less; the energy consumption of practical work is 10.7% more, and the maximum operating resistance is 20.5% lower. Therefore, although the full bucket rate of the trajectory with a parallel shovel depth of 400 mm is 1% smaller than that of the manually controlled shoveling, the performance of the shoveling in other aspects is better than that of the manually controlled shoveling. Therefore, the operational performance of the trajectory with a parallel shoveling depth of 400 mm meets the practical requirements.
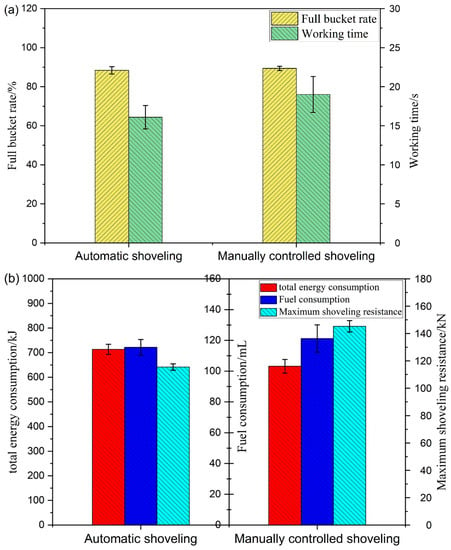
Figure 21.
(a) Full bucket rate and operating time of automatic shoveling and manually controlled shoveling; (b) total energy consumption, fuel consumption, maximum operating resistance of automatic shoveling, and manually controlled shoveling.
6. Conclusions
In this paper, the basic parameters, such as shovel weight, cylinder displacement and pressure, and torque of the drive shaft for different trajectories, were obtained through automatic shoveling tests of the loader. Next is to combine the formula of operational performance to calculate the performance parameters of different trajectories. The confidence intervals for these performance parameters were calculated by the normal distribution. Finally, these parameters were compared and analyzed to find the optimal operating trajectory in order to verify whether the optimal trajectory can achieve the construction requirements. In a consistent test environment, an experienced driver controls the loader to perform manually controlled shoveling in the manual mode of the loader performance test platform. Through comprehensive comparative analysis, the operational performance of the trajectory with a parallel shoveling depth of 400 mm is better than the operational performance of manually controlled shoveling. It proves that the trajectory has led to a significant improvement in the operational performance of the wheel loader.
This study provides an important method and practical value for automatic shoveling, energy saving, and green design of wheel loaders, which can be directly applied in engineering practice. Its methods and theories are also applicable to other construction machinery. In the subsequent research, different materials will be used to improve the method’s applicability.
Author Contributions
Conceptualization, Y.C. and H.J.; methodology, Y.C.; validation, Y.C. and H.J.; formal analysis, H.J.; investigation, T.Z.; resources, G.S.; data curation, Y.C.; writing—original draft preparation, H.J.; writing—review and editing, Y.C.; supervision, G.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 61962007), the Key Projects of Guangxi Natural Science Foundation (Grant No. 2018GXNSFDA294001), the S&T Fund of Guangxi Province (Grant No. 1598021-2).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article. The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dadhich, S.; Sandin, F.; Bodin, U.; Andersson, U.; Martinsson, T. Field test of neural-network based automatic bucket-filling algorithm for wheel-loaders. Autom. Constr. 2019, 97, 1–12. [Google Scholar] [CrossRef]
- Didhich, S.; Bodin, U.; Andersson, U. Key challenges in automation earth-moving machines. Automt. Constr. 2016, 68, 212–222. [Google Scholar] [CrossRef]
- Sandzimier, R.J.; Asada, H.H. A Data-Driven Approach to Prediction and Optimal Bucket-Filling Control for Autonomous Excavators. IEEE Robot. Autom. Lett. 2020, 5, 2681–2688. [Google Scholar] [CrossRef]
- Zhang, R.H.; Huang, M. Data processing method for dynamic weighing of materials shoveled by loader. J. Mech Electr. Eng. 2021, 38, 1486–1493. [Google Scholar]
- Bi, Q.S.; Wang, G.Q.; Wang, Y.P.; Yao, Z.W.; Hall, R. Digging Trajectory Optimization for Cable Shovel Robotic Excavation Based on a Multi-Objective Genetic Algorithm. Energies 2020, 13, 3118. [Google Scholar] [CrossRef]
- Cao, B.W.; Liu, X.H.; Chen, W.; Yang, K.; Liu, D. Intelligent energy-saving operation of wheel loader based on identifiable materials. J. Mech. Sci. Technol. 2020, 3, 1081–1090. [Google Scholar] [CrossRef]
- Backas, J.; Ghabcheloo, R.; Tikkanen, S.; Huhtala, K. Fuel optimal controller forhydrostatic drives and real-world experiments on a wheel loader. Int. J. Fluid Power 2016, 17, 187–201. [Google Scholar] [CrossRef]
- Alshaer, T.; Darabseh, T.; Alhanouti, M. Path planning modeling and simulation of anautonomous articulated heavy construction machine performing a loading cycle. Appl. Math. Model. 2013, 37, 5315–5325. [Google Scholar] [CrossRef]
- Liu, X.J.; Sun, D.Y.; Qin, D.T.; Liu, J.L. Achievement of Fuel Savings in Wheel Loader by Applying Hydrodynamic Mechanical Power Split Transmissions. Energies 2017, 10, 1267. [Google Scholar] [CrossRef]
- Osumi, H.; Uehara, T.; Sarta, S. Estimation of Reaction Force from Rock Piles in Scooping Operation by Wheel Loaders. Energies 2010, 5, 693–698. [Google Scholar] [CrossRef]
- Frank, B.; Kleinert, J.; Filla, R. Optimal control of wheel loader actuators in gravel applications. Autom. Constr. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Huang, J.F.; Kong, D.W.; Gao, G.Z. Data-driven reinforcement-learning-based automatic bucket-filling for wheel loaders. Appl. Sci. 2021, 11, 9191. [Google Scholar] [CrossRef]
- Gottschalk, M.; Jacbos, G.; Kramer, A. Test Method for Evaluating the energy Efficiency of Wheel Loaders. ATZoffhighway Worldwild 2018, 11, 44–49. [Google Scholar] [CrossRef]
- Shi, J.R.; Sun, D.Y.; Qin, D.T.; Hu, M.H.; Kan, Y.Z.; Ma, K.; Chen, R.B. Planning the trajectory of an autonomous wheel loader and tracking its trajectory via adaptive model predictive control. Robot. Auton. Syst. 2020, 131, 103570. [Google Scholar] [CrossRef]
- Park, S.; Choi, Y.; Park, H.S. Optimization of truck-loader haulage systems in an underground mine using simulation methods. Geosystem Eng. 2016, 9, 222–231. [Google Scholar] [CrossRef]
- Cao, B.; Liu, X.; Chen, W.; Yang, K.; Tan, P. Skid-Proof Operation of Wheel Loader Based on Model Prediction and Electro-Hydraulic Proportional Control Technology. IEEE Access 2020, 8, 81–92. [Google Scholar] [CrossRef]
- Siriborvornratanakul, T. A deep learning based road distress visual inspection system using Modified U-Net. In Proceedings of the International Conference on Human-Computer Interaction, Bari, Italy, 30 August–3 September 2021; pp. 345–355. [Google Scholar]
- Azulay, O.; Shapiro, A. Wheel Loader Scooping Controller Using Deep Reinforcement Learning. IEEE Access 2021, 9, 24145–24154. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, X.; Wang, Y. Human-like autonomous car-following model with deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2018, 97, 348–368. [Google Scholar] [CrossRef]
- Backman, S.; Lindmark, D.; Bodin, K.; Servin, M.; Mörk, J.; Löfgren, H. Continuous control of an underground loader using deep reinforcement learning. Machines 2021, 9, 216. [Google Scholar] [CrossRef]
- Dadhich, S.; Sandin, F.; Bodin, U.; Andersson, U.; Martinsson, T. Adaptation of a wheel loader automatic bucket filling neural network using reinforcement learning. In Proceedings of the 2020 IJCNN, Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar]
- Bhola, M.; Kumar, A.; Kumar, N. Energy-efficient control of hydrostatic transmission of a front-end loader machine using machine learning algorithm and its sensitivity analysis. J. Automob. Eng. 2022, 30, 1–23. [Google Scholar] [CrossRef]
- Dadhich, S.; Sandin, F.; Bodin, U. Predicting bucket-filling control actions of a wheel-loader operator using a neural network ensemble. In Proceedings of the 2018 IJCNN, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar]
- Yu, X.J.; Huai, Y.H.; Li, X.F.; Wang, D.W.; Yu, A. Shoveling trajectory planning of loader based on Kriging and particle swarm optimization. J. Jilin Univ. 2020, 50, 437–444. [Google Scholar]
- Gong, J.; Cui, Y.X. Trajectory planning of loader shovel excavation operation. J. Mech. Eng. 2009, 45, 29–34. [Google Scholar] [CrossRef]
- Meng, Y.; Fang, H.Z.; Liang, G.D.; Gu, Q.; Liu, L. Bucket Trajeory Optimization under the Automatic Scooping of LHD. Energies 2019, 12, 3919. [Google Scholar] [CrossRef]
- Chen, Y.H.; Meng, Y.; Xiang, S.S.; Bai, G.X.; Liang, G.D.; Xie, G.J. Shovel path planning of loader based on beetle antennae search. Int. J. Comput. Integr. Manuf. 2022, 10, 1–10. [Google Scholar]
- Wang, Q.G.; Li, B.W. Excavating Machinery and Supporting Equipment, 2nd ed.; China University of Mining and Technology Press: Xuzhou, China, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).