An Embedding-Based Approach to Repairing OWL Ontologies

Abstract

High-quality ontologies are critical to ontology-based applications, such as natural language understanding and information extraction, but logical conflicts naturally occur in the lifecycle of ontology development. To deal with such conflicts, conflict detection and ontology repair become two critical tasks, and we focus on repairing ontologies. Most existing approaches for ontology repair rely on the syntax of axioms or logical consequences but ignore the semantics of axioms. In this paper, we propose an embedding-based approach by considering sentence embeddings of axioms, which translates axioms into semantic vectors and provides facilities to compute semantic similarities among axioms. A threshold-based algorithm and a signature-based algorithm are designed to repair ontologies with the help of detected conflicts and axiom embeddings. In the experiments, our proposed algorithms are compared with existing ones over 20 real-life incoherent ontologies. The threshold-based algorithm with different distance metrics is further evaluated with 10 distinct thresholds and 3 pre-trained models. The experimental results show that the embedding-based algorithms could achieve promising performances.

1. Introduction

Ontologies play a fundamental role in many fields such as natural language understanding, semantic information extraction, and intelligent information integration to provide a formal representation of interested knowledge [1,2,3,4,5,6]. In particular, with the rapid development of knowledge graphs [7], ontologies became more essential for integrating, querying, and maintaining knowledge graphs [8,9,10]. High-quality ontologies are particularly critical. An ontology consists of a set of entities such as classes and properties. It is also composed of a set of axioms that describe the characteristics of some properties or the relationships among the entities. To represent an ontology, several ontology languages have been proposed, and OWL (Web Ontology Language) (https://www.w3.org/TR/owl-overview/, accessed on 15 November 2022) is a standard language recommended by W3C. Description logics [11], as the logic foundation of OWL, provide reasoning support for OWL ontologies. So far, ontologies have been widely applied in many fields such as intelligent city and life science [12,13]. Furthermore, ontologies provide schema restrictions for knowledge graphs [7] to facilitate their integration, querying, and maintenance. In particular, high-quality ontologies are critical to ontology-based applications, such as natural language understanding and information extraction. However, in practice, logical conflicts inevitably occur in the lifecycle of ontology development, such as ontology evolution [14] and ontology matching [15]. In general, logical conflicts can be classified into logical inconsistency and incoherence. An inconsistent ontology indicates that no model can explain it. Reasoning an inconsistent ontology with standard reasoners cannot obtain meaningful entailments. An incoherent ontology contains at least one concept interpreted as an empty set (called an unsatisfiable concept). Adding instances to an unsatisfiable concept will produce inconsistency, which has negative impacts on Semantic Web applications including terminological reasoning, data transformation, and query answering [16,17]. Therefore, it is paramount to handle such logical conflicts.

To deal with incoherence or inconsistency, conflict detection and ontology repair become two critical tasks [18]. The former demonstrates why an ontology is incoherent or inconsistent, and the latter is to compute a diagnosis for regaining logical coherence or consistency. We mainly focus on repairing ontologies in this paper and refer the readers to the references [19,20,21] to obtain more details about detecting conflicts. To repair an ontology automatically, it is often required to locate the logical conflicts in the ontology first and then choose at least one axiom from each conflict as a diagnosis [22,23,24]. That is, removing all axioms in the diagnosis will regain logical coherence or consistency. When choosing axioms for deleting, various ranking strategies have been proposed to assign a degree to each axiom in conflict. Most of the existing strategies to rank axioms for ontology repair rely on the syntax of axioms while ignoring the semantics of axioms. For example, the works in [22,25,26] use a scoring function by computing the frequency of occurrence of each axiom in all conflicts. The work in [27] proposes to rank the axioms by considering the usages of each signature in an axiom. Relatively, the authors in [23] rank different diagnoses by aggregating the truth values of the axioms in a diagnosis, where a truth value is calculated by an embedding model. Their experimental results have shown that the proposed approach is significantly more effective than classical random methods in ranking the best diagnoses. Although this work employs an embedding model to encode axioms as vectors for preserving their semantics, it only pays more attention to simple axioms as triples while ignoring complex axioms expressed in different ontology languages.

In this paper, we focus on dealing with incoherence in ontologies whose axioms can be much more complex than triples. Precisely, we propose an embedding-based approach that translates OWL axioms into natural language sentences, and then ranks the axioms in conflicts by employing the embeddings of such translated sentences. We further provide facilities to compute the semantic similarities among axioms. In this way, an axiom in a conflict could be associated with a degree by considering the semantic relationships between the axiom and others. Two algorithms, namely the threshold-based algorithm and the signature-based one, are designed to repair ontologies according to detected conflicts and axiom embeddings. To verify our proposed approach, we compared existing repair methods over 20 real-life incoherent ontologies. The experimental results indicate that the embedding-based algorithms could achieve promising performances. In addition, we discuss the advantages of each algorithm and provide recommendations for users to choose a suitable repair algorithm or ranking strategy.

The main contributions of this paper are summarized as follows:

• An embedding-based approach to repairing ontologies is proposed by considering both the syntax and the semantics of axioms in an ontology, and three metrics are defined to rank axioms based on the embeddings of axioms.
• A threshold-based algorithm and a signature-based algorithm are proposed to instantiate our embedding-based approach. Both of them can be configured with different pre-trained models and various thresholds.
• Abundant experiments have been conducted over 20 real-life incoherent ontologies. We implement our algorithms and existing repair algorithms using four ranking strategies. The experimental results show that two embedding-based algorithms could enhance the effectiveness of the traditional signature-based ranking strategy, and the threshold-based algorithm $\mathsf{ThrCosAlg}$ with model $\mathsf{m}\mathsf{4}$ is able to remove fewer axioms and differentiate various axioms.

The rest of the paper is organized as follows. Section 2 introduces the background knowledge about description logics and word embedding. Section 3 presents our general approach. Specific algorithms to instantiate the approach are proposed in Section 4. Section 5 shows various experimental results. Related works are introduced in Section 6, followed by conclusions and future works in Section 7.

2. Background Knowledge

This section introduces Description Logics (DLs) and the basic notations of logical conflicts. It also explains word embedding together with sentence embedding.

2.1. Description Logics

A DL-based ontology could describe three kinds of entities: concepts, roles and individuals in a domain. An individual describes an instance in a specific domain, and an individual name means a single individual. For example, $\mathsf{Tim-Bernerds} \mathsf{Lee}$ is an individual name describing a person, and Nanjing is an individual name describing a place. A concept indicates a set of individuals, and a role represents a binary relation between the individuals and individual names. The roles can be further divided into abstract roles and datatype roles. The domain and range of an abstract role are concepts. If the range of a role is a datatype literal such as string or integer, this role is called a datatype role [28]. The concepts and roles can be atomic or complex. A complex one is constructed based on the atomic ones by using various kinds of constructors such as existential restriction (∃) and universal restriction (∀). With different constructors, many DL languages can be formed, such as $\mathcal{ALC}$ allowing transitive roles, role hierarchy and inverse operation, and $\mathcal{SHI}$ further allowing role hierarchy and inverse operation.

A DL-based ontology could also describe the characteristics of some properties and the relationships among the entities by various axioms. Such axioms can be divided into TBox (terminology axioms) and ABox (assertion axioms). A TBox mainly describes those relationships among concepts and properties such as concept inclusion axioms in the form of $C⊑D$ and disjoint role axioms in the form of $C⊑\neg D$, where C and D are concepts. An ABox describes those relationships that are relevant to individuals, such as concept assertions in the form of $C\left(a\right)$ and equality assertions in the form of $a=b$, where a and b are individuals. It is noted that the concepts, abstract roles and datatype roles in DL-based ontologies correspond to the classes, object properties and data properties in OWL, respectively.

In an ontology, if there exist unsatisfiable concepts, minimal unsatisfiability-preserving sub-TBoxes (abbreviated as MUPS) are often computed to explain the unsatisfiability of such a concept.

Definition 1

((MUPS) [16]). For an unsatisfiable concept name C in a TBox $\mathcal{T}$, a sub-TBox ${\mathcal{T}}^{\prime }\subseteq \mathcal{T}$ is a MUPS of $\mathcal{T}$ with respect to C if C is unsatisfiable in ${\mathcal{T}}^{\prime }$ and there is no sub-TBox ${\mathcal{T}}^{″}\subset {\mathcal{T}}^{\prime }$ such that C is unsatisfiable in ${\mathcal{T}}^{″}$.

To explain the incoherence of an ontology, a set of minimal incoherence-preserving sub-TBoxes (abbreviated as MIPS) can be calculated.

Definition 2

((MIPS) [16]). For an incoherent TBox $\mathcal{T}$, its sub-TBox ${\mathcal{T}}^{\prime }\subseteq \mathcal{T}$ is a MIPS of $\mathcal{T}$ if ${\mathcal{T}}^{\prime }$ is incoherent and every sub-TBox ${\mathcal{T}}^{″}\subset {\mathcal{T}}^{\prime }$ is coherent.

From Definitions 1 and 2 we can observe that a MIPS is a MUPS, but not vice versa.

When repairing an incoherent ontology, a diagnosis is often computed. That is, removing or modifying the axioms in the diagnosis could regain coherence. The formal definition of a diagnosis is described below.

Definition 3

(Diagnosis). For an incoherent ontology, $O$ and a sub-ontology $O^{\prime }\subseteq O$, $O^{\prime }$ is a diagnosis of $O$ if $O\setminus O^{\prime }$ is coherent. $O\setminus O^{\prime }$ indicates removing all axioms in $O^{\prime }$ from $O$.

To repair an ontology automatically, it is often desired to achieve some kind of minimal change [22] and compute a minimal diagnosis by keeping information as much as possible.

Definition 4

((Minimal Diagnosis) [29]). For an incoherent ontology $O$ and a sub-ontology $O^{\prime }\subseteq O$, $O^{\prime }$ is a minimal diagnosis of $O$ if it is a diagnosis of $O$ and there is no $O^{″}\subset O^{\prime }$ such that $O\setminus O^{″}$ is coherent.

2.2. Word Embedding

In the field of natural language processing, vectorizing a text is a key step to convert the text into numbers such that the text can be processed by machine learning models [30]. The smallest semantic unit in a text is a word, so the vectorization task of a text can be changed into the vectorization of words. When representing the semantics of phrases, sentences or paragraphs, sentence embedding is used to compute embeddings of their word sequences [31]. Word embedding is to represent words with a continuous vector space, which is a low-dimensional dense vector and can represent the semantics of words. Such a representation method becomes unprecedentedly popular since the work in [32] was published in 2013. This work extends the original Skip-gram model to improve the quality of vectors and the efficiency of the model. It also provides a tool called Word2Vec to facilitate the usage of the extended model.

To represent words or sentences with vectors, a pre-trained model is welcomed due to its high-dimensional space and semantic representation. Such models have been widely accepted by both academic and industrial researchers in the past ten years [30,33,34]. They are pre-trained on an original task with a large corpus and used on a target task by tuning the corresponding parameters according to the characteristics of the target task. Namely, people can directly use a pre-trained model to compute vectors on their tasks without performing a training process by themselves. The popular models Word2Vec [32], BERT [35], Sentence-BERT [36] and CoSENT (https://kexue.fm/archives/8847, accessed on 15 November 2022) belong to pre-trained language models.

To represent the semantics of classes or individuals in an ontology, the work in [37] provides a tool called NaturalOWL (http://www.aueb.gr/users/ion/publications.html, accessed on 15 November 2022). This tool translates those OWL statements that are relevant to a class or individual into natural language sentences. Example 1 shows an example to generate sentences for a given class. From the description of the class $\mathsf{IceCream}$ we can see that the relationship of $\mathsf{DisjointClasses}$ and $\mathsf{SubClassOf}$ are translated to “isn’t a kind of” and “is a kind of” separately. The existential restriction (i.e., ObjectSomeValuesFrom) is converted to “at least one”.

Example 1.

Take the class $\mathsf{IceCream}$ in the widely used ontology $\mathsf{pizza}$ (https://protege.stanford.edu/ontologies/pizza/pizza.owl accessed on 15 November 2022) as an example. There are three axioms (We use the syntax adopted by OWL API to represent the axioms in an ontology, and ignore all namespaces for clarity) that are relevant to the class $\mathsf{IceCream}$ (see below):

$\mathsf{SubClassOf}\left(\mathsf{IceCream\; Food}\right)$

$\mathsf{DisjointClasses}\left(\mathsf{IceCream\; Pizza\; PizzaBase\; PizzaTopping}\right)$

$\mathsf{SubClassOf}\left(\mathsf{IceCream\; ObjectSomeValuesFrom}\right(\mathsf{hasTopping\; FruitTopping}\left)\right)$

By using NaturalOWL API, the description of $\mathsf{IceCream}$ is obtained:

IceCream isn’t a kind of PizzaBase, Pizza and PizzaTopping, and IceCream is a kind of Food. IceCream has topping at least one FruitTopping.

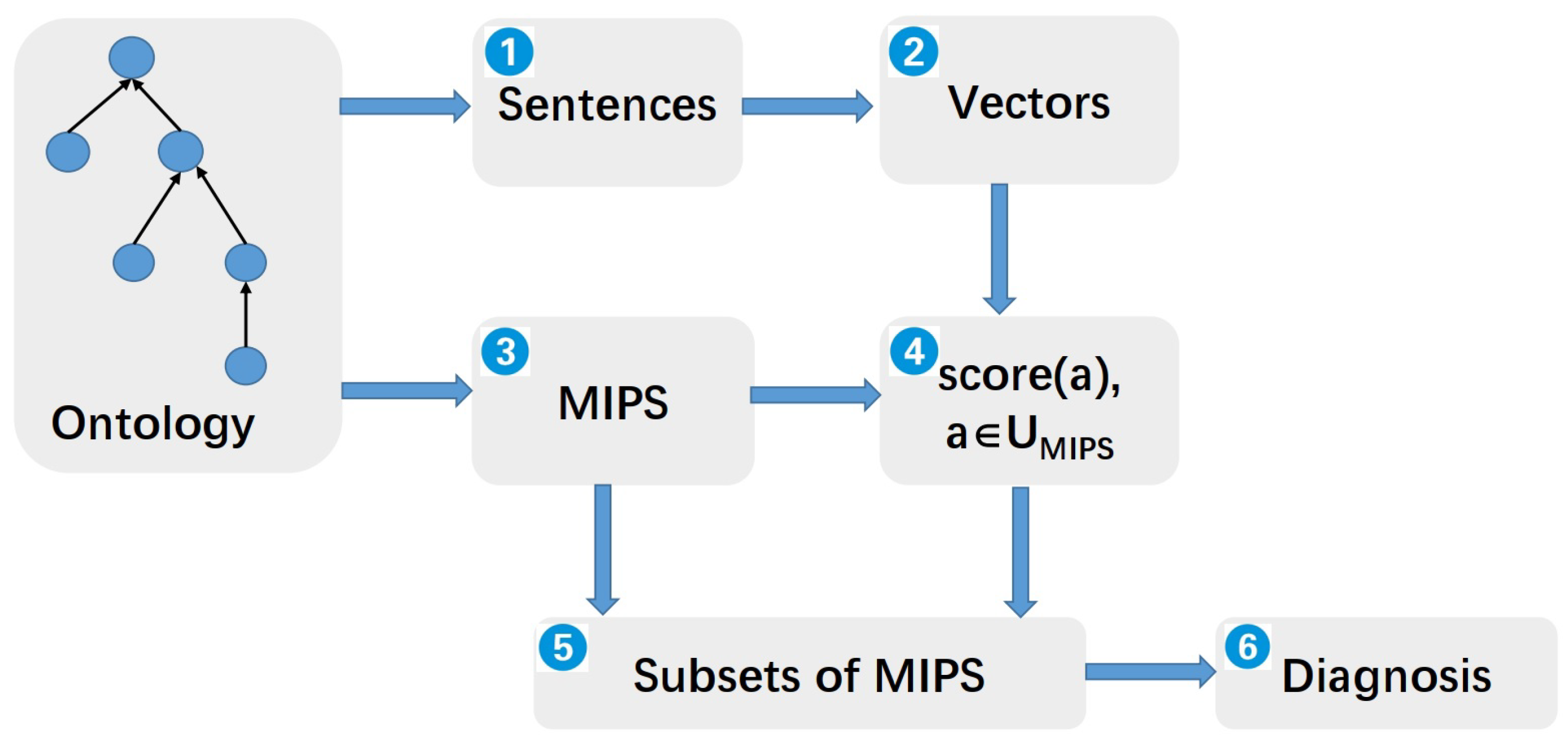
3. Approach

To rank axioms in conflicts based on embeddings, we propose a general approach to computing a diagnosis (see Figure 1). The proposed approach comprises six parts, the first three parts (labeled 1, 2 and 3) can be regarded as offline information preparation, and the other parts (labeled 4, 5 and 6) compute similarities between the axioms to generate a diagnosis automatically.

Figure 1. The embedding-based approach to repairing an ontology.

3.1. Information Preparing

When translating an axiom into one or multiple natural language sentences, we borrow the idea given in NaturalOWL [37]. Nonetheless, NaturalOWL does not translate all kinds of axioms or entities. It does not consider those axioms about properties such as property inclusion axioms and transitive properties. Furthermore, nested $\mathsf{ObjectIntersectionOf}$ and $\mathsf{ObjectUnionOf}$ operators are not allowed. Table 1 presents most of the rules implemented in NaturalOWL to transfer concepts or axioms to phrases or sentences separately. These rules are summarized manually by taking a toy example as this tool’s input and then observing its outputs. This example is an OWL ontology constructed by using a widely used ontology editor Protege (https://protege.stanford.edu/, accessed on 15 November 2022), and contains various kinds of axioms, complex concepts and properties. In case some axioms cannot be translated by NaturalOWL, we do transformation by keeping their main characteristic. For instance, the axiom “$\mathsf{SymmetricObjectProperty}\left(\mathsf{op}\right)$” is translated to “op is symmetric”, and the axiom “$\mathsf{SubClassOf}\left(\mathsf{A\; DataMaxCardinality}\right(\mathsf{3\; dp\; owl}:\mathsf{real}\left)\right)$” is transformed to “A dp at most 3 owl:real”.

Table 1. Rules to translate OWL concepts or axioms into phrases or sentences, respectively, where a and b are individual names, A and B are concepts, n indicates an integer, $op$ and $dp$ indicate an object property and a data property separately, and v is a value.

Ontology Elements	OWL Representation	Phrases or Sentences
Concepts	$\mathsf{ObjectSomeValuesFrom}\left(\mathsf{op\; A}\right)$	op at least one A
	$\mathsf{ObjectAllValuesFrom}\left(\mathsf{op\; A}\right)$	op only A
	$\mathsf{ObjectHasValue}\left(\mathsf{op\; a}\right)$	op a
	$\mathsf{ObjectIntersectionOf}\left(\mathsf{A\; B}\right)$	A and B
	$\mathsf{ObjectUnionOf}\left(\mathsf{A\; B}\right)$	A or B
	$\mathsf{ObjectExactCardinality}\left(\mathsf{n\; op\; A}\right)$	op exactly n A
	$\mathsf{ObjectMinCardinality}\left(\mathsf{n\; op\; A}\right)$	op at least n A
	$\mathsf{ObjectMaxCardinality}\left(\mathsf{n\; op\; A}\right)$	op at most n A
Axioms	$\mathsf{SubClassOf}\left(\mathsf{A\; B}\right)$	A is a kind of B
	$\mathsf{DisjointClasses}\left(\mathsf{A\; B}\right)$	A isn’t a kind of B
	$\mathsf{EquivalentClasses}\left(\mathsf{A\; B}\right)$	A is a kind of B
	$\mathsf{ClassAssertion}\left(\mathsf{A\; a}\right)$	a is a A
	$\mathsf{ObjectPropertyAssertion}\left(\mathsf{op\; a\; b}\right)$	a op b
	$\mathsf{DataPropertyAssertion}\left(\mathsf{dp\; a\; v}\right)$	a dp v

After obtaining the sentences for all axioms in an ontology, a pre-trained model could be adopted to represent the sentences with vectors, such as the models Word2Vec [32], BERT [35], Sentence-BERT [36] and CoSENT (Cosine Sentence) (https://kexue.fm/archives/8847, accessed on 15 November 2022). In this paper, we use the models Sentence-BERT and CoSENT to compute embeddings due to their excellent performances in computing similarities for sentences in the English language. Sentence-BERT makes balances between performance and efficiency and trains the upper classification function by supervised learning. CoSENT uses a ranking loss function, which makes the training process closer to prediction. More details about the experimental results to evaluate various pre-trained models can be found on the official website of PyPi (https://pypi.org/project/text2vec/, accessed on 15 November 2022), which indicates the Python Package Index and is a repository of software for the Python programming language. For instance, the following vector with large dimensions is obtained by applying the model Sentence-BERT (i.e., $\mathsf{m}\mathsf{1}$ introduced in Section 5.2) to represent the sentence “Parent is a kind of Animal”:

$$(0.08,0.25,0.15,0.39,-0.43,-0.20,0.14,0.03,0.38,0.09,...,-0.01,0.67,0.07).$$

With the obtained vectors, the semantic similarity between two axioms/sentences is calculated. Suppose we have two vectors $v_1$ and $v_2$, both of which have d dimensions. Two similarity metrics can be defined based on the widely used distance measures Cosine Distance and Euclidean Distance.

Definition 5.

The similarity metric based on Cosine Distance (marked as $si{m}_{cos}$) is formally defined as below:

$si{m}_{cos}(v_1,v_2)={\displaystyle \frac{1}{2}}(1+{\displaystyle \frac{v_1·v_2}{\left|\right|v_1\left|\right|\times \left|\right|v_2\left|\right|}})={\displaystyle \frac{1}{2}}(1+{\displaystyle \frac{{\sum }_{i=1}^d{v}_{1i}\times v_{2i}}{\sqrt{{\sum }_{i=1}^d{\left(v_{1i}\right)}^2}\times \sqrt{{\sum }_{i=1}^d{\left(v_{2i}\right)}^2}}})$

Here, $v_{1i}$ and $v_{2i}$ indicate the ith element in the vectors $v_1$ and $v_2$, respectively. d is the dimension of $v_1$ or $v_2$, both of them have the same dimension.

Definition 6.

The similarity metric based on Euclidean Distance (marked as $si{m}_{euc}$) is defined as below:

$si{m}_{euc}(v_1,v_2)={\displaystyle \frac{k}{k+\sqrt{{\sum }_{i=1}^d{(v_{1i}-v_{2i})}^2}}}$

Here, k indicates a positive integer. d is the dimension of $v_1$ or $v_2$, both of which have the same dimension.

The similarities computed by Definitions 5 and 6 range from 0 to 1 because the two original distance metrics have been normalized. Especially in Definition 6, a positive integer k is used for normalization. The greater the integer k, the larger the similarity $si{m}_{euc}$. Thus, k is set to be 4 in our evaluation because the similarities could be evenly distributed within (0, 1) according to our observations. In addition, the two metrics are reflexive because $sim(v,v)=1$ for any vector v. They are also symmetric since $sim(v_1,v_2)=sim(v_2,v_1)$ for any vectors $v_1$ and $v_2$. Here, $sim$ can be $si{m}_{cos}$ or $si{m}_{euc}$.

Example 2.

Take the following axioms in the ontology $\mathsf{km}\mathsf{1500}$ as examples.

$a1:\mathsf{SubClassOf}(\mathsf{information}\_\mathsf{kernel}\_\mathsf{technology}\_\mathsf{c}\mathsf{technology}\_\mathsf{c})$

$a2:\mathsf{ObjectPropertyDomain}(\mathsf{boost}\_\mathsf{r}\mathsf{technology}\_\mathsf{c})$

$a3:\mathsf{SubClassOf}(\mathsf{technology}\_\mathsf{c}\mathsf{information}\_\mathsf{resource}\_\mathsf{c})$

By applying the cosine similarity metric, we obtain

$si{m}_{cos}(a1,a2)=0.36$ and $si{m}_{cos}(a1,a3)=0.9$.

The similarity between axioms $a1$ and $a2$ is $0.36$, which is quite different from that between axioms $a1$ and $a3$ (i.e., $0.9$), although both pairs have shared entities. It is because $a1$ and $a2$ have different axiom types while both $a1$ and $a3$ belong to subsumption.

It is noted that, wekeep the similarities between axioms and the ranks of axioms to two decimal places by rounding. The main reason is that we ignore the slight difference between two values such as 0.563 and 0.564. In this way, multiple axioms can have more chance to share the same rank in a MUPS or MIPS, and it becomes possible to find multiple diagnoses and choose one of them as a final repair solution.

In our approach, another preparation task is to compute all MIPS for each ontology. The computation of MIPS could rely on all MUPS of all unsatisfiable concepts in an ontology [22], or be computed directly [20]. A single MUPS can be computed by applying a black-box approach or a glass-box approach, and all MUPS of an unsatisfiable concept are often computed based on the hitting set tree algorithm [19,38]. Of course, it may not be always desired to compute MIPS when resolving incoherence due to the efficiency problem, but we focus on computing diagnoses based on all MIPS of an ontology.

3.2. Diagnosis Generating

With the information obtained during the preparation step, each axiom in a MIPS needs to be associated with a degree. According to these degrees, a subset is then extracted from each MIPS. Those axioms in such subsets are regarded as candidates to form a diagnosis. Namely, selecting at least one axiom from each subset will resolve the incoherence of the considered ontology.

To compute a degree for an axiom in an ontology, we consider the semantic relationships between this axiom and others in the ontology. Based on a similarity metric $sim$, a degree of an axiom $\alpha$ in an ontology O can be defined by assuming that $emb\left(\alpha \right)$ indicates the embedding of the axiom $\alpha$ (See Definition 7). This definition computes the average semantic similarity between the axiom $\alpha$ and each axiom in O as the degree of $\alpha$.

Definition 7.

Given an axiom α in an ontology O, its degree with respect to the entire ontology O is defined as below:

$d_{global}(\alpha ,O)={\displaystyle \frac{1}{\left|O\right|}}{\sum }_{\beta \in O}sim(emb\left(\alpha \right),emb\left(\beta \right))$.

This degree is called a global degree and is denoted as $d_{global}$.

It is noted that two axioms with low similarity often indicate that their semantic relations are weak, or even both axioms have no semantic relations. Thus, a threshold can be used to filter those axioms that have low similarity with $\alpha$. The degree of $\alpha$ (see Definition 8) is then computed based on the selected axioms. In Definition 8, the similarity between any axiom in S and $\alpha$ is higher than the threshold, and only those axioms in S will contribute to the degree of $\alpha$. Namely, this definition computes the average semantic similarity between the axiom $\alpha$ and each axiom in S as the degree of $\alpha$.

Definition 8.

Given an axiom α in an ontology O, its degree with respect to a pre-defined threshold t, denoted as $d_{thr}$, is defined as below:

$d_{thr}(\alpha ,O,t)={\displaystyle \frac{1}{\left|S\right|}}{\sum }_{\beta \in S}sim(emb\left(\alpha \right),emb\left(\beta \right))$,

where$S=\left\{\beta \right|sim\left(emb\right(\alpha ),emb(\beta \left)\right)>t,\beta \in O\}$.

To ensure two axioms have semantic relations, we provide another definition to compute a degree for an axiom by considering those axioms that contain at least one entity appearing in the axiom (see Definition 9). A signature of an axiom can be a concept name, a property name or an individual name appearing in the axiom. Definition 9 computes the average semantic similarity between the axiom $\alpha$ and each axiom in T as the degree of $\alpha$.

Definition 9.

The signature-based degree of an axiom α in an ontology O, denoted as $d_{sig}$, is formally defined as below:

$d_{sig}(\alpha ,O)={\displaystyle \frac{1}{\left|T\right|}}{\sum }_{\beta \in T}sim(emb\left(\alpha \right),emb\left(\beta \right))$,

where $T=\left\{\beta \right|sig\left(\alpha \right)\cap sig\left(\beta \right)\ne \varnothing ,\beta \in O\}$, and $sig\left(\alpha \right)$ returns all signatures in α.

4. Algorithm

In this section, we design two concrete algorithms (i.e., a threshold-based algorithm and a signature-based algorithm) to repair an incoherent ontology based on the definitions of similarity degrees.

Algorithm 1 provides the details about the threshold-based repair algorithm. It takes an incoherent ontology O, all of its MIPS $MIPS\left(O\right)$, axiom embeddings ($emb\left(\alpha \right)$ indicates the embedding of the axiom $\alpha$), and a threshold t ranging from 0 to 1 as inputs, and outputs a diagnosis. This algorithm assumes all MIPS of O have been computed and are denoted as $MIPS\left(O\right)$. In this algorithm, the degree of each axiom in a MIPS needs to be computed first (see lines 4–13), which is the average similarity over those axiom pairs whose similarity values are greater than the threshold. According to these degrees, a subset $M^{\prime }$ is extracted from each MIPS M such that only the axioms with the lowest degree are contained in $M^{\prime }$ (see lines 15–18). Afterwards, a diagnosis can be generated over these subsets by applying the linear integer programming (abbreviated as ILP)-based approach [26] (see lines 20–30). We choose this approach to computing a minimal diagnosis instead of the traditional one (i.e., hitting set tree-based approach [22]) due to its high efficiency.

Algorithm 1: A threshold-based algorithm to repair an incoherent ontology.

The ILP-based approach first associates a binary variable to each axiom in the union of all MIPS (see lines 20–21). An objective function is then constructed over all binary variables by regarding them as the same important (see Line 22). For each set in $\mathcal{M}$, a constraint $c_i$ is constructed (see lines 23–27). Finally, the function $\mathsf{ILP}\_\mathsf{Solver}$ is invoked to generate an optimal assignment (see Line 28), and this can be achieved through invoking a traditional ILP solver such as the commercial linear programming tool Cplex. It is an optimization software developed by IBM ILOG (https://www.ibm.com/analytics/cplex-optimizer, accessed on 15 November 2022). For this function, one of its parameters $min$ indicates minimizing the objective function. The returned assignment $S_{assi}$ is the first one found by the ILP solver. Based on this assignment, we can find those axioms whose corresponding variables have the value 1 to form a final solution D (see Line 30).

The signature-based repair algorithm can be obtained easily by modifying Algorithm 1 slightly. Namely, the condition of $sim(emb\left(ax\right),emb\left(a{x}^{\prime }\right))>t$ in Line 7 is changed to $sig\left(ax\right)\cap sig\left(a{x}^{\prime }\right)\ne \varnothing$. That is, for an axiom $ax$, if another axiom $a{x}^{\prime }$ contains at least one signature from $ax$, it will contribute to the degree of $ax$, where a signature can be a class, a property or an individual.

5. Experiments

In this section, we first introduce the data set used in our experiments and experimental settings. We then provide experimental results of the preparation step. The subsequent three subsections introduce the experimental results of comparing repair algorithms, different thresholds and models. Finally, a detailed discussion of the results is provided.

5.1. Data Set

The data set comes from our previous work about benchmarking incoherent ontologies presented in [39]. Since the approach proposed in this paper considers the semantics of axioms, those ontologies with meaningless entity names are excluded from our experiments. For example, in ontology $\mathsf{DICE-A}$, “C521744” is a class name and “R19763” is a property name. They are meaningless, and we do not consider such an ontology. Since the proposed algorithms compute all MIPS in an ontology, we do not consider those ontologies all of whose MIPS cannot be found within a limited time or memory. For instance, we choose the sub-ontology $\mathsf{km}\mathsf{1500}–\mathsf{3500}$ instead of its complete version $\mathsf{km}\mathsf{1500}$. In this way, most of the existing incoherent ontologies (i.e., 13 incoherent ontologies) and 7 merged incoherent ontologies provided by [39] are chosen.

Table 2 presents the details about the chosen incoherent ontologies. The ontology names that consist of three parts and are connected with two symbols of “-” indicate those ontologies constructed by merging two source ontologies and an alignment between them. Here, an alignment consists of a set of correspondences, and correspondence can be translated into an OWL axiom (see [39] for more details). Take ontology $\mathsf{ALOD}\mathsf{2}\mathsf{Vec-confof-edas}$ as an example. Its name consists of $\mathsf{ALOD}\mathsf{2}\mathsf{Vec}$, $\mathsf{confof}$ and $\mathsf{edas}$. $\mathsf{ALOD}\mathsf{2}\mathsf{Vec}$ [40] is an ontology matching system, $\mathsf{confof}$ and $\mathsf{edas}$ indicate two source ontologies. This merged ontology is obtained by merging $\mathsf{confof}$, $\mathsf{edas}$, and the alignment generated by the system $\mathsf{ALOD}\mathsf{2}\mathsf{Vec}$. Similarly, the other 6 merged ontologies use the ontology matching systems $\mathsf{ATBox}$ [41], Lily [42], VeeAlign [43] and Wiktionary [44]. Those source ontologies come from the conference track provided by Ontology Alignment Evaluation Initiative (http://oaei.ontologymatching.org/2020/ accessed on 15 November 2022), which is a very popular platform to evaluate various ontology matching systems.

Table 2. Ontology information, where “SubPr” indicates the number of $\mathsf{SubObjectPropertyOf}$ axioms, “Cl”, “OP” and “DP” mean classes, object properties and data properties, respectively.

Ontology	TBox	ABox	SubCl	DisjCl	SubPr	Domain	Range	CL	OP	DP
ALOD2Vec-confof-edas	826	115	156	450	0	86	86	142	43	43
ATBox-cmt-confof	427	0	97	70	0	95	95	68	62	33
CHEM-A	110	0	46	6	4	18	18	48	9	11
dbpedia_2014	5763	1	745	20	964	2375	2527	814	1310	1725
Economy	577	1045	409	71	3	47	50	339	46	8
Geography	1621	0	682	939	0	0	0	400	0	0
km1500–3500	3500	0	2584	608	0	169	139	3671	261	0
koala	36	8	17	1	0	5	5	21	4	1
Lily-cmt-conference	511	0	91	41	13	123	123	88	95	28
Lily-edas-ekaw	869	115	177	481	8	74	74	177	63	20
MGED	1654	0	567	1087	0	0	0	225	68	0
miniTambis	173	0	125	3	0	0	0	183	44	0
pizza	697	11	259	398	4	6	7	100	8	0
proton	1777	0	278	1346	49	82	60	266	78	34
Terrorism	448	422	94	1	51	215	134	100	132	91
Transportation	926	226	452	317	5	81	76	445	89	4
University	46	4	32	5	0	1	1	30	11	1
VeeAlign-edas-iasted	990	119	339	408	0	91	91	243	68	23
Wiktionary-cmt-confof	431	0	97	70	0	95	95	68	62	33
Wiktionary-confof-edas	826	115	156	450	0	86	86	142	43	43

From Table 2, we observe that $\mathsf{dbpedia}\_\mathsf{2014}$ has a large TBox (i.e., 5763 axioms) and contains many $\mathsf{SubObjectPropertyOf}$ or $\mathsf{SubDataPropertyOf}$ axioms (i.e., 964 axioms). In its TBox, most axioms are used to describe the domains or ranges of the properties (nearly 5000 such axioms). As for ontologies $\mathsf{MGED}$ and $\mathsf{Geograph}$, most of their axioms describe disjointness relations among the classes. For ontology $\mathsf{km}\mathsf{1500}–\mathsf{3500}$, most of its axioms are subsumption, and there are also many disjointness axioms.

Furthermore, the information about MIPS in a selected ontology can be seen in Table 3, where all MIPS are obtained from the work presented in [39]. It can be observed that ontology $\mathsf{km}\mathsf{1500}–\mathsf{3500}$ has quite a lot of unsatisfiable concepts (i.e., 734), and most of the others have no more than 30 unsatisfiable concepts. For those ontologies containing more than 30 unsatisfiable concepts, they also contain many MIPS. For instance, $\mathsf{km}\mathsf{1500}–\mathsf{3500}$ and $\mathsf{Economy}$ have 146 and 47 MIPS, respectively. For the found MIPS, the maximal size is no more than 16, and a MIPS often contains no more than 10 axioms on average. Overall, these ontologies have various numbers of MIPS, and the size of a MIPS varies differently (i.e., from 2 to 16).

Table 3. Information about MIPS in all selected ontologies.

Ontology	Unsatisfiable Concepts	Number of MIPS	Size of MIPS
			Minimal	Maximal	Average
ALOD2Vec-confof-edas	7	18	6	11	8.1
ATBox-cmt-confof	5	2	7	7	7
CHEM-A	37	6	5	6	5.5
dbpedia_2014	2	1	7	7	7
Economy	51	47	3	5	3.5
Geography	11	31	3	5	4
km1500–3500	734	146	2	16	6.7
koala	3	3	4	4	4
Lily-cmt-conference	6	24	9	11	9.8
Lily-edas-ekaw	13	13	4	7	5.6
MGED	72	70	3	8	5.9
miniTambis	30	3	2	6	4
pizza	2	3	3	4	3.3
proton	24	17	2	8	5
Terrorism	14	5	3	3	3
Transportation	62	36	2	8	4.6
University	8	4	3	5	4
VeeAlign-edas-iasted	16	17	4	6	5.2
Wiktionary-cmt-confof	25	13	6	9	7.1
Wiktionary-confof-edas	7	82	5	13	10.5

5.2. Experimental Settings

All experiments were performed on a laptop with 1.99 GHz Intel Core ${}^{TM}$ CPU and 16 GB RAM, using a 64-bit Windows 11 operating system. A time limit of 1000 s is set to compute a diagnosis for an incoherent ontology based on the pre-computed MIPS and similarities between axioms. Each algorithm is evaluated with respect to its effectiveness and efficiency. When repairing an ontology by using a repair algorithm, the effectiveness of this algorithm indicates the number of removed axioms to resolve the incoherence in the ontology. The efficiency of the algorithm is the time to compute a diagnosis by taking an ontology and the information obtained by the preparation phase as inputs.

In our experiments, two pre-trained models Sentence-BERT and CoSENT are used with different configurations, and we call them four models (see below) for simplicity. The configurations are obtained according to the experimental results provided in PyPi.

• $\mathsf{m}\mathsf{1}$: The implementation of Sentence-BERT with model name “paraphrase-multilingual-MiniLM-L12-v2” and encoder type of averaging.
• $\mathsf{m}\mathsf{2}$: The implementation of CoSENT with model name “bert-base-nli-mean-tokens” and encoder type of “first-last-avg”.
• $\mathsf{m}\mathsf{3}$: The implementation of CoSENT with model name “bert-base-uncased” and encoder type of “first-last-avg”.
• $\mathsf{m}\mathsf{4}$: The implementation of Sentence-BERT with model name “bert-base-nli-mean-tokens” and encoder type of “cls”.

Here, “cls” is a special word and has no meaning. Its embedding should only contain semantic information of its context, which is regarded as sentence embedding. “first-last-avg” means averaging the word embeddings in the first and last layer of the model.

We evaluate the threshold-based repair algorithm and the signature-based one with two similarity metrics, and thus obtain the following four algorithms:

• $\mathsf{ThrCosAlg}$: Repair an ontology by using the threshold-based algorithm (i.e., Algorithm 1) with Cosine Distance (i.e., Definition 5).
• $\mathsf{ThrEucAlg}$: Repair an ontology by using the threshold-based algorithm with Euclidean Distance (i.e., Definition 6).
• $\mathsf{SigCosAlg}$: Repair an ontology by using the signature-based algorithm with Cosine Distance.
• $\mathsf{SigEucAlg}$: Repair an ontology by using the signature-based algorithm with Euclidean Distance.

Furthermore, four traditional ranking strategies are chosen to compare with ours because they have been frequently used in the existing works. Four repair algorithms (see below) are then designed by integrating each ranking strategy within the same framework. That is, such a repair algorithm is obtained by replacing the strategy of computing a degree for an axiom in Algorithm 1 while keeping the rest of Algorithm 1 nearly unchanged.

• $\mathsf{BaseAlg}$: This is a baseline algorithm to compute a minimal diagnosis based on all MIPS directly without ranking the axioms. Namely, it applies the ILP-based approach to all MIPS directly without computing degrees for axioms.
• $\mathsf{ScoreAlg}$: This is a score-based algorithm, and associates a score to an axiom in MIPS, where the score correspondences to the number of MIPS containing this axiom [22]. Different with Algorithm 1, $\mathsf{ScoreAlg}$ chooses those axioms with the highest score from each MIPS.
• $\mathsf{SigAlg}$: This is a signature-based algorithm, and ranks an axiom by summing the reference counts in other axioms for all entities appearing in the axiom [27]. An entity here can be a class name, a property name or an individual name. The rest of this algorithm is the same as Algorithm 1.
• $\mathsf{LogicAlg}$: It is a logic-based algorithm, and ranks an axiom by considering the impact on an ontology when the axiom is removed from the ontology [27]. The impact of an axiom is actually measured by how many entailments are lost when removing the axiom. The rest of this algorithm is the same as Algorithm 1.
• $\mathsf{ShapAlg}$: This algorithm ranks axioms by Shapley Minimum Inconsistency Value defined in [45]. This ranking strategy assigns a penalty to an axiom $\alpha$ in a MIPS, where the penalty is inversely proportional to the size of a MIPS where $\alpha$ is contained. The rest of this algorithm is the same as Algorithm 1.

All of these repair algorithms mentioned above (all implementations together with our data set and experimental results can be downloaded from https://github.com/QiuJi345/embRepair, accessed on 15 November 2022). They are implemented with OWL API (http://owlcs.github.io/owlapi/ accessed on 15 November 2022) in Java. In addition, computing similarities between axioms based on a pre-trained model is implemented in Python. It is noted that we implement the algorithms $\mathsf{SigAlg}$ and $\mathsf{LogicAlg}$ based on the corresponding implementation in SWOOP [46]. Furthermore, the widely used DL reasoner Pellet [47] is selected to perform reasoning tasks.

5.3. Results of Preparation

For the preparation phase, the consumption time of each task is discussed below. These tasks can be seen as offline ones. Because translating axioms in an ontology to sentences is very efficient, we will not provide the details about the time of this task. Usually, it took no more than 2 s to finish this task. For ontologies $\mathsf{km}\mathsf{1500}–\mathsf{3500}$ and $\mathsf{dbpedia}\_\mathsf{2014}$ with many axioms, it spent about 4 s and 7 s, respectively.

During the preparation process, computing embeddings for the obtained sentences is the most time-consuming task. Figure 2 presents the time to compute the embeddings of the sentences transformed from an ontology by applying the four pre-trained models mentioned in Section 5.2. Obviously, $\mathsf{m}\mathsf{1}$ is the most efficient model, and others perform similarly. Take the ontology $\mathsf{dbpedia}\_\mathsf{2014}$ as an example. $\mathsf{m}\mathsf{1}$ spent 128 s while around 340 s for the other three models. The amount of time spent is determined by the size of an ontology. The ontology $\mathsf{dbpedia}\_\mathsf{2014}$ has the most axioms (i.e., 5764 axioms) among all selected ontologies, and thus each model spent the most time computing embeddings for this ontology. The ontology $\mathsf{koala}$ contains no more than 50 axioms, and thus, less than 4 s were spent for each model.

Figure 2. Time in milliseconds (y-axis) for each ontology to compute similarities for all axiom pairs in each ontology by using Cosine Distance.

When computing similarities for sentence pairs, it is much more efficient than computing embeddings. Figure 3 shows the time to compute similarities for each ontology by using Cosine Distance or Euclidean Distance. From this figure and Figure 2 we can see that computing similarities for an ontology often took no more than 10 s while more than 10 s (even more than 100 s) for computing embeddings. In addition, it is obvious that no big difference can be observed between the two distance metrics. The amount of time consumed here is also determined by the size of an ontology.

Figure 3. Time in milliseconds (y-axis) for each ontology to compute similarities for axiom pairs in each ontology by using two distance metrics.

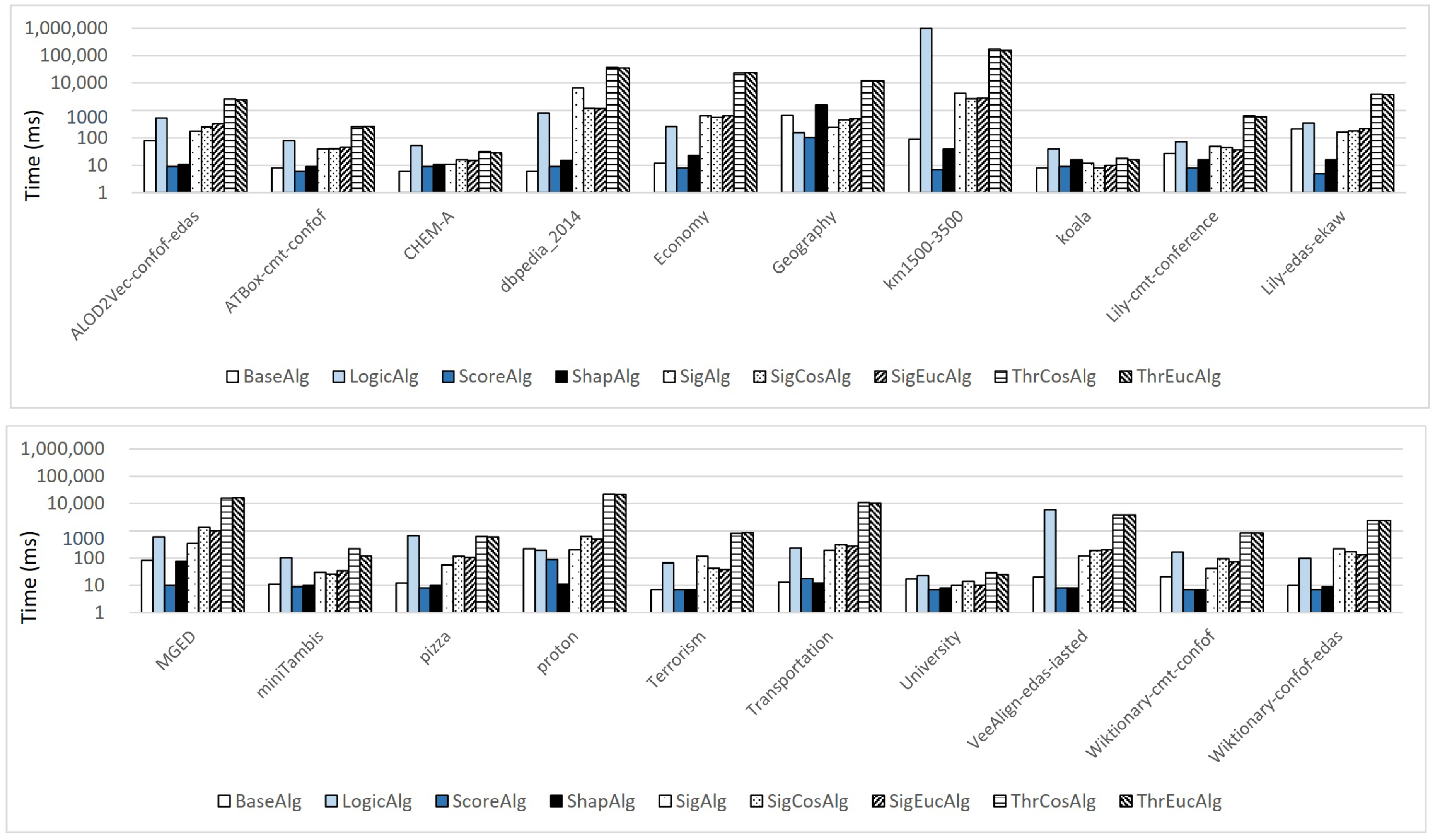
5.4. Results of Comparing Repair Algorithms

In this section, our algorithms are compared with the existing ones with respect to effectiveness and efficiency. The four embedding-based algorithms use the model $\mathsf{m}\mathsf{1}$ and set the threshold to be 0.5.

5.4.1. Results about Effectiveness

Table 4 presents the number of the axioms removed by each repair algorithm to restore the coherence of an incoherent ontology.

Table 4. Repair results about the number of the axioms removed by each repair algorithm (using the model $\mathsf{m}\mathsf{1}$ and the threshold 0.5), where “n.a.” indicates “not available”.

Ontology	BaseAlg	LogicAlg	ScoreAlg	ShapAlg	SigAlg	SigCosAlg	SigEucAlg	ThrCosAlg	ThrEucAlg
ALOD2Vec-confof-edas	1	1	1	1	2	4	4	5	1
ATBox-cmt-confof	1	1	1	1	1	2	2	2	1
CHEM-A	1	1	1	1	1	1	1	3	1
dbpedia_2014	1	1	1	1	1	1	1	1	1
Economy	8	34	8	8	47	22	23	36	20
Geography	9	11	9	10	11	12	13	11	13
km1500–3500	19	n.a.	26	26	39	38	38	38	30
koala	1	2	1	1	2	3	3	3	3
Lily-cmt-conference	1	1	1	1	2	1	1	2	2
Lily-edas-ekaw	4	4	5	5	6	5	5	8	7
MGED	3	7	3	4	9	21	20	7	7
miniTambis	3	3	3	3	3	3	3	3	3
pizza	2	2	2	2	2	3	3	3	3
proton	8	12	8	9	15	12	12	12	11
Terrorism	1	5	1	1	5	5	5	1	4
Transportation	13	15	13	14	24	23	23	19	20
University	3	3	3	3	3	3	3	3	4
VeeAlign-edas-iasted	2	2	2	2	12	5	5	2	3
Wiktionary-cmt-confof	3	3	3	3	5	6	6	4	8
Wiktionary-confof-edas	1	1	1	1	3	5	5	5	1
Total	85	109	93	97	193	175	176	168	143

Obviously, $\mathsf{LogicAlg}$ cannot deal with ontology $\mathsf{km}\mathsf{1500}–\mathsf{3500}$ because the reasoning process of computing entailments for each axiom MIPS cannot be finished within the limited time (i.e., 1000 milliseconds). Similar to the work in $\mathsf{LogicAlg}$ [27], we mainly consider those entailments that are subsumption. In ontology $\mathsf{km}\mathsf{1500}–\mathsf{3500}$, too many such entailments can be inferred for some axioms, and thus, the process is quite time-consuming. Take the following axiom in a MIPS in $\mathsf{km}\mathsf{1500}–\mathsf{3500}$ as an example:

$\mathsf{SubClassOf}(\mathsf{information}\_\mathsf{cservice}\_\mathsf{c})$

$\mathsf{LogicAlg}$ needs to compute all descendants (denoted as $S_{des}$) of the concept $\mathsf{information}\_\mathsf{c}$ and all ancestors (denoted as $S_{anc}$) of the concept $\mathsf{service}\_\mathsf{c}$ by invoking the reasoner first, then create axioms in the form of $\mathsf{SubClassOf}$$(C_1,C_2)$ ($C_1\in S_{des}$ and $C_2\in S_{anc}$) as this axiom’s entailments. Since $\mathsf{service}\_\mathsf{c}$ is an unsatisfiable concept and all concept names except unsatisfiable concepts are regarded as this concept’s ancestors, we obtain 2937 ancestors in total (i.e., 3671 concept names minus 734 unsatisfiable concepts) for $\mathsf{service}\_\mathsf{c}$. Moreover, the concept $\mathsf{information}\_\mathsf{c}$ has 18 descendants obtained by reasoning. Therefore, more than 50 thousand entailments (i.e., 18 × 2937 = 52,866) were obtained for the axiom. This is the main reason why $\mathsf{LogicAlg}$ failed to compute a diagnosis within limited resources.

Comparing various repair algorithms, the following observations can be obtained:

(1)

The baseline algorithm $\mathsf{BaseAlg}$ is able to find a minimal diagnosis as expected. This can be explained by the fact that it applies the ILP-based approach to all MIPS directly, and the ILP-based approach has been proven to find minimal diagnoses [26].

(2)

The score-based algorithm $\mathsf{ScoreAlg}$ has similar performances as $\mathsf{BaseAlg}$ since it selects the axioms with the highest score from each MIPS. Thus, it can find a minimal diagnosis in most cases. In addition, the ranking strategy in $\mathsf{ShapAlg}$ is similar to that in $\mathsf{ScoreAlg}$. The more times an axiom appears in MIPS, the higher the rank of the axiom is. One main difference between them is that the former is also dependent on the size of a MIPS. Thus, both algorithms perform similarly.

(3)

For those ontologies that $\mathsf{BaseAlg}$ removed more than five axioms, the original signature-based algorithm $\mathsf{SigAlg}$ often removed much more axioms than others, and it removed 193 axioms in total for all selected ontologies. For example, $\mathsf{SigAlg}$ removed 47 axioms for the ontology $\mathsf{Economy}$ while no more than 36 axioms for others.

(4)

For each ontology that $\mathsf{BaseAlg}$ removed less than five axioms, $\mathsf{LogicAlg}$ can always find a minimal diagnosis as $\mathsf{BaseAlg}$. It is because most of the axioms in MIPS do not have any entailments such that nearly all axioms in a MIPS have the same rank. For instance, although the ontology $\mathsf{Wiktionary-confof-edas}$ has 82 MIPS and 24 distinct axioms in these MIPS, only 3 axioms have entailments.

(5)

Two embedding-based algorithms by considering the signature of axioms performed similarly. Namely, two distance measures do not make any big difference. Furthermore, both of them outperformed the original signature-based algorithm $\mathsf{SigAlg}$. It shows that $\mathsf{SigCosAlg}$ and $\mathsf{SigEucAlg}$ can reduce the number of removed axioms.

(6)

As a whole, two threshold-based algorithms performed better than the three signature-based ones, especially $\mathsf{ThrEucAlg}$. Each of them removed less than 170 axioms in total (143 axioms for $\mathsf{ThrEucAlg}$) while more than 175 axioms for a signature-based algorithm.

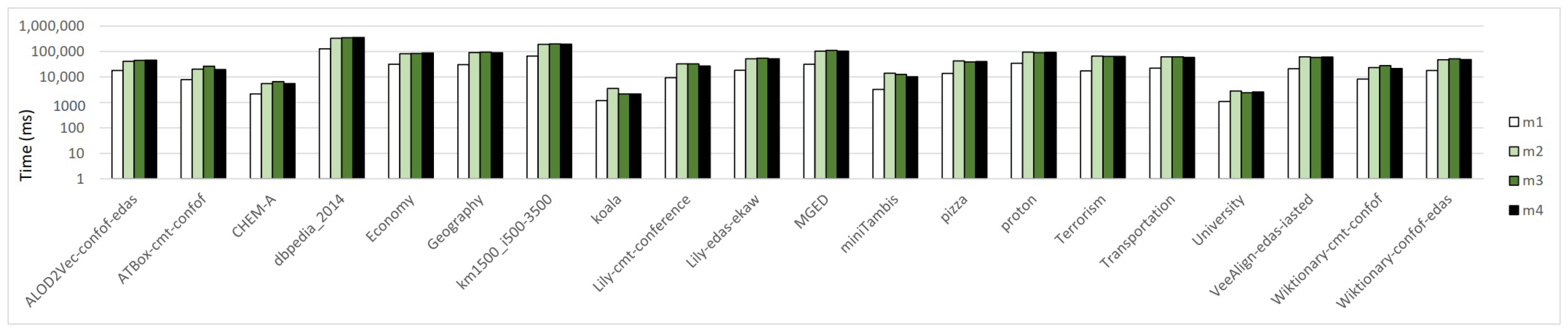
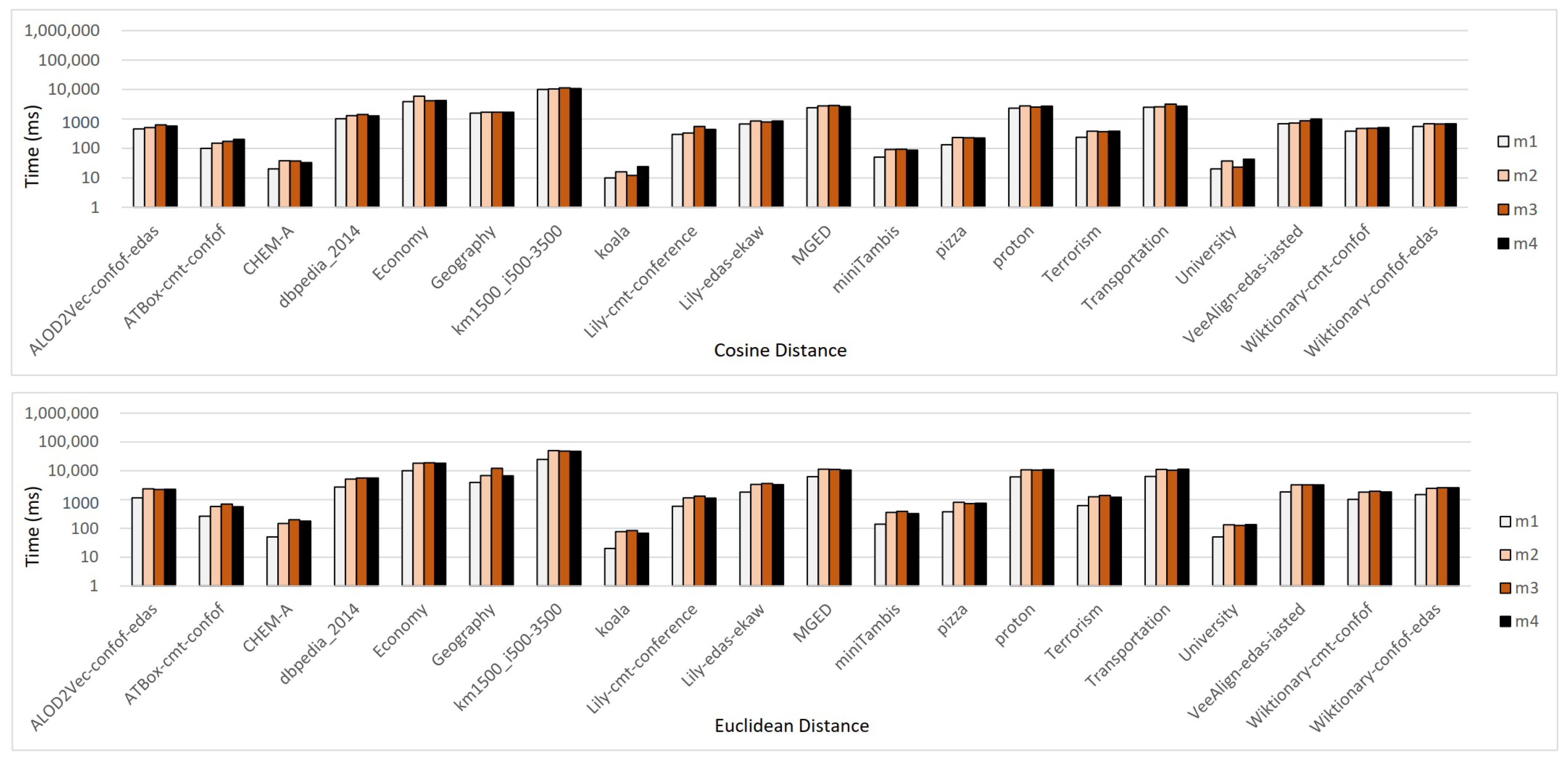
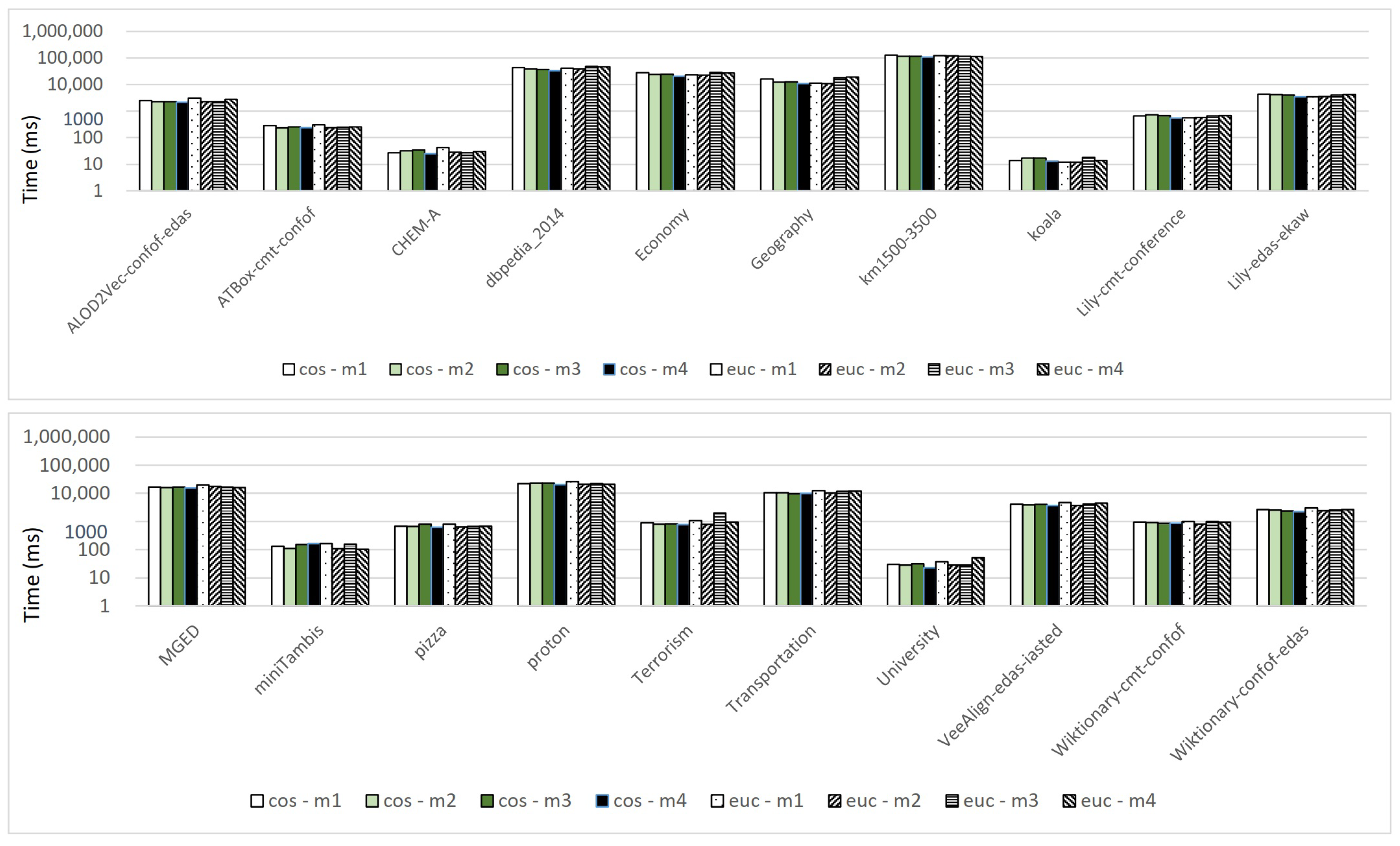
5.4.2. Results about Efficiency

Figure 4 presents the time to compute a diagnosis for each selected ontology. For the ontology $\mathsf{km}\mathsf{1500}–\mathsf{3500}$, $\mathsf{LogicAlg}$ cannot finish the repair process within the limited time (i.e., 1000 s).

Figure 4. Time in milliseconds (y-axis) for each incoherent ontology to compute diagnoses using the model $\mathsf{m}\mathsf{1}$ and the threshold 0.5.

From the figure, we observe that $\mathsf{ScoreAlg}$ performs best and is able to finish most of the processes within 10 milliseconds. $\mathsf{BaseAlg}$ performed slightly worse than $\mathsf{ScoreAlg}$, and it spent less than 100 milliseconds for most of the ontologies. This can be explained by the fact that $\mathsf{BaseAlg}$ applies the ILP-based approach to all MIPS directly while $\mathsf{ScoreAlg}$ is based on those subsets extracted from all MIPS. As the similarities of $\mathsf{ScoreAlg}$ and $\mathsf{ShapAlg}$ are similar, their performances are also close. $\mathsf{LogicAlg}$ is more time-consuming than all other algorithms except the two threshold-based ones in most cases. It is mainly due to the usage of logical reasoning. Take the ontology $\mathsf{VeeAlign-edas-iasted}$ as an example. $\mathsf{LogicAlg}$ took about 6 s while others took no more than 4 s. Three signature-based algorithms performed similarly, and the original one performed slightly better. Two threshold-based algorithms spent much more time than others since they need to spend time computing a degree for an axiom over all axioms in the corresponding ontology. The degree is summing the similarity values between the axiom and others if the values are larger than the given threshold (i.e., 0.5).

5.5. Results of Comparing Different Thresholds

To better analyze the performances of two threshold-based algorithms, more experiments have been conducted with 10 thresholds: 0.4, 0.45, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85 and 0.9. Since the consumption time for each algorithm with different thresholds has no big difference, we only present the number of removed axioms (see Table 5). These results were obtained using the same pre-trained model (i.e., $\mathsf{m}\mathsf{1}$).

Table 5. Number of axioms removed by two threshold-based algorithms using different thresholds.

Ontology	$\mathsf{ThrCosAlg}$ with Different Thresholds
	0.4	0.45	0.5	0.55	0.6	0.65	0.7	0.75	0.8	0.85	0.9
ALOD2Vec-confof-edas	5	5	5	4	1	1	1	2	1	5	2
ATBox-cmt-confof	2	2	2	1	1	2	1	1	1	1	2
CHEM-A	3	3	3	3	2	4	3	2	1	1	2
dbpedia_2014	1	1	1	1	1	1	1	1	1	1	1
Economy	37	37	36	28	39	39	31	42	28	19	21
Geography	11	11	11	11	11	12	12	14	14	12	14
km1500–3500	38	38	38	38	34	38	36	41	29	31	25
koala	2	2	3	3	3	2	2	2	1	2	2
Lily-cmt-conference	2	2	2	1	1	3	2	2	2	1	1
Lily-edas-ekaw	8	8	8	8	8	8	7	6	6	6	5
MGED	7	7	7	6	6	6	16	21	20	9	16
miniTambis	3	3	3	3	3	3	3	3	3	3	3
pizza	3	3	3	3	3	2	2	2	3	3	3
proton	14	14	12	13	9	10	9	10	9	9	11
Terrorism	1	1	1	3	2	1	1	4	3	4	4
Transportation	20	20	19	19	19	22	23	20	21	23	21
University	3	3	3	3	3	3	3	3	4	4	4
VeeAlign-edas-iasted	3	3	2	3	3	3	4	3	4	3	11
Wiktionary-cmt-confof	6	5	4	3	4	4	3	4	5	8	6
Wiktionary-confof-edas	5	5	5	4	1	1	2	3	4	4	4
Total	174	173	168	158	154	165	162	186	160	149	158
Ontology	$\mathsf{ThrEucAlg}$ with Different Thresholds
	0.4	0.45	0.5	0.55	0.6	0.65	0.7	0.75	0.8	0.85	0.9
ALOD2Vec-confof-edas	2	1	1	3	2	3	3	2	1	1	1
ATBox-cmt-confof	2	1	1	1	2	1	1	1	1	1	1
CHEM-A	2	3	1	1	1	2	2	1	1	1	1
dbpedia_2014	1	1	1	1	1	1	2	1	1	1	1
Economy	31	37	20	15	23	13	8	8	8	8	8
Geography	11	12	13	14	16	13	11	12	9	9	9
km1500–3500	34	37	30	30	31	32	24	21	20	19	19
koala	3	3	3	2	2	1	1	1	1	1	1
Lily-cmt-conference	1	1	2	1	2	3	3	1	1	1	1
Lily-edas-ekaw	6	8	7	5	5	5	4	4	4	4	4
MGED	9	7	7	17	17	10	10	11	5	3	3
miniTambis	3	3	3	3	3	3	3	3	3	3	3
pizza	3	3	3	3	3	2	2	2	2	2	2
proton	9	11	11	11	11	9	8	8	8	8	8
Terrorism	1	4	4	5	5	2	1	1	1	1	1
Transportation	21	22	20	23	16	22	19	16	13	13	13
University	3	3	4	4	4	4	3	3	3	3	3
VeeAlign-edas-iasted	3	8	3	11	8	6	6	2	2	2	2
Wiktionary-cmt-confof	3	5	8	7	6	5	3	3	3	3	3
Wiktionary-confof-edas	6	1	1	6	4	7	2	2	1	1	1
Total	154	171	143	163	162	144	116	103	88	85	85

From the table, it can be seen that $\mathsf{ThrEucAlg}$ could achieve better results with higher thresholds. For instance, when a threshold is greater than 0.75, no more than 90 axioms need to be removed to restore the coherence of all ontologies, while more than 100 axioms for the algorithm with the other thresholds. Surprisingly, when the threshold is no less than 0.85, $\mathsf{ThrEucAlg}$ removed the same number of axioms as $\mathsf{BaseAlg}$. It means that all diagnoses found by $\mathsf{ThrEucAlg}$ are minimal in such cases. When checking the experimental results, we found that the degrees computed by $\mathsf{ThrEucAlg}$ are all equal to 1, and thus the ILP-based approach actually was executed over all MIPS directly. As for $\mathsf{ThrCosAlg}$, when the threshold is set to be 0.6 and 0.85, better results could be reached. There is no obvious border to divide the results into good ones and bad ones for this algorithm. Compared to the two threshold-based algorithms, $\mathsf{ThrEucAlg}$ removed fewer axioms than $\mathsf{ThrCosAlg}$ in most cases. However, when the threshold is more than 0.65, $\mathsf{ThrEucAlg}$ failed to differentiate the axioms and associated the same degree to them.

5.6. Results of Comparing Different Models

To observe the influence of different pre-trained models on the results of repairing ontologies, the algorithms $\mathsf{ThrCosAlg}$ and $\mathsf{ThrEucAlg}$ were evaluated with the four models (i.e., $\mathsf{m}\mathsf{1}$, $\mathsf{m}\mathsf{2}$, $\mathsf{m}\mathsf{3}$ and $\mathsf{m}\mathsf{4}$). The threshold was set to 0.5.

Figure 5 illustrates the time to compute a diagnosis for each ontology by applying the threshold-based algorithm with a specific model and a given distance metric. In this figure, $\mathsf{cos-m1}$ indicates the threshold-based algorithm with Cosine Distance and model $\mathsf{m}\mathsf{1}$, and $\mathsf{euc-m1}$ indicates the threshold-based algorithm with Euclidean Distance and model $\mathsf{m}\mathsf{1}$. It is similar to other algorithms. In Figure 5, we observe that the algorithm with $\mathsf{cos-m4}$ is slightly more efficient than the algorithm with other configurations. The algorithms with $\mathsf{cos-m1}$, $\mathsf{euc-m1}$, $\mathsf{euc-m3}$ or $\mathsf{euc-m4}$ spent relatively more time. Generally speaking, the time difference between these algorithms is not significant.

Figure 5. Time in milliseconds (y-axis) for each incoherent ontology to compute a diagnosis by the threshold-based algorithm with different models and distance metrics while keeping the same threshold of 0.5.

Table 6 presents the number of axioms removed by each algorithm with a specific model. The results reveal that both threshold-based algorithms with $\mathsf{m}\mathsf{4}$ remove fewer axioms than the two algorithms with the other models according to the total number of removed axioms. In particular, $\mathsf{ThrCosAlg}$ with $\mathsf{m}\mathsf{4}$ provides more promising results, and a total of 118 axioms were deleted. Compared with the baseline algorithm $\mathsf{BaseAlg}$, this algorithm could find minimal diagnoses for 9 out of 20 ontologies. Although both algorithms remove the same number of axioms for these ontologies, the axioms removed may be different. Take the ontology $\mathsf{Economy}$ as an example. $\mathsf{BaseAlg}$ removed the following 8 axioms:

Table 6. Number of axioms removed by two threshold-based algorithms using different models.

Ontology	$\mathsf{ThrCosAlg}$				$\mathsf{ThrEucAlg}$
	m1	m2	m3	m4	m1	m2	m3	m4
ALOD2Vec-confof-edas	5	3	3	1	1	2	3	3
ATBox-cmt-confof	2	2	1	2	1	2	2	2
CHEM-A	3	3	4	3	1	3	2	1
dbpedia_2014	1	1	1	1	1	1	1	1
Economy	36	8	43	8	20	22	11	14
Geography	11	11	15	11	13	14	15	15
km1500–3500	38	23	29	23	30	32	33	27
koala	3	1	3	1	3	2	2	1
Lily-cmt-conference	2	1	2	1	2	1	4	1
Lily-edas-ekaw	8	9	8	9	7	5	5	5
MGED	7	5	8	5	7	20	6	10
miniTambis	3	3	3	3	3	3	3	3
pizza	3	3	3	3	3	3	2	2
proton	12	12	13	13	11	9	9	9
Terrorism	1	1	1	1	4	5	5	4
Transportation	19	26	21	19	20	17	14	16
University	3	3	4	3	4	4	4	4
VeeAlign-edas-iasted	2	3	9	4	3	2	2	3
Wiktionary-cmt-confof	4	5	5	6	8	7	8	7
Wiktionary-confof-edas	5	6	4	1	1	4	4	4
Total	168	129	180	118	143	158	135	132

a1: $\mathsf{SubClassOf}\left(\mathsf{HandwovenCarpet\; TextileProduct}\right)$

a2: $\mathsf{SubClassOf}\left(\mathsf{Lumber\; ForestProduct}\right)$

a3: $\mathsf{SubClassOf}\left(\mathsf{Ginger\; Vegetable}\right)$

a4: $\mathsf{DisjointClasses}\left(\mathsf{CapitalGood\; ManufacturedProduct}\right)$

a5: $\mathsf{DisjointClasses}\left(\mathsf{Fruit\; GroceryProduce}\right)$

a6: $\mathsf{DisjointClasses}\left(\mathsf{GroceryProduce\; RootVegetable}\right)$

a7: $\mathsf{DisjointClasses}\left(\mathsf{GroceryProduce\; Vegetable}\right)$

a8: $\mathsf{DisjointClasses}\left(\mathsf{AgriculturalProduct\; Fodder}\right)$

$\mathsf{ThrCosAlg}$ with the model $\mathsf{m}\mathsf{4}$ removed the axioms from a4 to a8 together with the following three axioms:

a9: $\mathsf{DisjointClasses}\left(\mathsf{ForestProduct\; ManufacturedProduct}\right)$

a10: $\mathsf{DisjointClasses}\left(\mathsf{HandicraftProduct\; ManufacturedProduct}\right)$

a11: $\mathsf{DisjointClasses}\left(\mathsf{Spice\; Vegetable}\right)$

$\mathsf{ThrCosAlg}$ with the model $\mathsf{m}\mathsf{2}$ removed the same set of axioms as $\mathsf{ThrCosAlg}$ with the model $\mathsf{m}\mathsf{4}$. As we can see, axioms from ax1 to a3 represent knowledge in a correct way, while axioms from a9 to a11 are not very correct. For instance, axiom ax11 means that $\mathsf{Spice}$ is disjoint with $\mathsf{Vegetable}$. However, in fact, those natural spices such as Chinese prickly ash and coriander belong to vegetables. Therefore, $\mathsf{ThrCosAlg}$ with the models $\mathsf{m}\mathsf{2}$ and $\mathsf{m}\mathsf{4}$ could differentiate axioms with various degrees, and assign lower degrees to those problematic axioms. $\mathsf{ThrCosAlg}$ with the model $\mathsf{m}\mathsf{4}$ performed even better. Take the ontology $\mathsf{Wiktionary-confof-edas}$ as another example. $\mathsf{ThrCosAlg}$ with the model $\mathsf{m}\mathsf{4}$ only removed 1 axiom, which is the same as the baseline algorithm, but $\mathsf{ThrCosAlg}$ with other models removed more than 3 axioms.

5.7. Discussion and Limitations

In this section, we discuss the main conclusions of our experiments. In particular, we analyze the main advantages and limitations of our proposed algorithms.

According to our results, the following main conclusions can be derived:

• Compared with other algorithms, $\mathsf{BaseAlg}$ can always find a minimal diagnosis, but it spent slightly more time than $\mathsf{ScoreAlg}$ and $\mathsf{ShapAlg}$ in most cases. Although no big difference in these algorithms’ efficiency has been reflected by our experiments, computing diagnoses based on subsets of all MIPS should be more efficient than that based on all MIPS directly. Thus, when time is a problem for $\mathsf{BaseAlg}$, $\mathsf{ScoreAlg}$ and $\mathsf{ShapAlg}$ would be preferred as they compute a diagnosis based on subsets of all MIPS.
• When logical consequences are considered important, $\mathsf{LogicAlg}$ can be used to compute a diagnosis such that removing all axioms in the diagnosis will lose the least entailments. One main disadvantage of this algorithm is that computing entailments, even given types of entailments, may be very time-consuming.
• In the case that the usage of entities is considered important, $\mathsf{SigCosAlg}$ and $\mathsf{SigEucAlg}$ are good choices, because they consider both syntax and semantics, and remove fewer axioms than the original signature-based algorithm $\mathsf{SigAlg}$. These algorithms assign higher degrees to those axioms that have more syntactical overlapping with other axioms. The embedding-based algorithms further consider semantic relevance.
• For the threshold-based algorithm, the threshold plays an important role. According to our observations, a value of around 0.5 is a good choice. Furthermore, the threshold-based algorithm with Euclidean Distance (i.e., $\mathsf{ThrEucAlg}$) often removes fewer axioms than that with Cosine Distance (i.e., $\mathsf{ThrCosAlg}$), but it cannot distinguish the difference of axioms when the threshold is more than 0.65.
• Among the four pre-trained models, $\mathsf{m}\mathsf{1}$ is the most efficient one. This reflects that its embedding model “paraphrase-multilingual-343 MiniLM-L12-v2” outperforms other BERT models used in $\mathsf{m}\mathsf{2}$, $\mathsf{m}\mathsf{3}$, and $\mathsf{m}\mathsf{4}$, according to their efficiency. In addition, $\mathsf{m}\mathsf{4}$ provides more promising results with respect to the number of removed axioms. It is able to not only differentiate the axioms but also remove fewer axioms.

Based on the discussion of the main results, we can summarize the following advantages of our proposed approach: (1) Our embedding-based approach provides a novel approach to considering semantic relationships among axioms. The source code of our implementations, together with the data set and experimental results, can be freely downloaded for reusing or retesting purposes. This approach is also a flexible framework to integrate different distance metrics and embedding models. (2) Integrating the embedding-based ranking strategy with existing ones may be a promising combination to enhance existing strategies’ effectiveness. $\mathsf{SigCosAlg}$ and $\mathsf{SigEucAlg}$ are good examples. They combine the traditional signature-based ranking strategy with the embedding-based one and really reduce the number of axioms to be removed. (3) Through our experiments, we show that our embedding-based algorithm with the model $\mathsf{m}\mathsf{4}$ is a promising choice to remove relatively fewer axioms and differentiate the axioms with different degrees.

Nevertheless, there exist several limitations to our study. (1) Computing similarities between axioms will be extremely time-consuming if too many axiom pairs are considered. Although this process can be performed offline, various strategies to choose axiom pairs should be considered. (2) It is not easy to select a suitable threshold for given incoherent ontologies. According to our experimental results, a suitable threshold has been recommended. However, it would be dynamically changed when the evaluated ontologies are updated. (3) It is not sufficient to evaluate the repair algorithms with the time and number of axioms to be removed. It would be better to compute precision and recall for each algorithm based on golden standards, but such golden standards are not available currently.

6. Related Work

Various algorithms to repair ontologies have been proposed. Existing algorithms generally consist of automatic repair algorithms and semi-automatic repair ones, or fine-grained ones and algorithms to delete whole axioms. Semi-automatic repair (e.g., [48,49,50,51,52]) requires an expert’s participation to decide which recommended axioms should be removed. Most of these works focus on repairing ontology mappings interactively. When repairing ontology mappings, those confidence values associated with the correspondences could help an expert to make a decision. Fine-grained repair algorithms (e.g., [53,54,55,56,57,58]) only remove or rewrite parts of an axiom instead of removing the entire axiom. When weakening axioms, various strategies such as using refinement operators, splitting axioms or applying the tableaux algorithm. In addition, a few works such as [55] consider weakening axioms with an expert’s help. In this work, we focus on deleting complete axioms without interaction of experts.

Many existing repair algorithms rely on ranking axioms by considering their syntax or logical influence. The authors in [22,26,59] ranked axioms by computing scores. A score of an axiom corresponds to the number of MIPS or conflicts which contain this axiom. This ranking strategy was implemented in $\mathsf{ScoreAlg}$. The work in [27] proposed a signature-based ranking strategy and a logic-based one, which were used in $\mathsf{SigAlg}$ and $\mathsf{LogicAlg}$, respectively. Furthermore, the latter can be extended to allow a user to specify a set of test cases that describe those desired entailments. The work in [25] introduced a graph-based method to debug and repair a DL-Lite ontology. The authors ranked an axiom with two strategies: one computed a score like $\mathsf{ScoreAlg}$, and the other computed logic impact when removing an axiom, which is similar to the ranking strategy implemented in $\mathsf{LogicAlg}$. The work presented in [45] proposed a novel ranking strategy and computed the penalty of an axiom in a conflict set as the sum of inverse proportions to the size of such sets. That is, if an axiom appears in one conflict set M, the penalty of this axiom is $\frac{1}{\left|M\right|}$. If it appears in n conflict sets, its total penalty should be the sum of n penalties. This ranking strategy has been implemented in $\mathsf{ShapAlg}$. It indicated that different ranking strategies could be combined in some way to form a hybrid one, such as the strategy used in SWOOP [46].

Another type of ranking strategy makes use of external knowledge. The work in [27] also proposed another strategy by making use of provenance information like the authors or reasons for adding an axiom. For instance, an axiom created by a supervisor should be more important or reliable than that created by a subordinate. The authors in [45] designed two novel ranking strategies by using background context ontologies. Each axiom can be assigned a support to represent how much support for an axiom exists in the background knowledge. Although these strategies are very useful, background knowledge may not be always available. In this work, we do not consider using external information.

Recently, several works ranked axioms in a special way. The work in [23] ranked axioms by providing their truth values based on an embedding model. The work in [60] dealt with the problem of resolving conflicts with a partial order of axioms. The authors considered that not all axioms were ranked in the same way, and thus the axioms cannot be compared directly. To deal with this problem, a general notion of logical inconsistency was defined, and a conflict was stratified into two parts. Finally, a prioritized hitting set was computed as a diagnosis.

To conclude, most of the existing ranking strategies for ontology repair mainly rely on the syntax of axioms or logic entailments, while ignoring the semantics of axioms. Although there exist few works that consider the semantics of axioms, they may not be suitable to deal with complex types of axioms. Therefore, we propose a novel approach to ranking various expressions of axioms by using pre-trained embedding models.

7. Conclusions and Future Works

In this paper, we presented an embedding-based approach to repairing ontologies by translating OWL axioms into natural language sentences. Specifically, the translation was inspired by the ideas from NaturalOWL, and then various pre-trained models such as Sentence-BERT and CoSENT were employed to the obtained sentences for computing embeddings. After that, the similarities between sentences could be calculated by encoded vectors. Benefiting from these similarities, three definitions were provided to compute a degree for an axiom based on the embeddings of axioms in the same semantic space. Afterwards, a threshold-based repair algorithm and a signature-based one were proposed to instantiate our embedding-based approach. Finally, we conducted abundant experiments over 20 real-life incoherent ontologies varying in size of axioms and number of unsatisfiable concepts. Experimental results indicated that our embedding approach could provide promising results, especially the threshold-based algorithm with the fourth model is able to differentiate axioms according to their semantics and remove fewer axioms.

As for future works, we plan to explore how to choose a threshold dynamically according to similarity distributions and characteristics of various distance metrics. In addition, the combination of different single-ranking strategies and employing external knowledge will be considered in order to improve the effectiveness and efficiency of our approach. We also will consider the parallel diagnosing process to deal with the cases where an ontology contains too many diagnoses by borrowing the idea from the work [61]. Last but not least, we will study how to provide a friendly user interface to facilitate users to repair an ontology like the work given in [62].