A Proactive Microgrid Management Strategy for Resilience Enhancement Based on Nested Chance Constrained Problems

Abstract

As the frequency of extreme weather events rises, the resilience of power systems is becoming increasingly important. This paper proposes a proactive microgrid management strategy for enhancing the resilience of microgrids (MGs) based on nested Mixed Integer Linear Programming problems with chance constraints. In the proposed method, MGs operate in a special operating mode referred to as the “preparation mode” to protect the vital load and maximize resource operation efficiency when an external grid outage warning is issued. The preparation mode problem is formulated to reflect both the normal and emergency mode operation conditions. The on-event phase-operation problem under emergency-mode operation conditions is nested within the pre-scheduling problem under normal-mode operation conditions in the preparation mode. Further, according to their importance, loads are divided into critical and non-critical ones in the problems. The former is represented by a chance constraint, and the latter is represented by the expected cost of load shedding in the cost function. The numerical examples demonstrate that the proposed preparation mode enables the MG to guarantee a high chance that the critical load will survive and to lower the cost of the non-critical load shedding with a minor increase in resource operation costs.

1. Introduction

Increased extreme weather events caused by climate change raise significant concerns about reliability in power system operation. Since 2002, about 58% of power outages have been attributed to extreme weather events, and they can result in an average annual economic loss of 18–33 billion dollars [1] in the United States. Hurricane Sandy in 2012 caused more than 7.5 million customers to lose electricity. The relevant economic loss of hurricane Sandy was approximately 65 billion USD [2]. In February 2021, a massive power-generation failure occurred in Texas because of severe winter storms across the state. This storm caused 70% of the Texas population to suffer from power outages for 42 h on average. The economic loss from the blackout and freeze was estimated to be between 80 and 130 billion USD, including both direct and indirect costs [3].

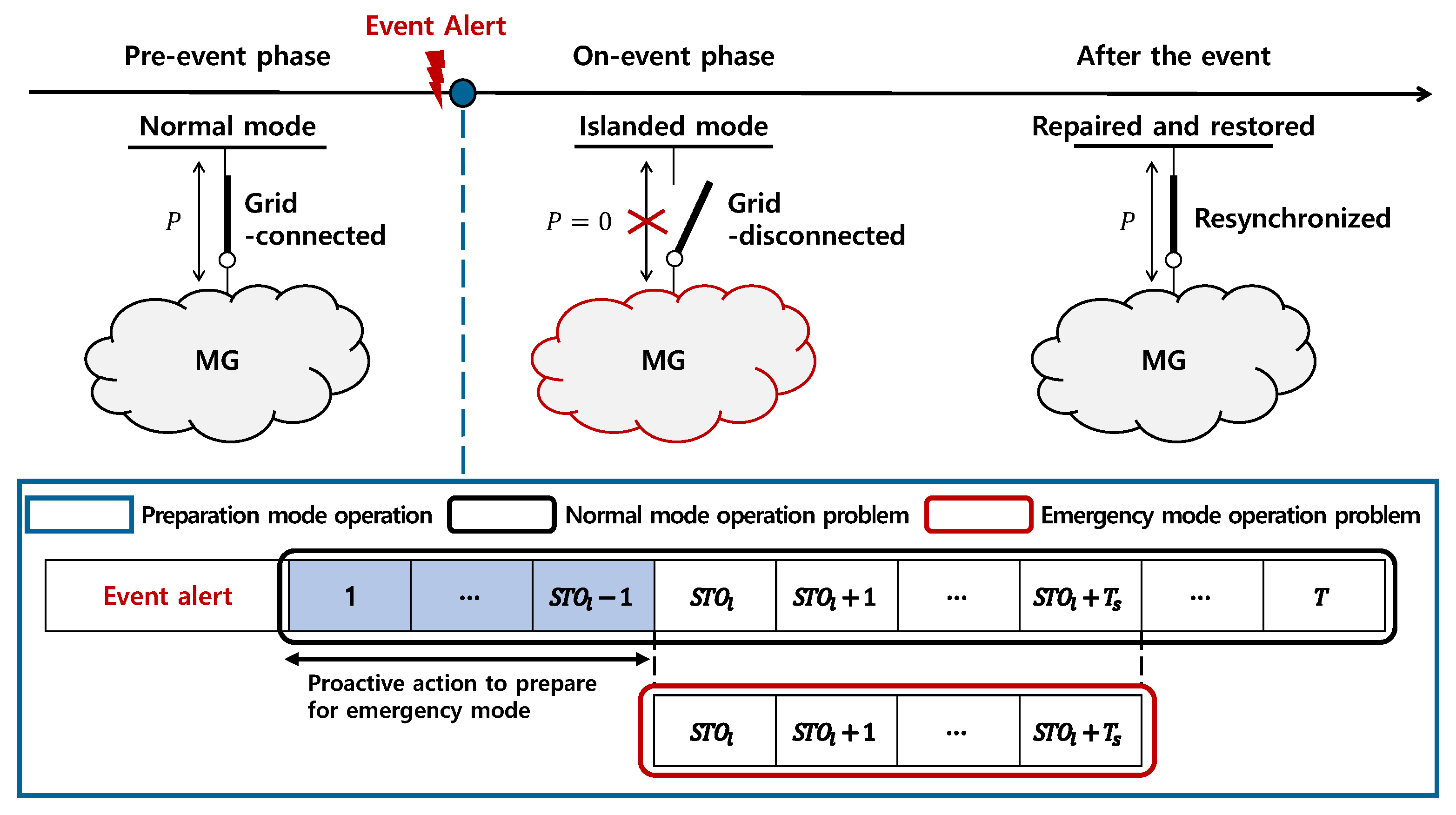
The “resilience” of the power system has drawn considerable attention from the power industry to cope with such catastrophic events. In the context of power systems, resilience is the ability of the system to withstand and recover from high-impact, low-probability events by employing preventive and corrective actions [4,5]. Holistic operational strategies for multiple phases are required to realize resilient power systems [6]. To this end, a microgrid (MG) is a technically viable option that can improve power-system resilience because of its unique functions. The MG can operate as a self-sufficient energy system because it has its own energy resources. The MGs equipped with a central energy management system can be operated for specific functions and increased energy efficiency through a coordinated operation of energy resources [7,8]. On the one hand, a grid-connected MG can serve as a power source to the main grid that contributes to improving the entire power system resiliency. On the other hand, the MG can improve its own resiliency when an external outage occurs isolated from the main grid, and it can protect its critical loads [9,10]. Holistic system management strategies that span multiple phases, from infrastructure hardening to system restoration from an event, are required to build a resilient MG. In the pre-event phase, the MG identifies feasible events and hardens the current system or installs new devices to prepare for these events. The MG employs proactive scheduling decisions for its resources as the identified event approaches to ensure their availability to supply critical loads during the event. During the on-event phase, the MG takes corrective actions to minimize the effect of the event. The original system configuration can be modified to restrict such an effect by re-dispatching the resources or conducting network reconfiguration. The MG returns to the normal state and resynchronizes with the main grid after the event ends [11,12]. Among these aforementioned strategies, the proactive scheduling of the MG resources is the most cost-effective approach because it does not require any associated capacity investment, which can be expensive. Therefore, many researchers are interested in developing optimal operation schemes for enhancing the resilience of MGs.

Energy management methods that can reduce the MG load interruption from the specified types of disasters have been reported in the existing literature [13,14]. The probability that the MG load is not supplied because of the failure in power devices and facilities caused by extreme floods was evaluated [13]. Further, the active energy management of MG was proposed for minimizing the load loss in the worst case. In [14], the authors suggested a method to schedule energy resources for a continuous power supply to a load that can be interfered with by windstorms. To this end, Amirioun et al. [14] analyzed the effect of high wind speed on power distribution facilities and wind power generators.

Many studies have proposed optimization models to enhance MG resilience for coping with unspecified incidents [15,16,17,18,19,20,21,22]. Khodaei [15] developed an optimization formulation for MG operations to minimize the power mismatch that can occur during the multiple duration of the event and extended the model that considers forecasting errors of the load and renewable energy generation in [16]. The authors of [17] studied an approach to managing energy storage systems and distributed generators to guarantee sufficient power resources when an event occurs. Further, Liu et al. [17] employed a two-stage robust optimization to confirm that the availability of power resources takes precedence over MG operating costs. A more balanced MG operation between ensuring load survivability and reducing MG operating costs was pursued through a two-stage adaptive robust optimization model in [18]. The authors of [19] suggested a novel optimization formulation for a proactive MG operation that includes resilience cuts for the state of charge of energy storage systems. Further, they considered the dynamic cost of load shedding to reduce the likelihood of critical load curtailment. In [20], the authors demonstrated that a two-stage stochastic programming approach could significantly mitigate the effect of natural disasters by reflecting a wide range of uncertainties attributed to various factors in optimal MG operation.

The authors of [21,22] suggested an MG operation to maintain supply capability above a certain level during the on-event phase. They defined supply capability as the probability that the net demand falls within the spinning reserve range provided by the MG. The problem was formulated as a MILP with chance constraints in [21], and they assumed the forecast error of the net load to be a Gaussian distribution. In [22], the authors extended the problem of considering the reconfigurable capability of the MG during the on-event phase. Younesi et al. [23] synthesized resilience indexes and developed a multi-objective economic-resilience scheduling model for the microgrid. For the resilience enhancement, the authors of [23] suggest the first objective function as the cost of the MG operation and the second objective function as a combination of indices that include fragility, recovery efficiency, voltage, and lost load.

However, conservatively operating MGs to be ready for all unforeseen events can be inefficient because this can lead to MGs having excess reserves, which is not economical in most situations. Furthermore, huge events, such as hurricanes, tropical storms, and blizzards, can typically be predicted at least 24–72 h in advance [6], and approximately 43.6 percent of events causing power outages and microgrid disconnections are predictable [24]. Therefore, in order to achieve resilient and cost-effective MG operations, it is crucial to establish a specified operating scheme for different operating conditions of MGs: the pre-event, after-warning, and on-event phases. In [24], the authors suggested an energy management method to procure adequate energy reserve for uninterruptible power supply to the critical load based on the predicted natural disaster. However, this study assumes that the levels of renewable generation and loads are given as determinative parameters without taking into account their uncertainty. We present a resilience-oriented MG operation strategy that proactively manages its energy resources to enhance the survival of important loads in anticipation of extended external grid outages. The goal is to reduce the impact on critical loads after the event occurs and to achieve cost-effectiveness in the MG operation by deliberately managing MG resources when a credible forecast of the event occurrence times is provided. The main contributions of this work are summarized as follows:

• Proposing a new formulation for proactive microgrid management strategy: We propose an optimal resource scheduling method of the MG for resiliency enhancement to protect loads according to their importance from predicted extreme events. The scheduling of MG energy resources is optimized for minimizing the MG operation cost while guaranteeing a very low probability of critical load interruption during an event. We developed a nested chance-constrained programming model for dealing with load interruption risks from the uncertainty in electricity loads and power generation from solar PV and wind at pre-event times. The MG operator increases the possibility of an uninterrupted power supply to critical loads because the suggested operating strategy integrates the MG operational cost and conditions for various times when an outage can occur in the problem formulation.
• Modeling the expected load shedding: The expected load shedding (ELS) is evaluated analytically. The ELS is discovered to be a nonlinear nonconvex function. However, we find that the expected cost of load shedding (ECLS) included in the cost function is a convex function if the forecasting errors of load and renewable generation follow a Gaussian distribution. We find that ECLS, which is included in the cost function, is a nonlinear convex function if the forecasting errors of load and renewable generation follow a Gaussian distribution. The ECLS is calculated by the multiplication of ELS and the probability of load shedding. The ECLS does not compromise the solvability of the optimization problem. However, we approximate ECLS to be a piecewise linear model for representing the problems as a mixed integer linear program (MILP).
• Demonstrating the effectiveness of the proposed proactive microgrid management strategy: We conducted simulations using two cases—when the loads are (1) low and (2) high during event periods—to verify the advantages of using the proposed method to improve MG resilience. The proposed method can increase load survivability and reduce ECLS during the event periods by the proactive decision of the battery and generator operations during the normal mode compared to the operation without preparation.

The remainder of this paper is organized as follows. Section 2 describes the MG system configuration and operations considered in this study. Section 3 and Section 4 introduce the optimization problem formulation for realizing the proposed energy scheduling method and the numerical examples, respectively, verifying the effectiveness of the proposed method. Finally, Section 5 concludes the paper.

2. System Description

2.1. Microgrid System

Figure 1 shows the microgrid test model considered in this study. The MG is composed of loads, four controllable generators (CGs), renewable energy sources, and battery energy-storage systems (BESSs). CG refers to dispatchable gas and diesel generators whose output can be adjusted according to instructions from a centralized MG operator. The loads are categorized into classes A (critical load) and B (non-critical load) based on their importance. Renewable energy sources such as wind turbines and PV systems are considered to be non-controllable in this study. Therefore, the flexibility of CG and BESS is essential for maintaining the balance between the supply and demand of MGs.

2.2. Microgrid Operation

The MG operates in three modes (normal, islanded, and restoration). We consider an additional MG operation scheme known as “preparation mode”, which is specifically designed to increase the resilience of the MG loads for external grid failures by the proactive scheduling of the MG’s resources and devices (Figure 2).

In its normal operating mode, the MG provides power to its loads with the lowest possible operating costs. Based on the predicted renewable energy generation and load, the MG determines the schedules for generating resources and power exchange with the external grid considering several physical constraints, such as the capacity of a point of common coupling and ramp rates of generating units. For the BESS, frequent charge/discharge cycles can be restricted in the normal operating mode to prevent the battery cells from degrading rapidly [24].

MG operation during the event periods is referred to as emergency mode. The main objective of the MG in this mode is modified for supporting critical loads using local resources because the MG is separated from the external grid. The physical constraints of the generator should be considered, as in the normal mode. However, some constraints can be relaxed to handle emergency scenarios. For example, the restriction on the charge/discharge cycles of BESS should no longer be considered in the emergency operation mode as the survival of the load has a higher value than that of maintaining the BESS lifespan.

The preparation mode of the MG operation is developed as a proactive microgrid management strategy to consider both the normal and emergency mode operation conditions that can effectively improve the survivability of loads. Under the warning of an external grid outage, the MG can enter the preparation mode and change the operating states, and it can generate levels of its resources for the ongoing power supply to the load after interruption. However, supporting all loads for the duration of the event may not be economical or even viable, given the constrained local resources of the MG. Therefore, the loads should be split into critical and non-critical loads and treated differently based on their importance in the preparation mode. Therefore, a requirement for satisfying the critical loads is a hard constraint of the problem, and meeting the non-critical loads is treated as a soft constraint. Violating a constraint incurs a penalty in the objective function.

3. Optimization Problem Formulations

3.1. Normal Mode Operation Formulation

Equation (1) expresses the objective function of the normal mode operation. In Equation (1), $X^{NM}$ represents the set of decision variables related to the normal-mode operation problem. The first and second terms indicate the cost of operating the controllable generating unit and the cost of power exchange with the main grid, respectively. The last term represents the sum of the load shedding costs for classes A and B.

$$\begin{array}{cc}\hfill f^{NM}\left(X^{NM}\right)=& \sum _{g=1}^G\sum _{t=1}^T(C_g^{gen}·P_{g,t}^{NM}+C_g^{SU}·y_{g,t}^{NM}+C_g^{SD}·z_{g,t}^{NM})\hfill \\ \hfill & +\sum _{t=1}^T(P{R}_t^{Buy}·P_t^{Buy.NM}-P{R}_t^{Sell}·P_t^{Sell.NM})\hfill \\ \hfill & +\sum _{t=1}^T(C^{LSA}·P_t^{LSA.NM}+C^{LSB}·P_t^{LSB.NM}).\hfill \end{array}$$

(1)

Equations (2)–(20) represent constraints related to the normal-mode operation. The power balance of the system is represented by Equation (2), and Equations (3) and (4) represent the load shedding.

$$\begin{array}{cc}\hfill & \sum _{g=1}^G{P}_{g,t}^{NM}+P_t^{WT}+P_t^{PV}+\eta ·P_t^{dch.NM}-P_t^{ch.NM}\hfill \\ \hfill & +P_t^{Buy.NM}-P_t^{Sell.NM}\ge P_t^{tA.NM}+P_t^{tB.NM},{\forall }_t.\hfill \end{array}$$

(2)

$$P_t^{LSA.NM}=P_t^{LA}-P_t^{tA.NM},{\forall }_t.$$

(3)

$$P_t^{LSB.NM}=P_t^{LB}-P_t^{tB.NM},{\forall }_t.$$

(4)

Further, Equation (5) represents the output limit of the generating units. Equation (6) indicates the ramp capability limit of the generating units. Equations (7) and (8) represent the minimum start-up time and minimum stop time of the generating units, respectively. Equations (9) and (10) represent the binary variables that indicate the start-up and shutdown behavior of the generator, respectively.

$$u_{g,t}^{NM}·P_g^{min}\le P_{g,t}^{NM}\le u_{g,t}^{NM}·P_g^{max},{\forall }_{g,t}.$$

(5)

$$P_{g,t-1}^{NM}-R{D}_G^{max}\le P_{g,t}^{NM}\le P_{g,t-1}^{NM}+R{U}_G^{max},{\forall }_{g,t}.$$

(6)

$$\sum _{to=0}^{T{O}_g-1}{u}_{g,t+to}^{NM}\ge T{O}_g(u_{g,t}^{NM}-u_{g,t-1}^{NM}),{\forall }_{g,t}.$$

(7)

$$T{S}_g-\sum _{ts=0}^{T{S}_g-1}{u}_{g,t+ts}^{NM}\ge T{S}_g(u_{g,t-1}^{NM}-u_{g,t}^{NM}),{\forall }_{g,t}.$$

(8)

$$y_{g,t}^{NM}=max\{(u_{g,t}^{NM}-u_{g,t-1}^{NM}),0\},{\forall }_{g,t}.$$

(9)

$$z_{g,t}^{NM}=max\{(u_{g,t-1}^{NM}-u_{g,t}^{NM}),0\},{\forall }_{g,t}.$$

(10)

Equations (11)–(18) are associated with the battery operations. The battery dynamics are modeled through a linear model as shown in Equation (11). The maximum charging and discharging power are restricted by the capacity of the power conversion system (PCS), as shown in Equations (12) and (13), respectively. Further, Equations (14) and (15) constrain the maximum allowable charging/discharging power according to the SoC level, $So{C}_t^{NM}$. Equations (16) and (17) are introduced to prevent the battery from being charged and discharged frequently, respectively, which extends the battery lifespan. Thus, once charging begins, it must last for at least TCM hours, and once discharging starts, it must not be terminated within TDM hours. Equation (18) indicates that charging and discharging must not occur simultaneously within the ESS.

$$So{C}_t^{NM}=So{C}_{t-1}^{NM}+\frac{\eta ·P_t^{ch.NM}-P_t^{dch.NM}}{Ba{t}_c}·\mathsf{\Delta }t,{\forall }_t.$$

(11)

$$0\le P_t^{ch.NM}\le uc{h}_t^{NM}·PC{S}_c,{\forall }_t.$$

(12)

$$0\le P_t^{dch.NM}\le ud{c}_t^{NM}·PC{S}_c,{\forall }_t.$$

(13)

$$So{C}_t^{NM}·Ba{t}_c+\eta ·P_t^{ch.NM}·\mathsf{\Delta }t\le DoD·Ba{t}_c,{\forall }_t.$$

(14)

$$P_t^{dch.NM}·\mathsf{\Delta }t\le So{C}_t^{NM}·Ba{t}_c,{\forall }_t.$$

(15)

$$\sum _{tcm=0}^{TCM-1}uc{h}_{t+tcm}^{NM}\ge TCM(uc{h}_t^{NM}-uc{h}_{t-1}^{NM}),{\forall }_t.$$

(16)

$$\sum _{tdm=0}^{TDM-1}ud{c}_{t+tdm}^{NM}\ge TDM(ud{c}_t^{NM}-ud{c}_{t-1}^{NM}),{\forall }_t.$$

(17)

$$0\le uc{h}_t^{NM}+ud{c}_t^{NM}\le 1,{\forall }_t.$$

(18)

Finally, the maximum permitted power exchange between the main grid and the MG is shown in Equation (19). In Equation (19), power exchange between the main grid and the MG is limited by the capacity of the substation at the point of common coupling. Equation (20) indicates that all variables are positive.

$$0\le P_t^{Sell.NM},P_t^{Buy.NM}\le P_c^{sub}.$$

(19)

$$p_t^{LSA.NM},p_t^{LSB.NM},p_t^{tA.NM},p_t^{tB.NM}\ge 0.$$

(20)

3.2. Emergency-Mode Operation Formulation

The MG is considerably more vulnerable to unexpected fluctuations in loads and renewable energy generation when it is disconnected from the main grid than that when it is connected. Therefore, the MG operation in the emergency mode should consider the uncertainty in loads and renewable energy generation captured by forecasting errors.

The objective function of the emergency-mode operation is expressed in Equation (21). The objective function is constructed to minimize the sum of operating costs over all periods of the islanded mode operation. The predicted start time of the outage ($STO$) is the first time in the islanded mode operation. The continuous $STO$ is set to operate the preparation mode MG conservatively, and it reflects some possible inaccuracies in the STO. In Equation (21), $X^{EM}$ represents the set of decision variables related to the emergency-mode operation problem.

$$\begin{array}{cc}\hfill f^{EM}\left(X^{EM}\right)=& \sum _{l=1}^L\left\{\sum _{g=1}^G\sum _{t{s}_l=st{o}_l}^{ST{O}_l+Ts}(C_g^{gen}·P_{g,t{s}_l}^{ST{O}_l}+C_g^{SU}·y_{g,t{s}_l}^{ST{O}_l}+C_g^{SD}·z_{g,t{s}_l}^{ST{O}_l})\right\}\hfill \\ \hfill & +\sum _{l=1}^L\left\{\sum _{t{s}_l=st{o}_l}^{ST{O}_l+Ts}(C_{t{s}_l}^{ELSA.ST{O}_l}+C_{t{s}_l}^{ELSB.ST{O}_l})\right\}.\hfill \end{array}$$

(21)

Equations (22)–(37) represent the emergency-mode operation conditions. The power balance of the system in the emergency mode is represented by Equation (22), and load shedding reflecting forecast error is captured by Equations (23) and (24).

Equations (23) and (24) define the expected cost of load shedding (ECLS) based on the type of load. ${\varphi }_{{\widehat{ϵ}}_{t{s}_l}^A}$ and ${\varphi }_{{\widehat{ϵ}}_{t{s}_l}^B}$ represent the Probability density function (PDFs) of ${\widehat{ϵ}}_{t{s}_l}^A$ and ${\widehat{ϵ}}_{t{s}_l}^B$, respectively. ${\Phi }_{{\widehat{ϵ}}_{t{s}_l}^A}$ and ${\Phi }_{{\widehat{ϵ}}_{t{s}_l}^B}$ are the Cumulative density function (CDF) of ${\widehat{ϵ}}_{t{s}_l}^A$ and ${\widehat{ϵ}}_{t{s}_l}^B$, respectively. ${\widehat{ϵ}}_{t{s}_l}^A$ represents the sum of the forecast error. We assume the forecast error of renewable generators to be independent Gaussian distribution with zero mean.

$P_{t{s}_l}^{ELSA.ST{O}_l}$ and $P_{t{s}_l}^{ELSB.ST{O}_l}$ represent the expected load shedding (ELS) based on the type of load. These are nonlinear and nonconvex with respect to $P_t^{tA.ST{O}_l}$ and $\left(P_t^{tB.ST{O}_l}\right)$. However, ECLS, which is included in the objective function, is nonlinear and convex with respect to $P_t^{tA.ST{O}_l}$ and $\left(P_t^{tB.ST{O}_l}\right)$. A more detailed explanation is provided in Appendix A.

$$\sum _{g=1}^G{P}_{g,t{s}_l}^{ST{O}_l}+P_{t{s}_l}^{WT}+P_{t{s}_l}^{PV}+\eta ·P_{t{s}_l}^{dch.ST{O}_l}-P_{t{s}_l}^{ch.ST{O}_l}\ge P_{t{s}_l}^{tA.ST{O}_l}+P_{t{s}_l}^{tB.ST{O}_l},{\forall }_{l,t{s}_l}.$$

(22)

$$\left\{\begin{array}{c}{C}_{t{s}_l}^{ELSA.ST{O}_l}=C^{LSA}·{\Phi }_{{\widehat{ϵ}}_{t{s}_l}^A}·\left(P_{t{s}_l}^{ELSA.ST{O}_l}\right),{\forall }_{l,t{s}_l}.\hfill \\ where{P}_{t{s}_l}^{ELSA.ST{O}_l}=(P_{t{s}_l}^{LA}-P_{t{s}_l}^{tA.ST{O}_l})+{\sigma }^2·\frac{{\varphi }_{{\widehat{ϵ}}_{t{s}_l}^A}(P_{t{s}_l}^{LA}-P_{t{s}_l}^{tA.ST{O}_l})}{{\Phi }_{{\widehat{ϵ}}_{t{s}_l}^A}}.\hfill \end{array}\right.$$

(23)

$$\left\{\begin{array}{c}{C}_{t{s}_l}^{ELSB.ST{O}_l}=C^{LSB}·{\Phi }_{{\widehat{ϵ}}_{t{s}_l}^B}·\left(P_{t{s}_l}^{ELSB.ST{O}_l}\right),{\forall }_{l,t{s}_l}.\hfill \\ where{P}_{t{s}_l}^{ELSB.ST{O}_l}=(P_{t{s}_l}^{LA}-P_{t{s}_l}^{tB.ST{O}_l})+{\sigma }^2·\frac{{\varphi }_{{\widehat{ϵ}}_{t{s}_l}^B}(P_{t{s}_l}^{LB}-P_{t{s}_l}^{tB.ST{O}_l})}{{\Phi }_{{\widehat{ϵ}}_{t{s}_l}^B}}.\hfill \end{array}\right.$$

(24)

We use piecewise linearized Equations (23) and (24) to represent the problems as MILP because these equations have exponential terms. An example of piecewise linearization of $C^{ELSA}$ is illustrated in Figure 3.

For resilience enhancement, the critical load must be supplied power under forecasting uncertainty. By using chance constrained programming, the resulting decision can guarantee the probability following a constraint [25]. The authors of [21,22,26], using chance constrained programming to make decisions, guarantee the probability of the incident to be greater than or equal to specific probability. With the same purpose, we used chance constrained programming to make power transmitted to load A guarantee the probability $\alpha$%. This is represented in Equation (25). Equations (26)–(36) have the same purpose as those from the normal-mode operation conditions, i.e., Equations (5)–(18). In the emergency-mode operation problem, Equations (16) and (17) are ignored because reducing ELS is more important than preventing the degradation of the battery life attributed to repeated battery charging and discharging.

$$\begin{array}{c}\hfill {\Phi }_{{\widehat{ϵ}}_{t{s}_l}^A}^{-1}(1-\alpha )\ge P_{t{s}_l}^{tA.ST{O}_l},{\forall }_{t{s}_l},{\forall }_l.\end{array}$$

(25)

$$u_{g,t{s}_l}^{ST{O}_l}·P_g^{min}\le P_{g,t{s}_l}^{ST{O}_l}\le u_{g,t{s}_l}^{ST{O}_l}·P_g^{max}{\forall }_g,{\forall }_l,{\forall }_{t{s}_l}$$

(26)

$$P_{g,t{s}_l-1}^{ST{O}_l}-R{D}_G^{max}\le P_{g,t{s}_l}^{ST{O}_l},{\forall }_{g,l},t{s}_l>st{o}_l.$$

(27)

$$P_{g,t{s}_l}^{ST{O}_l}\le P_{g,t{s}_l-1}^{ST{O}_l}+R{U}_G^{max},{\forall }_{g,l},t{s}_l>st{o}_l.$$

(28)

$$\sum _{to=0}^{T{O}_g-1}{u}_{g,t+to}^{ST{O}_l}\ge T{o}_g(u_{g,t{s}_l}^{ST{O}_l}-u_{g,t{s}_l-1}^{ST{O}_l}),{\forall }_g,{\forall }_l,t{s}_l>st{o}_l.$$

(29)

$$T{s}_g-\sum _{ts=0}^{T{s}_g-1}{u}_{g,t{s}_l+ts}^{ST{O}_l}\ge T{s}_g(u_{g,t{s}_l-1}^{ST{O}_l}-u_{g,t{s}_l}^{ST{O}_l}),{\forall }_g,{\forall }_l,t{s}_l>st{o}_l.$$

(30)

$$y_{g,t{s}_l}^{ST{O}_l}=max\{(u_{g,t{s}_l}^{ST{O}_l}-u_{g,t{s}_l-1}^{ST{O}_l}),0\},{\forall }_g,{\forall }_l,t{s}_l>st{o}_l.$$

(31)

$$z_{g,t{s}_l}^{ST{O}_l}=max\{(u_{g,t{s}_l-1}^{ST{O}_l}-u_{g,t{s}_l}^{ST{O}_l}),0\},{\forall }_g,{\forall }_l,t{s}_l>st{o}_l.$$

(32)

$$So{C}_{t{s}_l}^{ST{O}_l}=So{C}_{t{s}_l-1}^{ST{O}_l}+\frac{\eta ·P_{t{s}_l}^{ch.ST{O}_l}-P_{t{s}_l}^{dch.ST{O}_l}}{Ba{t}_c}·\mathsf{\Delta }t,{\forall }_l,t{s}_l>st{o}_l.$$

(33)

$$So{C}_{t{s}_l}^{ST{O}_l}·Ba{t}_c+\eta ·P_{t{s}_l}^{ch.ST{O}_l}·\mathsf{\Delta }t\le DoD·Ba{t}_c,{\forall }_{t{s}_l}.$$

(34)

$$0\le P_{t{s}_l}^{dch.ST{O}_l},P_{t{s}_l}^{ch.ST{O}_l}\le PC{S}_c,{\forall }_{t{s}_l}.$$

(35)

$$P_{t{s}_l}^{dch.ST{O}_l}·\mathsf{\Delta }t\le So{C}_{t{s}_l}^{ST{O}_l}·Ba{t}_c,{\forall }_{t{s}_l}.$$

(36)

$$0\le C_{t{s}_l}^{ELSA.ST{O}_l},C_{t{s}_l}^{ELSB.ST{O}_l},P_{t{s}_l}^{tA.ST{O}_l},P_{t{s}_l}^{tB.ST{O}_l}.$$

(37)

3.3. Preparation-Mode Operation Formulation

The optimal MG operation in the preparation mode is formulated as nested MILP problems with chance constraints. It is a combination of normal-mode and emergency-mode problems. Further, the on-event problem under the emergency-mode operation condition is nested in the pre-scheduling problem under the normal-mode operation condition. In other words, with the decision-making of the pre-scheduling problem, normal- and emergency-mode operations are determined together under the preparation-mode problem. The cost function of the preparation mode, which is a sum of the normal-mode and emergency-mode operating cost, is expressed as Equation (38).

$$min[f^{NM}\left(X^{NM}\right)+f^{EM}\left(X^{EM}\right)]$$

(38)

The objective function of the preparation mode is subject to constraints Equations (2)–(20), Equations (22)–(37), and Equations (39)–(47).

$$P_{g,st{o}_l-1}^{NM}-R{D}_G^{max}\le P_{g,t{s}_l}^{ST{O}_l},{\forall }_g,{\forall }_l,t{s}_l=st{o}_l.$$

(39)

$$P_{g,t{s}_l}^{ST{O}_l}\le P_{g,st{o}_l-1}^{NM}+R{U}_G^{max},{\forall }_g,{\forall }_l,t{s}_l=st{o}_l.$$

(40)

$$\sum _{to=0}^{T{O}_g-1}{u}_{g,t+to}^{ST{O}_l}\ge T{o}_g(u_{g,t{s}_l}^{ST{O}_l}-u_{g,st{o}_l-1}^{NM}),{\forall }_g,{\forall }_l,t{s}_l=st{o}_l.$$

(41)

$$To(u_t^{NM}-u_{t-1}^{NM})\le \sum _{to=0}^{To-(j+1)}{u}_{t{s}_l+to}^{ST{O}_l}+\sum _{k=1}^j{u}_{t+j-k}^{NM},{\forall }_g,{\forall }_l.$$

(42)

$$T{s}_g-\sum _{ts=0}^{T{s}_g-1}{u}_{g,t{s}_l+ts}^{ST{O}_l}\ge T{s}_g(u_{g,st{o}_l-1}^{NM}-u_{g,t{s}_l}^{ST{O}_l}),{\forall }_g,{\forall }_l,t{s}_l=st{o}_l.$$

(43)

$$T{s}_g-\sum _{to=0}^{To-(j+1)}{u}_{g,t{s}_l+j+to}^{ST{O}_l}+\sum _{k=1}^j{u}_{t+j-k}^{NM}\le T{s}_g(u_t^{NM}-u_{t-1}^{NM}),{\forall }_g,{\forall }_l.$$

(44)

$$y_{g,t{s}_l}^{ST{O}_l}=max\{(u_{g,t{s}_l}^{ST{O}_l}-u_{g,st{o}_l-1}^{NM}),0\},{\forall }_g,{\forall }_l,t{s}_l=st{o}_l.$$

(45)

$$z_{g,t{s}_l}^{ST{O}_l}=max\{(u_{g,st{o}_l-1}^{NM}-u_{g,t{s}_l}^{ST{O}_l}),0\},{\forall }_g,{\forall }_l,t{s}_l=st{o}_l.$$

(46)

$$So{C}_{t{s}_l}^{ST{O}_l}=So{C}_{st{o}_l-1}^{NM}+\frac{\eta ·P_{t{s}_l}^{ch.ST{O}_l}-P_{t{s}_l}^{dch.ST{O}_l}}{Ba{t}_c}·\mathsf{\Delta }t,{\forall }_l,t{s}_l=st{o}_l.$$

(47)

In the preparation-mode operation problem, some decision variables of the emergency mode are affected by the decision variables of normal-mode problems before the STO. Thus, the preparation-mode operation problem needs to include constraints for considering the relationship between the normal- and emergency-mode operation problems. The decision variables in the emergency-mode operation affected by the decision variables in the normal mode operation are SoC dynamics, on/off state, and output of generators. Equations (39)–(47) indicate the relationship of decision variables between the emergency normal mode operation.

Equations (39) and (40) represent the ramp capability’s limit relationship between the normal- and emergency-mode variables about the generation output. Equations (41) and (44) indicate the minimum startup/shutdown time relationships between the normal- and emergency-mode variables in the generators’ on/off state. In constraints (42) and (44), j = 1:To − 1, t = STO−j, $t{s}_l$ = $st{o}_l$. Equations (45) and (46) represent the startup and shutdown binary variables’ relationship between the normal and emergency modes, respectively. Equation (47) indicates the SoC relationship between the normal and emergency modes.

4. Case Study

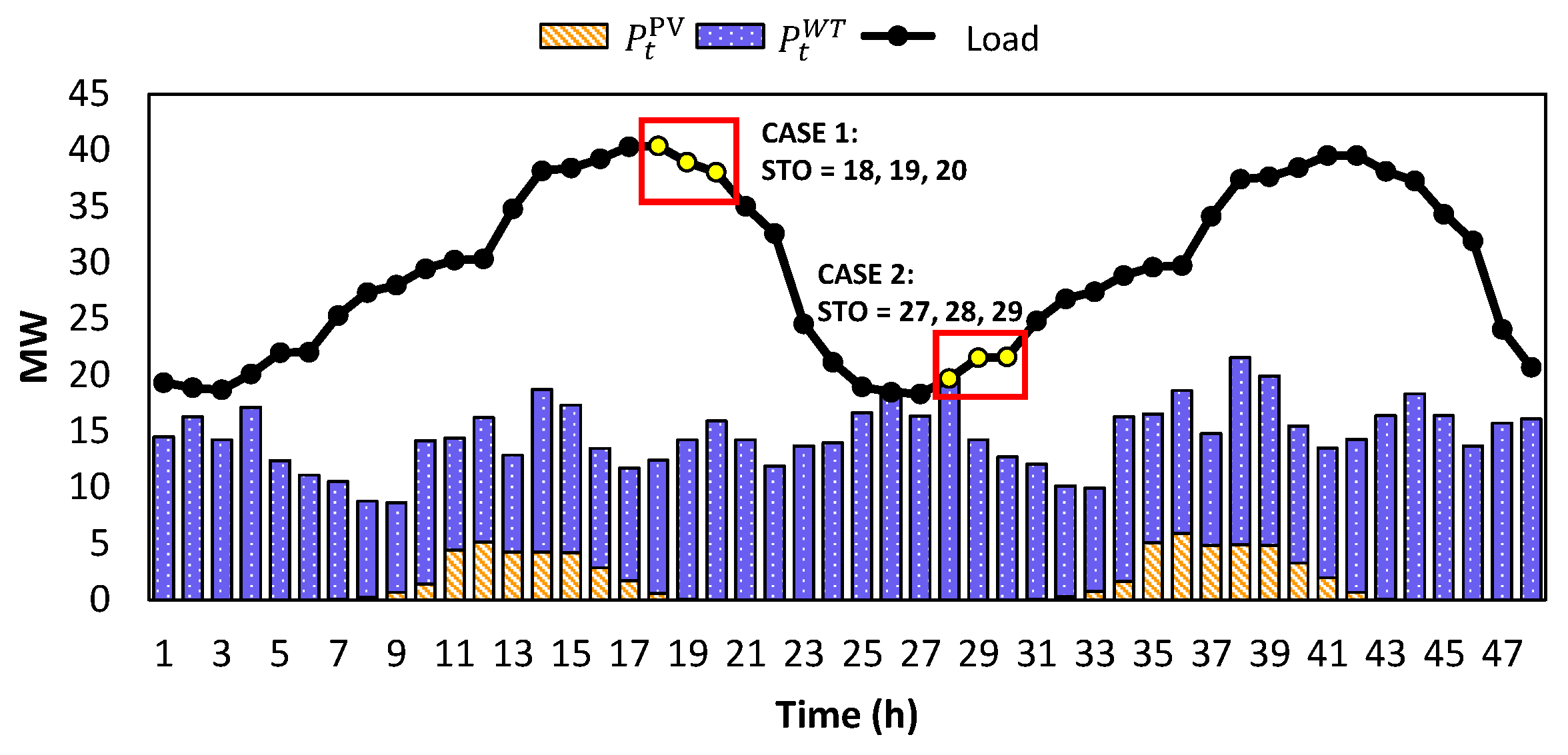
We set the optimization time to 48 h and performed simulations for two cases, considering the $STO$ as a high load time and a low time period for evaluating the performance of the proposed mode. Figure 4 shows the hourly forecasted electricity market price. Figure 5 shows the renewable generation and load.

In the first case, the $ST{O}_l$ are 18 h, 19 h, and 20 h. In the second case, the $ST{O}_l$ are 27 h, 28 h, and 29 h. The parameters of CG used in the MG, namely generation cost, minimum/maximum generation capacity, ramp up/down capability, startup/shutdown cost, and minimum operating time (TO)/stop time (TS), are shown in

Table 1. Parameters of the controllable generators.

Unit	Gen. Cost (USD/MWh)	Start Up/Down Cost (USD)	Min./Max. Capacity (MW)	TO/TS (h)	Ramp Up/Down Rate (MW/h)
G1	27.7	15/5	1/8	3/3	3
G2	39.1	45/8	1/4	3/3	2
G3	61.3	25/5	0.8/2	1/1	2
G4	65.6	10/2	0.8/2	1/1	2

. The parameters of ESS, namely the battery capacities, PCS capacities, and the minimum charging time (TCM) and minimum discharge time (TDM), are shown in

Table 2. Parameters associated with ESS.

Storage	Capacity (MWh)	TCM/TDM (h)	PCS (MW)
ESS	24	3/3	12

. The depth of the discharge (DoD) is set to 0.9. In the MG, the capacities of solar photovoltaic and wind turbine generators are 8.21 MW and 20.76 MW, respectively.

The $C^{LSA}$ and $C^{LSB}$ are set as USD 9000 and USD 3000, respectively. At the forecast error of load, the standard deviations are set to 8%. At the forecast error of renewable generation, the standard deviations are set to 20%. $\alpha$ indicates the survival index of load A. In the preparation mode, the survivability of the critical load must be above $\alpha$%. The $\alpha$ is set to 0.95.

4.1. Case 1 (STO = 18, 19, 20)

The case study compares the difference between the two methods of MG operation (with and without preparation). Further, we evaluate the effect of proactive actions on the load during the event periods.

Usually, proactive actions are realized by securing the available power through rescheduling generators and maintaining the battery SoC. In Case 1, all generators in the MG are scheduled for maximum output regardless of the preparation in the pre-event time to supply a high load at the lowest cost in high electricity prices. In the pre-event time, different operations of the MG with and without preparation are ($P_t^{dch.NM}$) and ($P_t^{Buy.NM}$). ($P_t^{dch.NM}$) means the power discharged from the battery at t in the normal-mode operations. ($P_t^{Buy.NM}$) means the power bought from the utility grid at t in the normal-mode operation. 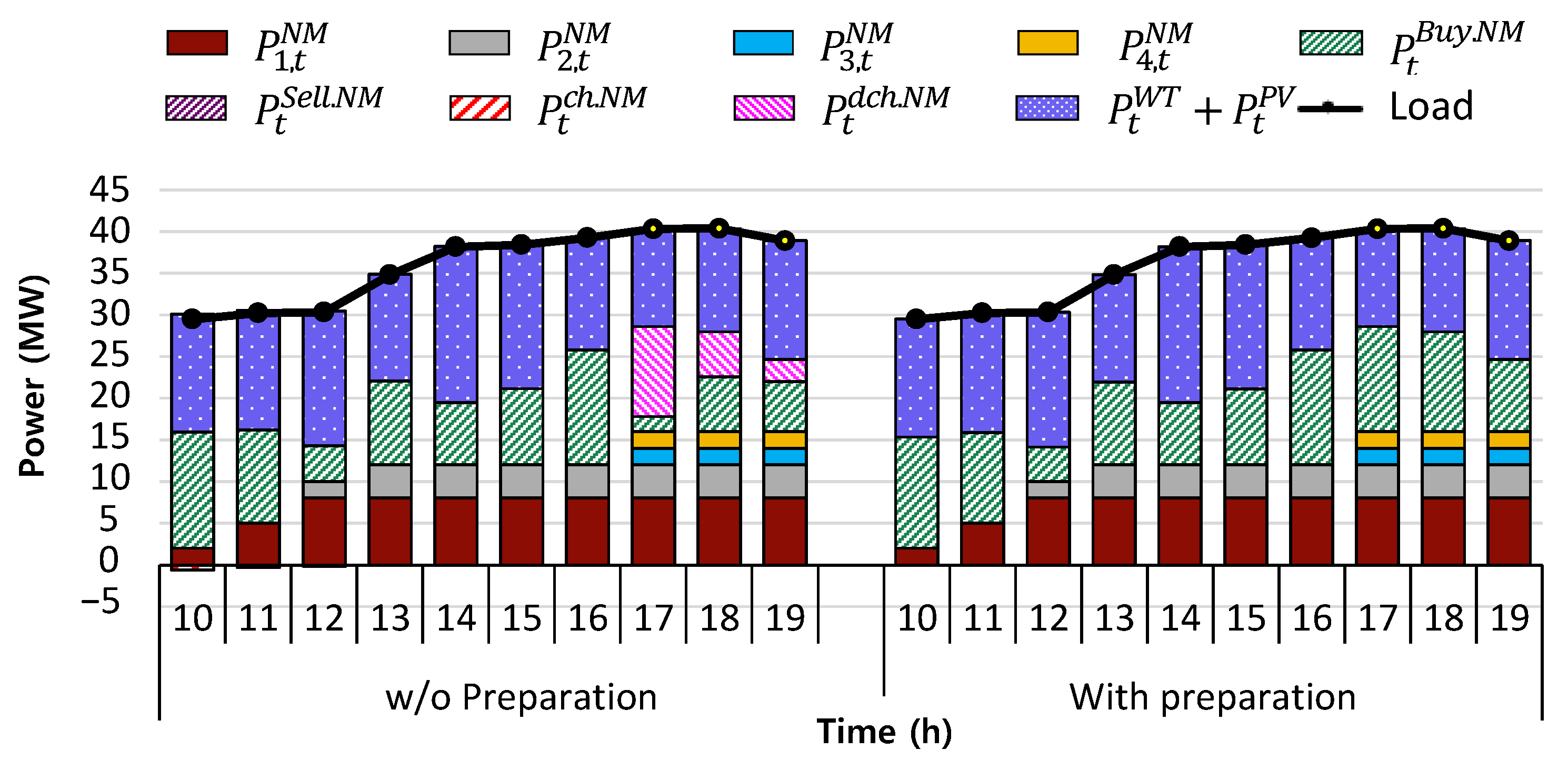Figure 6 shows ($P_t^{dch.NM}$, ($P_t^{Buy.NM}$) and other dynamics of generators of the MG operation with and without preparation.

In the MG operation without preparation, the battery discharge occurs when electricity prices are high for supplying the load in the normal mode with minimal cost. At pre-event times without preparation, $P_t^{dch.NM}$ is 10.79 MW, 5.4 MW, and 2.7 MW and $P_t^{Buy.NM}$ is 1.81 MW, 6.56 MW, and 5.96 MW. In the MG operation with preparation, $P_t^{dch.NM}$ does not occur at pre-event times, (1) to prepare for the interruption of the external power supply attributed to events and (2) to maintain the SoC of the battery at an appropriate level. In the MG operation with preparation, instead of decreasing $P_t^{dch.NM}$, $P_t^{Buy.NM}$ increases at pre-event times $P_t^{Buy.NM}$. Thus, at the pre-event times, the sums of $P_t^{dch.NM}$ and $P_t^{Buy.NM}$ are 12.61 MW, 11.96 MW, and 8.66 MW in the MG operation without preparation.

In this section, the probability that the power delivered to a load is higher than the actual load is called load survivability. We calculated the load survivability to evaluate the effect of proactive actions on the load during the event periods. The formal expression of the critical and normal load survivability is ${\Phi }_{{\widehat{ϵ}}_{t{s}_l}^A}(P_{t{s}_l}^{LA}-P_{t{s}_l}^{tA.ST{O}_l})$ and ${\Phi }_{{\widehat{ϵ}}_{t{s}_l}^B}(P_{t{s}_l}^{LB}-P_{t{s}_l}^{tB.ST{O}_l})$.

Figure 7 shows the different components of the MG operation based on a proactive action at each event period in Case 1. In Case 1, the different components of MG operations are SoC (%), load A survivability (%), and operating costs (USD ). The difference in load B survivability appears very low in Case 1 because load A is large, and there is insufficient power to transfer to load B regardless of preparation.

At the pre-event time, the SoC is 90%, 90%, and 90% with preparation and the SoC is 45%, 22%, and 11% without preparation. For maintaining the SoC at a high level, the preparation mode requires more $P_t^{Buy.NM}$ than without preparation when the electricity price is relatively high. Thus, in the normal mode, the preparation mode has a higher operating cost than the MG operation without preparation. The normal-mode operating costs are USD 22,837 and USD 22,263 with and without preparation, respectively.

However, the emergency MG operation without preparation cannot adequately guarantee load A survivability because of the lack of available power during the event periods. In the emergency MG operation without preparation, load A survivability is under 95%, which excludes t = 24 of $ST{O}_{20}$. The minimum values of load A survivability are 67%, 39%, and 24%, which appear the first time in each event period because the load decreases over time. In the emergency MG operation with preparation, load A survivability is greater than the set value of $\alpha$%, which is equal to 95%. The load A survivability is 95%, which excludes t = 23 and t = 24. The load A survivability values are 97%, 98%, and 99% at t = 23 of $ST{O}_{19}$ and t = 23, t = 24 of $ST{O}_{20}$. These load A survivability values are determined by reflecting the ECLS of load A.

The emergency-mode operation costs contain the ECLS and the other generation costs. These depend on the available power, such as the generation output capability and the stored energy in the ESS secured at pre-event times. The emergency mode operation costs without and with preparation are USD 156,555, USD 116,769, and USD 86,401, and USD 145,392, USD 90,315, and USD 47,795, respectively. The maximum values for the emergency mode operation costs are shown at $ST{O}_{18}$ because the total load of the event periods is the highest in $ST{O}_{18}$, $ST{O}_{19}$, and $ST{O}_{20}$. The maximum difference in the emergency mode operation costs is shown at $ST{O}_{20}$ because the SoC difference is the highest at t = 19 in the normal mode.

The simulation results in Case 1 show that the proposed method employs proactive actions to ensure the survivability of the critical loads and lower the total operation cost, which includes the ECLS. When comparing normal-mode MG operating cost, an additional cost of USD 574 is incurred during normal mode to operate in preparation mode. However, in the case of MG operation without preparation, there are cases where the critical load survivability under $\alpha$% and operation costs for all $ST{O}_l$ are higher than that of MG operation with preparation.

Table 3. Total MG operation costs according to $ST{O}_l$ in Case 1.

	$\mathit{S}\mathit{T}{\mathit{O}}_{18}$	$\mathit{S}\mathit{T}{\mathit{O}}_{19}$	$\mathit{S}\mathit{T}{\mathit{O}}_{20}$
with preparation	USD 168,229	USD 113,152	USD 70,632
$w/o$ preparation	USD 178,818	USD 139,032	USD 108,664
Cost improvement	5.92%	18.61%	35.00%

shows the total MG operation costs in Case 1 according to $ST{O}_l$.

4.2. CASE 2 (STO = 27, 28, 29)

At pre-event times in Case 2, regardless of preparation, the output of the generators with relatively high fuel costs stopped, and the renewable generation and $P_t^{Buy.NM}$ supply the loads. Further, the battery is operated to charge power with a low economic value and to utilize it during times of high load and high electricity price. However, based on the preparation, the output patterns of some generators with minimum downtime and SoC are different. Figure 8 shows the optimization results between the two modes in Case 2 in pre-event times.

In the normal MG operation without preparation, G1 and G2 shut off at t = 26 and 25. At t = 26, while $P_t^{Buy.NM}$ increases, all CG shuts off, and the battery starts charging through renewable generation. At pre-event times, the normal MG operation without preparation, $P_t^{Buy.NM}$, is 0.25 MW, 11.09 MW, 7.63 MW, and 2.8 MW and $P_t^{ch.NM}$ is 0 MW, 11.35 MW, 5.67 MW, and 2.84 MW. In the normal MG operation with preparation, G1 maintains the on-state, and the G2 shuts off at t = 24 for generating t = 27, 28, and 29 for $ST{O}_{27}$, $ST{O}_{28}$, and $ST{O}_{29}$, respectively. The battery starts charging at t = 25. It is earlier than that in the normal mode of operation without preparation. At pre-event times with preparation, $P_t^{Buy.NM}$ is 11.61 MW, 4.41 MW, 2.79 MW, and 0 MW; $P_t^{ch.NM}$ is 11.32 MW, 5.66 MW, 2.83 MW, and 1.42 MW. Therefore, in the MG operation mode with preparation, the SoC is 68%, 79%, and 84%, which is 23%, 11%, and 6% higher than that of the MG operation without preparation at pre-event times. As in Case 1, the preparation requires more costs because of the uneconomical power adjustment of the generator and for maintaining SoC at a high level. Therefore, the preparation mode has higher operating costs in Case 2. The normal MG operating costs are USD 22,581 with preparation and USD 22,263 without preparation.

The load survivability and total available power of CGs, considering minimum stop time and ramp capability, are calculated to evaluate the effect of proactive actions on the load during the event periods in Case 2.

Table 4. Total available power of CGs at each $ST{O}_l$.

$\mathit{S}\mathit{T}{\mathit{O}}_{27}$	t = 27	t = 28	t = 29	t = 30
with preparation	10 MW	15 MW	16 MW	16 MW
$w/o$ preparation	4 MW	6 MW	11 MW	14 MW
$\mathit{S}\mathit{T}{\mathit{O}}_{28}$	t = 28	t = 29	t = 30	t = 31
with preparation	11 MW	16 MW	16 MW	16 MW
$w/o$ preparation	6 MW	11 MW	14 MW	16 MW
$\mathit{S}\mathit{T}{\mathit{O}}_{29}$	t = 29	t = 30	t = 31	t = 32
with preparation	14 MW	16 MW	16 MW	16 MW
$w/o$ preparation	9 MW	14 MW	16 MW	16 MW

shows the total available power of CGs at each $ST{O}_l$.

With preparation, most CGs can generate the maximum output in the emergency MG operation. In the emergency MG operation without preparation, the total available power of CGs is under the maximum output of CGs due to the minimum stop time and ramp capability of G1 and G2. Without preparation, the total available power of CGs can be maxed at t = 31. Figure 9 shows the different components of the MG operation based on the proactive action at each event period in Case 2. The different components are SoC (%), load A survivability (%), load B survivability (%), and operating costs (USD) in Case 2.

In Case 1, the SoC continued to decline over time, where the load was relatively high. However, in Case 2, the SoC increased at times when the load was very low. This means that, at t = 31, t = 32, and t = 33, the surplus available power required to guarantee the survivability of the increased load was adequately stored. An increase in SoC at t = 31, t = 32, and t = 33 is observed in emergency MG operations with preparation because the total available power of CGs can quickly reach its maximum with preparation.

The differences in load survivability between the two modes during the event periods are caused by the SoC and total available power of CG at the pre-event time. The mean values of load A survivability are 98.31% and 95.91% with and without preparation, respectively. The mean values of load B survivability are 92.83% and 82.36% with and without preparation, respectively. Load A survivability is greater than the setting value of $\alpha$%, which is equal to 95% regardless of preparation because the load is relatively low. Further, the difference in load B survivability is low. However, a low difference in load survivability significantly affects emergency MG operation costs. These costs without preparation are USD 5037, USD 5905, and USD 9901, and those with preparation are USD 2407, USD 3580, and USD 6312. Although available power difference is the most at $ST{O}_{27}$, since loads increase significantly over time, the maximum values for the emergency-mode operation costs and the maximum difference in the emergency-mode operation costs are shown at $ST{O}_{29}$.

When comparing normal mode operating cost, an additional cost of USD 318 is incurred during normal mode to operate in preparation mode. However, even without preparation in Case 2, the critical load’s survivability is above $\alpha$% during the event periods due to the low load. Thus, the resilience-enhancement effect of the proposed method is lower than that of Case 1. However, in event periods, there are differences in normal load survivability, and operation costs for all $ST{O}_l$ are higher than those of MG operation with preparation. The simulation results in Case 2 show that the proposed method employs proactive actions to ensure the survivability of normal loads and lower the total operation cost, which includes the ECLS.

Table 5. Total MG operation costs according to $ST{O}_l$ in Case 2.

	$\mathit{S}\mathit{T}{\mathit{O}}_{27}$	$\mathit{S}\mathit{T}{\mathit{O}}_{28}$	$\mathit{S}\mathit{T}{\mathit{O}}_{29}$
with preparation	USD 24,988	USD 26,161	USD 28,893
$w/o$ preparation	USD 27,300	USD 28,168	USD 32,164
Cost improvement	8.47%	7.13%	10.17%

shows the total MG operation costs in Case 2 according to $ST{O}_l$.

5. Conclusions

A proactive microgrid-management strategy was proposed based on nested MILP problems with chance constraints to enhance resilience during the event periods. In the proposed method, the MG operates in preparation mode when an external grid outage warning is issued. We formulated the preparation-mode problem as a nested chance-constrained problem reflecting normal and emergency-mode operation conditions. The pre-scheduling problem under normal-mode operation conditions includes the on-event phase operation problem under emergency-mode operation conditions as a subproblem. In the proposed method, proactive actions of the MG are realized by rescheduling the generator and maintaining the high SoC of the battery.

The value of load shedding during event periods was reflected as ECLS in the proposed method. Further, we reflected the critical load shedding value in chance constraints of the preparation-mode problem. These induce MG to operate conservatively to ensure survivability.

It was confirmed that the proposed method efficiently and proactively determined the operation of the battery and generator during the normal mode to improve resilience during the event periods when compared to the MG operation without preparation. A comparison of the operation with and without preparation indicated that the proposed method slightly increased the operating cost in the normal mode but was effective in increasing the load survivability and reducing the operating cost during the event periods. Further, we find that the resilience improvement effect of the proposed method may vary depending on the predicted start time of outages. When the predicted start times of outage are high-load time periods, the survivability of critical loads during the event periods is guaranteed above 95% in the proposed method but only guaranteed some time in MG operation without preparation mode. Since all loads are high during the event periods, the survivability of normal loads is low with and without preparation. When predicted start times of outages are low-load time periods, since all loads are low during the event periods, the survivability of critical loads is guaranteed to be above 95% regardless of preparation. However, depending on the preparation, the survivability and ECLS of the normal load are different during the event periods, and the proposed method shows resilience enhancement.

In the proposed method, we assumed the predicted the start time of outages and event duration. Therefore to maximize the efficiency of the proposed method, the event-prediction information should be delivered to the centralized MG operator a few hours before the actual event occurs. On the other hand, the proposed method may be less effective for events with predictable characteristics seconds or minutes before the event occurs. Furthermore, the characteristics based on the load type and voltage were not considered in the proposed method. In future studies, we plan to reflect on the characteristics of critical loads in the proposed method and extend the proposed method for considering the voltage by applying network constraints.