Numerical Study on the Flow Past Three Cylinders in Equilateral-Triangular Arrangement at Re = 3 × 106
Abstract
1. Introduction
2. Numerical Models
2.1. Numerical Method
2.2. Boundary Conditions and Grid System


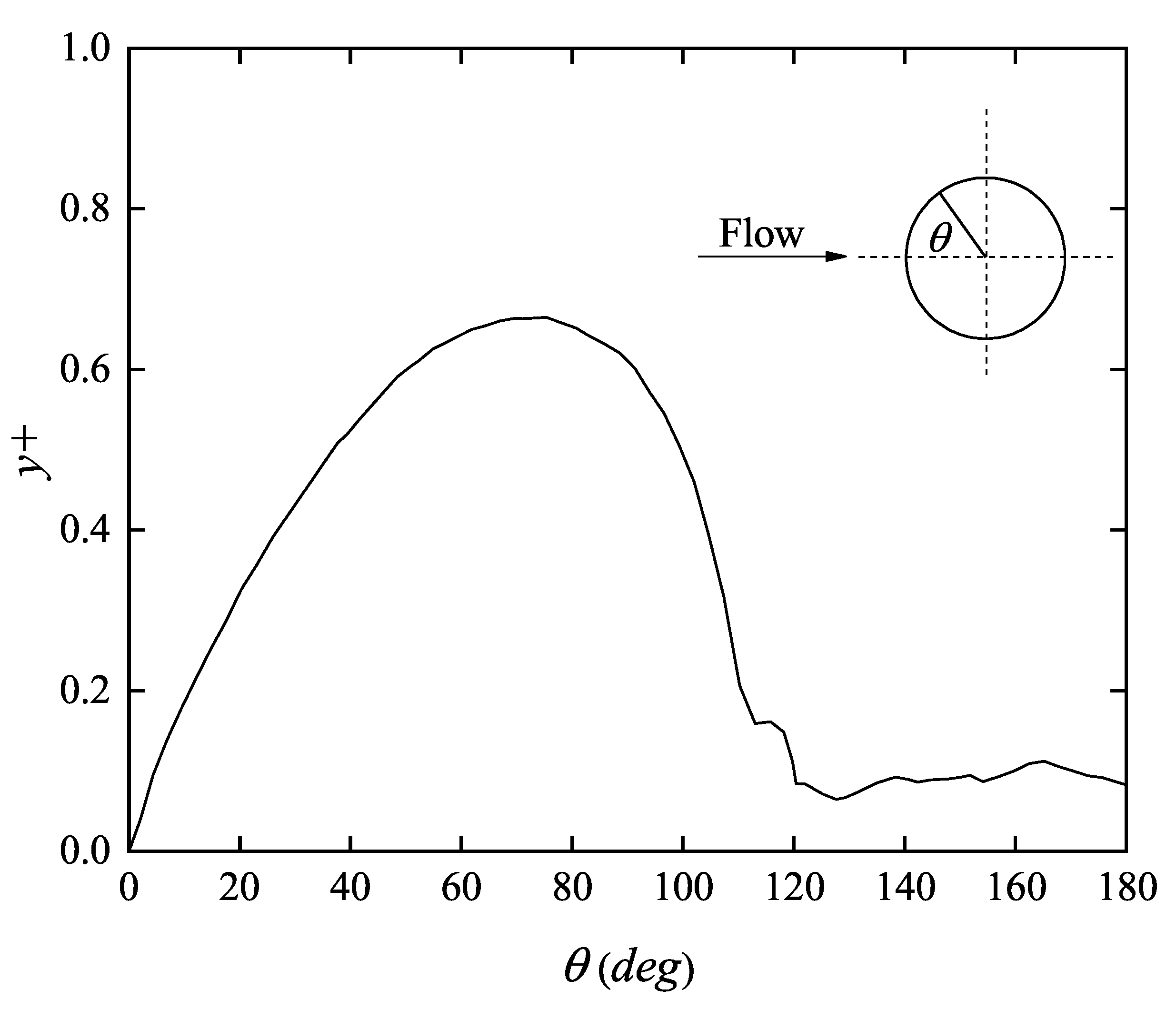
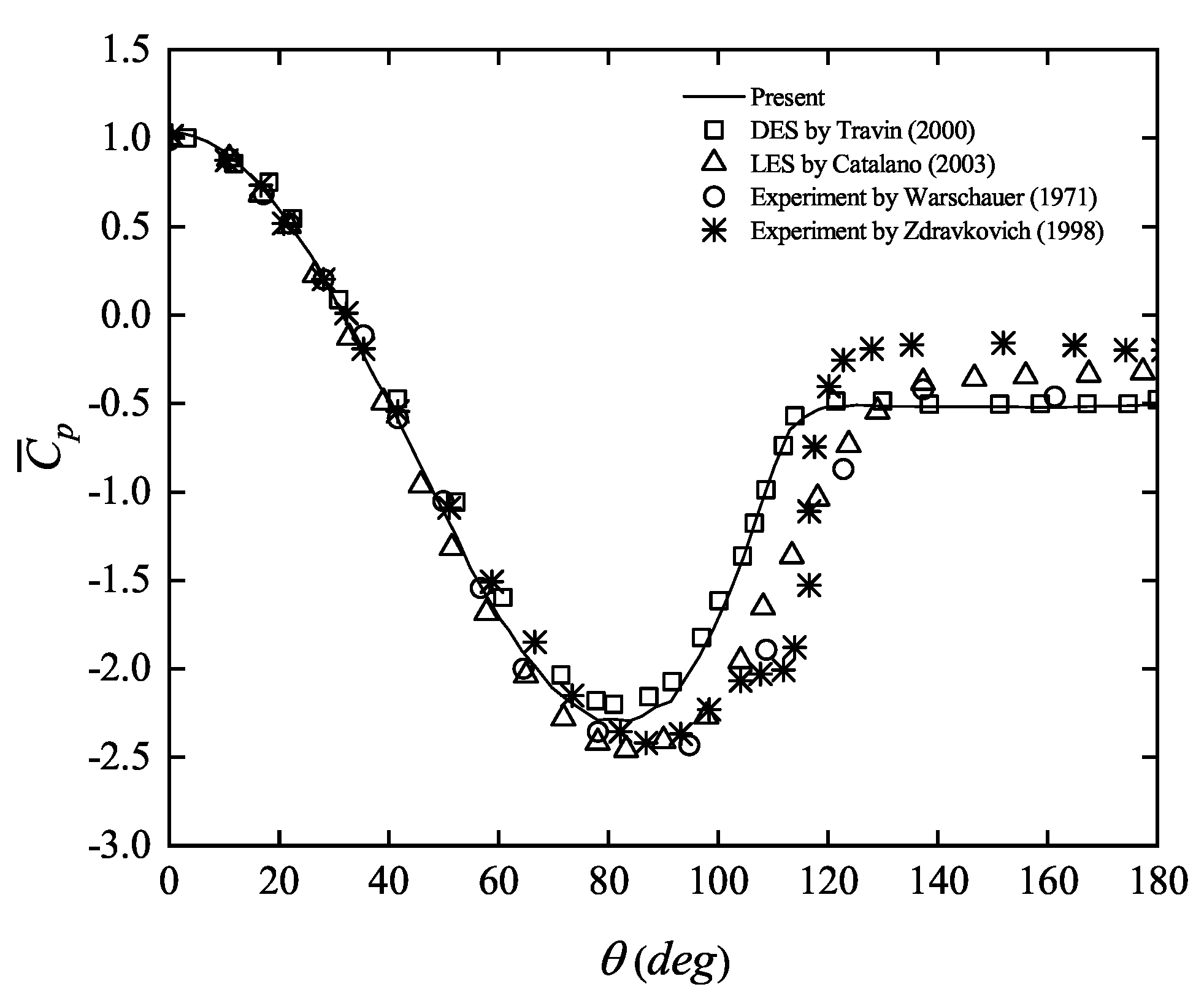
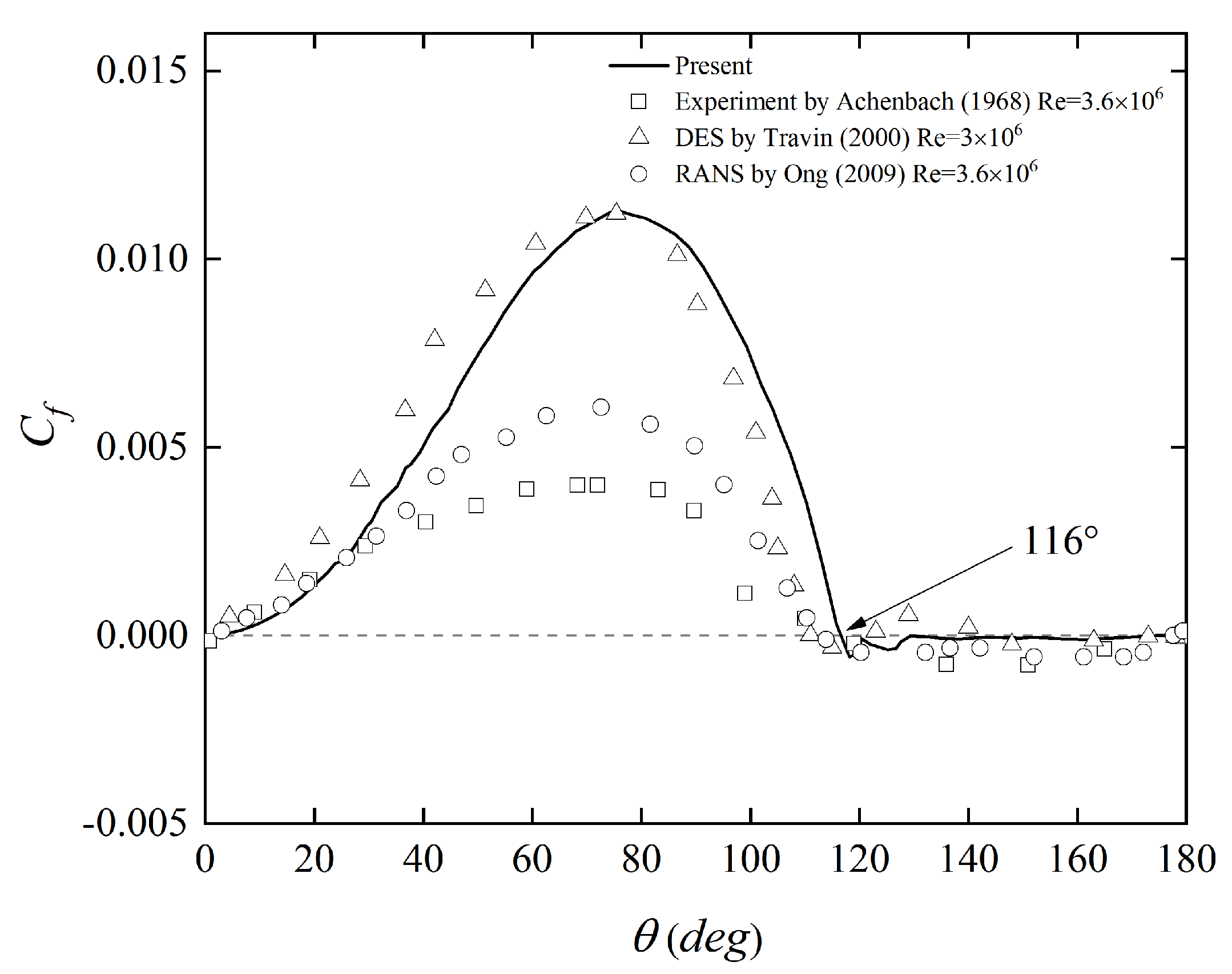
3. Convergence Study and Calculation Validation
4. Results and Discussion
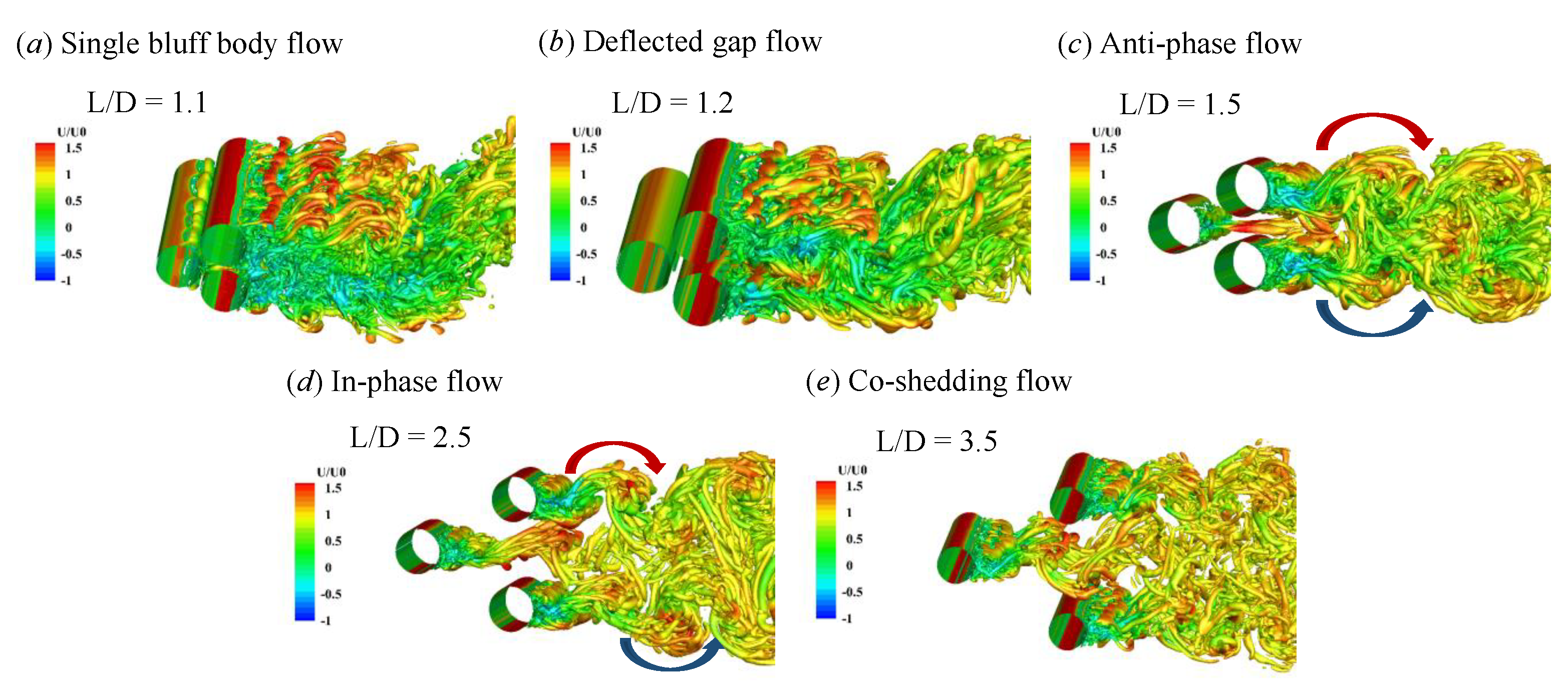
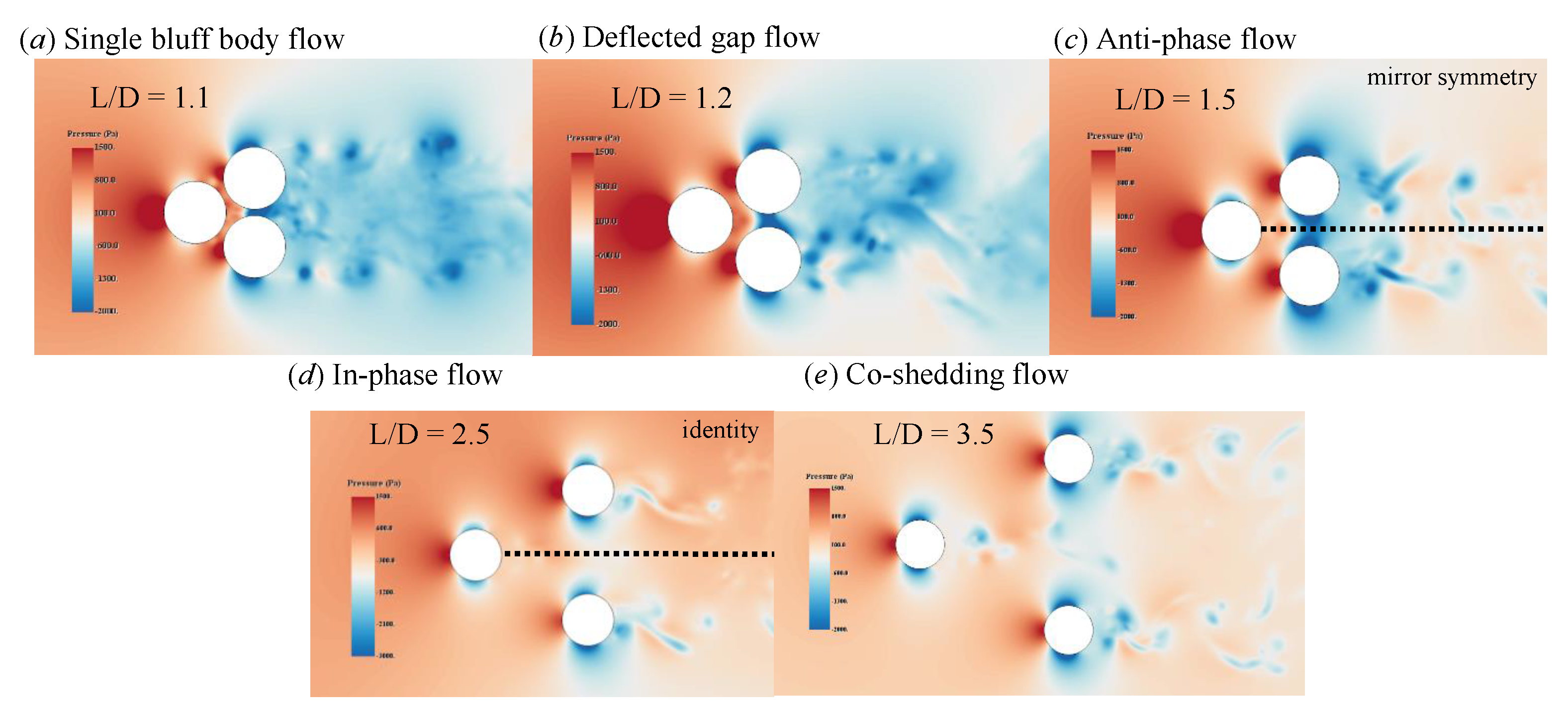
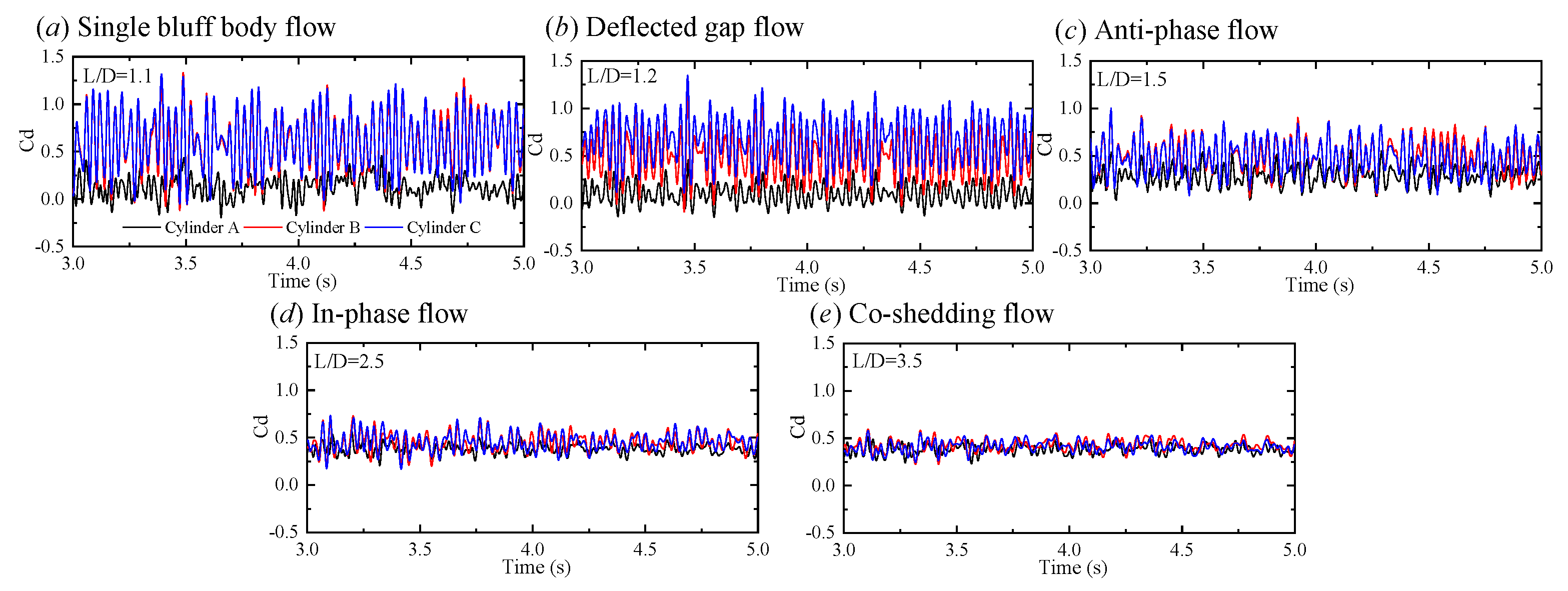
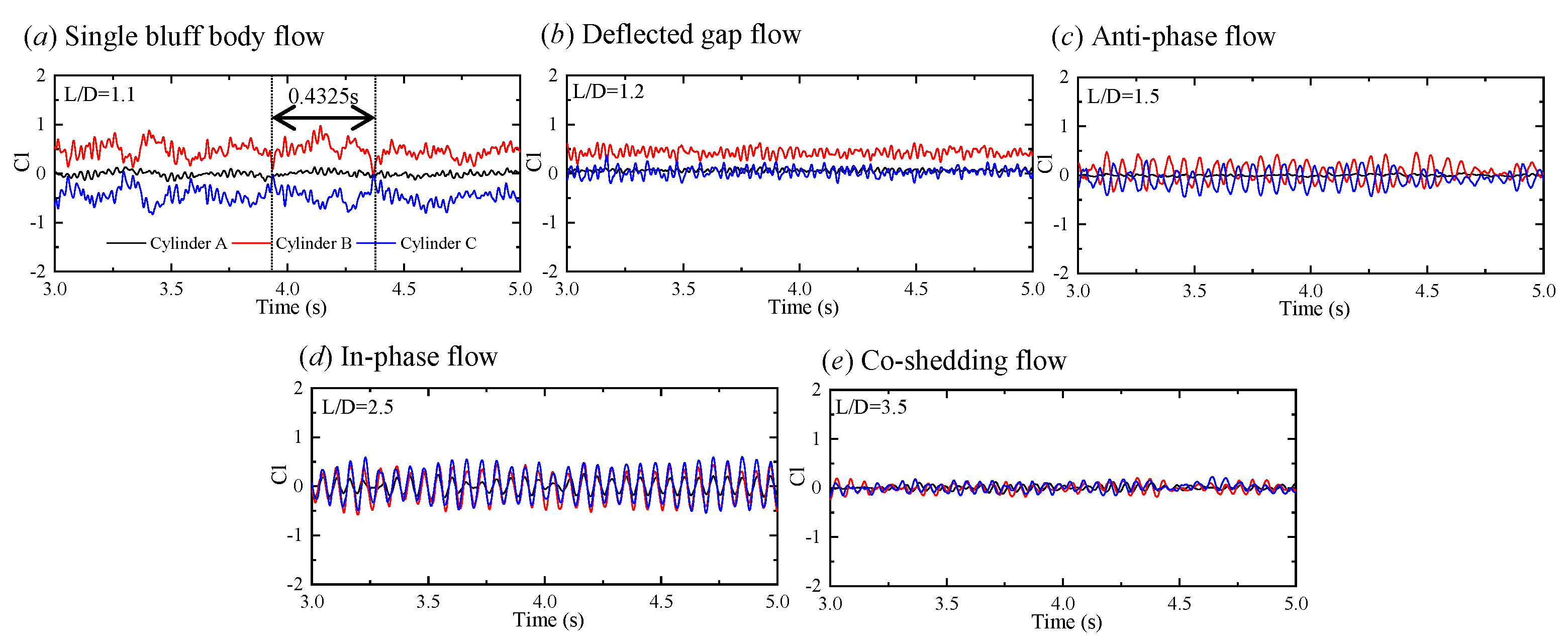
4.1. Flow Patterns
- Single bluff body flow

- Deflected gap flow
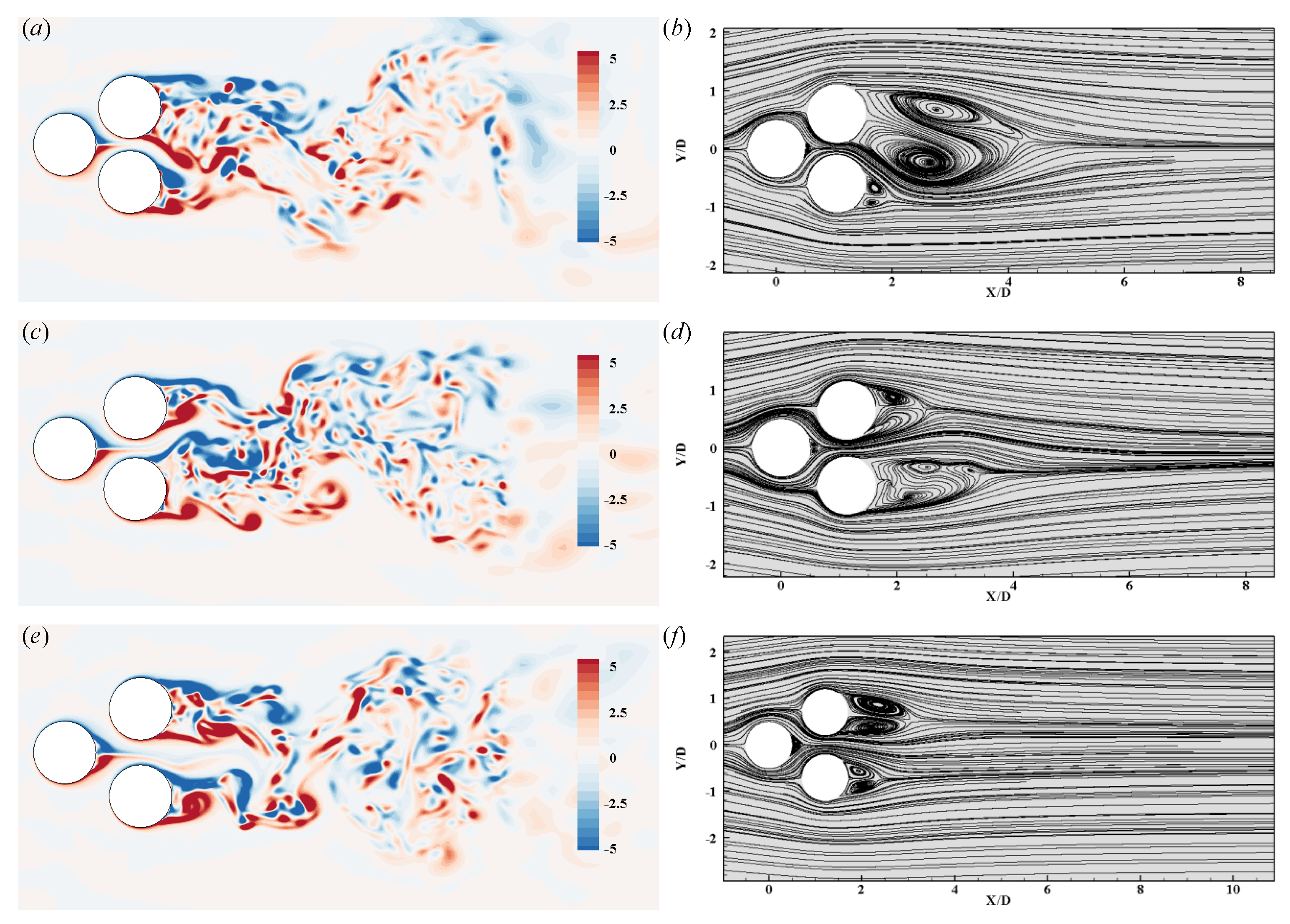
- Anti-phase flow

- In-phase flow
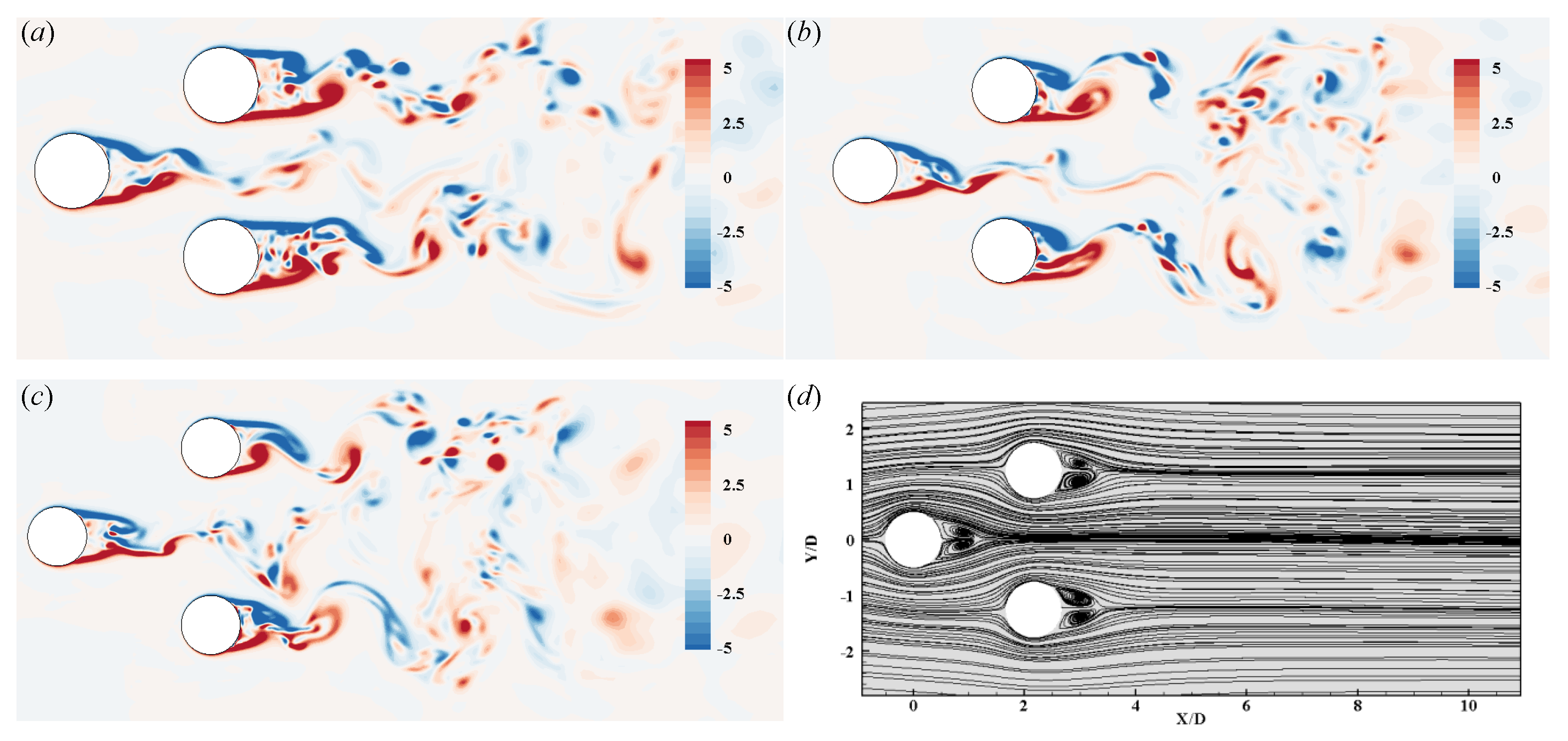
- Co-shedding flow

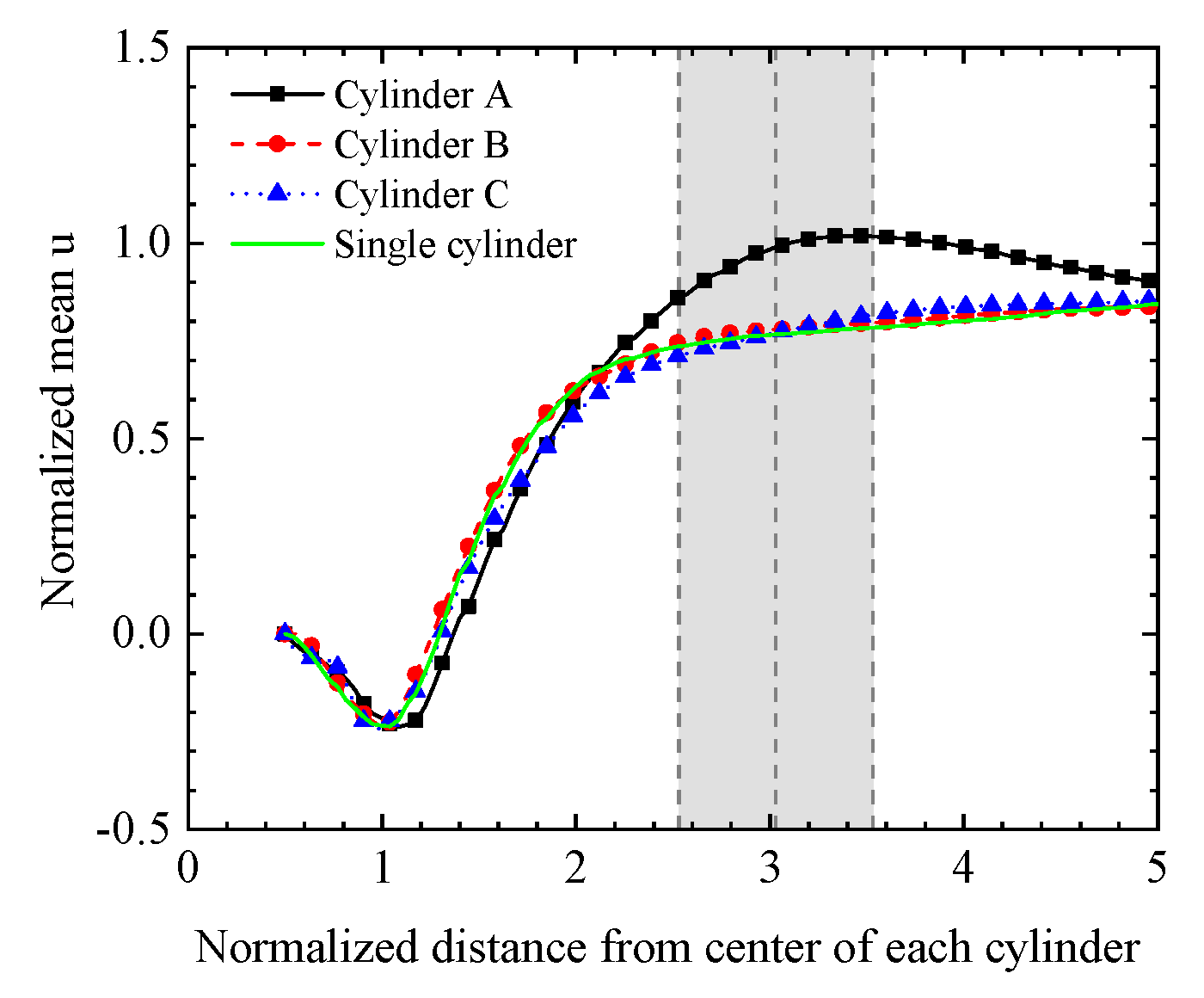
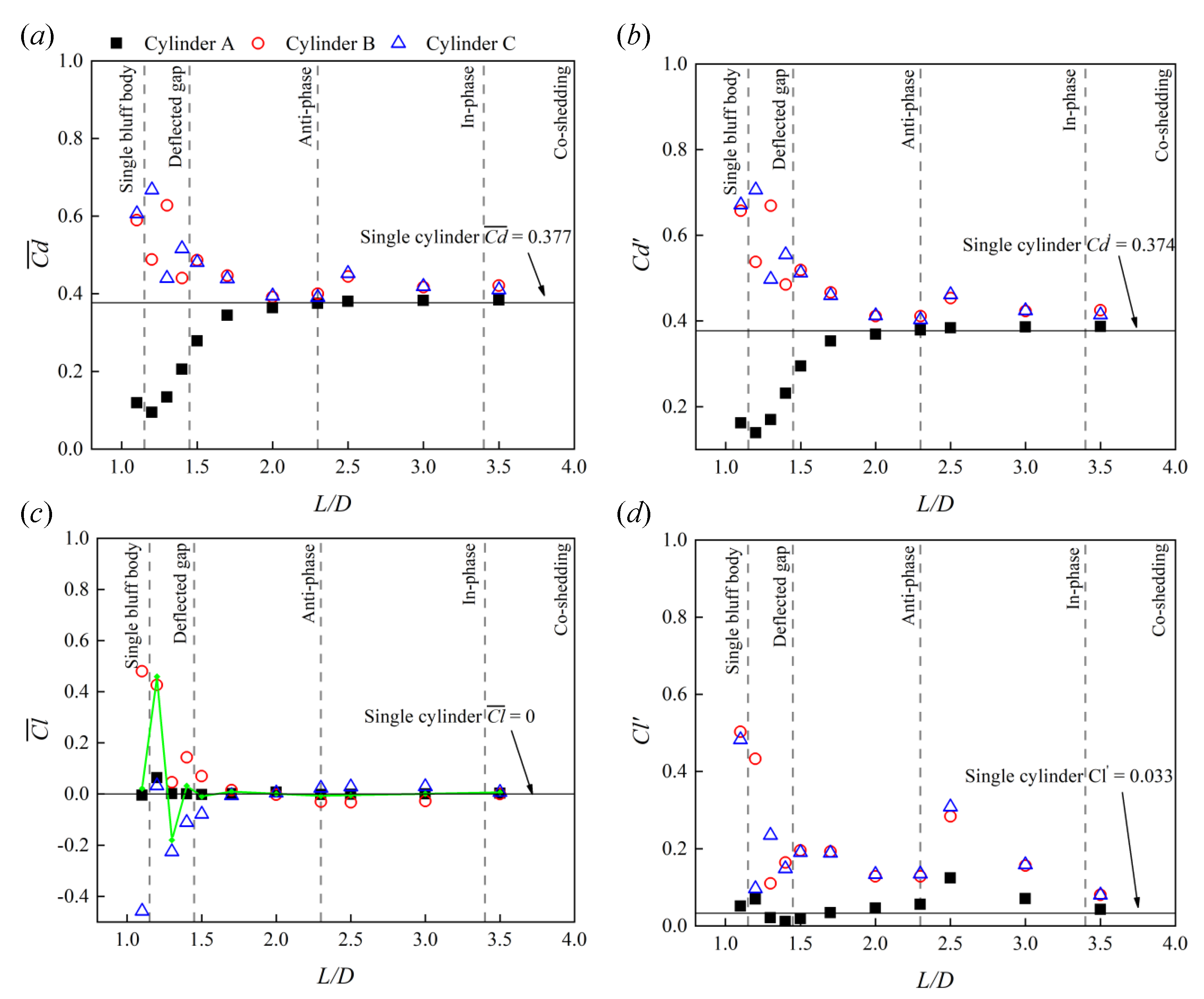
4.2. Fluid Force Coefficients
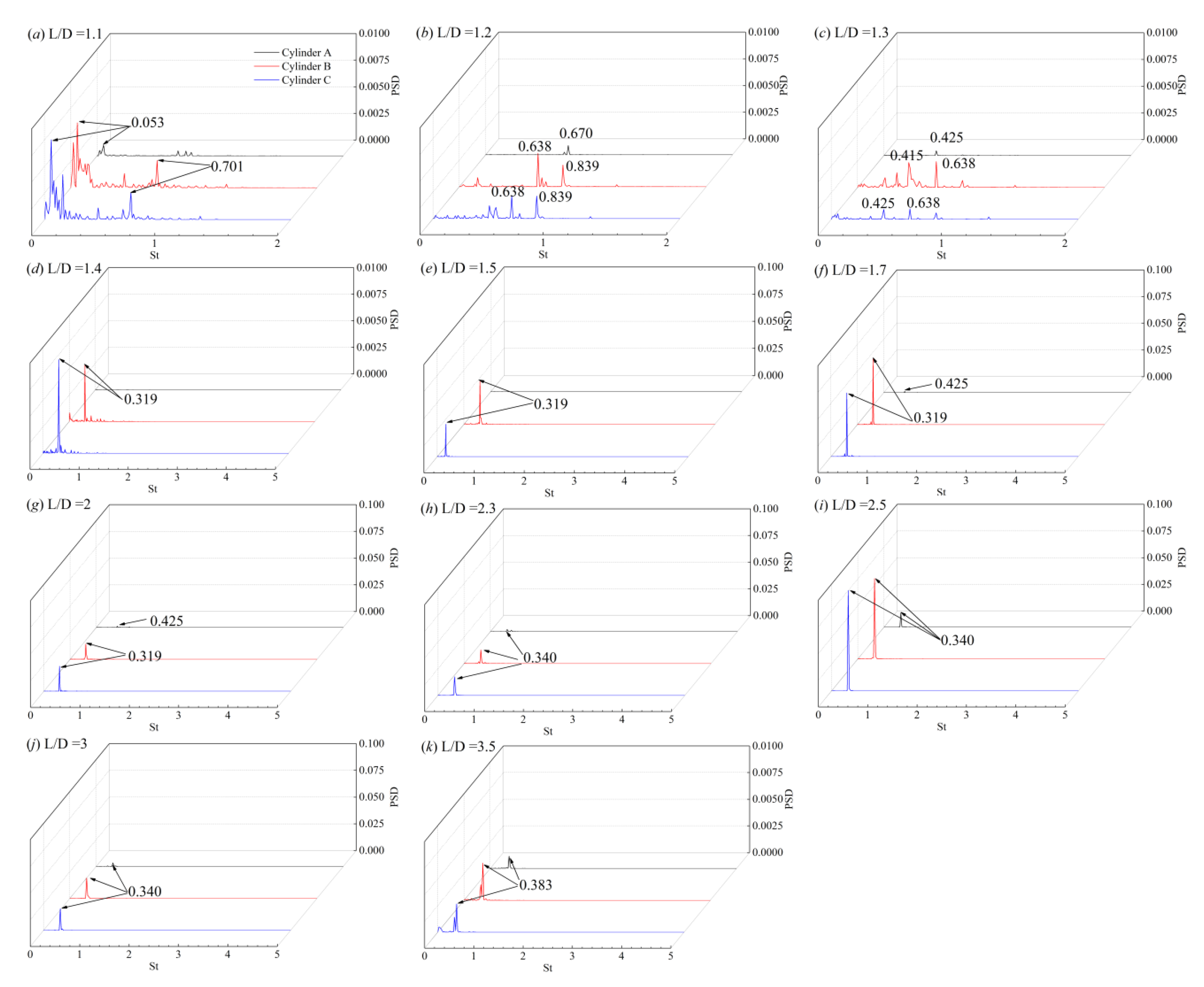
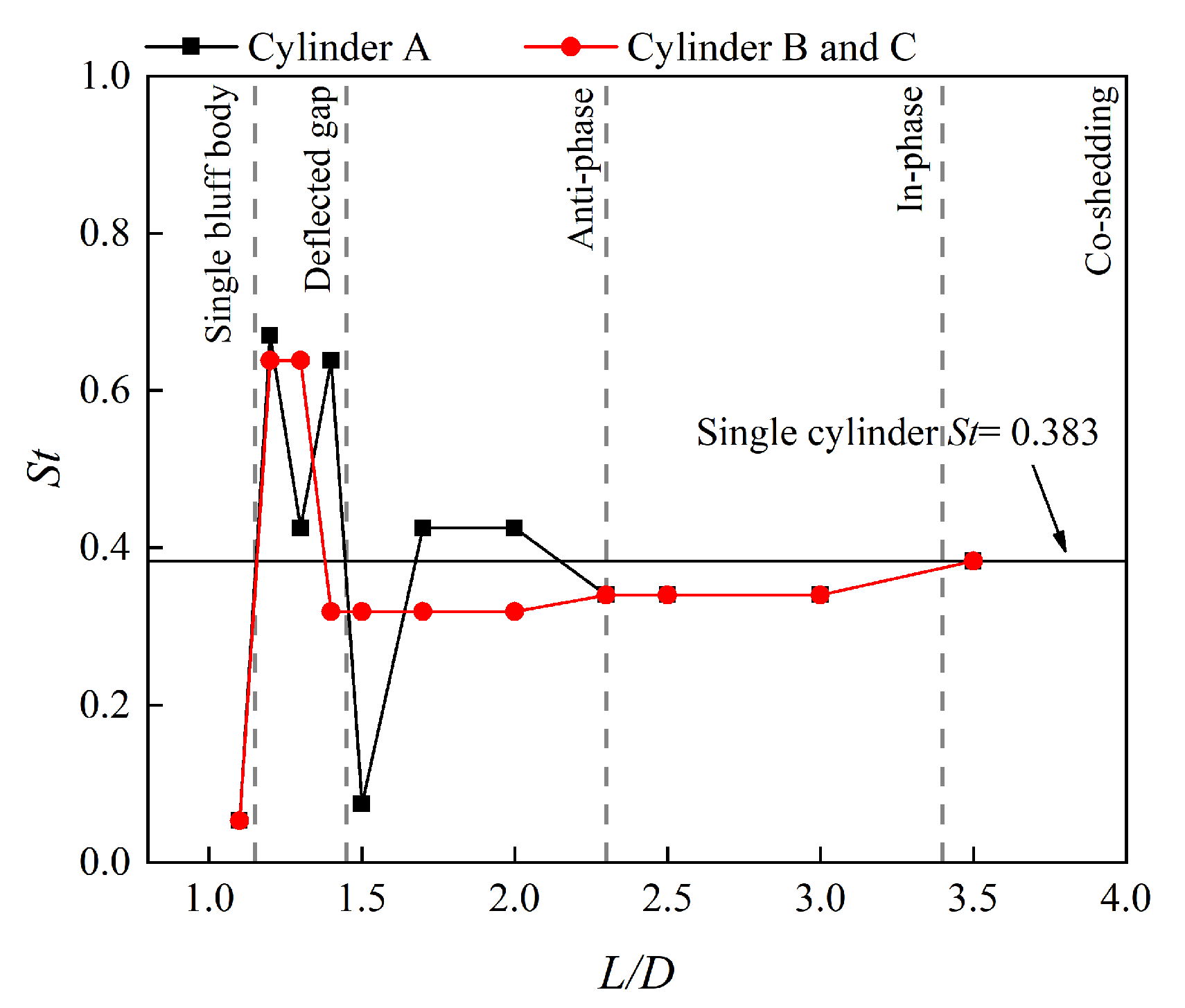
4.3. Vortex Shedding Frequencies
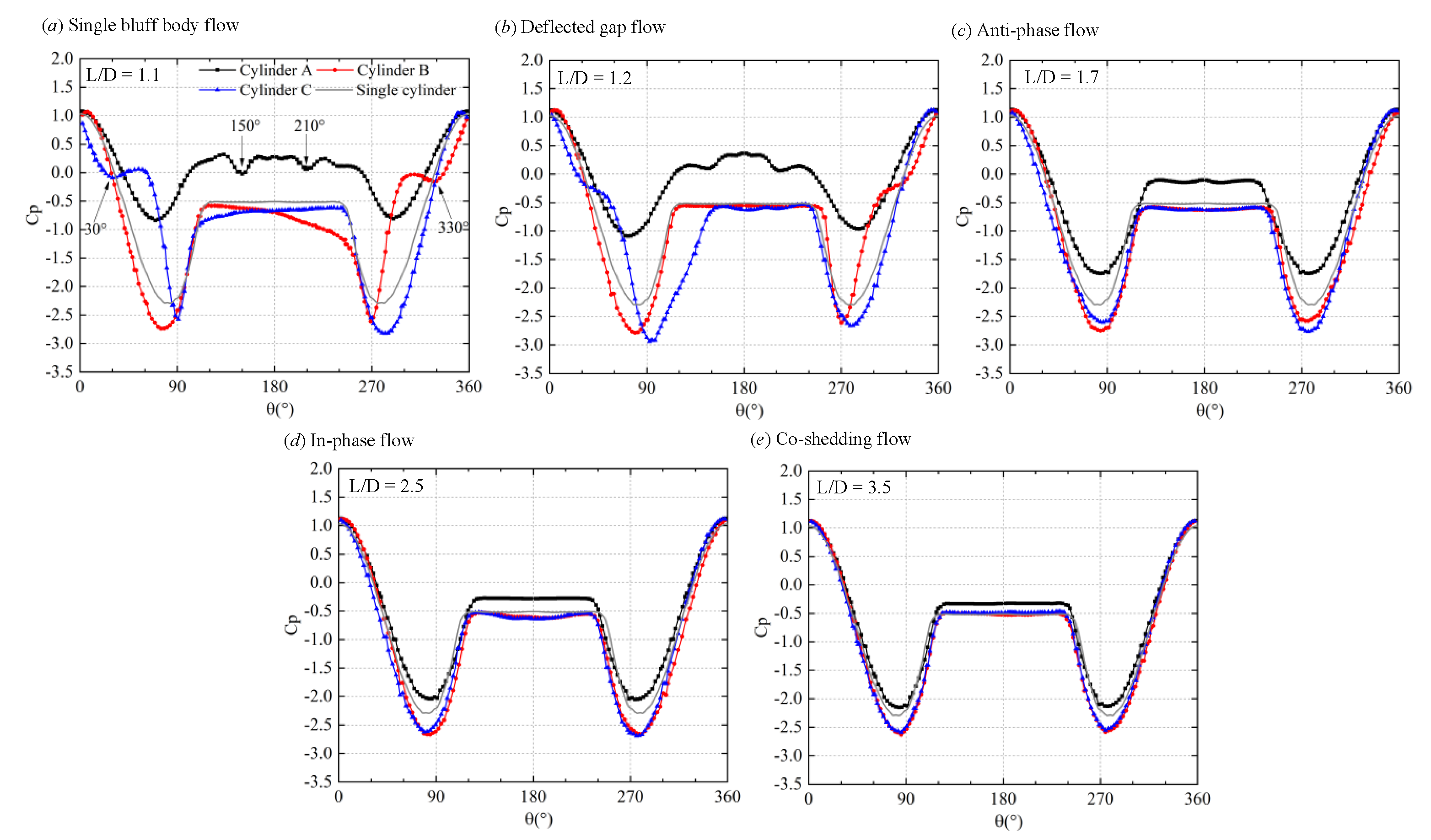
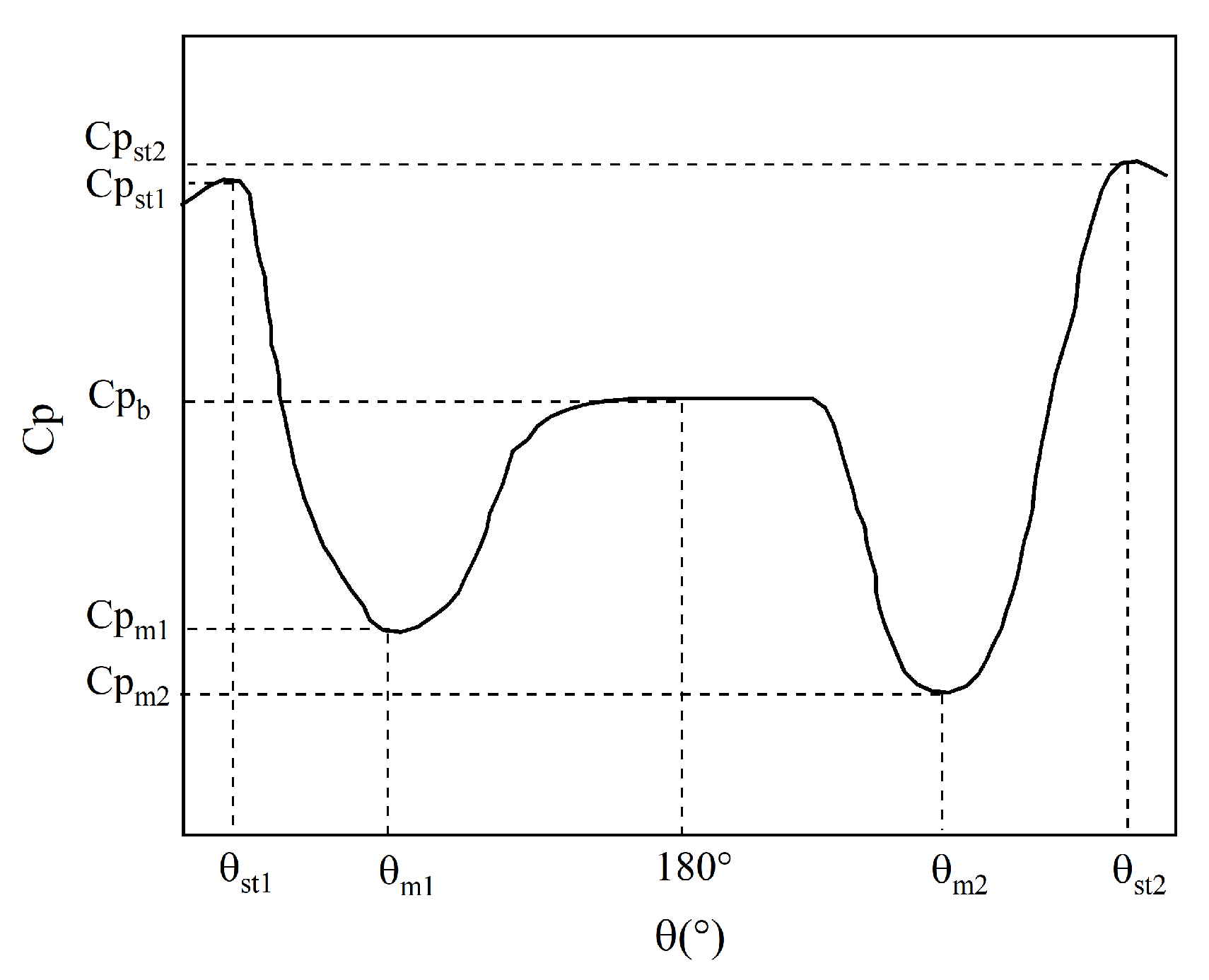
4.4. Separation Angles
5. Conclusions
- (i)
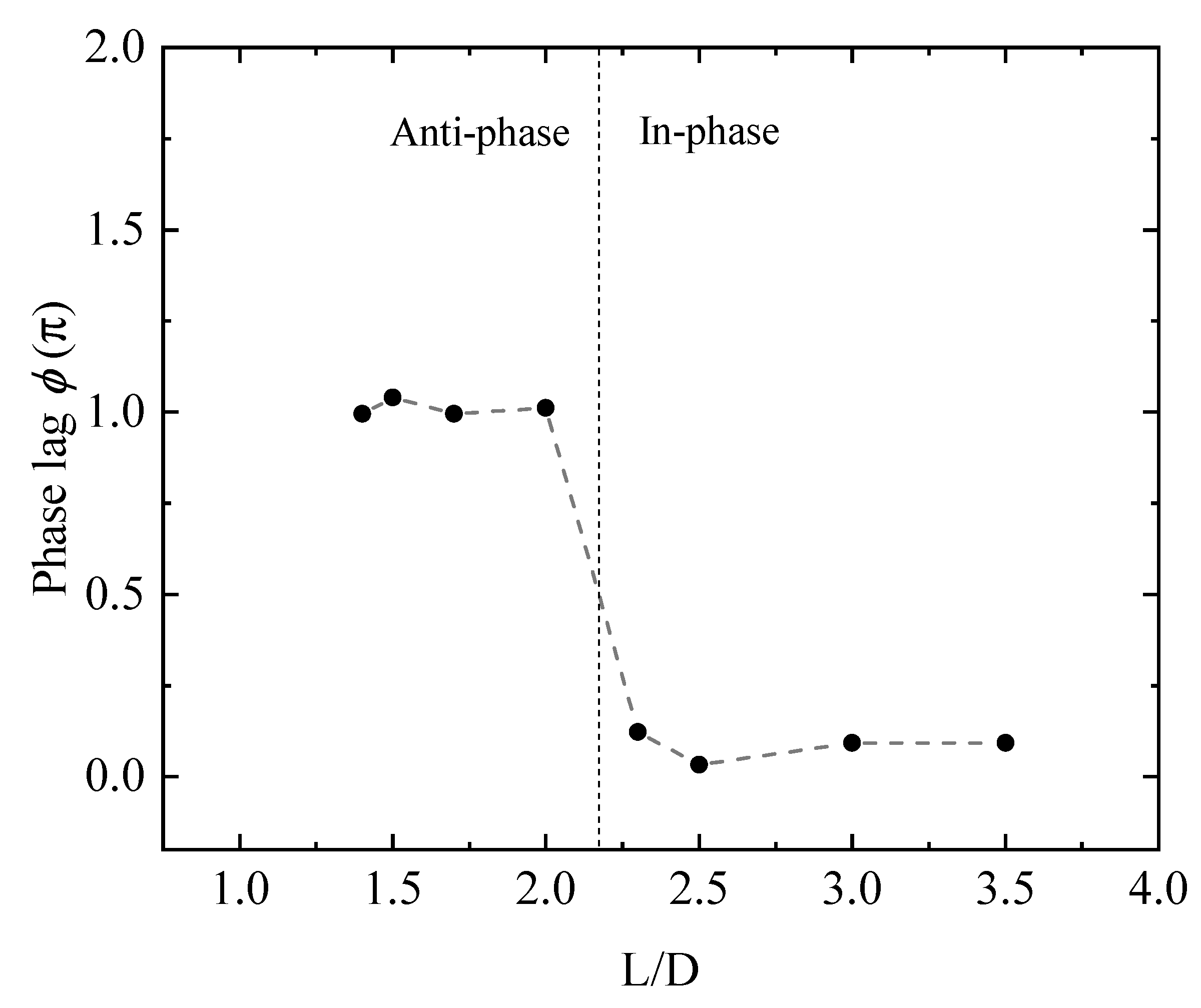
- Five flow regimes are identified depending on the spacing ratios, i.e, single bluff body flow (), deflected gap flow ( = 1.2–1.4), anti-phase flow ( = 1.5–2), in-phase flow ( = 2–3.5), and co-shedding flow ().
- (ii)
- When in deflected gap flow, the downstream cylinder with a wide wake experiences lower drag and higher lift (absolute value and RMS), compared to the cylinder with narrow wake. However, their vortex shedding frequencies are identical. In addition, the sum of lift forces of the three cylinders at the deflected gap flow is not zero, either a positive or negative lift may exist.
- (iii)
- When , the separation points on the free-flow-side of the downstream cylinders are always lower than that of the single cylinder, indicating that the violent flow at the gap also causes the flow separation on the outer side of the cylinder to advance. When , the separation point of the cylinder in upper stream is close to that of single cylinder, indicating that the minimum for negligible interaction among the cylinders is .
Author Contributions
Funding
Conflicts of Interest
References
- Han, P.; Pan, G.; Tian, W. Numerical simulation of flow-induced motion of three rigidly coupled cylinders in equilateral-triangle arrangement. Phys. Fluids 2018, 30, 125107. [Google Scholar]
- Liang, Y.; Tao, L.; Xiao, L.; Liu, M. Experimental and numerical study on vortex-induced motions of a deep-draft semi-submersible. Appl. Ocean Res. 2017, 67, 169–187. [Google Scholar] [CrossRef]
- Goldschmidt, M.; Muskulus, M. Coupled mooring systems for floating wind farms. Energy Procedia 2015, 80, 255–262. [Google Scholar] [CrossRef]
- Gonalves, T.R.; Chame, M.E.F.; Hannes, N.H.; de Paula Lopes, P.P.S.; Hirabayashi, S.; Suzuki, H. Experimental study on flow-induced motion of an array of three cylinders with circular, square, and diamond sections. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Zdravkovich, M.M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Sumner, D.; Price, S.J.; Paidoussis, M.P. Tandem cylinders in impulsively started flow. J. Fluids Struct. 1999, 13, 955–965. [Google Scholar] [CrossRef]
- Sumner, D. Two circular cylinders in cross-flow: A review. J. Fluids Struct. 2010, 26, 849–899. [Google Scholar] [CrossRef]
- Harichandan, A.B.; Roy, A. Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme. Int. J. Heat Fluid Flow 2010, 31, 154–171. [Google Scholar] [CrossRef]
- Igarashi, T.; Suzuki, K. Characteristics of the Flow around Three Circular Cylinders. Bull. JSME 1984, 27, 2397–2404. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zhou, Y. Effect of unequal cylinder spacing on vortex streets behind three side-by-side cylinders. Phys. Fluids 2001, 13, 3675–3686. [Google Scholar] [CrossRef]
- Sayers, A.T. Flow interference between three equispaced cylinders when subjected to a cross flow. J. Wind Eng. Ind. Aerodyn. 1987, 26, 1–19. [Google Scholar] [CrossRef]
- Lam, K.; Cheung, W.C. Phenomena of vortex shedding and flow interference of three cylinders in different equilateral arrangements. J. Fluid Mech. 1988, 196, 1–26. [Google Scholar] [CrossRef]
- Tatsuno, M.; Amamoto, H.; Koji, I.I. Effects of interference among three equidistantly arranged cylinders in a uniform flow. Fluid Dyn. Res. 1998, 22, 297–315. [Google Scholar] [CrossRef]
- Gu, Z.; Sun, T. Classification of flow pattern on three circular cylinders in equilateral-triangular arrangements. J. Wind Eng. Ind. Aerodyn. 2001, 89, 553–568. [Google Scholar] [CrossRef]
- Pouryoussefi, S.G.; Mirzaei, M.; Pouryoussefi, M.H. Force coefficients and Strouhal numbers of three circular cylinders subjected to a cross-flow. Arch. Appl. Mech. 2011, 81, 1725–1741. [Google Scholar] [CrossRef]
- Bansal, M.S.; Yarusevych, S. Experimental study of flow through a cluster of three equally spaced cylinders. Exp. Therm. Fluid Sci. 2017, 80, 203–217. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, X.; Si, J.H.; Li, Y. Flow around three circular cylinders in equilateral-triangular arrangement. Ocean Eng. 2020, 215, 107838. [Google Scholar] [CrossRef]
- Yan, B.; Zhou, D.; Cheng, H. Numerical simulation of flow over three circular cylinders in equilateral arrangements at low Reynolds number by a second-order characteristic-based split finite element method. Comput. Fluids 2010, 39, 882–899. [Google Scholar]
- Yan, W.; Wu, J.; Yang, S.; Wang, Y. Numerical investigation on characteristic flow regions for three staggered stationary circular cylinders. Eur. J. Mech. B/Fluids 2016, 60, 207–214. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, W.; Lv, X. Numerical simulation of cross-flow around three equal diameter cylinders in an equilateral-triangular configuration at low Reynolds numbers. Comput. Fluids 2016, 130, 94–108. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Alam, M.M.; Williams, J.; Xu, D. Numerical simulations of flow past three circular cylinders in equilateral-triangular arrangements. J. Fluid Mech. 2020, 891, A14. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, X.; Zhao, M.; Wang, L. Three-dimensional numerical simulation on flow past three circular cylinders in an equilateral-triangular arrangement. Ocean Eng. 2019, 189, 106375. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X.; You, Y. On the flow around two circular cylinders in tandem arrangement at high Reynolds numbers. Ocean Eng. 2019, 189, 106301. [Google Scholar] [CrossRef]
- Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
- Hinsberg, N.P.V. The Reynolds number dependency of the steady and unsteady loading on a slightly rough circular cylinder: From subcritical up to high transcritical flow state. J. Fluids Struct. 2015, 55, 526–539. [Google Scholar] [CrossRef]
- Rodriguez, I.; Lehmkuhl, O.; Chiva, J.; Borrell, R.; Oliva, A. On the flow past a circular cylinder from critical to super-critical Reynolds numbers: Wake topology and vortex shedding. Int. J. Heat Fluid Flow 2015, 55, 91–103. [Google Scholar] [CrossRef]
- Okajima, A. Flows around Two Tandem Circular Cylinders at Very High Reynolds Numbers. Bull. JSME Jpn. Soc. Mech. Eng. 1979, 22, 504–511. [Google Scholar] [CrossRef]
- Spalart, P.R. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Liang, X.F.; Chen, G.; Li, X.B.; Zhou, D. Numerical simulation of pressure transients caused by high-speed train passage through a railway station. Build. Environ. 2020, 184, 107228. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Li, Q.B.; Yang, Y.J.; Xiao, Z.X. Numerical studies of reverse flows controlled by undulating leading edge. Sci.-China-Phys. Mech. Astron. 2019, 62, 974712. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.B.; Liu, Z.; Zhou, D.; Wang, Z.; Liang, X.F.; Krajnovic, S. Dynamic analysis of the effect of nose length on train aerodynamic performance. J. Wind Eng. Ind. Aerodyn. 2019, 184, 198–208. [Google Scholar] [CrossRef]
- Tan, C.; Zhou, D.; Chen, G.; Sheridan, J.; Krajnovic, S. Influences of marshalling length on the flow structure of a maglev train. Int. J. Heat Fluid Flow 2020, 85, 108604. [Google Scholar] [CrossRef]
- Dong, T.; Minelli, G.; Wang, J.; Liang, X.; Krajnovi, S. The effect of reducing the underbody clearance on the aerodynamics of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2020, 204, 104249. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T.; Kitagishi, T. Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn 1998, 74, 531–542. [Google Scholar] [CrossRef]
- Norberg, C. An experimental investigation of the flow around a circular cylinder: Influence of aspect ratio. J. Fluid Mech. 1994, 258, 287–316. [Google Scholar] [CrossRef]
- Spalart, P.R. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Lehmkuhl, O.; Rodriguez, I.; Borrell, R.; Chiva, J.; Oliva, A. Unsteady forces on a circular cylinder at critical Reynolds numbers. Phys. Fluids 2014, 26, 125110. [Google Scholar] [CrossRef]
- Roshko, A. Experiments on the Flow Past a Circular Cylinder at Very High Re Number. J. Fluid Mech. 1961, 10, 345–356. [Google Scholar] [CrossRef]
- Schmidt, L.V. Flucting force measurements upon a circular cylinder at Reynolds number up to 5 × 106. In Proceedings of the Meeting on Ground Wind Load Problems in Relation to Launch Vehicles, Langley, WA, USA, 7–8 June 1966. [Google Scholar]
- Jones, G.W.; Cincotta, J.J.; Walker, R.W. Aerodynamic Forces on a Stationary and Oscillating Circular Cylinder at High Reynolds Numbers; Technical report; NASA: Washington, DC, USA, 1969. [Google Scholar]
- Shih, W.; Wang, C.; Coles, D.; Roshko, A. Experiments on flow past rough circular cylinders at large Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 1993, 49, 351–368. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P. Detached-Eddy Simulations Past a Circular Cylinder. Flow Turbul. Combust. 2000, 63, 293–313. [Google Scholar] [CrossRef]
- Catalano, P.; Wang, M.; Iaccarino, G.; Moin, P. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. Int. J. Heat Fluid Flow 2003, 24, 463–469. [Google Scholar] [CrossRef]
- Ong, M.; Utnes, T.; Holmedal, L.E.; Myrhaug, D.; B, P. Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers. Mar. Struct. 2009, 22, 142–153. [Google Scholar] [CrossRef]
- Warschauer, K.A.; Leene, J.A. Experiments on mean and fluctuating pressures of circular cylinders at cross flow at very high Reynolds numbers. In Proceedings of the International Conference on Wind Effects on Buildings and Structures, Tokyo, Japan, 6–11 September 1971. [Google Scholar]
- Zdravkovich, M.M.; Bearman, P.W. Flow Around Circular Cylinders -Volume 1: Fundamentals. ASME J. Fluids Eng. 1998, 120, 216. [Google Scholar] [CrossRef]
- Achenbach, E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re=5×106. J. Fluid Mech. 1968, 34, 625–639. [Google Scholar] [CrossRef]
- Janocha, M.J.; Ong, M.C. Vortex-induced vibrations of piggyback pipelines near the horizontal plane wall in the upper transition regime. Mar. Struct. 2021, 75, 102872. [Google Scholar] [CrossRef]
- Yang, X.; Ji, C.; Chen, W.; Zhang, Z. Wake patterns and hydrodynamic forces of flow around circular cylinders in an equilateral triangular arrangement. Chin. J. Hydrodynom. 2019, 34, 69–76. (In Chinese) [Google Scholar]
- Kim, H.J. Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 1988, 196, 431–448. [Google Scholar] [CrossRef]
- Alam, M.M.; Moriya, M.; Sakamoto, H. Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. J. Fluids Struct. 2003, 18, 325–346. [Google Scholar] [CrossRef]
- Hunt, J.; Wray, A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program, Stanford, CA, USA, 27 June–22 July 1988; pp. 193–208. [Google Scholar]

| Case | Cell Count (Million) | |||||
|---|---|---|---|---|---|---|
| Coarse Mesh | ||||||
| Medium Mesh | ||||||
| Fine Mesh |
| Researchers | Description | |||||
|---|---|---|---|---|---|---|
| Present study | k– IDDES | |||||
| Roshko [40] | Experiments | 0.30 | − | − | 0.37 | |
| Experiments | 0.42 | − | − | 0.62 | ||
| Experiments | 0.69 | − | − | 0.85 | ||
| Schmidt [41] | (2.6–3.3) × 10 | Experiments | 0.25–0.44 | − | − | 0.51–0.61 |
| Jones et al. [42] | Experiments | 0.21 | − | − | 0.53 | |
| Experiments | 0.53 | − | − | 0.59 | ||
| Experiments | 0.56 | − | − | 0.61 | ||
| Schewe [24] | Experiments | 0.45 | − | − | − | |
| Shih et al. [43] | (3–3.1) × 10 | Experiments | 0.35–0.38 | − | − | 0.45–0.46 |
| Travin et al. [44] | DES | |||||
| Catalanoet al. [45] | LES | − | ||||
| Ong et al. [46] | k– URANS | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Yin, B.; Guo, D.; Ji, Z.; Yang, G. Numerical Study on the Flow Past Three Cylinders in Equilateral-Triangular Arrangement at Re = 3 × 106. Appl. Sci. 2022, 12, 11835. https://doi.org/10.3390/app122211835
Zhang M, Yin B, Guo D, Ji Z, Yang G. Numerical Study on the Flow Past Three Cylinders in Equilateral-Triangular Arrangement at Re = 3 × 106. Applied Sciences. 2022; 12(22):11835. https://doi.org/10.3390/app122211835
Chicago/Turabian StyleZhang, Mohan, Bo Yin, Dilong Guo, Zhanling Ji, and Guowei Yang. 2022. "Numerical Study on the Flow Past Three Cylinders in Equilateral-Triangular Arrangement at Re = 3 × 106" Applied Sciences 12, no. 22: 11835. https://doi.org/10.3390/app122211835
APA StyleZhang, M., Yin, B., Guo, D., Ji, Z., & Yang, G. (2022). Numerical Study on the Flow Past Three Cylinders in Equilateral-Triangular Arrangement at Re = 3 × 106. Applied Sciences, 12(22), 11835. https://doi.org/10.3390/app122211835







