Research on Lazy Theta* Route Planning Algorithm Based on Grid Point Optimization
Abstract
Featured Application
Abstract
1. Introduction
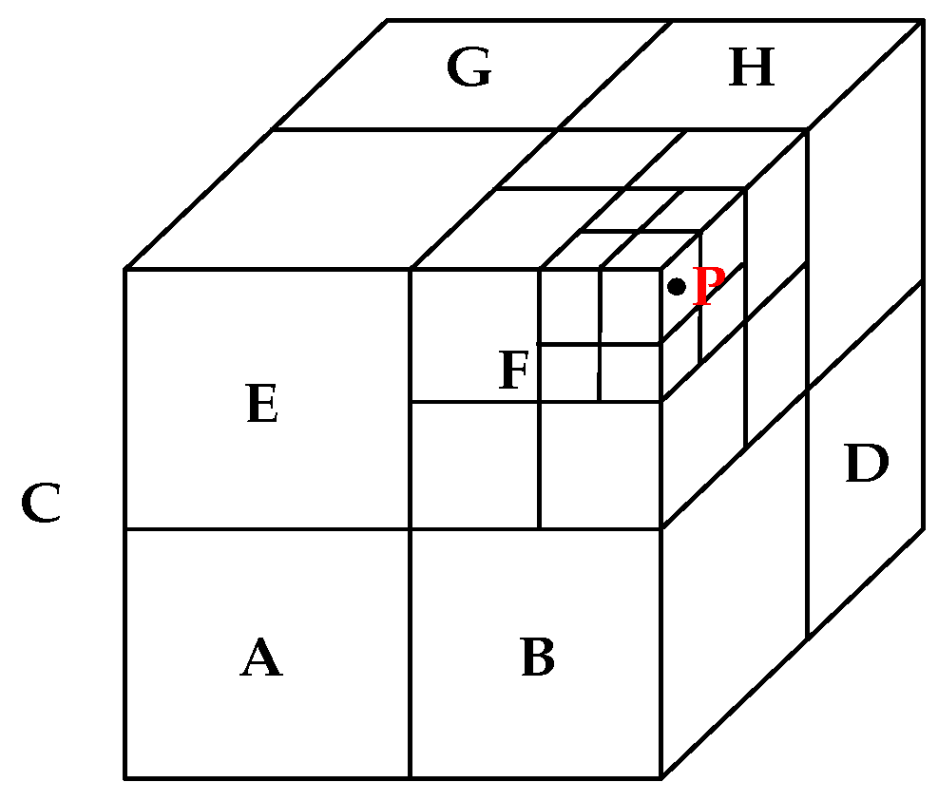
2. Octree Meshing Modeling
2.1. Octree Meshing
2.2. Encoding Method
- Convert to binary number .
- According to the order , the bits are crossed to obtain the code .
- Shift to the left by three bits to obtain the encoded .
- Convert the binary code to the octal code .
- Reverse the cross-bit of the binary cell code to obtain the binary coordinate .
- The calculation formula of the first hexagram limit grid point code is presented in Equation (1).
2.3. Building a Grid Point Map
- Determine the grid level within the environmental range required by the task; i.e., the grid scale is determined, and the minimum step size of the flight is limited. Let the grid side length of grid level be . Then, the minimum step size satisfies Equation (2). According to the flight mission requirements, determine the flight range, reduce the unnecessary grids, and shorten the planning path.
- To determine the grid level and planning range, divide the grid into a point grid.
- Based on the gridded scene, assign a value to the grid point, where zero means the grid point is passable, and one means the grid point is occupied and not passable.
3. Route Planning Modeling
3.1. Flight Condition Constraints
3.1.1. Maximum Range Constraint
3.1.2. Maximum Steering Angle Constraint
3.1.3. Maximum Climb/Dive Angle Constraints
3.1.4. Turning Radius Constraints
3.1.5. Flight Altitude Constraints
3.2. Threat Modeling
3.2.1. Terrain Threat
3.2.2. Detection Threat
3.2.3. Fire Threat
- Surface-to-air missile threat model
- Anti-aircraft gun threat model
3.2.4. No-Fly Zone Threat
4. Lazy Theta* Algorithm Based on Grid Point Optimization
4.1. Map Grid Point
4.2. Theta* Algorithm
- Initialize and ; put to .
- When the is empty, the search cannot determine the shortest route.
- Choose the smallest node in the and insert it into the and make it the current node.
- Given a current node with a target node , determine the route from the original point to the final destination using ’s parent node , and the search terminates. If s is not the destination node, step 5 is executed.
- Search the with each nearby node to . If is in the lists, disregard . If not, go to step 6.
- Compute the cost of , then check the visibility of the and .
- When there are two visible points: the route cost of is recorded as , and the path cost of is recorded as , where is the path cost of . If , update . If already appears on the , update . If not, add to .
- There are two points that are not visible. Check whether is present already in the ; if so, write down the cost of as and the cost of as , if , . Otherwise, add to the .
- Sort nodes in the based on the path cost, and go to step 2.
4.3. Grid Point-Based Lazy Theta* Algorithm
5. B-Spline Route Smoothing
5.1. B-Spline Uniform Sampling
5.2. B-Spline Equally Spaced Sampling
- According to B-spline uniform sampling, a uniform sampling point sequence about parameter is obtained, denoted as , where is the -th sampling point about the parameter , , and .
- Let point , and put into , where is the first sampling point. Let be used to mark the sampling point in , and is used for the iterative process of the dichotomy.
- In , starting from point , find the next sampling point , which is required to satisfy Equation (27).where represents the cumulative distance and is the path length from point to point along the polyline specified by .
- (1)
- If any point has , then: let , ; put point into ; point is the last sampling point of ; and move to step 5.
- (2)
- If , the last point of has been searched. Let , and place point into , where point is the last sampling point of . Skip to step 5.
- (3)
- If , then , meaning that the point whose cumulative distance to point is is located on . Move to step 4 to search for this point by dichotomy.
- (4)
- On the line segment , use the dichotomy to find the point , such that or , where is the sampling spacing error, which is used to control the search accuracy of the dichotomy. Let , put into as a new sampling point, and let . Move to step 3 to continue execution.
- (5)
- Obtain by calculation; that is, the sequence of the equally spaced sampling points of the B-spline route.
6. Simulation Experiment and Analysis
6.1. Meshing Experiment
- Simulation
- 2
- Analysis of results
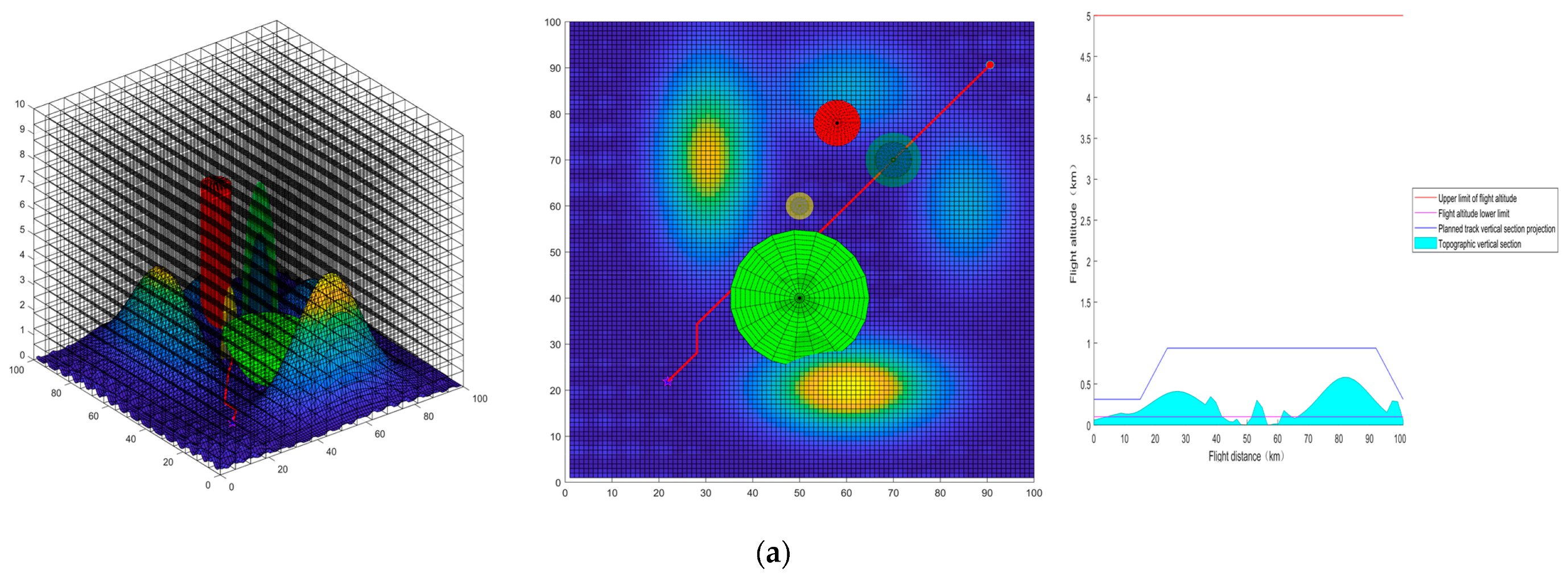
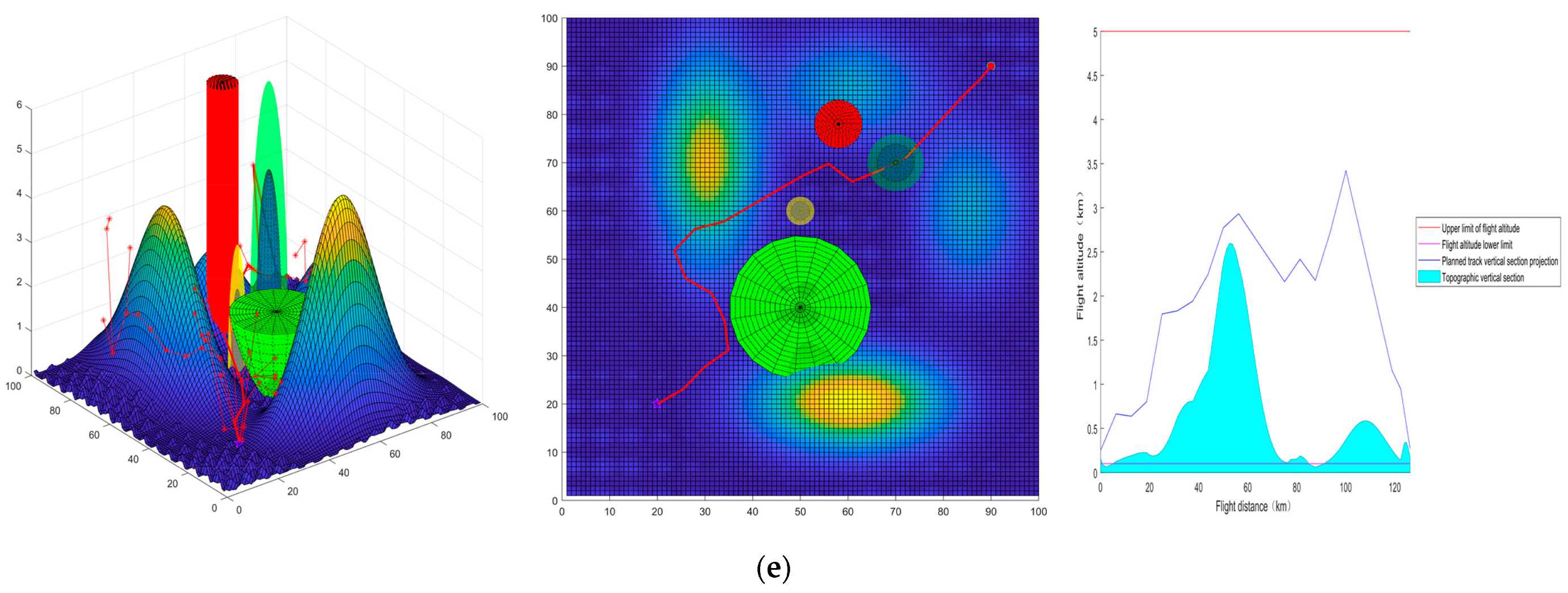
6.2. Route Planning Algorithm Comparison Experiment
6.2.1. Route Planning Algorithm Comparison Experiment
- Simulation
- 2
- Analysis of results
6.2.2. Grid Point-Based Lazy Theta* Route Planning at Different Grid Levels
- Simulation
- 2
- Analysis of results
6.2.3. Route Smoothing Experiment
- Simulation
- 2
- Analysis of results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


Appendix B
- Route planning algorithm comparison experiment
- (1)


- (2)


- (3)
- .

- 2
- Grid point-based Lazy Theta* route planning at different grid levels.



- 3
- Route Smoothing Experiment



References
- Gao, Y. Research on Path Planning Technology in Penetration. Master’s Thesis, Xidian University, Xi’an, China, 2021. [Google Scholar]
- Hu, S.; Xu, T.; Wang, B. Route-Planning Method for Plant Protection Rotor Drones in Convex Polygon Regions. Sensors 2021, 21, 2221. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhou, S.; Xiao, Z.; Qi, Y.; Dai, F. A Review of Research on UAV Obstacle Avoidance Methods. J. Ordnance Equip. Eng. 2022, 43, 40–47. [Google Scholar]
- Zhaoying, L.; Ruoling, S.; Zhao, Z. A New Path Planning Method Based on Sparse A* Algorithm with Map Segmentation. Trans. Inst. Meas. Control 2022, 44, 916–925. [Google Scholar] [CrossRef]
- Bing, H.; Lai, L. Improvement and Application of Dijkstra Algorithms. Acad. J. of Comput. Inf. Sci. 2022, 5, 97–102. [Google Scholar]
- BinKai, Q.; Mingqiu, L.; Yang, Y.; XiYang, W. Research on UAV Path Planning Obstacle Avoidance Algorithm Based on Improved Artificial Potential Field Method. J. Phys. Conf. Ser. 2021, 1948, 012060. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Liu, Y. Research on Improved Genetic Simulated Annealing Algorithm for Multi-UAV Cooperative Task Allocation. J. Phys. Conf. Ser. 2022, 2246, 012081. [Google Scholar] [CrossRef]
- Lin, N.; Zhang, Y.L. The Frontier of Route Planning Algorithm for UAV. Adv. Mater. Res. 2014, 926–930, 3577–3580. [Google Scholar]
- Wang, X.; Zhang, H.; Liu, S.; Wang, J.; Wang, Y.; Shangguan, D. Path Planning of Scenic Spots Based on Improved A* Algorithm. Sci. Rep. 2022, 12, 1320. [Google Scholar] [CrossRef]
- Yijun, Z.; Jiadong, X.; Chen, L. A Fast Bi-Directional A* Algorithm Based on Quad-Tree Decomposition and Hierarchical Map. IEEE Access 2021, 9, 102877–102885. [Google Scholar] [CrossRef]
- Cai, C.; Chen, J. An AUV Path Planner for Large-Scale Search and Rescue Based on A* Algorithm. J. Phys. Conf. Ser. 2021, 2050, 012017. [Google Scholar] [CrossRef]
- Ou, Y.; Fan, Y.; Zhang, X.; Lin, Y.; Yang, W. Improved A* Path Planning Method Based on the Grid Map. Sensors 2022, 22, 6198. [Google Scholar] [CrossRef] [PubMed]
- Xiang, D.; Lin, H.; Ouyang, J.; Huang, D. Combined Improved A* and Greedy Algorithm for Path Planning of Multi-Objective Mobile Robot. Sci. Rep. 2022, 12, 13273. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H. Application of UAV Remote Sensing Mapping Technology in Engineering Surveying and Mapping. Surv. Mapp. Geol. Miner. Resour. 2020, 3, 37. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Hou, J.; Chen, L.; Hu, N. A Path Planning Method for Underground Intelligent Vehicles Based on an Improved RRT* Algorithm. Electronics 2022, 11, 294. [Google Scholar] [CrossRef]
- Wu, Z.; Meng, Z.; Zhao, W.; Wu, Z. Fast-RRT: A RRT-Based Optimal Path Finding Method. Appl. Sci. 2021, 11, 11777. [Google Scholar] [CrossRef]
- Xiong, J.; Duan, X. Path planning for UAV based on improved dynamic step RRT algorithm. J. Phys. Conf. Ser. 2021, 1983, 012034. [Google Scholar] [CrossRef]
- Nasir, J.; Islam, F.; Malik, U.; Ayaz, Y.; Hasan, O.; Khan, M.; Muhammad, M.S. RRT*-SMART: A Rapid Convergence Implementation of RRT*. Int. J. Adv. Robot. Syst. 2013, 10, 299. [Google Scholar] [CrossRef]
- Ryu, H.; Park, Y. Improved Informed RRT* Using Gridmap Skeletonization for Mobile Robot Path Planning. Int. J. Precis. Eng. Manuf. 2019, 20, 2033–2039. [Google Scholar] [CrossRef]
- Shorakaei, H.; Vahdani, M.; Imani, B.; Gholami, A. Optimal Cooperative Path Planning of Unmanned Aerial Vehicles by a Parallel Genetic Algorithm. Robotica 2016, 34, 823–836. [Google Scholar] [CrossRef]
- Duan, H.; Yu, Y.; Zhang, X.; Shao, S. Three-Dimension Path Planning for UCAV Using Hybrid Meta-Heuristic ACO-DE Algorithm. Simul. Model. Pract. Theory 2010, 18, 1104–1115. [Google Scholar] [CrossRef]
- Faria, M.; Marín, R.; Popović, M.; Maza, I.; Viguria, A. Efficient Lazy Theta* Path Planning over a Sparse Grid to Explore Large 3D Volumes with a Multirotor UAV. Sensors 2019, 19, 174. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Wu, F.; Wang, R.; Qin, Y.; Tong, X.; Chen, B. Study on Globe Spatial Grid Reference System Construction. Acta Sci. Nat. Univ. Pekin. 2016, 52, 1041–1049. [Google Scholar] [CrossRef]
- Wu, X.; Liu, W.; Wang, T. Octree Structure Based Voxelization of Polygonal Meshes. J. Graph. 2005, 4, 1–7. [Google Scholar]
- Ulmer, B.; Samavati, F. Toward Volume Preserving Spheroid Degenerated-Octree Grid. Geoinformatica 2020, 24, 505–529. [Google Scholar] [CrossRef]
- Li, Q.; Li, D. 3D run-length encoding of octrees. Geomat. Inf. Sci. Wuhan Univ. 1997, 2, 12–16. [Google Scholar]
- Wu, X. Research on Scene Grid Modeling and Application Method for Urban Space Management and Control. Master’s Thesis, PLA Strategic Support Force Information Engineering University, Zhengzhou, China, 2020. [Google Scholar]
- Wu, Y.; Cao, X. A Hilbert Octree-Oriented Adjacent Cell Calculation Algorithm. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 613–622. [Google Scholar] [CrossRef]
- Zhai, W.; Chen, B.; Tong, X.; Cheng, C. Research on Continuity of Multi-Scale Space-Filling Curves. Acta Sci. Nat. Univ. Pekin. 2018, 54, 331–335. [Google Scholar] [CrossRef]
- Wu, X.; Tong, X.; Lei, Y.; Li, H.; Guo, C.; Zhang, Y.; Lai, G.; Zhou, S. Rapid Computation of Set Boundaries of Multi-Scale Grids and Its Application in Coverage Analysis of Remote Sensing Images. Comput. Geosci. 2021, 146, 104573. [Google Scholar] [CrossRef]
- Ahmed, R.; Mahmud, K.H.; Tuya, J.H. A GIS-Based Mathematical Approach for Generating 3D Terrain Model from High-Resolution UAV Imageries. J. Geovis. Spat. Anal. 2021, 5, 24. [Google Scholar] [CrossRef]
- Dong, S. The Research of Route Planning Method under Complex Constraints. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Wu, W.; Guo, X.; Zhou, S. Path planning algorithm based on NURBS and GOBL-ACDE. Syst. Eng. Electron. 2020, 42, 1073–1082. [Google Scholar]
- Zhang, H.; Gan, X.; Li, S.; Feng, Z.; Jin, Y. UAV route planning considering regional risk assessment under complex low altitude environment. Chin. J. Sci. Instrum. 2021, 42, 257–266. [Google Scholar] [CrossRef]
- Han, X.; Zhang, X. Multi-Scale Theta* Algorithm for the Path Planning of Unmanned Surface Vehicle. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021, 236, 147509022110396. [Google Scholar] [CrossRef]
- Ren, T.; He, J.; Zou, J. 3D Route Planning for Helicopters Based on Improved Theta* Algorithm. Electron. Opt. Control 2022, 29, 45–48. [Google Scholar]
- Daniel, K.; Nash, A.; Koenig, S.; Felner, A. Theta*: Any-Angle Path Planning on Grids. J. Artif. Intell. Res. (JAIR) 2014, 39, 533–579. [Google Scholar] [CrossRef]
- Le, P.T.H.; Lee, K. Weight Value and Map Complexity in Theta*. MATEC Web Conf. 2016, 54, 05003. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, Y.; Liu, H. Late Line-of-Sight Check and Partially Updating for Faster Any-Angle Path Planning on Grid Maps. Electron. Lett. 2019, 55, 690–692. [Google Scholar] [CrossRef]
- De Filippis, L.; Guglieri, G.; Quagliotti, F. Path Planning Strategies for UAVS in 3D Environments. J. Intell. Robot. Syst. 2012, 65, 247–264. [Google Scholar] [CrossRef]
- Yiu, Y.; Du, J.; Mahapatra, R. Evolutionary Heuristic A* Search: Pathfinding Algorithm with Self-Designed and Optimized Heuristic Function. Int. J. Semant. Comput. 2019, 13, 5–23. [Google Scholar] [CrossRef]
- Tran, N.H.; Nguyen, A.D.; Nguyen, T.N. A Genetic Algorithm Application in Planning Path Using B-Spline Model for Autonomous Underwater Vehicle (AUV). Appl. Mech. Mater. 2020, 902, 54–64. [Google Scholar]
- Sun, Y.; Zhang, C.; Liu, C. Collision-Free and Dynamically Feasible Trajectory Planning for Omnidirectional Mobile Robots Using a Novel B-Spline Based Rapidly Exploring Random Tree. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211016608. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, X.; Chen, Z. Non-uniform cubic B-spline smoothing algorithm for UAV 3D track. Control Eng. China 2020, 27, 1259–1266. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Q.; Zhang, X.; Guo, L.; Sun, Q. Through Research of Determining Step Size for Approaching of Cubic Spline Curve. Mach. Tool Hydraul. 2016, 44, 136–139. [Google Scholar]
























| Grid Level | Number of Grids | Model Fit |
|---|---|---|
| 1 | 1 | 40.2% |
| 2 | 8 | 40.2% |
| 3 | 41 | 65.40% |
| 4 | 264 | 73.76% |
| 5 | 1245 | 78.65% |
| 6 | 6457 | 83.70% |
| 7 | 30,994 | 87.24% |
| 8 | 147,925 | 91.08% |
| 9 | 711,874 | 93.16% |
| 10 | 3,405,644 | 94.56% |
| Algorithm | Grid Level | Path Length | Path Cost | Max Pitch Angle | Max Turn Angle | Running Time |
|---|---|---|---|---|---|---|
| Grid A* | 3 | 120.89 | 103.00 | 4.04 | 45.14 | 0.91 |
| 4 | 113.48 | 93.93 | 4.04 | 45.14 | 1.53 | |
| 5 | 100.93 | 82.35 | 4.04 | 45.14 | 1.95 | |
| Grid point A* | 3 | 113.57 | 96.64 | 5.71 | 45.14 | 0.98 |
| 4 | 95.71 | 82.60 | 3.02 | 45.14 | 1.02 | |
| 5 | 91.93 | 76.35 | 2.02 | 45.14 | 1.72 | |
| Grid Lazy Theta* | 3 | 116.40 | 97.35 | 4.04 | 63.46 | 1.34 |
| 4 | 110.63 | 89.86 | 3.03 | 56.32 | 2.36 | |
| 5 | 98.15 | 79.37 | 1.59 | 22.83 | 2.54 | |
| Grid point Lazy Theta* | 3 | 105.02 | 86.39 | 2.86 | 63.64 | 1.25 |
| 4 | 91.26 | 74.01 | 1.99 | 36.87 | 2.02 | |
| 5 | 87.90 | 68.01 | 1.46 | 16.58 | 2.38 | |
| RRT* | step size = 25 | 164.97 | 132.02 | 14.33 | 62.41 | 1.91 |
| step size = 12.5 | 145.73 | 116.61 | 14.37 | 58.43 | 3.44 | |
| step size = 6.25 | 105.10 | 84.14 | 10.58 | 58.59 | 5.23 |
| Algorithm | Grid Level | Path Length | Path Cost | Max Pitch Angle | Max Turn Angle | Running Time |
|---|---|---|---|---|---|---|
| Grid point Lazy Theta* | 3 | 105.02 | 86.39 | 2.86 | 63.64 | 1.25 |
| 4 | 91.26 | 74.01 | 1.99 | 36.87 | 2.02 | |
| 5 | 87.90 | 68.01 | 1.46 | 16.58 | 2.38 | |
| 6 | 83.67 | 66.58 | 4.04 | 4.62 | 4.45 | |
| 7 | 79.45 | 64.75 | 2.70 | 2.29 | 6.85 | |
| 8 | 78.36 | 63.82 | 8.05 | 7.44 | 13.45 | |
| 9 | 78.94 | 63.25 | 5.11 | 18.82 | 58.64 |
| Route Planning Algorithm | Smoothing Method | Path Length after Smoothing | Maximum Height after Smoothing |
|---|---|---|---|
| Grid point Lazy Theta* | Original route | 105.02 | 5.00 |
| Uniform quadratic B-Splines | 100.59 | 4.38 | |
| Uniform cubic B-splines | 98.61 | 4.17 | |
| Equally spaced quadratic B-splines | 96.89 | 4.17 | |
| Equally spaced cubic B-splines | 90.50 | 3.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Wan, L.; Cai, M.; Xu, X. Research on Lazy Theta* Route Planning Algorithm Based on Grid Point Optimization. Appl. Sci. 2022, 12, 10601. https://doi.org/10.3390/app122010601
Gao Z, Wan L, Cai M, Xu X. Research on Lazy Theta* Route Planning Algorithm Based on Grid Point Optimization. Applied Sciences. 2022; 12(20):10601. https://doi.org/10.3390/app122010601
Chicago/Turabian StyleGao, Zhizhou, Lujun Wan, Ming Cai, and Xinyu Xu. 2022. "Research on Lazy Theta* Route Planning Algorithm Based on Grid Point Optimization" Applied Sciences 12, no. 20: 10601. https://doi.org/10.3390/app122010601
APA StyleGao, Z., Wan, L., Cai, M., & Xu, X. (2022). Research on Lazy Theta* Route Planning Algorithm Based on Grid Point Optimization. Applied Sciences, 12(20), 10601. https://doi.org/10.3390/app122010601





