Featured Application
Authors are encouraged to provide a concise description of the specific application or a potential application of the work. This section is not mandatory.
Abstract
The ghost effect in marine seismic data causes low-frequency suppression and frequency notch, resulting in incomplete frequency information for seismic records, which poses challenges for high-resolution imaging. The deghosting effect depends on the approximation of the ghost delay operator. Due to the strict requirements of dense sampling, the 2D deghosting method for a densely sampled inline dataset is still the mainstream method for marine data processing. As the trade-off, inversion-based methods are widely used in the industry to reduce the influence of the inaccurate ghost delay operator. In order to overcome the sampling limits and improve the 2D deghosting effect, we propose a pseudo-3D deghosting framework based on an l1 norm sparse inversion. In the framework, the inversion problem is divided into two subproblems, i.e., pseudo-3D operator building and optimization inversion. Considering the data coherence along the shot direction, we derive a pseudo-3D ghost delay operator to deghost simultaneously for multi-shot gathers. We then introduce a sparse inversion method in the pseudo-3D radon domain (multi-shot gathers) to further improve the inversion accuracy. The proposed framework is easy to implement, is not sensitive to noise, and shows superior performance in synthetic and field examples.
1. Introduction
For signal-to-noise ratio considerations, the receivers are sunk to a certain depth below the air–water interface during marine seismic acquisition [1]. When the upgoing wavefield propagates to the air–water interface, it reflects and propagates downward. The downgoing wavefield is called ghost [2], and it interferes with the upgoing wavefield, resulting in frequency notch and reducing the vertical resolution of the seismic dataset [3].
In marine acquisition, the sampling interval in the crossline direction is usually much larger than that in the inline direction (usually between 4:1 and 16:1) [4], and the sparse sampling poses a large challenge for deghosting [5]. Therefore, the 2D deghosting method for a densely sampled inline dataset is still the mainstream method for marine data processing. The current deghosting methods are mainly implemented in the frequency domain, and the idea of plane wave decomposition is directly or indirectly applied [6]. The deghosting methods based on plane wave decomposition can be roughly divided into two categories: the deconvolution-based method and the inversion-based method.
The basic idea of the deconvolution-based method is to transform the seismic dataset containing ghost into other data domains (time domain [7], frequency domain [8], f-k domain [9], etc.), construct a ghost delay operator, use the deconvolution algorithm to achieve deghosting in this domain, and transform it into the space–time domain. However, the deconvolution-based method requires the accurate estimation of ghost delay time, which cannot overcome the error of actual acquisition [10]. The basic idea of the inversion-based method is to combine the parameter of the observing system with the plane wave decomposition and express it as a transformation matrix. Due to the combination of a plane wave coding operator and a deghost delay operator, the ghost-free wavefield can be obtained by a linear inversion algorithm. The advantage of this method is the applicability of various observation systems (e.g., variable-depth streamer [10]) and the convenient introduction of an advanced inversion algorithm [11,12,13]. However, accurately obtaining a ghost-free wavefield by conventional 2D deghosting method technology is still difficult.
Compressed sensing [14] is widely used in signal analysis [15,16], noise suppression [17,18], seismic acquisition [19], seismic imaging [20], and optimized inversion [21,22]. Such methods decompose seismic datasets into different units with different characteristics (frequency, direction, wavelet, curvature, etc.), and they extract corresponding units according to the characteristics of the target signal to achieve sparse representation, which means highlighting the useful information and removing the redundant information. Van den Berg et al. [23], Wang et al. [24], and Hu et al. [25] adopted the compressed sensing-based sparse inversion method to find the informative local minimum in the inversion of seismic signals. The key to these methods is to choose the appropriate data domain and sparse transformation for the sparse representation of seismic signals. By amplifying the coherence difference between the signal and the noise, the seismic signal can be highlighted in the inversion, thereby improving the inversion accuracy.
In this paper, we propose a pseudo-3D deghosting framework based on an l1 norm sparse inversion to improve the deghosting effect. In this framework, we include the data coherence along the shot direction into inversion and introduce the idea of compressed sensing to further improve the inversion accuracy. Firstly, based on the consistency of the receiver depth in conventional streamer data, we derive a pseudo-3D ghost delay operator for multi-shot gathers for simultaneous deghosting. Then, we introduce an l1 norm sparse inversion in the pseudo-3D radon domain to improve the inversion accuracy. It is worth noting that this method of using an l1 norm to regulate objective functions is not limited to the field of seismic exploration, but it can be used in various fields as a potential methodology, such as sensor development and image recognition. The synthetic and field examples indicate that the performance of our framework appears to be successful on a conventional 2D streamer dataset.
2. Methods
2.1. Pseudo-3D Deghosting Framework with the Data Coherence along the Shot Direction
In marine seismic exploration, the most conventional acquisition method is the streamer observation system, which is where a power boat drags several streamers for movement. The mainstream processing strategy is streamer-by-streamer, and a single streamer record can be viewed as a dataset of several shot gathers. For conventional multi-shot gathers, the radon domain deghosting algorithm can be expressed as
where represents the i-th shot of the seismic data in the frequency domain, represents the i-th shot of the deghosting result in the frequency domain, and , , and represent the offset index of the j-th trace, the slowness index of the ip-th trace, and the angular frequency, respectively. represents the delay time between the ghost and primary, which is known to be a function of the water velocity , the receiver depth , and the incident angle (Figure 1b). In the radon domain, the slowness is calculated by the water velocity and the incident angle as follows:
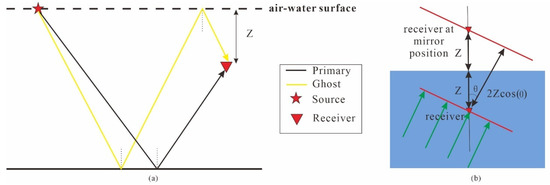
Figure 1.
Schematic illustration of ghost propagation. (a) The propagation of ghost. (b) The estimation of ghost delay time.
The delay time in the radon domain is calculated by
To simplify Equation (1), we redefine the 2D deghosting operator in the radon domain, which can be regarded as a combination of the radon transform operator and the ghosting operator as follows:
Equation (1) can then be rewritten as a form of matrix multiplication:
The conventional 2D deghosting method indicates a shot-by-shot deghosting manner. Because every shot gather is processed independently, the inversion accuracy of the 2D deghosting algorithm is easily limited by the field noise and accuracy of the 2D operator, which is necessary to introduce a priori information to constrain the inversion. During the horizontal streamer acquisition, the location of the sources and receivers is relatively stable, and so the offset parameters of the different shots are consistent. According to this property, we can rearrange the dataset into the data cube shown in Figure 2. In this data cube, the seismic records are arranged in a source-offset-time manner. Then, we can adopt a Fourier transform to the data cube, and the frequency slice can be expressed as:
where represents the number of common shot gathers (CSGs) and represents the number of common offset gathers (COGs). Since the offsets and receiver depths of the different shot gathers data are consistent, the ghost delay operator in Equation (1) is applicable to the data slice described in Figure 2:
where and represent the location of the source and offset, respectively. As shown in Equation (7), the deghosting case for multi-shot gathers is integrated into a linear system of equations, which can be simplified as:
where represents the ghost delay operator. In this way, we can simultaneously deghost for the data cube. In the source direction of the data cube, each slice represents a COG. The characteristics of events in COGs are similar to those of the underground interface, which means the COGs are composed as several smooth and approximately linear events [26]. The event coherence in COGs provides the basis for the introduction of sparse representations, and we can utilize the data coherence along the shot direction as an inversion constraint. In the common offset gathers, more information that can be used for coherence analysis is obtained [27], which effectively improves the inversion accuracy.
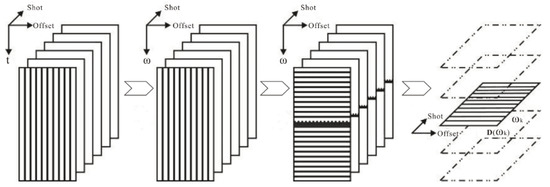
Figure 2.
Demonstration of a pseudo-3D data cube.
2.2. Compressed Sensing-Based Sparse Inversion Method
In recent years, compressed sensing-based inversion methods, which improve inversion accuracy by sparse representation, have been emerging. The basic idea is to discretize the seismic signal by a sampling matrix, then remove redundant information and retain fewer elements to represent the main characteristics of the signal. Because the signal becomes sparse, it does not easily fall into the local minimum during inversion. In this way, the signal becomes sparse and redundant information is not included during inversion, and it does not easily fall into the non-information local minimum during inversion [28].
Sparse inversion requires the sparse representation (Figure 3) of the seismic signals using the sampling matrix . The sparse representation can be described as a linear equation:
where the sampling matrix can be expressed as
where represents the coefficients in the transformed domain and in , represents the norm of , which measures the number of non-zero elements and represents the degree of matrix sparsity, and represents the vector of the sampling matrix . Because the l0 norm is difficult to solve optimally (non-deterministic polynomial-hard problem, NP-hard), an l1 norm is usually used to replace the l0 norm as the constraint condition to simplify the optimization problem, as follows:

Figure 3.
Demonstration of sparse representation.
To demonstrate the sparsity change before and after the sparse representation of the seismic signal, we adopt a curvelet transform [29] to noisy synthetic data for sparse representation, where the noise distribution is . We select 5% as the curvelet and time–space coefficients, in order of amplitude, to reconstruct the data. From Figure 4, the sparsity of the curvelet coefficients is significantly better than that of the time–space coefficients.

Figure 4.
Sparsity comparison of the synthetic data. (a) Input data. (b) Sparse reconstruction in the time domain. (c) Sparse reconstruction in the curvelet domain.
In the optimization inversion process, the objective function is generally minimized in the sense of least squares. However, the seismic signals not only contain useful signals, but also noise. The sparse representation of seismic signals regards the noise as redundant information, which means inversion in the transform domain can obtain more stable inversion results. Therefore, the sparse inversion methods are suitable for solving such problems.
2.3. Pseudo-3D Deghosting Based on Sparse Inversion
To highlight the data coherence, we introduce the compressed sensing-based sparse inversion methods into the deghosting method. In the pseudo-3D deghosting framework, the linear system of Equation (6) can be rewritten as
where represents the vector of the deghosting result in the radon domain, represents the vector of the input dataset in the time–space domain, represents the identity matrix, represents the Kronecker product of the matrix, and represent the Fourier transform pair in the time direction, and represents the combination of the ghost delay operator and the Fourier transform operator.
In actual seismic acquisition, field noise cannot be avoided. Assuming that the input datasets are a collection of the noise and useful signals , then:
Based on the compressed sensing theory, the seismic signals are over-complete and satisfy the requirement of sparse representation. Therefore, the useful signal can be reconstructed by the sampling matrix :
where represents the coefficients in the transformed domain. In general, can be constructed by a sparse transform (wavelet transform [30], curvelet transform [29], etc.). Without considering the noise, the main purpose of this problem is to solve the sparse solution of , where represents a matrix of the size and represents a vector of the size . When , this problem is under-determined, which can be summarized as a basic pursuit problem (BP). To solve this BP problem [31], we propose the objective function:
Considering the existence of noise, the BP problem can be transformed into a BPDN problem (basis pursuit denoising) [32] to avoid the noise interference during inversion:
where represents the l2 norm residual of the objective function, which is generally set as 5–10% of the l2 norm of . The proposed method uses the l2 norm to approximate the reconstructed data to the original data while the l1 norm constrains the noise. In this way, the noise in the data can be suppressed. To solve the above problem, we adopt the spectral gradient projection method (SPGL1) [33]
where and represent the inversion results in the data domain and the sparse domain, respectively, represents the noise level, which controls the sparsity, and SLGL1 is a solver for the l1-regularized least-squares inversion problem, which is suitable for large-scale datasets.
In order to improve the inversion accuracy, we adopt a sparse transform to achieve the sparse representation of the curved events with multi-scale and multi-directional characteristics. It can be seen from Section 2.2 that sparse representation can increase the sparseness of the signal. Considering representation accuracy and computational efficiency, we combine a 2D curvelet transform and a 1D wavelet transform as the sampling matrix. Therefore, the pseudo-3D deghosting based on a sparse inversion can be expressed as
where represents the 3D coefficients in the sparse domain, represents the combined operators of the 2D curvelet transform and the 1D wavelet transform, and and are the inverse transforms of . The inversion result is the coefficients in the radon domain, and then we obtain the result in the time–space domain by adopting a conventional inverse radon transform.
3. Results
In order to verify the effectiveness of the proposed method for deghosting, we first apply the pseudo-3D algorithm to the synthetic data obtained from the forward modeling of the saltdome model (Figure 5). The saltdome model is a classic acoustic model for testing multiple attenuation methods for marine data [34], and it has a width of 5400 m, a depth of 1250 m, and a grid spacing of 5 m. The model contains high-speed layers and faults, and the corresponding records are complex. As for the observation system, in order to highlight the influence of ghost, the sinking depth of the sources is 14 m and the sinking depth of the receivers is 25 m. The maximum offset is 2550 m and the trace interval is 10 m. To further verify the effectiveness of the algorithm, we also adopt the algorithm to the field streamer data. For data preparation, we choose the open-source software Madagascar, which is applicable to digital image and data processing in geophysics and related fields, as a tool for forward modeling and data preprocessing.
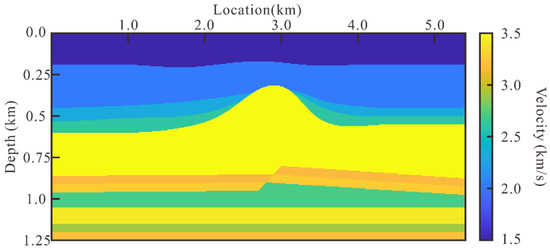
Figure 5.
The demonstration of the saltdome model.
3.1. Synthetic Example
To ensure the completeness of the synthetic data, we choose the wave equation-based simulation method, i.e., the fine difference algorithm, to conduct forward modeling. The synthetic multi-shot synthetic records include 256 CSGs, 256 COGs, 512 samplings, and a sampling interval of 0.004 s. Then, we apply the conventional 2D method and the sparse inversion method to obtain the deghosting results, and we compare the results of the two methods from the CSGs, COGs, f-k spectrum, etc.
Figure 6 shows the original data before deghosting. Figure 6a–c shows the data cube, the zoom section of the COG, and the corresponding f-k spectrum of the CSG. From Figure 6a, we can observe that when the sinking depth is large, ghost is easy to recognize. The separation of the primaries and the ghosts can be clearly observed in the near-offset section. Figure 6b shows that the frequency bandwidth of the deghost-interfered datasets is narrowed, with a lack of low frequency (5–10 Hz) and a main frequency notch (25–50 Hz). Therefore, in order to obtain a frequency-rich seismic record, it is necessary to deghost.
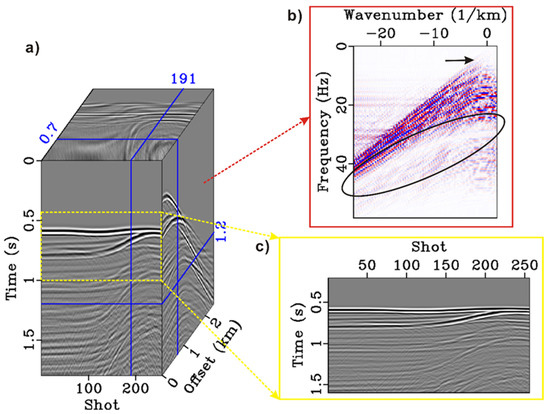
Figure 6.
The synthetic data before deghosting. (a) 3D data cube including 256 CSGs and 256 COGs. (b) f-k spectrum in which the black oval marks the effect of ghost. (c) COG wherein the events are similar to the underground interface.
Figure 7 and Figure 8 respectively demonstrate the deghosting results of the conventional 2D algorithm and the proposed method. Comparing Figure 7a and Figure 8a, it can be seen that both methods have suppressing effects on deghosting. However, the conventional algorithm has some artifacts in the deep position (blue arrow). The reason is that the complexity of the underground structure increases and the inversion process is unstable. These artifacts in the sparse inversion result are effectively suppressed, which proves that the introduction of the proposed method improves the deghosting effect. From Figure 7b and Figure 8b, we see that the notch frequency is mainly 25–50 Hz. Both results compensate for the notch effect, but some energy leakage can still be observed in the conventional results. The sparse inversion results have the complete frequency band and more balanced high-frequency energy, which proves the effectiveness of the proposed method. Figure 7c and Figure 8c show the zoomed section of the COGs. The difference in the deep events (1.5 s, 150–250th shots) is obvious. The conventional method has artifacts but the sparse inversion results do not.
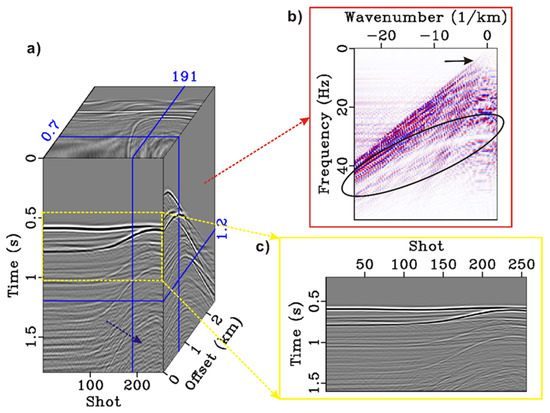
Figure 7.
The conventional deghosting results. (a) 3D data cube including 256 CSGs and 256 COGs. (b) f-k spectrum in which the black oval marks the effect of ghost. (c) COG wherein the events are similar to the underground interface.
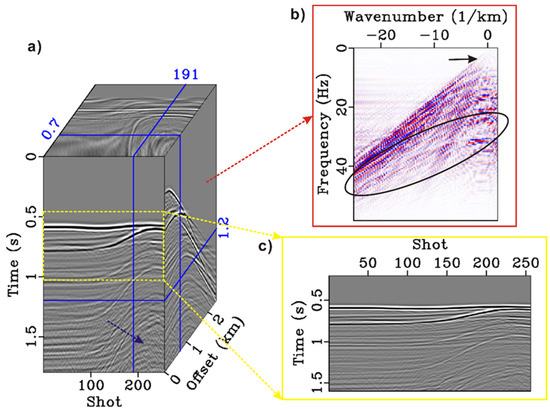
Figure 8.
The sparse inversion-based pseudo-3D deghosting results. (a) 3D data cube including 256 CSGs and 256 COGs. (b) f-k spectrum in which the black oval marks the effect of ghost. (c) COG wherein the events are similar to the underground interface.
To further demonstrate the effectiveness of the proposed method, we calculate the frequency spectrum in the time window (1.25–1.5 s) to quantitatively compare the frequency compensation ability of the conventional deghosting method and the pseudo-3D deghosting method (Figure 9). Figure 9b clearly shows the energy comparison of the three curves. Compared with the f-k spectrum shown above, we can observe a good correspondence between them. It is shown in Figure 6b that the frequency bandwidth of deghost-interfered datasets is narrowed at the main frequency notch (25–50 Hz), and in Figure 9b, the original data has the lowest energy (near 0.25) at approximately 40 Hz. Both the red curve and the yellow curve in Figure 9b have higher energy than the original data in the main frequency notch (25–50 Hz), which is consistent with the phenomenon seen in Figure 7b and Figure 8b, where both methods compensate for the notch effect. Similarly, the energy leakage caused by traditional methods also leads to a large difference between the 2D method and the pseudo-3D method in a quantitative comparison of the main frequency energy. The results of the quantitative comparison also prove the effectiveness of the proposed method.
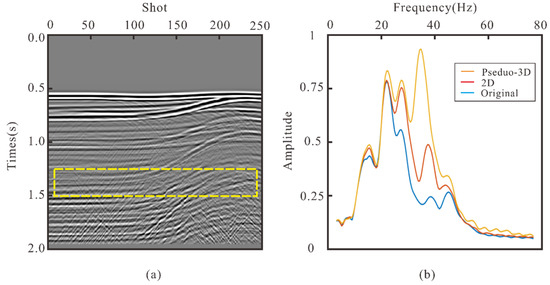
Figure 9.
Frequency comparison of the different methods. (a) COG. (b) Frequency spectrum.
3.2. Field Example
In this section, we adopt a field dataset to test the deghosting effect. The dataset contains a total of 193 shot gathers, 128 offset gathers, 1000 sampling points, and a sampling interval of 4 ms. The sink depth of the geophone is 7 m. The maximum spacing is 3175 m, and the track spacing is 25 m. Figure 10, Figure 11 and Figure 12 show the original data, the conventional 2D method, and the deghosting result of the algorithm, respectively.
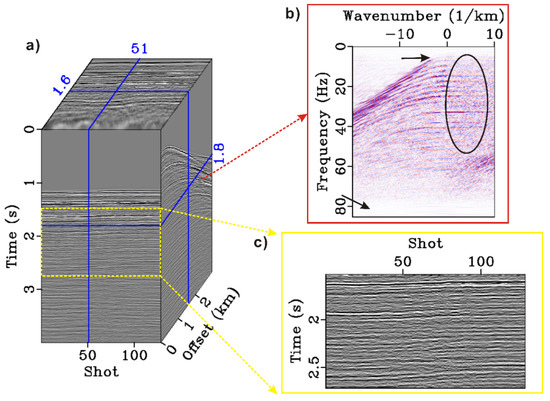
Figure 10.
The field data before deghosting. (a) 3D data cube including 193 CSGs and 128 COGs. (b) f-k spectrum in which the black oval marks the effect of ghost. (c) COG wherein the events are similar to the underground interface.
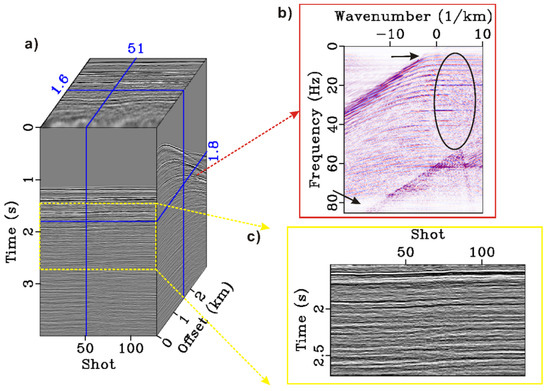
Figure 11.
The 2D deghosting results. (a) 3D data cube including 193 CSGs and 128 COGs. (b) f-k spectrum in which the black oval marks the effect of ghost. (c) COG wherein the events are similar to the underground interface.
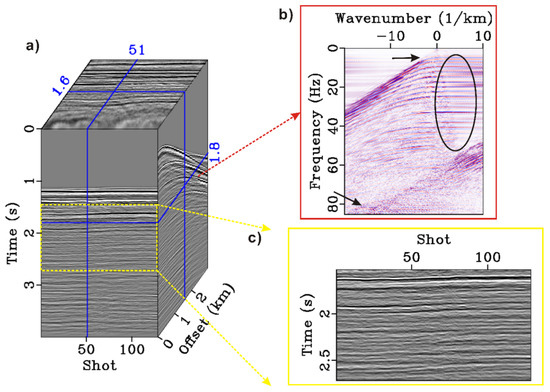
Figure 12.
The sparse inversion-based deghosting results. (a) 3D data cube including 193 CSGs and 128 COGs. (b) f-k spectrum in which the black oval marks the effect of ghost. (c) COG wherein the events are similar to the underground interface.
As a result, there are three main differences: frequency extension, event continuity, and signal-to-noise ratio (SNR). In terms of frequency extension, since the source depth of the data is 7 m, the first non-zero notch frequency is relatively large. The influence of ghost on the seismic records is mainly manifested in the suppression of the low frequency (2–10 Hz) and high frequency (60–80 Hz). The two methods have similar effects on low-frequency energy compensation, but the proposed method has better effects on high-frequency energy compensation. The continuity of the events (Figure 11c and Figure 12c) also proves the effectiveness of the proposed method. Because noise is unavoidable in the field datasets, the continuity of the event becomes worse. The proposed method uses the sparse representation of the seismic signal and retains the main components for reconstruction to improve the event continuity. The SNR difference can be clearly observed in the f-k spectrum, which means the sparse inversion method has a stronger anti-noise performance. The noise reduces the image quality of the f-k spectrum, and the f-k spectrum of the sparse inversion result is smoother, indicating that the redundant information (noise) is attenuated during the inversion process. In summary, the deghosting method in this paper has more advantages in frequency extension. In addition, this method is more suitable for field data processing, which can simultaneously improve the SNR in the process of deghosting.
4. Discussion
In this paper, we introduce the l1 norm sparse inversion method to improve the inversion accuracy. The curvelet and wavelet transforms are excellent tools for the sparse representation of seismic signals, which is fully data-driven. The core assumption of the sparse representation is that the noise energy is smaller than the signal energy in the transformed domain, otherwise signal damage may occur during the inversion. For complex geological conditions, the wavefield contains some weak signals generated by the small-scale structure, which more easily covered by noise. In this case, the parameter setting criteria of the proposed method is a trade-off between being signal-preserving and noise-free.
In addition, although sparse representation improves the sparsity of seismic signals, the redundancy is also improved, which means an increase in data size. Therefore, the calculation efficiency of the proposed deghosting method is limited. To further improve the proposed method, we recommend two future research directions:
- (1)
- Based on symmetry arguments, one would expect that they could also be applied for source-side deghosting in the common-receiver domain.
- (2)
- A combination of this method with a multiple suppression method to propose a set of pre-processing flow data suitable for offshore exploration, including degusting and demultiple.
5. Conclusions
In this paper, we propose a novel pseudo-3D deghosting framework based on 3D sparse inversion to improve the effect of the conventional 2D deghosting method. The pseudo-3D data cube required by the framework is easily implemented from conventional 2D streamer data. To improve the inversion accuracy, the data coherence along the shot direction and the compressed sensing-based inversion method are introduced.
The synthetic and field examples show that the main advantages of the proposed method are the frequency compensation and noise stability. Field noise cannot be avoided in marine seismic acquisition, and the processing process requires the amplitude-preservation of useful events. The algorithms with low noise sensitivity are more suitable for deghosting in industrial data processing.
Author Contributions
D.W. and R.W. conceived and designed the study; W.Z. programmed the code of the deghosting algorithm; Y.L. evaluated and interpreted the results; B.H. provided the idea; L.W. processed the synthetic and field datasets; and R.W. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Natural Science Foundation of China (No. 42074151 and No. 41374108) and Major Projects of the National Science and Technology of China (Grant No. 2016ZX05026-002-003).
Data Availability Statement
The seismic data used in this paper are the property of Jilin University.
Acknowledgments
We are grateful for the SPGL1 solver package provided by University of British Columbia, the Madagascar software package provided by University of Texas at Austin, and the open-source code.
Conflicts of Interest
All of the authors declare that the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Hamarbitan, N.S.; Margrave, G.F. Spectral analysis of a ghost. Geophysics 2001, 66, 1267–1273. [Google Scholar] [CrossRef]
- Berkhout, A.J.; Blacquière, G. Deghosting by echo-deblending. Geophys. Prospect. 2016, 64, 406–420. [Google Scholar] [CrossRef][Green Version]
- Posthumus, B.J. Deghosting using a twin streamer configuration. Geophys. Prospect. 2010, 41, 267–286. [Google Scholar] [CrossRef]
- Zhang, Z.; Masoomzadeh, H.; Wang, B. Evolution of deghosting process for single-sensor streamer data from 2D to 3D. Geophys. Prospect. 2018, 66, 975–986. [Google Scholar] [CrossRef]
- Sun, Y.; Verschuur, E. Three-dimensional receiver deghosting of seismic streamer data using L1 inversion and redundant extended radon dictionary. Geophys. Prospect. 2018, 66, 987–1003. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Wang, B.; Ji, J. Time variant de-ghosting and its applications in WAZ data. In Proceedings of the 85th SEG Annual International Meeting Expanded Abstracts, New Orleans, LA, USA, 18–23 October 2015; pp. 4600–4604. [Google Scholar]
- Robertsson, J.; Amundsen, L. Deghosting of arbitrarily depth-varying marine hydrophone streamer data by time-space domain modelling. In Proceedings of the 84th SEG Annual International Meeting Expanded Abstracts, Denver, CO, USA, 26–31 October 2014; pp. 4248–4252. [Google Scholar]
- Ghosh, K.S. Deconvolving the ghost effect of the water surface in marine seismic. Geophysics 2000, 65, 1831–1836. [Google Scholar] [CrossRef]
- Amundsen, L.; Weglein, A.; Reitan, A. On seismic deghosting using integral representation for the wave equation. Use of Green’s functions with Neumann or Dirichlet boundary conditions. Geophysics 2013, 78, T89–T98. [Google Scholar] [CrossRef]
- Poole, G. Premigration receiver deghosting and redatuming for variable depth streamer data. In Proceedings of the 83th Annual International Meeting Expanded Abstracts, Houston, TX, USA, 22–27 September 2013; pp. 4216–4220. [Google Scholar]
- Wang, P.; Ray, S.; Nimsaila, K. 3D joint de-ghosting and crossline interpolation for marine single-component streamer data. In Proceedings of the 84th SEG Annual International Meeting Expanded Abstracts, Denver, CO, USA, 26–31 October 2014; pp. 3594–3598. [Google Scholar]
- Hardwick, A.; Charron, P.; Masoomzadeh, H.; Aiyepeku, A.; Cox, P.; Laha, S. Accounting for sea surface variation in deghosting—A novel approach applied to a 3D dataset offshore West Africa. In Proceedings of the 85th SEG Annual International Meeting Expanded Abstracts, New Orleans, LA, USA, 18–23 October 2015; pp. 4615–4619. [Google Scholar]
- King, S.; Poole, G. Hydrophone-only receiver de-ghosting using a variable see surface datum. In Proceedings of the 85th SEG Annual International Meeting Expanded Abstracts, New Orleans, LA, USA, 18–23 October 2015; pp. 4610–4614. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, Z.; Gholami, A.; Yan, J.; Li, S. Seismic signal sparse time-frequency analysis by Lp-quasinorm constraint. IEEE Trans. Circuits Syst. 2018, 87, 43–59. [Google Scholar]
- Hu, B.; Wang, D.; Zhang, L.; Zeng, Z. Rock location and quantitative analysis of regolith at the chang’e 3 landing site based on local similarity constraint. Remote Sens. 2019, 11, 530. [Google Scholar] [CrossRef]
- Nazari Siahsar, M.A.; Gholtashi, S.; Roshandel Kahoo, A.; Chen, W.; Chen, Y.K. Data-driven multi-task sparse dictionary learning for noise attenuation of 3D seismic data. Geophysics 2017, 82, V385–V396. [Google Scholar] [CrossRef]
- Allouche, N.; Øzdemir, K.; Özbek, A.; Hopperstad, J.-F. Multimeasurement aliased-noise attenuation for sparse land seismic acquisition using compressed sensing. Geophysics 2020, 85, V183–V200. [Google Scholar] [CrossRef]
- Ning, T.; Herrmann, F.J. Fast imaging with surface-related multiples by sparse inversion. Geophys. J. Int. 2015, 201, 304–317. [Google Scholar]
- Anagaw, A.Y.; Sacchi, M.D. Edge-preserving seismic imaging using the total variation method. J. Geophys. Eng. 2012, 9, 138–146. [Google Scholar] [CrossRef]
- Zhang, F.; Dai, R.; Liu, H. Seismic inversion based on L1-norm misfit function and total variation regularization. J. Appl. Geophys. 2014, 109, 111–118. [Google Scholar] [CrossRef]
- Feng, F.; Wang, D.L.; Zhu, H.; Cheng, H. Estimating primaries by sparse inversion of the 3D curvelet transform and the L1-norm constraint. Appl. Geophys. 2013, 10, 201–209. [Google Scholar] [CrossRef]
- Van den Berg, E.; Friedlander, M.P. Sparse optimization with least-squares constraints. SIAM J. Optim. 2011, 21, 1201–1229. [Google Scholar] [CrossRef]
- Wang, T.; Wang, D.; Sun, J.; Hu, B.; Liu, C.M. Closed-loop SRME based on 3D L1-norm sparse inversion. Acta Geophys. 2017, 65, 1145–1152. [Google Scholar] [CrossRef]
- Hu, B.; Wang, D.; Wang, R. An Iterative Focal Denoising Strategy for Passive Seismic Data. Pure Appl. Geophys. 2020, 177, 4607–4622. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, H.; Xia, Y.; Liu, W.; Wang, Y. Random Noise Attenuation of Common Offset Gathers Using Iteratively Reweighted 2,1 Norm Minimization. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1988–1992. [Google Scholar] [CrossRef]
- Rastegar, S.A.; Javaherian, A.; Farajkhah, N.K.; Monfared, M.S.; Zarei, A. Ground-roll attenuation using modified common-offset-common-reflection-surface stacking. Appl. Geophys. 2016, 13, 353–363. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Comput. Pure Appl. Math. 2010, 59, 1207–1223. [Google Scholar] [CrossRef]
- Candès, E.J.; Demanet, L.; Donoho, D.L.; Ying, L. Fast discrete curvelet transforms. Multiscale Model. Simul. 2006, 5, 861–899. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal L1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Hennenfent, G.; Berg, E.V.D.; Friedlander, M.P.; Herrmann, F.J. New insights into one-norm solvers from the Pareto curve. Geophysics 2008, 73, A23–A26. [Google Scholar] [CrossRef]
- Tim, T.Y.; Felix, J.H. Robust estimation of primaries by sparse inversion via one-norm minimization. Geophysics 2013, 78, R133–R150. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).