Design and Analysis of Microchannels for Heat Dissipation of High-Energy VCSELs Based on Laser 3D Printing

Abstract

For the problem of high waste heat in the active area of high-power VCSEL arrays and the difficulty of heat dissipation, we took advantage of laser 3D printing technology and combined it with the relevant principles of fluid-structure coupling, three kinds of microchannel heat sink with different structures of pin-fin, honeycomb, and double-layer reflow were designed. The heat dissipation capacity of three kinds of heat sinks to the heat flux density 200 W/cm² VCSEL array and the influence of the key characteristics of the microchannel on the heat dissipation capacity was studied. The results show that the double-layer reflow microchannel heat sink has the strongest heat dissipation capability, with the minimum thermal resistance value of 0.258 °C/W when the microchannel diameter and the cooling mass flow rate were 0.5 mm and 24 L/h, respectively. The inner wall roughness of the pure copper microchannel prepared by 3D printing technology was 7.08 μm, and the heat sink thermal resistance was reduced by 0.7% compared with the smooth channel wall. The deviation of the microchannel diameter from the design size (500 μm) was −10 μm, and the heat sink thermal resistance was reduced by 0.8% compared to the theoretical value, which shows that the surface roughness and size deviation of the 3D printed microchannel had beneficial effect on enhancing heat dissipation. The actual thermal conductivity of the 3D printed pure copper after heat treatment was 310.4 W/m-K, at which point the thermal resistance was 0.306 °C/W, and the maximum temperature was 35.3 °C, which satisfied the operating temperature range of the chip. This study provides a theoretical basis and implementation method for the fabrication of heat sinks for high-energy VCSEL arrays using laser 3D printing technology.

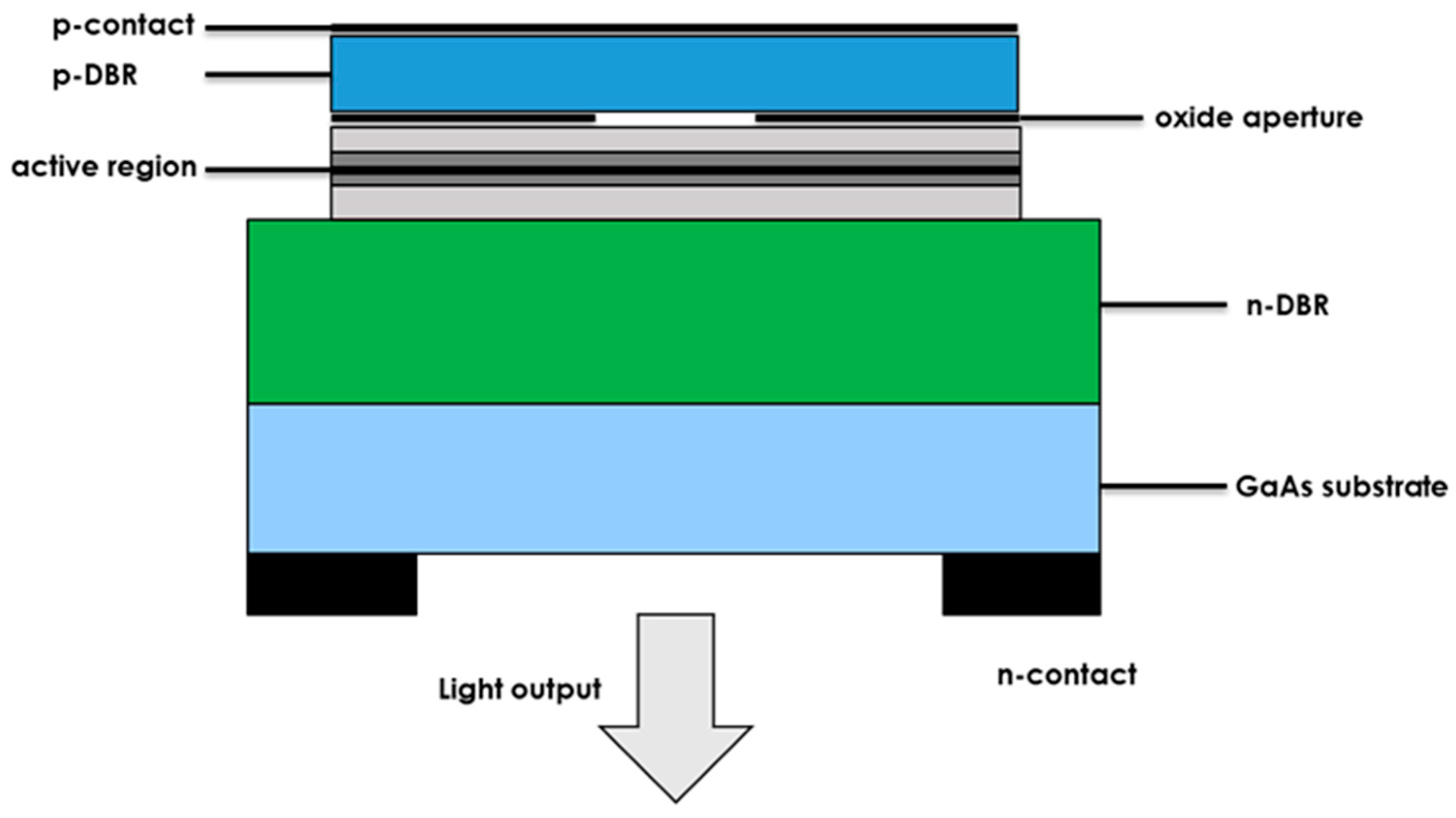
1. Introduction

High-Power Vertical Cavity Surface Emitting Semiconductor Laser [1] (VCSEL) has high photoelectric conversion efficiency, low threshold current, and emits circular light spot. Due to its excellent photoelectric performance, VCSEL is widely used in laser radar, 3D camera, face recognition, and other fields. In 2008, Princeton Optoelectronics in the United States achieved a continuous output of 45 W on a two-dimensional array of 5 × 5 mm VCSEL [2]. In 2015, the above company achieved a continuous output of 280 W for an 808 nm VCSEL array by adding a diamond film as a transition heat sink between a 5 × 5 mm VCSEL array and a microchannel heat sink [3], this is by far the highest level of public reporting in the world. However, high-power VCSELs could generate excessive temperatures in the DBR and active areas during operation, resulting in wavelength red shift, threshold current increase and output power decrease. Therefore, efficient heat dissipation is particularly important for high-power VCSEL. At present, the heat dissipation method of lasers mainly includes: Forced air cooling, semiconductor cooling, macrochannel water cooling, microchannel water cooling, etc. Among them, microchannel water cooling can realize the heat dissipation of chips above 100 watts, which is the most potential heat dissipation method at present.

Tuckerman and Pease [4] first proposed the concept of liquid-cooled microchannel heat sink in 1981, and achieved an excellent heat transfer coefficient of up to 10 W/cm² · K, but the disadvantage of single-layer microchannels was the uneven heat distribution along the channel. Vafai [5] designed a double-layer microchannel structure, which had a certain effect on improving heat dissipation uniformity. Kumar et al. [6] studied the effect of dual inlets at different positions and spacing on the heat transfer performance of microchannel heat sink, the result shows that splitting a single inlet into two could effectively alleviates the phenomenon of uneven flow distribution on the heat sink and improves the heat dissipation capacity. Tengwei Qiu et al. [7,8] prepared a diamond microchannel heat sink with excellent heat dissipation capability using porous copper as a substrate. Inspired by biomimicry, some scholars refer to some excellent structures in nature. Abo Zahhad [9] designed a diamond-shaped microchannel, Xie [10] introduced microneedle fins of different shapes into microchannels, Chen Ran et al. [11] designed a double-layer microchannel heat sink with pyramid-shaped disturbance structure. Compared with the ordinary double-layer trapezoidal microchannel heat sink, the double-layer trapezoidal microchannel heat sink with pyramid-shaped disturbance structure had a stronger heat transfer capacity. The study found that the microchannel heat sink has the advantages of high specific surface area, large convective heat transfer coefficient, and requires just a small amount of coolant. However, it is also shown that the poor channel structure causes uneven temperature distribution, which, in turn, leads to significant temperature gradients at the heat source surface, optimizing the structural design to increase the contact area between the coolant and the heat sink can solve this problem and help to further improve the heat dissipation capability of the microchannel heat sink.

Although the microchannel water-cooled heat sink obtains obvious advantages, limited by the high difficulty of precision machining of microchannels, the application of microchannel water-cooling technology in the field of VCSEL chip cooling is not mature yet. At present, the microchannel heat sink is usually produced by using plasma etching technology to etch different hollow structures on multi-layer high thermal conductivity rectangular sheets, respectively, then, through hot press welding technology for precision welding. However, the multi-layer welding will also introduce additional thermal resistance, which will reduce the mechanical strength and service life of the heat sink manufactured by hot-press welding. For this situation, it is urgent to introduce a new technology to break through the current technological bottleneck. Laser 3D printing technology is an additive manufacturing technology based on the idea of near-net forming [12,13,14], which uses laser as the energy source to scan the metal powder bed layer by layer according to the planned path in the 3D CAD slice model, and the scanned metal powder is melted and solidified to achieve metallurgical bonding and finally obtain the metal parts of the model design. 3D printing technology has the characteristics of flexible design and high degree of freedom for complex structures. Compared with the traditional laminated soldering technology, 3D printing one-piece formed channel structure avoids the additional thermal resistance introduced by multi-layer pressed soldering and the risk of solder diffusion into the microchannel blocking the channel. Therefore, the use of 3D printing technology to prepare microchannel heat sinks is expected to drive a significant development in chip thermal management. In 2011, the Fraunhofer Institute in Germany fabricated a steel, titanium, and aluminum alloy heat exchanger for automobiles by 3D printing technology. The experimental results show that 3D printing technology increases the possibility of complex and precise design fabrication [15]. In 2019, the University of Nottingham proposed a method to fabricate pure copper under a low-power small laser spot diameter 3D printing device and obtained parts with a high density of 85.8% and high electrical conductivity [16], providing a research idea to fabricate pure copper parts under a low-power device. In 2021, a topologically bionic pure copper microchannel heat sink was fabricated by 3D printing of fused wire fabrication at Texas State University, providing a new way to manufacture heat sinks [17]. Yao et al. studied the preparation of single-layer diamond-shaped fork-row microchannel heat sink using laser 3D printing technology to dissipate heat for a chip with a heat flux of 60 W/cm². The results show that the maximum temperature of the heat source surface is 75.62 °C, and the experimental results are in good agreement with the simulation results. This work can provide a comparative reference for the development of our research [18].

Based on the design principles of 3D printing technology and the theory of fluid-solid coupling, this paper designs three types of heat sink with microchannel structures: honeycomb type, pin-fin type, and multi-layer reflux type. FEA software ANSYS was used to simulate the influence of heat sink structure, coolant flow and hydraulic diameter of microchannel on-chip thermal resistance and temperature distribution. The influence of key characteristics (dimensional accuracy, surface roughness) and thermal conductivity of 3D printed samples on the heat sink’s heat dissipation capability was also studied, providing theoretical support and implementation methods for the preparation of heat sinks for high-power VCSEL arrays using 3D printing technology.

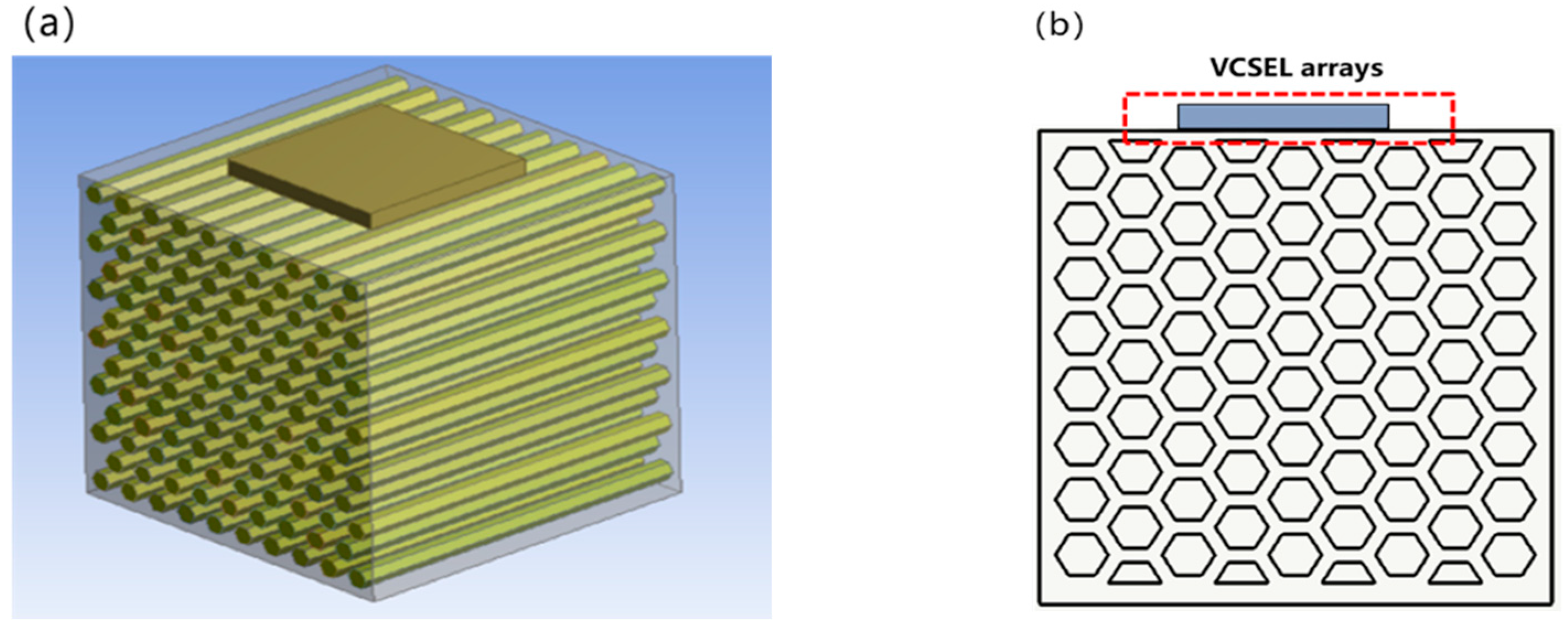
2. Micro-Channel Heat Sink Structure Design

The heat source in the microchannel heat sink system is the bottom-emitting VCSEL array, and the structure is schematically shown in Figure 1. It generates a large amount of waste heat in the DBR and active areas. The design requirements of heat sink for the high-power VCSEL array are shown in

Table 1. Heat dissipation requirements of VCSEL arrays.

Type	Calculation Conditions
Chip Heat Source	100 W
Photovoltaic conversion efficiency	50%
Chip Size	5 × 5 × 0.5 mm
Chip Materials	GaAs
Cooling mass	Deionized water
Heat sink size	10 × 10 mm
Heat sink materials	Oxygen-free copper

.

3D printing technology has high manufacturing flexibility of complex structures, so based on the idea of increasing the coolant heat exchange area to strengthen heat transfer, in this study, we designed microchannel heat sinks with three structures: Double-layer reflow type, honeycomb type, and needle-fin type.

Vafai pointed out that one disadvantage of monolayer microchannels was the high and uneven temperature distribution along the channel direction. It is because the flow rate of the coolant is relatively low, and large amount of heat generated by the chip cannot be dissipated, resulting in a temperature gradient that causes thermal stress inside the VCSEL chip. High local thermal stress is a major cause of chip failure. One way to reduce the temperature gradient is to increase the flow of coolant. Therefore, in the study, we designed a double-layer reflow microchannel with dual inlets. As shown in Figure 2, the liquid flows in the two adjacent layers of the heat sink were in opposite directions, as shown by the arrow in Figure 2b, and the upper channel is dissipated through the lower channel for secondary heat dissipation, thereby achieving uniform heat dissipation to the chip.

The honeycomb structure is a bionic design of a natural beehive, which consists of a series of hollow cell arrays and has the advantages of structural stability and large contact area of internal channels. As shown in Figure 3, the honeycomb microchannel heat sink was designed with staggered arrangement of microchannels in a hexagonal imitation honeycomb structure, and the multi-layer channels were stacked to significantly increase the heat transfer area. The side length and wall thickness of the hexagonal microchannels were both 0.3 mm.

Pin-fin microchannel heat sink increases the effective heat transfer area and turbulence intensity by setting up spoiler columns to achieve stronger heat dissipation than conventional long straight channels. As shown in Figure 4, the cross-section of the pin-fin spoiler column distributed in the channel was a square with a side length of 0.5 mm. In order to reduce the resistance to water, the diagonal of the pin-fin section was set parallel to the direction of water flow.

In order to distribute the cooling mass flow and flow rate evenly, the inlets of the above three models adopt a tapering structure with the center gradually expanding to both sides, and the slow flow area of the outlet adopts a tapering structure with the center gradually narrowing to both sides, so that the cooling masses converge together.

3. Mathematical Model and Boundary Conditions

3.1. Mathematical Model

The design of the microchannel heat dissipation system in this paper was based on the relevant principles of fluid-solid coupling, and the thermal analysis was based on the three laws of fluid mechanics. The governing equations of mass, momentum, and energy can be written as follows:

Continuity equation:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$$

(1)

where u, v, and w are velocity components in x, y, and z directions, respectively.

Momentum equations:

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=-\frac{1}{{\rho }_f}\frac{\partial p}{\partial x}+\frac{{\mu }_f}{{\rho }_f}\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)$$

(2)

$$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=-\frac{1}{{\rho }_f}\frac{\partial p}{\partial y}+\frac{{\mu }_f}{{\rho }_f}\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)$$

(3)

$$u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}=-\frac{1}{{\rho }_f}\frac{\partial p}{\partial z}+\frac{{\mu }_f}{{\rho }_f}\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)$$

(4)

where ${\rho }_f$ and ${\mu }_f$ are the density and dynamic viscosity of the coolant, respectively, and $\mathrm{p}$ is the coolant pressure.

Energy equation for the coolant

$$u\frac{\partial T_f}{\partial x}+v\frac{\partial T_f}{\partial y}+w\frac{\partial T_f}{\partial z}=\frac{k_f}{{\rho }_f{c}_{Pf}}\left(\frac{{\partial }^2{T}_f}{\partial x^2}+\frac{{\partial }^2{T}_f}{\partial y^2}+\frac{{\partial }^2{T}_f}{\partial z^2}\right)$$

(5)

where $T_f$ is the coolant’s temperature, $c_{Pf}$ is fluid-specific heat and $k_f$ is fluid thermal conductivity.

Energy equation for the solid region

$$0=k_s\left(\frac{{\partial }^2{T}_s}{\partial x^2}+\frac{{\partial }^2{T}_s}{\partial y^2}+\frac{{\partial }^2{T}_s}{\partial z^2}\right)$$

(6)

where $T_s$ is solid temperature, and $k_s$ is solid thermal conductivity

3.2. Boundary Conditions for Fluent Calculations

The boundary conditions in the Fluent simulation calculation were as follows:

(1) High power VCSEL array surface: $-k\frac{\partial T}{\partial z}=200\mathrm{W}/{\mathrm{cm}}^2$

(2) Channel inlet, $u=0,v=0,w=1.2\mathrm{m}/\mathrm{s},T_{water}=293 K$

(3) Channel outlet, $\frac{\partial u}{\partial z}=\frac{\partial v}{\partial z}=\frac{\partial w}{\partial z}=0,$ $\frac{\partial T_{water}}{\partial z}=0$

(4) The contact surface between VCSEL chip and heat sink, heat sink and fluid: $u=v=w=0$, $-{\lambda }_{water}\frac{\partial T_{water}}{\partial z}=-{\lambda }_{solid}\frac{\partial T_{solid}}{\partial z}$

(5) Remaining walls: $u=v=w=0$, $\frac{\partial T}{\partial n}=0$, and the natural convection and radiation heat transfer are ignored in the next calculation.

In this paper, the momentum equation and energy equation were solved by using the second-order upwind scheme, the standard SIMPLE algorithm was used to solve the coupling equation of pressure and velocity. Since the chip and heat sink are regular cubic structures, the mesh was divided using hexahedral cells, as shown in Figure 5. Since the chip and heat sink are regular cubic structures, the mesh was divided using hexahedral cells, as shown in Figure 5.

As mentioned above, Yao et al. made the diamond-shaped fork row microchannel heat sink by 3D printing and compared the experimental results with the heat dissipation characteristics calculated by ANSYS FLUENT software. The results show that the experimental data are in good agreement with the simulation data, the deviation is less than 5%, and the trend of the experimental data curve is consistent with that of the simulation data curve. When the heat flow density and velocity are constant, the experimental data of the maximum temperature of the contact surface of the heat source is slightly higher than the simulation data, the cause of this phenomenon may be: (1) During the experiment, the heating plate and the heat sink are bonded by thermal grease, and there is inevitably thermal contact resistance, which is not considered in the simulation, this will introduce some error. (2) There is a certain accuracy error in the process of the micro-channel heat sink, which cannot be completely consistent with the model size in the simulation. In order to compare and verify Yao’s work, the same boundary conditions are selected to simulate the temperature distribution of the bottom surface of the heat sink when the heat flux is 60 W/cm², and the flow rate is 1.2 m/s. The maximum temperature calculated is 73.12 °C, the temperature deviation from the original is 1.15 °C, and the deviation rate is 1.5%. Therefore, it can be considered that the model established in this paper is accurate and can be used to study the heat transfer performance of the microchannel heat sink.

4. Numerical Simulation and Result Analysis

4.1. Influence of Coolant Flow on Thermal Resistance

ANSYS finite element analysis software was used to analyze the thermal simulation of the microchannel heat sink models of the above three structures. As shown in Figure 6, first, we compare the chip thermal resistance variation curves of the three microchannel heat sinks at different coolant flow rates.

It can be seen from Figure 6 that the three thermal resistance curves varying with coolant flow were approximately parallel, and the thermal resistance decreased with the increase of coolant flow, The corresponding chip thermal resistance of honeycomb, pin fin and double-layer reflux heat sink decreased from 0.439 °C/W, 0.466 °C/W and 0.376 °C/W at 10 L/h to 0.340 °C/W, 0.376 °C/W, and 0.312 °C/W at 40 L/h, respectively. However, with the increase of coolant flow to 22 L/h, the decreasing trend of thermal resistance gradually leveled off, and continuously increasing the coolant flow rate will cause the pressure of the pipe in the microchannel to rise, so the coolant flow rate cannot be increased indefinitely.

Figure 7 shows the temperature nephogram of the heat source surface of the microchannel heat sink with three structures when the cooling working flow rate was 14 L/h. The maximum chip temperatures were 37.6 °C, 40.2 °C, and 47.7 °C on the dual-layer reflow, honeycomb, and pin-fin microchannel heat sinks, respectively. By simulating the flow velocity cloud in the channel of the pin-finned radiator, the highest temperature at its heat source surface might be analyzed because the pin-fin can change the flow state of the cooling mass and enhance the turbulent flow state of the cooling mass for enhanced heat transfer, but there was no water passing through the dead space behind the needle fin, and the cooling mass is prone to large cavities (shown in Figure 8), and these cavities significantly reduce the heat dissipation capacity. The reason for the best heat dissipation effect of the double-layer return microchannel radiator may be that the two water inlets provided by the adjacent bi-directional flow channels increase the flow of cooling mass while achieving secondary cooling of the lower channel to the upper channel. The combined thermal resistance and temperature results show that the double-layer return microchannel heat sink had the best thermal performance among the three structural designs.

4.2. Influence of Microchannel Hydraulic Diameter on Heat Dissipation Capacity

In order to further optimize the structure design of the double-layer reflow microchannel heat sink, we continued to study the variation of the chip thermal resistance with the coolant flow under different microchannel hydraulic diameters.

It can be seen from Figure 9 that with the decrease of the hydraulic diameter of the microchannel, the thermal resistance of the chip gradually decreased, and with the increase of the coolant flow rate, the thermal resistance of the chip under the conditions of different hydraulic diameters of the microchannel presented an approximately parallel downward trend, and the downward trend was slowing down. The results show that the smaller the hydraulic diameter of the microchannel, the better the heat dissipation effect of the chip. For example, when the coolant flow rate was 14 L/h, the hydraulic diameter of the microchannel was 0.4 mm compared to 0.8 mm, and the thermal resistance of the chip was 73.3% of the latter. However, the hydraulic diameter of the microchannel cannot be reduced indefinitely. The microchannel heat sink is sensitive to pipeline pressure. Large pipeline pressure may damage the microchannel structure, thus causing channel blockage [19]. Therefore, the variation of microchannel pipe pressure with coolant flow rate was simulated for different hydraulic diameters, and the curves are shown in Figure 10. In the double-layer reflow microchannel heat sink, the pipeline pressure increased greatly with the decrease of the hydraulic diameter, and it showed an obvious upward trend with the increase of the coolant flow rate. According to research, 1.3 bar was a relatively safe pipeline pressure threshold. It can be seen that when the hydraulic diameter is 0.4 mm, the coolant flow rate to keep the pressure in the pipeline lower than 1.3 bar was 10 L/h and 14 L/h, when the hydraulic diameter was 0.5 mm, the cooling mass flow rate of 10 L/h, 14 L/h, 18 L/h, 22 L/h, and 24 L/h could meet the requirements. When the hydraulic diameter was greater than 0.7 mm, the coolant flow rate was in the range of 10 L/h–40 L/h, and the pressure of the pipes in the microchannel was less than 1.3 bar.

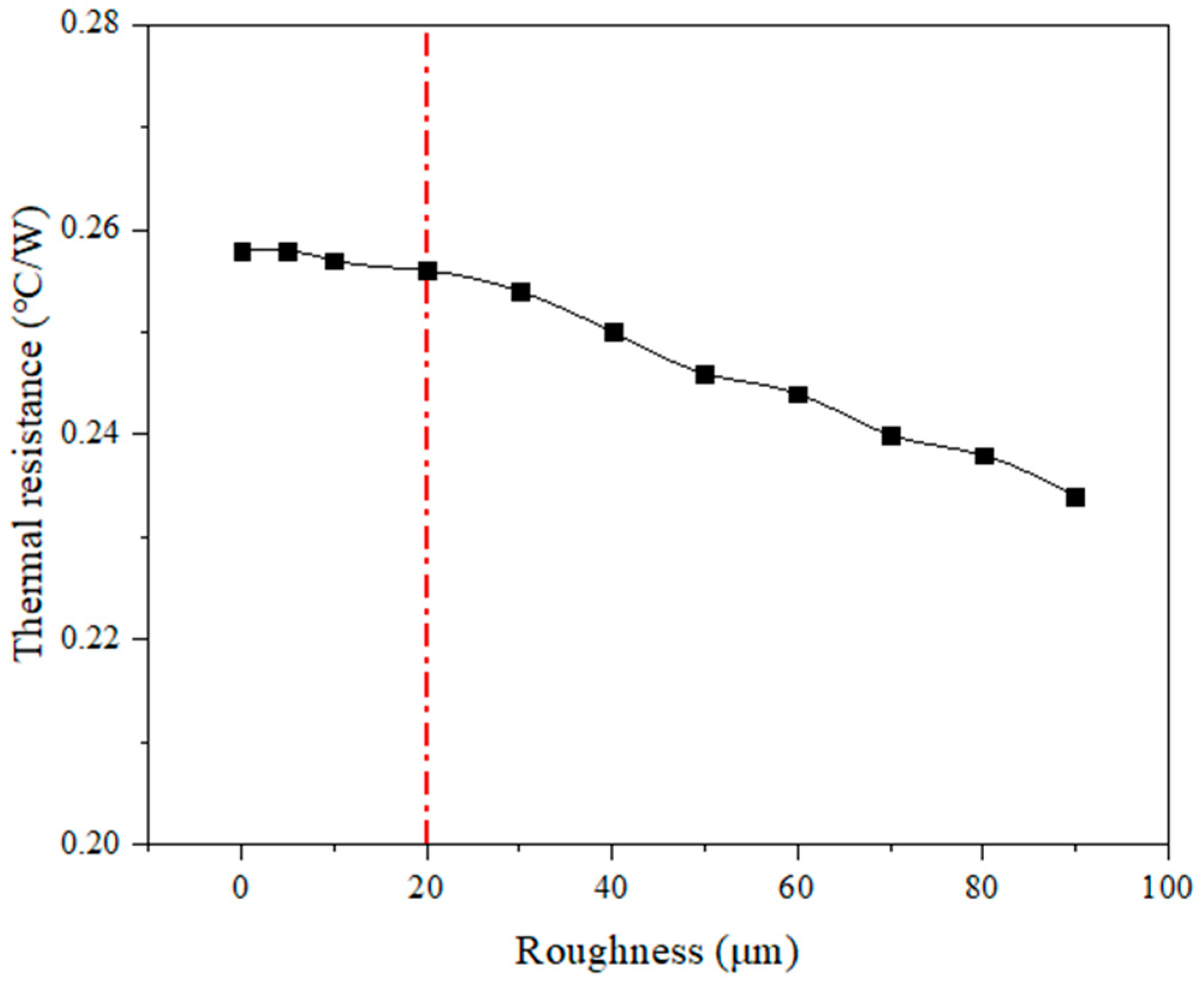
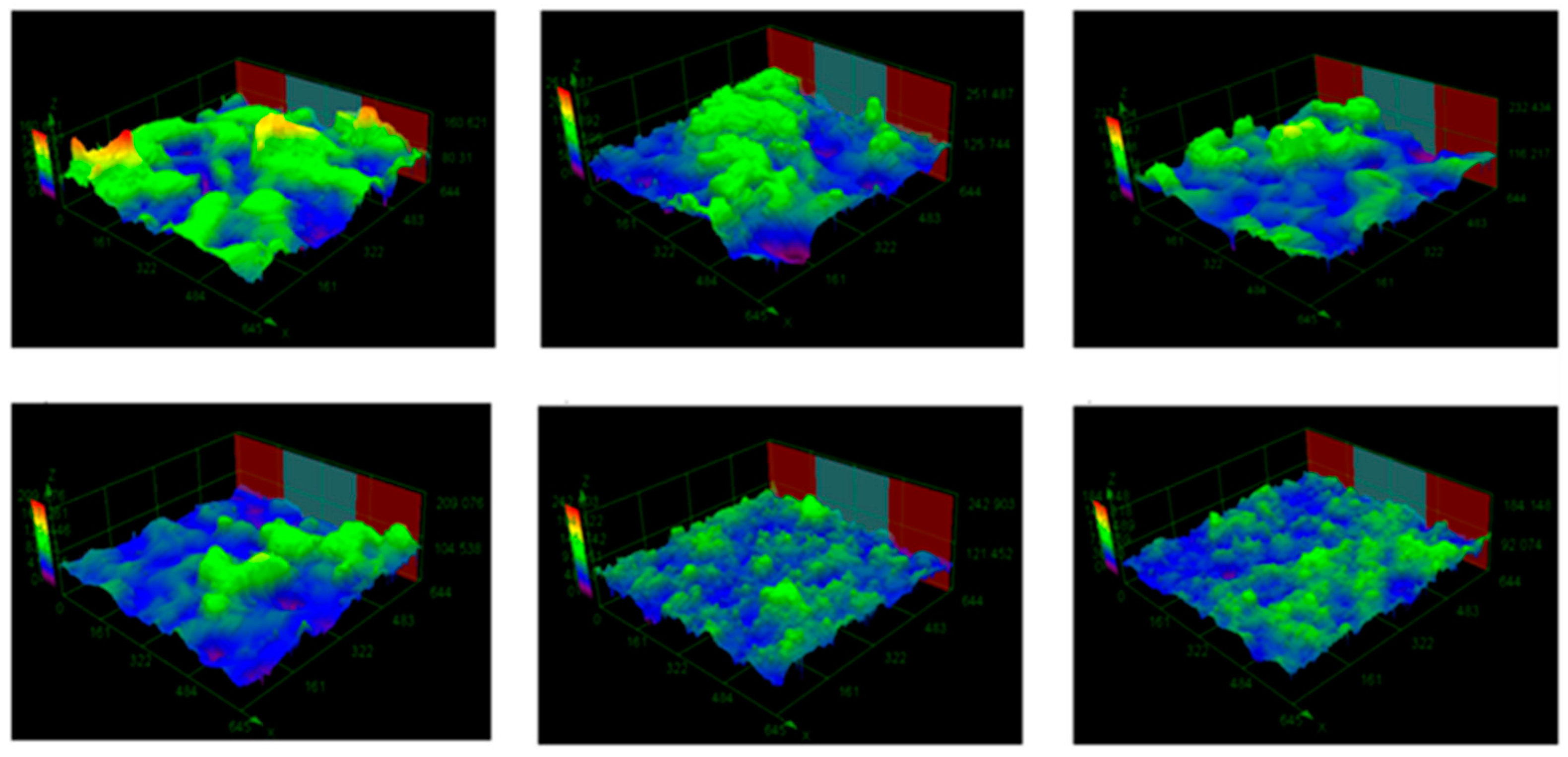
4.3. Effect of Microchannel Roughness on Heat Dissipation Capability

The double-layer reflow microchannel heat sink in this paper was fabricated by laser 3D printing technology, and the roughness of the inner wall of the pipe was unavoidable. The roughness may increase the heat exchange area between the heat sink and the cooling mass and may also change the flow state of the cooling mass near the wall. Therefore, it is necessary to study the effect of roughness on the heat dissipation capacity of the microchannel heat sink. Roughness is involved in the solution of NS equation in the form of wall function. When roughness is considered, the logarithmic distribution law of wall function is:

$$u^{+}=\frac{u_p}{u^{*}}=\frac{1}{k}In\left(E\frac{y_p{u}^{*}}{\nu }\right)-\mathsf{\Delta }B$$

(7)

where $\mathsf{\Delta }B$ is a function of roughness. A dimensionless number $K_S^{+}=\frac{K_s{u}^{*}}{\nu }$ is introduced for roughness, where $K_s$ is roughness (mm):

(1) 0 < $K_S^{+}=\frac{K_s{u}^{*}}{\nu }$ < 2.25, $\mathsf{\Delta }B$ = 0, the viscous sublayer covers the whole roughness peak,

(2) 2.25 < $K_S^{+}=\frac{K_s{u}^{*}}{\nu }$ < 90,

$$\mathsf{\Delta }B=\frac{1}{k}In\left[\frac{K_S^{+}-2.25}{87.75}+C_s{K}_s\right]\times sin\left[0.4258In\left(K_S^{+}-0.811\right)\right]$$

(8)

(3) $K_S^{+}=\frac{K_s{u}^{*}}{\nu }$ > 90,

$$\mathsf{\Delta }B=\frac{1}{k}In\left[1+C_s{K}_s\right]$$

(9)

peak is almost completely exposed in the turbulent region, where $C_s$ is the roughness constant, which is generally 0.5.

Figure 11 shows the influence curve of the inner wall roughness of the microchannel on the thermal resistance of the chip. It can be seen that when the channel wall roughness was 0–20 μm, the thermal resistance of the chip did not change significantly and only decreased from 0.258 °C/W to 0.256 °C/W. However, when the microchannel wall roughness exceeded 20 μm, the curve dropped slowly from 0.256 °C/W at 20 μm to 0.234 °C/W at 90 μm with a decrease of 8%. The result shows that the increase in channel wall roughness could reduce the thermal resistance of the chip. The reason might be when the roughness was small, the heat exchange area and the flow state of the cooling mass did not change significantly compared with the smooth wall surface. With the increase of micro-channel wall roughness, on the one hand, the heat transfer area between the cooling medium and heat sink is increased, on the other hand, the degree of disturbance and turbulence of the cooling medium is increased, and the heat dissipation effect was enhanced. However, the roughness continued to increase, which means that the surface grain was less constrained, and the surface was prone to plastic deformation [20], which is easy to cause pipeline blockage caused by erosion and corrosion of the cooling medium, affecting the service life of the microchannel heat sink.

According to the above analysis, the optimal design of the three microchannel radiator structures is double-layer backflow, and the optimal parameters are as follows: Hydraulic diameter of the microchannel is 0.5 mm, flow rate of the cooling medium is 24 L/h, inner wall roughness is 0–20 μm, and the thermal resistance of the chip is 0.256 ℃/W. The temperature cloud diagram is shown in Figure 12.

5. 3D Printing Microchannel Heat Sink

The material properties and the structure of the heat sink determine the heat dissipation capacity of the heat sink. In this paper, we continue to investigate the effects of surface roughness, microchannel dimensional accuracy, and material thermal conductivity on the heat sink performance of laser 3D printed formed copper parts. Figure 13 shows the microchannel radiators with three kinds of structures prepared by laser 3D printing technology.

5.1. Roughness

The printed and formed bilayer reflux microchannels were measured by confocal microscopy, as shown in Figure 14. The roughness of the inner wall of the pipe was 7.08 μm, at this time, the temperature on the chip was 32.8 °C, which was 0.1 °C lower than that of the pipe with smooth wall, and the thermal resistance of the heat sink was 0.256 °C/W.

5.2. Dimensional Accuracy

Figure 15 shows the scanning electron microscope (SEM) images of microchannels designed with diameters of 600, 500, 400, and 300 μm formed by laser 3D printing. The deviation between the actual size and the design value was in the range of −10 um and −1 um. The reason for this dimensional deviation might be that copper has excellent thermal conductivity, and during the printing process, the high temperature formed in the melt pool after laser incidence was rapidly conducted, and under high-speed cooling conditions, copper’s shrink caused the actual size of the channel to be smaller than the design size. Therefore, it is important to study the effect of microchannel dimensional accuracy on the performance of heat sink. In this study, the microchannel diameter was 0.5 mm with a dimensional accuracy of 20 μm, at which the maximum temperature on the chip was reduced by 0.1 °C compared to the theoretical value as shown in Figure 16. It can be seen that the roughness and dimensional accuracy of 3D printed microchannels have a certain enhancement effect on the device’s thermal performance and help to reduce the chip’s thermal resistance.

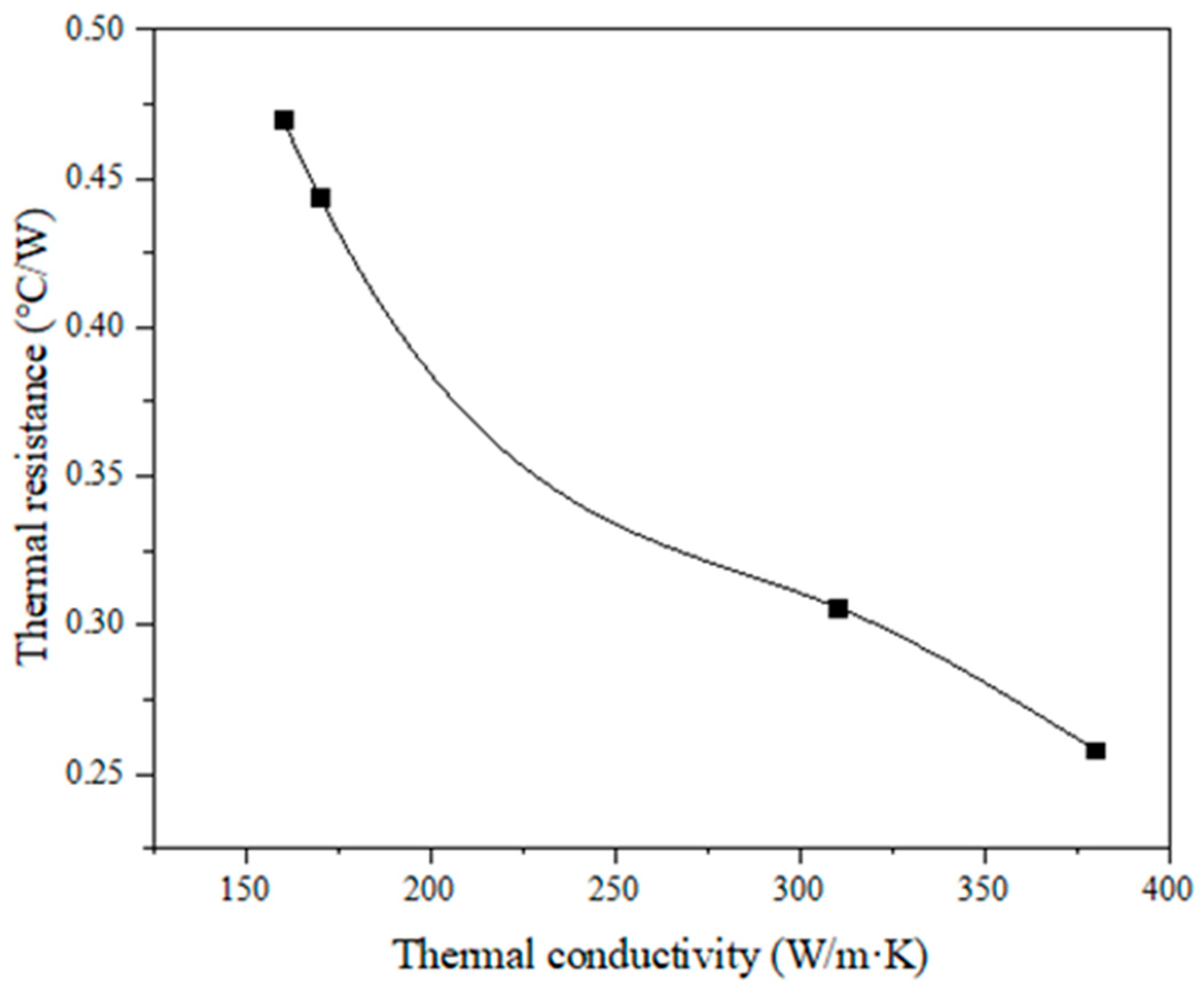
5.3. Thermal Conductivity

Material thermal conductivity is the most critical factor affecting the thermal performance of microchannel heat sink. In this study, the heat treatment process of heating at 1000 °C for 12 h was used to modify the property of copper specimens formed by 3D printing. Compared with that before heat treatment, the thermal conductivity of the material increased from 160 W/m·K to 310 W/m·K, with a performance improvement of 93%, and this thermal conductivity value was similar to that in the literature [21]. Heat treatment can make incompletely melted particles reach a molten state to form neck connections and promote densification [19]. Figure 17 compares the variation curve of the thermal resistance of the chip with the thermal conductivity of the radiator material. When the thermal conductivity of the radiator material is 160 W/m·K, the thermal resistance of the chip is 0.47 °C/W. When the thermal conductivity of the heat sink material is 310 W/m·K, the thermal resistance of the chip is 0.306 °C/W, and the maximum temperature of the chip surface is 35.3 °C, which can fully meet the operating temperature range of the chip (−45 °C~80 °C).

6. Conclusions

In this paper, we first analyzed the influence of channel structure, coolant flow rate, and hydraulic diameter of the channel on the heat dissipation capacity of microchannel heat sink by means of finite element analysis, and then optimized the design of heat sink structure, and studied the influence of surface roughness, dimensional accuracy and thermal conductivity of copper parts prepared by laser 3D printing on heat dissipation capacity of heat sink, and the following conclusions can be obtained.

• Among the three structures of microchannel heat sinks of pin-fin, honeycomb, and double-layer reflow type, the double-layer reflow type has the lowest heat source surface temperature, the smallest chip thermal resistance, and the best heat dissipation effect. The optimal solution for the structural design of the double-layer reflow microchannel heat sink is obtained by comprehensively weighing the chip thermal resistance and the pipe pressure that the micro-channel can withstand: The hydraulic diameter is 0.5 mm, the coolant flow rate is 24 L/h, and the chip thermal resistance is 0.258 °C/W.
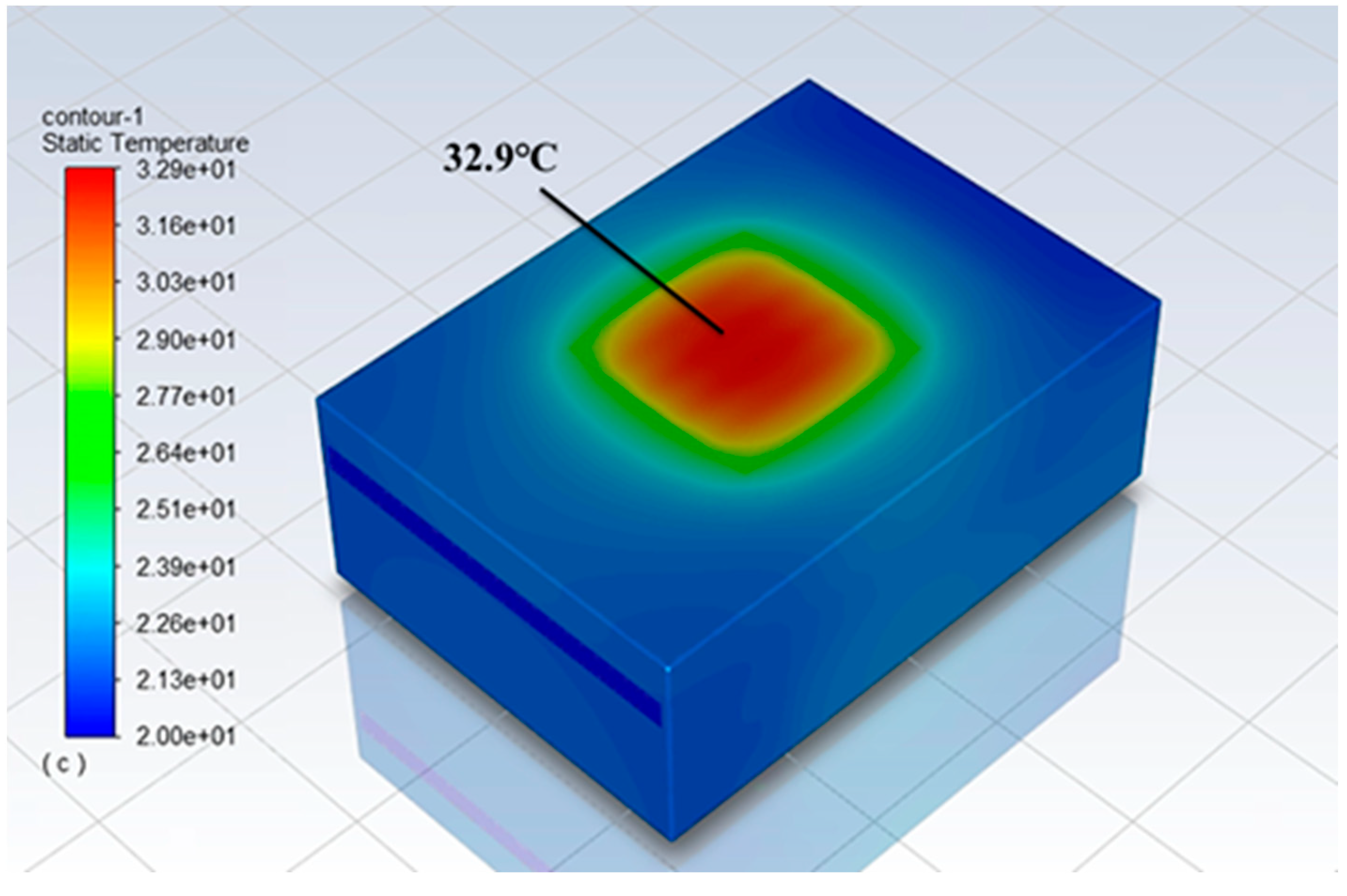
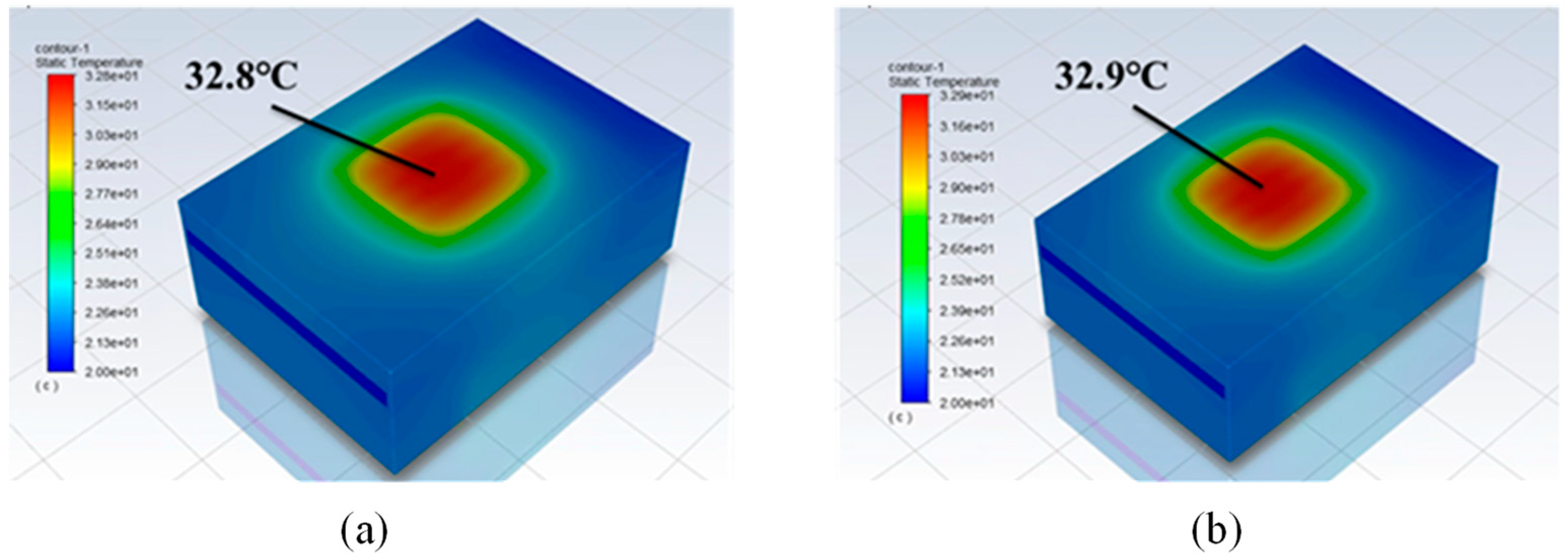
• The inner wall roughness of pure copper microchannel prepared by 3D printing technology is 7.08 μm, and the heat sink thermal resistance is reduced by 0.7% compared to that when the smooth channel wall is used. The deviation of microchannel diameter from the design size (500 μm) is −10 μm, and the heat sink thermal resistance is reduced by 0.8% compared to the theoretical value, which shows that the surface roughness and size deviation of 3D printed microchannel can be regarded as a beneficial factor to enhance heat dissipation. At present, the highest thermal conductivity achievable for laser 3D printed formed copper parts is 310 W/m-K, at which the maximum chip surface temperature is 35.3 °C and the heat sink thermal resistance is 0.306 °C/W, which can fully meet the chip (−45 °C~80 °C) operating temperature range.