Evaluation of the Flexural Rigidity of Underground Tanks Manufactured by Rotomolding
Abstract
:1. Introduction
2. Materials and Methods
Flexural Rigidity of the Sandwich Structure
3. Results
3.1. Optimization of Sandwich Structures
3.2. Stability of Shell Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | cross-sectional width of the sandwich element |
| E1 | calculated modulus of elasticity—non-lightweight layers |
| E2 | calculated modulus of elasticity—lightweight layer (core) |
| Eef | effective modulus of elasticity |
| Eef theoretical | theoretical effective modulus of elasticity |
| Eef experimental | experimental effective modulus of elasticity |
| h | cross-sectional height of the sandwich element |
| JR | quadratic modulus of the reduced cross-sectional area |
| Jef | effective quadratic modulus of the cross-section of the sandwich element |
| K0 | flexural rigidity of the cross-section of the sandwich element |
| m | unit mass of the sandwich structure |
| mef | unit mass of the homogeneous wall of effective thickness |
| sef | effective thickness of the sandwich structure |
| t1 | thickness of surface—non-lightweight layers |
| t1OPT | optimum thickness of the surface—non-lightweight layers |
| ρ1 | density of the non-lightweight layers |
| ρ2 | density of the lightweight core |
References
- Černohlávek, V.; Štěrba, J.; Svoboda, M.; Zdráhal, T.; Suszyński, M.; Chalupa, M.; Krobot, Z. Verification of the Safety of Storing a Pair of Pressure Vessels. Manuf. Technol. 2022, 21, 762–773. [Google Scholar] [CrossRef]
- Daghighi, S.; Weaver, P.M. Three-dimensional effects influencing failure in bend-free, variable stiffness composite pressure vessels. Compos. Struct. 2021, 262, 113346. [Google Scholar] [CrossRef]
- Margolis, J.M. Engineering Thermoplastics: Properties and Applications; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Shaker, R.; Rodrigue, D. Rotomolding of Thermoplastic Elastomers Based on Low-Density Polyethylene and Recycled Natural Rubber. Appl. Sci. 2019, 9, 5430. [Google Scholar] [CrossRef]
- Crawford, R.J.; Throne, J.L. Rotational Molding Technology; William Andrew Publishing: New York, NY, USA, 2001. [Google Scholar]
- Novo, A.V.; Bayon, J.R.; Castro-Fresno, D.; Rodriguez-Hernandez, J. Review of Seasonal Heat Storage in Large Basins: Water Tanks and Gravel–Water Pits. Appl. Energy 2010, 87, 390–397. [Google Scholar] [CrossRef]
- Tkac, J.; Samborski, S.; Monkova, K.; Debski, H. Analysis of mechanical properties of a lattice structure produced with the additive technology. Comp. Struct. 2020, 242, 112138. [Google Scholar] [CrossRef]
- Xue, B.; Peng, Y.X.; Ren, S.F.; Liu, N.N.; Zhang, Q. Investigation of impact resistance performance of pyramid lattice sandwich structure based on SPH-FEM. Comp. Struct. 2021, 261, 113561. [Google Scholar] [CrossRef]
- Saifullah, A.; Wang, L.; Barouni, A.; Giasin, K.; Lupton, C.; Jiang, C.; Zhang, Z.; Quaratino, A.; Dhakal, H.N. Low Velocity Impact (LVI) and Flexure-after-Impact (FAI) Behaviours of Rotationally Moulded Sandwich Structures. J. Mater. Res. Technol. 2021, 15, 3915–3927. [Google Scholar] [CrossRef]
- Błachut, J.; Magnucki, K. Strength, stability, and optimization of pressure vessels: Review of selected problems. Appl. Mech. Rev. 2008, 61, 060801. [Google Scholar] [CrossRef]
- Renhuai, L.; Jianghong, X. Development of nonlinear mechanics for laminated composite plates and shells. Chin. J. Theor. Appl. Mech. 2017, 49, 487–506. [Google Scholar] [CrossRef]
- Carrera, E.; Soave, M. Use of functionally graded material layers in a two-layered pressure vessel. J. Press. Vessel Technol. 2011, 133, 051202. [Google Scholar] [CrossRef]
- Magnucki, K.; Stasiewicz, P. Critical sizes of ground and underground horizontal cylindrical tanks. Thin-Walled Struct. 2003, 41, 317–327. [Google Scholar] [CrossRef]
- Brar, G.S.; Hari, Y.; Williams, D.K. Calculation of working pressure for cylindrical vessel under external pressure. In Proceedings of the ASME 2010 Pressure Vessels and Piping Division/K-PVP Conference, Bellevue, Washington, DC, USA, 18–22 July 2010. [Google Scholar] [CrossRef]
- Subbaiah, T.; Vijetha, P.; Marandi, B.; Sanjay, K.; Minakshi, M. Ionic Mass Transfer at Point Electrodes Located at Cathode Support Plate in an Electrorefining Cell in Presence of Rectangular Turbulent Promoters. Sustainability 2022, 14, 880. [Google Scholar] [CrossRef]
- Banghai, J.; Zhibin, L.; Fangyun, L. Failure mechanism of sandwich beams subjected to three-point bending. Comp. Struct. 2015, 133, 739–745. [Google Scholar] [CrossRef]
- Behravan, A.; Dejong, M.M.; Brand, A.S. Laboratory Study on Non-Destructive Evaluation of Polyethylene Liquid Storage Tanks by Thermographic and Ultrasonic Methods. CivilEng 2021, 2, 823–851. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Z.; Chen, F.; Guo, W.; Cao, G. Buckling of cylindrical shells with general axisymmetric thickness imperfections under external pressure. Eur. J. Mech. A/Solids 2013, 38, 90–99. [Google Scholar] [CrossRef]
- Yang, L.; Luo, Y.; Qiu, T.; Zheng, H.; Zeng, P. A novel analytical study on the buckling of cylindrical shells subjected to arbitrarily distributed external pressure. Eur. J. Mech. A/Solids 2022, 91, 104406. [Google Scholar] [CrossRef]
- Jiroutova, D. Methodology of Experimental Analysis of Long-Term Monitoring of Sandwich Composite Structure by Fibre-Optic Strain Gauges. Manuf. Technol. 2016, 16, 512–518. [Google Scholar] [CrossRef]
- Beall, G.L. Rotational Molding: Design, Materials, Tooling, and Processing; Hanser: Munich, Germany, 1998. [Google Scholar]
- Scott, D. Products and Applications—Composite and Thermoplastic Tanks, Silos and Other Vessels. Adv. Mater. Water Handl. 2000, 175–216. [Google Scholar] [CrossRef]
- Beňo, P.; Kozak, D.; Konjatić, P. Optimization of thin-walled constructions in CAE system ANSYS. Tech. Gaz. 2014, 21, 1051–1055. [Google Scholar]
- Mešić, E.; Muratović, E.; Redžepagić-Vražalica, L.; Pervan, N.; Muminović, A.J.; Delić, M.; Glušac, M. Experimental & FEM analysis of orthodontic mini-implant design on primary stability. Appl. Sci. 2021, 11, 5461. [Google Scholar] [CrossRef]
- Regassa, Y.; Gari, J.; Lemu, H.G. Composite Overwrapped Pressure Vessel Design Optimization Using Numerical Method. J. Compos. Sci. 2022, 6, 229. [Google Scholar] [CrossRef]
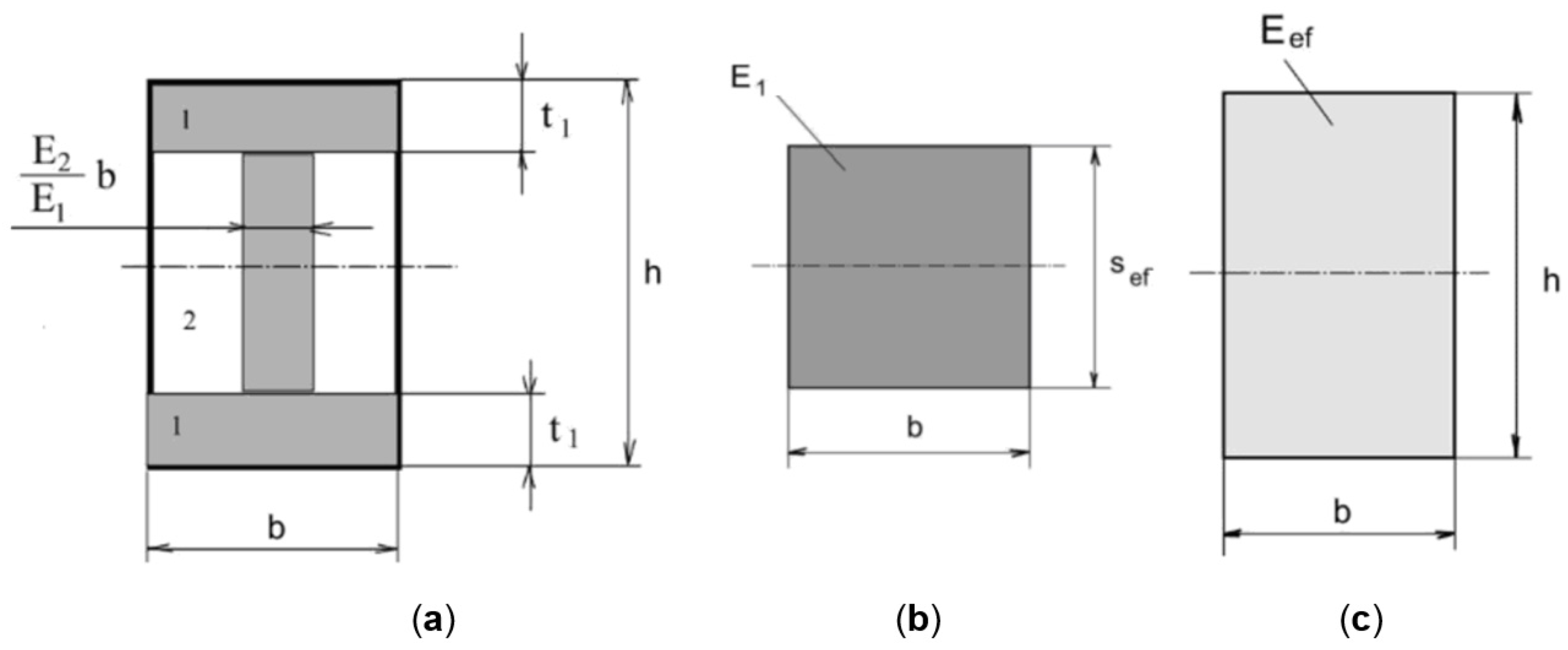
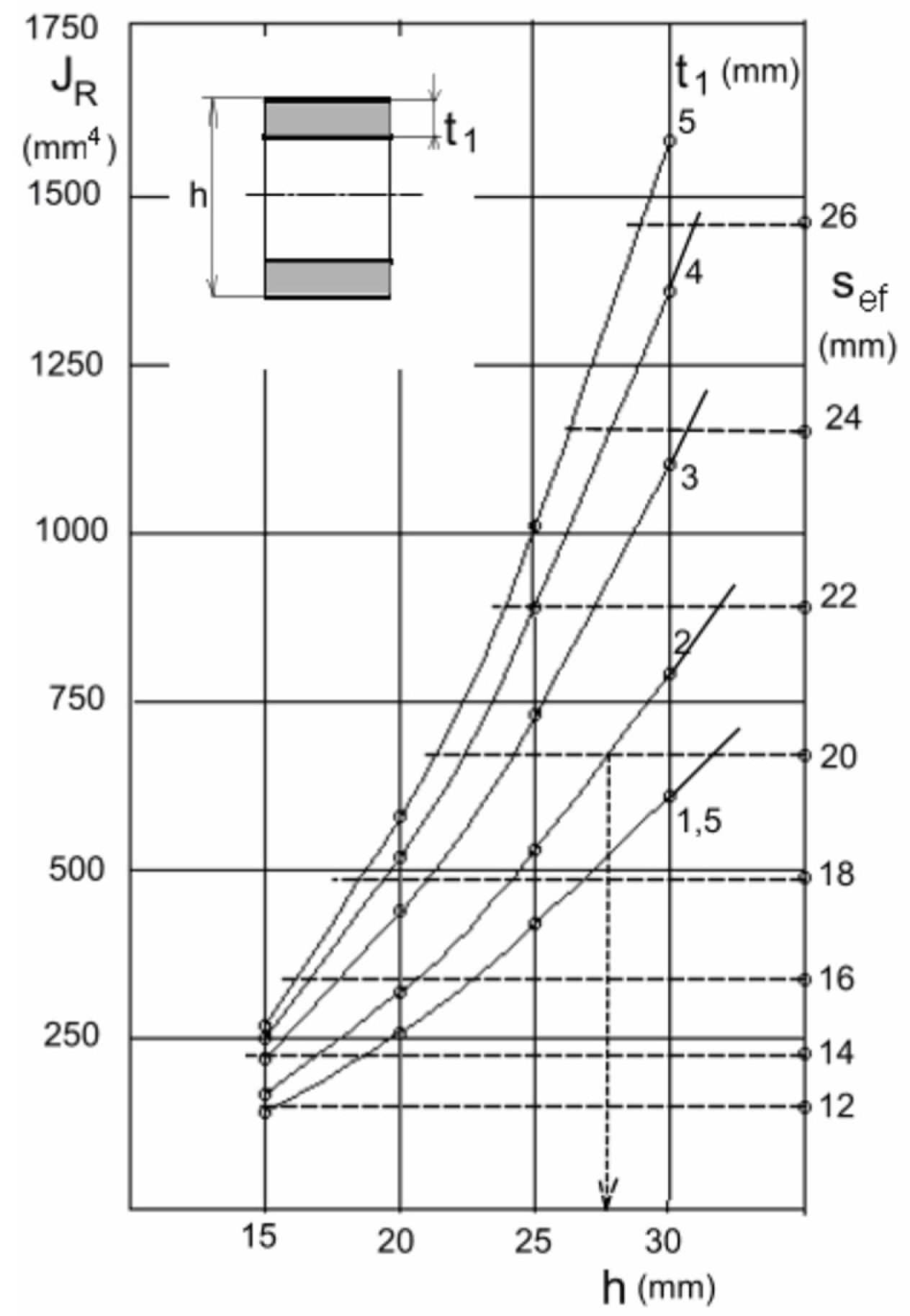



| Structure | h (mm) | t1 (mm) | t1OPT (mm) |
|---|---|---|---|
| 3v_7 | 7 | 2.4 | 1.32 |
| 3v_10 | 10 | 2.5 | 1.90 |
| 3v_11 | 11 | 1.6 | 2.08 |
| 3v_15 | 15 | 2.0 | 2.84 |
| Structure | Eef theoretical (MPa) | Eef experimental (MPa) | Difference δ (%) |
|---|---|---|---|
| 3v_7 | 678 | 640 | 5.94 |
| 3v_10 | 612 | 576 | 6.25 |
| 3v_11 | 450 | 422 | 6.64 |
| 3v_15 | 424 | 396 | 7.07 |
| Structure | sef (mm) | msef/m3v (-) |
|---|---|---|
| 3v_7 | 6.7 | 1.21 |
| 3v_10 | 8.9 | 1.12 |
| 3v_11 | 9.1 | 1.42 |
| 3v_15 | 12.1 | 1.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šuba, O.; Bílek, O.; Kubišová, M.; Pata, V.; Měřínská, D. Evaluation of the Flexural Rigidity of Underground Tanks Manufactured by Rotomolding. Appl. Sci. 2022, 12, 9276. https://doi.org/10.3390/app12189276
Šuba O, Bílek O, Kubišová M, Pata V, Měřínská D. Evaluation of the Flexural Rigidity of Underground Tanks Manufactured by Rotomolding. Applied Sciences. 2022; 12(18):9276. https://doi.org/10.3390/app12189276
Chicago/Turabian StyleŠuba, Oldřich, Ondřej Bílek, Milena Kubišová, Vladimír Pata, and Dagmar Měřínská. 2022. "Evaluation of the Flexural Rigidity of Underground Tanks Manufactured by Rotomolding" Applied Sciences 12, no. 18: 9276. https://doi.org/10.3390/app12189276
APA StyleŠuba, O., Bílek, O., Kubišová, M., Pata, V., & Měřínská, D. (2022). Evaluation of the Flexural Rigidity of Underground Tanks Manufactured by Rotomolding. Applied Sciences, 12(18), 9276. https://doi.org/10.3390/app12189276








