High Speed Decoding for High-Rate and Short-Length Reed–Muller Code Using Auto-Decoder
Abstract
:1. Introduction
2. RM Decoder Based on AD
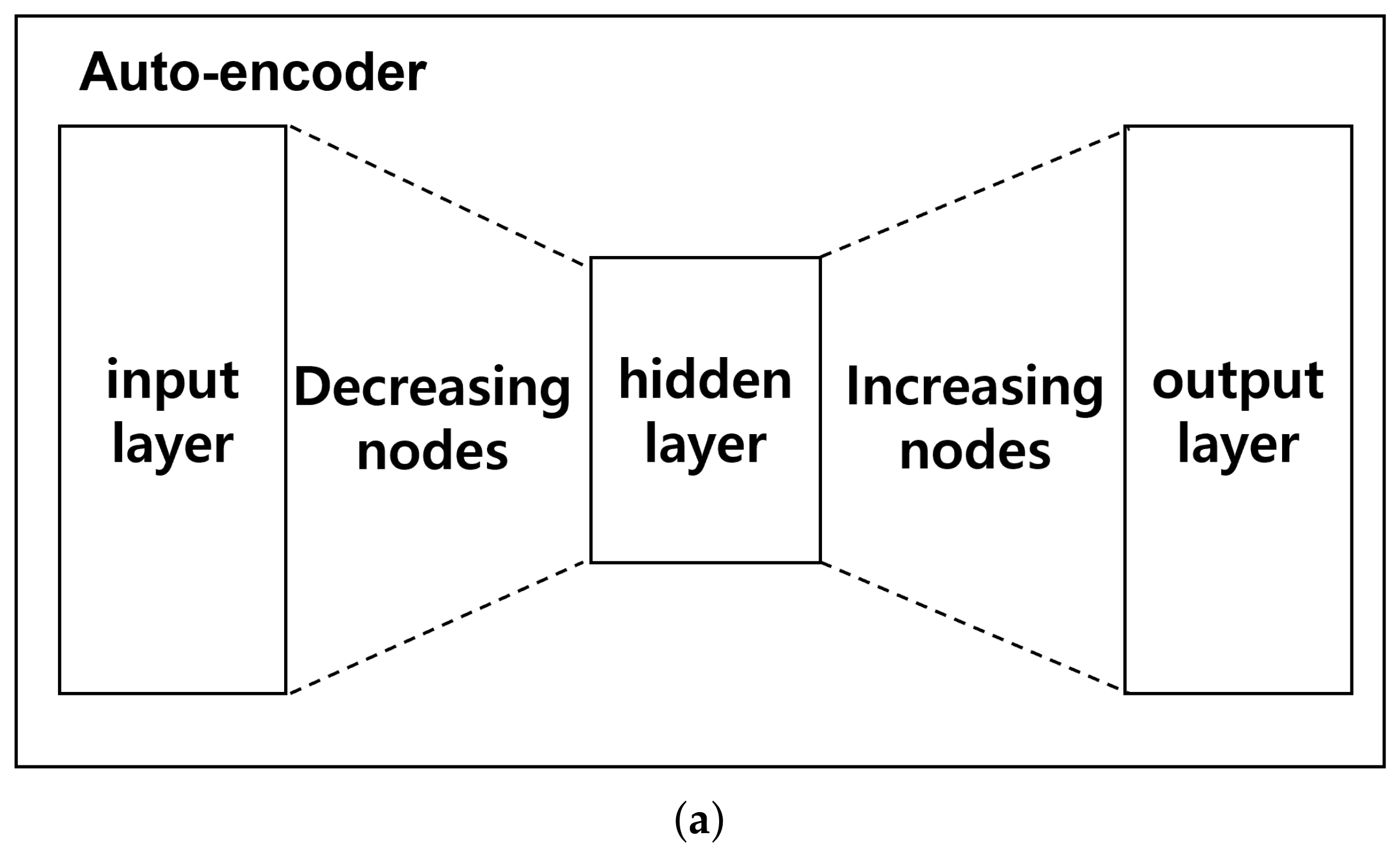
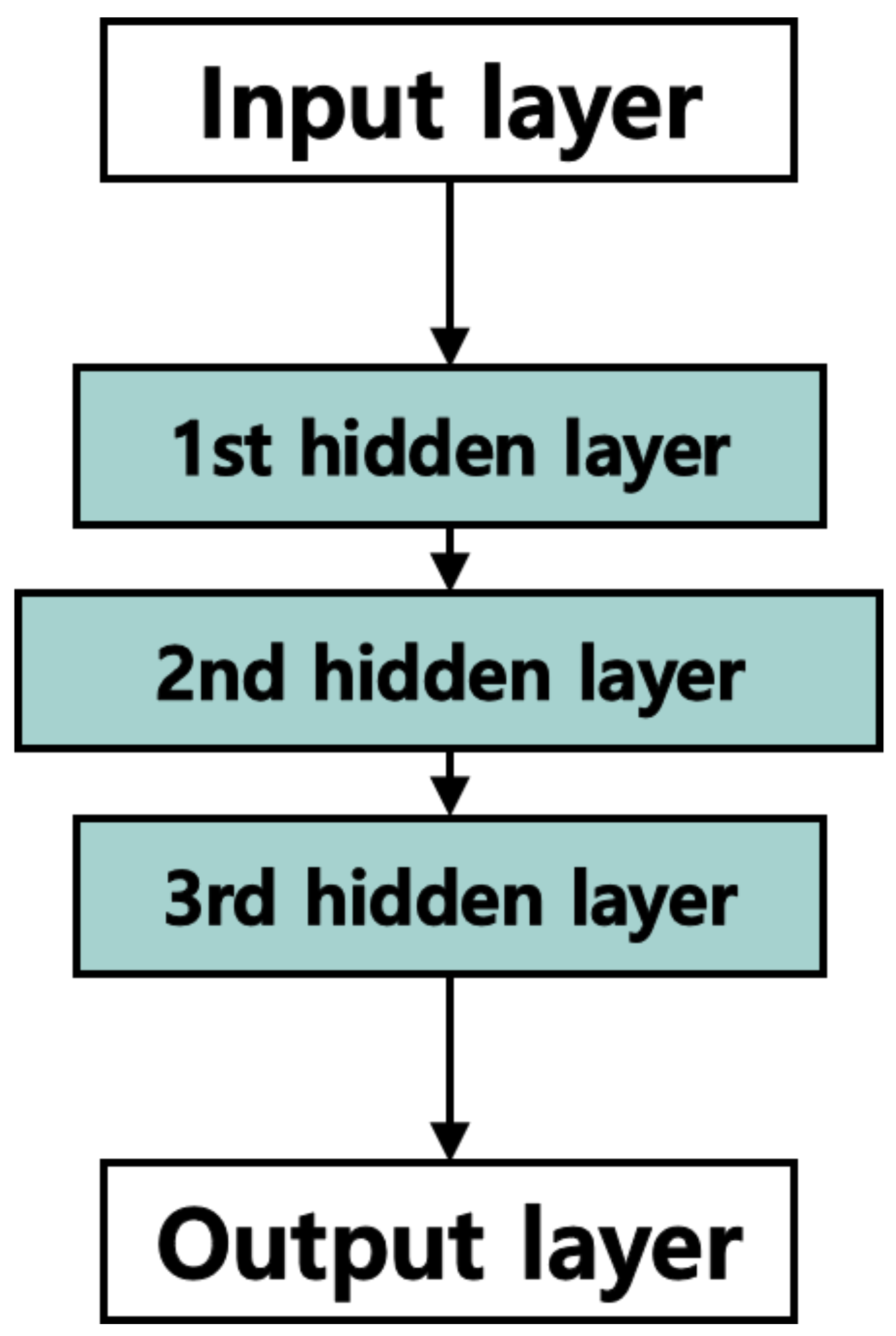
2.1. Auto-Decoder
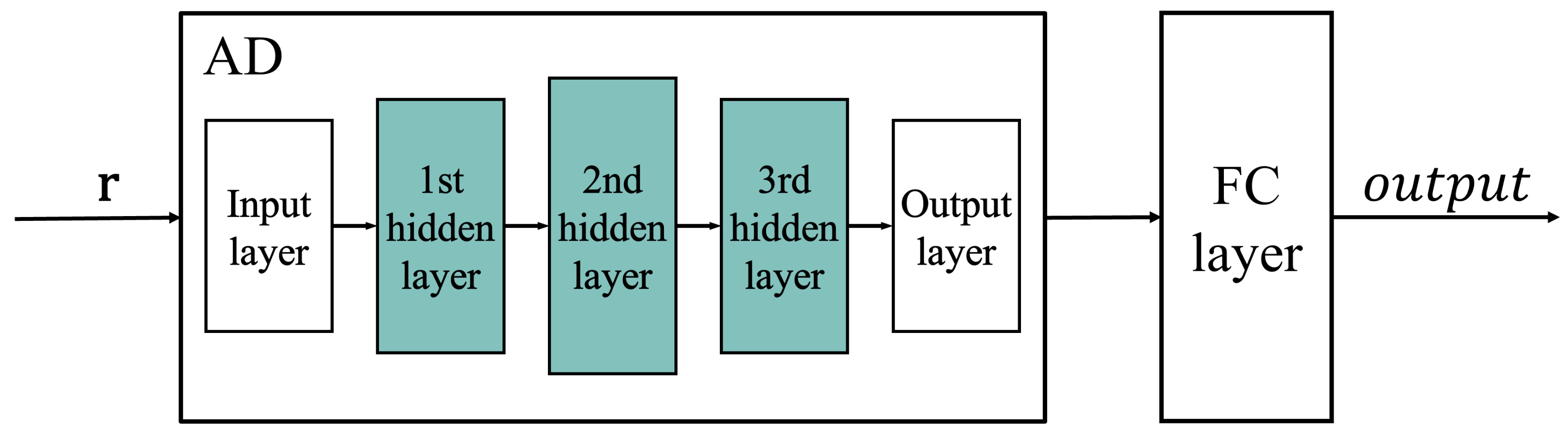
2.2. RM Decoding Model
2.3. Hyperparameters
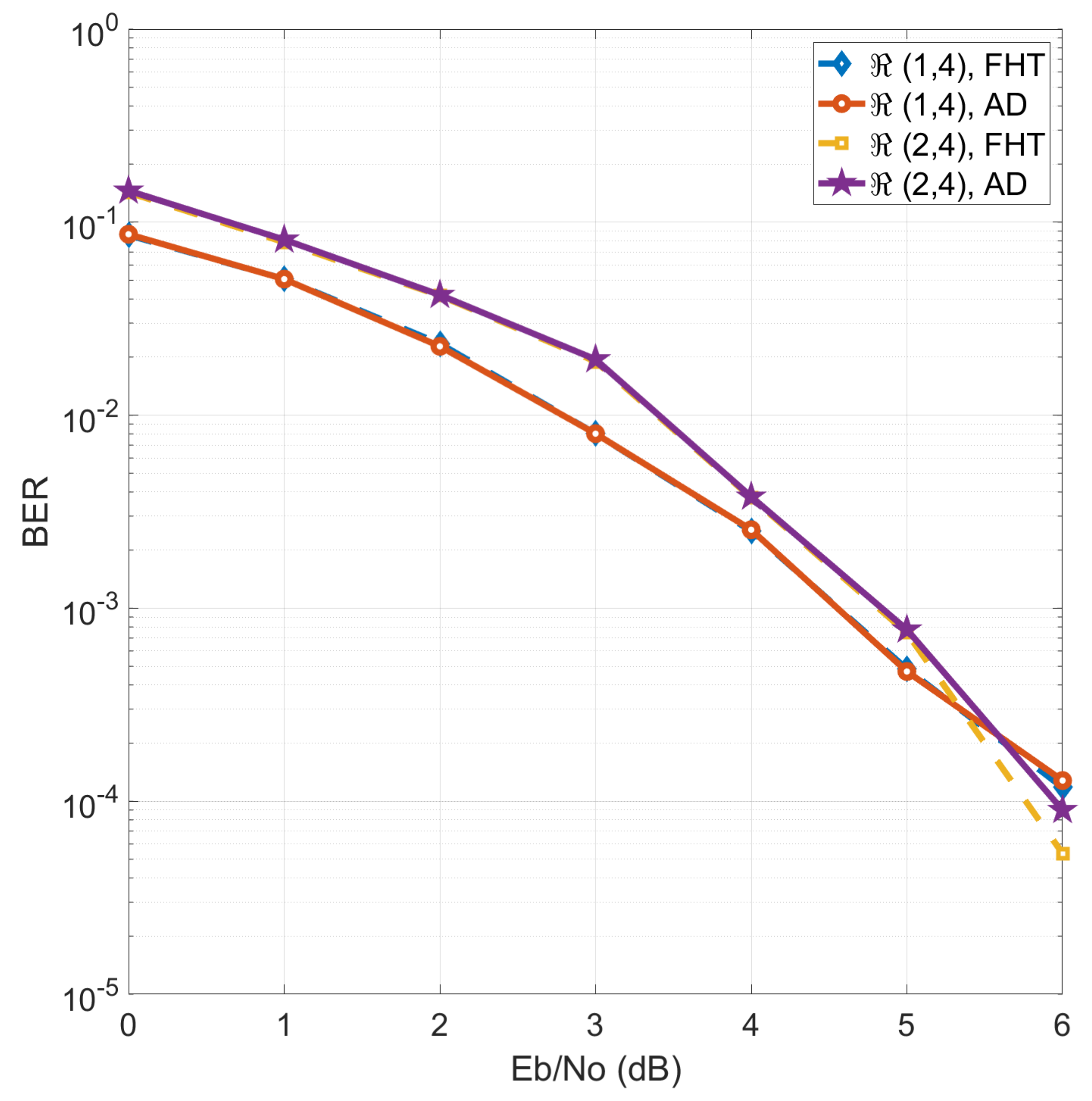
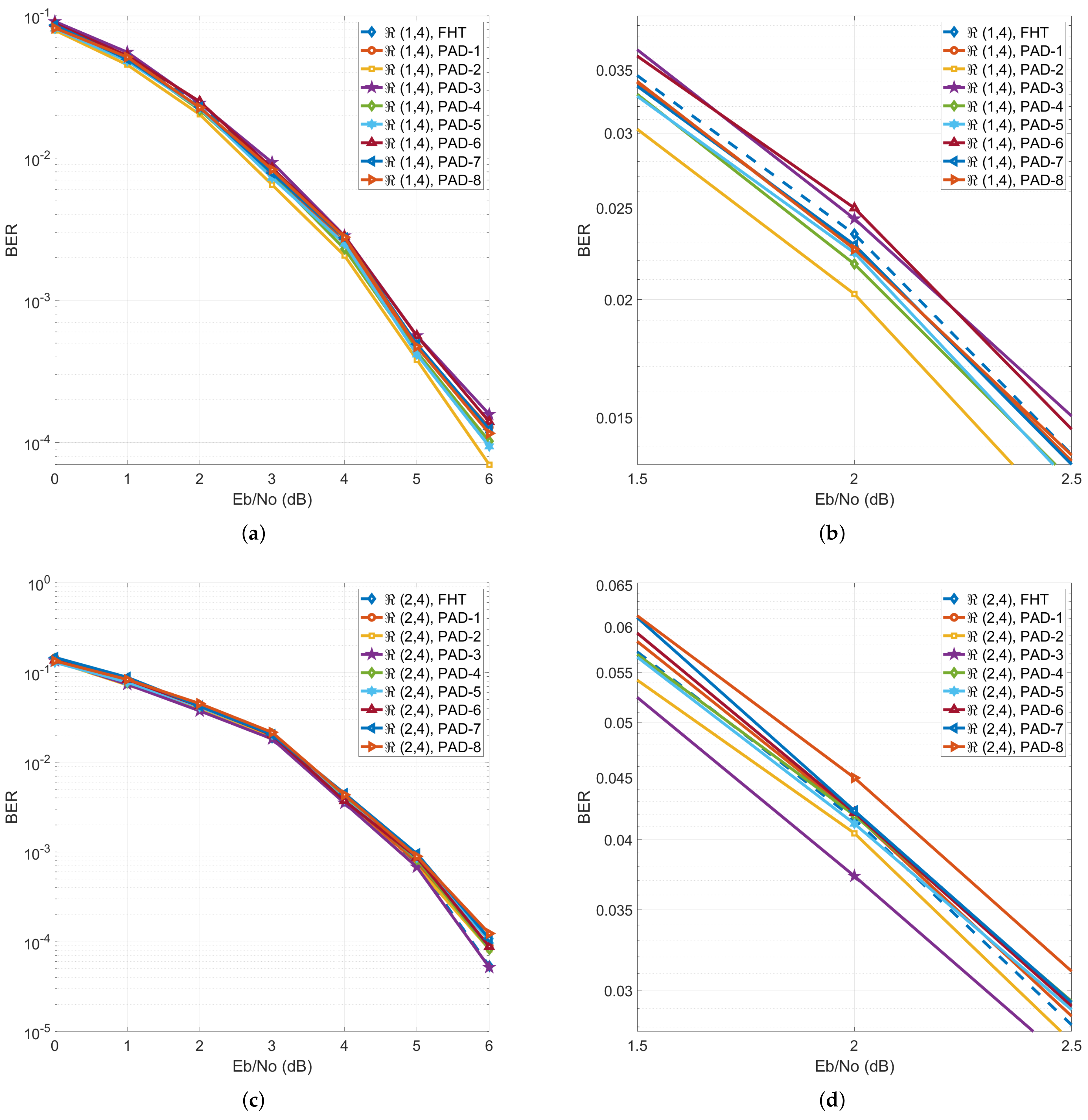
2.4. Performance Evaluation
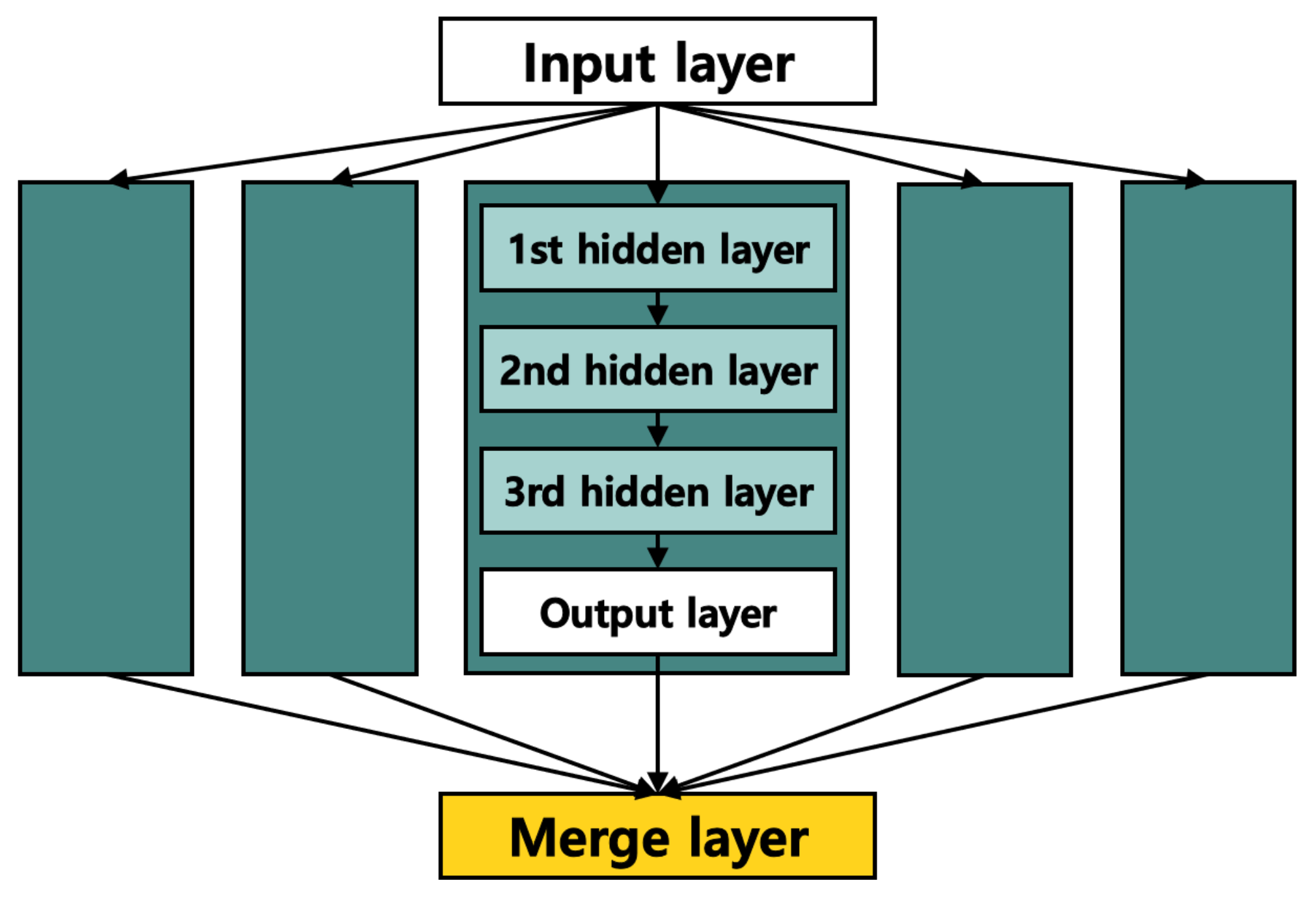
3. PAD
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, NIPS’12, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Jiang, K.; Lu, X. Natural language processing and its applications in machine translation: A diachronic review. In Proceedings of the 2020 IEEE 3rd International Conference of Safe Production and Informatization (IICSPI), Chongqing, China, 28–30 November 2020; pp. 210–214. [Google Scholar]
- Al-Qizwini, M.; Barjasteh, I.; Al-Qassab, H.; Radha, H. Deep learning algorithm for autonomous driving using GoogLeNet. In Proceedings of the IEEE Intelligent Vehicle Symposium, Los Angeles, CA, USA, 11–14 June 2017; pp. 89–96. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P. Extracting and composing robust features with denosing autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomuting 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Gondara, L. Medical Image Denoising Using Convolutional Denoising Autoencoders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 241–246. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- An, J.; Cho, S. Variational Autoencoder Based Anomaly Detection Using Reconstruction Probability; Technical Report; SNU Data Mining Center: Seoul, Korea, 2015. [Google Scholar]
- Ly, A.; Yao, Y.-D. A Review of Deep Learning in 5G Research: Channel Coding, Massive MIMO, Multiple Access, Resource Allocation, and Network Security. IEEE Open J. Commun. Soc. 2021, 2, 396–408. [Google Scholar] [CrossRef]
- Huang, X.-L.; Ma, X.; Hu, F. Machine learning and intelligent communications. Mob. Netw. Appl. 2018, 23, 68–70. [Google Scholar] [CrossRef]
- 3GPP TS36.212: Multiplexing and Channel Coding, V13.11.0 (2021-03). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2426 (accessed on 12 September 2022).
- 3GPP TS38.212: Multiplexing and Channel Coding, V15.10.0 (2020-09). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3214 (accessed on 12 September 2022).
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Abbas, R.; Huang, T.; Shahab, B.; Shirvanimoghaddam, M.; Li, Y.; Vucetic, B. Grant-free non-orthogonal multiple access: A key enabler for 6G-IoT. arXiv 2020, arXiv:2003.10257. [Google Scholar]
- Kang, I.; Lee, H.; Han, S.; Park, C.; Soh, J.; Song, Y. Reconstruction method for Reed-Muller codes using fast Hadamard transform. In Proceedings of the 13th International Conference on Advanced Communication Technology (ICACT2011), Gangwon, Korea, 13–16 February 2011; pp. 793–796. [Google Scholar]
- Dumer, I. Recursive decoding and its performance for low-rate Reed-Muller codes. IEEE Trans. Inf. Theory 2004, 50, 811–823. [Google Scholar] [CrossRef]
- Dumer, I.; Shabunov, K. Soft-decision decoding of Reed-Muller codes: Recursive lists. IEEE Trans. Inf. Theory 2006, 52, 1260–1266. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Costello, D.J. Error Control Coding: Fundamentals and Applications; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1983. [Google Scholar]
- Gruber, T.; Cammerer, S.; Hoydis, J.; Brick, S.t. On deep learning-based channel coding. In Proceedings of the IEEE 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]


| Symbol | Description |
|---|---|
| n | length of codeword (bits) |
| r, m | parameters of RM code () |
| k | length of message (bits) |
| N | number of nodes in FC layer |
| one-hot encoding vector | |
| message vector | |
| output of FC layer | |
| S | number of validation sets |
| , | SNRs for the training set and the s-th validation set |
| Layer | Number of Nodes |
|---|---|
| input | n |
| 1st hidden | |
| 2nd hidden | |
| 3rd hidden | |
| output | n |
| loss function | cross-entropy |
| optimizer | Adam |
| training data set | |
| epoch | |
| batch size |
| Training SNR () | 0 | 1 | 2 | 3 |
| NVE | 0.972 | 0.945 | 0.982 | 1.138 |
| Training SNR () | 4 | 5 | 6 | 7 |
| NVE | 0.981 | 1.320 | 1.529 | 2.489 |
| RM Code | Method | Time (ms) |
|---|---|---|
| FHT | 0.6012 | |
| AD | 0.3327 | |
| FHT | 46.625 | |
| AD | 0.3704 |
| Layer | Number of Nodes | ||||
|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | |
| CAD | CAD | CAD | CAD | CAD | |
| 1st hidden | n | ||||
| 2nd hidden | n | ||||
| 3rd hidden | n | ||||
| output | n | n | n | n | n |
| Method | Time (ms) | Parameters | ||
|---|---|---|---|---|
| FHT | 0.6012 | 46.625 | - | - |
| PAD-1 | 0.3327 | 0.3704 | 5808 | 40,080 |
| PAD-2 | 0.3472 | 0.3785 | 6896 | 41,168 |
| PAD-3 | 0.3838 | 0.4037 | 22,512 | 56,784 |
| PAD-4 | 0.4075 | 0.4367 | 57,728 | 92,000 |
| PAD-5 | 0.4520 | 0.4854 | 124,864 | 159,136 |
| PAD-6 | 0.4972 | 0.5241 | 239,312 | 273,584 |
| PAD-7 | 0.5508 | 0.6225 | 419,536 | 388,032 |
| PAD-8 | 0.6198 | 0.6352 | 687,072 | 502,480 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.W.; Song, Y.J. High Speed Decoding for High-Rate and Short-Length Reed–Muller Code Using Auto-Decoder. Appl. Sci. 2022, 12, 9225. https://doi.org/10.3390/app12189225
Cho HW, Song YJ. High Speed Decoding for High-Rate and Short-Length Reed–Muller Code Using Auto-Decoder. Applied Sciences. 2022; 12(18):9225. https://doi.org/10.3390/app12189225
Chicago/Turabian StyleCho, Hyun Woo, and Young Joon Song. 2022. "High Speed Decoding for High-Rate and Short-Length Reed–Muller Code Using Auto-Decoder" Applied Sciences 12, no. 18: 9225. https://doi.org/10.3390/app12189225
APA StyleCho, H. W., & Song, Y. J. (2022). High Speed Decoding for High-Rate and Short-Length Reed–Muller Code Using Auto-Decoder. Applied Sciences, 12(18), 9225. https://doi.org/10.3390/app12189225






