Prediction and Surveillance Sampling Assessment in Plant Nurseries and Fields
Abstract
:1. Background
2. Method
2.1. Bayesian Kriging for a Binary Response
2.2. Implementation of Bayesian Kriging with INLA
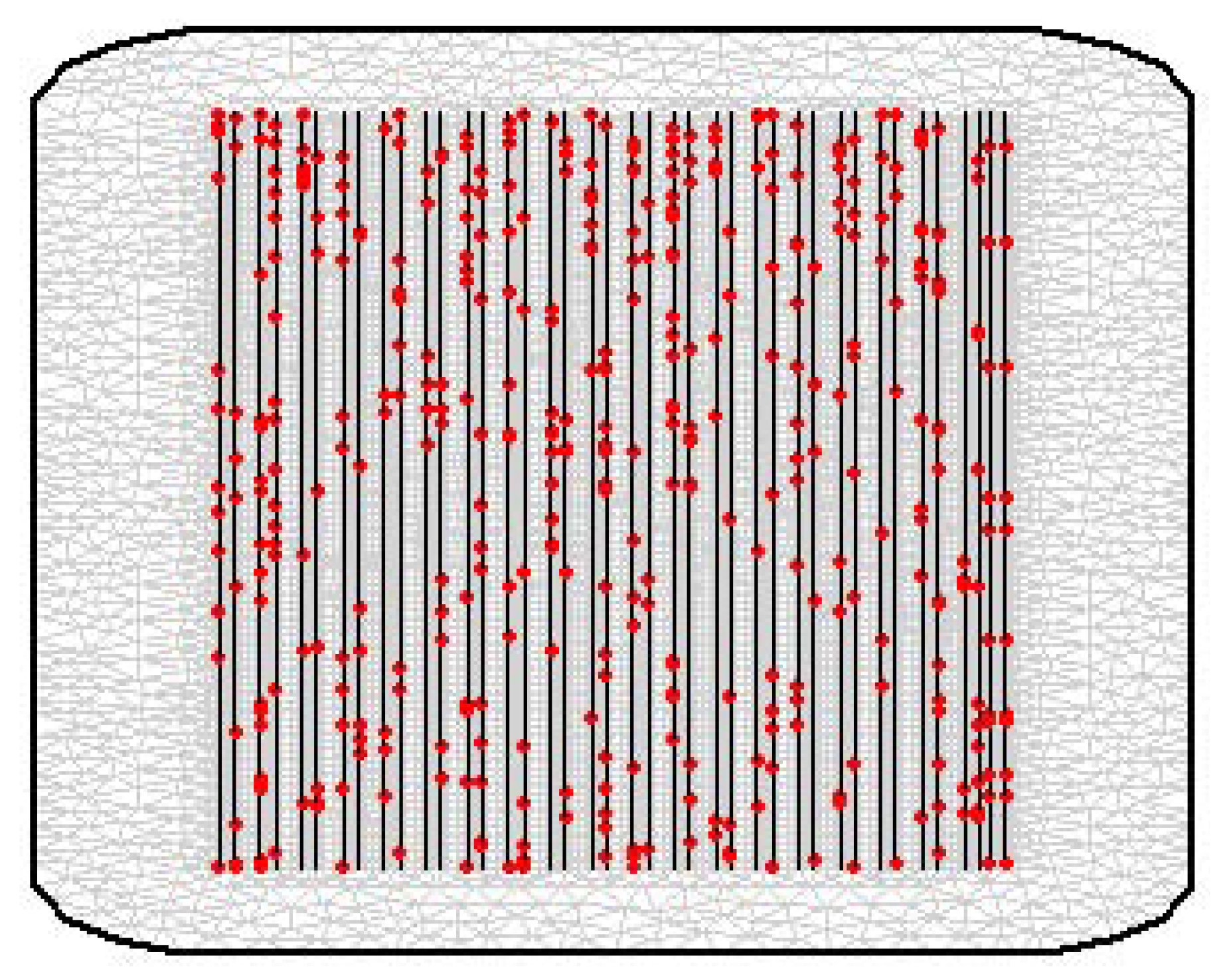
2.3. Research Object
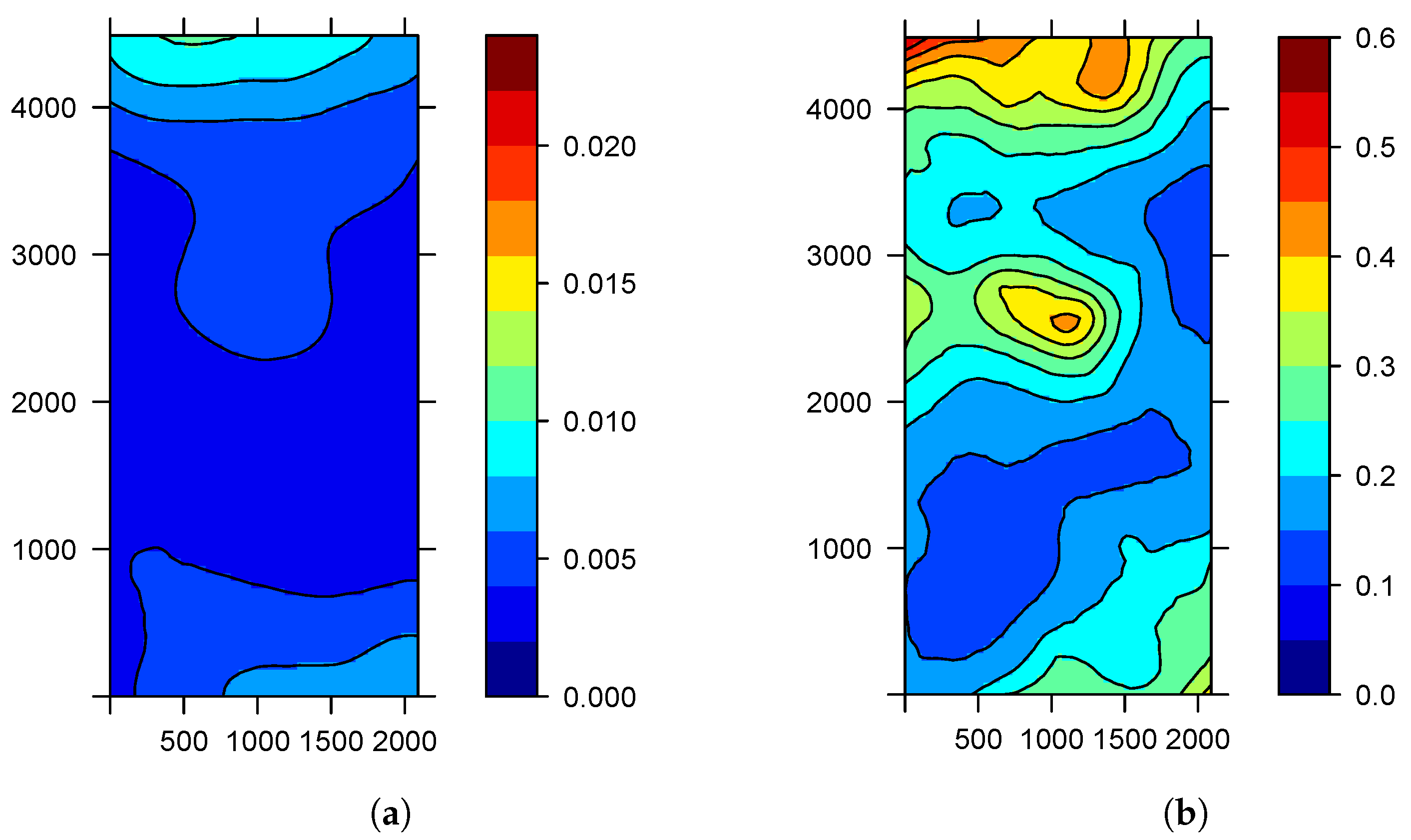
3. Results
3.1. Sampling Assessment in the Study of Agricultural Diseases
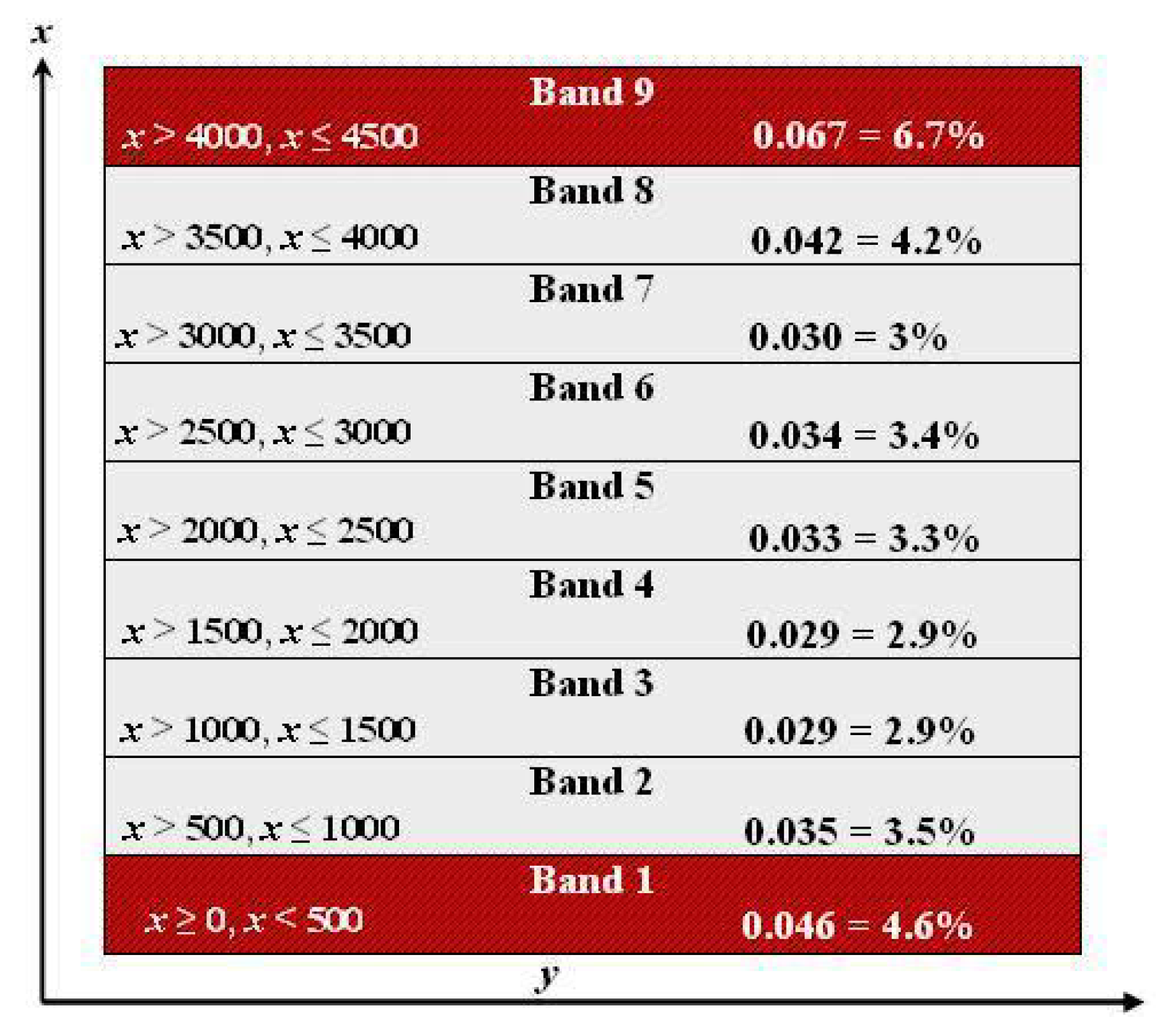
3.2. Calibration Sampling
3.3. Application of the Sampling Methods
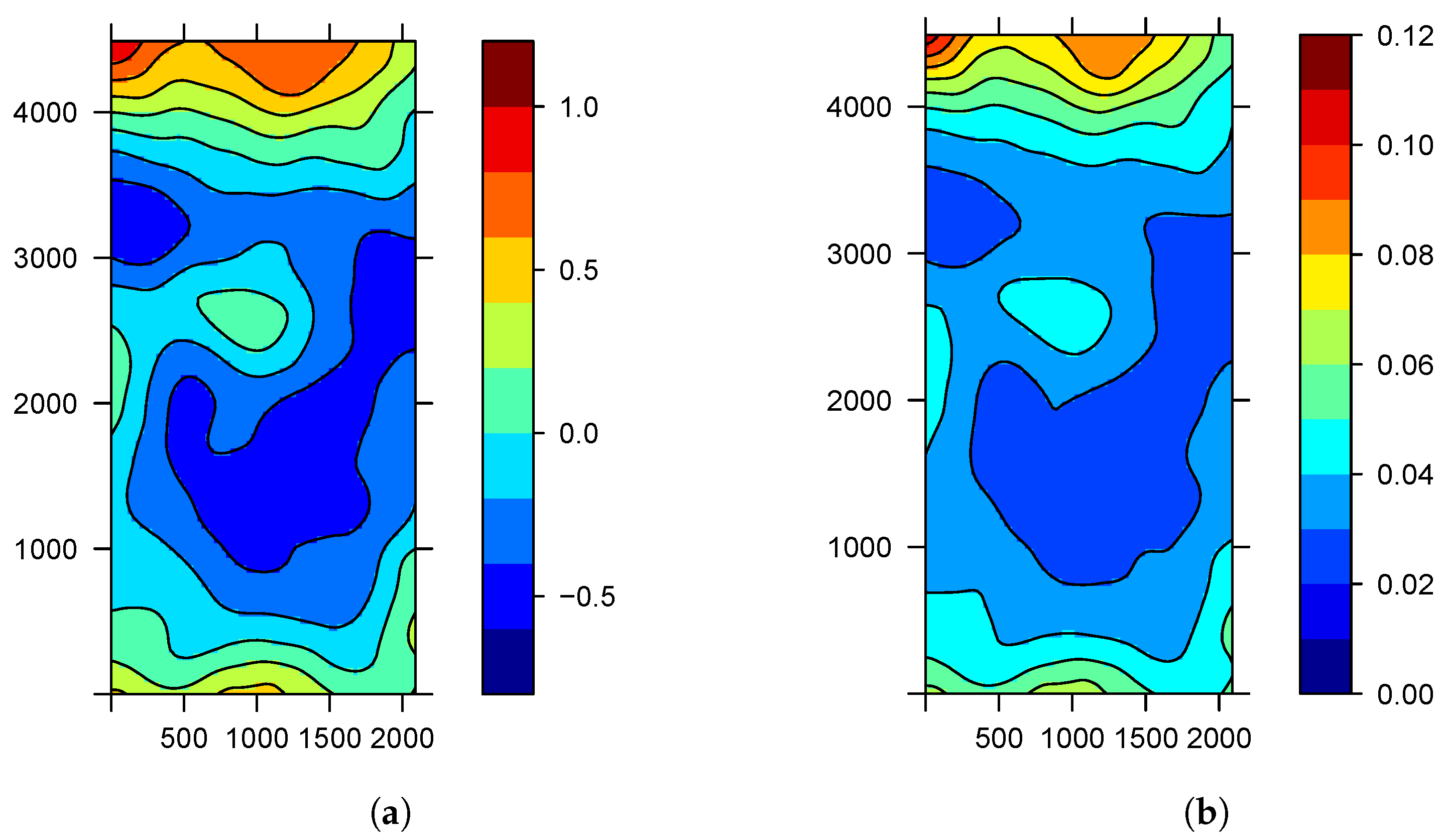
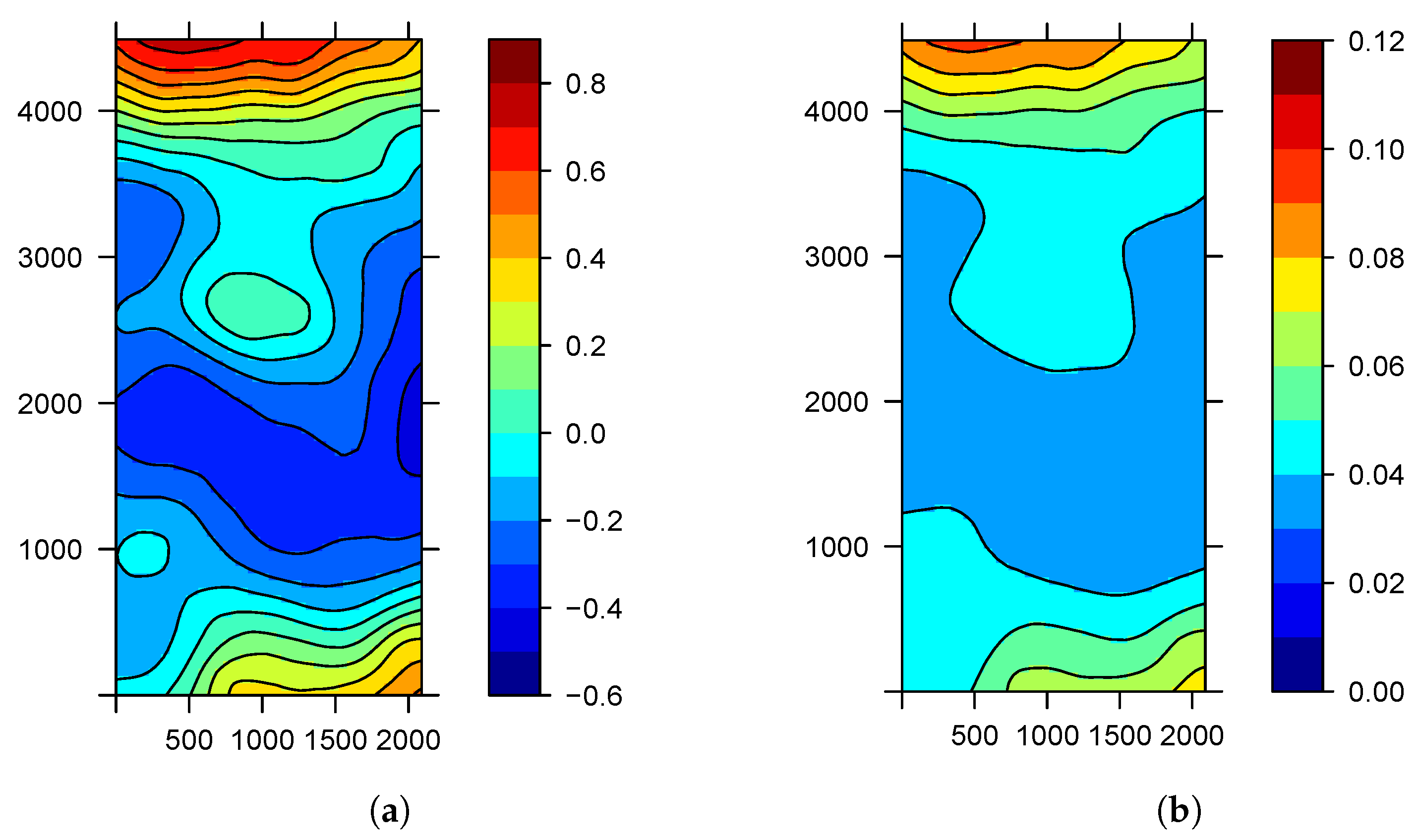
3.4. Estimation and Prediction from Sampling Assessment
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABSE | Absolute Square Error |
| CTV | Citrus Tristeza Virus |
| CV | Coefficient of Variation |
| DIC | Deviance Information Criterion |
| GF | Gaussian Field |
| GMRF | Gaussian Markov Random Field |
| INLA | Intregrated Nested Laplace Approximation |
| MCMC | Markov Chain Monte Carlo |
| MSE | Mean Square Error |
| PIT | Probability Integral Transform |
| SPDE | Stochastic Partial Differential Equation |
| STAR | Structured Additive Regression |
References
- Banerjee, S.; Carlin, B.P.; Gelf, A.E. Hierarchical Modeling and Analysis for Spatial Data, 2nd ed.; Chapman & Hall/CRC Monographs on Statistics & Applied Probability; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Chien, L.C.; Bangdiwala, S.I. The implementation of Bayesian structural additive regression models in multi-city time series air pollution and human health studies. Stoch. Environ. Res. Risk Assess. 2012, 26, 1041–1051. [Google Scholar] [CrossRef]
- King, R.; Illian, J.B.; King, S.E.; Nightingale, G.F.; Hendrichsen, D.K. A Bayesian Approach to Fitting Gibbs Processes with Temporal Random Effects. J. Agric. Biol. Environ. Stat. 2012, 17, 601–622. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer: New York, NY, USA, 1999. [Google Scholar]
- Diggle, P.J.; Ribeiro, P.J. Model-based Geostatistics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Lindgren, F.; Bolin, D.; Rue, H. The SPDE approach for Gaussian and non-Gaussian fields: 10 years and still running. Spat. Stat. 2022, 50, 100599. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The SPDE approach (with discussion). J. R. Stat. Soc. Ser. B 2011, 73, 423–498. [Google Scholar] [CrossRef]
- Moraga, P.; Dean, C.; Inoue, J.; Morawiecki, P.; Noureen, S.R.; Wang, F. Bayesian spatial modelling of geostatistical data using INLA and SPDE methods: A case study predicting malaria risk in Mozambique. Spat Spatio-Temporal Epidemiol. 2021, 39, 100440. [Google Scholar] [CrossRef] [PubMed]
- Roos, M.; Held, L. Sensitivity analysis in Bayesian generalized linear mixed models for binary data. Int. Soc. Bayesian Anal. 2011, 6, 259–278. [Google Scholar] [CrossRef]
- Finley, A.O.; Banerjee, S.; Ek, A.R.; McRoberts, R.E. Bayesian multivariate process modeling for prediction of forest attributes. J. Agric. Biol. Environ. Stat. 2008, 13, 60–83. [Google Scholar] [CrossRef]
- Gaudard, M.; Ramsey, P.; Stephens, M. Interactive Data Mining and Design of Experiments: The JMP® Partition and Custom Design Plataforms, Group. 26. 2006. Available online: http://northhavengroup.com/pdfs/PartitionandDOEFinalCopy.pdf (accessed on 1 August 2022).
- Diggle, P.J.; Tawn, J.A.; Moyeed, R.A. Model-based geostatistics (with discussion). J. R. Stat. Soc. Ser. C (Appl. Stat.) 1998, 47, 299–350. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S. Approximate Bayesian inference for hierarchical Gaussian Markov random fields models. J. Stat. Plan. Inference 2007, 137, 3177–3192. [Google Scholar] [CrossRef]
- Tierney, L.; Kadane, J.B. Accurate approximations for posterior moments and marginal densities. J. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Guttorp, P.; Gneiting, T. Studies in the history of probability and statistics XLIX on the Matern correlation family. Biometrika 2006, 93, 989–995. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Thomas, A.; Best, N.; Lunn, D. WinBUGS User Manual; Version 1.4; MRC Biostatistics Unit, Institute of Public Health and Department of Epidemiology and Public Health, Imperial College School of Medicine: London, UK, 2003; Available online: https://www.mrc-bsu.cam.ac.uk/software/bugs/ (accessed on 1 February 2019).
- Munoz, F.M.; Pennino, M.G.; Conesa, D.; López-Quílez, A.; Bellido, J.M. Estimation and prediction of the spatial occurrence of fish species using Bayesian latent Gaussian model. Stoch. Environ. Res. Risk Assess. 2013, 27, 1171–1180. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: http://www.R-project.org (accessed on 12 August 2022).
- Rue, H.; Riebler, A.; Sørbye, S.H.; Illian, J.B.; Simpson, D.P.; Lindgren, F.K. Bayesian computing with INLA: A review. Annu. Rev. Stat. Its Appl. 2017, 4, 395–421. [Google Scholar] [CrossRef]
- Gottwald, T.R.; DaGraça, J.V.; Bassanezi, R.B. Citrus huanglongbing: The pathogen and its impact. Plant Health Prog. 2007, 8, 31. [Google Scholar] [CrossRef]
- Lezama-Ochoa, N.; Pennino, M.G.; Hall, M.; López, J.; Murua, H. Using a Bayesian modelling approach (INLA-SPDE) to predict the occurrence of the Spinetail Devil Ray (Mobular mobular). Sci. Rep. 2020, 10, 18822. [Google Scholar] [CrossRef] [PubMed]
- Kifle, Y.W.; Hens, N.; Faes, C. Using additive and coupled spatiotemporal SPDE models: A flexible illustration for predicting occurrence of Culicoides species. Spat. Spatio-Temporal Epidemiol. 2017, 23, 11–34. [Google Scholar] [CrossRef] [PubMed]
- Fioravanti, G.; Martino, S.; Carmeletti, M.; Cattani, G. Spatio-temporal modelling of PM10 daily concentrations in Italy using the SPDE approach. Atmos. Environ. 2021, 248, 118192. [Google Scholar] [CrossRef]

| Parameter | Mean | S.D. | |||
|---|---|---|---|---|---|
| (Intercept) | −3.13 | 0.31 | −3.77 | −3.14 | −2.45 |
| 0.00217 | 0.0063 | 0.00074 | 0.0019 | 0.0049 | |
| (cm) | 3.55 | 0.0153 | 1.198 | 3.12 | 8.38 |
| Measure | Sample 10% | Sample 15% | Sample 20% | Sample 25% |
|---|---|---|---|---|
| 0.0058 | 0.0084 | 0.0044 | 0.0029 | |
| (cm) | 6.26 | 3.83 | 8.39 | 12.44 |
| (cm) | 19.44 | 11.81 | 6.76 | 4.82 |
| MSE | 3.1419 | 2.8638 | 2.8448 | 2.4847 |
| ABSE | 0.0134 | 0.0116 | 0.0118 | 0.0106 |
| CV | 0.2025 | 0.2183 | 0.2075 | 0.1689 |
| Measure | Sample 50% | Sample 25% | Sample 20% | Sample 9% |
|---|---|---|---|---|
| 0.0032 | 0.0046 | 0.0036 | 0.0026 | |
| (cm) | 8.58 | 6.03 | 7.70 | 10.81 |
| (cm) | 7.98 | 4.33 | 4.20 | 4.80 |
| MSE | 2.4409 | 2.7979 | 2.9392 | 3.7203 |
| ABSE | 0.0109 | 0.0109 | 0.0110 | 0.0130 |
| CV | 0.1775 | 0.2017 | 0.2391 | 0.3313 |
| Block 1 | Block 2 | Block 3 | Total | |
|---|---|---|---|---|
| 100% | 20% | 20% | 10% | 12.23% |
| N | 1240 | 1200 | 8480 | 10,920 |
| n | 248 | 240 | 848 | 1336 |
| 100% | 25% | 25% | 15% | 16.67% |
| N | 1240 | 1200 | 8480 | 10,920 |
| n | 310 | 300 | 1211 | 1821 |
| 100% | 30% | 30% | 20% | 22.97% |
| N | 1240 | 1200 | 8480 | 10,920 |
| n | 413 | 400 | 1696 | 2509 |
| 100% | 35% | 35% | 25% | 30.58% |
| N | 1240 | 1200 | 8480 | 10,920 |
| n | 620 | 600 | 2120 | 3340 |
| Measure | 20%, 20%, 10% | 25%, 25%, 15% | 30%, 30%, 20% | 35%, 35%, 25% |
|---|---|---|---|---|
| 0.0042 | 0.0031 | 0.0024 | 0.0091 | |
| (cm) | 6.98 | 10.36 | 14.68 | 9.35 |
| (cm) | 9.82 | 3.80 | 3.917 | 2.91 |
| MSE | 8.2617 | 4.0836 | 3.4858 | 3.0376 |
| ABSE | 0.0195 | 0.0140 | 0.0130 | 0.0124 |
| CV | 0.3985 | 0.3264 | 0.2969 | 0.2505 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monsalve, N.C.; López-Quílez, A. Prediction and Surveillance Sampling Assessment in Plant Nurseries and Fields. Appl. Sci. 2022, 12, 9005. https://doi.org/10.3390/app12189005
Monsalve NC, López-Quílez A. Prediction and Surveillance Sampling Assessment in Plant Nurseries and Fields. Applied Sciences. 2022; 12(18):9005. https://doi.org/10.3390/app12189005
Chicago/Turabian StyleMonsalve, Nora C., and Antonio López-Quílez. 2022. "Prediction and Surveillance Sampling Assessment in Plant Nurseries and Fields" Applied Sciences 12, no. 18: 9005. https://doi.org/10.3390/app12189005
APA StyleMonsalve, N. C., & López-Quílez, A. (2022). Prediction and Surveillance Sampling Assessment in Plant Nurseries and Fields. Applied Sciences, 12(18), 9005. https://doi.org/10.3390/app12189005







