Digital Watermarking System for Copyright Protection and Authentication of Images Using Cryptographic Techniques

Abstract

Digital images are transferred with ease through the network. Many users are using the images without the knowledge of the owners. Therefore, a novel watermarking scheme is proposed to ensure copyright protection and authentication of images using cryptography techniques. Here, a quick response (QR) image is generated for a watermark image that contains public and private keys prepared using a cryptosystem. Later, this QR image is scrambled using a chaotic logistic map. The public and private keys are used to cipher and decipher the data. Next, the scrambled QR watermark is embedded into a color image using a single-level discrete wavelet transform followed by singular value decomposition using the key value. Finally, the inverse process is applied to extract the watermark. The proposed method is validated using various image processing attacks. The results are then compared with state-of-the-art watermarking schemes. The experimental results show that the scheme provides good results in terms of robustness and imperceptibility.

1. Introduction

Recently, with the development of long-range informal communication on the web, the capacity and dissemination of interactive media content have become extremely simple. On the other hand, this simplicity has led to the need for copyright protection, blocking information theft, and data genuineness [1,2].

To handle the above issues, digital watermarking has emerged as an appropriate solution. Digital watermarking is a way of embedding a watermark into a significant image/media. A watermark acts as copyright data, shielding advanced information from illicit replication and conveyance [3,4]. A watermark is a sort of marker clandestinely inserted in a signal (audio, video, or image information). A watermark embedded into media may or may not relate to it. Watermarks are utilized to check the realness or uprightness of the watermarked signal [5,6].

Watermarking is a strategy that is broadly utilized and ceaselessly created by utilizing different strategies and executions [7,8]. In the proposed method, discrete wavelet transform (DWT) and singular value decomposition (SVD) techniques are combined to accomplish the vigor and imperceptibility of the watermark. The scheme is generally achievable for clients and has an oddity edge over the other existing digital watermarking methods [9]. The idea of embedding the watermark information is to prevent intruders or other members from claiming to be the rightful owner of the data [10,11].

The literature review is provided in Section 2. The methods used in the proposed scheme are provided in Section 3. Section 4 provides the process of embedding and extraction of the propounded method. Section 5 presents the experimental results with various images, attacks, and metrics. Finally, the conclusion is provided in Section 6.

2. Literature Survey

Concealing information in other media is extremely old, as depicted on account of steganography. The term advanced watermarking first appeared in 1993 when Tirkel et al. [12] introduced two methods to conceal information in pictures.

In the recent past, telehealth systems have increasingly improved watermarking approaches [13]. These approaches provide authentication and security and give optimal bandwidth utilization, another essential criterion of the telehealth communication system. In [13], the authors proposed a watermarking scheme (WS) for telehealth applications. This method embedded a signature watermark image and patient report of 80 characters in length using lifting wavelet transform (LWT) and discrete cosine transform (DCT) schemes. This work decomposed the host image into subbands using LWT, and DCT further transformed the significant subbands. Simultaneously, the patient report and the signature watermark were encrypted and embedded into the final DCT-transformed subbands. The reverse process was applied to extract the watermarked information.

A blend of watermarking, cryptography, and error-correcting code for electronic patient records (EPRs) is proposed in the method [14]. The watermarking image (WI) and EPR are embedded in this method after performing DWT and turbo encoding, respectively. Later, an inverse DWT is applied to this embedded data and processed to obtain an encrypted watermark using pallier encryption. Simultaneously, the cover image is encrypted using a pallier cryptosystem to obtain an encrypted cover image. Finally, these encrypted images (cover and watermark) are again embedded and sent via a communication channel. The reverse process is held at the destination to obtain the desired information.

A crypto watermarking scheme for telemedical applications is proposed in [15]. In [16], a blind WS is framed to hide EPR data in the retinal image for telehealth applications. The retinal image is decomposed into subbands, and the lower subband (LL) is subjected to SVD; the EPR watermark is placed into this band. At the initial step, a bit-plane extraction is performed on the host image, and the watermark image is integrated into the host image using a chaotic mapping scheme. Further, the watermarked image (WI) is encrypted using the fractional Hartley transform to obtain the crypto-watermarked image.

Another work in [17] is proposed for the detection of tampered medical images using a crypto WS. However, it is a non-blind watermarking scheme, where the EPR is embedded into the radiological images for authentication and security. The approach is based on DCT and compressive sensing (CS), where CS is used to encrypt the watermark data and DCT is applied to a host image. In [18], the authors attempted to embed patients’ two biometrics, fingerprints and face, using a two-stage watermarking approach. Initially, the fingerprint was encrypted using minutiae extraction and encoding into the original face image and a key. Later, the watermarked image was further encrypted and embedded into the original fingerprint to obtain the second level of the WI. Finally, the watermark was embedded by combining the DCT subbands and the encrypted watermark image.

All the literature above is related to image watermarking with different transform domains. They follow different types of watermarking approaches based on extraction, and in embedding the watermark, different transformation techniques methods are utilized (most commonly, DWT, DCT, and LWT). Previous watermarking schemes are weak in terms of the security of watermark data, which inspired us to add crypto techniques to protect the watermark. The proposed watermarking approach can overcome authentication problems by embedding the QR code watermark. The proposed scheme converts the text information to a scrambled QR image using a chaotic logistic map. The public and private keys are used to cipher and decipher the data. As the images are vulnerable to attacks, the proposed method overcomes this by combining DWT and SVD using adaptive embedding factor values for images. Four subbands in the proposed scheme, LL, LH, HL, and HH, are obtained after one level LWT. LL is selected based on its efficient properties. The LL subband is again decomposed using QR, and then embedding of the scrambled QR code watermark. The motivation behind this combination is to enhance the imperceptibility and robustness. The robustness improvements are provided by applying DWT coefficients. The watermark is embedded by modifying the coefficients of DWT using secret keys. The inverse process is utilized at the receiver end to retrieve the watermark data.

3. Preliminaries

This section gives the details of the techniques used in the propounded scheme. The propounded scheme consists of two modules: embedding and extraction. The depiction of these two processes is shown in sub sections. As the transform domain is more robust than the spatial domain, the DWT algorithm is utilized in the embedding process as it has better reconstruction without losing information. SVD is utilized in combination with DWT to overcome noise and compression attacks. Moreover, a cryptographic algorithm (RSA) is used to verify the algorithm’s robustness against the channel’s vulnerability.

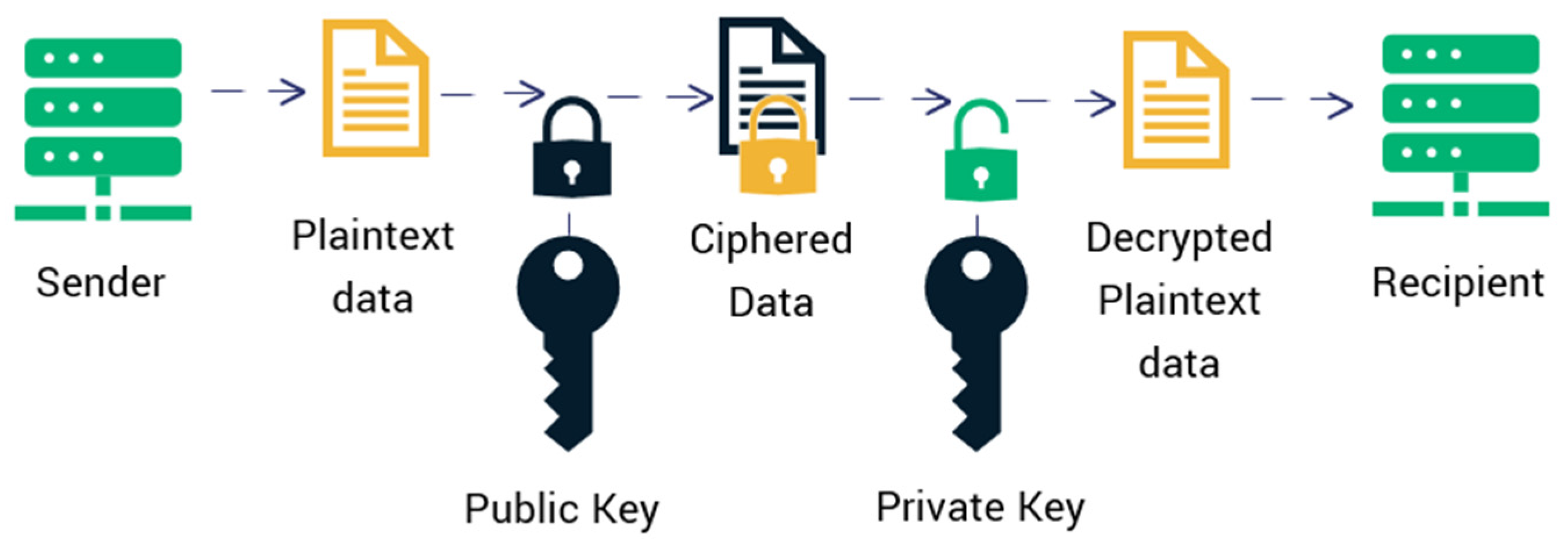
3.1. RSA Algorithm

RSA is named after Rivest, Shamir, and Adleman, the three creators of the RSA calculation [19]. It is an asymmetric cryptographic algorithm that contains two keys: public and private. A public key is used to encrypt the data at the transmitter, and for decryption, both these keys are used at the receiver. The primary rationale behind the RSA algorithm is that it generates these two keys by factorizing a given large integer. Since a public key has two numbers, one of them is a product of two prime numbers.

RSA keys are commonly 1024 or 2048 bits in length. If the key’s size increases, the encryption’s strength increases exponentially. Similarly, using the same prime numbers, a private key is also generated. Therefore, the algorithm’s robustness lies in foolproofing the large number factorizing. RSA Algorithm is shown in Figure 1 respectively. The generated public and private keys using RSA algorithm are provided in

Table 1. Generation of public and private keys using RSA.

Inputs and Outputs of RSA Algorithm
X(o) (0–1)	U (3.56–4)	Prime Numbers	Public Key	Private Key	Encrypted Message	Decrypted Message
0.2	3.6	(3, 5)	(1, 15)	(1, 15)	31514649	(0.2, 3.6)
0.4	3.7	(5, 7)	(23, 35)	(27, 55)	2716334111620	(0.4, 3.7)
0.5	3.6	(5, 13)	(19, 65)	(43, 65)	226273451624	(0.5, 3.6)
0.6	3.8	(5, 11)	(11, 55)	(11, 55)	3746544451461	(0.6, 3.8)
0.8	3.9	(7, 13)	(35, 91)	(35, 91)	55249602528	(0.8, 3.9)

.

The RSA algorithm employs the following procedure to generate public and private keys:

• Pick two big prime numbers, r, and s.
• Find t = r × s by multiplying these values, where t is referred to as the modulus for encryption and decoding.
• Use a number k less than t so that t is roughly prime to (r − 1) × (s − 1), which indicates that the only factor in common between k and (r − 1) × (s − 1) is 1. Select “k” so that 1 < k < φ (t), k is prime to φ (t), and gcd (e,d(t)) = 1.
• The public key is <e, t> for t = r × s. The public key <e, t> encrypts a plaintext message m. The mathematical methodology is employed to obtain ciphertext C from the original message: C = m^k mod t.
• The following formula is employed to calculate the d and set the private key in a way that D_k mod {(r − 1) × (s − 1)} = 1.
• <d, t> is the private key. The private key <d, t> is used to decipher the ciphertext message c. The below formula is used to generate plain text m out from ciphertext c: m = c^d mod t.
• Different inputs of x(o), u, prime numbers, and the generated public and private keys with an encrypted message and decrypted messages are shown in Table 1.

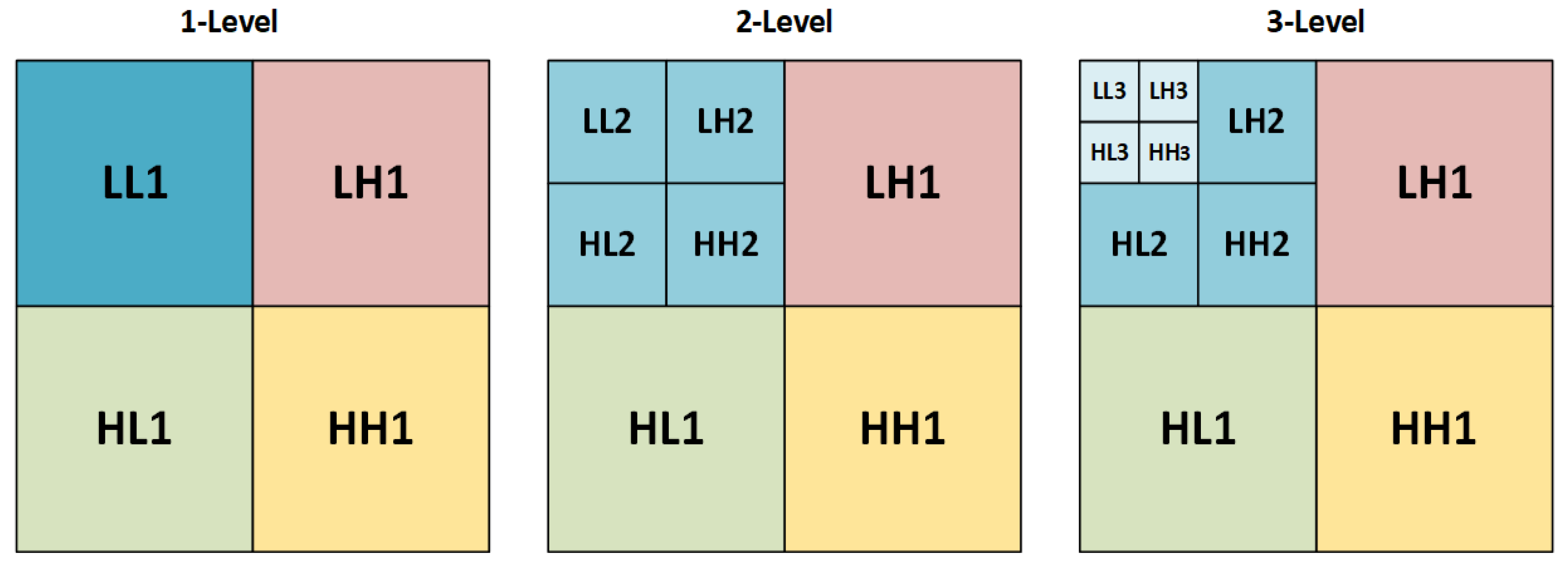
3.2. Discrete Wavelet Transform (DWT)

The primary benefit of wavelet analysis over Fourier analysis is its capability to capture time and frequency localization. Daubechies and Mallat introduced the DWT in the late 1980s [20,21]. DWT subdivides a signal into a set of mutually orthogonal wavelet basis functions [22]. The 2D-DWT is commonly used for image processing applications [23]. The DWT decomposition on images yields information about low-frequency LL subbands; horizontal and vertical edge details as LH and HL subbands, respectively; and diagonal edge features as HH subbands. This process is called one-level decomposition, which can be extended to various levels to extract further higher-level feature information from images [23]. The 2D-DWT subband decomposition process for the first three levels is shown in Figure 2. The further mathematical details of DWT can be found in [24,25]. The three levels of DWT decompositions are shown in Figure 2 Respectively.

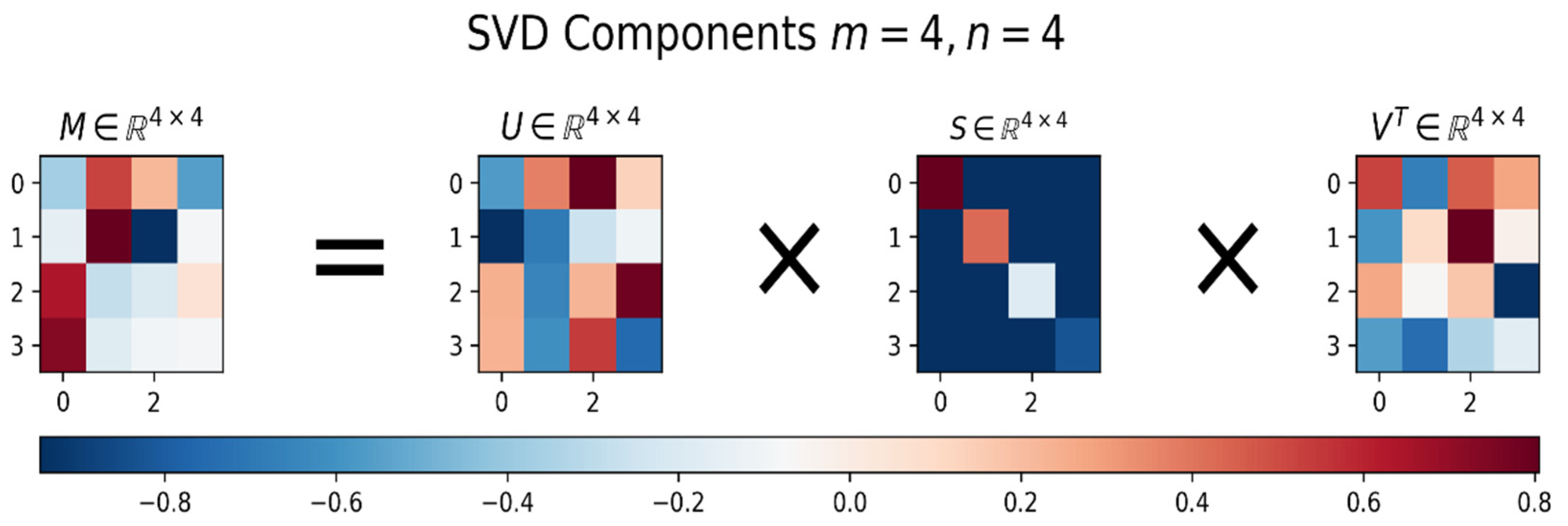
3.3. Singular Value Decomposition (SVD)

SVD is a factorization of a given matrix with various applications in image processing [26]. The singular values (SVs) of an image have excellent soundness, i.e., (i) they will not change even after modifying the original image, and (ii) SVs address inborn arithmetical image properties. Here, an image can be addressed as a framework of positive scalar qualities.

The SVD of a matrix M can be factorized into three matrices: U, S, and V product, where U and V are orthonormal matrices. S is a diagonal matrix with positive values in descending order, as shown in Figure 3. The equation form of SVD for the matrix M is M = U × S × V^T, where S is utilized to embed the watermark information.

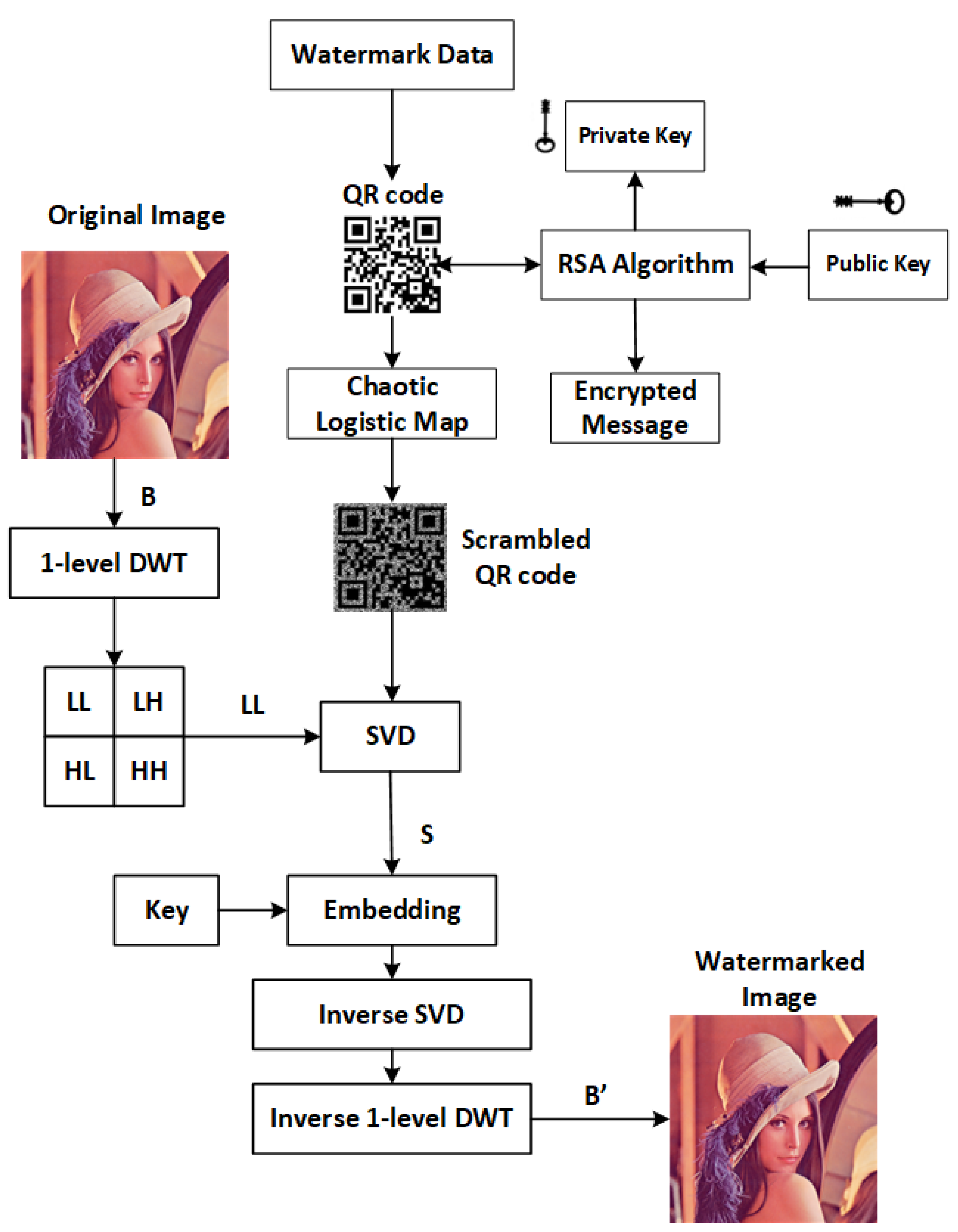
4. Proposed Method

This section discusses the details of the proposed digital watermarking processes. The proposed system embeds the QR code watermark in the transform domain using DWT and SVD using the cryptography technique (RSA). The embedding process is provided in Section 4.1, and the reverse process of embedding is implemented in watermark extraction, which is detailed in Section 4.2.

4.1. Embedding

This section discusses the process of watermark embedding using the cryptographic algorithm stepwise. The watermark embedding architecture is shown in Figure 4.

Step 1:

The watermark data consisting of name and country is created as a QR code.

Step 2:

Generate a public key and an encrypted message by inputting private key values into the RSA algorithm.

Step 3:

The QR code is scrambled using a Chaotic Logistic Map (CLM) to provide watermark data security.

Step 4:

Import the significant image where the watermark has to be concealed.

Step 5:

Convert the imported color image into red, green, and blue components.

Step 6:

Consider the blue layer and apply one-level Haar wavelet decomposition to obtain the four subbands (LL, LH, HL, and HH).

Step 7:

The LL subband and scrambled QR image are selected and decomposed using SVD decomposition.

Step 8:

Both images’ singular values are considered and combined with a key value to generate watermarked singular values.

Step 9:

A watermarked LL subband is created using an invertible SVD.

Step 10:

By fusing the watermarked LL subband and the other subbands to create the watermarked blue layer, an inverse DWT is implemented for one level.

Step 11:

A watermarked color image is created by combining a blue layer with the red, green, and other layers.

Step 12:

The watermarked image with the public key and key value are communicated to the receiver.

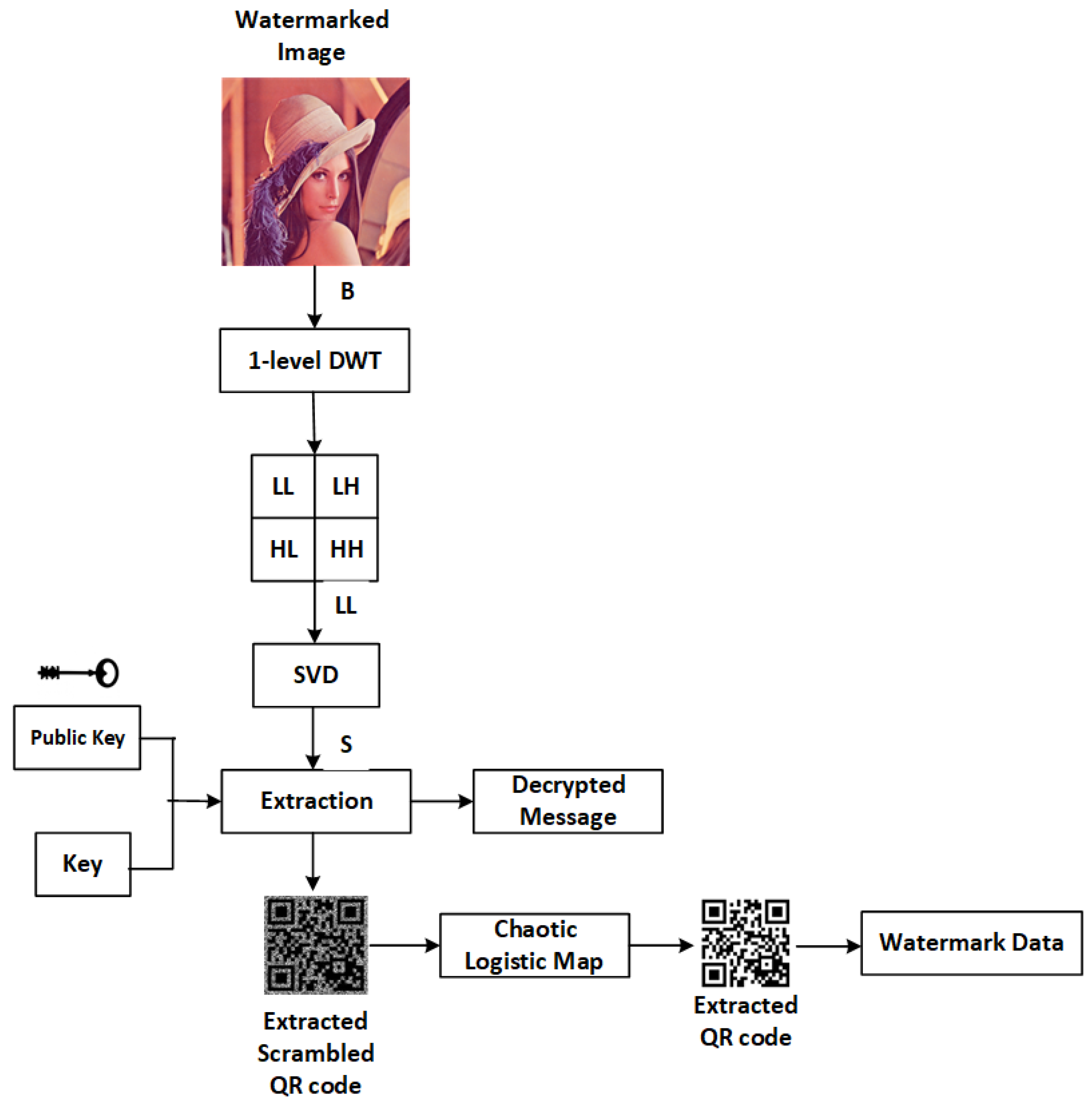
4.2. Extraction

This section goes details the extraction procedure. In semi-blind watermark extraction, partial data of significant data is required. The extraction procedure is provided in Figure 5.

Step 1:

Examine the image that is watermarked.

Step 2:

The color watermarked image is converted to red, green, and blue layers.

Step 3:

As the watermark is embedded in the blue component, the same is considered for extraction.

Step 4:

The blue component is applied with one-level DWT with a Haar wavelet.

Step 5:

The LL subband is considered, and SVD is applied to generate a singular value matrix.

Step 6:

A scrambled QR watermark is extracted based on the key values and partial data of the significant image.

Step 7:

Inverse scrambling is applied to the extracted watermark using the CLM algorithm.

Step 8:

The watermark is extracted with the decrypted message using the public key, which contains the private key values to verify the watermarked data.

5. Experimental Results

A sample color images with a size of $512\times 512\times 3$ and watermark QR code with a size of $256\times 256$ are considered for the evaluation of the proposed method, which is shown in Figure 6 and Figure 7. Several attacks such as noise attacks and geometric attacks are applied to the sample images to test the method’s robustness, which is discussed in detail.

5.1. Evaluation Metrics

The peak-signal-to-noise ratio (PSNR) and normalized correlation coefficient (NCC) metrics evaluate how effectively the proposed watermarking system works. These are discussed in detail in this section.

5.1.1. Peak-Signal-to-Noise Ratio

PSNR is an articulation of the proportion between a signal’s most extreme conceivable worth and the watermarked signal. The PSNR is normally represented in the logarithmic decibel scale. PSNR between the watermarked picture and cover picture is utilized to assess intangibility and is effortlessly characterized through the mean square error (MSE).

MSE permits the analysis of the valid pixel upsides of a unique image to a corrupted image. The higher the PSNR values, the higher the quality of the watermarked image:

$$MSE=\frac{{{\displaystyle \sum }}_{m=0}^{M-1}{{\displaystyle \sum }}_{n=0}^{N-1}{\left(I_{m,n}-WM{I}_{m,n}\right)}^2}{I_{m,n}}$$

$$PSN{R}_{I,WMI}=20lo{g}_{10}\left(\frac{ma{x}_I}{\sqrt{ MSE }}\right)$$

(1)

The $MA{X}_{ML}$ refers to the extreme value of the image that is possible.

5.1.2. Normalized Correlation Coefficient

NCC is the measurement utilized to discover the relationship coefficient between the original watermark and the extracted watermark. When NCC is close to 1, the extracted watermark equals the original watermark. The NCC is defined as follows:

$$NC{C}_{qr,eqr}=\frac{{{\displaystyle \sum }}_{x=1}^m{{\displaystyle \sum }}_{y=1}^{n}qr\left(x,y\right)\times Eqr\left(x,y\right)}{\left(\sqrt{{{\displaystyle \sum }}_{x=1}^{m}qr{(x,y)}^2}\right)\left(\sqrt{{{\displaystyle \sum }}_{x=1}^{m}Eqr{(x,y)}^2}\right)}$$

(2)

The PSNR and NCC values without attacks and with attacks on watermarked images are shown in

Table 2. PSNR and NCC values without attacks.

Images	PSNR and NCC Values without Attacks
House	42.25, 1.00	Lake	41.68, 1.00
Tree	43.56, 1.00	Pepper	40.35, 1.00
Girl	42.85, 1.00	House 2	41.74, 1.00
Mandrill	43.12, 1.00	Einstein	43.36, 1.00
Lena	42.22, 1.00	Monalisa	43.81, 1.00
Jetplane	41.81, 1.00	Monarch	42.65, 1.00

,

Table 3. PSNR and NCC values with different attacks.

Images	PSNR and NCC Values after Attacks
	Salt and Pepper	Gaussian	Mean Filtering	JPEG Compression
House	36.11, 0.9789	39.01, 0.9898	33.12, 0.9901	37.12, 0.9938
Tree	36.05, 0.9796	38.87, 0.9885	33.25, 0.9905	37.28, 0.9942
Girl	35.56, 0.9898	38.86, 0.9896	33.18, 0.9908	37.25, 0.9935
Mandrill	35.66, 0.9899	38.96, 0.9901	33.22, 0.9906	37.24, 0.9932
Lena	35.28, 0.9887	38.15, 0.9914	33.15, 0.9910	37.16, 0.9949
Jetplane	35.47, 0.9815	38.42, 0.9912	33.16, 0.9903	37.21, 0.9936
Lake	35.22, 0.9829	38.36, 0.9908	33.11, 0.9907	37.27, 0.9937
Pepper	35.84, 0.9867	38.51, 0.9925	33.08, 0.9915	37.28, 0.9932
House 2	36.24, 0.9814	39.12, 0.9904	33.13, 0.9911	37.24, 0.9941
Einstein	36.05, 0.9885	39.21, 0.9916	33.17, 0.9916	37.28, 0.9934
Monalisa	35.69, 0.9829	39.11, 0.9892	33.22, 0.9914	37.22, 0.9914
Monarch	35.88, 0.9785	39.05, 0.9845	33.20, 0.9909	37.24, 0.9909

and

Table 4. PSNR and NCC values with geometric attacks on watermarked images.

Images	PSNR and NCC Values after Attacks
	Cropping	Rotation	Scaling	Translation
House	28.36, 0.9801	29.06, 0.9896	38.66, 0.9964	36.42, 0.9777
Tree	29.05, 0.9815	28.58, 0.9889	38.59, 0.9948	36.28, 0.9765
Girl	29.23, 0.9836	29.12, 0.9885	39.28, 0.9947	36.19, 0.9787
Mandrill	29.26, 0.9885	29.14, 0.9889	39.22, 0.9957	36.33, 0.9789
Lena	28.21, 0.9869	28.12, 0.9904	38.92, 0.9954	36.23, 0.9778
Jetplane	29.60, 0.9878	27.86, 0.9911	37.99, 0.9958	36.19, 0.9781
Lake	29.35, 0.9886	28.26, 0.9919	38.84, 0.9961	36.28, 0.9776
Pepper	29.48, 0.9891	27.87, 0.9921	37.94, 0.9955	36.22, 0.9785
House 2	29.54, 0.9912	28.56, 0.9902	38.65, 0.9961	36.18, 0.9788
Einstein	29.22, 0.9905	29.14, 0.9919	39.19, 0.9951	36.19, 0.9781
Monalisa	29.35, 0.9897	29.04, 0.9901	39.21, 0.9968	36.24, 0.9782
Monarch	29.32,0.9856	28.87, 0.9842	38.92, 0.9964	36.28, 0.9778

respectively.

5.2. Noise Attacks

Noise in images is an arbitrary variety of brilliance or shading data in the image. It is corruption of a signal by the addition of data. Images containing multiplicative noise consist of more noise data. Noise attacks on sample images and extracted watermarks are shown in Figure 8.

5.2.1. Salt and Pepper Noise

Salt and pepper noise is added to an image by the option of both choosing noise (with 255-pixel worth) and irregular dullness (with 0-pixel esteem) all around the image. This model is otherwise called information drop noise because it is measured by the number of salt and pepper crystals on the image. The sample salt and pepper noise attacks on images and the watermark extracted from it with PSNR and NCC values are provided in Figure 8 with a density of 0.5.

5.2.2. Gaussian Noise Attack

Gaussian noise is a measurable commotion with a feasible density equivalent to an ordinary state, otherwise called Gaussian dissemination. Gaussian noise values with a variance of 0.01 are tested on various images.

5.2.3. Mean Filtering Attack

Mean filtering with a size of 3 × 3 is applied, producing an average value of their neighbors, including themselves. Average or mean filtering also reduces the intensity disparity between adjacent pixels.

5.2.4. JPEG Compression

This is an image processing standard designed by the Joint Photography Experts Group. It uses DCT for compression, which is lossy image compression. Different compression ratios can be applied to the images based on the requirement. The proposed method is tested with compression 90.

5.3. Geometric Attacks

Geometric attacks on sample images and extracted watermarks are shown in Figure 9.

5.3.1. Cropping Attack

A piece of the picture is trimmed, which is expected to influence the watermark installed in the picture. As the watermark is installed into the picture utilizing DWT and SVD strategies, we can, in any case, recuperate the watermark picture, and the genuineness remains unblemished.

5.3.2. Rotation Attack

A rotation attack is an entirely distinguishable assault performed to change the files of the first picture. It ensures that none of the mathematical mutilations influence the trustworthiness of the watermark picture. The watermarked picture cannot experience change in the framework esteems.

5.3.3. Scaling Attack

In an image scaling attack, the intruders try to manipulate the image without knowing by downscaling and upscaling. The image is downsampled twice in the proposed system to test the robustness.

5.3.4. Translation Attack

In an image, a translation attack shifts the image to a specific direction on the X and Y axes. The proposed system shifts the image to two pixels in the X direction and two in the Y direction.

Different types of attacks are applied to test the robustness of the method. In addition to this, the method is also compared with related watermarking schemes [4,8,27,28], as shown in

Table 5. Comparison of NCC values with related watermarking methods.

Image Attacks	Schemes	Lena	Mandrill	Peppers	Airplane
No Attack	Vaidya et al. [4]	1.00	1.00	1.00	1.00
	Mun et al. [27]	0.9885	0.9886	0.9895	0.9879
	Agoyi et al. [28]	0.8694	0.8837	0.9030	0.9025
	Hosny et al. [6]	0.9995	0.9995	0.9995	0.9995
	Proposed Method	1.00	1.00	1.00	1.00
Salt and Pepper noise	Vaidya et al. [4]	0.8458	0.7156	0.9465	0.9325
	Mun et al. [27]	-	-	-	-
	Agoyi et al. [28]	-	-	-	-
	Hosny et al. [6]	0.9916	0.9916	0.9916	0.9916
	Proposed Method	0.9887	0.9899	0.9867	0.9815
Gaussian noise	Vaidya et al. [4]	0.8489	0.8053	0.9279	0.9114
	Mun et al. [27]	-	-	-	-
	Agoyi et al. [28]	0.7955	0.7796	0.8083	0.7956
	Hosny et al. [6]	0.9905	0.9905	0.9905	0.9905
	Proposed Method	0.9914	0.9901	0.9925	0.9912
Cropping	Vaidya et al. [4]	0.8944	0.8946	0.8942	0.8965
	Mun et al. [27]	0.9921	0.9860	0.9948	0.9888
	Agoyi et al. [28]	-	-	-	-
	Hosny et al. [6]	-	-	-	-
	Proposed Method	0.9869	0.9885	0.9891	0.9878
Scaling	Vaidya et al. [4]	0.9827	0.9956	0.9980	0.9963
	Mun et al. [27]	0.9837	0.9742	0.9768	0.9879
	Agoyi et al. [28]	0.9263	0.9675	0.9644	0.9381
	Hosny et al. [6]	0.9940	0.9940	0.9940	0.9940
	Proposed Method	0.9954	0.9957	0.9955	0.9958
JPEG Compression (90)	Vaidya et al. [4]	0.9053	0.8983	0.8819	0.8956
	Mun et al. [27]	0.9457	0.6537	0.9194	0.9472
	Agoyi et al. [28]	0.8469	0.8469	0.8901	0.8854
	Hosny et al. [6]	0.9928	0.9928	0.9928	0.9928
	Proposed Method	0.9949	0.9932	0.9932	0.9936

. The comparison is tested with various attacks where the proposed scheme has better robustness results than other methods.

6. Conclusions

A novel watermarking scheme is proposed to ensure copyright protection and authentication of images using cryptographic techniques. This scheme fuses the asymmetric encryption RSA algorithm with spatial domain schemes called the DWT and SVD algorithm. This hybrid algorithm ensures visual inspection, copyright protection, and authentication robustness. Moreover, the proposed watermarking scheme was tested with various image and signal processing attacks. The proposed method showed better results compared to related watermarking techniques. However, we only tested our method on a few image datasets. Therefore, in our subsequent works, we will attempt to add more diversified data such as medical images and include more noise attacks to provide a generalized watermarking method for the research field.