Modulation Decoding Based on K-Means Algorithm for Bit-Patterned Media Recording
Abstract
:1. Introduction
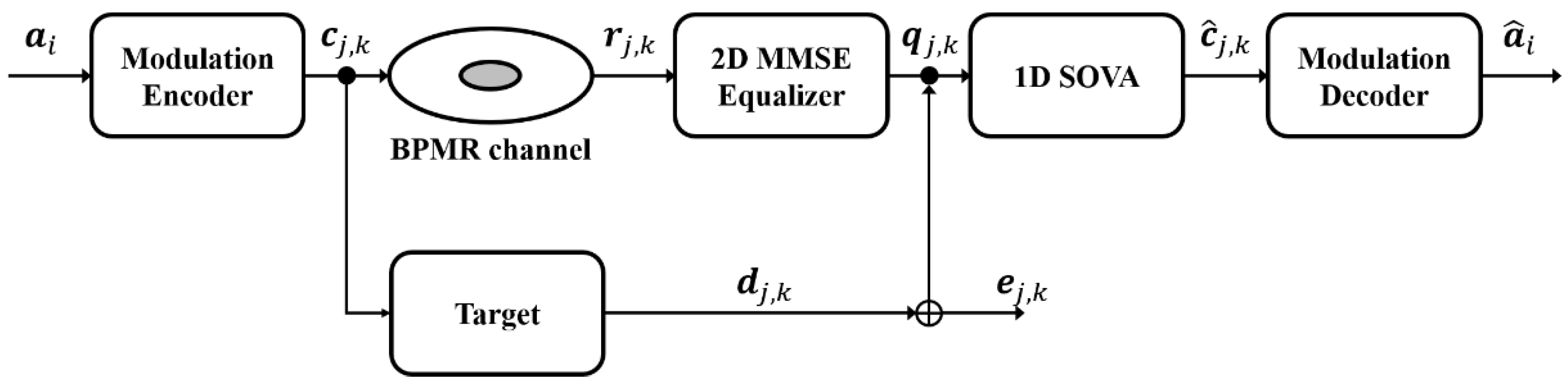
2. Channel Model and Detector
3. Proposed Modulation Decoding Scheme
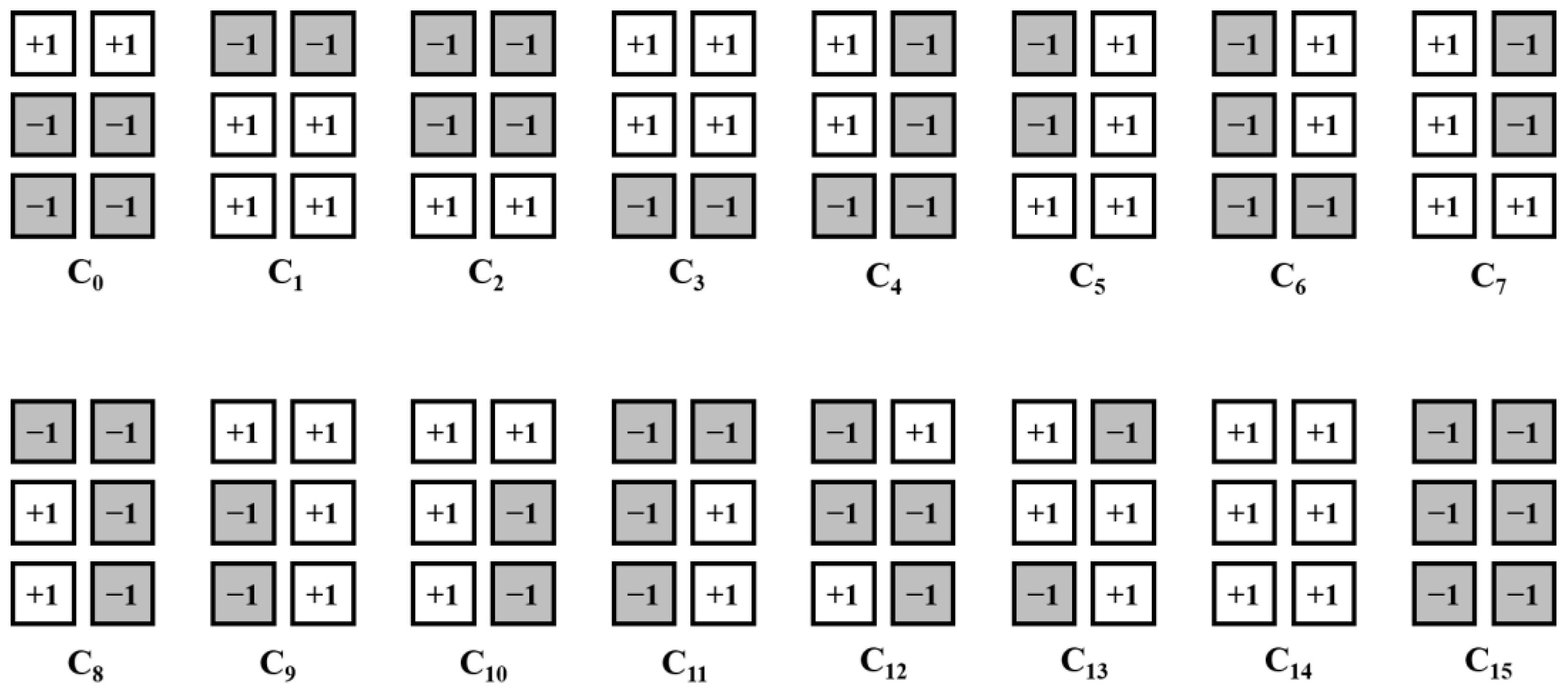
3.1. Conventional Modulation Encoding and Decoding Scheme
3.2. Modulation Decoding Schemes Based on K-Means Algorithm
| Algorithm 1 K-Means Algorithm |
| Input (received sequence): = (n is the number of received sequences) The number of clusters: k Centroid: While (true) For (i = 1 to n) Assign each received sequence to the nearest cluster For (j = 1 to k) Recalculate centroids for observations assigned to each cluster |
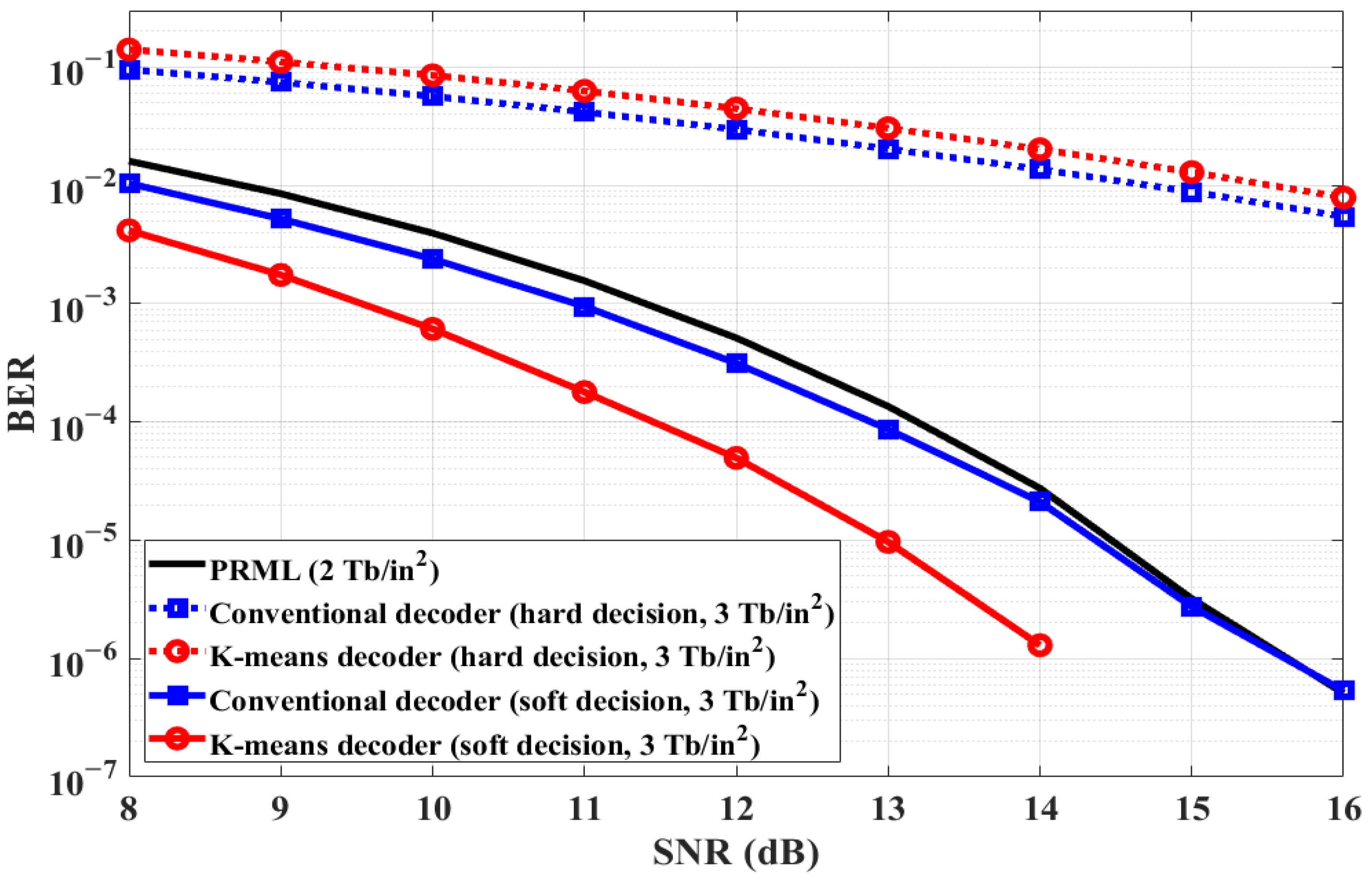
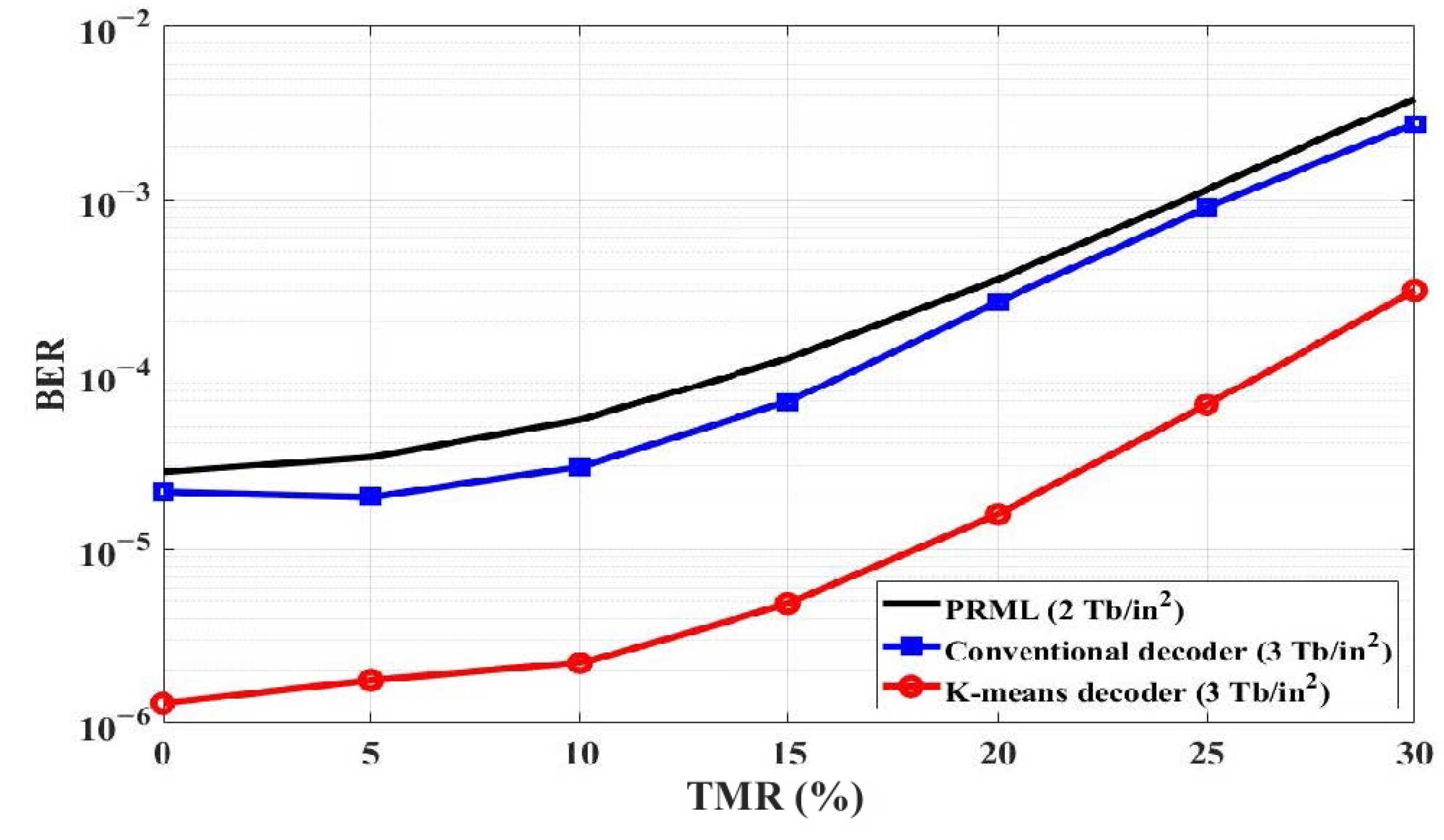
4. Simulation and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- White, R.L.; New, R.M.H.; Pease, R.F.W. Patterned media: A viable route to 50 Gbit/in2 and up for magnetic recording. IEEE Trans. Magn. 1997, 33, 990–995. [Google Scholar]
- Richter, H.J.; Dobin, A.Y.; Heinonen, O.; Gao, K.Z.; Veerdonk, R.J.M.V.D.; Lynch, R.T.; Xue, J.; Weller, D.; Asselin, P.; Erden, M.F.; et al. Recording on bit-patterned media at densities of 1 Tb/in2 and beyond. IEEE Trans. Magn. 2006, 42, 2255–2260. [Google Scholar]
- Zhu, J.; Lin, Z.; Guan, L.; Messner, W. Recording, noise, and servo characteristics of patterned thin film media. IEEE Trans. Magn. 2000, 36, 23–29. [Google Scholar]
- Chang, W.; Cruz, J.R. Inter-track interference mitigation for bit-patterned magnetic recording. IEEE Trans. Magn. 2010, 46, 3899–3908. [Google Scholar]
- Yang, S.; Han, Y.; Wu, X.; Wood, R.; Galbraith, R. A soft decodable concatenated LDPC code. IEEE Trans. Magn. 2015, 51, 9401704. [Google Scholar]
- Keskinoz, M. Two-dimensional equalization/detection for patterned media storage. IEEE Trans. Magn. 2008, 44, 533–539. [Google Scholar]
- Nguyen, T.A.; Lee, J. Modified Viterbi algorithm with feedback using a two-dimensional 3-way generalized partial response target for bit-patterned media recording systems. Appl. Sci. 2021, 11, 728. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Iterative LDPC–LDPC product code for bit patterned media. IEEE Trans. Magn. 2017, 53, 3100704. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Modulation code for reducing intertrack interference on staggered bit-patterned media recording. Appl. Sci. 2020, 10, 5295. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Lee, J. Error-correcting 5/6 modulation code for staggered bit-patterned media recording systems. IEEE Magn. Lett. 2019, 10, 6510005. [Google Scholar]
- Burse, K.; Yadav, R.; Shrivastava, S. Channel equalization using neural networks: A review. IEEE Trans. Syst. Man Cybern. Part C-Appl. Rev. 2010, 40, 352–357. [Google Scholar] [CrossRef]
- Cao, C.; Li, D.; Fair, I. Deep learning-based decoding of constrained sequence codes. IEEE J. Sel. Areas Commun. 2019, 37, 2532–2543. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Iterative signal detection scheme using multilayer perceptron for a bit-patterned media recording system. Appl. Sci. 2020, 10, 8819. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Bit-flipping scheme using k-means algorithm for bit-patterned media recording. IEEE Trans. Magn. 2022, 58, 3101704. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Modulation code and multilayer perceptron decoding for bit-patterned media recording. IEEE Magn. Lett. 2020, 11, 6502705. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Nabavi, S.; Kumar, B.V.K.V.; Bain, J.A. Two-dimensional pulse response and media noise modeling for bit-patterned media. IEEE Trans. Magn. 2008, 44, 3789–3792. [Google Scholar] [CrossRef]
- Nabavi, S.; Kumar, B.V.K.V.; Bain, J.A.; Hogg, C.; Majetich, S.A. Application of image processing to characterize patterning noise in self-assembled nano-masks for bit-patterned media. IEEE Trans. Magn. 2009, 45, 3523–3526. [Google Scholar] [CrossRef]
- Moon, J.; Zeng, W. Equalization for maximum likelihood detectors. IEEE Trans. Magn. 1995, 31, 1083–1088. [Google Scholar] [CrossRef]
- Ng, Y.; Cai, K.; Kumar, B.V.K.V.; Chong, T.C.; Zhang, S.; Chen, B.J. Channel modeling and equalizer design for staggered islands bit-patterned media recording. IEEE Trans. Magn. 2012, 48, 1976–1983. [Google Scholar] [CrossRef]
- Hagenauer, J.; Hoeher, P. A Viterbi algorithm with soft-decision outputs and its applications. In Proceedings of the 1989 IEEE Global Telecommunications Conference and Exhibition ‘Communications Technology for the 1990s and Beyond’, Dallas, TX, USA, 27–30 November 1989; pp. 1680–1686. [Google Scholar]
- Figueiredo, M.A.T.; Jain, A.K. Unsupervised learning of finite mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 381–396. [Google Scholar] [CrossRef]
- Krishna, K.; Narasimha Murty, M. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 1999, 29, 433–439. [Google Scholar] [CrossRef] [PubMed]
- Sinaga, K.P.; Yang, M. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Na, S.; Xumin, L.; Yong, G. Research on K-means clustering algorithm: An improved K-means clustering algorithm. In Proceedings of the 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Ji’an, China, 2–4 April 2010; pp. 63–67. [Google Scholar]
- Scikit-Learn: Machine Learning in Phtyon. Available online: https://scikit-learn.org/stable/modules/clustering.html#k-means (accessed on 24 August 2022).
- Scikit-Learn: Machine Learning in Phtyon. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html# (accessed on 24 August 2022).
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-sne. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
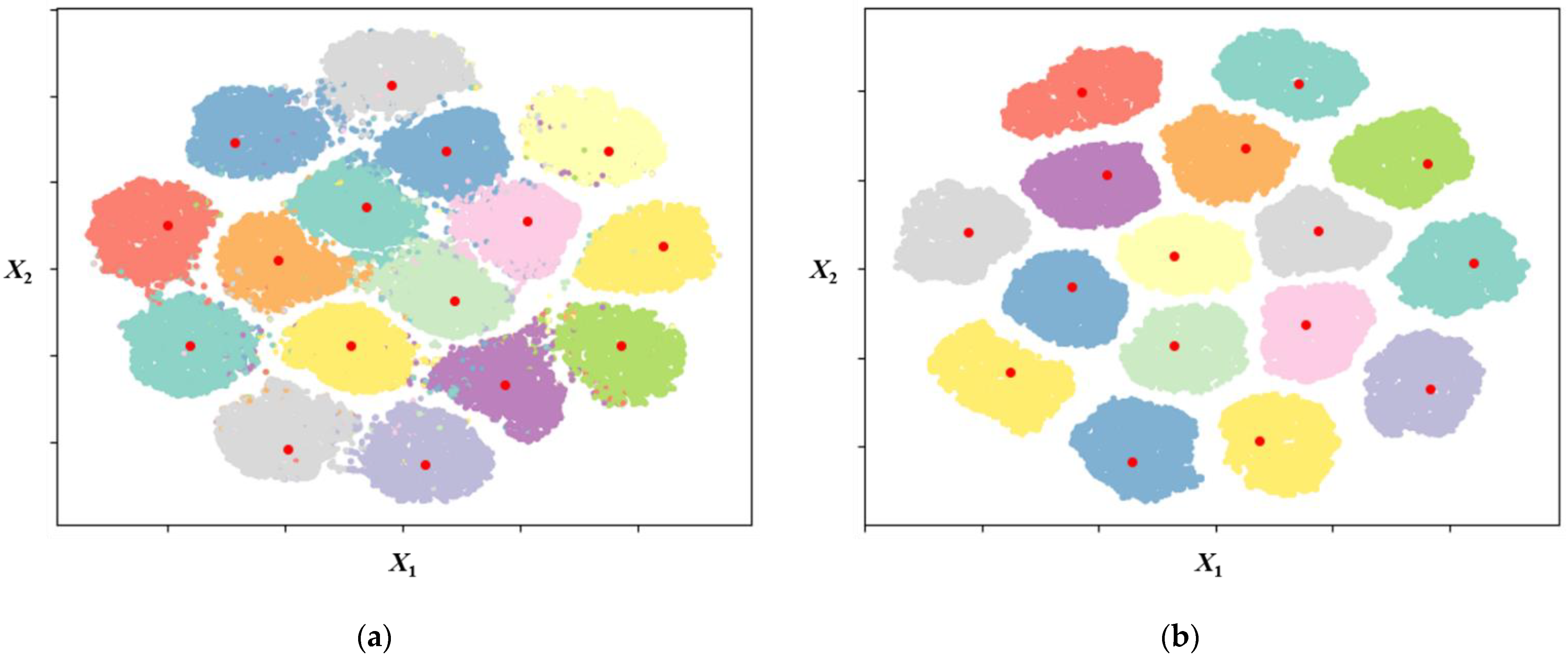
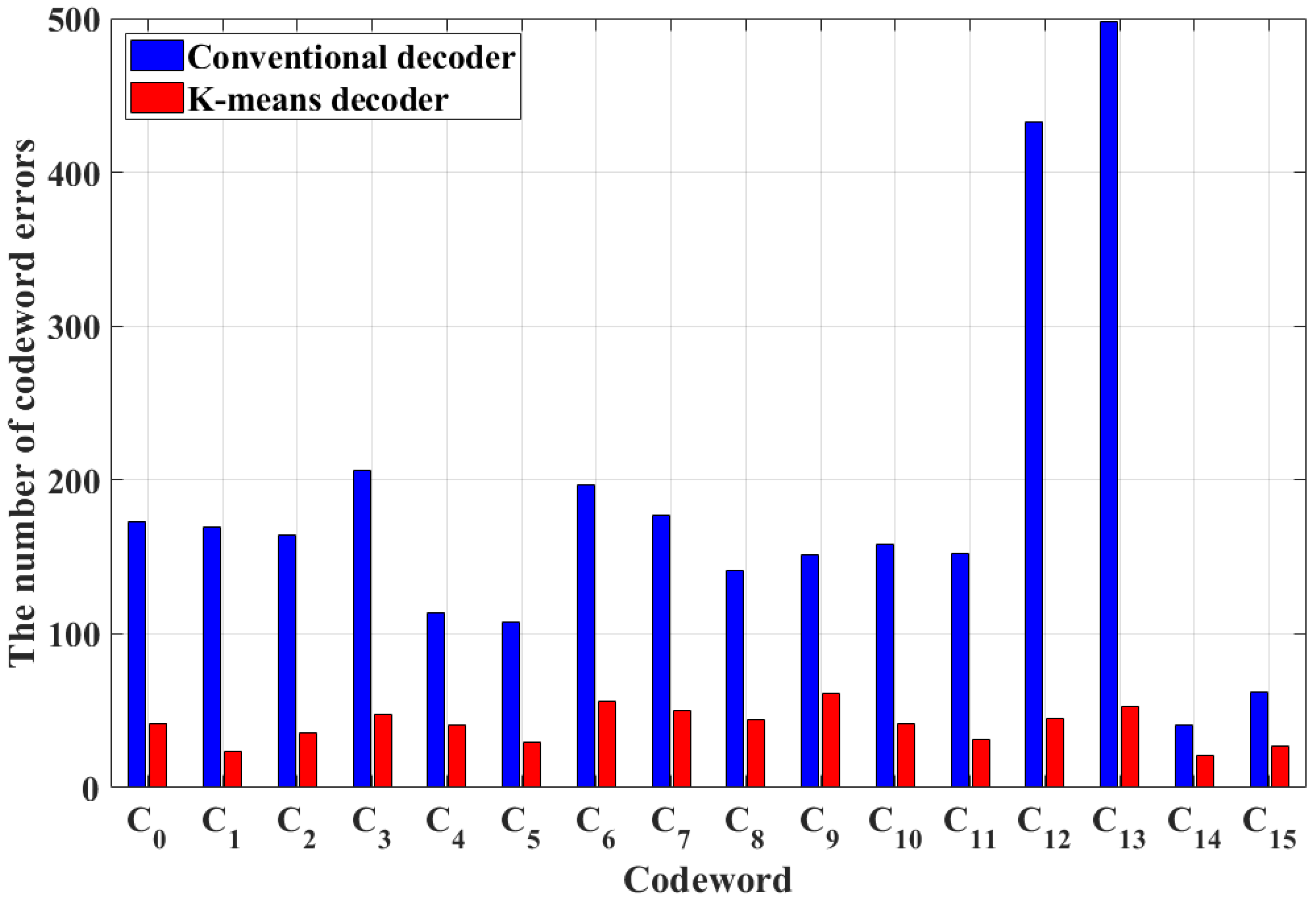
| Parameters | |
|---|---|
| Square island with length | 11 nm |
| Square island with thickness | 10 nm |
| Read-head element thickness | 4 nm |
| Read-head element width | 15 nm |
| Read-head gap distance | 6 nm |
| Read-head fly height | 10 nm |
| K-Means Algorithm in Scikit-Learn |
|---|
| from sklearn.cluster import Kmeans codeword = np.array([[+1, +1, −1, −1, −1,− 1], [−1, −1, +1, +1, +1, +1], [−1, −1, −1, −1, +1, +1], [+1, +1, +1, +1, −1, −1], [+1, −1, +1, −1, −1, −1], [−1, +1, −1, +1, +1, +1], [−1, +1,− 1, +1,− 1, −1], [+1, −1, +1,− 1, +1, +1], [−1,− 1, +1, −1, +1, −1], [+1, +1,−1, +1, −1, +1], [+1, +1, +1, −1,+ 1, −1], [−1, −1, −1, +1, −1, +1], [−1, +1, −1,− 1, +1, −1], [+1, −1, +1, +1, −1, +1], [+1, +1, +1, +1, +1, +1], [−1, −1, −1, −1, −1, −1]]) kmeans = KMeans(n_clusters=16, init=codeword, n_init=1) y_pred = kmeans.fit_predict(received sequence) |
| Codeword or Initial Centroid | Finalized Centroid with Hard Decision | Finalized Centroid with Soft Decision |
|---|---|---|
| [+1, +1, −1, −1, −1, −1] | [+0.99, +0.99, −0.95, −0.94, −1.00, −0.99] | [+2.80, +2.79, −2.88, −2.86, −3.95, −3.96] |
| [−1, −1, +1, +1, +1, +1] | [−0.98, −0.97, +1.00, +1.00, +0.99, +0.99] | [−2.77, −2.78, +2.85, +2.83, +3.96, +3.97] |
| [−1, −1, −1, −1, +1, +1] | [−1.00, −1.00, −0.94, −0.95, +0.99, +0.99] | [−3.95, −3.96, −2.87, −2.88, +2.81, +2.78] |
| [+1, +1, +1, +1, −1, −1] | [+0.99, +0.99, +1.00, +1.00, −0.97, −0.98] | [+3.96, +3.97, +2.84, +2.85, −2.79, −2.77] |
| [+1, −1, +1, −1, −1, −1] | [+0.99, −1.00, +1.00, −0.99, −0.89, −0.97] | [+3.81, −2.79, +2.71, −3.90, −2.52, −3.16] |
| [−1, +1, −1, +1, +1, +1] | [−0.99, +0.99, −0.99, +0.99, +0.99, +0.99] | [−3.80, +2.80, −2.74, +3.86, +2.53, +3.19] |
| [−1, +1, −1, +1, −1, −1] | [−1.00, +0.99, −0.99, +0.99, −0.98, −0.89] | [−2.78, +3.83, −3.91, +2.71, −3.19, −2.52] |
| [+1, −1, +1, −1, +1, +1] | [+0.99, −0.99, +0.99, −0.99, +0.99, +0.99] | [+2.80, −3.80, +3.87, −2.73, +3.21, +2.53] |
| [−1, −1, +1, −1, +1, −1] | [−1.00, −0.98, +1.00, −0.99, +0.99, −1.00] | [−2.53, −3.18, +2.71, −3.91, +3.82, −2.78] |
| [+1, +1, −1, +1, −1, +1] | [+0.99, +0.99, −0.99, +0.99, −1.00, +0.99] | [+2.55, +3.19, −2.73, +3.88, −3.82, +2.80] |
| [+1, +1, +1, −1, +1, −1] | [+0.99, +0.99, +1.00, −0.99, +0.99, −1.00] | [+3.19, +2.52, +3.86, −2.73, +2.80, −3.81] |
| [−1, −1, −1, +1, −1, +1] | [−0.96, −1.00, −0.99, +1.00, −1.00, +0.99] | [−3.19, −2.51, −3.89, +2.70, −2.78, +3.82] |
| [−1, +1, −1, −1, +1, −1] | [−0.99, +0.99, −0.99, −1.00, +0.99, −1.00] | [−3.54, +2.41, −2.90, −2.88, +2.40, −3.54] |
| [+1, −1, +1, +1, −1, +1] | [+0.99, −1.00, +1.00, +1.00, −1.00, +0.99] | [+3.57, −2.39, +2.84, +2.84, −2.38, +3.56] |
| [+1, +1, +1, +1, +1, +1] | [+0.99, +0.99, +1.00, +1.00, +0.99, +0.99] | [+2.95, +2.93, +4.01, +4.02, +2.93, +2.93] |
| [−1, −1, −1, −1, −1, −1] | [−0.94, −0.88, −0.99, −0.99, −0.88, −0.94] | [−2.94, −2.92, −4.04, −4.05, −2.91, −2.92] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, S.; Lee, J. Modulation Decoding Based on K-Means Algorithm for Bit-Patterned Media Recording. Appl. Sci. 2022, 12, 8703. https://doi.org/10.3390/app12178703
Jeong S, Lee J. Modulation Decoding Based on K-Means Algorithm for Bit-Patterned Media Recording. Applied Sciences. 2022; 12(17):8703. https://doi.org/10.3390/app12178703
Chicago/Turabian StyleJeong, Seongkwon, and Jaejin Lee. 2022. "Modulation Decoding Based on K-Means Algorithm for Bit-Patterned Media Recording" Applied Sciences 12, no. 17: 8703. https://doi.org/10.3390/app12178703
APA StyleJeong, S., & Lee, J. (2022). Modulation Decoding Based on K-Means Algorithm for Bit-Patterned Media Recording. Applied Sciences, 12(17), 8703. https://doi.org/10.3390/app12178703





