Abstract
This article aims at analytically solving the free vibration problem of rectangular thin plates with one corner free and its opposite two adjacent edges rotationally-restrained, which is difficult to handle by conventional semi-inverse approaches such as the Levy solution and Naiver solution, etc. Based on the classical Fourier series theory, this work presents a first endeavor to treat the two-dimensional half-sinusoidal Fourier series, which is quite similar to the Navier’s form solution, as the solution form of plate deflection. By utilizing the orthogonality of the present trial function and the Stoke’s transformation technique, the present solution procedure converts the complicated plate problem into solving sets of linear algebra equations, which heavily decreases the difficulties. Therefore, the present approach enables one to solve the title problem in a unified, simple and straightforward way, which is very easily implemented by researchers. Another advantage of the present method over other analytical approaches is that it has general applicability to various boundary conditions through utilizing different types of Fourier series and it can be extended for further dynamic/static analysis of plates under different shear deformation theories. Moreover, without any extra derivation processes, new, precise analytical free vibration solutions for plates under three non-Levy-type boundary conditions are also obtained by choosing different rotating fixed coefficients. Consequently, we present more than 400 comprehensive free vibration results for plates with classical/non-classical boundaries, all the present results are confirmed by FEM/analytical solutions and can be used as benchmark data for further research.
1. Introduction
A rectangular thin plate is considered to be the basic structural element in practical applications because of its relevance in various engineering fields such as civil and structural engineering, mechanical engineering, naval and aerospace, etc. The extensive application of such structures requires the investigation of the dynamic characteristics of thin plates to establish an accurate and reliable design. It is confirmed that free vibration of plates causes a reduction in structure stiffness which reduces its load carrying capacity, as a result may cause premature structure failure. Simultaneously, a clear understanding of natural frequencies and associated mode shapes is the basis for reliable design toward avoiding a plate’s resonance problem. However, it is difficult to deal with the free vibration problem of plates under various boundary conditions, especially for the ones with complex non-classical boundaries. Numerous approaches have been developed to solve such types of intractable problems, all of them face the challenge of pursuing exact solutions that satisfy the governing partial differential equations (PDEs) under specific boundaries. Analytical methods are indispensable since they can provide theoretical, reliable and benchmark results, but are far from completed due to the complicated mathematical procedure involved. The literature review reveals that exact analytical solutions of plates under non-classical boundary restraints are not as easily available as those of Levy-type plates (two simply supported parallel edges). The boundary condition investigated in the present article is one of the most representative challenging cases, in which both the free corner and its opposite two adjacent rotationally restrained edges increase the solving difficulty of the vibration problem of plate. Accordingly, very few analytical benchmark results are available for the title problem. Consequently, seeking effective and simple analytical approaches becomes more and more crucial.
The aforementioned situation motivates the development of numerical/approximate approaches. Since there are excellent capabilities of the advanced numerical approaches such as simplicity, versatility, high precision and good convergence, they have been continuously applied to solve intractable mechanical problems of plates. Here we introduce some typical studies to illustrate new developments in this field. Wang [1] predicts the nonlinear dynamic behaviors of elastically restrained composite panels by using the classical Rayleigh–Ritz approach, the proposed solving procedure allowed one to transform the complicated nonlinear PDEs into handling several nonlinear ordinary differential equations. On basis of first-order shear deformation theory, Qin [2] developed a novel Jacobi–Ritz approach to predict free vibration responses of laminated plates with different edge conditions, excellent convergent and precise approximate results were presented for further investigation. Huang [3] provided new, precise buckling and vibration analysis for internally cracked square plates through combining the conventional Ritz method with the moving least square approach, in which novel enriched basis functions are selected as a solution for in-plane and out-of-plane displacements. It is promising to extend such an effective approach to investigate more intractable stability/dynamic problems of plates since it exhibits a powerful mathematical ability. Bidzard [4] carried out the FEM analysis on the dynamic response of multilayer FG-GPLRC toroidal panels under non-classical boundaries. The present FEM results revealed that frequency parameters decrease with the decreasing of rotational spring factor and the GPLs volume fractions. Amoushahi [5] investigated vibration and buckling behavior of composite plates by applying the traditional finite strip approach, in which the effects of moisture and temperature are well illustrated. Nguyen [6] employed a novel isogeometric Bézier finite element approach to solve the vibration problem of functionally gradient piezoelectric plates, all the numerical results obtained were precise enough since the proposed approach inherited all the advantages of the accurate geometry of isogeometric analysis and traditional FEM. Within the framework of the isogeometric approach, Alesadi [7] adopted the Carrera’s unified formulation as the approximate field solution, which yielded accurate numerical results for free vibration and buckling problems of cross-ply laminated plates. Jassas [8] developed the coupled motion equations for concrete slabs reinforced by agglomerated SiO2 nanoparticles through using the third order shear deformation theory. The authors provided new, precise approximate results for forced vibration of concrete slabs by combining the Newmark method and the harmonic differential quadrature approach. Results indicated that linear frequencies of such type structures increased when the volume percent of SiO2 nanoparticles grew up to 0.37. Civalek explored new, precise numerical solutions of plate [9,10,11] and shell [12] problems by adopting the advanced discrete singular convolution approach which was treated as a reliable and applicable tool for its excellent accuracy and efficiency.
Compared with the numerical/approximate methods, the progress made by analytical solutions is relatively few owing to the mathematical difficulty in solving the governing PDEs under the given boundaries. Semi-inverse approaches on the basis of Fourier series theory [13,14,15] are treated as the most popular analytical ways to solve plate problems, in which the preselected solutions are mainly in the form of single or double Sine series and the majority of boundaries investigated are mainly restricted to simple classical boundaries, such as the fully simply supported boundaries and Levy-type boundaries. For example, Li [16] employed a modified Fourier series method to acquire new exact analytical free vibration solutions for rectangular plates with general elastic boundary supports. Based on nonlocal elasticity theory and the generalized heat conduction model with phase delays, Ahmed [17] provided Sinusoidal form solutions for the thermomechanical problem of rotating size-dependent nanobeams with clamped–clamped boundary conditions. Except for the classical single/double Sine series solutions for plate problems, various types of trial functions such as Quasi-Green’s function [18], beam function [19], power series [20], displacement potential functions [21], etc. allow researchers to pursue accurate results for problems of plates with some certain boundaries. Based on the generalized thermoelasticity theory, Abbas [22] obtained the analytical solution for the temperature, displacement components, and stresses of thermoelastic material plates by utilizing an eigenvalue approach. By using the same method, the author [23] also provided new accurate analytical solutions for the free vibration problem of thermoelastic hollow sphere, in which the dispersion relations for various types of possible vibration modes of the hollow sphere were well derived. Ungbhakorn [24] developed the extended Kantorovich approach to handle the buckling problem of laminated composite plates. Liu [25] proposed a new Spectral stiffness approach for buckling analysis of Winkler foundation plates with general boundaries. By using an extended separation-of-variable approach, Xing [26,27] obtained close-form solutions of thin plates with several non-Levy boundaries, the given solution procedure enables one to solve eigenvalue equations simultaneously. Gorman [28] developed a modified Superposition-Galerkin approach to investigate vibration behaviors of thin plates, in which the difficulties in determining vast families of roots of traditional superposition method can be avoided. Hashemi [29] derived an exact in-plane vibration solution for Mindlin plates through utilizing the Helmholtz decomposition. The classical finite integral transform approach [30,31,32,33,34,35,36,37] and the new developed symplectic superposition approach [38,39,40,41] allowing one to solve plate and shell problems without the requirement of trial functions. However, many of the mentioned analytical approaches are applied in handling problems of plate under classical boundaries.
Considerable literatures confirm that the Navier’s form solutions are still accurate analytical solutions of the ideal form because of their simplicity and excellent orthogonality. It is well acknowledgement that Navier’s solution is most commonly used in analyzing static and dynamic problems of plates since its simple solution procedure. However, Navier’s solution is only suitable for plates with all edges simply supported. Consequently, it is of great significance to extent such effective classical approach to solve the problem of plates under more complex boundaries. Motivated by the above situation, a two-dimensional improved Fourier series approach is developed to provide exact vibration analysis of plates under the complicated non-classical boundary restraints. For the first time, we treat the two-dimensional half-sinusoidal Fourier series as the trial function for the deflection of plates. Interestingly, the adopted trial function is quite similar to the Navier’s form solution and automatically satisfies the zero deflection at rotationally restrained edges, zero effective shear force at free edges and zero twisting moment at the free corner. We also make a first endeavor to introduce the Stoke’s transformation technique on deriving detailed expressions for the first four order derivatives of the deflection, in which some associated unknown constants with obvious physical meaning can also be acquired. The obtained constants can be solved by dealing with sets of linear simultaneous equations after putting the obtained derivatives of the deflection into the remain boundaries. The present solution procedure and new Fourier series expansions, which can be directly adopted for solving mechanical problems of thick plates, are the main contribution of the present study. Another advantage of the present study is that new, precise free vibration results for rectangular thin plates under classical boundaries can be obtained by selecting different coefficients of the rotational springs introduced. Therefore, four different types of boundaries including RRFF, CCFF, CSFF and SSFF are considered for the investigated plate, where the free, rotationally restrained, simply supported and clamped edge are, respectively, designated as F, R, S and C. The present work chooses a clockwise representation for the boundaries studied, starting from the edges of x = 0. Finally, we list new precise results for the dimensionless natural frequency parameters and plot the corresponding mode shapes, all of which are testified to be qualified as new exact benchmarks after comparing with the ones solved by the conventional finite element method and other analytical methods.
2. Basic Equations
Consider a rectangular thin plate with length a, width b and uniform thickness h, and the coordinate of plates under title boundary conditions is depicted in Figure 1. Through the derivation with the consideration of the classic Kirchhoff assumptions, the free vibration governing equation can be expressed as:
where is Poisson’s ratio, is flexural rigidity, E is elasticity modulus and is the mass density of the plate. Resultant internal forces including bending moments, effective shear forces and twisting moments can be described by the deflection w (x, y) as follow:
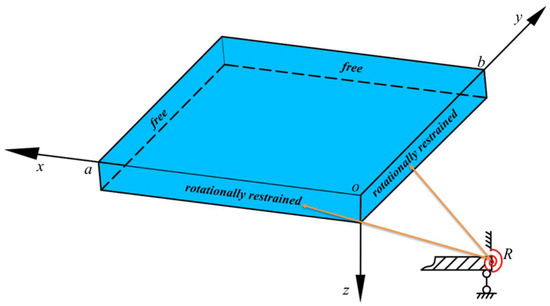
Figure 1.
Rectangular plate with one corner free and its opposite two adjacent edges rotationally restrained.
On basis of the classical vibration theory, the deflection for a free vibration plate could be preselected as . Then one will obtain
Expressions for the RRFF plate, in which rotationally-restrained at edges and , and its opposite corner free, are described as:
where are the rotational springs that are reflected through setting the rotating fixed factor from reference [36] as follows:
As to problems of rectangular thin plates, Fourier series is usually adopted as the trial function for the deflection due to its simple form and orthogonality properties. To deal with title problem, is assumed to have the following form:
where , ; is the unknown Fourier coefficient for the deflection.
The term-by-term differentiation of the trial function is achieved by utilizing the Stoke’s transformation [42], which is the main contribution of the current study. Now utilizing the Stoke’s transformation, the detail expressions for the first four order derivatives of the deflection are given as below:
where
Substituting the assumed and its fourth high-order derivatives, that appeared in Equations (8)–(10), into Equation (3) yields the following expression for the free vibration governing equation:
It is obvious that is zero since the zero-twisting moment at free corner. Similarly, due to the zero deflection at rotationally-restrained edges (, ) and zero effective shear force at free edges (, ), it is easy to derive that
It is clearly that are the Fourier coefficients of the slope along the free edges. Obviously and are the Fourier coefficients of bending moments along the rotationally restrained edges, the corresponding bending moments can be directly acquired by the following formula:
One can obtain the following simplified expression for the free vibration governing equations by substituting Equations (13)–(15) into the Equation (12), which is shown below:
After the simple derivation, one can obtain the expression of with , , and to be determined.
where
Through the above solving procedure, it is clear that the preselected trial function satisfies the boundaries in Equation (4) automatically. The assumed deflection is still required to satisfy the boundaries in Equation (5), which can determine the unknown constants in . The boundary condition at the rotationally restrained edge will be satisfied by substituting the Equation (16) and the slopes in Equations (8) and (9) into Equation (5), which produces Equations (20) and (22). Similarly, utilizing the second-order derivatives of in Equations (8) and (9) to acquire the bending moments at free edges and letting them to be equal to zero, which can satisfy the remain bending moments requirements and produce Equations (21) and (23).
Multiplying each side of Equations (20) and (21) by and integrating from 0 to b gives Equations (24) and (25) while multiplying each side of Equations (22) and (23) by and integrating from 0 to a gives Equations (26) and (27), which are shown as follows:
The complicated title problem can be turned into dealing with sets of infinite linear algebra equations composed of Equations (24)–(27) via the above derivations. A zero determinant of above matrix is needed since the requirement of non-zero solutions, which gives the natural frequencies. Subsequently, the constants , , and () can be acquired by substituting the obtained natural frequencies into the corresponding matrix. Finally, the associate free vibration mode shapes will be determined through using the determined by the acquired constants. It is theoretically possible for one to obtain exact results when m and n are close to infinity. Actually, convergent results with desired accuracy can be obtained by solving sets of finite equations containing the identical count of unknowns. In the present study, the identical terms s is selected for m and n, with their upper limit setting at and .
3. Comprehensive Frequency Parameter and Mode Shape Results
Aimed at testifying the capability of the proposed approach in predicting free vibration response for rectangular thin plates with classic/non-classic type edge conditions, new precise comprehensive results including frequency parameters and the associated mode shapes are in comparison with FEM results and the existing analytical solutions [16,43]. It is worth noting that the reliable FEM results for comparison are acquired by using ABAQUS 6.13 (2013), where 4-node thin shell element S4R is employed. To guarantee the accuracy of the FEM results, we testify the convergence for the FEM results of CCFF plate with aspect ratio b/a = 1, as is shown in Table 1. It is found that most of the obtained FEM results for converge when the mesh size is 1/400 of the plate length. Thus, the uniform mesh size with short edge length of 1/400 is adopted throughout the present study. It is notable that the investigation on classic boundaries is attained through changing the coefficient r, in which means clamped and means simply-supported. Meanwhile, effects on free vibration of plates aroused by aspect ratio b/a and different degrees of boundary constraint are also conducted, in the present study Poisson’s ratio equals 0.3, the aspect ratio of the CCFF, CSFF and SSFF rectangular plate ranges from 0.5 to 5 and the coefficient of the RRFF square plate ranges from 0.1 to 0.9.

Table 1.
Convergence of the dimensionless frequency parameter obtained by FEM for the CCFF square plates with different mesh sizes.
We first carry out vibration analysis on evaluating the non-dimensional frequency parameter, , for CSFF, SSFF and CCFF plates under 10 different aspect ratios such that 100 results are present for each case, which are tableted in Table 1, Table 2 and Table 3. The corresponding vibration mode shapes for the CSFF, CCFF and SSFF square plates are shown in Figure 2, Figure 3 and Figure 4. As to the RRFF square plates, two different cases are considered: (1) the coefficient ranges from 0.1 to 0.9, new exact results for are given in Table 4; (2) the coefficient ranging from 0.1 to 0.9 with , and new benchmark results for are shown in Table 5. The first five vibration modes for the second case of RRFF square plates are given in Figure 5, where the coefficient , respectively.

Table 2.
Frequency parameter of CCFF rectangular plates with defined rotational fixity factors and aspect ratio changing from 0.5 to 5.

Table 3.
Frequency parameter of CSFF rectangular plates with defined rotational fixity factors and aspect ratio changing from 0.5 to 5.
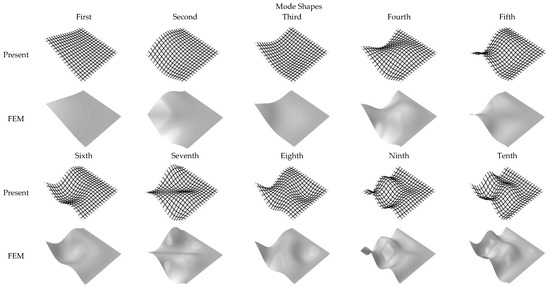
Figure 2.
First ten mode shapes of the square CCFF plate with , .
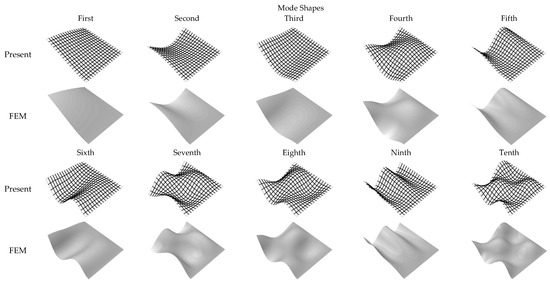
Figure 3.
First ten mode shapes of the square CSFF thin plate with , .
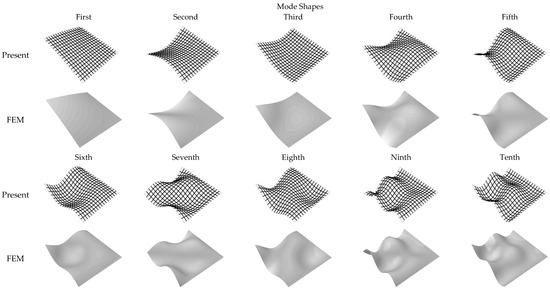
Figure 4.
First ten mode shapes of the square SSFF plates with , .

Table 4.
Frequency parameter of SSFF rectangular plates with defined rotational fixity factors and aspect ratio changing from 0.5 to 5.

Table 5.
Frequency parameter of square RRFF plates with the defined rotational fixity factors changing from 0.1 to 0.9.
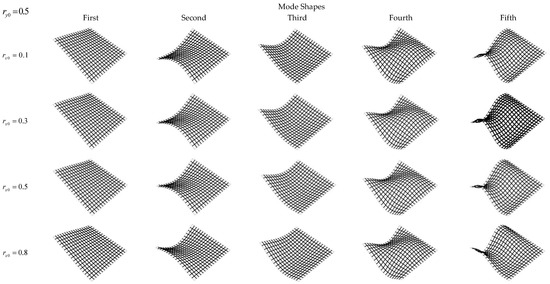
Figure 5.
First five mode shapes of the RRFF square plates with , and equaling 0.1, 0.3, 0.5 and 0.0.8., respectively.
As is shown in Table 2, Table 3 and Table 4, the non-dimensional frequency parameter decreases as the aspect ratio increases and vice versa. Therefore, the minimum values of corresponds to the aspect ratio (5.0). The non-dimensional frequency parameter decreases rapidly when the aspect ratio is 1 or less than one. Additionally, it can be observed that the values of changes very little when changes from 2.5 to 5. It can be concluded that the aspect ratio from 0.5 to 2.0 has more influence on the natural frequencies as compared to the aspect ratio from 2.5 to 5. Through Table 2, Table 3 and Table 4, it also found that boundary conditions have great influence on the non-dimensional frequency parameter. The acquired for all boundary conditions is higher as the aspect ratio gets smaller than one. The magnitude of is always greater for CCFF than those under CSFF and SSFF when aspect ratio is same. Moreover, the non-dimensional frequency parameter for CSFF is higher than the SSFF for all aspect ratio. It can be concluded that the plate with more clamped edges requires more energy to vibrate. Through the comparisons in Table 2, Table 3 and Table 4, it is clearly seen that all the results obtained are in good agreement with ones solved numerically or analytically, especially with those in Ref. [43]. Similarly, through Table 5 and Table 6, it is obvious that the obtained increases with the increase of the rotating fixed coefficient r, which indicates that the RRFF plate with stricter boundary constraints needs more energy to vibrate. The aforesaid parametric analysis indicates that both the aspect ratios and the degree of boundary restraint effect free vibration behaviors of plates significantly.

Table 6.
Frequency parameter of square RRFF plates with the defined rotational fixity factors and changing from 0.1 to 0.9.
As is shown in Figure 2, Figure 3 and Figure 4, it is easily found that all the obtained free vibration mode shapes for the CCFF, CSFF and SSFF plates match well with the ones provided by the Finite element method. It is also obviously found the present mode shapes strictly satisfy the boundary conditions, which confirm the accuracy of the present method. Through Figure 5, it is found that the mode shapes for the RRFF plate under different degree boundary restraints change gradually, which further confirm the affections of boundary conditions on the free vibration characteristics of plates.
We finally carry out convergence study for the dimensionless frequency parameter of all the five cases, as illustrated by Table 7, Table 8, Table 9, Table 10 and Table 11, in which the convergent results are precise up to five significant figures and are marked in bold. It should be pointed that all the given solutions converge at a slower rate due to the Fourier series form solution. However, the acquired simultaneous equations are easily handled through using the commercial software such as Mathematica 10.3. For each case, it is obviously seen that most of are convergent at , which leads to 150 series of terms that are adopted throughout the present work. Excellent agreement is found between the present numerical/graphical results with FEM solutions and other analytical solutions, which confirms the qualification of the present method in solving complex plate problems. Obviously, all the present the non-dimensional natural frequency parameters and the associated vibration mode shapes can be adopted for engineers and scientists for academic and practical applications. The laws indicated by the present parametric analysis enable designers to effectively avoid resonance problems of rectangular thin plate structures.

Table 7.
Convergence of the dimensionless frequency parameter for the CCFF plates with aspect ratio equaling 0.5 and 4.5, respectively.

Table 8.
Convergence of the dimensionless frequency parameter for the CSFF plates with aspect ratio equaling 0.5 and 4.5, respectively.

Table 9.
Convergence of the dimensionless frequency parameter for the SSFF plates with aspect ratio equaling 0.5 and 4.5, respectively.

Table 10.
Convergence of the dimensionless frequency parameter for the RRFF square plates with equaling 0.1 and 0.8, respectively.

Table 11.
Convergence of the dimensionless frequency parameter for the RRFF square plates with and equaling 0.1 and 0.8, respectively.
4. Conclusions
A new two-dimensional improved Fourier series approach is developed to seek an exact analytical free vibration solution of thin plates under classical/non-classical edge conditions. The significant merits of the present method differing from other analytical methods are: (1) it provides a more simple and straightforward solution procedure for precise plate free vibration analysis since it avoids some complicated mathematical manipulations such as the transformation procedure in finite integral transform method or superposition procedure in symplectic superposition approach; (2) within the framework of Fourier series theory, it reduces the mathematical difficulty of the plate problem by converting the boundary value problems of higher-order partial differential equations into solving linear algebra equations; (3) it provides more precise analytical solutions for mechanical problems of moderately-thick/thick plates under more complicated boundary conditions by using different types of Fourier series. The present trial function exactly satisfies both the governing vibration formula and the non-classical boundaries after determining the unknown constants with obvious physics meaning. In addition, new analytical solutions for the CCFF, CSFF and SSFF plates are also acquired by choosing introduced rotating fixed coefficients. Consequently, we provided new exact results, including 50 mode shapes and more than 400 natural frequencies, for the intractable title problem. In the present parametric analysis, it is found that both the aspect ratio and boundary restraint significantly influence the free vibration behaviors of plates. All the analytical results are precise enough since they agree well with the results obtained by using the FEM and other analytical methods, which are promising to validate solutions of other methods.
Author Contributions
Conceptualization, T.Y.; methodology, B.L.; software, B.L.; validation, S.U. and K.L.; formal analysis, K.L.; investigation, K.L.; resources, S.U.; data curation, B.L.; writing—original draft preparation, B.L.; writing—review and editing, S.U.; visualization, K.L.; supervision, T.Y.; project administration, T.Y.; funding acquisition, T.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.; Cao, D.; Peng, J.; Cheng, H.; Lin, H.; Huang, W. Nonlinear random responses and fatigue prediction of elastically restrained laminated composite panels in thermo-acoustic environments. Compos. Struct. 2019, 229, 111391. [Google Scholar] [CrossRef]
- Qin, B.; Zhong, R.; Wu, Q.; Wang, T.; Wang, Q. A unified formulation for free vibration of laminated plate through Jacobi-Ritz method. Thin-Walled Struct. 2019, 144, 106354. [Google Scholar] [CrossRef]
- Huang, C.S.; Lee, M.C.; Chang, M.J. Vibration and Buckling Analysis of Internally Cracked Square Plates by the MLS-Ritz Approach. Int. J. Str. Stab. Dyn. 2018, 18, 1850105. [Google Scholar] [CrossRef]
- Bidzard, A.; Malekzadeh, P.; Mohebpour, S.R. Vibration of multilayer FG-GPLRC toroidal panels with elastically restrained against rotation edges. Thin-Walled Struct. 2019, 143, 106209. [Google Scholar] [CrossRef]
- Amoushahi, H.; Goodarzian, F. Dynamic and buckling analysis of composite laminated plates with and without strip delamination under hygrothermal effects using finite strip method. Thin-Walled Struct. 2018, 131, 88–101. [Google Scholar] [CrossRef]
- Nguyen, L.B.; Thai, C.H.; Zenkour, A.M.; Nguyen-Xuan, H. An isogeometric Bézier finite element method for vibration analysis of functionally graded piezoelectric material porous plates. Int. J. Mech. Sci. 2019, 157–158, 165–183. [Google Scholar] [CrossRef]
- Alesadi, A.; Galehdari, M.; Shojaee, S. Free vibration and buckling analysis of cross-ply laminated composite plates using Carrera’s unified formulation based on Isogeometric approach. Comput. Struct. 2017, 183, 38–47. [Google Scholar] [CrossRef]
- Jassas, M.R.; Bidgoli, M.R.; Kolahchi, R. Forced vibration analysis of concrete slabs reinforced by agglomerated SiO2 nanoparticles based on numerical methods. Constr. Build. Mater. 2019, 211, 796–806. [Google Scholar] [CrossRef]
- Civalek, Ö.; Dastjerdi, S.; Akgöz, B. Buckling and free vibrations of CNT-reinforced cross-ply laminated composite plates. Mech. Based Des. Struct. Mach. 2020, 50, 1914–1931. [Google Scholar] [CrossRef]
- Civalek, Ö.; Baltacıoglu, A.K. Free vibration analysis of laminated and FGM composite annular sector plates. Compos. Part B Eng. 2019, 157, 182–194. [Google Scholar] [CrossRef]
- Mercan, K.; Baltacıoglu, A.K.; Civalek, Ö. Free vibration of laminated and FGM/CNT composites annular thick plates with shear deformation by discrete singular convolution method. Compos. Struct. 2018, 186, 139–153. [Google Scholar] [CrossRef]
- Civalek, Ö. Discrete singular convolution method for the free vibration analysis of rotating shells with different material properties. Compos. Struct. 2017, 160, 267–279. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. A microstructure-dependent sinusoidal plate model based on the strain gradient elasticity theory. Acta Mech 2015, 226, 2277–2294. [Google Scholar] [CrossRef]
- Xiang, Y.; Wei, G.W. Exact solutions for buckling and vibration of stepped rectangular Mindlin plates. Int. J. Solids Struct. 2004, 41, 279–294. [Google Scholar] [CrossRef]
- Rezvani, S.S.; Kiasat, M.S. Analytical and experimental investigation on the free vibration of a floating composite sandwich plate having viscoelastic core. Arch. Civ. Mech. Eng. 2018, 18, 1241–1258. [Google Scholar] [CrossRef]
- Li, W.L.; Zhang, X.; Du, J.; Liu, Z. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. J. Sound Vib. 2009, 321, 254–269. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Atta, D.; Sedighi, H.M. Vibrational behavior of thermoelastic rotating nanobeams with variable thermal properties based on memory-dependent derivative of heat conduction model. Arch. Appl. Mech. 2022, 1–24. [Google Scholar] [CrossRef]
- Li, S.; Yuan, H. Quasi-Green’s function method for free vibration of clamped thin plates on Winkler foundation. Appl. Math. Mech.-Engl. Ed 2011, 32, 265–276. [Google Scholar] [CrossRef]
- Cheung, Y.K.; Zhou, D. Vibrations of moderately thick rectangular plates in terms of a set of static Timoshenko beam functions. Comput. Struct. 2000, 78, 757–768. [Google Scholar] [CrossRef]
- He, D.; Shi, D.; Wang, Q.; Ma, C. A unified power series method for vibration analysis of composite laminate conical, cylindrical shell and annular plate. Structures 2021, 29, 305–327. [Google Scholar] [CrossRef]
- Yekkalam Tash, F.; Navayi Neya, B. An analytical solution for bending of transversely isotropic thick rectangular plates with variable thickness. Appl. Math. Model. 2020, 77, 1582–1602. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abdalla, A.E.N.N.; Alzahrani, F.S.; Spagnuolo, M. Wave propagation in a generalized thermoelastic plate using eigenvalue approach. J. Therm. Stresses 2016, 39, 1367–1377. [Google Scholar] [CrossRef]
- Abbas, I.A. Analytical Solution for a Free Vibration of a Thermoelastic Hollow Sphere. Mech. Based Des. Struct. Mach. 2015, 43, 265–276. [Google Scholar] [CrossRef]
- Ungbhakorn, V.; Singhatanadgid, P. Buckling analysis of symmetrically laminated composite plates by the extended Kantorovich method. Compos. Struct. 2006, 73, 120–128. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Zhou, W. An analytical spectral stiffness method for buckling of rectangular plates on Winkler foundation subject to general boundary conditions. Appl. Math. Model. 2020, 86, 36–53. [Google Scholar] [CrossRef]
- Xing, Y.F.; Liu, B. New exact solutions for free vibrations of thin orthotropic rectangular plates. Compos. Struct. 2009, 89, 567–574. [Google Scholar] [CrossRef]
- Wang, Z.; Xing, Y.; Sun, Q. Highly accurate closed-form solutions for the free in-plane vibration of rectangular plates with arbitrary homogeneous boundary conditions. J. Sound Vib. 2020, 470, 115166. [Google Scholar] [CrossRef]
- Gorman, D.J.; Ding, W. The Superposition-Galerkin method for free vibration analysis of rectangular plates. J. Sound Vib. 1996, 194, 187–198. [Google Scholar] [CrossRef]
- Hosseini Hashemi, S.; Moradi, A.R. Exact solutions for the in-plane vibrations of rectangular Mindlin plates using Helmholtz decomposition. Acta Mech. 2010, 215, 345–361. [Google Scholar] [CrossRef]
- Ullah, S.; Zhang, J.; Zhong, Y. Accurate buckling analysis of rectangular thin plates by double finite sine integral transform method. Struct. Eng. Mech. 2019, 72, 491–502. [Google Scholar]
- Qian, X.; Jinghui, Z.; Ullah, S.; Yang, Z.; Litao, G. Analytical bending solutions of thin plates by two-dimensional generalized integral transform method. Z. Angew. Math. Mech. 2020, 101, e202000246. [Google Scholar] [CrossRef]
- Ullah, S.; Zhong, Y.; Zhang, J. Analytical buckling solutions of rectangular thin plates by straightforward generalized integral transform method. Int. J. Mech. Sci. 2019, 152, 535–544. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, J.; Ullah, S.; Gao, Y.; Zhao, D. Buckling analysis of rectangular thin plates with two opposite edges free and others rotationally restrained by finite Fourier integral transform method. Z. Angew. Math. Mech. 2020, 101, e202000153. [Google Scholar] [CrossRef]
- An, D.; Xu, D.; Ni, Z.; Su, Y.; Wang, B.; Li, R. Finite integral transform method for analytical solutions of static problems of cylindrical shell panels. Eur. J. Mech. A/Solids 2020, 83, 104033. [Google Scholar] [CrossRef]
- Zhang, J.; Ullah, S.; Zhong, Y. New analytical free vibration solutions of orthotropic rectangular thin plates using generalized integral transformation. J. Comput. Appl. Math. 2020, 367, 112439. [Google Scholar] [CrossRef]
- Ullah, S.; Zhang, J.; Zhong, Y. New Analytical Solutions of Buckling Problem of Rotationally-Restrained Rectangular Thin Plates. Int. J. Appl. Mechanics 2019, 11, 1950101. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, C.; Ullah, S.; Zhong, Y.; Li, R. Two-dimensional generalized finite integral transform method for new analytic bending solutions of orthotropic rectangular thin foundation plates. Appl. Math. Lett. 2019, 92, 8–14. [Google Scholar] [CrossRef]
- Yang, Y.; An, D.; Xu, H.; Li, P.; Wang, B.; Li, R. On the symplectic superposition method for analytic free vibration solutions of right triangular plates. Arch Appl. Mech. 2020, 91, 187–203. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, Y.; Zhou, C.; Zheng, X.; Li, R. On the symplectic superposition method for new analytic free vibration solutions of side-cracked rectangular thin plates. J. Sound Vib. 2020, 489, 115695. [Google Scholar] [CrossRef]
- Li, R.; Zhou, C.; Zheng, X. On New Analytic Free Vibration Solutions of Doubly Curved Shallow Shells by the Symplectic Superposition Method Within the Hamiltonian-System Framework. J. Vib. Acoust. 2021, 143, 011002. [Google Scholar] [CrossRef]
- Hu, Z.; Zheng, X.; An, D.; Zhou, C.; Yang, Y.; Li, R. New analytic buckling solutions of side-cracked rectangular thin plates by the symplectic superposition method. Int. J. Mech. Sci. 2021, 191, 106051. [Google Scholar] [CrossRef]
- Khalili, M.R.; Malekzadeh, K.; Mittal, R.K. A new approach to static and dynamic analysis of composite plates with different boundary conditions. Compos. Struct. 2005, 69, 149–155. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, J.; Ullah, S.; Gao, Y.; Zhao, D.; Jamal, A.; Civalek, O. Free vibration analysis of thin rectangular plates with two adjacent edges rotationally-restrained and the others free using finite Fourier integral transform method. Struct. Eng. Mech. 2021, 80, 455–462. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).