Controlling Electronic Energy Transfer: A Systematic Framework of Theory
Abstract
1. Introduction
2. Electronic Energy Transfer
3. Controlled Energy Transfer
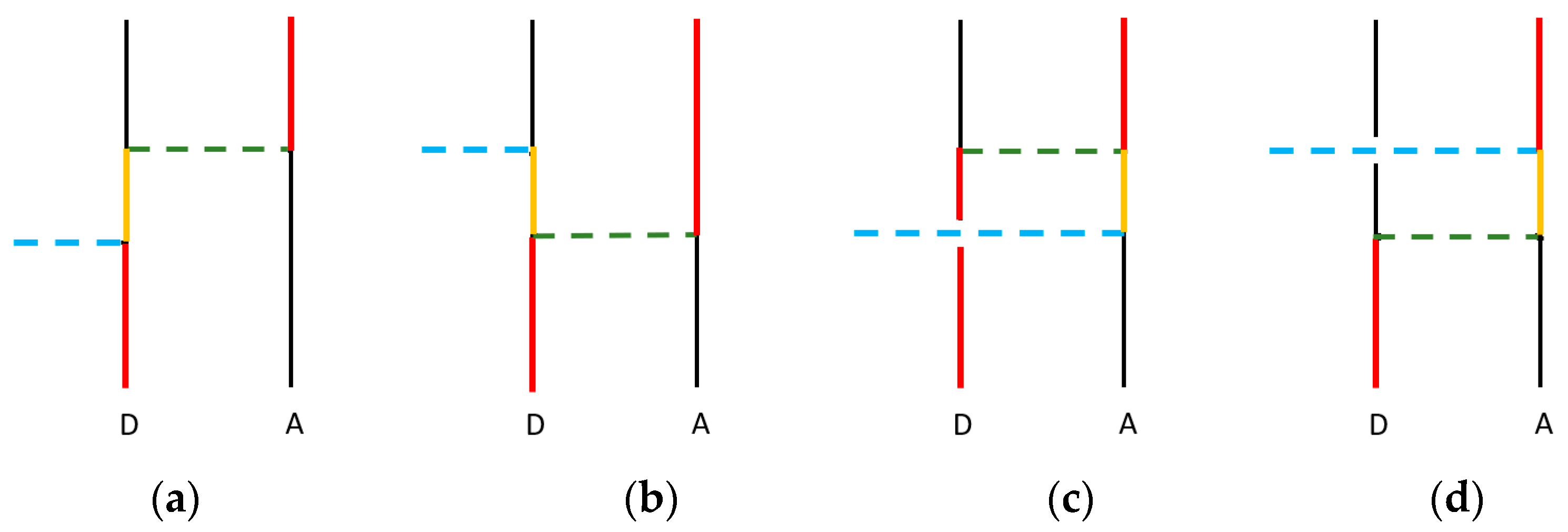
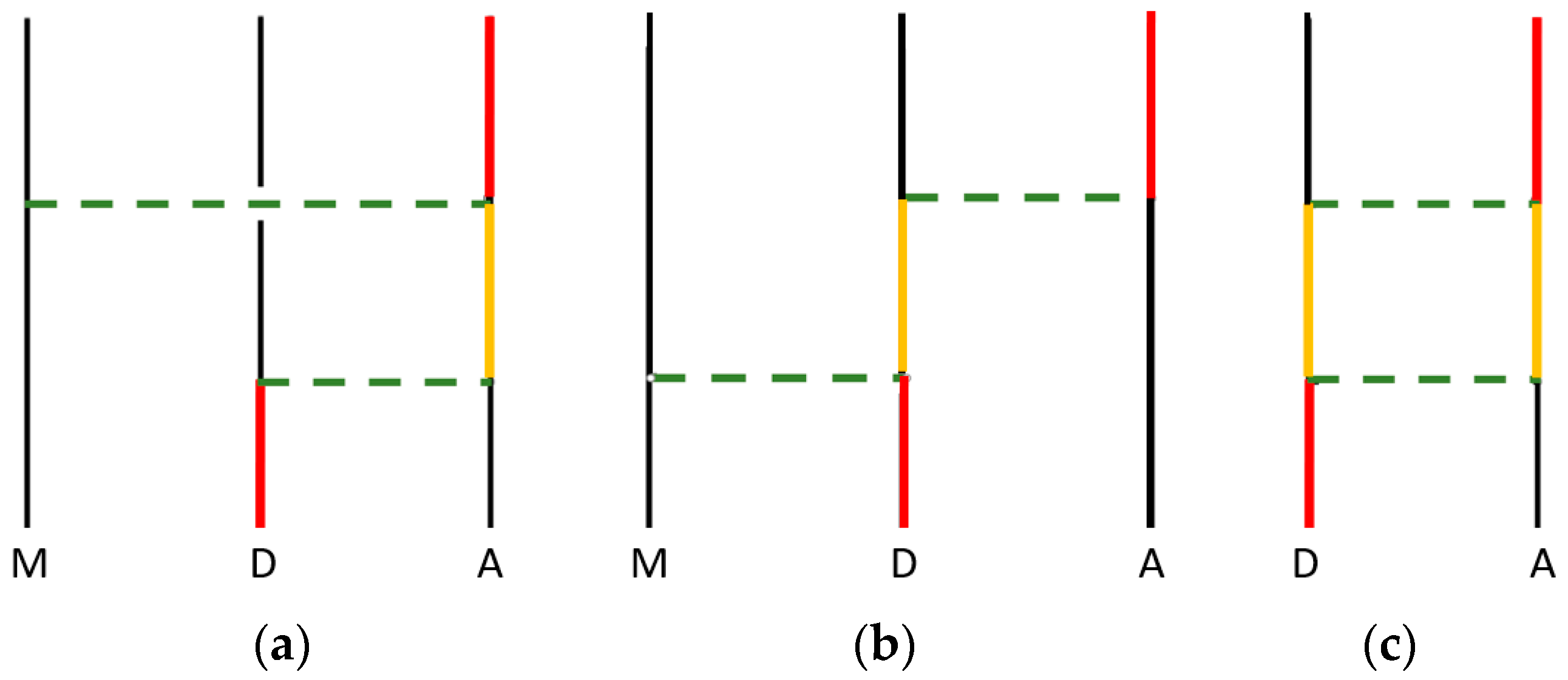
3.1. Static-Field Induced EET
3.2. Static-Dipole Induced EET
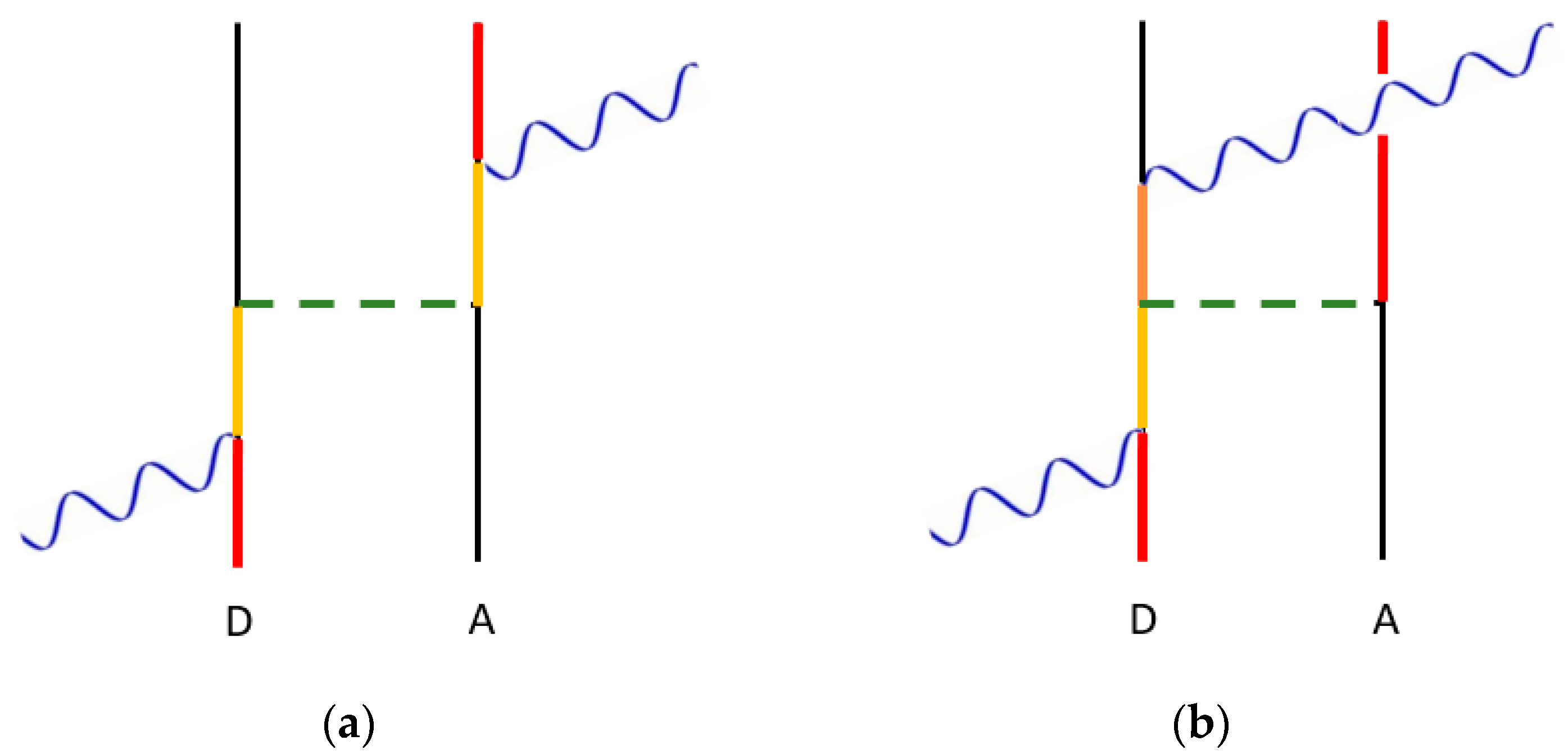
3.3. Optically Controlled EET
4. Interatomic Coulombic Decay
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andrews, D.L.; Demidov, A.A. Resonance Energy Transfer; Wiley: Chichester, UK, 1999. [Google Scholar]
- May, V.; Kühn, O. Charge and Energy Transfer Dynamics in Molecular Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Salam, A. Molecular Quantum Electrodynamics. Long-Range Intermolecular Interactions; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Medintz, I.; Hildebrandt, N. Förster Resonance Energy Transfer: From Theory to Applications; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Valeur, B.; Berberan-Santos, M.N. Molecular Fluorescence: Principles and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Andrews, D.L.; Lipson, R.H. Molecular Photophysics and Spectroscopy, 2nd ed.; IOP Publishing: Bristol, UK, 2021. [Google Scholar]
- Juzeliūnas, G.; Andrews, D.L. Quantum electrodynamics of resonance energy transfer. Adv. Chem. Phys. 2000, 112, 357–410. [Google Scholar]
- Andrews, D.L. Mechanistic principles and applications of resonance energy transfer. Can. J. Chem. 2008, 86, 855–870. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. Resonance energy transfer. In Encyclopedia of Applied Specteoscopy; Andrews, D.L., Ed.; Wiley-VCH: Weinheim, Germany, 2009; pp. 533–554. [Google Scholar]
- Jones, G.A.; Bradshaw, D.S. Resonance energy transfer: From fundamental theory to recent applications. Front. Phys. 2019, 7, 100. [Google Scholar] [CrossRef]
- Marburger, S.; Kugeler, O.; Hergenhahn, U.; Möller, T. Experimental evidence for interatomic coulombic decay in Ne clusters. Phys. Rev. Lett. 2003, 90, 203401. [Google Scholar] [CrossRef] [PubMed]
- Bennett, R.; Votavová, P.; Kolorenč, P.; Miteva, T.; Sisourat, N.; Buhmann, S.Y. Virtual photon approximation for three-body interatomic coulombic decay. Phys. Rev. Lett. 2019, 122, 153401. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Rodríguez, J. Resonance energy transfer: Spectral overlap, efficiency, and direction. J. Chem. Phys. 2007, 127, 084509. [Google Scholar] [CrossRef] [PubMed]
- Lovett, B.W.; Reina, J.H.; Nazir, A.; Kothari, B.; Briggs, G.A.D. Resonant transfer of excitons and quantum computation. Phys. Lett. A 2003, 315, 136–142. [Google Scholar] [CrossRef]
- Scholes, G.D.; Andrews, D.L. Resonance energy transfer and quantum dots. Phys. Rev. B 2005, 72, 125331. [Google Scholar] [CrossRef]
- Kawazoe, T.; Kobayashi, K.; Ohtsu, M. Optical nanofountain: A biomimetic device that concentrates optical energy in a nanometric area. Appl. Phys. Lett. 2005, 86, 103102. [Google Scholar] [CrossRef]
- Wegner, K.D.; Jin, Z.; Lindén, S.; Jennings, T.L.; Hildebrandt, N. Quantum-dot-based Förster resonance energy transfer immunoassay for sensitive clinical diagnostics of low-volume serum samples. ACS Nano 2013, 7, 7411–7419. [Google Scholar] [CrossRef]
- Higgins, L.J.; Marocico, C.A.; Karanikolas, V.D.; Bell, A.P.; Gough, J.J.; Murphy, G.P.; Parbrook, P.J.; Bradley, A.L. Influence of plasmonic array geometry on energy transfer from a quantum well to a quantum dot layer. Nanoscale 2016, 8, 18170–18179. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Bradshaw, D.S. Virtual photons, dipole fields and energy transfer: A quantum electrodynamical approach. Eur. J. Phys. 2004, 25, 845–858. [Google Scholar] [CrossRef]
- Andrew, P.; Barnes, W.L. Förster energy transfer in an optical microcavity. Science 2000, 290, 785–788. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Fujii, M.; Miura, S.; Inui, M.; Hayashi, S. Enhancement and suppression of energy transfer from Si nanocrystals to Er ions through a control of the photonic mode density. Phys. Rev. B 2006, 74, 045302. [Google Scholar] [CrossRef]
- Zhao, L.; Ming, T.; Shao, L.; Chen, H.; Wang, J. Plasmon-controlled Förster resonance energy transfer. J. Phys. Chem. C 2012, 116, 8287–8296. [Google Scholar] [CrossRef]
- Ghenuche, P.; de Torres, J.; Moparthi, S.B.; Grigoriev, V.; Wenger, J. Nanophotonic enhancement of the Förster resonance energy-transfer rate with single nanoapertures. Nano Lett. 2014, 14, 4707–4714. [Google Scholar] [CrossRef]
- Hsu, L.-Y.; Ding, W.; Schatz, G.C. Plasmon-coupled resonance energy transfer. J. Phys. Chem. Lett. 2017, 8, 2357–2367. [Google Scholar] [CrossRef]
- Cortes, C.L.; Jacob, Z. Fundamental figures of merit for engineering Förster resonance energy transfer. Opt. Express 2018, 26, 19371–19387. [Google Scholar] [CrossRef]
- Roth, D.J.; Nasir, M.E.; Ginzburg, P.; Wang, P.; Le Marois, A.; Suhling, K.; Richards, D.; Zayats, A.V. Förster resonance energy transfer inside hyperbolic metamaterials. ACS Photonics 2018, 5, 4594–4603. [Google Scholar] [CrossRef]
- Wei, Y.-C.; Lee, M.-W.; Chou, P.-T.; Scholes, G.D.; Schatz, G.C.; Hsu, L.-Y. Can nanocavities significantly enhance resonance energy transfer in a single donor–acceptor pair? J. Phys. Chem. C 2021, 125, 18119–18128. [Google Scholar] [CrossRef]
- Daniels, G.J.; Jenkins, R.D.; Bradshaw, D.S.; Andrews, D.L. Resonance energy transfer: The unified theory revisited. J. Chem. Phys. 2003, 119, 2264–2274. [Google Scholar] [CrossRef]
- Weeraddana, D.; Premaratne, M.; Andrews, D.L. Direct and third-body mediated resonance energy transfer in dimensionally constrained nanostructures. Phys. Rev. B 2015, 92, 035128. [Google Scholar] [CrossRef]
- Fiscelli, G.; Rizzuto, L.; Passante, R. Resonance energy transfer between two atoms in a conducting cylindrical waveguide. Phys. Rev. A 2018, 98, 013849. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S.; Leeder, J.M.; Rodríguez, J. Dynamics of the dispersion interaction in an energy transfer system. Phys. Chem. Chem. Phys. 2008, 10, 5250–5255. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Salam, A. The unified theory of resonance energy transfer according to molecular quantum electrodynamics. Atoms 2018, 6, 56. [Google Scholar] [CrossRef]
- Fermi, E. Nuclear Physics; University of Chicago Press: Chicago, IL, USA, 1950. [Google Scholar]
- Scholes, G.D. Long-range resonance energy transfer in molecular systems. Annu. Rev. Phys. Chem. 2003, 54, 57–87. [Google Scholar] [CrossRef]
- Andrews, D.L.; Thirunamachandran, T. On three-dimensional rotational averages. J. Chem. Phys. 1977, 67, 5026–5033. [Google Scholar] [CrossRef]
- Salam, A. A general formula for the rate of resonant transfer of energy between two electric multipole moments of arbitrary order using molecular quantum electrodynamics. J. Chem. Phys. 2005, 122, 044112. [Google Scholar] [CrossRef]
- Grinter, R.; Jones, G.A. Interpreting angular momentum transfer between electromagnetic multipoles using vector spherical harmonics. Opt. Lett. 2018, 43, 367–370. [Google Scholar] [CrossRef]
- Wade, J.; Brandt, J.R.; Reger, D.; Zinna, F.; Amsharov, K.Y.; Jux, N.; Andrews, D.L.; Fuchter, M.J. 500-fold amplification of small molecule circularly polarised luminescence through circularly polarised FRET. Angew. Chem. Int. Ed. 2021, 60, 222–227. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J.; Keeler, L. Atkins’ Physical Chemistry, 11th ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Andrews, D.L.; Bittner, A.M. Energy-transfer in a static electric-field. J. Lumin. 1993, 55, 231–242. [Google Scholar]
- Van der Meer, B.W. Kappa-squared: From nuisance to new sense. Rev. Mol. Biotechnol. 2002, 82, 181–196. [Google Scholar] [CrossRef]
- Loura, L.M. Simple estimation of Förster resonance energy transfer (FRET) orientation factor distribution in membranes. Int. J. Mol. Sci. 2012, 13, 15252–15270. [Google Scholar] [PubMed]
- Andrews, D.L.; Harlow, M.J. Phased and Boltzmann-weighted rotational averages. Phys. Rev. A 1984, 29, 2796–2806. [Google Scholar] [CrossRef]
- Andrews, D.L. Effects of intrinsic local fields on molecular fluorescence and energy transfer: Dipole mechanisms and surface potentials. J. Phys. Chem. B 2019, 123, 5015–5023. [Google Scholar]
- Daniels, G.J.; Andrews, D.L. The electronic influence of a third body on resonance energy transfer. J. Chem. Phys. 2002, 116, 6701–6712. [Google Scholar] [CrossRef]
- Caprasecca, S.; Curutchet, C.; Mennucci, B. Toward a unified modeling of environment and bridge-mediated contributions to electronic energy transfer: A fully polarizable QM/MM/PCM approach. J. Chem. Theory Comput. 2012, 8, 4462–4473. [Google Scholar] [CrossRef] [PubMed]
- Salam, A. Mediation of resonance energy transfer by a third molecule. J. Chem. Phys. 2012, 136, 014509. [Google Scholar]
- Andrews, D.L.; Ford, J.S. Resonance energy transfer: Influence of neighboring matter absorbing in the wavelength region of the acceptor. J. Chem. Phys. 2013, 139, 014107. [Google Scholar]
- Salam, A. Near-zone mediation of RET by one and two proximal particles. J. Phys. Chem. A 2019, 123, 2853–2860. [Google Scholar]
- Salam, A. Bridge-mediated RET between two chiral molecules. App. Sci. 2021, 11, 1012. [Google Scholar]
- Salam, A. Pair and mediated RET between two chiral molecules. Mol. Phys. 2022, 120, e2094842. [Google Scholar]
- Suppan, P. Invited review solvatochromic shifts: The influence of the medium on the energy of electronic states. J. Photochem. Photobiol. A Chem. 1990, 50, 293–330. [Google Scholar]
- Allcock, P.; Jenkins, R.D.; Andrews, D.L. Laser assisted resonance energy transfer. Chem. Phys. Lett. 1999, 301, 228–234. [Google Scholar]
- Allcock, P.; Jenkins, R.D.; Andrews, D.L. Laser-assisted resonance-energy transfer. Phys. Rev. A 2000, 61, 023812. [Google Scholar]
- Andrews, D.L. Symmetry characterization in molecular multiphoton spectroscopy. Spectrochim. Acta Part A 1990, 46, 871–885. [Google Scholar]
- Bradshaw, D.S.; Andrews, D.L. Optically controlled resonance energy transfer: Mechanism and configuration for all-optical switching. J. Chem. Phys. 2008, 128, 144506. [Google Scholar]
- Bradshaw, D.S.; Andrews, D.L. All-optical switching based on controlled energy transfer between nanoparticles in film arrays. J. Nanophotonics 2009, 3, 031503. [Google Scholar]
- Bradshaw, D.S.; Andrews, D.L. All-optical switching between quantum dot nanoarrays. Superlatt. Microstruct. 2010, 47, 308–313. [Google Scholar]
- Bradshaw, D.S.; Forbes, K.A.; Andrews, D.L. Off-resonance control and all-optical switching: Expanded dimensions in nonlinear optics. App. Sci. 2019, 9, 4252. [Google Scholar]
- Andrews, D.L.; Bradshaw, D.S. Off-resonant activation of optical emission. Opt. Commun. 2010, 283, 4365–4367. [Google Scholar]
- Cederbaum, L.S.; Zobeley, J.; Tarantelli, F. Giant intermolecular decay and fragmentation of clusters. Phys. Rev. Lett. 1997, 79, 4778–4781. [Google Scholar]
- Santra, R.; Zobeley, J.; Cederbaum, L.S.; Moiseyev, N. Interatomic coulombic decay in van der Waals clusters and impact of nuclear motion. Phys. Rev. Lett. 2000, 85, 4490–4493. [Google Scholar] [PubMed]
- Santra, R.; Zobeley, J.; Cederbaum, L.S. Electronic decay of valence holes in clusters and condensed matter. Phys. Rev. B 2001, 64, 245104. [Google Scholar]
- Jahnke, T.; Czasch, A.; Schöffler, M.; Schössler, S.; Knapp, A.; Käsz, M.; Titze, J.; Wimmer, C.; Kreidi, K.; Grisenti, R. Experimental observation of interatomic Coulombic decay in neon dimers. Phys. Rev. Lett. 2004, 93, 163401. [Google Scholar] [CrossRef]
- Trinter, F.; Williams, J.; Weller, M.; Waitz, M.; Pitzer, M.; Voigtsberger, J.; Schober, C.; Kastirke, G.; Müller, C.; Goihl, C. Evolution of interatomic Coulombic decay in the time domain. Phys. Rev. Lett. 2013, 111, 093401. [Google Scholar]
- Scheit, S.; Cederbaum, L.S.; Meyer, H.D. Time-dependent interplay between electron emission and fragmentation in the interatomic Coulombic decay. J. Chem. Phys. 2003, 118, 2092–2107. [Google Scholar]
- Andrews, D.L.; Leeder, J.M. Resonance energy transfer: When a dipole fails. J. Chem. Phys. 2009, 130, 184504. [Google Scholar]
- Franz, J.; Bennett, R.; Buhmann, S.Y. Auger decay in dispersing and absorbing environments. Phys. Rev. A 2021, 104, 013103. [Google Scholar]
- Jahnke, T. Interatomic and intermolecular Coulombic decay: The coming of age story. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 082001. [Google Scholar]
- Hemmerich, J.L.; Bennett, R.; Buhmann, S.Y. The influence of retardation and dielectric environments on interatomic Coulombic decay. Nat. Commun. 2018, 9, 2934. [Google Scholar] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrews, D.L.; Bradshaw, D.S. Controlling Electronic Energy Transfer: A Systematic Framework of Theory. Appl. Sci. 2022, 12, 8597. https://doi.org/10.3390/app12178597
Andrews DL, Bradshaw DS. Controlling Electronic Energy Transfer: A Systematic Framework of Theory. Applied Sciences. 2022; 12(17):8597. https://doi.org/10.3390/app12178597
Chicago/Turabian StyleAndrews, David L., and David S. Bradshaw. 2022. "Controlling Electronic Energy Transfer: A Systematic Framework of Theory" Applied Sciences 12, no. 17: 8597. https://doi.org/10.3390/app12178597
APA StyleAndrews, D. L., & Bradshaw, D. S. (2022). Controlling Electronic Energy Transfer: A Systematic Framework of Theory. Applied Sciences, 12(17), 8597. https://doi.org/10.3390/app12178597






