Double-Diffusive Effects on the Onset of Rayleigh-Benard Convection of Water-Based Nanofluids
Abstract
:1. Introduction
2. Materials and Methods
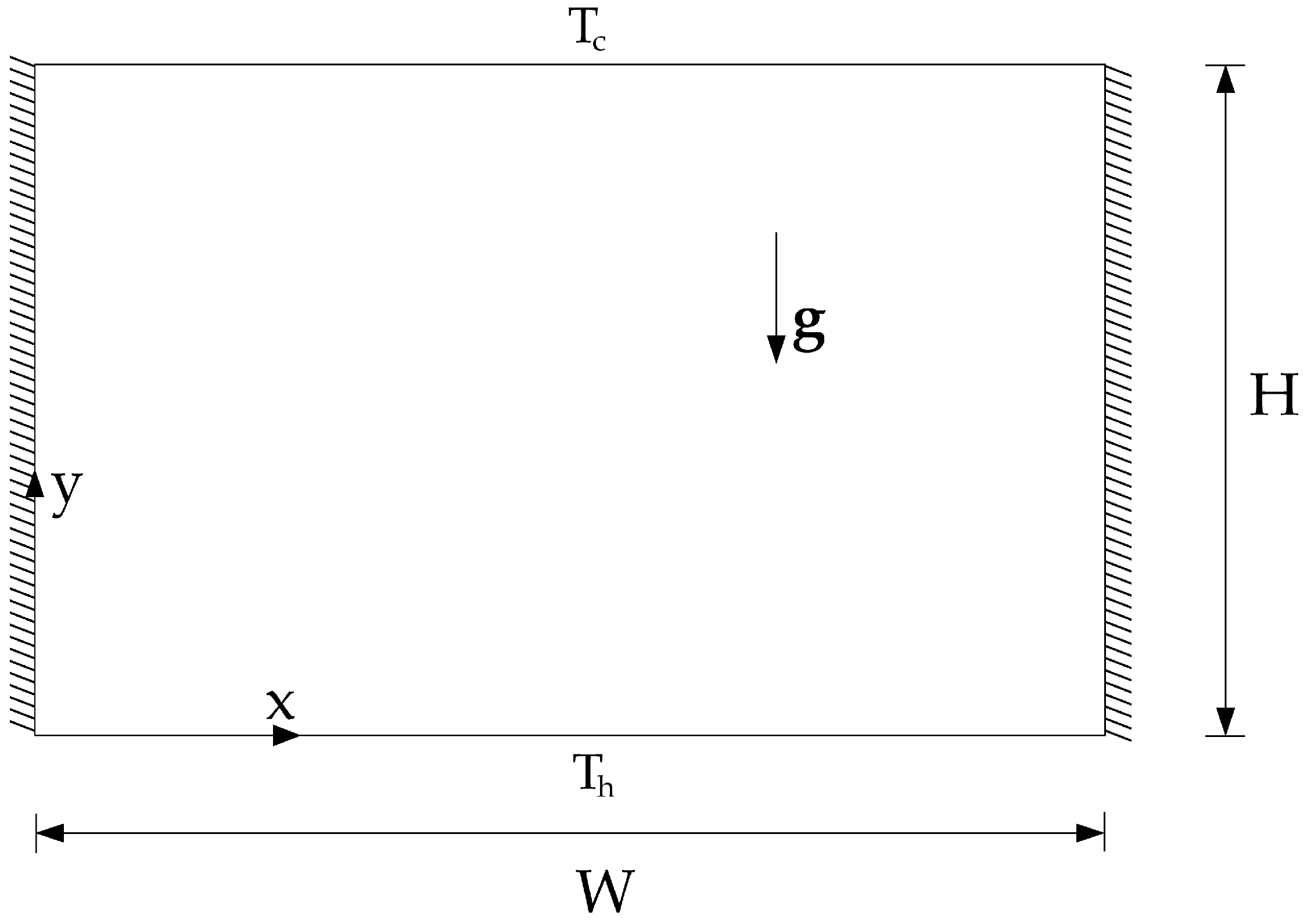
2.1. Mathematical Formulation
2.2. Computational Procedure
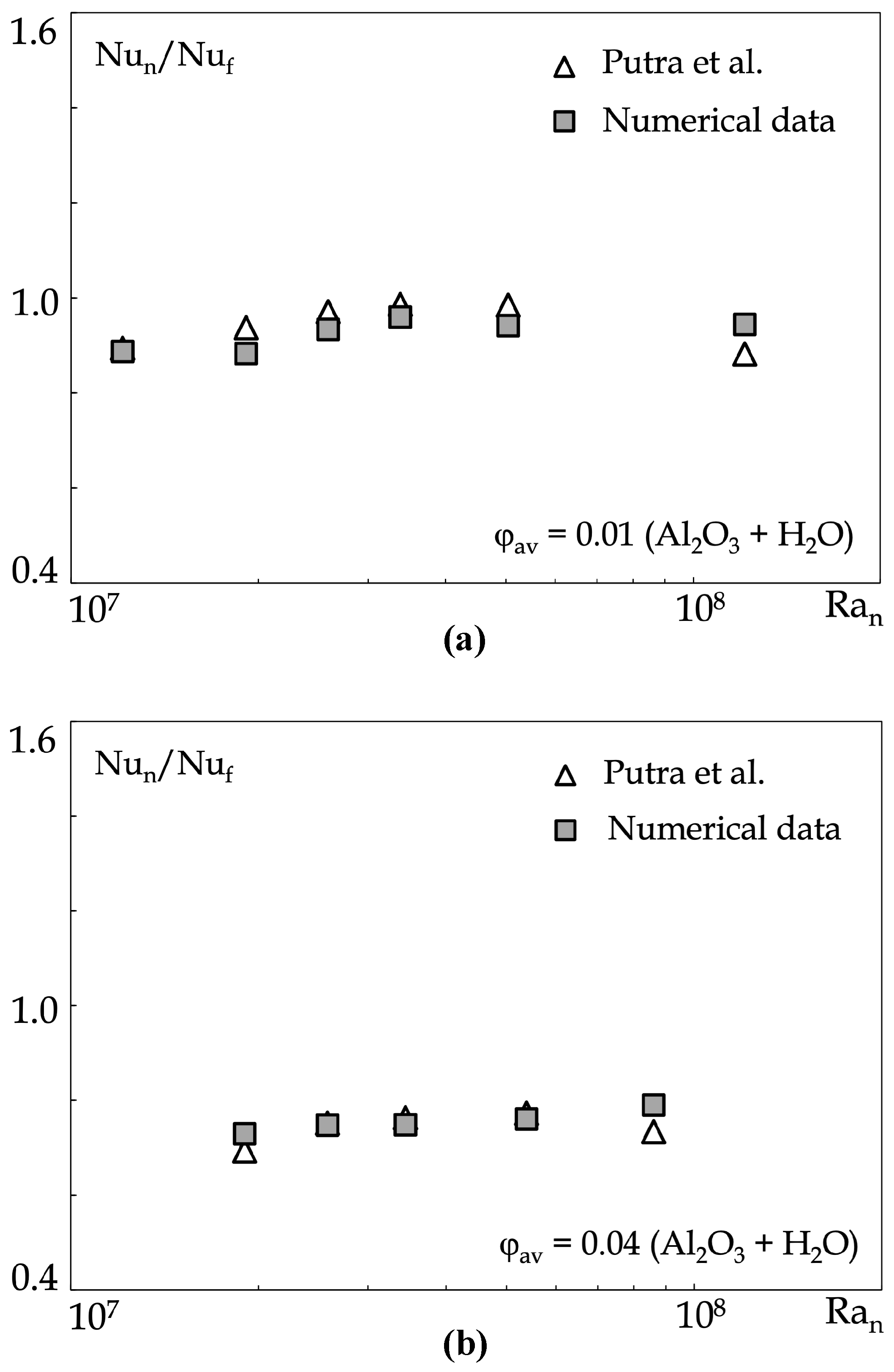
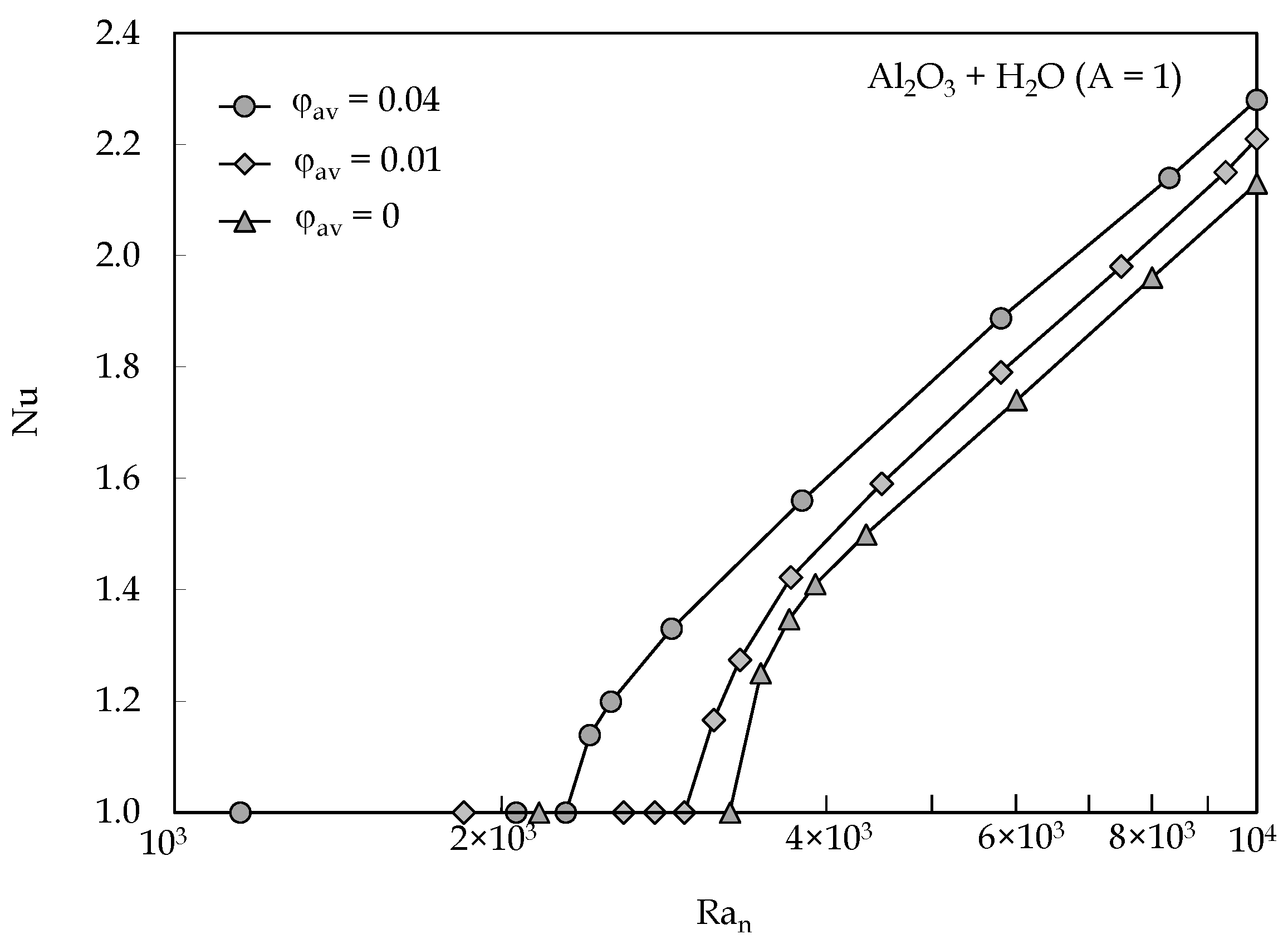
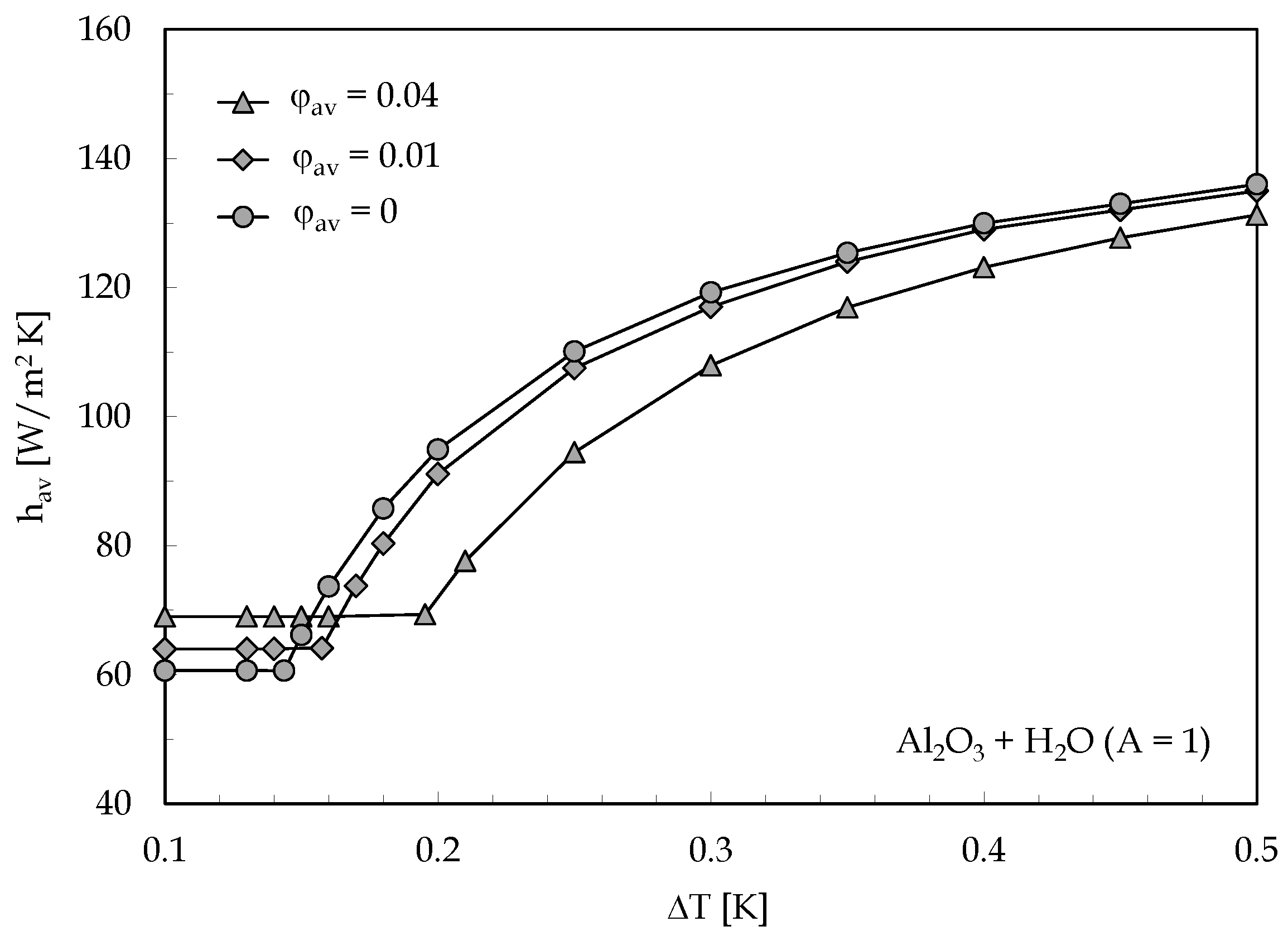
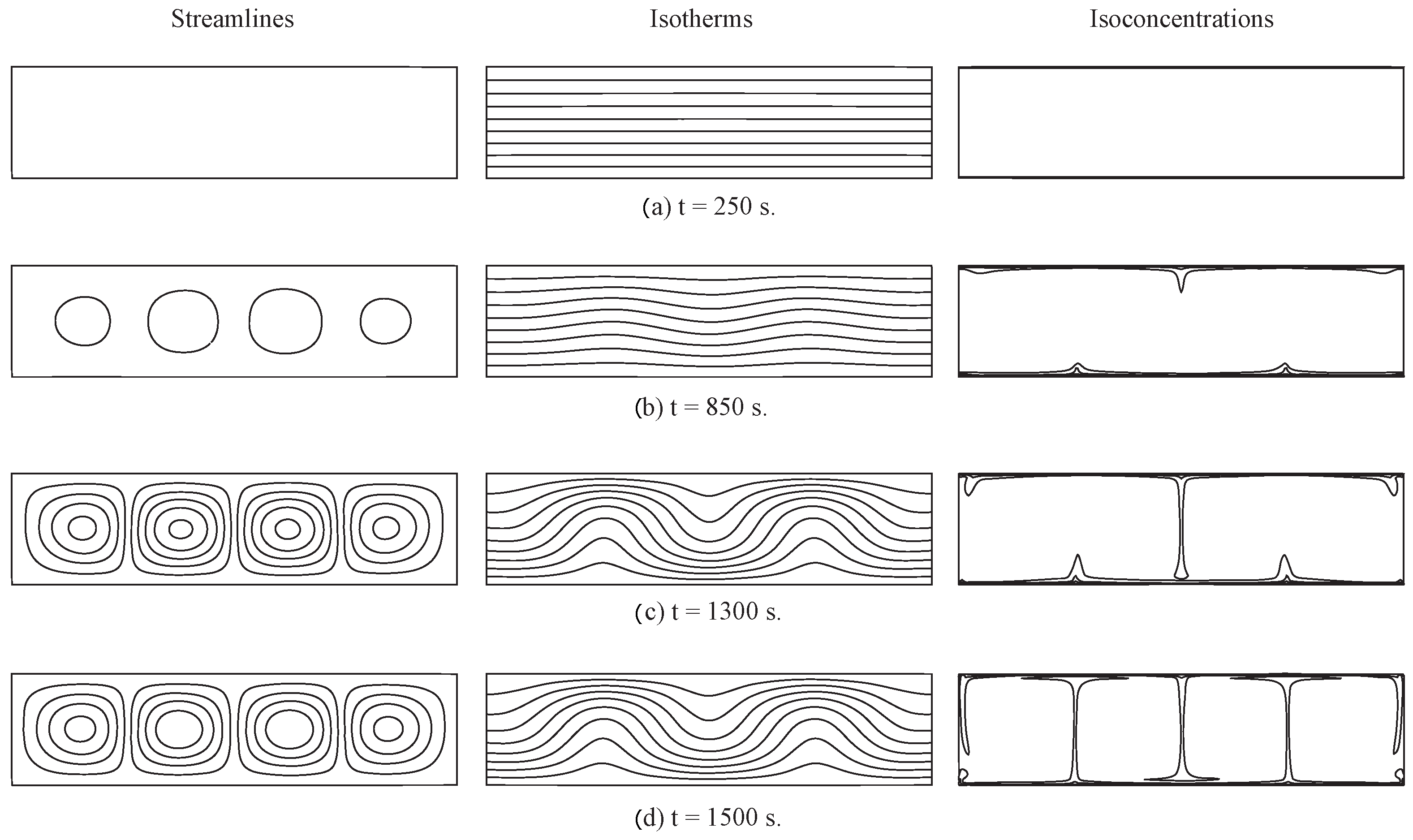
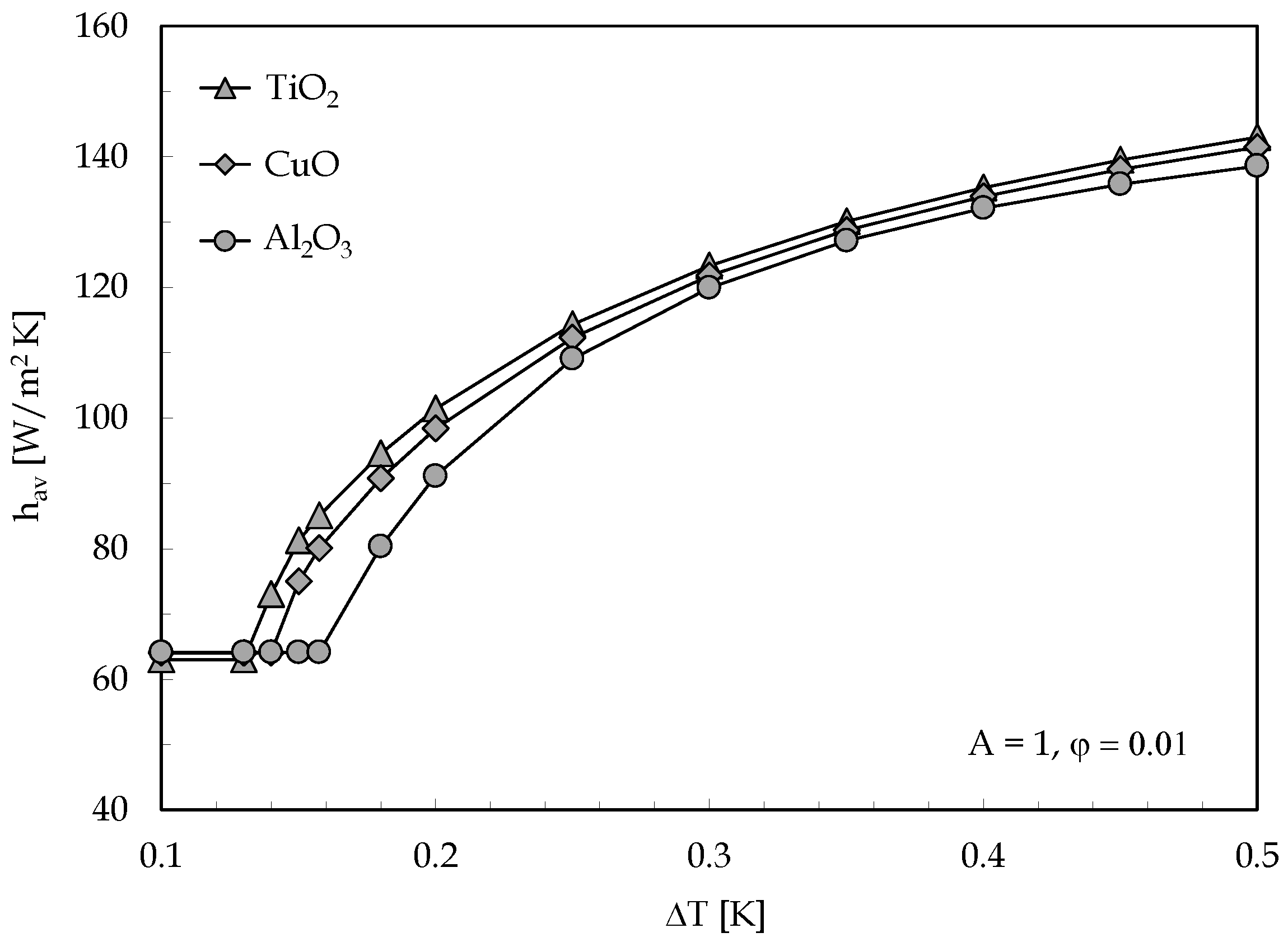
3. Results
4. Conclusions
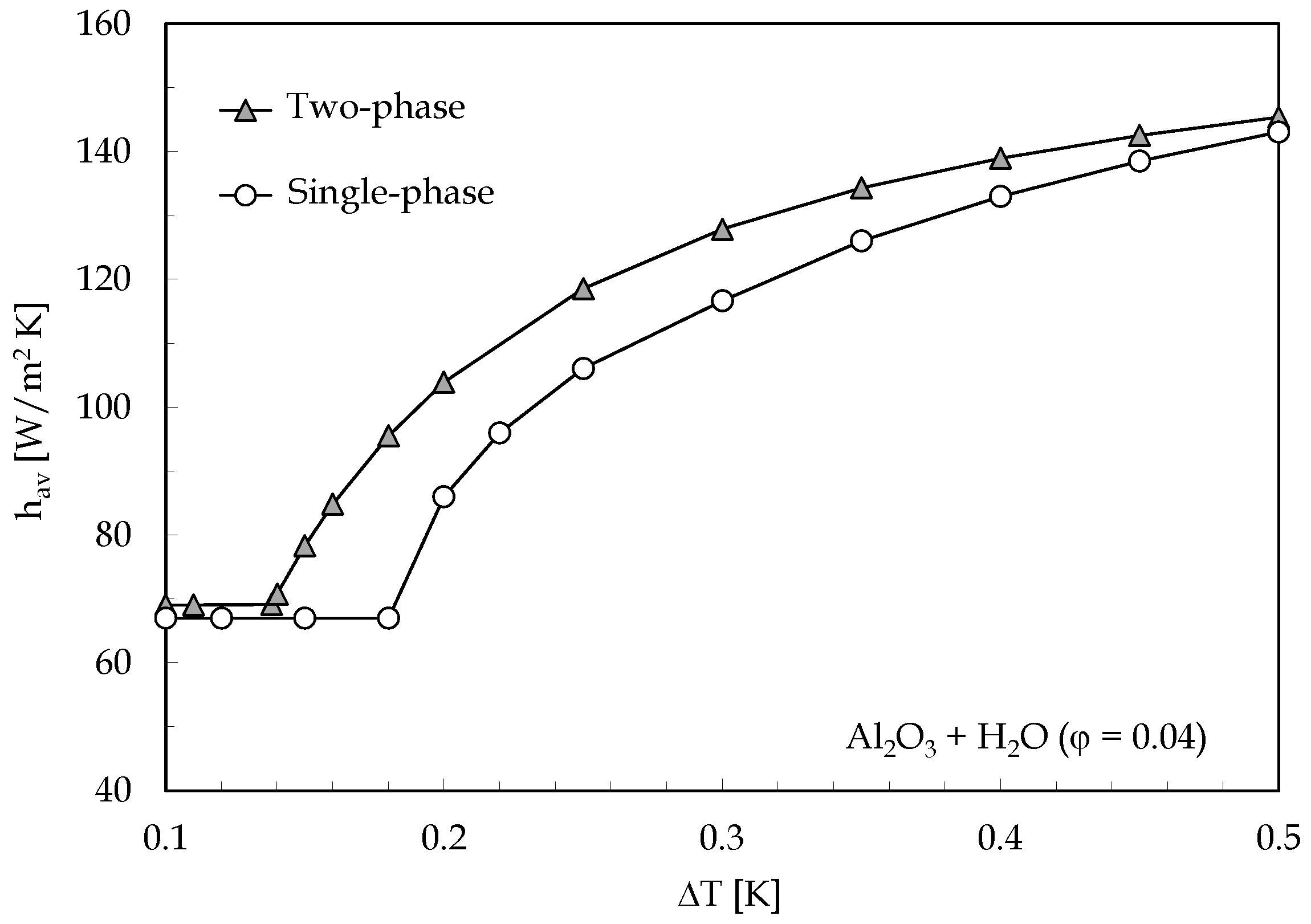
- The value of the difference in temperature between the heated and cooled horizontal walls corresponding to the onset of convection increases as the average volume fraction is increased, which is a consequence of the growth of the dynamic viscosity;
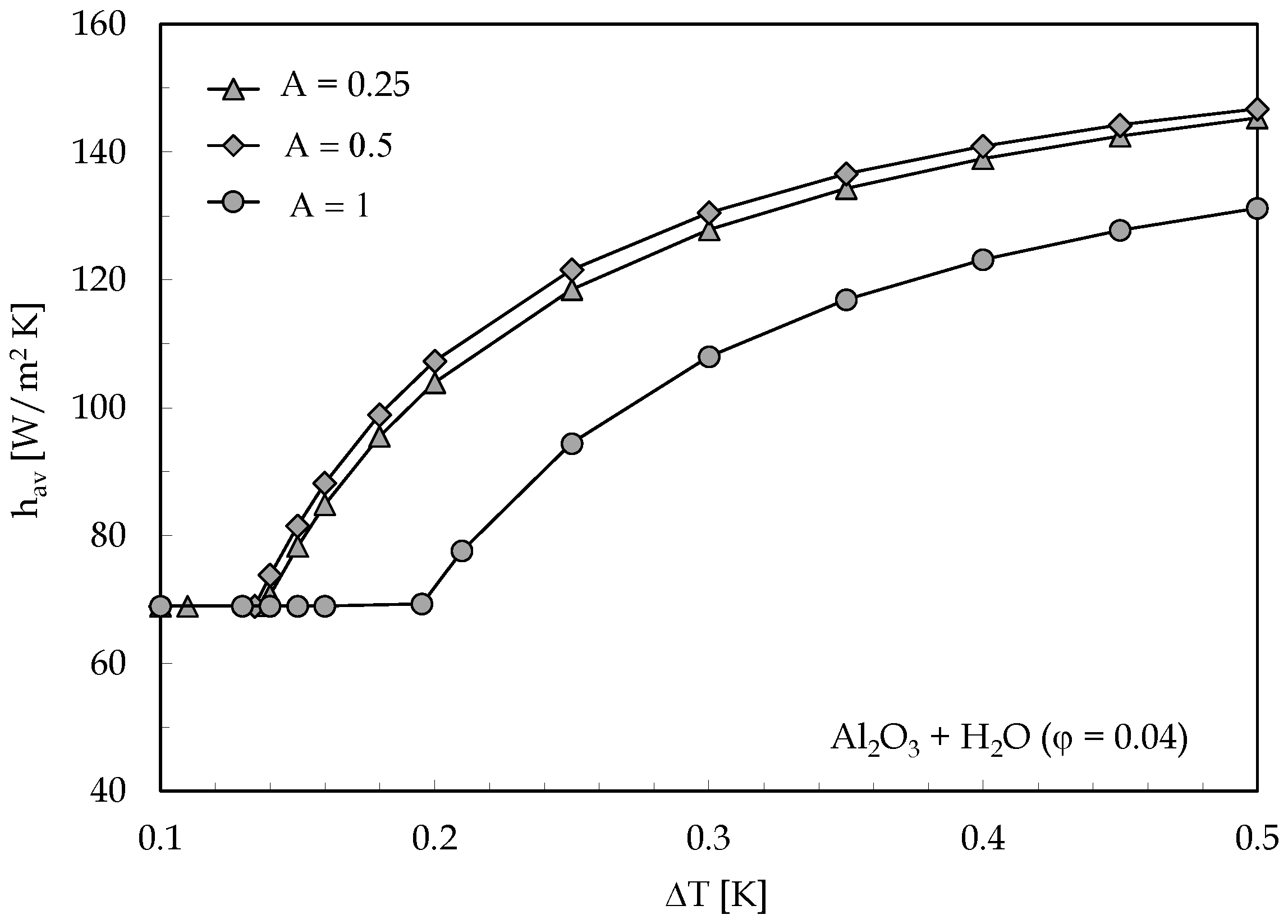
- The nanoparticles migration from hot to cold results in a pronounced reduction in the critical condition for the onset of convection in comparison with the case of the single-phase approach;
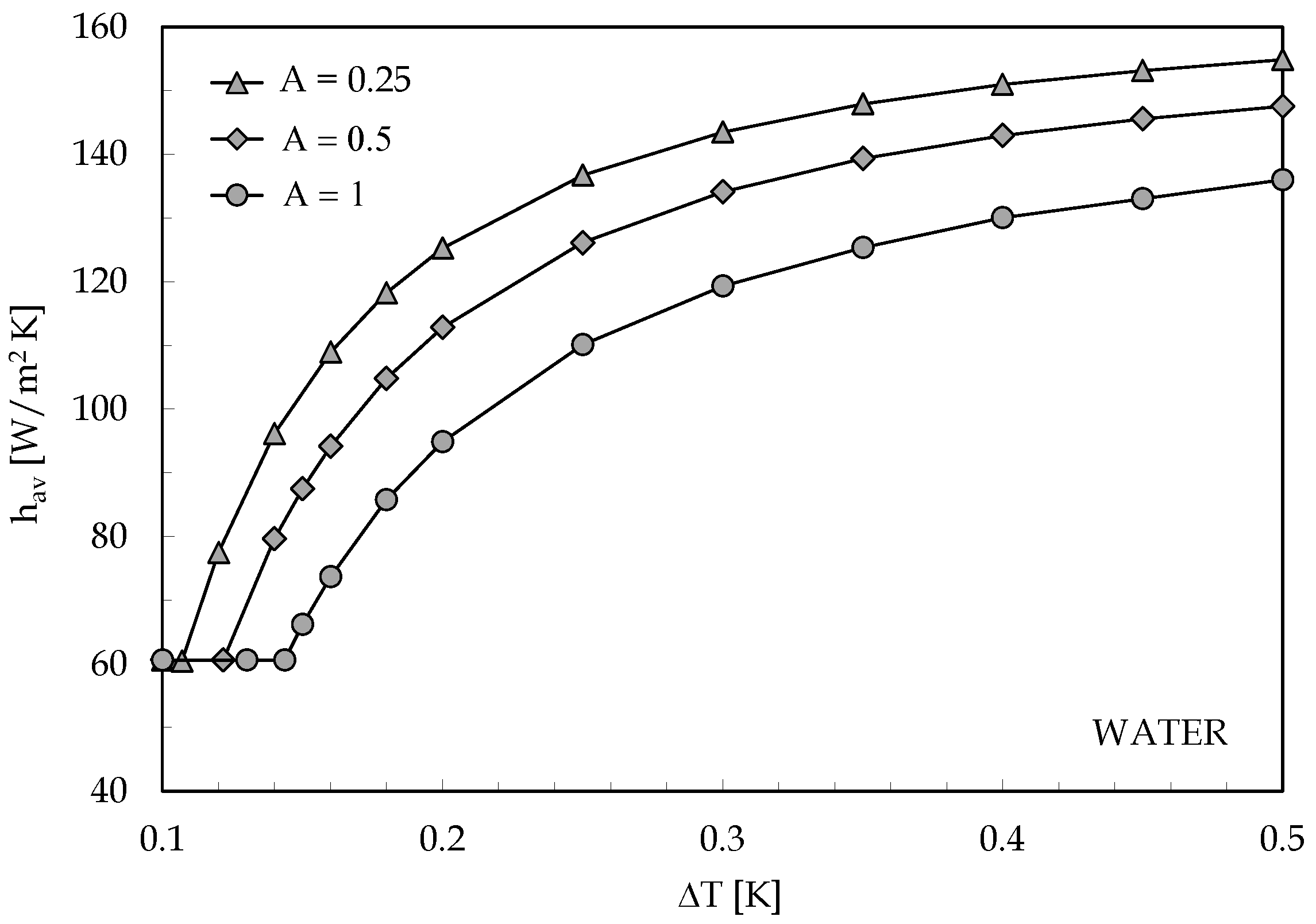
- The value of the difference of temperature corresponding to the onset of convection decreases with decreasing the aspect ratio of the cavity;
- The onset of convection is anticipated for TiO2 + H2O than for CuO + H2O and Al2O3 + H2O, due to the higher value of thermophoresis parameter .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wen, D.; Ding, Y. Natural convective heat transfer of suspensions of titanium dioxide nanoparticles (nanofluids). IEEE Trans. Nanotechnol. 2006, 5, 220–227. [Google Scholar]
- Rao, S.; Srivastava, A. Interferometric study of natural convection in a differentially-heated cavity with Al2O3–water based dilute nanofluids. Int. J. Heat Mass Transf. 2016, 92, 1128–1142. [Google Scholar] [CrossRef]
- Chang, B.H.; Mills, A.F.; Hernandez, E. Natural convection of microparticles suspensions in thin enclosures. Int. J. Heat Mass Transf. 2008, 51, 1332–1341. [Google Scholar] [CrossRef]
- Hwang, K.S.; Lee, J.; Jang, S.P. Buoyancy-driven heat transfer of water-based Al2O3 nanofluids in a rectangular cavity. Int. J. Heat Mass Transf. 2007, 50, 4003–4010. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U.S. The role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316–4318. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particle. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Park, H.M. Rayleigh-Benard convection of nanofluids based on the pseudo-single-phase continuum model. Int. J. Therm. Sci. 2015, 90, 267–278. [Google Scholar] [CrossRef]
- Kim, J.; Kang, Y.T.; Choi, C.K. Analysis of convective instability and heat transfer characteristics of nanofluids. Phys. Fluids 2004, 16, 2395. [Google Scholar] [CrossRef]
- Tzou, D.Y. Thermal instability of nanofluids in natural convection. Int. J. Heat Mass Transf. 2008, 51, 2967–2979. [Google Scholar] [CrossRef]
- Tzou, D.Y. Instability of nanofluids in natural convection. J. Heat Transf. 2008, 130, 072401. [Google Scholar] [CrossRef]
- McNab, G.S.; Meisen, A. Thermophoresis in liquids. J. Colloid Interf. Sci. 1973, 44, 339–346. [Google Scholar] [CrossRef]
- Ryskin, A.; Muller, H.W.; Pleiner, H. Thermal convection in binary fluid mixtures with a weak concentration diffusivity, but strong solutal buoyancy forces. Phys. Rev. E 2003, 67, 046302. [Google Scholar] [CrossRef] [PubMed]
- Nield, D.A.; Kuznetsov, A.V. The effect of local thermal nonequilibrium on the onset of convection in a nanofluid. J. Heat Transf. 2010, 132, 052405. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of double-diffusive convection in a nanofluid layer. Int. J. Heat Fluid Flow 2011, 32, 771–776. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of convection in a nanofluid layer of finite depth: A revised model. Int. J. Heat Mass Transf. 2014, 77, 915–918. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of convection in an internally heated nanofluid layer. J. Heat Transf. 2014, 136, 014501. [Google Scholar] [CrossRef]
- Agarwal, S.; Rana, P.; Bhadauria, B.S. Rayleigh–Benard convection in a nanofluid layer using a thermal nonequilibrium model. J. Heat Transf. 2014, 136, 122501. [Google Scholar] [CrossRef]
- Haddad, Z.; Abu-Nada, E.; Oztop, H.F.; Mataoui, A. Natural convection in nanofluids: Are the thermophoresis and Brownian motion effects significant in nanofluid heat transfer enhancement? Int. J. Therm. Sci. 2012, 57, 152–162. [Google Scholar] [CrossRef]
- Ho, C.J.; Chen, D.; Yan, W.; Mahian, O. Rayleigh–Bénard convection of Al2O3/water nanofluids in a cavity considering sedimentation, thermophoresis, and Brownian motion. Int. Commun. Heat Mass Transf. 2014, 57, 22–26. [Google Scholar] [CrossRef]
- Eslamian, M.; Ahmed, M.; El-Dosoky, M.F.; Saghir, M.Z. Effect of thermophoresis on natural convection in a Rayleigh–Benard cell filled with a nanofluid. Int. J. Heat Mass Transf. 2015, 81, 142–156. [Google Scholar] [CrossRef]
- Savithiri, S.; Pattamatta, A.; Das, S. Rayleigh–Benard convection in water-based alumina nanofluid: A numerical study. Numer. Heat Transf. Part A 2017, 71, 202–214. [Google Scholar] [CrossRef]
- Sun, M.; Wang, G.; Zhang, X. Rayleigh-Bénard convection of non-Newtonian nanofluids considering Brownian motion and thermophoresis. Int. J. Therm. Sci. 2019, 139, 312–325. [Google Scholar] [CrossRef]
- Ahuja, J.; Sharma, J. Rayleigh-Bénard instability in nanofluids: A comprehensive review. Micro Nano Syst. Lett. 2020, 8, 1–15. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Das, S.K.; Putra, N.; Roetzel, W. Pool boiling characteristics of nano-fluids. Int. J. Heat Mass Transf. 2003, 46, 851–862. [Google Scholar] [CrossRef]
- Prasher, R.; Song, D.; Wang, J.; Phelan, P. Measurements of nanofluid viscosity and its implications for thermal applications. Appl. Phys. Lett. 2006, 89, 133108. [Google Scholar] [CrossRef]
- He, Y.; Jin, Y.; Chen, H.; Ding, Y.; Cang, D.; Lu, H. Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transf. 2007, 50, 2272–2281. [Google Scholar] [CrossRef]
- Chen, H.; Ding, Y.; He, Y.; Tan, C. Rheological behaviour of ethylene glycol based titania nanofluids. Chem. Phys. Lett. 2007, 444, 333–337. [Google Scholar] [CrossRef]
- Chevalier, J.; Tillement, O.; Ayela, F. Rheological properties of nanofluids flowing through microchannels. Appl. Phys. Lett. 2007, 91, 233103. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Pastoriza-Gallego, M.J.; Piñero, M.M.; Lugo, L. Characterization and measurements of thermal conductivity, density and rheological properties of zinc oxide nanoparticles dispersed in (ethane-1,2-diol + water) mixture. J. Chem. Thermodyn. 2013, 58, 405–415. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 17, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Brenner, H.; Bielenberg, J.R. A continuum approach to phoretic motions: Thermophoresis. Physica A 2005, 355, 251–273. [Google Scholar] [CrossRef]
- Corcione, M.; Cianfrini, M.; Quintino, A. Enhanced natural convection heat transfer of nanofluids in enclosures with two adjacent walls heated and the two opposite walls cooled. Int. J. Heat Mass Transf. 2015, 88, 902–913. [Google Scholar] [CrossRef]
- Corcione, M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. NIST Chemistry WebBook; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: http://webbook.nist.gov (accessed on 10 December 2021).
- Das, S.K.; Putra, N.; Thiesen, P.; Roetzel, W. Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat Transf. 2003, 125, 567–574. [Google Scholar] [CrossRef]
- Mintsa, H.A.; Roy, G.; Nguyen, C.T.; Doucet, D. New temperature dependent thermal conductivity data for water-based nanofluids. Int. J. Therm. Sci. 2009, 48, 363–371. [Google Scholar] [CrossRef]
- Greenshields, C. OpenFOAM User Guide; Version 8; OpenFOAM Foundation Ltd.: Reading, UK, 2022. [Google Scholar]
- Hollands, K.G.T.; Raithby, G.D.; Konicek, L. Correlation equations for free convection heat transfer in horizontal layers of air and water. Int. J. Heat Mass Transf. 1975, 18, 879–884. [Google Scholar] [CrossRef]
- Putra, N.; Roetzel, W.; Das, S.K. Natural convection of nano-fluids. Heat Mass Transf. 2003, 39, 775–784. [Google Scholar] [CrossRef]
- Corcione, M.; Cianfrini, M.; Quintino, A. Temperature effects on the enhanced or deteriorated buoyancy-driven heat transfer in differentially heated enclosures filled with nanofluids. Numer. Heat Transf. Part A 2016, 70, 223–241. [Google Scholar] [CrossRef]
- Ho, C.J.; Liu, Y.S.; Chang, Y.S.; Lin, C.C. Natural convection heat transfer of alumina-water nanofluid in vertical square enclosures: An experimental study. Int. J. Therm. Sci. 2010, 49, 1345–1353. [Google Scholar] [CrossRef]

| Nanoparticles | (kg/m3) | k (W/m K) | Cp (J/kg K) |
|---|---|---|---|
| Al2O3 | 3880 | 36 | 773 |
| CuO | 6500 | 17.6 | 540 |
| TiO2 | 4175 | 8.4 | 692 |
| A | av | Mesh Size | Q (W) | max | min |
|---|---|---|---|---|---|
| 1 | 0.01 | 0.661 | 0.00975 | 0.00930 | |
| 0.676 | 0.01007 | 0.00947 | |||
| 0.687 | 0.01030 | 0.00966 | |||
| 0.692 | 0.01040 | 0.00970 | |||
| 1 | 0.01 | 0.623 | 0.03950 | 0.03718 | |
| 0.641 | 0.04012 | 0.03802 | |||
| 0.650 | 0.04059 | 0.03863 | |||
| 0.656 | 0.04080 | 0.03890 | |||
| 0.25 | 0.04 | 2.731 | 0.03865 | 0.03710 | |
| 2.816 | 0.03955 | 0.03790 | |||
| 2.891 | 0.04051 | 0.03836 | |||
| 2.920 | 0.04070 | 0.03870 |
| Mesh Size | t (s) | Q (W) | max | min |
|---|---|---|---|---|
| 2.749 | 0.03843 | 0.03642 | ||
| 2.817 | 0.03954 | 0.03728 | ||
| 2.868 | 0.04015 | 0.03818 | ||
| 2.891 | 0.04051 | 0.03836 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corcione, M.; Quintino, A. Double-Diffusive Effects on the Onset of Rayleigh-Benard Convection of Water-Based Nanofluids. Appl. Sci. 2022, 12, 8485. https://doi.org/10.3390/app12178485
Corcione M, Quintino A. Double-Diffusive Effects on the Onset of Rayleigh-Benard Convection of Water-Based Nanofluids. Applied Sciences. 2022; 12(17):8485. https://doi.org/10.3390/app12178485
Chicago/Turabian StyleCorcione, Massimo, and Alessandro Quintino. 2022. "Double-Diffusive Effects on the Onset of Rayleigh-Benard Convection of Water-Based Nanofluids" Applied Sciences 12, no. 17: 8485. https://doi.org/10.3390/app12178485
APA StyleCorcione, M., & Quintino, A. (2022). Double-Diffusive Effects on the Onset of Rayleigh-Benard Convection of Water-Based Nanofluids. Applied Sciences, 12(17), 8485. https://doi.org/10.3390/app12178485







