Abstract
Although widely used in various fields due to its powerful capability of signal processing, empirical mode decomposition has to decompose signals separately, which limits its application for multivariate data such as the structural monitoring data recorded by multiple sensors. In order to avoid this shortcoming, a multivariate extension of empirical mode decomposition is proposed to deal with the multidimensional signals synchronously by employing a real-valued projection on hyperspheres. This study presents a hybrid modal identification method combining the multivariate empirical mode decomposition with stochastic subspace identification and fast Bayesian FFT methods to more conveniently and accurately identify structural dynamic parameters from multi-sensor vibration measurements. Deployed as a preprocessing tool, the multivariate signals are decomposed into several aligned intrinsic mode functions, which contain only a dominant component in the frequency domain. Then, the modal parameters can be identified by advanced fast Bayesian FFT and stochastic subspace identification directly. The combined method is first validated by a numerical illustration of a frame structure and then is applied in a shaking table test and a full-scale measurement under nonstationary earthquake excitation. Compared with the finite element method, the peak–pick, the half-power bandwidth methods, and Hilbert–Huang transform method, the results show that this hybrid method is more robust and reliable in the modal parameters identification. The main contribution of this paper is to develop a more effective integrated approach for accurate modal identification with the output-only multi-dimensional nonstationary signal.
1. Introduction
Modal identification is attracting growing attention in civil engineering for its wide application in the field of model updating, damage detection, structural control, and dynamic performance prediction. In the full-scale measurement of high-rise buildings or bridges, the input excitations are generally unavailable hence more efforts are devoted to developing the output-only modal identification methods. In the past decades, numerous algorithms were put forward, which could be mainly divided into two main categories (i.e., the time domain methods and the frequency domain methods). In the frequency domain, frequency decomposition and its reversions are the most representative and widely used [1,2]. In terms of the time domain, the random decrement technique and the natural excitation [3] are utilized to obtain the free vibration response, and then the modal parameters can be obtained by some other traditional identification algorithms, including the eigensystem realization algorithm, the Ibrahim time domain, the least square complex exponential, etc.
Additionally, the majority of the conventional methods are on the basis of the stationary assumption which is often violated in hazardous conditions, such as strong winds or earthquake excitations. To meet this situation, more improvements were made to overcome the limits of the stationary assumption. Abazarsa et al. [4] employed a clustering technique to expand the blind modal identification method [5] to identify the modal parameter from the seismic response. Assuming the nonstationary response is a sum of exponential functions, Chiang and Lin [6] improved the Ibrahim time-domain method with a channel-expansion technique for a nonstationary white noise excitation.
Notably, for the nonstationary signals or the time-dependent system, the Hilbert–Huang transform (HHT) is a powerful and adaptive approach to capture the time-dependent characteristics [7,8]. The HHT contains two main procedures: the empirical mode decomposition (EMD) and the Hilbert spectrum analysis by means of the Hilbert transform. Without choosing basis functions, the EMD is data-driven and suitable to deal with the nonstationary signals: therefore, it is widely used in the field of modal identification combined with other methods, such as the random decrement technique [9,10], stochastic subspace identification (SSI) [11] and natural excitation technique [12]. It should be noted that in the full-scale measurements, the multi-dimensional dynamic responses could be recorded synchronously by multiple sensors whereas the conventional EMD, which works only for a single signal, faces a severe problem of mode misalignment, i.e., the decomposed intrinsic mode functions (IMFs) from multiple sensors usually do not match in terms of their frequency order. More difficulties lie in the identification of mode shapes. For the IMFs derived from various signals, the number of IMFs tends to be different and usually does not match in a frequency scale; therefore, the direct usage of IMFs for mode shapes may lead to a faulty result. Subsequently, the EMD and the EMD-based modal identification algorithm might become invalid while dealing with measurements of multiple sensors or multi-dimensional signals. To overcome the limitation of EMD, the bivariate and trivariate EMD are proposed with the concept of rotating mode components [13,14], and eventually, the multivariate empirical mode decomposition (MEMD) was developed as a generic extension of EMD which could compute the multivariate IMFs directly by projecting the signal in a multi-dimensional space [14]. Then, the MEMD was applied in many practical fields. Huang et al. [15] employ MEMD to decompose downburst wind records, extract the time-varying means and carry out the time–frequency analysis. Sadhu [16] and Barbosh et al. [17] explored a hybrid MEMD with the EEMD and independent component analysis (ICA) to identify the modal parameters from the numerical and experimental illustrations containing measurement noise, low energy and closely spaced modes. It is thus effective and reliable that the MEMD is adopted in this study to decompose the multi-dimensional nonstationary signal. After obtaining each single-frequency component, the peak–pick (PP), the half-power bandwidth (HPBW) methods and the HHT method are usually employed to identify the parameters of each component. Notably, SSI, an advanced output-only time domain method, can derive the modal parameters directly from the time history response. Based on the singular value decomposition (SVD), it is capable to filter extra noise from the dynamic response which causes a serious ending effect affecting the calculation accuracy of modal parameters by the HHT method. Additionally, as a more attractive tool, the Fast Bayesian FFT(FBFFT) method can obtain, not only the modal frequencies, but also corresponding posterior uncertainty, which is widely employed by many researchers [18,19,20] to identify the modal parameters. Thus, the SSI and FBFFT are reliable, and worth being adopted in this study.
This paper aims to develop a more effective approach for accurate modal parameter identification with the output-only multi-dimensional nonstationary signal by integrating appropriate analysis tools and then comparing it with the commonly used methods. Firstly, a brief review of the MEMD is introduced. Then, the MEMD-based modal identification, including the SSI and the FBFFT methods is combined in Section 2. Notably, using MEMD, the manual-picked system order in SSI is significantly simplified. Section 3 employs a numerical illustration of a 5-storey frame structure and the experimental shaking table test to demonstrate the accuracy and robustness of the MEMD-based modal identification approach. In addition, the MEMD-based method is applied to a full-scale high-rise tower with multi-sensor data recorded under the earthquake in Section 4. Finally, some discussion and concluding remarks are provided.
2. Methodology
2.1. MEMD
For an n-dimensional signal , each component can be easily decomposed into several IMFs by the EMD method individually. The main drawback here is that the IMFs derived from the different components are non-uniform in the number of IMFs or cannot match in frequency scale, which is also called mode misalignment. To decompose the signal synchronously and uniformly, the standard EMD method is developed to handle the complex signals.
In the standard EMD method [7,8], the envelope is generated with a spline by interpolating the local maximums and minimums, whereas for the multi-dimensional signal , it is difficult to define the local extreme values directly. To overcome the problem, the rotational mode is developed as an extension of the oscillatory mode, based on the assumption that the original signal consists of the slow and fast rotation components. The envelopes are generated by projecting the signal along multiple directions in n-dimensional space and interpolating the local maximums and minimums in splines. Then, the n-dimensional local mean can be obtained by averaging the multiple envelopes [14,21]. Owing to the fact that the local mean is the approximation of the integration of all multiple envelopes, the choice of directional vectors in the n-dimensional space has a significant impact on the accuracy of the local mean values, especially when the number of direction vectors is quite limited. To yield a more uniform distribution of directional vectors, the low-discrepancy sequences [22], including the Halton and Hammersley sequences are adapted to generate the directional vectors. The main procedures of the MEMD method can be listed in the following steps [14,23,24,25]:
- (1)
- Generate n-point low-discrepancy Hammersley sequences to sample on an () dimensional sphere.
- (2)
- Project the original signal along each directional vector , where is the number of directional vectors, denoted as of each vector.
- (3)
- Pick up the time instants of the maximums of every projection .
- (4)
- Interpolate to generate the multiple envelope by a spline.
- (5)
- Calculate the mean curve for all envelopes
- (6)
- Subtract the mean curve from the original signal . If the detail satisfies the stoppage criterion, it can be regarded as the first IMF, otherwise, repeat step 2 to step 5 to regenerate . Then, apply the above steps with to obtain other IMFs.
One should be pointed out that the stoppage criterion adopted in MEMD is adopted from the standard EMD method [8]. Due to the unavailable extreme values of multi-dimensional signals, the equality of the number of extremes and zero crossing is ignored.
2.2. Memd-Based Identification Methods
This section aims to integrate a more effective approach for accurate modal identification with the output-only multi-dimensional nonstationary signal. To this end, two modal identification methods, the SSI and FBFFT method are used and combined with the MEMD procedure to extract the modal parameters involving the natural frequency, damping ratio, and mode shapes.
2.2.1. MEMD-Based SSI (MSSI) Method
Numerous variants of the SSI method are developed, which are mainly based on two visions (i.e., the data-driven SSI (SSI-DATA) method and the covariance-driven SSI method). In this research, the latter is used to identify the modal parameters.
For a linear system, after modeling under white noise excitation, the dynamic response (i.e., acceleration response) with the discrete time can express in the following state–space equation [26,27,28]:
in which and are the state and output matrix, respectively; and are the input and output vectors, respectively, and are assumed to be the zero-mean white noises.
In the covariance-driven SSI, the modal parameters are identified from the state and output matrix (i.e., and ) of the stochastic state–space model. To this end, the first step is to construct the Hankel data matrix with the measured data and then calculate the block Toeplitz matrix with the block output covariance, as respectively shown in Equations (3) and (4).
where and are the past and future measured matrix; is the block covariance between all outputs as . The SVD is applied to the Toeplitz matrix , decomposed as
where and are the orthonormal matrices; is the diagonal matrix containing the singular values in descending order.
By factorizing the Toeplitz matrix into an extend observation matrix and reversed extend control matrix, the system matrix in Equation (2) can be computed as
Meanwhile, the output matrix equals the first rows of . A more detailed process of reasoning can be found in the reference [26]. Then, the estimation of the modal parameters starts with the eigenvalue decomposition of , where is a diagonal matrix containing the discrete time complex eigenvalues and denotes the eigenvectors as columns. The natural frequencies and damping ratio can be obtained from the continuous time conjugated eigenvalues () [27], and the mode shapes are the multiplication of eigenvectors and output matrix .
The number of the singular values in Equation (5) denotes the system order n. Note that in practical structures, it is quite difficult to determine the system order directly from the singular value of the Toeplitz matrix since the singular values associated with tend to be small numbers rather than zero under the influence of noise. If the selected system order deviates from the required order, the identified results will miss some physical modes or yield some spurious modes. Generally, the stabilization diagram of the identified modal parameters with the increasing order is employed to decide the order of the system to search the stable poles. However, the quality of the stabilization diagram is still highly related to the noise and for the structures with quite close modes, it is still not easy to pick up the exact system order [29,30,31,32]. Thus, the MEMD is deployed as a preprocessing tool, aiming to reduce the effect of noise and obtain a credible system order. For the MSSI method, the multivariate signals are firstly decomposed into several aligned IMFs. Basically, the divided signals contain only a dominant component in the frequency domain, and the majority of the noise is filtered out.
2.2.2. MEMD-Based FBFFT (MFBFFT) Method
Based on Bayes’ theorem, several modal identification methods are proposed to determine the most probable value (MPV) of modal parameters as well as the posterior uncertainties [33]. Notably, this theorem is originally based on the assumption of the white noise excitation and stationary process. Whereas, the wind load or earthquake load, as the wide-band excitation, does not generally satisfy the condition of the stationary white noise process. Fortunately, under this condition, the FBFFT also proves to be credible and robust [34]. The FBFFT method is thus adapted to identify the modal parameters under the nonstationary process in this study.
In the FBFFT method, the measured acceleration response is modeled as the practical part and the error resulted from the measurement or noise:
where denotes the modal parameters including the natural frequency , damping ratio , spectrum values of modal force and error.
Define an augmented vector , in which and are the real and imaginative part of the FFT of the and k is the number of associated frequencies. By virtue of the Bayes’ theorem, the posterior probability density function of given by is proportional to the likelihood function.
For the recorded response data in a high sampling rate and long duration, is proved to be asymptotically independent and zero mean Gaussian vector. Hence the likelihood function can be given as
where is the covariance function of , referenced to Yuen et al. [35]; is the number of frequency point.
For the purpose of simplifying the procedure of optimization, the negative log-likelihood function is defined as and can be expressed as
The MPV of the modal parameter can be obtained by the minimization of . However the direct usage of Equation (10) is not convenient and efficient until Au and Ping [34] proposed a fast algorithm for well-separated modes. Meanwhile, the posterior uncertainty can be defined as the coefficient of variation (COV) (coefficient of variation = standard deviation/MPV). Since seismic excitation is a typical non-stationary process, the MEMD is also adopted as a pre-processing tool to the FBFFT method for identifying the modal parameters from the seismic-induced response.
3. Case Study
3.1. Numerical 5-Storey Frame Structure
The finite element model of a 5-storey, 3-bay by 5-bay frame structure as shown in Figure 1 is established by SAP 2000 to validate the MEMD-based modal identification method. The overall height of the modal is 15 m with a story height of 3 m and a bay of 2.5 m. The sections of the beam and column elements are the size: 0.3 m × 0.5 m and 0.4 m × 0.4 m, respectively. All of them are made of C30 concrete. The natural frequencies of the first two sway modes are 3.5374 Hz and 3.7821 Hz, respectively. The modal damping ratios for calculating the dynamic response are assumed uniformly to be 3%. The input excitation of the model is 1 dB white Gaussian noise with a sampling frequency of 50 Hz. The structural responses of 5 gauge points as shown in Figure 1 are picked up from the SAP 2000.
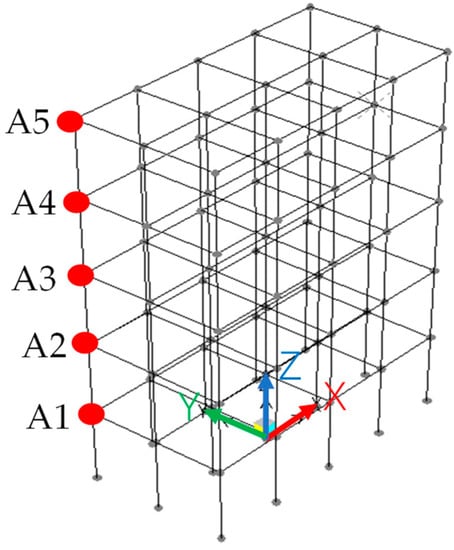
Figure 1.
A 5-storey frame structure.
To validate the accuracy and robustness of the MEMD-based method, a sinusoidal noise is added to the extracted response and the amplitude is a quarter of the standard deviation of the associated response as Equation (11).
where is the response of th point, is the associated standard derivation and is the noise-added response.
Figure 2 displays the noise-added structural responses of point A5 along the direction of the X and Y axis. The associated noise-added signal at each point is decomposed by the MEMD method and the X-direction results of the first five IMFs are displayed in Figure 3, in which (X1)2 stands for the 2nd IMF of X-direction response of point A1, and so on. Figure 4 shows the time–frequency spectrum using the Hilbert transform, from which the time–frequency distribution and the associated amplitude of each IMFs can be easily figured out. Figure 4b,d show the components with a dominant frequency of 11 Hz and 3.5 Hz, which are corresponded to the second and first sway vibration mode of X-direction, respectively. Subsequently, IMF2 and IMF4 are used for identifying the modal parameters of the X-direction. By repeating a similar procedure, the modal parameters of the Y-direction can be obtained.
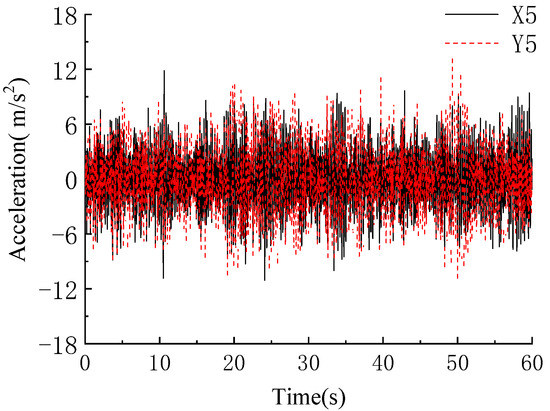
Figure 2.
Noise-added acceleration time histories at Point A5.
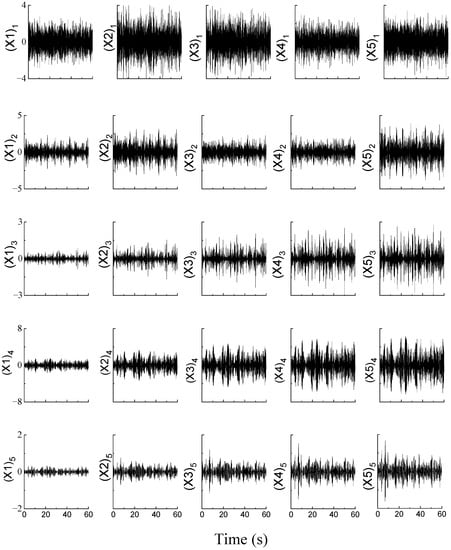
Figure 3.
First five IMFs of the 5-storey frame structure by MEMD decomposition.
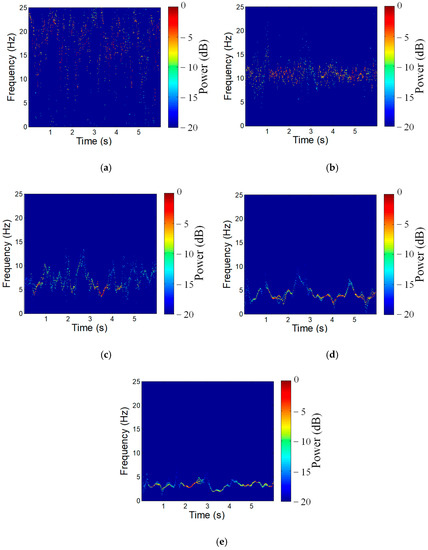
Figure 4.
Hilbert spectrum of the first five IMFs. (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5.
The identified frequencies and damping ratios of sway modes are summarized in Table 1 and Table 2, together listing the results identified by the finite element method (FEM), the peak–pick, and the half-power bandwidth methods. Meanwhile, the mean absolute relative deviation (MARD) [36] is calculated to evaluate the accuracy of modal identification, as following equation.
where and are the identified and exact modal parameters at the jth mode, respectively; is the number of the identified modes.

Table 1.
Identified natural frequencies (Hz) of four sway modes for a numerical model of the structure.

Table 2.
The identified damping ratio of four sway modes for a numerical model of the structure.
It can be noted that the frequencies identified from the noise-added response by several methods are satisfactory and the relative error, MARD, is almost less than 1%, revealing the high precision of the identified frequencies. However, compared with the frequency, more deviations in damping ratio can be seen, especially by the HPBW and the HHT methods which may be strongly affected by the limited length and nonstationary characteristics of the acceleration response. By employing the MEMD, it can be observed that by the FBFFT method the MARD of damping ratio falls to 3.92% from 6.42%, and by the SSI method, it reduces from 6.17% to 1.50%, indicating that with the employment of the MEMD the errors of damping ratio caused by sinusoidal noise effect in the original signal can be significantly decreased.
The mode shapes of sway vibration modes are shown in Figure 5. The mode shapes of the frame structure are normalized by making the modal contribution coefficient of the top measuring point A5 the unit. The results in Figure 5 demonstrate that the mode shapes identified by MSSI and MFBFFT methods are almost consistent with that given by the FEM. In order to verify the correlation between the identified and the FEM mode shapes, corresponding modal assurance criteria (MAC) and the normalized modal difference (NMD) [37,38] are calculated as
where and are the jth identified and FEM analyzed mode shape vectors, respectively. The MAC and NMD values are summarized in Table 3. Generally, a greater MAC value and a smaller NMD represent a reasonable match. Meanwhile, considering that the minimum of MAC and the maximum of NMD from Table 3 are 99.45% and 7.42% respectively, it is thus clearly known that the mode shape vectors identified by the MEMD-based methods are very close to the FEM vectors.
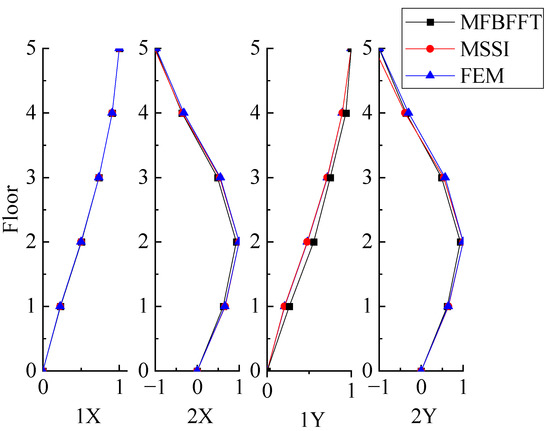
Figure 5.
Comparison of the mode shapes for a numerical model of the structure.

Table 3.
Correlation index of the identified and FEM mode shapes.
Moreover, system order is an important parameter when performing the SSI method, which is usually determined from the gap of singular value decomposition of the Toeplitz matrix. As shown in Figure 6, it is clearly observed that there lie three significant gaps in Figure 6a when N = 10, 40, 46, and only one when N = 4 when employing the MEMD. Though it is easy to obtain the real system order with the aid of other stability diagrams due to the fewer degrees of freedom in this FEM model, by means of the MEMD method, it can be picked out directly and precisely.
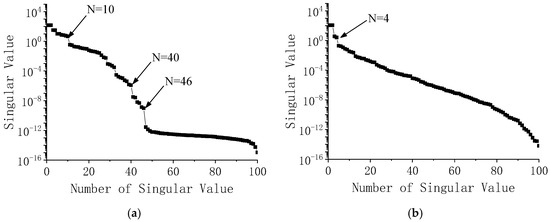
Figure 6.
Singular spectrum from SVD of Toeplitz matrix. (a) Original data; (b) IMFs decomposed by MEMD.
3.2. Shaking Table Modal Test
To examine the robustness of the proposed MEMD-based identification methods in seismic excitations, the acceleration response of a 12-storey reinforced frame in shaking table model tests [39] is utilized as a case study. The length scale of the model is 1/10 with an overall height of 3.6 m, beams of 30 mm × 30 mm, and columns of 50 mm × 60 mm, as shown in Figure 7. To measure the dynamic response of the model, more than 61 operating conditions were carried out and 25 channels of accelerometers were instrumented in the model. More information about the shaking table modal was presented by Lu [40]. In this study, the acceleration response of seven channels in X-direction with the sampling frequency of 255 Hz during El Centro excitation is adopted to identify the modal parameters. The original responses and corresponding IMFs of A6 and A7 points are shown in Figure 8. Absolutely, the signals to be decomposed (i.e., X6 and X7 in Figure 8) contain nonstationary features.
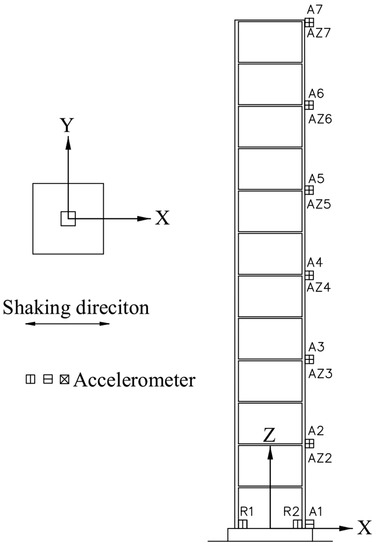
Figure 7.
View of frame model and accelerometers of the shaking table test.
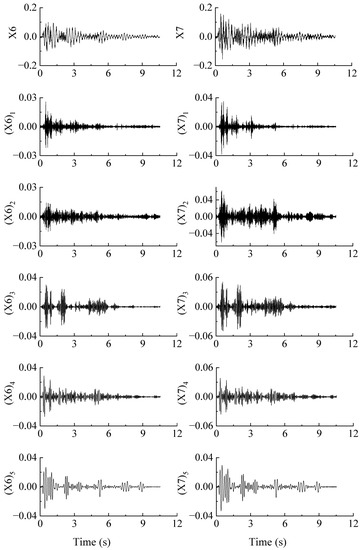
Figure 8.
First five IMFs of the shaking table test by MEMD decomposition.
The identified frequencies and damping ratios of the first four modes are summarized in Table 4 and Table 5, together listing the frequencies of FEM and other results identified by ERA methods [12]. It can be observed that the frequencies identified from the seismic response are still comparable with the FEM despite the original data being a typical nonstationary process and the length of data being only 2688. Similarly, the MARD is used to evaluate the accuracy of the results on the basis of the FEM. The MARD of frequencies is 4.7% by the MFBFFT method and 3.7% by the MSSI method, indicating the proposed MEMD-based methods are capable to identify the natural frequencies from the seismic response. For the damping ratio, the variation between different methods is relatively large and the identified COVs of the damping ratio remain at a high level, implying greater posterior uncertainties. It can be seen from Table 5 that there is a tendency for the modal damping ratio to decrease with the increase in modes. Due to the exact value of the damping ratio being unavailable, the mean values of the results identified by the different methods are regarded as the benchmark instead. The MARDs of damping ratio are larger than 10% except that, by the HHT method, it is only 3.7%. By employing the EMD method, the MARD of the FBFFT method decreases to 10.2% from 15.6% and by the SSI method, it falls to 21.6% from 23.3%, respectively.

Table 4.
Identified results of the natural frequencies (Hz) for the shaking table test.

Table 5.
Identified results of the damping ratios for the shaking table test.
The stabilization diagrams during the SSI method are displayed in Figure 9. Owing to the limited length of the response, the frequency resolution of the power spectrum density function is not high enough, making it difficult to find out the exact system orders as shown in Figure 9a. As for the selected IMFs decomposed by the MEMD method, extra vibration modes are filtered out, leaving only one dominant frequency component as shown in Figure 9b, which indicates a system order of two or four (a result from the remaining noise).
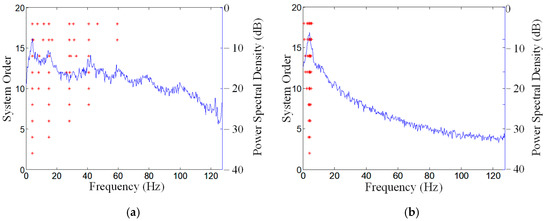
Figure 9.
Stabilization diagram of original and decomposed acceleration response for the shaking table test. (a) Original data; (b) IMF10.
4. Full-Scale Measurement of the Canton Tower
To further validate the MEMD-based approach for a nonstationary process, the acceleration data of the Canton Tower during the Heyuan earthquake are used in the present study. The Canton Tower, a 610 m tube-in-tube structure, was installed with a long-term structural health monitoring system comprised of more than 700 sensors, including 20 accelerometers [41], as shown in Figure 10. Since its constructive period, the monitoring system records rich data on the temperature, wind speed and dynamic performance of the structure during ambient excitation and several hazard events. More details can be referred to in Ni et al. [41,42].
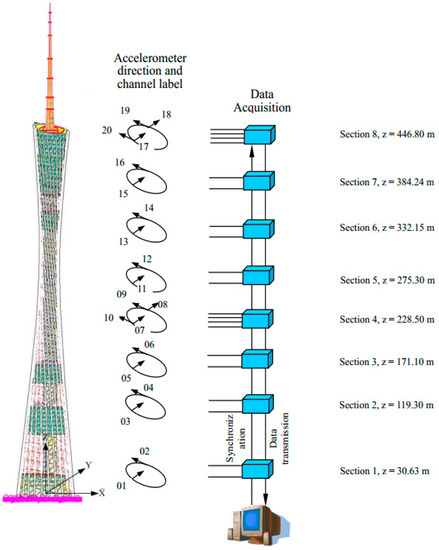
Figure 10.
View of Canton Tower and monitoring system.
The Heyuan earthquake, a 4.2-magnitude quake, occurred at 13:50 on 31st August 2012. The epicenter was only about 160 km away from the Canton Tower which was a typical short-distance earthquake for the structure. The acceleration responses recorded from 13:00 to 14:00 were utilized for extracting the modal parameters. The acceleration time histories atop the Canton Tower during the earthquake are shown in Figure 11. The maximum acceleration response at section 8 of the tower is only 0.53 milli-g due to the small magnitude of the quake. As shown in Figure 11, the strike instance of earthquake is reflected as a spike in the one-hour acceleration history. Since the paper is focusing on the modal identification method under the nonstationary excitation, it is reasonable to take Canton Tower with the Heyuan earthquake as an example to demonstrate the proposed MEMD-based modal identification method.
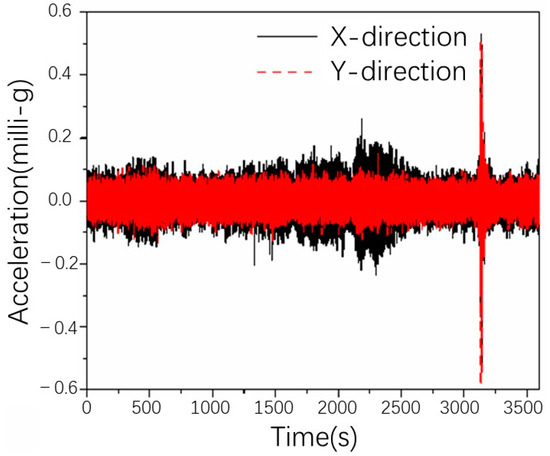
Figure 11.
Acceleration response measured atop Canton Tower during the earthquake.
The selected time histories recorded by the X-direction sensors and the Y-direction sensors were decomposed by the MEMD method independently. The vibration modes of Canton Tower are quite complex and close [43], and the original responses are mainly divided into 13 component IMFs in which the vibration modes are not perfectly decomposed. Fortunately, the mode mixing of the selected segment exists only in higher modes which provides a reasonable estimation of the first several modes. Figure 12 and Figure 13 show the time histories and the associated Hilbert spectrum of 7th–10th IMFs. It can be seen that the main frequency ranges from 0.07 Hz to 0.1 Hz. With the aid of power spectrum analysis, it can be inferred that the IMF8 and IMF10 are corresponding to the second and the first vibration mode of the X direction, respectively.
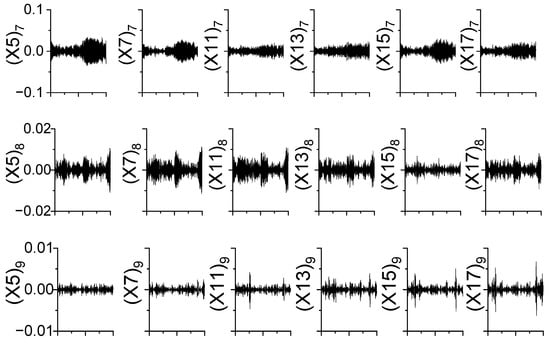
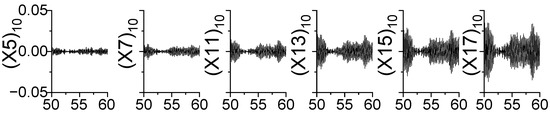
Figure 12.
7th–10th IMFs of X-direction response of Canton Tower.
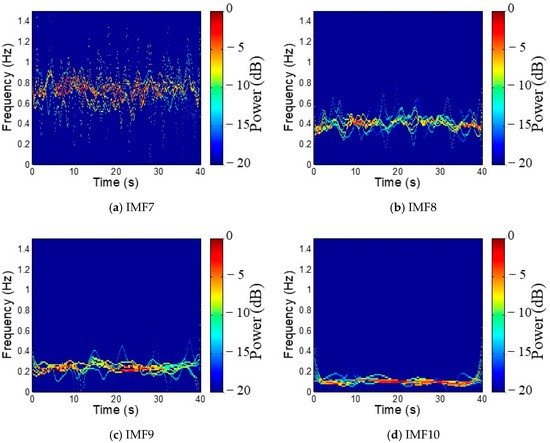
Figure 13.
Hilbert spectrum of the 7th–10th IMFs of X-direction. (a) IMF7; (b) IMF8; (c) IMF9; (d) IMF10.
Then, the modal parameters are mainly identified by the SSI and FBFFT methods. Due to the close and multiple vibration modes of the Canton Tower, it is still difficult to determine the exact system order in SSI methods using the singular spectrum and stabilization diagram as displayed in Figure 14a and Figure 15a. Loh et al. [29] adapted the system orders of 90 and 120 in the SSI method after reducing the noise with the singular spectrum analysis; nonetheless, the drawbacks that spurious modes cannot be avoided and some actual modes may be improperly filtered out still exist. Figure 14b and Figure 15b show the singular value and stabilization diagram of IMF10, the first vibration mode of X direction. It is obviously observed that, in Figure 14b, there is a significant gap in the distribution of singular value when N = 2 and in Figure 15b the frequency of stable poles almost indicates the same frequency, which is the only one peak in the figure of PSD function of the reference point. Therefore, for the decomposed signal, the system order can be set clearly as two.
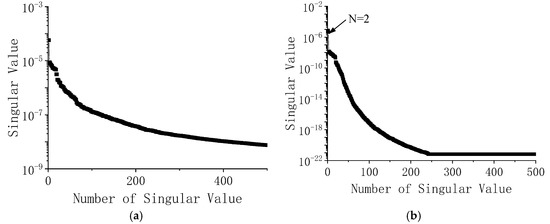
Figure 14.
Singular spectrum from SVD of Toeplitz matrix. (a) Original data; (b) IMF10.
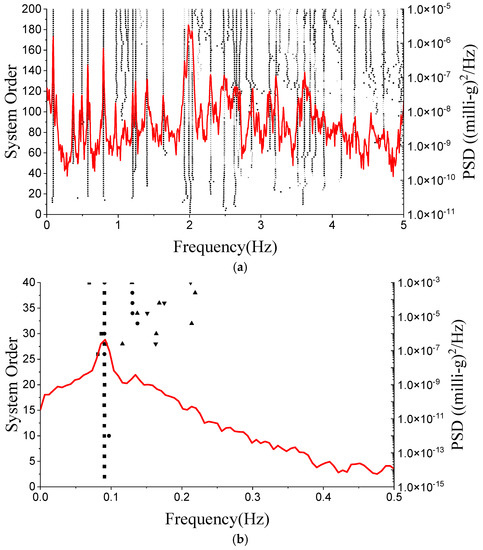
Figure 15.
Stabilization diagram of original and decomposed acceleration response for the Canton Tower. (a) Original data; (b) IMF10.
As mentioned before, the row of the Toeplitz matrix plays a significant role in discriminating between the noise and true vibration signal, so the effect between the various Toeplitz matrix row numbers with the modal parameters is taken into consideration as shown in Figure 16, in which each mode is identified separately with the system orders of two, except that the Mode4 and Mode5 are extracted synchronously from the 8th IMF of Y-direction so the system order is decided as four. It can be seen that the frequencies are quite stable with the increasing of the rows of the Toeplitz matrix in the stability diagram.
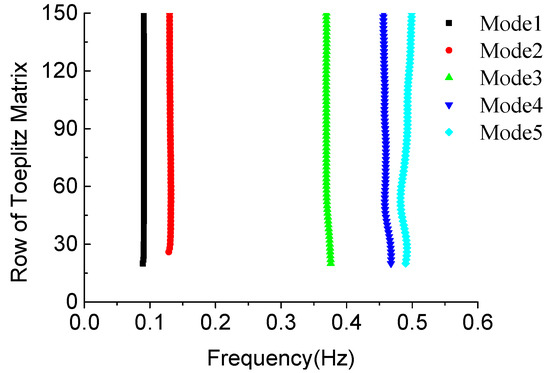
Figure 16.
The identified frequency with the varying row of Toeplitz matrix by SSI method.
The modal parameters of Canton Tower under earthquake excitation are identified by the MEMD-based SSI and FBFFT methods. In the FBFFT method, the initial frequencies are picked up from the power spectrum density function directly and frequency bands are manually selected approximately with a length of 10 percent of the initial frequency, as listed in Table 6. The identified frequencies and damping ratios together with other results by the HHT combined with the RDT method and HPBW are summarized in Table 7 and Table 8, respectively. In addition, for comparison, the modal parameters under the Shenzhen earthquake by the frequency decomposition method are listed together as well [44].

Table 6.
Initial frequency and frequency band by the FBFFT method of the Canton Tower.

Table 7.
Identified frequencies under earthquake of the Canton Tower.

Table 8.
Identified damping ratios under earthquake of the Canton Tower.
Similar to previous illustrations, the frequencies identified by various methods are consistent with each other, while damping ratios display great discreteness. The COVs of the frequencies in the Bayesian are less than 1%, showing high confidence, and associated COVs of the damping ratios of the first two modes are as much as 50%. Figure 17 shows the comparison of the identified mode shapes of Canton Tower. It can be seen that the mode shapes can be effectively identified by two methods that are consistent with each other, especially for the first two modes.
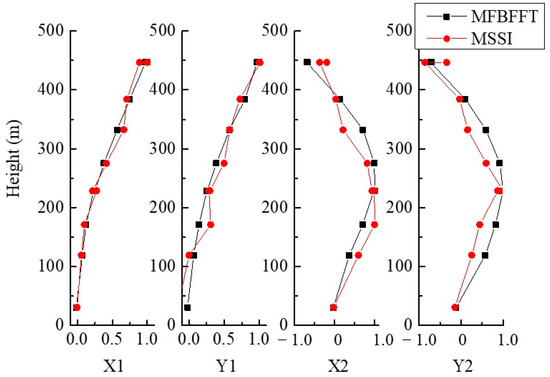
Figure 17.
Comparison of the identified mode shapes of the Canton Tower.
5. Discussion
This paper focuses on developing a trustworthy method for identifying the modal identification and comprehensive analysis on three types of acceleration responses, and was conducted to verify the validness and practicability of the combined methods.
A numerical 5-storey frame structure simulated by SAP2000 was first analyzed. The frequencies estimation results from the noise-added response by several methods are consistent with each other and with the small relative error of less than 1%. In terms of the damping ratio, more deviations can be found, where the associated accuracy of the HPBW and HHT methods strongly depend on the limited length and nonstationarity of the acceleration response. It can be also noted that by employing the MEMD, the mean absolute relative deviation of damping ratios identified by the FBFFT method falls to 3.92% from 6.42% and by the SSI method, it reduces to 1.50% from 6.17%, indicating that it significantly reduces the errors of damping ratio caused by sinusoidal noise effect in the original signal. On the other hand, with the help of MEMD, the system order which was hard to be determined in SSI can be simply set as two or four (due to some residue noise or mode mixing) in both two cases. Meanwhile, the analysis of the shaking table model test in seismic excitations demonstrates that the accuracy of the damping identification is affected by the adopted method and there exists a trend that the modal damping ratio decreases with the increase in modes.
The MEMD-based modal identification approach was applied to the Canton Tower under nonstationary earthquake excitation. The modal parameters of the first five vibration modes are identified and compared with other traditional methods (i.e., HPBW and HHT) and previous study for the same structure by Li [44]. The frequencies identified by various methods are quite consistent while damping ratios display more uncertainties: for instance, Li [44] obtained a small fourth-order damping ration of 0.37%, while a large value, 1.13%, may be seen in Table 8 by the HPBW.
6. Conclusions
The main contribution of this paper is to integrate the multivariate empirical mode decomposition (MEMD) for identifying modal parameters from the output-only multi-dimensional responses with a combination of fast Bayesian FFT (FBFFT) and stochastic subspace identification (SSI) methods. The MEMD is deployed as a preprocessing tool, aiming to reduce the effect of noise and extract the synchronous modal response. The multivariate signals are firstly decomposed into several aligned intrinsic mode functions, which only contain a dominant component in the frequency domain. Then, the modal parameters can be identified by advanced FFBFT and SSI directly.
The illustrations of a numerical frame structure and a shaking table test were utilized to validate the MEMD-based methods. In the numerical illustration, by adopting the MEMD, the MARD of damping ratio by the FBFFT or SSI method significantly falls, implying that the combined method is superior to the traditional method. Compared with the original SSI method, it is easy to determine the associated system order of the MSSI method after employing the MEMD to decompose the original acceleration response. The combined method was also employed to determine the modal parameters of the Canton Tower using the full-scale measurement acceleration data. The same as before, the frequencies identified by various methods are identical, while damping ratios present high discreteness.
Notably, the above study clearly demonstrates that although the identification accuracy of each modal frequency is reliable and accurate, associated damping ratios highly depend on the selected approach, whether the adopted tools are the probabilistic method such as the FBFFT or the traditional time–frequency method, such as the Hilbert–Huang transform, half-power bandwidth, and peak–pick. Therefore, the identification accuracy of damping ratios should be further improved in the future.
Author Contributions
M.H.: Conceptualization, Resources, Supervision. J.S.: Methodology, Software, Data curation, Formal analysis, Visualization, Writing—original draft. K.C.: Writing—review & editing. Q.L.: review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
The work described in this paper was partially supported by National Natural Science Foundation of China (Project No. 52178512), and Natural Science Foundation of Zhejiang Province (Project No. LZ22E080006).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Brincker, R.; Ventura, C.E.; Andersen, P. Damping estimation by Frequency Domain Decomposition. In Proceedings of the IMAC 19: A Conference on Structural Dynamics, Hyatt Orlando, Kissimmee, FL, USA, 5–8 February 2001. [Google Scholar]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar]
- James, G.H.I.; Carne, T.G.; Lauffer, J.P. The natural excitation technique (NExT) for modal parameter extraction from operating wind turbines. Int. J. Anal. Exp. Modal Anal. 1993, 93, 260–277. [Google Scholar]
- Abazarsa, F.; Nateghi, F.; Ghahari, S.F.; Taciroglu, E. Extended blind modal identification technique for nonstationary excitations and its verification and validation. J. Eng. Mech. 2016, 142, 04015078. [Google Scholar]
- Ghahari, S.F.; Abazarsa, F.; Ghannad, M.A.; Celebi, M.; Taciroglu, E. Blind modal identification of structures from spatially sparse seismic response signals. Struct. Control Health Monit. 2014, 21, 649–674. [Google Scholar]
- Chiang, D.Y.; Lin, C.S. Identification of modal parameters from nonstationary ambient vibration data using the channel-expansion technique. J. Mech. Sci. Technol. 2011, 25, 1307–1315. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar]
- Huang, N.E.; Wu, M.L.C.; Long, S.R.; Qu, W.; Gloersen, P.; Fan, K.L. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 459, 2317–2345. [Google Scholar]
- Yang, J.N.; Lei, Y.; Lin, S.; Huang, N. Identification of natural frequencies and dampings of in situ tall buildings using ambient wind vibration data. J. Eng. Mech. 2004, 130, 570–577. [Google Scholar]
- He, X.H.; Hua, X.G.; Chen, Z.Q.; Huang, F.L. EMD-based random decrement technique for modal parameter identification of an existing railway bridge. Eng. Struct. 2011, 33, 1348–1356. [Google Scholar]
- Yu, D.J.; Ren, W.X. EMD-based stochastic subspace identification of structures from operational vibration measurements. Eng. Struct. 2005, 27, 1741–1751. [Google Scholar]
- Han, J.; Zheng, P.; Wang, H. Structural modal parameter identification and damage diagnosis based on Hilbert-Huang transform. Earthq. Eng. Eng. Vib. 2014, 13, 101–111. [Google Scholar]
- Rilling, G.; Flandrin, P.; Gonçalves, P.; Lilly, J.M. Bivariate empirical mode decomposition. IEEE Signal Processing Lett. 2007, 14, 936–939. [Google Scholar]
- Rehman, N.; Mandic, D.P. Empirical mode decomposition for trivariate signals. IEEE Trans. Signal Processing 2010, 58, 1059–1068. [Google Scholar]
- Huang, G.; Su, Y.; Kareem, A.; Liao, H. Time-frequency analysis of nonstationary process based on multivariate empirical mode decomposition. J. Eng. Mech. 2015, 142, 04015065. [Google Scholar]
- Sadhu, A. An integrated multivariate empirical mode decomposition method towards modal identification of structures. J. Vib. Control 2017, 23, 2727–2741. [Google Scholar]
- Barbosh, M.; Sadhu, A.; Vogrig, M. Multisensor-based hybrid empirical mode decomposition method towards system identification of structures. Struct. Control. Health Monit. 2018, 25, e2147.1–e2147.21. [Google Scholar]
- Aruljayachandran, M.; Kareem, A.; Kwon, D.K. Identification of vortex-induced vibration of tall building pinnacle using cluster analysis for fatigue evaluation: Application to burj khalifa. J. Struct. Eng. 2020, 146, 04020234. [Google Scholar]
- Zhang, L.; Hu, X.; Xie, Z. Identification method and application of aerodynamic damping characteristics of super high-rise buildings under narrow-band excitation. J. Wind Eng. Ind. Aerodyn. 2019, 189, 173–185. [Google Scholar]
- Au, S.K.; Brownjohn, J.; Mottershead, J.E. Quantifying and managing uncertainty in operational modal analysis. Mech. Syst. Signal Processing 2017, 102, 139–157. [Google Scholar]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. A 2010, 466, 1291–1302. [Google Scholar]
- Dalal, I.L.; Stefan, D.; Harwayne-Gidansky, J. Low discrepancy sequences for Monte Carlo simulations on reconfigurable platforms. In Proceedings of the 2008 International Conference on Application-Specific Systems, Architectures and Processors, Leuven, Belgium, 2–4 July 2008. [Google Scholar]
- Komaty, A.; Boudraa, A.O.; Flandrin, P.; Amblard, P.O.; Astolfi, J.A. On the Behavior of MEMD in Presence of Multivariate Fractional Gaussian Noise. IEEE Trans. Signal Processing 2021, 69, 2676–2688. [Google Scholar]
- Xia, Y.; Zhang, B.; Pei, W.; Mandic, D.P. Bidimensional Multivariate Empirical Mode Decomposition with Applications in Multi-Scale Image Fusion. IEEE Access 2019, 7, 114261–114270. [Google Scholar]
- Lang, X.; Zheng, Q.; Zhang, Z.; Lu, S.; Xie, L.; Horch, A.; Su, H. Fast multivariate empirical mode decomposition. IEEE Access 2018, 6, 65521–65538. [Google Scholar]
- Peeters, B.; Roeck, G.D. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Signal Processing 1999, 13, 855–878. [Google Scholar]
- Peeters, B.; De Roeck, G. Reference based stochastic subspace identification in civil engineering. Inverse Probl. Eng. 2000, 8, 47–74. [Google Scholar]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory, Implementation and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Loh, C.H.; Liu, Y.C.; Ni, Y.Q. SSA-based stochastic subspace identification of structures from output-only vibration measurements. Smart Struct. Syst. 2012, 10, 331–351. [Google Scholar]
- Reynders, E.; Pintelon, R.; Roeck, G.D. Uncertainty bounds on modal parameters obtained from stochastic subspace identification. Mech. Syst. Signal Processing 2008, 22, 948–969. [Google Scholar]
- Zini, G.; Betti, M.; Bartoli, G. A quality-based automated procedure for operational modal analysis. Mech. Syst. Signal Processing 2022, 164, 108173. [Google Scholar]
- Priori, C.; Angelis, M.D.; Betti, R. On the selection of user-defined parameters in data-driven stochastic subspace identification. Mech. Syst. Signal Processing 2018, 100, 501–523. [Google Scholar]
- Yuen, K.V. Structural Modal Identification Using Ambient Dynamic Data. Master’s Thesis, Hong Kong University of Science and Technology, Hong Kong, 1999. [Google Scholar]
- Au, S.K.; Ping, T. Full-scale validation of dynamic wind load on a super-tall building under strong wind. J. Struct. Eng. 2012, 138, 1161–1172. [Google Scholar]
- Yuen, K.V.; Katafygiotis, L.S.; Beck, J.L. Spectral density estimation of stochastic vector processes. Probabilistic Eng. Mech. 2002, 17, 265–272. [Google Scholar]
- Korwar, R.M. On characterizations of distributions by mean absolute deviation and variance bounds. Ann. Inst. Stat. Math. 1991, 43, 287–295. [Google Scholar]
- Water, T.P. Finite Element Model Updating Using Measured Frequency Response Functions. Ph.D. Thesis, University of Bristol, Bristol, UK, 1995. [Google Scholar]
- Li, Q.S.; Wu, J.R. Correlation of dynamic characteristic of a super tall building from full-scale measurements and numerical analysis with various finite element models. Earthq. Eng. Struct. Dyn. 2004, 33, 1311–1336. [Google Scholar]
- Lu, X.L.; Li, P.Z.; Chen, Y.Q. Complete Data of Shaking Table Test on a 12-Story Reinforced Concrete Frame Model; State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University: Shanghai, China, 2004. [Google Scholar]
- Lu, X.L.; Zhang, J.; Lu, W.S. Seismic behavior of vertically mixed structures with upper steel and lower concrete components. J. Build. Struct. 2011, 32, 20–26. (In Chinese) [Google Scholar]
- Ni, Y.Q.; Xia, Y.; Liao, W.Y.; Ko, J.M. Technology innovation in developing the structural health monitoring system for Guangzhou new TV tower. Struct. Control Health Monit. 2009, 16, 73–98. [Google Scholar]
- Ni, Y.Q.; Xia, Y.; Lin, W.; Chen, W.H.; Ko, J.M. SHM benchmark for high-rise structures: A reduced-order finite element model and field measurement data. Smart Struct. Syst. 2012, 10, 411–426. [Google Scholar]
- Guo, Y.L.; Kareem, A.; Ni, Y.Q.; Liao, W.Y. Performance evaluation of canton tower under winds based on full-scale data. J. Wind. Eng. Ind. Aerodyn. 2012, 104–106, 116–128. [Google Scholar]
- Li, H.; Liu, J.K.; Chen, W.H.; Lu, Z.R.; Xia, Y.; Ni, Y.Q. Analysis of dynamic characteristics of the Canton Tower under different earthquakes. Adv. Struct. Eng. 2015, 18, 1087–1100. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).