Abstract
It is well known that the parameters of Nb3Sn superconducting strands are strain sensitive, and the internal brittle Nb3Sn filament can easily break under deformations. A temperature difference from the preparation temperature of about 1000 K to the cryogenic working environment of 4.2 K damages brittle Nb3Sn fibers before working. Based on the Curtin–Zhou model, the damage theory for fiber-reinforced composites is utilized to study the influence of filament fractures caused by thermal stress. According to the typical multi-scale geometric of the EAS-Nb3Sn strand (European Advanced Superconductor, EAS), an efficient hierarchical homogenized calculation model considering filament fracture and matrix plasticity was established. In this work, we took the filament fracture caused by both thermal stresses and mechanical loads into consideration using the secant modulus and simultaneously had the impact of the plastic constitutive of the bronze matrix and the copper protective layer. Mechanical parameters, such as the homogenized secant modulus, shear modulus, and Poisson’s ratio in different directions of level scale, were predicted at various temperatures. The elastoplastic mechanical behavior of the strands subjected to axial load was analyzed, and the results were in good agreement with the experiment. The initial thermal fiber fracture has non-negligible effects on the mechanical properties of the EAS-Nb3Sn superconducting strand and play the role in accelerating the increase in fiber breakage.
1. Introduction
Since the discovery of superconductivity more than 100 years ago, many diverse classes of superconducting materials have been found and subsequently studied in detail. Based on the different superconducting transition temperatures, the superconding materials can be classified into the low-temperature superconductors (LTS), which are represented by metals, alloys, and metal alloy materials, such as Nb3Sn, NbTi, et al., and the high-temperature superconductors (HTS). To date, more than 5000 superconducting materials have been discovered or synthesized all over the world [1]. Based on Bi (Bi-Sr-Ca-Cu-O [2,3]), Tl (Tl-Ba-Ca-Cu-O [4]), RE (RE-Ba-Cu-O [5], as well as with the participation of several RE [6]), and Y (Y-Ba-Cu-O [7]), high-temperature superconducting materials are becoming more and more popular in recent years. HTS-superconducting tapes are used without and with a stabilizer as windings in transformers and superconducting electromagnets and superconducting current limiters. Compared with HTSs, Nb3Sn low-temperature superconducting materials are widely used in the core of large high-field magnets because of their mature and simple preparation, high-critical magnetic field (Hc2 ≈ 25 T), critical current [8], and stable mechanical properties in low-temperature environments. However, even today, after thousands of papers devoted to the materials have been published, understanding their nonlinear mechanical behavior remains a challenge.
The magnetic coils of the TOKAMAK of the International Thermonuclear Experimental Reactor (ITER) project and the Large Hadron Collider (LHC) of the European Organization for Nuclear Research all use Nb3Sn superconducting materials [9,10]. The Nb3Sn superconducting strand works under strong magnetic fields, cryogenic environmental, and high electric potential when ITER superconducting magnets are operating at 4.2 K. In addition, the temperature difference between the preparation temperature of about 1000 K and the operating temperature of 4.2 K will also produce corresponding thermal stress in the strands, which obviously affects the axial mechanical behavior of the strands [11,12]. These articles illustrate that cracks and fractures in the filaments are the essential reasons for the reduction in the current-carrying capacity that restrict the design and application of the Nb3Sn superconductor used in engineering.
Numerous experimental investigations have been performed to describe the mechanical properties of Nb3Sn strands [13,14,15,16,17,18,19,20,21]. Eijnden et al. [15] developed a test system (Tarsis) to procure the axial tensile stress–strain relation of Nb3Sn strands and measured the mechanical properties of four different kinds of superconducting strands at various temperatures to determine the tensile constitutive. It is found that the mechanical characteristics of the four different kinds of superconducting strands are all temperature dependent. Subsequently, Ilyin et al. [11] developed a system to determine the constitutive relations of ITER-related CICC cables under axial tension and compression, cyclic loading, and cable radial deformation. Osamura et al. [18] used the quantum beam technique to quantify the local strain of the helical and non-helical Nb3Sn strands in the cryogenic environment. Both axial and transverse thermal stress components in Nb3Sn filaments are numerically measured. In addition, the ENEA Centro Ricerche Frascati group in Italy and the Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences group in Poland have carried out extensive research on ITER and achieved promising results [22,23,24,25,26,27,28].
Several theoretical and numerical models have been presented to predict the mechanical properties of Nb3Sn strands [11,29,30,31,32,33,34,35,36,37,38,39,40]. For instance, Boso et al. [29,30,31,32] proposed a multi-scale numerical method for the composite strands based on the asymptotic homogenization theory. Effective behaviors of various scales were generated by identifying the representative volume elements (RVE) simulated using the finite element method. Although the computational results were relatively ideal, the helical structure of the Nb3Sn wire and the fiber fracture damage were not considered. Collins et al. [34,35] developed a three-dimensional, multi-scale nonlinear model to investigate the mechanical behavior of a superconducting strand and its filaments, simulating the thermal stress due to changes from the heat treatment temperature to the operational temperature (4.2 K). The stress state of superconductors and their critical current-carrying capacity were calculated by the multiscale model. Taking the helical structure into consideration, Jing et al. [36] developed a three-dimensional theoretical model based on the Mori–Tanaka approach to evaluate the internal strain and performance degradation of a Nb3Sn superconducting strand subjected to mechanical and thermal stress. The helical structure of the superconducting strands was shown to be effective in this investigation. Liu et al. [37] investigated the elastic–plastic behavior of Nb3Sn superconducting strands using the finite element technique. The fluctuation of effective parameters with temperature was calculated using the Mori–Tanaka technique and the finite element numerical approach with consistent results. However, the Nb3Sn fiber is prone to brittle fracture, and the effects of the filaments breakage on anticipated mechanical properties were necessary as was the inaccuracy introduced when bronze was treated as a linear elastic material.
The mechanical properties of Nb3Sn materials are similar to those of ceramics; therefore, brittle fracture occurs when they are subjected to tiny deformations. As such, many experts have started to concentrate on investigating Nb3Sn filament fracture [41,42,43,44,45,46,47,48]. Curtin and Zhou [41,42] hypothesized that filament breakage is a random process related to axial stress, and the filament fracture length could be described using the Weibull distribution function. Based on the Curtin–Zhou theory and the ‘shear-lag model’, Luo [43], and Wang et al. [44] investigated the influence of filament fracture and damage progression on the mechanical characteristics of LMI-Nb3Sn strands. Yong et al. [45] established a two-dimensional crack bridge model to investigate the fracture behavior of filaments within the strand and calculated the stress intensity factors of modes I, II, and III crack tips, as well as the relative opening displacements between the crack surfaces. Abdyukhanov et al. [46] investigated the influence of artificially generated surface defects on the microstructure and the electrical parameters of two kinds of Nb3Sn superconductors in 2021. Through SEM observations, it was found that the current-carrying capacity of the superconductor decreased proportionally with the increases in defect size and number. When the depth of the prefabricated crack reached 0.44 mm, the critical current was reduced by 10%. Consequently, the effect of internal fiber damage on the physical properties and mechanical behavior of the strand must be considered. To analyze the temperature stress caused by heat treatment and the influence of the twisting process on the fracture damage of strands, Shen et al. [47,48] used laser-scanning microscopy to study Nb3Sn strands in TF CICC cable. Comparing the micrographs of strands before and after heat treatment under artificial bending, it could clearly be observed that the internal fibers of strands after heat treatment and repeated bending were severely damaged.
Previous studies on Nb3Sn strands have mostly focused on their mechanical properties, including the damage and fracture caused by mechanical and electromagnetic loads. However, the mechanical properties of their nonlinear mechanical behavior considering the fiber fracture, thermal stress, and material plastic remains a challenge. In this paper, Curtin–Zhou’s damage theory is extended to consider the initial damage to fibers caused by thermal stress. Based on the secant modulus theory, an efficient method of considering the matrix plasticity in the multi-scale homogenization model is presented, and the elastic–plastic analysis of the Nb3Sn strand in a homogenization model with initial thermal damage was carried out. The effective parameters of each homogenization level of EAS-Nb3Sn strands with filament fracture and plastic of the matrix were numerically predicted, as well as the tensile curves.
2. Numerical Analysis of the Constitutive Relationship of EAS-Nb3Sn Strands
2.1. The Hierarchical Homogenization Model of EAS-Nb3Sn Strands
The overall properties of composite Nb3Sn strand not only depend on the components but also on the internal geometric structure [29]. Even though Nb3Sn fiber, bronze, and copper are all isotropic materials, Nb3Sn strands are constituted of orthotropic materials. As shown in Figure 1, the EAS-Nb3Sn strand contains around 8305 Nb3Sn fibers embedded in the bronze matrix, each fiber measuring just 2~3 μm in diameter. As a result, complete numerical analyses of the mechanical properties of superconducting strands would be extremely computing intensive and unfeasible. To model the mechanical characteristics of the strand more effectively, the representative volume elements (RVEs) are employed in this study. Due to the clear hierarchical structure of EAS-Nb3Sn strands and the periodicity of fiber bundles [29], a three-level homogenization model could be utilized, as illustrated in Figure 2.

Figure 1.
Cross section of the EAS-Nb3Sn superconducting strand [32].
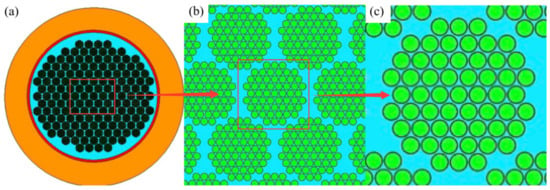
Figure 2.
The hierarchical structure of the EAS-Nb3Sn strand: (a) EAS-Nb3Sn superconducting stranded wire, (b) Nb3Sn fiber bundles, (c) the Nb3Sn fibers reinforced in a bronze matrix.
As shown in Figure 2, different hierarchical levels can be identified, from level 1 to level 3, starting from the fiber bundle composed of 55 Nb3Sn fibers and a bronze matrix (level 1), as shown in Figure 2c. The level 2 composite is composed of 151 groupings of level 1 fiber bundles embedded in bronze matrix, as shown in Figure 2b. Level 3 is the Nb3Sn strand compounded by the level 2 effective homogenous material surrounded by a copper and tantalum barrier layer, as shown in Figure 2a. The component materials and volume fractions of EAS-Nb3Sn strand are shown in Table 1.

Table 1.
Volume fractions of each component material of EAS-Nb3Sn strand.
For the level 1 fiber bundle, considering the volume fraction and geometric structure of the Nb3Sn fibers, the level 1 RVE (geometric size of 5.2 × 5.2 × 1 μm3; fiber volume fraction VF1 = 0.5223), as shown in Figure 3c, would be selected to calculate its effective constitutiveness. Similarly, for the level 2 superconducting region, considering the volume fraction and the geometric structure of the Nb3Sn fiber bundle in the strands, the level 2 RVE (geometric size of 55 × 100 × 10 μm3; level 1 fiber bundle volume fraction VF2 = 0.7837) can be selected, as shown in Figure 3b, to calculate its effective stiffness matrix when the effective constitutiveness of level 1 is substituted, as depicted in the blue region in Figure 3b. The cross section of the homogenized EAS-Nb3Sn strand is shown in Figure 3a, and the 3D model is shown in Figure 4. The stress–strain behaviors of the EAS-Nb3Sn strand can be examined precisely from the micro- to macro-levels using the homogenization model.
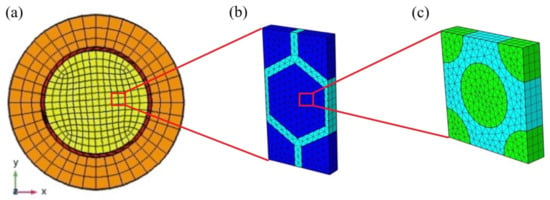
Figure 3.
(a) Effective homogenization model of the EAS-Nb3Sn strand (yellow region represents the level 2 effective superconducting region, red region represents the tantalum isolation layer, and orange region represents copper); (b) the RVE of the level 2 (blue region represents the level 1 homogeneous fiber bundle, and cyan represents the matrix); (c) the RVE of the level 1 (green region represents the Nb3Sn fiber, and cyan region represents bronze).
Figure 4.
3D model of the homogenized EAS-Nb3Sn strands (length L = 20 mm).
Calculating the effective elastic coefficients for level 1 and level 2 in the strand is important for mechanical analyses of the homogenization model. It is generally believed that Nb3Sn strands are an orthotropic material based on its internal structures (Figure 1). Therefore, the following calculation assumes that the stiffness matrix of level 1 and level 2 are both orthotropic. The constitutive relationship of the materials is as follows [32]:
where is the stiffness matrix of level i, and the relationship with the flexibility matrix is
The flexibility matrix of the orthotropic materials can be expressed through nine elastic constants, , , , , , , , , and . The subscripts 1, 2, and 3 denote three orthogonal directions. When the Cartesian coordinate system was adopted for the model system, subscripts 1, 2, and 3 would be replaced by x, y, and z.
After applying the boundary conditions, the effective elastic constants of the RVE may be derived by combining Equations (1)–(3). The effective properties of the Nb3Sn strand are determined by applying six various types of boundary conditions to the RVE, as described in reference [32].
2.2. Fiber Damage Caused by Thermal Stress
With the increasing loads, the brittleness of the Nb3Sn material results in fiber cracks and fractures, impacting the overall stress–strain behavior of the strand. Therefore, this research employed the Curtin–Zhou model [41,42] to investigate the effect of the axial fracture of Nb3Sn fibers. The Curtin–Zhou model was extended to include the effect of early thermal damage caused by a temperature difference between the preparation and operating environments.
Curtin et al. [41,42] assumed that the growing stress is equally distributed across all fibers in the unbroken region around the breaking fiber, and stress concentration is neglected, as shown in Figure 5b. The fiber stress away from the breakpoint is a constant, S. The Poisson distribution of fiber breakpoints may be used to characterize the composites’ axial dimensionless stress [43]:
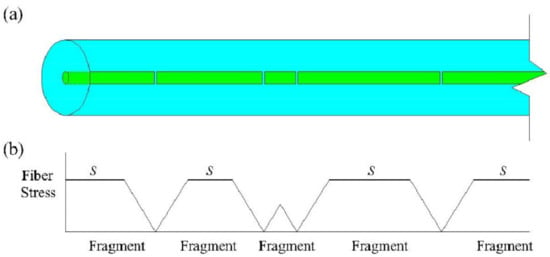
Figure 5.
(a) Schematic of the random fracture distribution of a single fiber, (b) stress distribution during fiber fracture.
Here, represents the dimensionless stress of the composite material, which depends on the value of the average of the fiber stress, , and characteristic stress, . represents the dimensionless stress of the fiber far from the breaking point, where is the far-field homogeneous strain. represents the dimensionless damage density of the fiber, represents the dimensionless yield stress of the matrix, and represent the volume fractions of fiber and matrix, respectively. The characteristic stress, , and feature length, , can be obtained through the material-stretching mirror experiment.
The relationship between and is given as follows [43]:
where m is the Weibull modulus.
The influence of fiber fracture on the constitutive relationship of composites can be considered by reducing the average stiffness of the fibers in this model. With the Nb3Sn fiber fracture, the average stress in the fiber may be calculated by setting the fiber volume fraction to one and the matrix volume fraction to zero in Equation (4):
Nb3Sn strands operate in liquid helium (4.2 K); therefore, the temperature differential between the preparation temperature (~1000 K) and the extremely low-temperature conditions may result in significant thermal stress to Nb3Sn fibers, which is referred to as ‘initial thermal damage’. According to the Curtin–Zhou theory, the association between fiber thermal stress and initial thermal damage is comparable to that seen in Equation (5):
The axial thermal stress, , can be derived as
Here, () is the temperature difference between the preparation temperature, , and the working temperature, . and indicate the thermal expansion coefficients of the fiber and matrix, respectively; and is the thermal expansion coefficient of the composite calculated by the law of mixtures.
Then, the dimensionless stress of Nb3Sn fiber with initial thermal damage under axial load is expressed as
Equation (10) can be used to analyze the mechanical behavior of Nb3Sn strands by considering both the initial thermal damage and mechanical damage to the fiber. The secant modulus, Es, was used to describe the properties of the broken Nb3Sn strands in nonlinear analysis.
The initial thermal damage, , and mechanical damage, , can be included in the homogenization model through the changes in the secant modulus, . Without examining the effect of damage on the fiber’s transverse properties, it is presumed that the Nb3Sn fiber remains transversely isotropic after damage, and the Young’s modulus is [, , (εz)]. Here, represents the elastic modulus of the Nb3Sn fiber perpendicular to the axis, and (εz) represents the axial elastic modulus, taking the damage into account, which is a function of axial strain, εz. Using the method discussed in Section 2.1, the effective elastic coefficients of the level 1 homogeneous fiber bundle and the level 2 effective superconducting region could be computed.
2.3. Nb3Sn Strand Elastoplastic Uniaxial Tensile Study with Fiber Damage
In the homogenization EAS-Nb3Sn strand model shown in Figure 4, the superconducting region was replaced by an effective homogeneous material, making it difficult to account for the plasticity of bronze at a specific strain, εz. One approach for considering matrix plasticity in a hierarchical homogenization model is the utilization of the secant modulus theory. It may be used to determine the degraded effective stiffness of a Nb3Sn strand homogenization model when fiber damage is present.
The effective plastic stress and effective plastic strain of the elastic–plastic deformation materials can be expressed through the deviator stress and strain components, respectively:
The secant modulus of the elastic–plastic deformation material is
Assessed using the relationship between applied loads and fiber fracture, Section 2.2 effectively accounts for the influence of fiber damage in level 1 and level 2. The plastic behavior of the bronze matrix should also be incorporated in the analysis by considering the relationship between axial loads and the secant modulus. On the other hand, as an elastic–plastic material, the parameters of bronze depend on the stress state at different positions. It may consider more than only the effect of axial deformation on material properties. Therefore, it is necessary to determine the partial strain component of bronze to calculate the secant modulus using Equations (12)–(14). For this reason, we need to employ the iterative approach shown in Figure 6 to determine the actual relationship between strand stress and strain. The main steps are as follows:
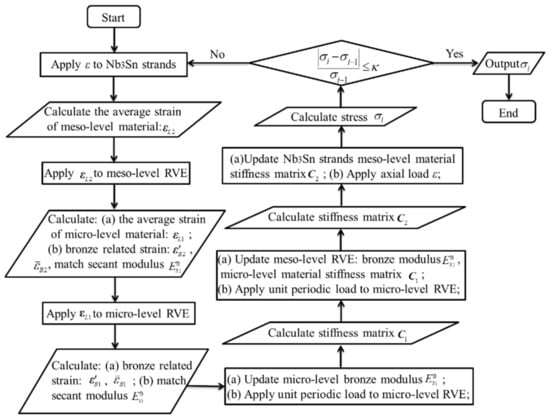
Figure 6.
Flow chart of meso-mechanical homogenization algorithm considering matrix plasticity (κ represents error).
- 1.
- Apply uniaxial tensile strain, εz, to the EAS-Nb3Sn strand by fixing the axial displacements pointwise at the left end:and the axial displacements pointwise at the left end:While considering the fiber damage and plasticity of copper, then calculate and output the average strain tensor, , of level 2 homogenization part of the strand.
- 2.
- Apply to level 2 RVE (Figure 3b) by setting the displacements of the points on the level 2 RVE surface:in which xj (j = 1, 2, 3) are the x, y, and z coordinate values. ui (i = 1, 2, 3) represents the displacements along the x, y, and z directions. Calculate and output the average strain, , of the level 1 homogeneous part of the strand and the deviant strain, , of the bronze matrix.
- 3.
- Apply to the level 1 RVE (Figure 3c) by setting the displacements of the points on the level 2 RVE surface:where, xj and ui are the x, y, and z coordinate values and displacements in the corresponding directions, respectively. Calculate and output the deviant strain, , of the first-class bronze matrix.
Through the above stepwise calculations, the deviator strain components of the different levels of the bronze matrix of strands could be obtained. Combined with Equations (12)–(14), the plastic secant modulus, , of the different levels of the bronze matrix can be obtained when strands are subjected to uniaxial tensile load, εz. Update the material parameters of each layer and calculate the equivalent elastic–plastic parameters using the method introduced in Section 2.1. The application of the periodic boundary conditions is shown in detailed in literature [32]. The main steps are as follows:
- 1.
- Update the secant modulus of the level 1 bronze and apply the periodic boundary conditions to the level 1 RVE; calculate and output the stiffness matrix, C1.
- 2.
- Update the secant modulus of the secondary bronze and the stiffness matrix, C1, of the homogeneous part of the strand in the level 1 RVE, apply the periodic boundary conditions to level 2 RVE, and calculate and output the stiffness matrix, C2.
- 3.
- Update the stiffness matrix, C2, of the level 2 homogenization part of the strand in the EAS-Nb3Sn strand model, apply the uniaxial tensile load, εz, and then calculate and output the stress values.
To achieve a higher computational accuracy, the above program was repeated iteratively. One could also set the error value, κ, to control the time of the cyclic iteration and the expected output value.
The hierarchical homogenization model takes about half an hour for each individual run when the models were meshed using that shown in Figure 3. Moreover, the FEM for the full geometrical model takes several days for each individual run and even ignore the fiber fracture. In brief, the multi-scale homogenization model has significant advantages computational efficiency, even after considering the fiber fracture and plastic of materials.
3. Multi-Scale Numerical Analysis of EAS-Nb3Sn Strands
In Section 2.2, the constitutive relationship of Nb3Sn fiber with initial thermal damage and mechanical damage is established. Figure 7 is the average stress–strain curve with initial thermal damage, , and mechanical damage, , when the m = 2 and = 900 MPa [12]. It can be found that the existence of initial thermal damage accelerates the stress degradation of Nb3Sn fibers, and low temperature aggravates the fracture in fiber. In the above calculation, the preparation temperature was taken to be T0 = 923 K. The elastic properties and thermal property parameters of each component are detailed in the literature [11,32].
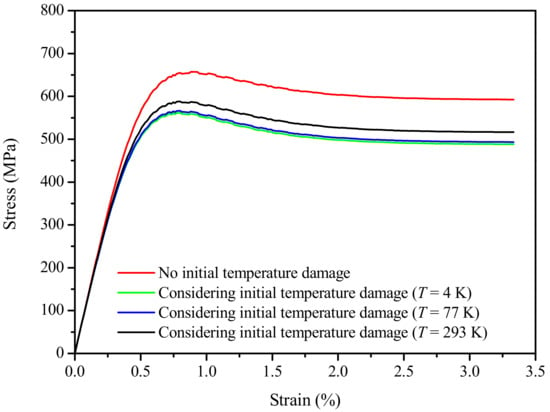
Figure 7.
Stress–strain curve of EAS-Nb3Sn fiber with initial thermal damage.
The secant modulus, , of fiber with initial thermal and mechanical damage may be determined using the stress–strain data in Figure 7. The COMSOL software was used to apply six different boundary loads, same as that in Boso’s work [32], and the effective elastic–plastic parameters in the superconducting regions of the EAS-Nb3Sn strands at various temperatures were obtained.
3.1. The Effective Elastic–Plastic Parameters of the Level 1 Homogeneous Fiber Bundles
When computing the effective elastic–plastic characteristics of the level 1 homogeneous fiber bundle, it was important to include the fiber scant modulus with consideration of damage, as well as the bronze plastic parameters. By applying axial strain to an EAS-Nb3Sn strand, the secant modulus of the plastic bronze matrix in the level 1 homogeneous fiber bundle was calculated.
Figure 6 illustrates how the element periodic boundary conditions could be applied to the given element model and how the level 1 effective elastic–plastic parameters can be derived while considering fiber damage and bronze plasticity at various temperatures. The effective stiffness coefficients of the level 1 homogeneous fiber bundle with initial thermal damage are shown in Table 2 where the temperature is T = 4 K, and the axial strain is equal to ε = 0.003. Using COMSOL software, the deformation and von Mises stress distributions of example elements under various boundary conditions are depicted in Figure 8 when the fiber damage was considered at T = 4 K. As shown in the figure, the z direction is parallel to the fiber axis, and the axial direction is perpendicular to the x and y axes.

Table 2.
When T = 4 K and ε = 0.003, the stiffness matrix, C1 (MPa), of the EAS-Nb3Sn level 1 homogeneous fiber bundle considering fiber damage is shown.
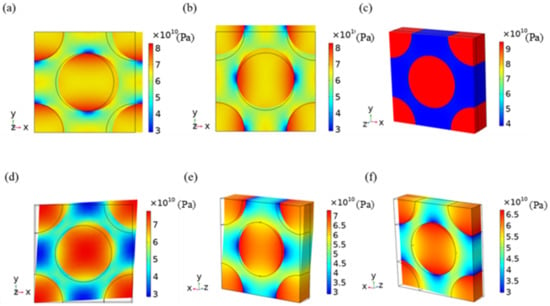
Figure 8.
The von Mises stress (Pa) distribution cloud diagram of the EAS-Nb3Sn level 1 homogeneous fiber bundle considering fiber damage, when T = 4 K, and ε = 0.003. (a) Load case 1: von Mises stress (N/m2). (b) Load case 2: von Mises stress (N/m2). (c) Load case 3: von Mises stress (N/m2). (d) Load case 4: von Mises stress (N/m2). (e) Load case 5: von Mises stress (N/m2). (f) Load case 6: von Mises stress (N/m2).
The effective elastic–plastic properties in various directions are shown in Figure 9 with the initial thermal damage considered at 4 K. The effective Young’s modulus and shear modulus of the level 1 homogeneous fiber bundle are shown in Figure 9a,b, respectively. It can be seen from the figure that the level 1 homogeneous fiber bundles’ axial Young’s modulus, , shear modulus, , and decrease with increasing strain. Furthermore, the existence of early thermal damage promotes the modulus deterioration. The axial Young’s modulus, with initial thermal damage, as well as the shear moduli, and , are less than the values without initial thermal damage, as shown in Figure 9a,b. It is mainly because we chose to neglect the influence of the fiber breakage on the homogeneous fiber material parameters perpendicular to fiber orientation, as shown in Equation (10). The reason for this assumption is the direction of cracks is mostly perpendicular to the direction of fiber. This makes the fiber breakage mainly affect the axial Young’s modulus, , in Figure 9a. Meanwhile, the influence of initial thermal damage on the shear moduli, and , and Poisson’s ratio, , , are more substantial than and . From the figure, it can be noticed that the influence of the initial thermal damage on the values is minor under a small axial extensile strain. However, the differences increased with the axial strain increases. Thermal stress may result in fiber fragmentation, possibly playing a role in accelerating the increase in fiber breakage.
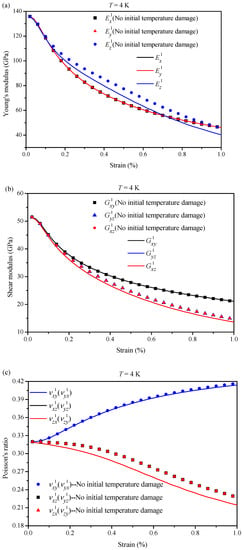
Figure 9.
T = 4 K, EAS-Nb3Sn level 1 homogeneous fiber bundle considering damage in different directions: (a) Young’s modulus; (b) shear modulus; (c) Poisson’s ratio. (Note: The symbol “1” indicates the level 1 homogeneous fiber bundle.).
3.2. The Effective Elastic–Plastic Parameter of the Level 2 Homogeneous Superconducting Region
In Section 3.1, the effective elastic–plastic parameters of the level 1 homogeneous fiber bundle are presented; the obtained parameters were substituted into the corresponding area of the level 2 RVE and the secant modulus of bronze in the level 2 is updated. Different boundary conditions were applied in the RVE to calculate the effective stiffness coefficient of the level 2 superconducting region. Table 3 shows the level 2 effective stiffness coefficients take the initial thermal damage at 4 K when the axial load was ε = 0.003. The von Mises stress distribution in Level 2 RVE are shown in Figure 10 at six different boundary conditions using COMSOL software when the fiber damage was considered at T = 4 K. The z direction is parallel to the fiber axis, and the axial direction is perpendicular to the x and y axes. The effects of initial thermal damage on the effective elastic–plastic parameters of the level 2 with axial strain at T = 4 K are shown in Figure 11, revealing that initial thermal damage has a considerable effect on the material parameters. The trends of change are similar to the level 1 material parameters in Figure 9. It can be seen that the initial thermal damage would influence the Young’s modulus, , shear modulus , , and Poisson’s ratio , . Meanwhile, the value of with and without initial thermal damage considered shows a slight difference. A possible reason for this might be fiber orientation and anisotropic material properties of the homogenous fiber bundle.

Table 3.
The stiffness matrix, C2 (MPa), of the EAS-Nb3Sn level 2 homogeneous superconducting region at T = 4 K, ε = 0.003.
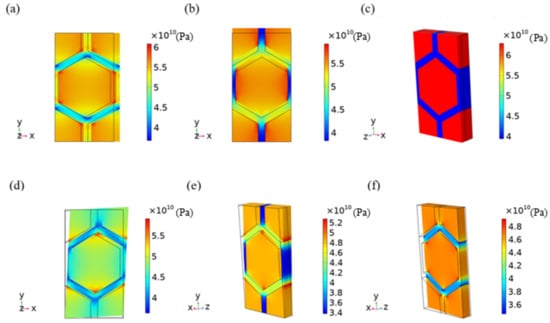
Figure 10.
Stress distribution cloud diagrams of the EAS-Nb3Sn level 2 homogeneous superconducting region considering fiber damage when T = 4 K and ε = 0.003. (a) Load case 1: von Mises stress (N/m2). (b) Load case 2: von Mises stress (N/m2). (c) Load case 3: von Mises stress (N/m2). (d) Load case 4: von Mises stress (N/m2). (e) Load case 5: von Mises stress (N/m2). (f) Load case 6: von Mises stress (N/m2).
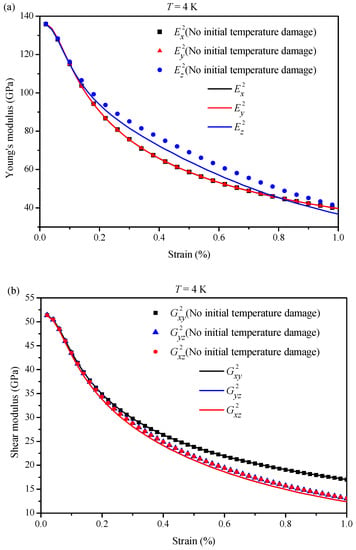
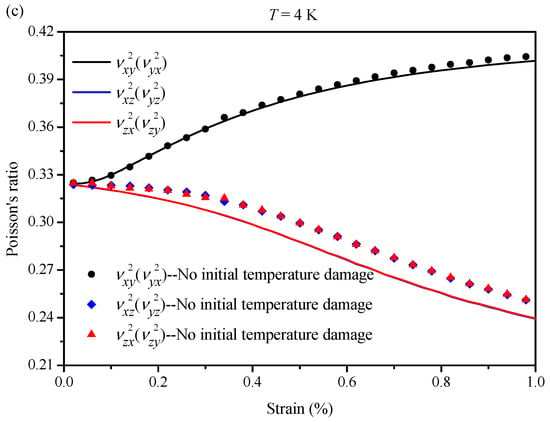
Figure 11.
EAS-Nb3Sn level 2 homogeneous superconducting region considering damage in different directions when T = 4 K: (a) Young’s modulus; (b) shear modulus; (c) Poisson’s ratio. (Note: The symbol “2” indicates the level 2 homogeneous core bundle).
3.3. Elastoplastic Numerical Analysis Results of the EAS-Nb3Sn Strand Considering Fiber Damage
In the previous section, the effective parameters of the EAS-Nb3Sn strand superconducting region were calculated. In this section, the effective elastic–plastic parameters of the superconducting region are updated for the EAS-Nb3Sn strand. The elastic–plastic numerical analysis of EAS-Nb3Sn strands considering fiber damage was carried out with the wire homogenization model when the axial tensile load was applied. Figure 12 shows the uniaxial tensile stress distribution of the EAS-Nb3Sn strand considering fiber damage and matrix plasticity when the working temperature was T = 4 K, and the axial strain was ε = 0.003.

Figure 12.
von Mises stress and effective plastic strain (isoclines) distributions of the EAS-Nb3Sn strand considering fiber damage at T = 4 K and axial strain ε = 0.003.
The numerical results showed good agreement with the experimental results from Eijnden et al. [15] (Figure 13), indicating that the proposed homogenization model of mulita-level composite can be used to analysis the mechanic behaviors considering the plasticity of the matrix. The helical structure of Nb3Sn fiber bundles was neglected in the establishment of the level 1 and 2 RVEs of EAS-Nb3Sn strands, as was the influence of the contact stress between the fiber bundle helixes; moreover, the damage caused by other preparation processes are neglected. Therefore, a certain error is exhibited between the simulation and experimental results in Figure 13. It can be seen from Figure 13 the experiment results are consistent with numerical analysis with less than 0.1% strain, and then, the differences increased with the increase of axial strain ε. The main reason for that is the pure component plastic parameters are not absolutely the same as that in the strand; at the same time, the content of each component is also difficult to identify. This could also result in an gradually approaches between the numerical analysis and the experiment results when the strain is more than 0.8%. In the subsequent sections, the influence of these factors on the mechanical properties of the strands will be considered. When the axial strain is identical, the average stress of the strand decreased with the increase of temperature. In general, experimental tests and trends agree with the results predicted by the simulation.
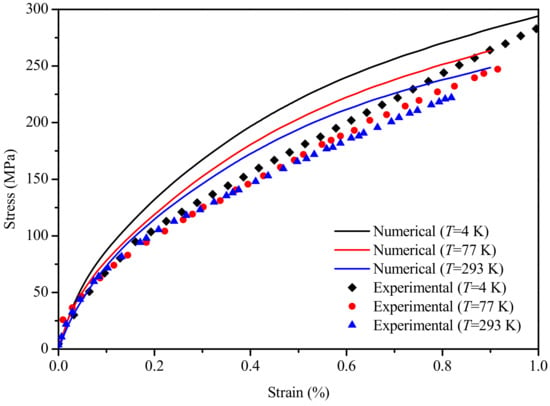
Figure 13.
Numerical simulation and experimental comparison of the EAS-Nb3Sn strand under different working temperatures considering damage.
Figure 14 depicts the stress–strain curve from the numerical simulation of homogenized EAS-Nb3Sn strands under uniaxial tensile load at operating temperatures, T = 4 K, 77 K, and 293 K, respectively. Comparing the stress–strain curves of fibers with initial thermal damage with those under different working temperatures in the comparison chart, it was found that the lower the working temperature, the greater the effect of the initial thermal damage of the fiber on the EAS-Nb3Sn strand stress; the existence of initial thermal damage accelerated the degradation of the strand stress. When the working temperature was T = 4 K and the axial load was ε = 0.005, the stress of the EAS-Nb3Sn strand with initial thermal damage was degraded by 3.7% compared with the stress value without initial damage; under the same load with a working temperature of T = 293 K, the stress value reduced by 2.9%. In addition, due to chill brittleness, the stress of the strand in the low–temperature environment (4 K) was greater than the value in the temperature environments of 77 K and 293 K.
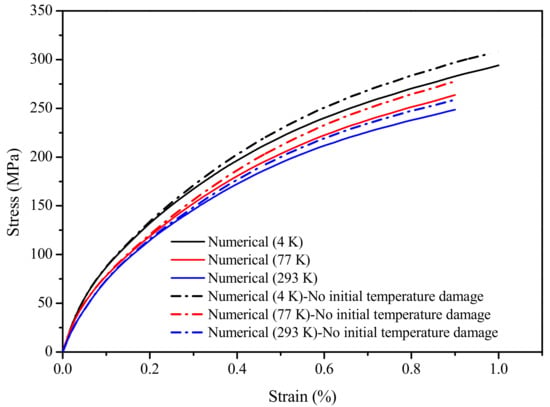
Figure 14.
Numerical simulation stress–strain curves of EAS-Nb3Sn strand considering damage at different working temperatures.
4. Conclusions
In this paper, an efficient hierarchical homogenized calculation model is presented that the initial thermal damage for the fibers and non-linear elastic-plastic model of the material in Nb3Sn strands are considered. Because of the strain sensitivity in Nb3Sn fibers and the large temperature difference between the preparation environment and the working environment, the thermal stress in the fiber obviously influences the nonlinear behaviors of strand. The homogenized effective stiffness matrixes are predicted at each level to investigate the effect of intimal thermal damage. The stress–strain curve of the numerical simulation was verified with the experiment, and the results were in good agreement. The following conclusions on the mechanical behavior of hierarchical cables are established in this paper.
The hierarchical homogenized model was presented to maximize the computing efficiency in this study. The presented method is desirable to avoid the extra-fine meshing due to the great difference between the Nb3Sn fiber and the strand. This leads to significant improvement in computational efficiency. Based on the Curtin–Zhou model, the initial thermal damage and mechanical damage for the fiber in the EAS-Nb3Sn strands was considered by introducing the scant module. Both initial thermal breakage and mechanical breakage can be considered. The initial thermal fiber fracture has non-negligible effects on the mechanical properties of the EAS-Nb3Sn superconducting strand and play the role in accelerating the increase in fiber breakage. Because of the plastic of the matrix and fiber fracture, the effective constitutive parameters of each level vary nonlinearly with strain. More precise results can be obtained considering both fiber fracture and matrix plastic.
Author Contributions
Conceptualization, Z.Z.; investigation, Z.Z. and L.S.; formal analysis, L.S.; writing-original draft preparation, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12102380), Natural Science Foundation of Jiangsu Province (BK20180894).
Institutional Review Board Statement
Not application.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Pablo, J. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Pęczkowski, P.; Łuszczek, M.; Szostak, E.; Naveen, K.C.M.; Anna, K.; Łukasz, G. Superconductivity and appearance of negative magnetocaloric effect in Ba1–xKxBiO3 perovskites, doped by Y, La and Pr. Acta Mater. 2022, 222, 117437. [Google Scholar] [CrossRef]
- Kowalik, M.; Zalecki, R.; Woch, W.M.; Tokarz, W.; Gondek, Ł. Critical Currents of (Bi1−xPbx)2Sr2Ca2Cu3Oy(x = 0.2 and 0.4) Films Deposited on Silver Substrate by Sedimentation. J. Supercond. Nov. Magn. 2017, 30, 2387–2391. [Google Scholar] [CrossRef][Green Version]
- You, F.; Ji, L.; Wang, Z.; Xie, Q.L.; Yan, S.L. Fabrication of double-sided Tl2Ba2CaCu2O8 Superconducting thin films on large-area sapphire substrates. Supercond. Sci. Technol. 2010, 23, 065002. [Google Scholar] [CrossRef]
- Pęczkowski, P.; Zachariasz, P.; Jastrzębski, C.; Piętosa, J.; Drzymała, E.; Gondek, Ł. On the Superconductivity Suppression in Eu1−xPrxBa2Cu3O7−δ. Materials 2021, 14, 3503. [Google Scholar] [CrossRef]
- Pęczkowski, P.; Kowalik, M.; Zachariasz, P.; Jastrzebski, C.; Jaegermann, Z.; Szterner, P.; Woch, W.M.; Szczytko, J. Synthesis and Physicochemical Properties of Nd-, Sm-, Eu-Based Cuprate High-Temperature Superconductors. Phys. Status Solidi A 2018, 215, 1700888. [Google Scholar] [CrossRef]
- Pęczkowski, P.; Szterner, P.; Jaegermann, Z.; Kowalik, M.; Zalecki, R.; Woch, W.M. Effects of Forming Pressure on Physicochemical Properties of YBCO Ceramics. J. Supercond. Nov. Magn. 2018, 31, 2719–2732. [Google Scholar] [CrossRef]
- Arbelaez, D.; Godeke, A.; Prestemon, S.O. An improved model for the strain dependence of the superconducting properties of Nb3Sn. Supercond. Sci. Technol. 2008, 22, 025005. [Google Scholar] [CrossRef][Green Version]
- Mitchell, N. The ITER Magnets: Design and Construction Status. IEEE Trans. Appl. Supercond. 2012, 22, 4200809. [Google Scholar] [CrossRef]
- Abelev, B.; Abramyan, A.; Adam, J.; Adamov´a, D.; Zyzak, M. Performance of the ALICE Experiment at the CERN LHC. Int. J. Mod. Phys. A 2014, 29, 1430044. [Google Scholar]
- Mitchell, N. Finite element simulations of elasto-plastic processes in Nb3Sn strands. Cryogenics 2005, 45, 501–515. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Gao, Y. Mechanical behaviors of multi-filament twist superconducting strand under tensile and cyclic loading. Cryogenics 2016, 73, 14–24. [Google Scholar] [CrossRef]
- Awaji, S.; Watanabe, K.; Katagiri, K. Improvement of mechanical and superconducting properties in CuNb/(Nb, Ti)3Sn wires by applying bending strain at room temperature. Supercond. Sci. Technol. 2003, 16, 733. [Google Scholar] [CrossRef]
- Chiesa, L.; Takayasu, M.; Minervini, J.V.; Gung, C.; Michael, P.C.; Fishman, V.; Titus, P.H. Experimental Studies of Transverse Stress Effects on the Critical Current of a Sub-Sized Nb3Sn Superconducting Cable. IEEE Trans. Appl. Supercond. 2007, 17, 1386–1389. [Google Scholar] [CrossRef]
- Eijnden, N.C.V.D.; Nijhuis, A.; Ilyin, Y.; Wessel, W.A.J.; Kate, H. Axial tensile stress–strain characterization of ITER model coil type Nb3Sn strands in TARSIS. Supercond. Sci. Technol. 2005, 18, 1523. [Google Scholar] [CrossRef]
- Ilyin, Y.; Nijhuis, A.; Wessel, W.A.J.; Van Den Eijnden, N.; Kate, H. Axial Tensile Stress-Strain Characterization of a 36 Nb3Sn Strands Cable. IEEE Trans. Appl. Supercond. 2006, 16, 1249–1252. [Google Scholar] [CrossRef]
- Nijhuis, A.; Pompe van Meerdervoort, R.P.; Krooshoop, H.J.G.; Wessel, W.A.J.; Zhou, C.; Rolando, G.; Mitchell, N.; Sanabria, C.; Lee, P.J.; Larbalestier, D.C. The effect of axial and transverse loading on the transport properties of ITER Nb3Sn strands. Supercond. Sci. Technol. 2013, 26, 084004. [Google Scholar] [CrossRef]
- Osamura, K.; Machiya, S.; Tsuchiya, Y.; Suzuki, H.; Shobu, T. Local strain and its influence on mechanical-electromagnetic properties of twisted and untwisted ITER Nb3Sn strands. Supercond. Sci. Technol. 2012, 25, 54010–54018. [Google Scholar] [CrossRef]
- Muzzi, L.; Corato, V.; Corte, A.D.; De Marzi, G.; Spina, T.; Daniels, J.; Michiel, M.D.; Buta, F.; Mondonico, G.; Seeber, B. Direct observation of Nb3Sn lattice deformation by high-energy x-ray diffraction in internal-tin wires subject to mechanical loads at 4.2 K. Kew Bull. 2012, 13, 54006–54013(8). [Google Scholar] [CrossRef]
- Scheuerlein, C.; Di Michiel, M.; Buta, F.; Seeber, B.; Senatore, C.; Flükiger, R.; Siegrist, T.; Besara, T.; Kadar, J.; Bordini, B.; et al. Stress distribution and lattice distortions in Nb3Sn multifilament wires under uniaxial tensile loading at 4.2 K. Supercond. Sci. Technol. 2015, 27, 98–102. [Google Scholar] [CrossRef]
- Vasil’ev, A.L.; Ballarino, A.; Bottura, L.; Gavrilkin, S.Y.; Degtyarenko, P.N.; Karateev, I.A.; Kruglov, V.S.; Latushkin, S.T.; Lunev, A.V.; Ryazanov, A.I. On the possible separation of the phase enriched with Nb in superconducting intermetallic Nb3Sn irradiated with fast protons. Bull. Lebedev Phys. Inst. 2017, 44, 118–121. [Google Scholar] [CrossRef]
- Pompili, F.; Esposito, B.; Marocco, D.; Podda, S.; Riva, M.; Baccaro, S.; Cemmi, A.; DiSarcina, I.; Quintieri, L.; Bocianc, D.; et al. Radiation and thermal stress test on diamond detectors for the Radial Neutron Camera of ITER. Nucl. Instrum. Methods Phys. Res. 2018, 936, 62–64. [Google Scholar] [CrossRef]
- Caiffi, B.; Angelone, M.; Colangeli, A.; Flammini, D.; Fonnesu, N.; Luìs, R.; Mariano, G.; Marocco, D.; Moro, F.; Tardocchic, M.; et al. Neutronic analyses in support of the conceptual design of the DTT tokamak radial neutron camera. Fusion Eng. Des. 2020, 157, 111629. [Google Scholar] [CrossRef]
- Jardin, A.; Bielecki, J.; Mazon, D.; Dankowski, J.; Kro, K.; Peysson, Y.; Scholz, M. Synthetic X-ray Tomography Diagnostics for Tokamak Plasmas. J. Fusion Energy 2020, 8, 240–250. [Google Scholar] [CrossRef]
- Vondracek, P.; Panek, R.; Hron, M.; Havlicek, J.; Zhang, H. Preliminary design of the COMPASS upgrade tokamak. Fusion Eng. Des. 2021, 169, 112490. [Google Scholar]
- Tan, W.; Ma, R.; Pan, H.; Zhao, H.; He, X.; Chen, X.; Zhao, C.; Lu, X. The observation of tin islands in Nb3Sn thin films deposited by magnetron sputtering. Phys. C 2020, 576, 1353667. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, C.; Huang, R.; Li, L. A comparative study of compositions and microstructures of two types internal-tin process Nb3Sn wires. Cryogenics 2020, 110, 103145. [Google Scholar] [CrossRef]
- Xiao, L.; Lu, X.; Yang, Z.; Tan, W.; Xie, D. Annealing study on the properties of Cu-based Nb3Sn films under argon pressures for SRF applications. Phys. C 2021, 586, 1353894. [Google Scholar] [CrossRef]
- Boso, D.P.; Lefik, M.; Schrefler, B.A. A multilevel homogenised model for superconducting strand thermomechanics. Cryogenics 2005, 45, 259–271. [Google Scholar] [CrossRef]
- Boso, D.P.; Lefik, M.; Schrefler, B.A. Homogenisation methods for the thermo-mechanical analysis of Nb3Sn strand. Cryogenics. 2006, 46, 569–580. [Google Scholar] [CrossRef]
- Boso, D.P.; Lefik, M.; Schrefler, B.A. Multiscale analysis of the influence of the triplet helicoidal geometry on the strain state of a Nb3Sn based strand for ITER coils. Cryogenics 2005, 45, 589–605. [Google Scholar] [CrossRef]
- Boso, D.P. A simple and effective approach for thermo-mechanical modelling of composite superconducting wires. Supercond. Sci. Technol. 2013, 26, 045006. [Google Scholar] [CrossRef]
- Ahoranta, M.; Lehtonen, J.; Tarhasaari, T.; Wiess, K. Modelling of local strain and stress relaxation in bronze processed Nb3Sn wires. Supercond. Ence Technol. 2008, 21, 025005. [Google Scholar] [CrossRef]
- Collins, B.; Krishnan, J.; Arbelaez, D.; Ferracin, P.; PrestemonS, O.; Godeke, A.; Dietderich, D.R.; Zohdi, T. Introduction of Nonlinear Properties into Hierachical Models of Nb3Sn Strands. IEEE Trans. Appl. Supercond. 2011, 21, 2320–2323. [Google Scholar] [CrossRef]
- Collins, B.; Krishnan, J.; Arbelaez, D.; Ferracin, P.; Dietderich, D.R.; Zohdi, T.I. Computation of Strain State in a Strand Using Nonlinear Hierarchical Models. IEEE Trans. Appl. Supercond. 2012, 22, 4905104. [Google Scholar] [CrossRef]
- Jing, Z.; Yong, H.; Zhou, Y. Theoretical Modeling for the Effect of Twisting on the Properties of Multi-filamentary Superconducting Strand. IEEE Trans. Appl. Supercond. 2013, 23, 6000307. [Google Scholar] [CrossRef]
- Liu, B.; Jing, Z.; Yong, H.; Zhou, Y.H. Strain distributions in superconducting strands with twisted filaments. Compos. Struct. 2017, 174, 158–165. [Google Scholar] [CrossRef]
- Wang, W.; Qin, J.; Yu, M.; Li, J. Heat transfer analysis during heat treatment of Nb3Sn coils for the CFETR CSMC. Fusion Eng. Des. 2021, 165, 112248. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Xue, C.; Chen, Y.Q.; Ou, X.J.; Wu, W.; Liu, W.; Ma, P.; Sun, L.T.; Zhao, H.W.; Zhou, Y.H. Thermomagnetic instabilities of Nb3Sn wires inside the superconducting solenoid. Phys. C 2021, 593, 1354002. [Google Scholar] [CrossRef]
- Xu, X.; Sumption, M.D.; Lee, J.; Rochester, J.; Peng, X. Persistent compositions of non-stoichiometric compounds with low bulk diffusivity: A theory and application to Nb3Sn superconductors. J. Alloy. Compd. 2020, 845, 156182. [Google Scholar] [CrossRef]
- Curtin, W.A. Theory of Mechanical Properties of Ceramic-Matrix Composites. J. Am. Ceram. Soc. 1991, 74, 2837–2845. [Google Scholar] [CrossRef]
- Curtin, W.A.; Zhou, S.J. Influence of processing damage on performance of fiber-reinforced composites. J. Mech. Phys. Solids 1995, 43, 343–363. [Google Scholar] [CrossRef]
- Luo, W.; Zheng, X.J. Initial damage influence of stiffness reduction for bronze route Nb3Sn strands. Phys. C 2011, 471, 558–562. [Google Scholar] [CrossRef]
- Yong, H.D.; Yang, P.L.; Xue, C.; Zhou, Y.H. Fractue behavior of filament in Nb3Sn strands with crack-bridging model. Fusion Eng. Des. 2016, 102, 66–73. [Google Scholar] [CrossRef]
- Popova, E.N.; Popov, V.V. Dislocation and grain structure formation in Nb filaments of different geometry at fabrication of Nb3Sn-based superconducting wires. Mater. Charact. 2020, 167, 110488. [Google Scholar] [CrossRef]
- Abdyukhanov, I.M.; Tsapleva, A.S.; Mareev, K.A.; Alekseev, M.V.; Luk'yanov, P.A.; Polikarpova, M.V.; Zakharova, G.A.; Panashchuk, I.A.; Nasibulin, M.N.; Dergunova, E.A. Investigation of Local Damage Effect on Nb3Sn Superconductor Properties. At. Energy 2021, 128, 343–348. [Google Scholar] [CrossRef]
- Kaverin, D.; Potanina, L.; Shutov, K.; Vysotsky, V.; Tronza, V.; Mitin, A.; Abdyukhanov, I.; Alekseev, M. Analysis of Nb3Sn Strand Microstructure After Full-size SULTAN Test of ITER TF Conductor Sample. Phys. Procedia 2015, 67, 914–919. [Google Scholar] [CrossRef][Green Version]
- Shen, F.; Zhang, H.; Huang, C.; Li, L. Experimental study on strain sensitivity of Internal-Tin Nb3Sn superconducting strand based on non-destructive technology. Phys. C 2021, 584, 1353784. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).