Characteristics of Magnetic Fields Induced by the Wake of an Underwater Vehicle
Abstract
1. Introduction
- (1)
- We used a multi-physical field simulation method and combined dynamic overset grid methods to calculate the magnetic field generated by the wake during submarine movement. This method can obtain substantial information about the wake and magnetic fields.
- (2)
- Based on the numerical simulation results, we analyzed the space-time distribution of the wake magnetic field and described the time-frequency domain characteristics of the magnetic field at different monitoring points during submarine navigation.
- (3)
- We studied the relationship between the velocity, acceleration, and wake magnetic field characteristics in submarine motion and proposed the gravity center frequency and half energy bandwidth to represent them.
2. Numerical Methods
2.1. Governing Equations and Turbulence Models
2.2. Magnetic Fields Induced by the Wake
3. Computational and Validation
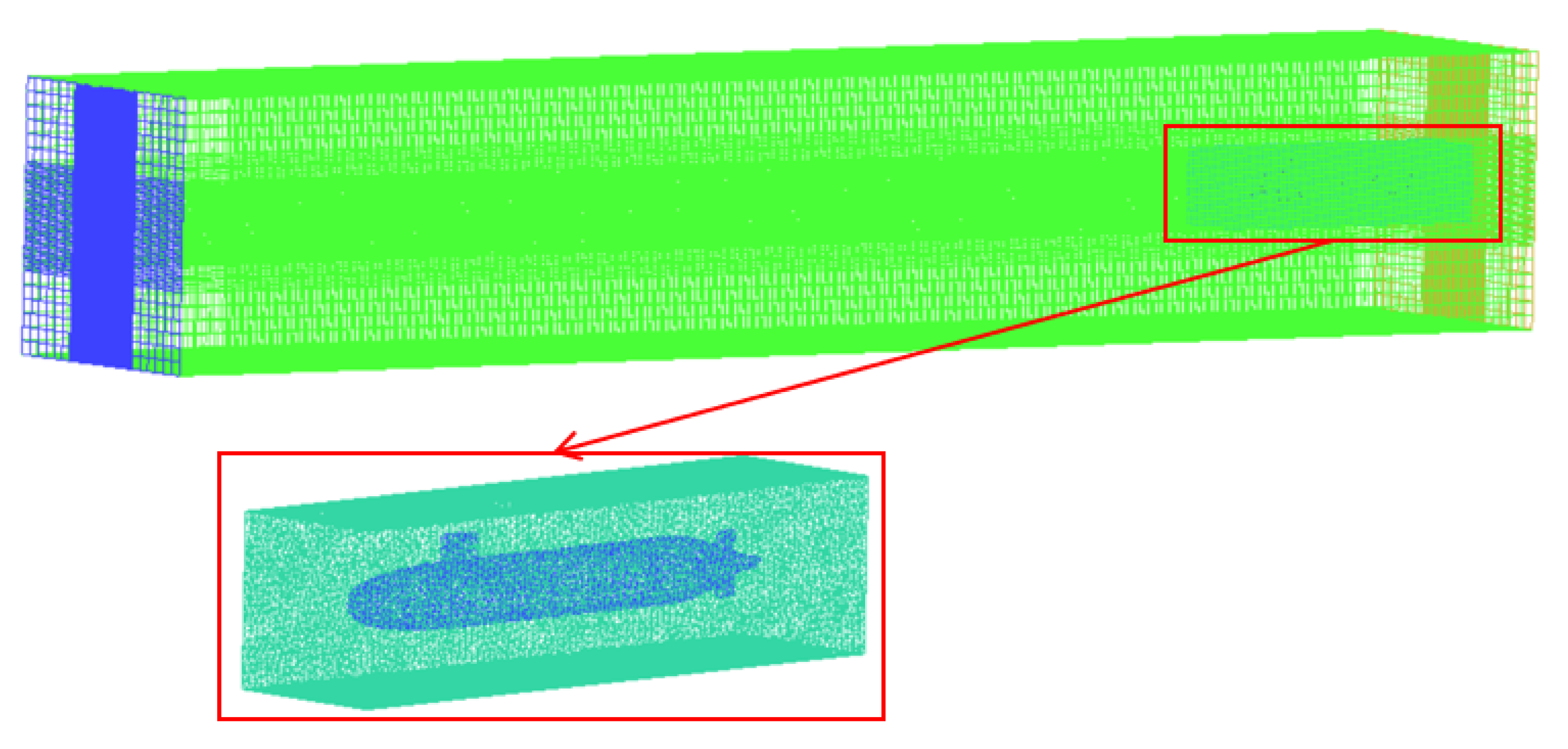
3.1. The Research Model and Discretized Mesh
3.2. Solution Validation
4. Results and Discussions
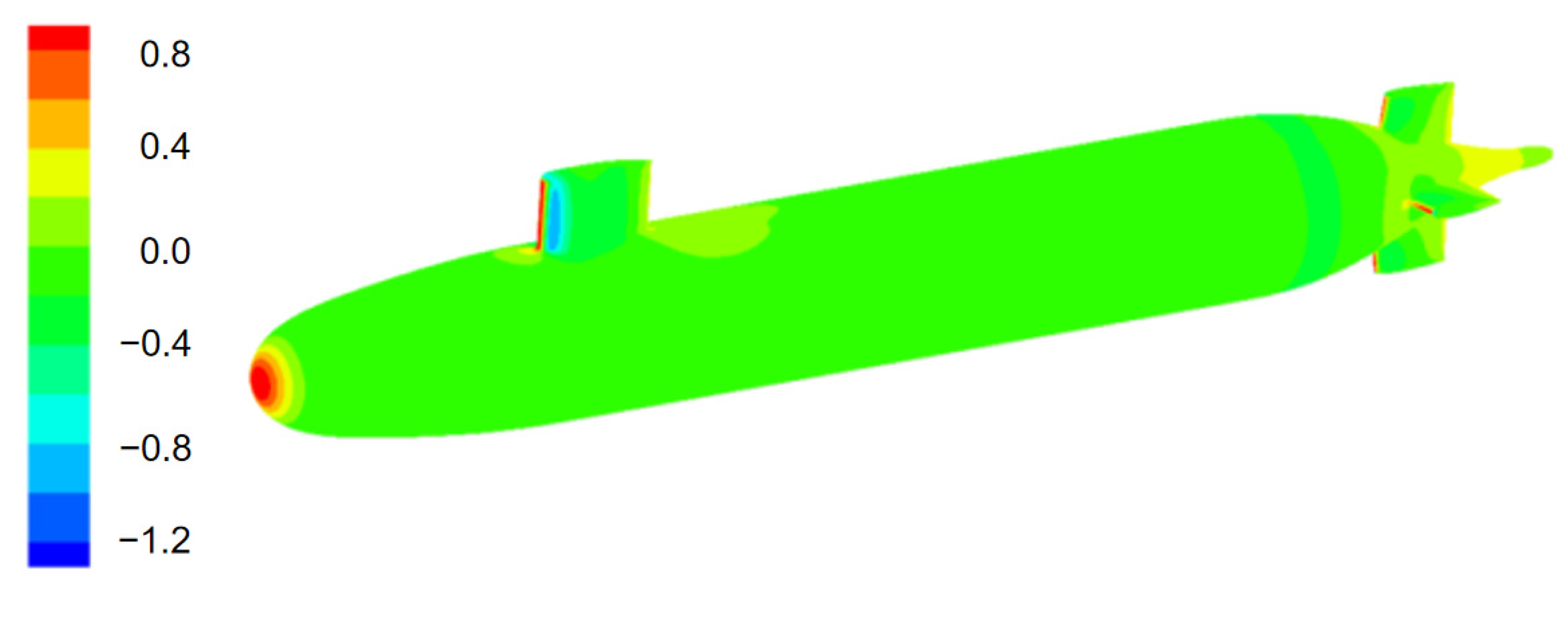
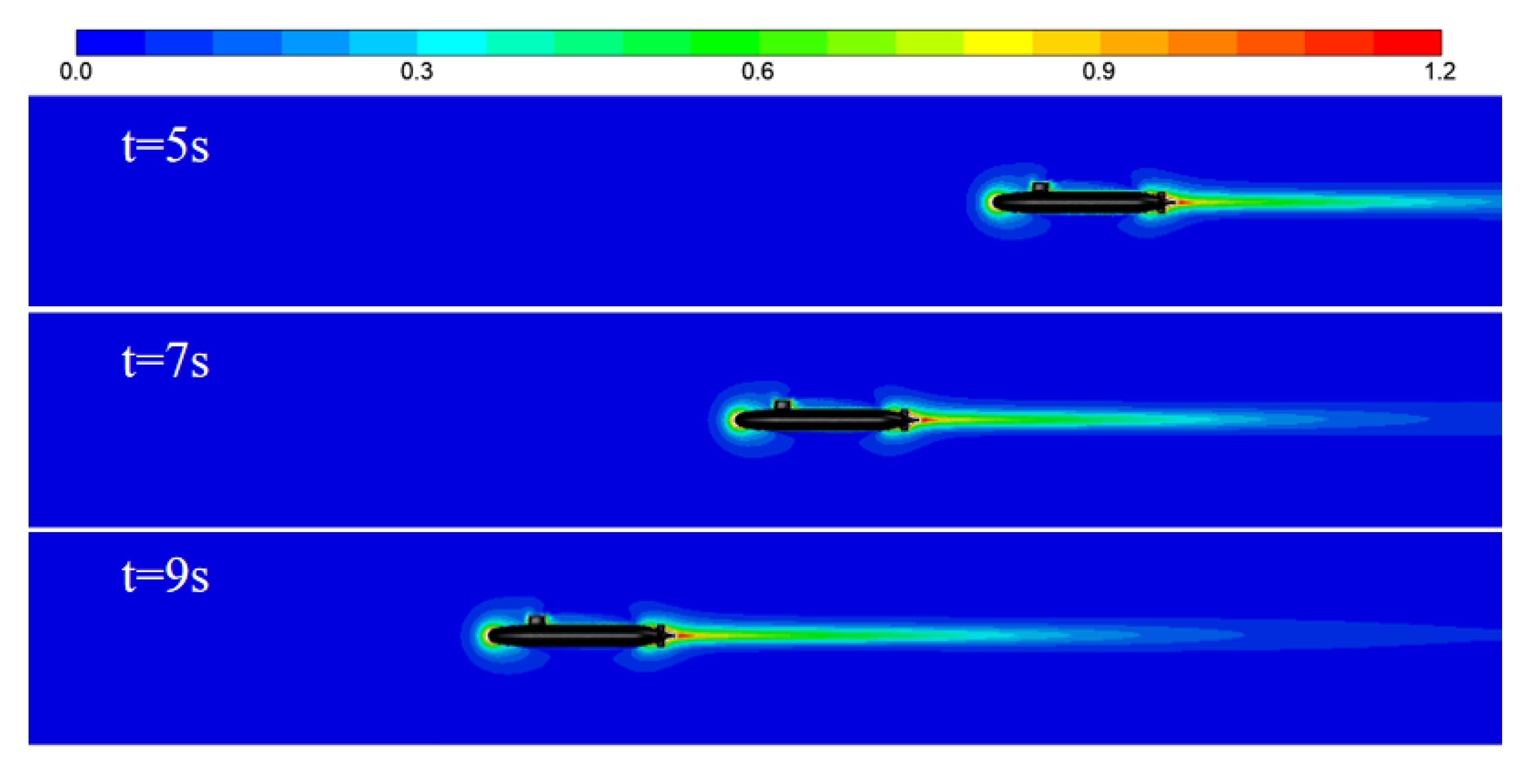
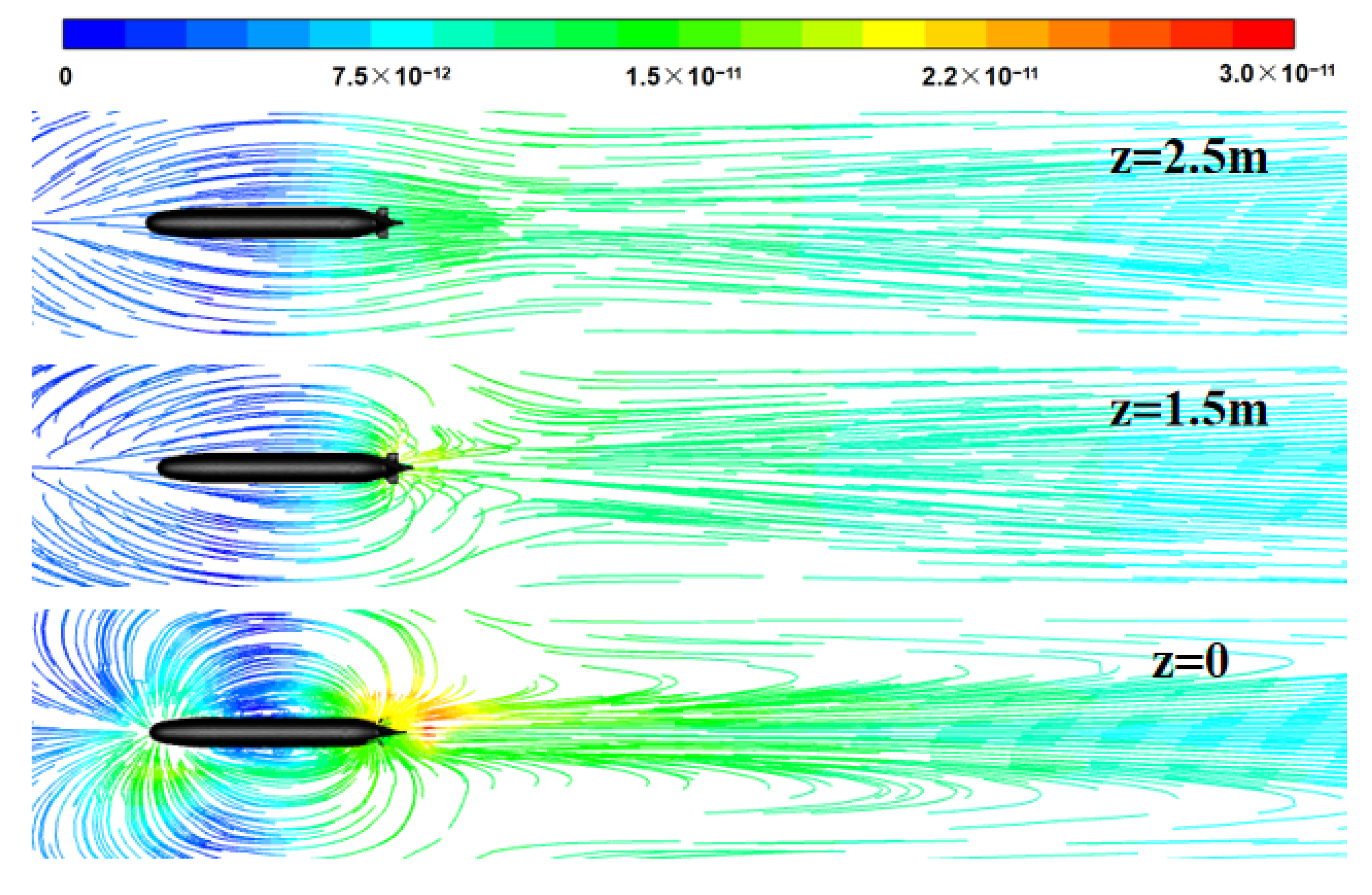
4.1. Spatial Distribution of the Flow and Magnetic Fields
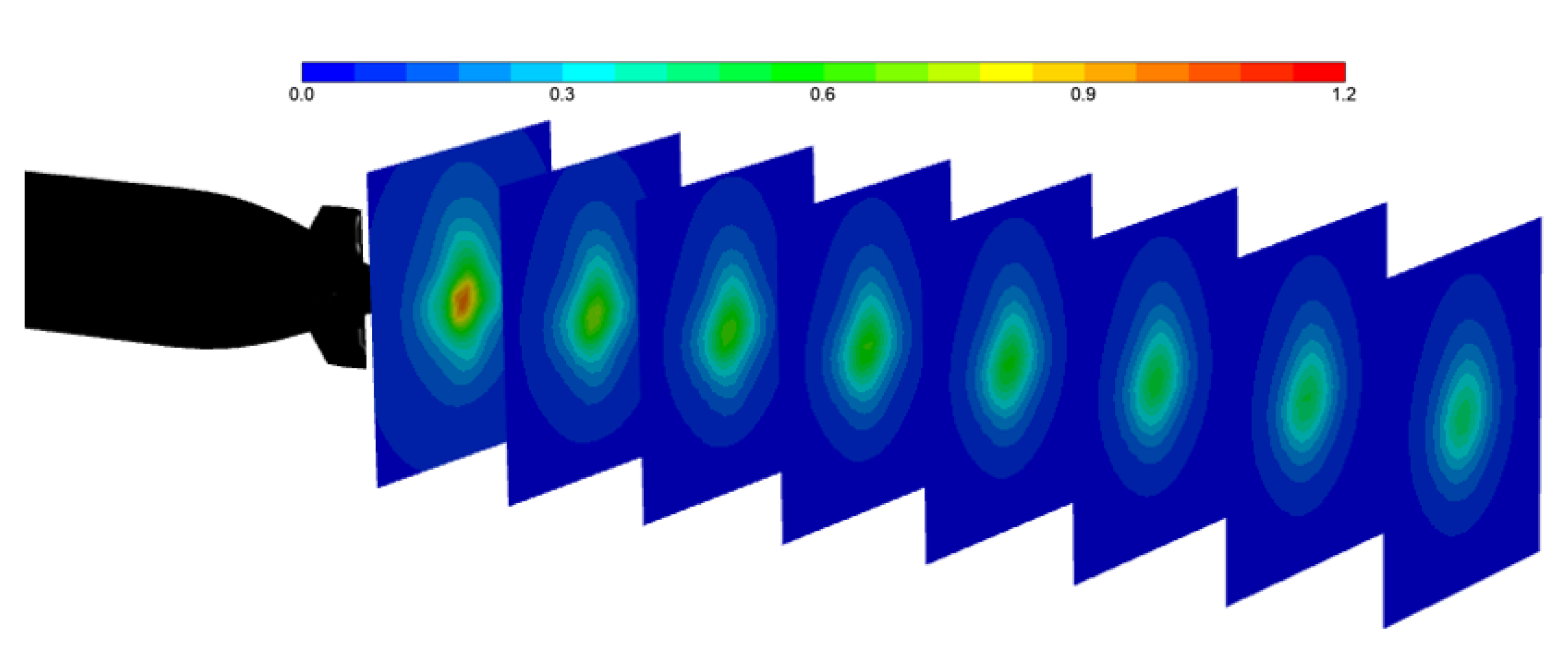
4.2. Characteristics of the Wake Magnetic Field
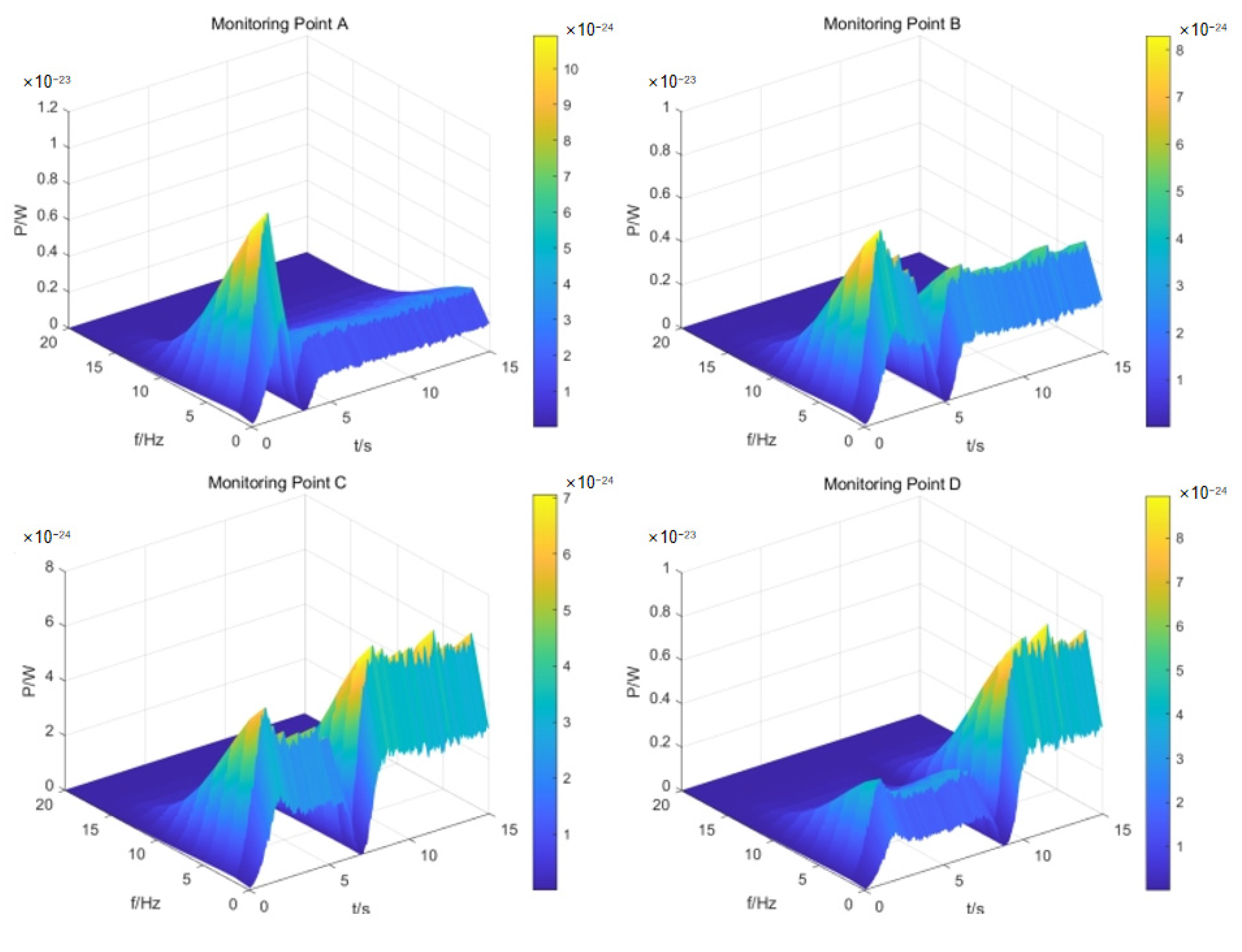
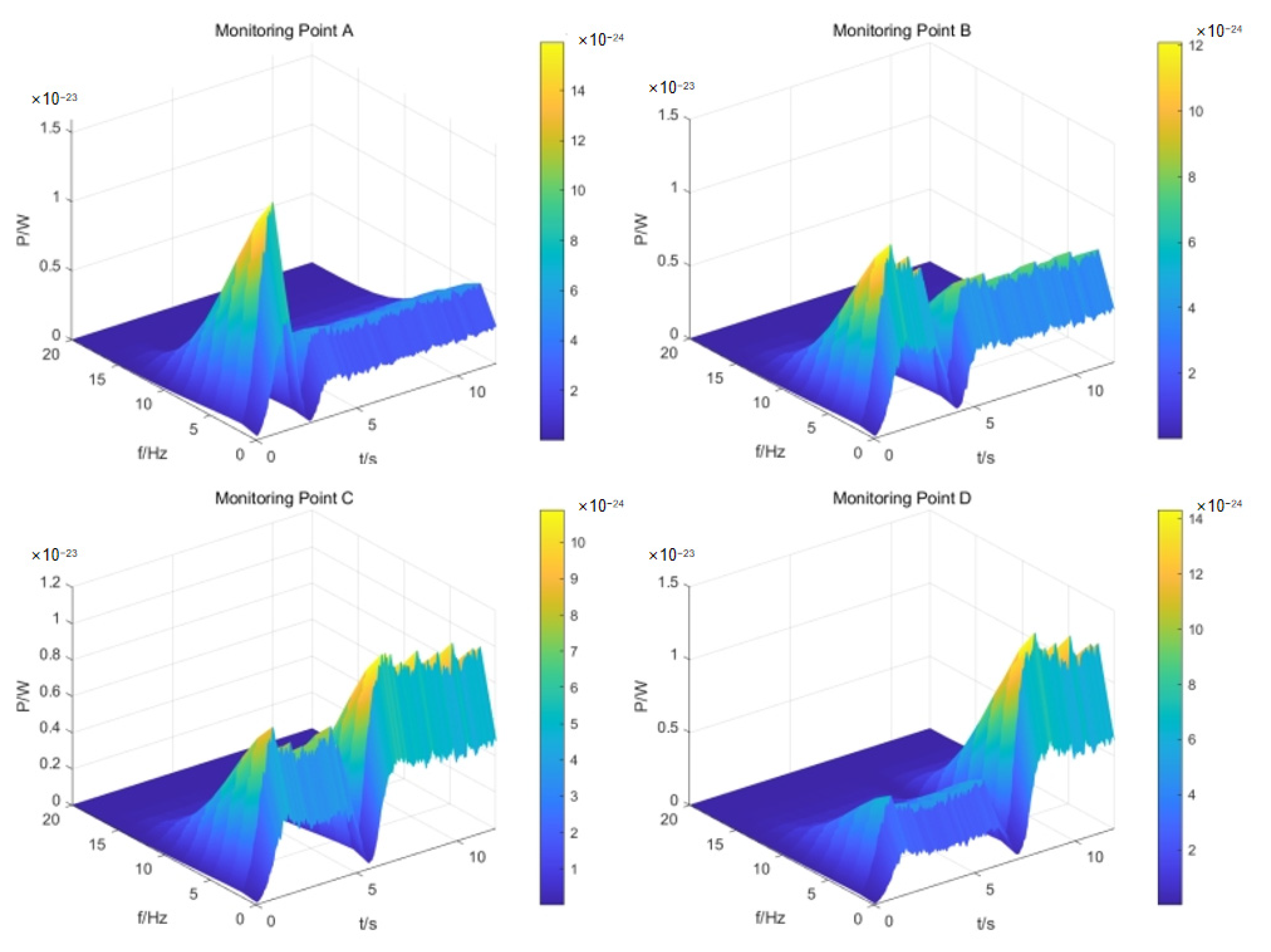
4.2.1. Time-Frequency Characteristics of the Wake Magnetic Field
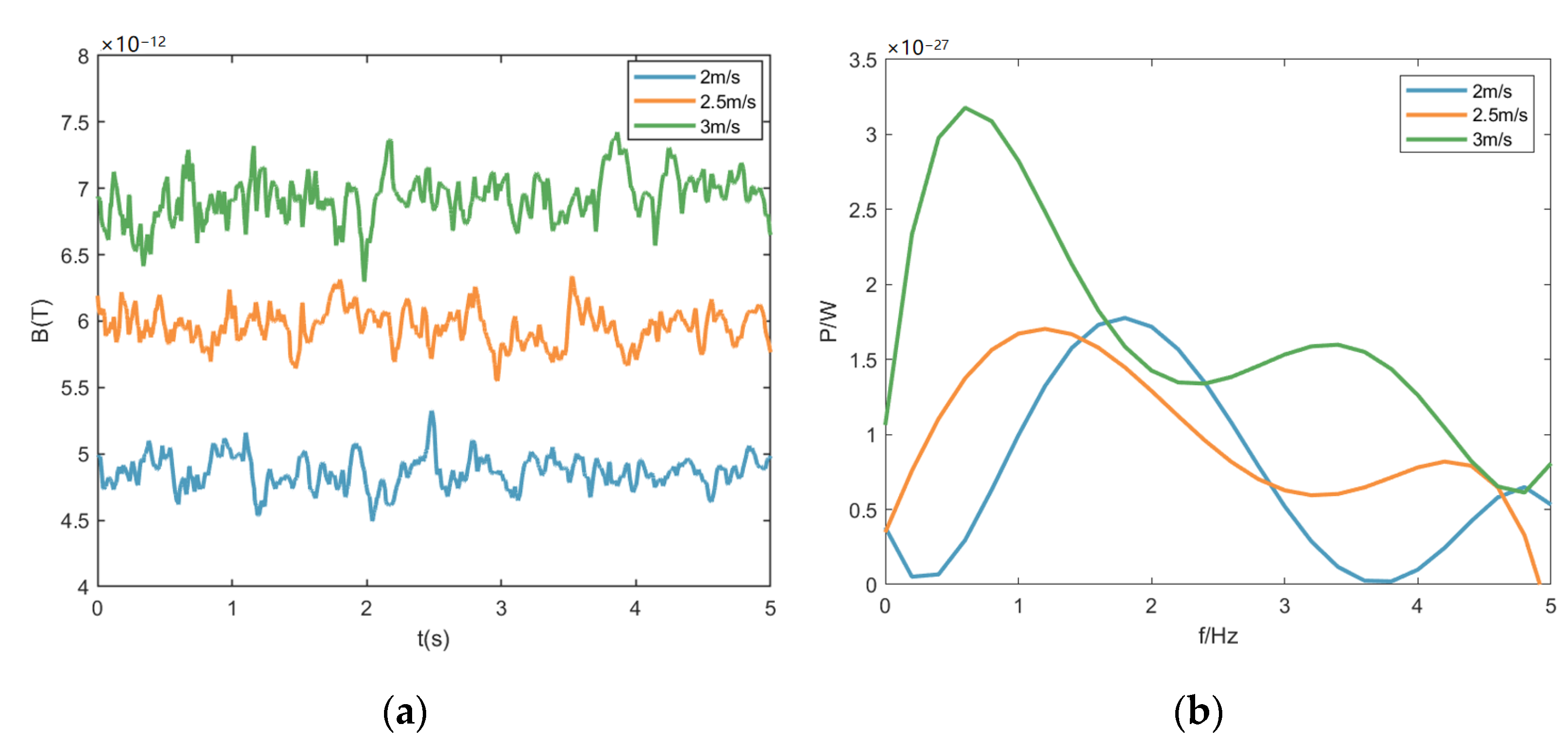
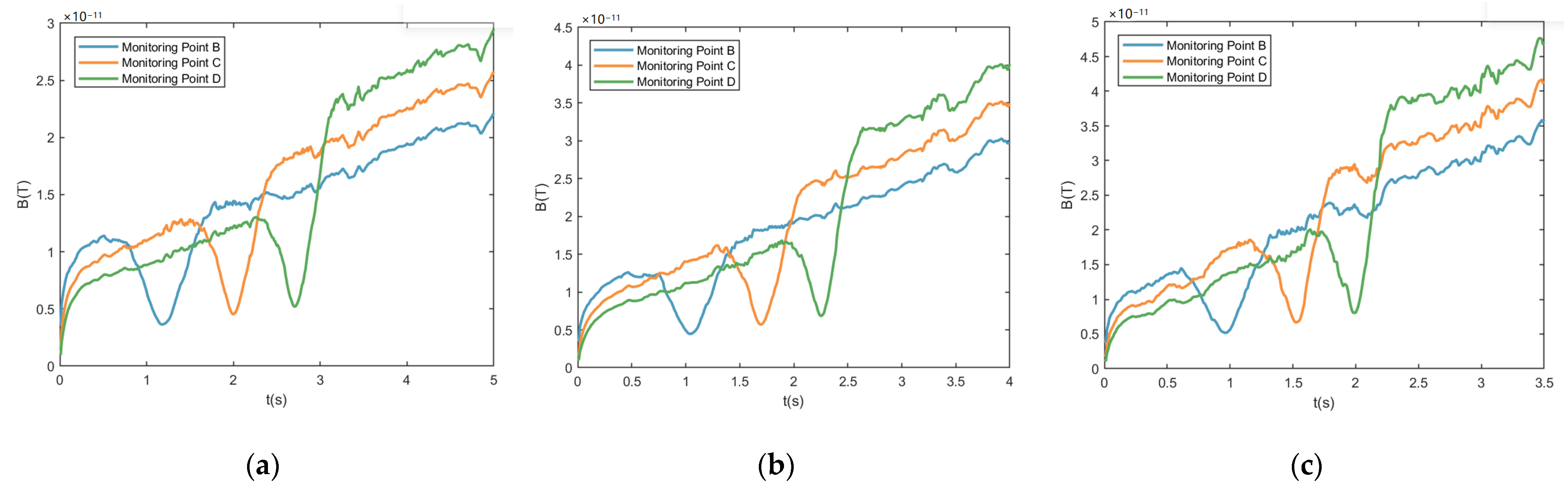
4.2.2. Effect of Ship Speed on the Wake Magnetic Field
4.2.3. Effect of Acceleration on the Wake Magnetic Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Faraday, M. Experimental Researches in Electricity. Philos. Trans. R. Soc. Lond. 1832, 122, 125–162. [Google Scholar]
- Podney Walter; Sager Ronald Measurement of Fluctuating Magnetic Gradients Originating from Oceanic Internal Waves. Science 1979, 205, 1381–1382. [CrossRef] [PubMed]
- Beal, H.T.; Weaver, J.T. Calculations of Magnetic Variations Induced by Internal Ocean Waves. J. Geophys. Res. 1970, 75, 6846–6852. [Google Scholar] [CrossRef]
- Chave, A.D. On the Electromagnetic Fields Induced by Oceanic Internal Waves. J. Geophys. Res. Ocean. 1984, 89, 10519–10528. [Google Scholar] [CrossRef]
- Fraser, D. Magnetic Fields of Ocean Waves. Nature 1965, 206, 605–606. [Google Scholar] [CrossRef]
- Semkin, S.; Smagin, V. The Effect of Self-Induction on Magnetic Field Generated by Sea Surface Waves. Izv. Atmos. Ocean. Phys. 2012, 48, 207–213. [Google Scholar] [CrossRef]
- Bhatt, K.; Hördt, A.; Weidelt, P.; Hanstein, T. Motionally Induced Electromagnetic Field within the Ocean; 2009. In Proceedings of the 23 Schmucker-Weidelt-Kolloquium für Elektromagnetische Tiefenforschung, Haltern am See, Germany, 23–27 September 2019. [Google Scholar] [CrossRef]
- Saynisch, J.; Petereit, J.; Irrgang, C.; Thomas, M. Impact of Oceanic Warming on Electromagnetic Oceanic Tidal Signals: A CMIP5 Climate Model-Based Sensitivity Study: Global warming impact on emots. Geophys. Res. Lett. 2017, 44, 4994–5000. [Google Scholar] [CrossRef]
- Zou, N.; Nehorai, A. Detection of Ship Wake Using an Airborne Magnetic Transducer. In Proceedings of the Conference Record of Thirty-Second Asilomar Conference on Signals, Systems and Computers (Cat. No.98CH36284), Pacific Grove, CA, USA, 1–4 November 1998; Volume 2, pp. 1316–1321. [Google Scholar]
- Madurasinghe, D. Induced Electromagnetic Fields Associated with Large Ship Wakes. Wave Motion 1994, 20, 283–292. [Google Scholar] [CrossRef]
- Fallah, M.-A.; Monemi, M. Optimal Magnetic Wake Detection in Finite Depth Water. PIER M 2021, 106, 25–44. [Google Scholar] [CrossRef]
- Zhu, X.-J.; Xia, M.-Y. Magnetic Field Induced by Wake of Moving Body in Wind Waves. Prog. Electromagn. Res. 2014, 149, 10. [Google Scholar] [CrossRef][Green Version]
- Zhu, X.J.; Du, C.P.; Xia, M.Y. Modeling of Magnetic Field Induced by Ship Wake. In Proceedings of the 2015 IEEE International Conference on Computational Electromagnetics, Hong Kong, China, 2–5 February 2015; pp. 374–376. [Google Scholar]
- Xu, Z.; Du, C.; Xia, M. Evaluation of Electromagnetic Fields Induced by Wake of an Undersea-Moving Slender Body. IEEE Access 2018, 6, 2943–2951. [Google Scholar] [CrossRef]
- Yaakobi, O.; Zilman, G.; Miloh, T. Detection of the Electromagnetic Field Induced by the Wake of a Ship Moving in a Moderate Sea State of Finite Depth. J. Eng. Math. 2011, 70, 17–27. [Google Scholar] [CrossRef]
- Fallah, M.A.; Abiri, H. Multi-Sensor Approach in Vessel Magnetic Wake Imaging. Wave Motion 2014, 51, 60–76. [Google Scholar] [CrossRef]
- Madurasinghe, D.; Tuck, E.O. The Induced Electromagnetic Field Associated with Submerged Moving Bodies in an Unstratified Conducting Fluid. IEEE J. Ocean. Eng. 1994, 19, 193–199. [Google Scholar] [CrossRef]
- Madurasinghe, D.; Haack, G.R. The Induced Electromagnetic Field Associated with Wakes-Signal Processing Aspects. In Proceedings of the IGARSS ’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 4, pp. 2335–2337. [Google Scholar]
- Chen, Q.; Xuan, Y.; Lin, Q.; Han, Y. Evolutions of the Electromagnetic Signatures Induced by the Propagating Wake behind a Submerged Body. Int. J. Heat Mass Transf. 2022, 194, 123105. [Google Scholar] [CrossRef]
- Xu, Y.; Pan, M.; Zhang, Q.; Chen, D.; Liu, Z.; Hu, J.; Chen, Z.; Wang, Z.; Wang, Z. The Characteristics of Debye Effect Magnetic Field Under Acoustic Excitation. J. Phys. Conf. Ser. 2021, 1885, 042021. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Pan, M.; Ding, Q.; Huang, B.; Chen, D.; Liu, Z. Analysis of Ion Separation Magnetic Field Induced by Submarine Hydrodynamic Perturbations. In Proceedings of the OCEANS 2021: San Diego–Porto, San Diego, CA, USA, 20 September 2021; pp. 1–5. [Google Scholar]
- Elsaady, W.; Oyadiji, S.O.; Nasser, A. A One-Way Coupled Numerical Magnetic Field and CFD Simulation of Viscoplastic Compressible Fluids in MR Dampers. Int. J. Mech. Sci. 2020, 167, 105265. [Google Scholar] [CrossRef]
- Liu, D.; Bu, C.; Chen, X. Development and Test of CFD–DEM Model for Complex Geometry: A Coupling Algorithm for Fluent and DEM. Comput. Chem. Eng. 2013, 58, 260–268. [Google Scholar] [CrossRef]
- Wang, L.; Martin, J.E.; Felli, M.; Carrica, P.M. Experiments and CFD for the Propeller Wake of a Generic Submarine Operating near the Surface. Ocean Eng. 2020, 206, 107304. [Google Scholar] [CrossRef]
- Li, J.; Martin, J.E.; Carrica, P.M. Large-Scale Simulation of Ship Bubbly Wake during a Maneuver in Stratified Flow. Ocean Eng. 2019, 173, 643–658. [Google Scholar] [CrossRef]
- Carrica, P.M.; Kim, Y.; Martin, J.E. Near-Surface Self Propulsion of a Generic Submarine in Calm Water and Waves. Ocean Eng. 2019, 183, 87–105. [Google Scholar] [CrossRef]







| Description | Symbol | Scale |
|---|---|---|
| Length | L (m) | 4.356 |
| Max diameter | D (m) | 0.508 |
| Max height | H (m) | 0.968 |
| CFD Total Resistance (N) | Test Value (N) | Error (%) |
|---|---|---|
| 105.2 | 102.3 | 2.8% |
| Speed (m/s) | 2 | 2.5 | 3 |
|---|---|---|---|
| Barycenter Frequency (Hz) | 2.20 | 2.03 | 1.99 |
| Half-Energy Bandwidth (Hz) | 0.86 | 1.63 | 2.42 |
| Acceleration (m/s2) | 1 | 2 | 3 |
|---|---|---|---|
| Growth Rate at Point A (T/s) | 1.78 × 10−12 | 3.77 × 10−12 | 5.55 × 10−12 |
| Growth Rate at Point B (T/s) | 2.01 × 10−12 | 5.05 × 10−12 | 7.36 × 10−12 |
| Growth Rate at Point C (T/s) | 2.34 × 10−12 | 6.23 × 10−12 | 7.60 × 10−12 |
| Growth Rate at Point D (T/s) | 3.43 × 10−12 | 6.85 × 10−12 | 9.17 × 10−12 |
| Acceleration (m/s2) | 1 | 2 | 3 |
|---|---|---|---|
| Magnetic Field Size (T) | 9.88 × 10−12 | 1.34 × 10−11 | 1.66 × 10−11 |
| Increase in Percentage (%) | 42.6 | 94.0 | 139.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Liu, Z.; Xu, Y.; Ding, Q.; Pan, M.; Hu, J.; Zhang, Q. Characteristics of Magnetic Fields Induced by the Wake of an Underwater Vehicle. Appl. Sci. 2022, 12, 7964. https://doi.org/10.3390/app12167964
Huang B, Liu Z, Xu Y, Ding Q, Pan M, Hu J, Zhang Q. Characteristics of Magnetic Fields Induced by the Wake of an Underwater Vehicle. Applied Sciences. 2022; 12(16):7964. https://doi.org/10.3390/app12167964
Chicago/Turabian StyleHuang, Bo, Zhongyan Liu, Yujing Xu, Qiaochu Ding, Mengchun Pan, Jiafei Hu, and Qi Zhang. 2022. "Characteristics of Magnetic Fields Induced by the Wake of an Underwater Vehicle" Applied Sciences 12, no. 16: 7964. https://doi.org/10.3390/app12167964
APA StyleHuang, B., Liu, Z., Xu, Y., Ding, Q., Pan, M., Hu, J., & Zhang, Q. (2022). Characteristics of Magnetic Fields Induced by the Wake of an Underwater Vehicle. Applied Sciences, 12(16), 7964. https://doi.org/10.3390/app12167964





