Machine Learning Enabled 3D Body Measurement Estimation Using Hybrid Feature Selection and Bayesian Search
Abstract
:1. Introduction
- A novel mix of Bayesian search and the importance-based feature selection is utilized to improve the efficacy of XGBoost and RF while maintaining a high standard their performance in the 3D BM prediction.
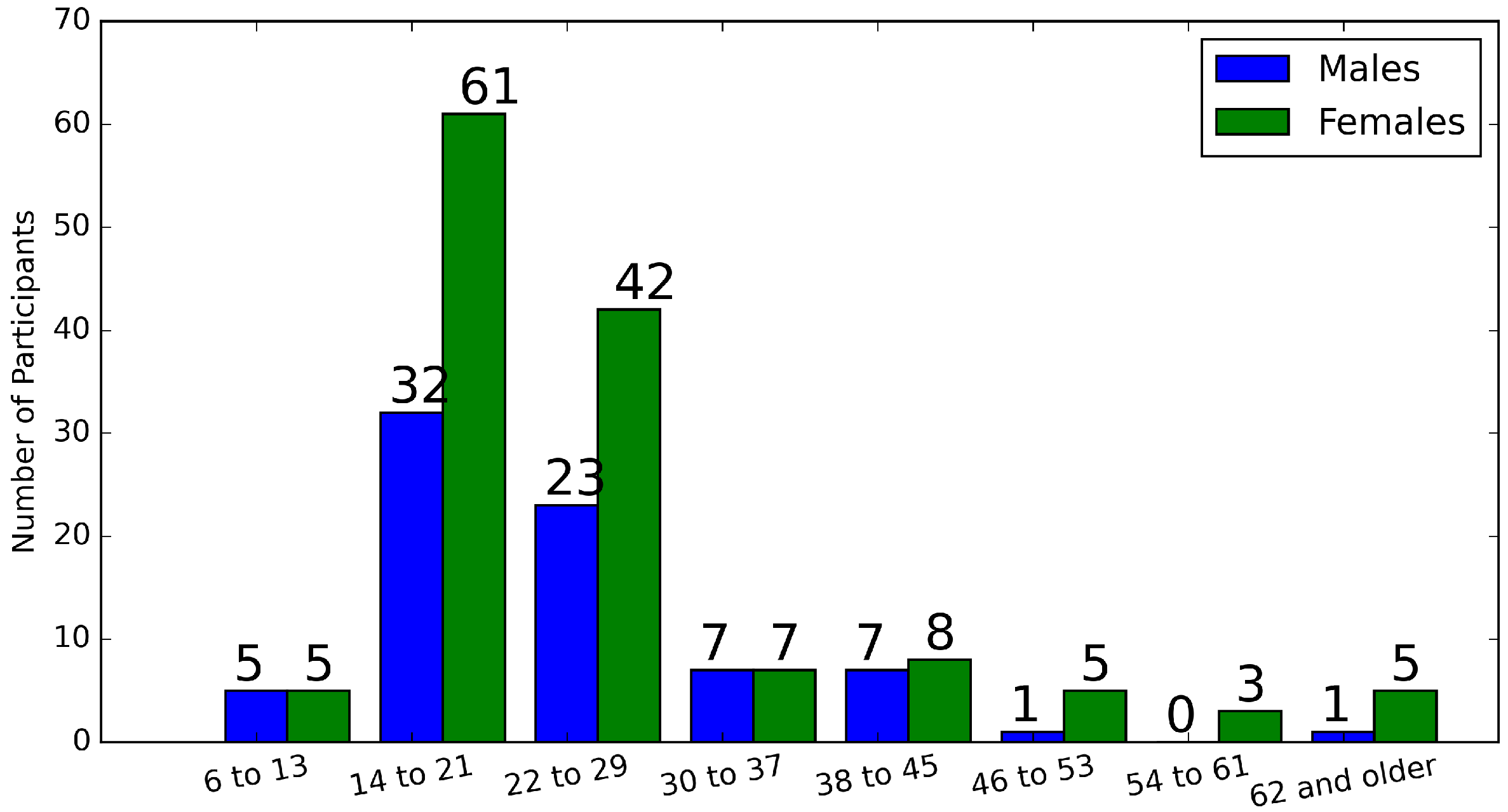
- A real-world 3D body measurement of 212 participants in the Kansas-Missouri area in the United States is collected, trained and tested in this research.
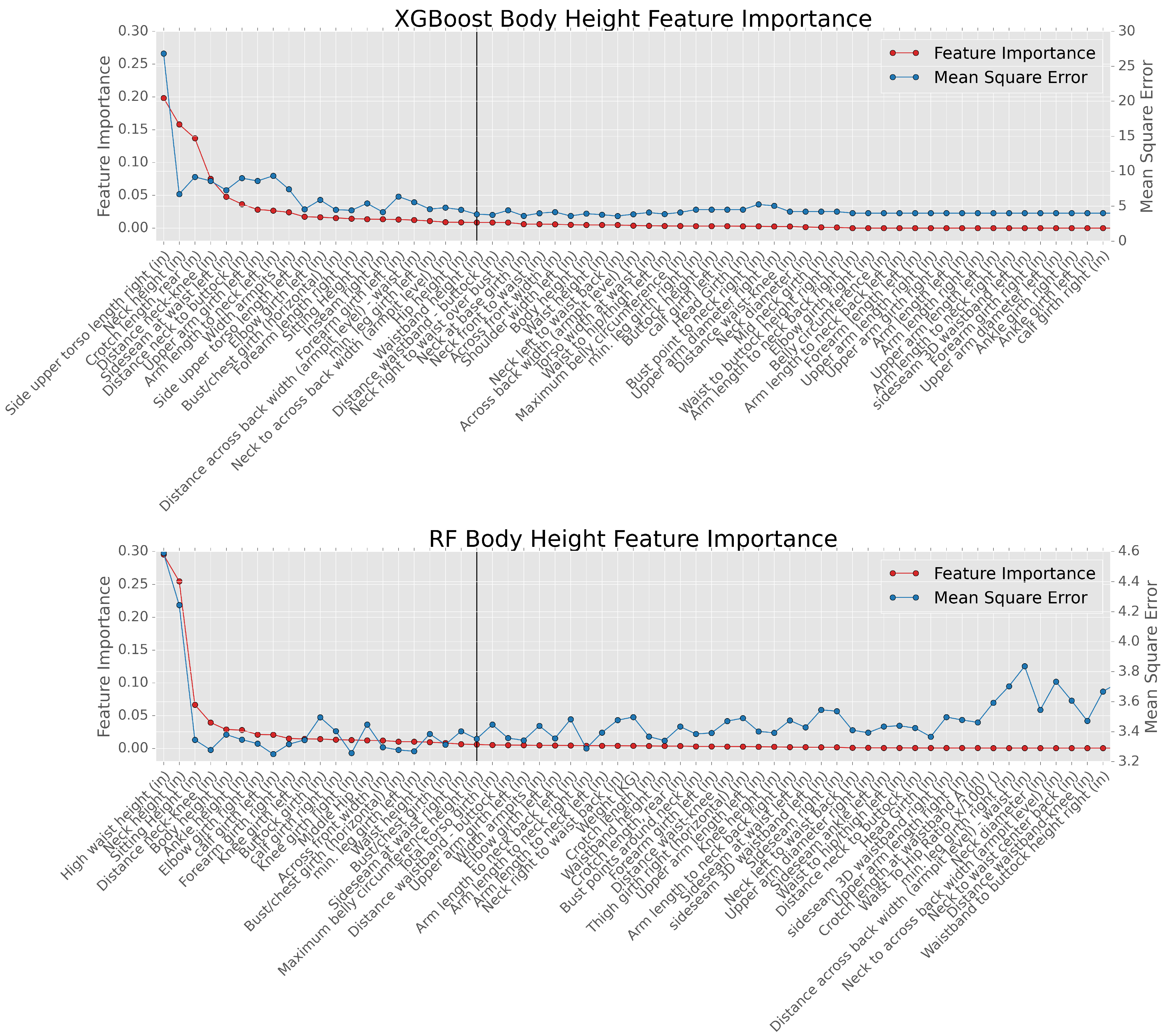
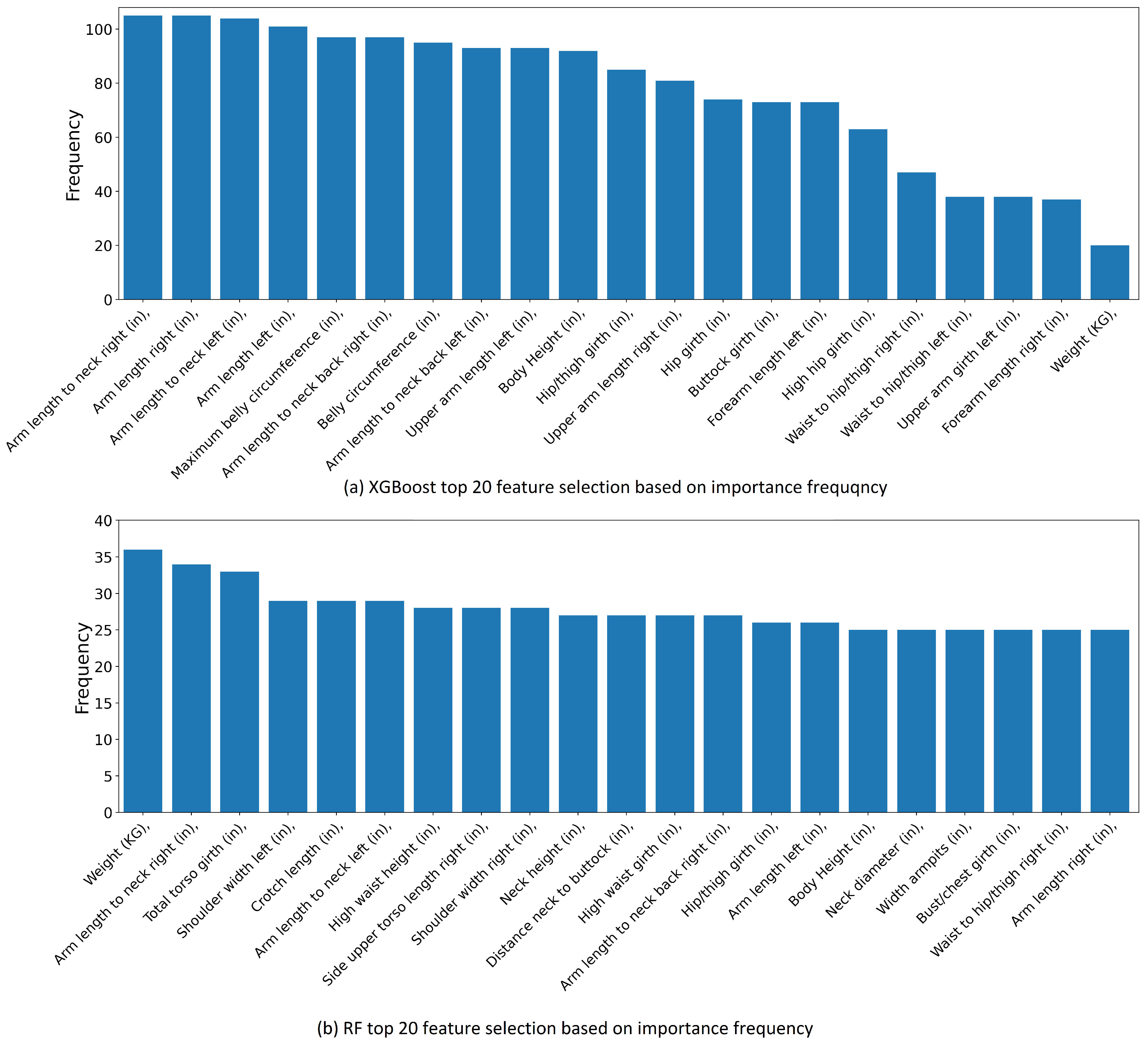
- The experimental results indicate that only 20 body features for the ML methods are required to accurately estimate all 3D body measurements. This new observation can dramatically reduce the amount of time, labor and manual errors in retrieving the body measurements essential to many fields such as ergonomics, anthropometry and the fashion industry.
2. Background and Methods
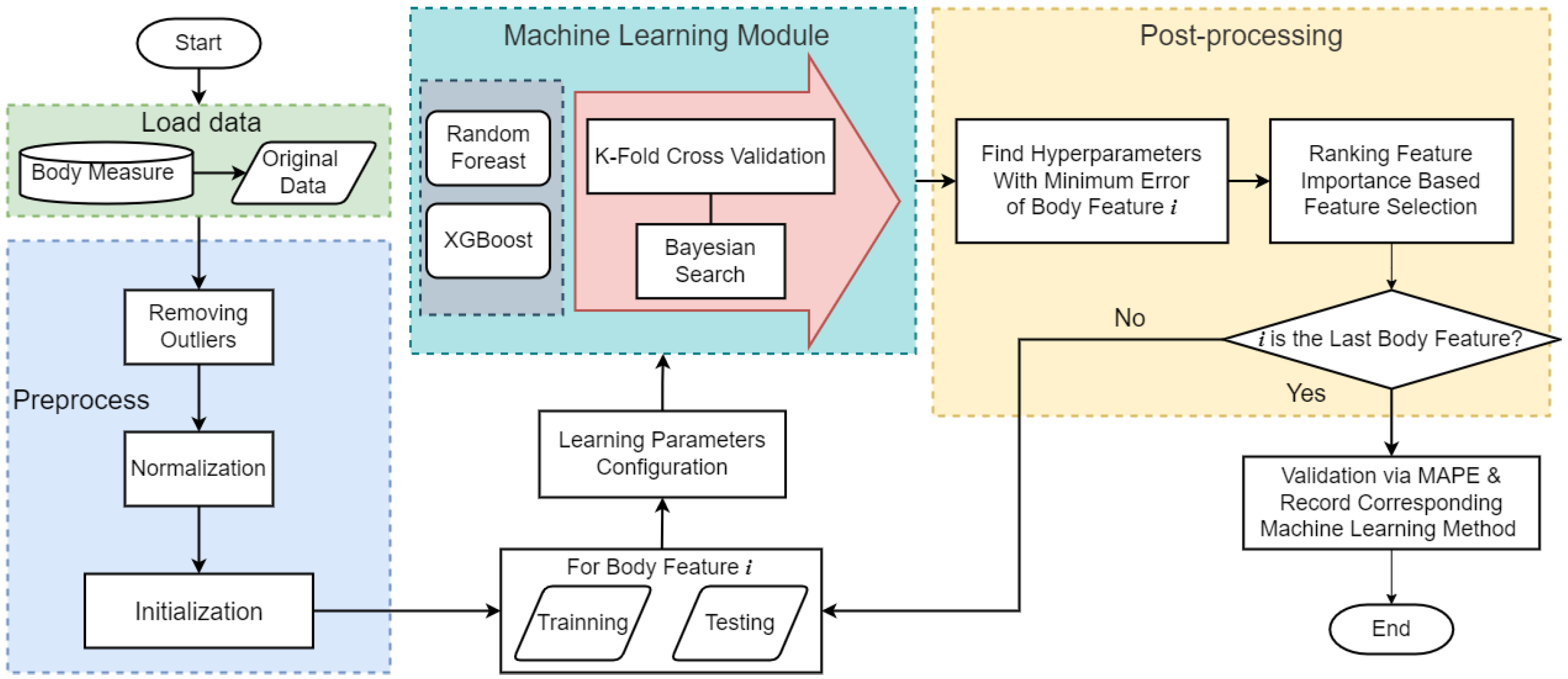
2.1. Proposed Framework
2.2. Machine Learning Methods for 3D BM Prediction
2.2.1. Random Forest
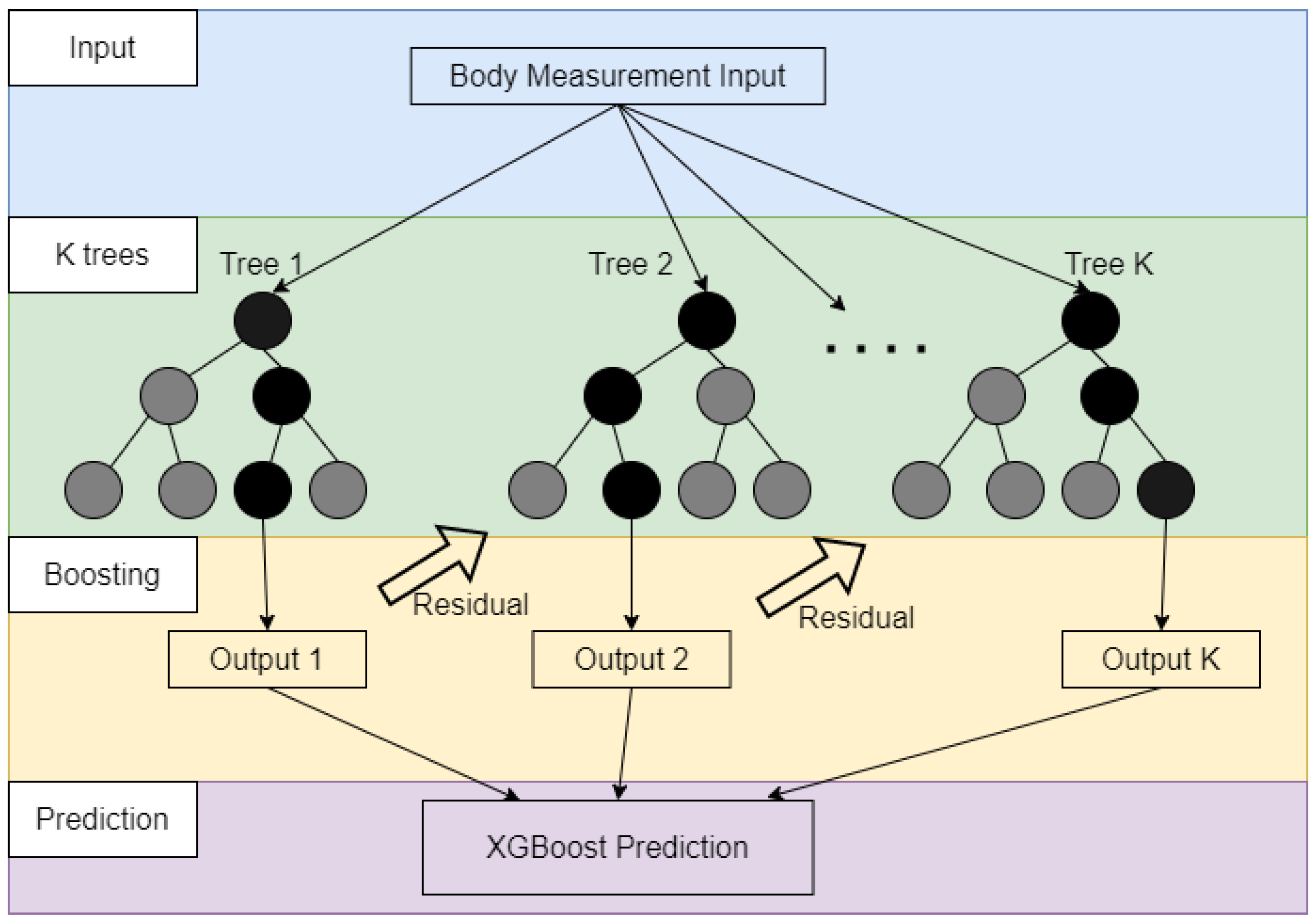
- Using K-bootstrap to sample sub-datasets from the original dataset.
- Individual learning from Tree 1 to Tree K via splitting on best feature for corresponding sub-dataset.
- Majority voting of the output from all learning trees.

2.2.2. XGBoost
2.3. Bayesian Search
2.4. Importance-Based Feature Selection
2.5. Performance Metrics
3. Case Study and Results
3.1. Basics of the Dataset
3.2. Results of the Bayesian Search
3.3. Result of the Feature Selection
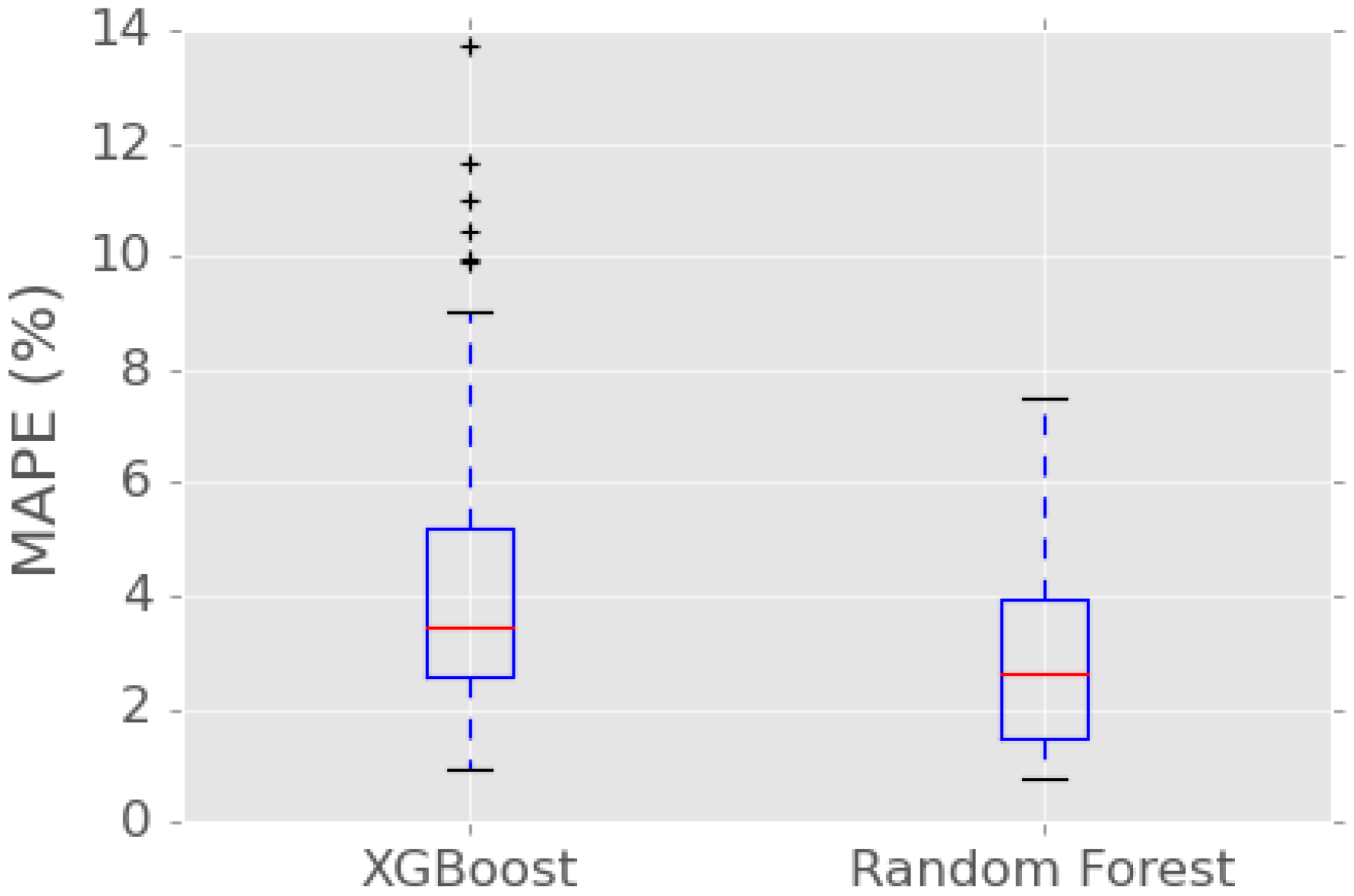
3.4. Validation of the Proposed Feature Selection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kershaw, G. Pattern Cutting for Menswear, 2nd ed.; Laurence King Publications: London, UK, 2021. [Google Scholar]
- Pleuss, J.D.; Talty, K.; Morse, S.; Kuiper, P.; Scioletti, M.; Heymsfield, S.B.; Thomas, D.M. A machine learning approach relating 3D body scans to body composition in humans. Eur. J. Clin. Nutr. 2019, 73, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Nijman, S.W.; Leeuwenberg, A.M.; Beekers, I.; Verkouter, I.; Jacobs, J.J.; Bots, M.L.; Asselbergs, F.W.; Moons, K.G.; Debray, T.P. Missing data is poorly handled and reported in prediction model studies using machine learning: A literature review. J. Clin. Epidemiol. 2022, 142, 218–229. [Google Scholar] [CrossRef] [PubMed]
- Jerez, J.M.; Molina, I.; García-Laencina, P.J.; Alba, E.; Ribelles, N.; Martín, M.; Franco, L. Missing data imputation using statistical and machine learning methods in a real breast cancer problem. Artif. Intell. Med. 2010, 50, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Qadri, S.F.; Ai, D.; Hu, G.; Ahmad, M.; Huang, Y.; Wang, Y.; Yang, J. Automatic Deep Feature Learning via Patch-Based Deep Belief Network for Vertebrae Segmentation in CT Images. Appl. Sci. 2019, 9, 69. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, M.; Qadri, S.F.; Ashraf, M.U.; Subhi, K.; Khan, S.; Zareen, S.S.; Qadri, S. Efficient Liver Segmentation from Computed Tomography Images Using Deep Learning. Comput. Intell. Neurosci. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 3 February 2022).
- Geng, D.; Zhang, H.; Wu, H. Short-Term Wind Speed Prediction Based on Principal Component Analysis and LSTM. Appl. Sci. 2020, 10, 4416. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Zhang, H.; Wu, H. Hourly occupant clothing decisions in residential HVAC energy management. J. Build. Eng. 2021, 40, 102708. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Wu, H. PV-EV integrated home energy management considering residential occupant behaviors. Sustainability 2021, 13, 13826. [Google Scholar] [CrossRef]
- Shi, R.; Xu, X.; Li, J.; Li, Y. Prediction and analysis of train arrival delay based on XGBoost and Bayesian optimization. Appl. Soft Comput. 2021, 109, 107538. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhong, H.; Li, Y.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- Nassif, A.B.; Shahin, I.; Attili, I.; Azzeh, M.; Shaalan, K. Speech Recognition Using Deep Neural Networks: A Systematic Review. IEEE Access 2019, 7, 19143–19165. [Google Scholar] [CrossRef]
- Fujiyoshi, H.; Hirakawa, T.; Yamashita, T. Deep learning-based image recognition for autonomous driving. IATSS Res. 2019, 43, 244–252. [Google Scholar] [CrossRef]
- Wuhrer, S.; Shu, C. Estimating 3D human shapes from measurements. Mach. Vis. Appl. 2013, 24, 1133–1147. [Google Scholar] [CrossRef] [Green Version]
- Kocabas, M.; Karagoz, S.; Akbas, E. Self-Supervised Learning of 3D Human Pose Using Multi-View Geometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1077–1086. [Google Scholar]
- Xu, T.; An, D.; Jia, Y.; Yue, Y. A Review: Point Cloud-Based 3D Human Joints Estimation. Sensors 2021, 21, 1684. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.Y.; Lee, K. Parametric human body shape modeling framework for human-centered product design. Comput.-Aided Des. 2012, 44, 56–67. [Google Scholar] [CrossRef]
- Lu, Y.; McQuade, S.; Hahn, J.K. 3D Shape-based Body Composition Prediction Model Using Machine Learning. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), Honolulu, HI, USA, 17–21 July 2018; pp. 3999–4002. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Kamalha, E.; Li, V.; Zeng, X. Construction of a prediction model for body dimensions used in garment pattern making based on anthropometric data learning. J. Text. Inst. 2017, 108, 2107–2114. [Google Scholar] [CrossRef]
- Fan, Z.; Chiong, R.; Hu, Z.; Keivanian, F.; Chiong, F. Body fat prediction through feature extraction based on anthropometric and laboratory measurements. PLoS ONE 2022, 17, e0263333. [Google Scholar] [CrossRef]
- Suzuki, A.; Ryu, K. Feature selection method for estimating systolic blood pressure using the taguchi method. IEEE Trans. Ind. Inform. 2014, 10, 1077–1085. [Google Scholar] [CrossRef]
- Guo, J.; Yang, L.; Bie, R.; Yu, J.; Gao, Y.; Shen, Y.; Kos, A. An XGBoost-based physical fitness evaluation model using advanced feature selection and Bayesian hyper-parameter optimization for wearable running monitoring. Comput. Netw. 2019, 151, 166–180. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.; Pham, H. Optimizing ensemble weights and hyperparameters of machine learning models for regression problems. Mach. Learn. Appl. 2022, 7, 100251. [Google Scholar] [CrossRef]
- Gokalp, O.; Tasci, E. Weighted Voting Based Ensemble Classification with Hyper-parameter Optimization. In Proceedings of the 2019 Innovations in Intelligent Systems and Applications Conference, Izmir, Turkey, 31 October–2 November 2019. [Google Scholar] [CrossRef]
- Du, L.; Gao, R.; Suganthan, P.N.; Wang, D.Z. Bayesian optimization based dynamic ensemble for time series forecasting. Inf. Sci. 2022, 591, 155–175. [Google Scholar] [CrossRef]
- Gao, L.; Ding, Y. Disease prediction via Bayesian hyperparameter optimization and ensemble learning. BMC Res. Notes 2020, 13, 1–6. [Google Scholar] [CrossRef]
- Nishio, M.; Nishizawa, M.; Sugiyama, O.; Kojima, R.; Yakami, M.; Kuroda, T.; Togashi, K. Computer-aided diagnosis of lung nodule using gradient tree boosting and Bayesian optimization. PLoS ONE 2018, 13, e0195875. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 2021, 6, 506–515. [Google Scholar] [CrossRef]
- Ashdown, S.P. Full body 3-D scanners. In Anthropometry, Apparel Sizing and Design; Woodhead Publishing: Cambridge, UK, 2020; pp. 145–168. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests; Springer: New York, NY, USA, 2001; pp. 5–32. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the Advances in Neural Information Processing Systems 24th (NIPS), Granada, Spain, 12–15 December 2011; pp. 1–9. [Google Scholar]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 115–123. [Google Scholar]
- Fox, E.W.; Hill, R.A.; Leibowitz, S.G.; Olsen, A.R.; Thornbrugh, D.J.; Weber, M.H. Assessing the accuracy and stability of variable selection methods for random forest modeling in ecology. Environ. Monit. Assess. 2017, 189, 316. [Google Scholar] [CrossRef]


| Feature Name | Min | Max | Mean | Std |
|---|---|---|---|---|
| Body Height (in) | 28.58 | 74.88 | 65.55 | 4.98 |
| Weight (kg) | 26.10 | 117.70 | 68.53 | 15.25 |
| Head Girth (in) | 12.09 | 25.47 | 21.79 | 1.31 |
| Arm Girth (in) | 7.09 | 23.82 | 11.49 | 1.99 |
| Sitting Height (in) | 25.59 | 39.49 | 34.59 | 2.25 |
| Head Height (in) | 7.89 | 12.33 | 9.46 | 0.71 |
| ML Method | Search Space Parameter | Search Type | Search Space Range |
|---|---|---|---|
| XGBoost | gamma | continuous | [5.0, 11.0] |
| learning rate | continuous | [0.07, 0.6] | |
| n estimators | discrete | 50, 100, 150 | |
| regulation alpha | discrete | 1 × 10, 1 × 10, 0.75 | |
| regulation lambda | discrete | 1 × 10, 1 × 10, 0.45 | |
| min child weight | discrete | 1.5, 6, 10 | |
| subsample | discrete | 0.6, 0.95 | |
| max depth | discrete | 3, 6, 9 | |
| Random Forest | n estimators | discrete | 100, 200, 500 |
| max depth | discrete | 4, 5, 6, ..., 11 | |
| min samples | discrete | 2, 3, 4, 5 | |
| min samples leaf | discrete | 1, 3, 5, 7 |
| Feature Input | ML Method | MAPE |
|---|---|---|
| without feature selection | XGBoost | 2.98% |
| Random Forest | 2.17% | |
| with feature selection | XGBoost | 3.85% |
| Random Forest | 2.88% |
| ML Method | Running Time |
|---|---|
| XGBoost | 2 h 6 min |
| Random Forest | 10 h 11 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wu, Y.; Wu, H. Machine Learning Enabled 3D Body Measurement Estimation Using Hybrid Feature Selection and Bayesian Search. Appl. Sci. 2022, 12, 7253. https://doi.org/10.3390/app12147253
Liu X, Wu Y, Wu H. Machine Learning Enabled 3D Body Measurement Estimation Using Hybrid Feature Selection and Bayesian Search. Applied Sciences. 2022; 12(14):7253. https://doi.org/10.3390/app12147253
Chicago/Turabian StyleLiu, Xuebo, Yingying Wu, and Hongyu Wu. 2022. "Machine Learning Enabled 3D Body Measurement Estimation Using Hybrid Feature Selection and Bayesian Search" Applied Sciences 12, no. 14: 7253. https://doi.org/10.3390/app12147253
APA StyleLiu, X., Wu, Y., & Wu, H. (2022). Machine Learning Enabled 3D Body Measurement Estimation Using Hybrid Feature Selection and Bayesian Search. Applied Sciences, 12(14), 7253. https://doi.org/10.3390/app12147253







