Time-Weighted Community Search Based on Interest
Abstract
:1. Introduction
- (1)
- Fully considering the characteristics of geographic social networks, we propose a new community search model, Time-Weighted Community Search Based on Interest (TWC), by considering the four dimensions of structural cohesiveness, spatial cohesiveness, interest, and time.
- (2)
- We design the attribute time-weighted decay function and then extract the user’s time-weighted representative attributes, which express the user’s interest trend clearly in the query window. In addition, we propose a new attribute similarity scoring function and a community scoring function.
- (3)
- In order to solve the TWC problem, we design a Local Extend algorithm from inside to outside and a Shrink algorithm from outside to inside to deal with different search scenarios.
- (4)
- We carry out many experiments on the real dataset. Comparison with similar algorithms shows that the community nodes of TWC are similar to the current interests of query points and can better express the short-term interests of query users.
2. Related Work
3. Problem Formulation
3.1. Structure Cohesiveness
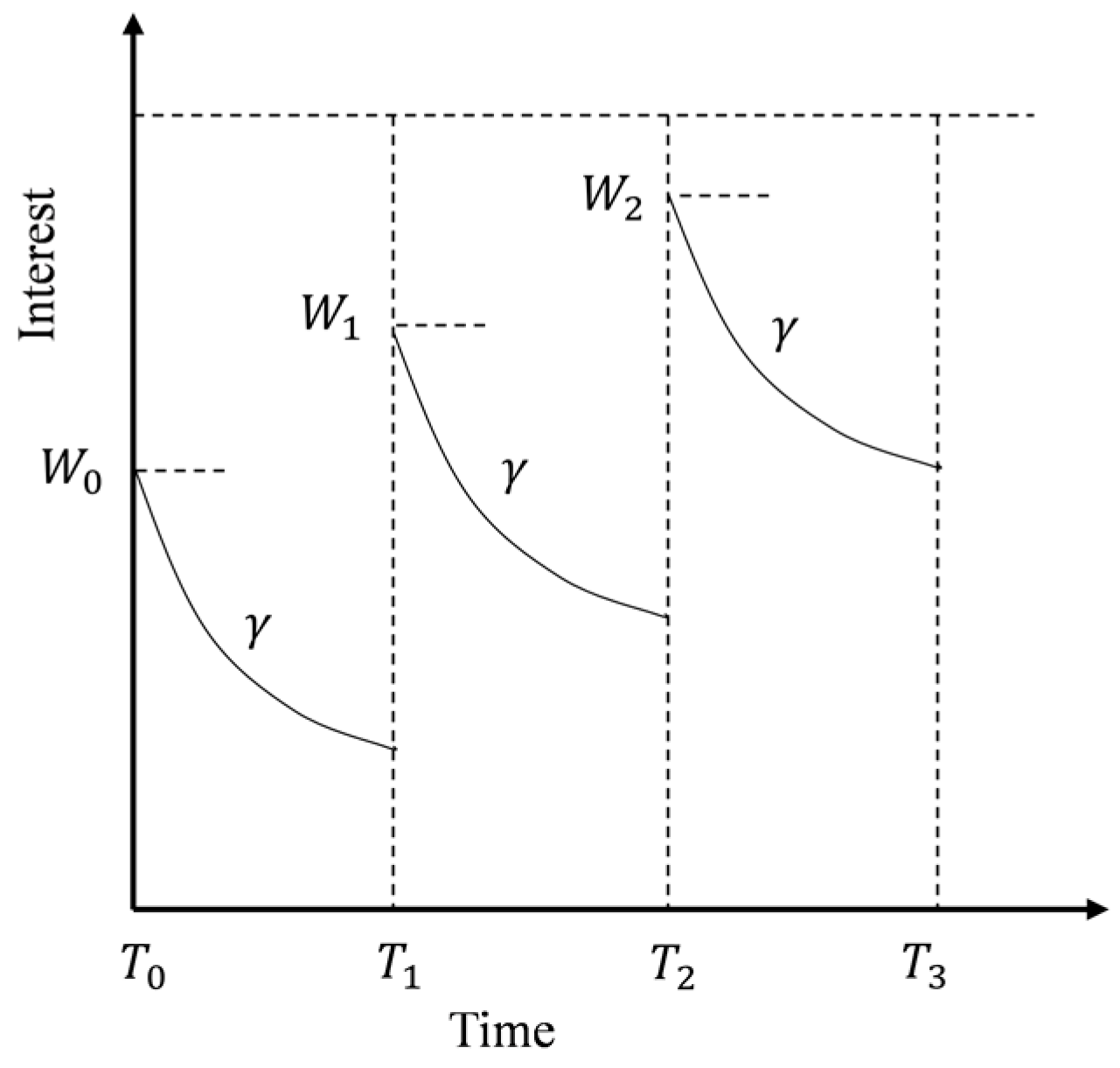
3.2. Time-Weighted Decay Function
3.3. Attributes Similarity Scoring Function
- (1)
- Connectivity: is a connected graph containing .
- (2)
- Structure cohesiveness: .
- (3)
- Attribute score maximum: While satisfying (1) and (2), the attribute similarity score of ,, is the highest, where .
- (4)
- There does not exist another subgraph satisfying the above three properties.
4. Methods
4.1. Local Extend Algorithm
- Strategy 1: Select the neighbor node of from with the highest ;
- Strategy 2: If there are multiple nodes satisfying strategy (1), we choose the node with the largest degree.
- Extend Rule 1: If and , then add node to and continue to expand.
- Extend Rule 2: If , then add node to , update and continue to expand.
- Extend Rule 3: If and , then add node to , update and continue to expand.
- Stop Rule 1: If and , then stop extension.
- Stop Rule 2: If , then stop extension.
| Algorithm 1 Local Extend Algorithm |
|
Input: A graph
a query node
, a non-negative integer
Output: A with the maximum . 1: Find the maximum feasible community as initial subgraph. 2: For each node in compute descending order according to the score. 3: 4: Extend ( ) 5: return . Procedure 6: if , then 7: Update 8: else 9: Select the best node from according to the vertex selection strategy. 10: if and , then 11: ; 12: else if then 13: ; 14: ; 15: else if and , then 16: ; 17: ; 18: else if , then 19: update over. |
4.2. Shrink Algorithm
| Algorithm 2 Shrink Algorithm |
|
Input: A graph
a query node
, a non-negative integer
Output: A with the maximum . 1: Find the maximum feasible community as initial subgraph. 2: Compute , form them as an ascending list . 3: Compute and form their core numbers as . 4: while exists do 5: ; 6: Select the first node in as the node to be deleted. 7: Delete and its incident edges from ; 8: Delete from ; 9: Update with the core maintenance algorithm, and organize nodes as 10: For nodes in , remove them from and ; 11: Maintain as a feasible community; 12: Return the latest feasible community as |
5. Results
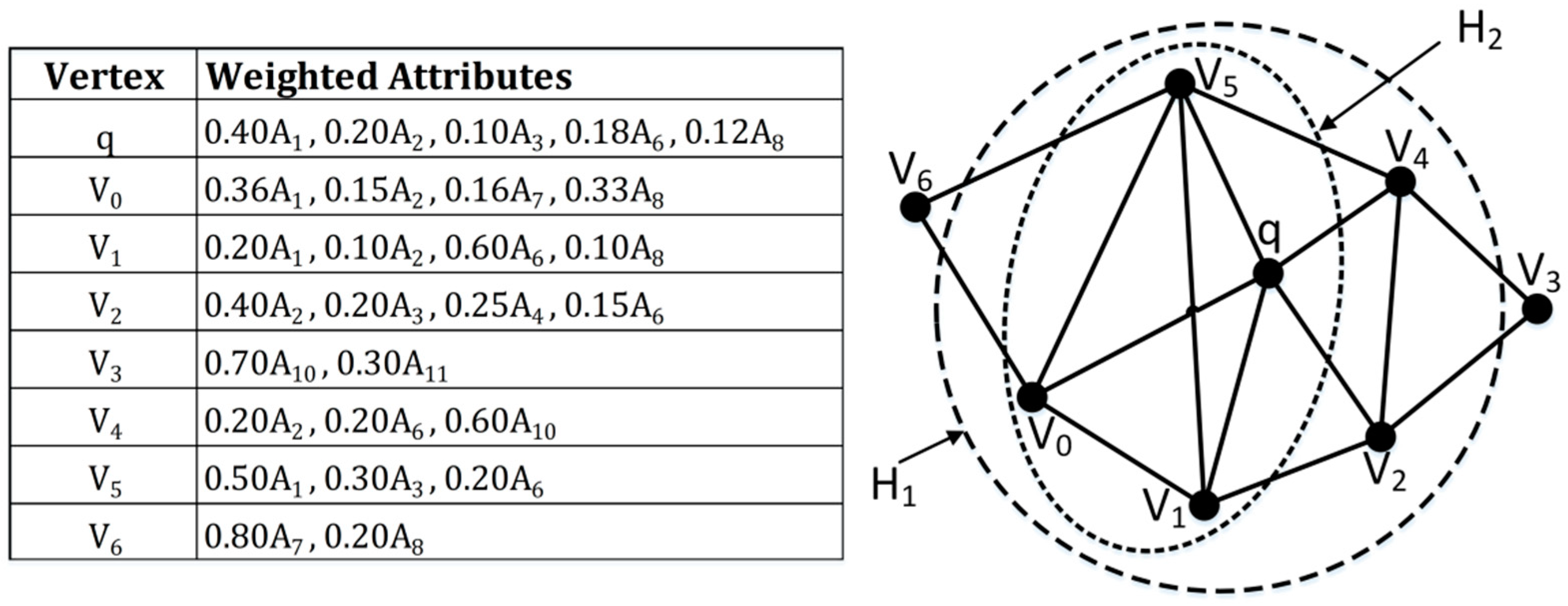
5.1. Case Study
5.2. Effectiveness and Efficiency Evaluation of the Model
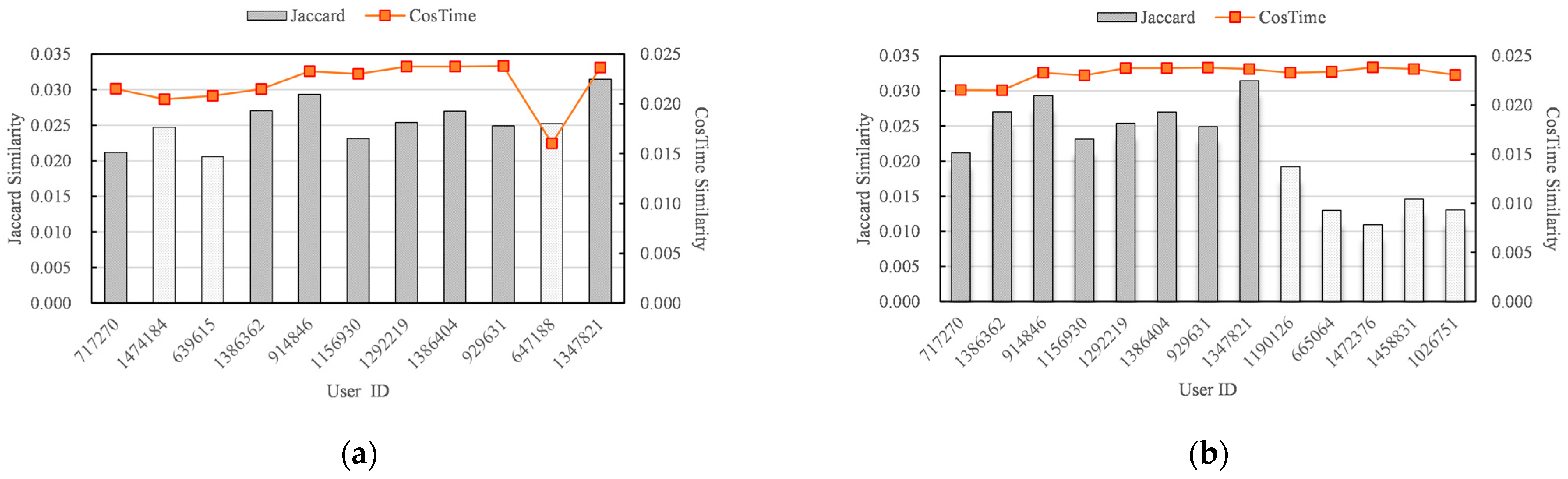
- Experiment 1: time distribution of community shared attributes
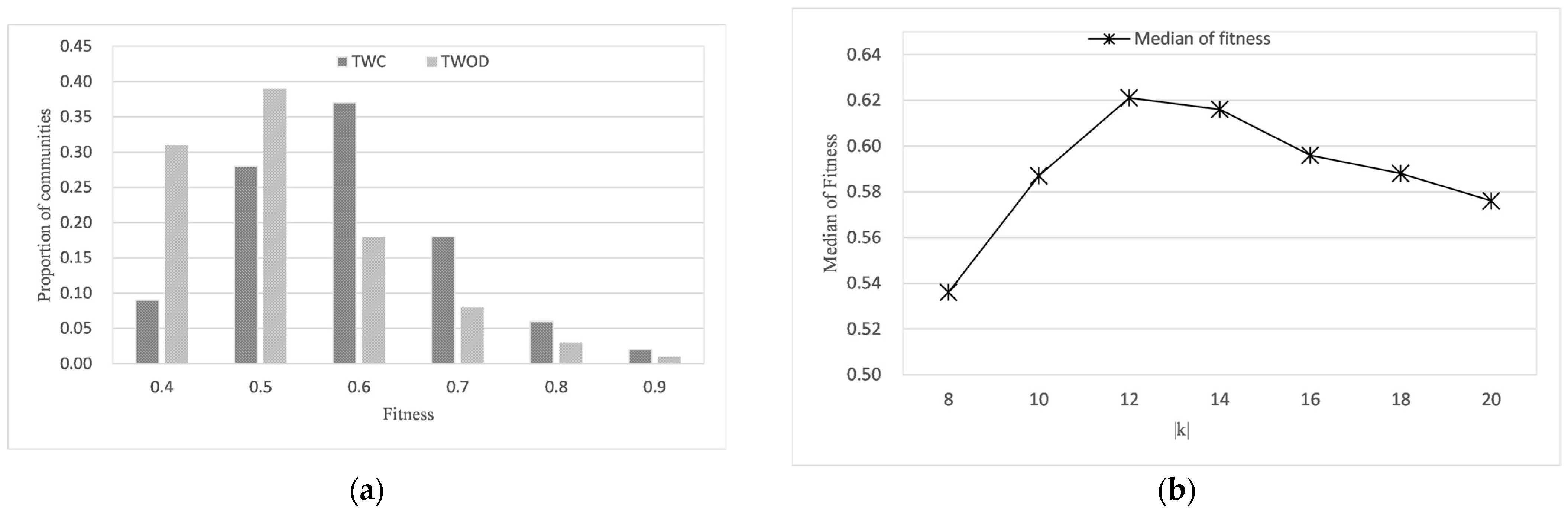
- Experiment 2: community fitness comparison caused by interest drift
- Experiment 3: the effect of k on effectiveness
- Experiment 4: the effect of query time window on effectiveness.
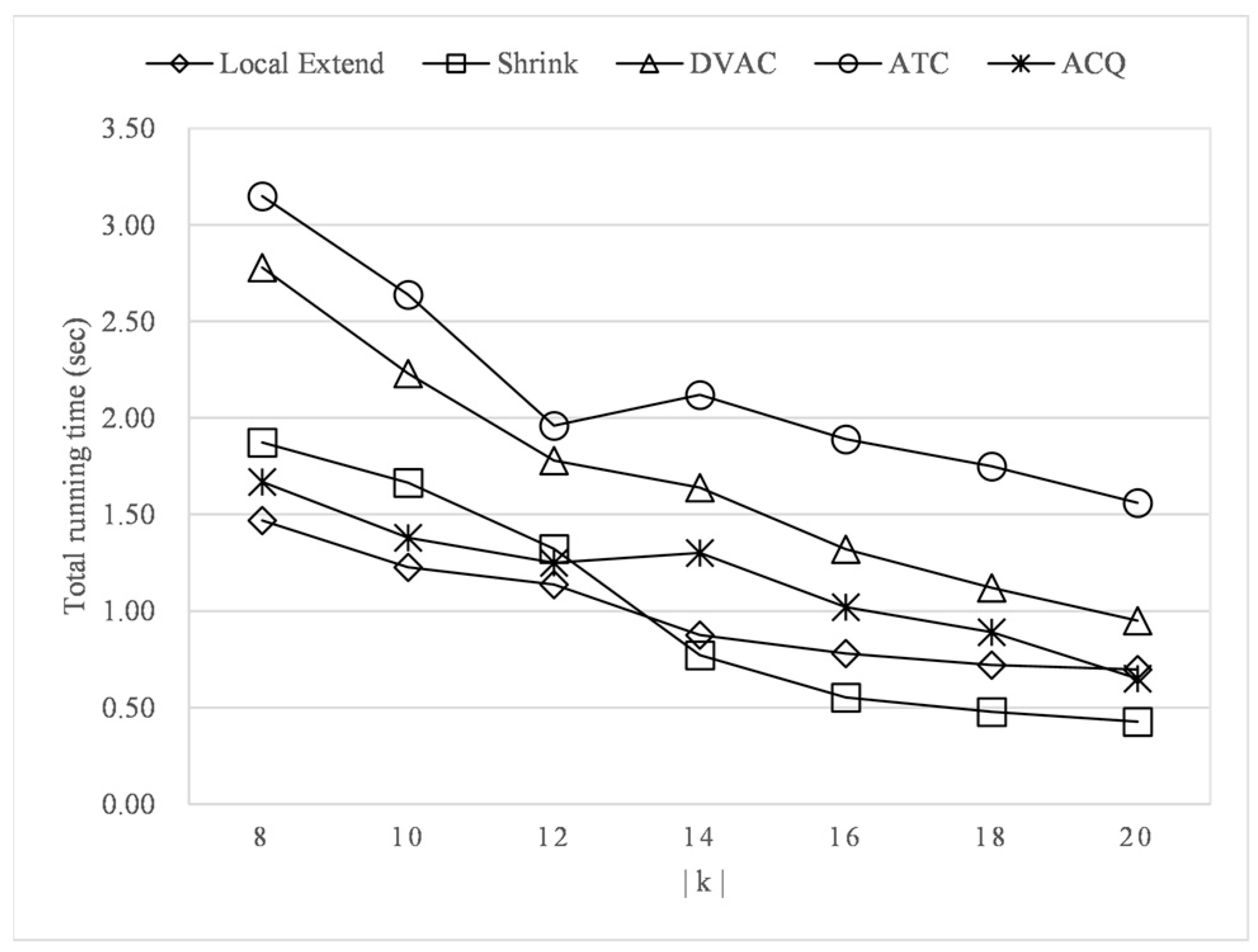
- Experiment 5: the effect of k on efficiency.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sozio, M.; Gionis, A. The Community-Search Problem and How to Plan a Successful Cocktail Party. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’10, Washington, DC, USA, 25–28 July 2010; ACM Press: Washington, DC, USA, 2010; p. 939. [Google Scholar] [CrossRef]
- Yang, D.-N.; Shen, C.-Y.; Lee, W.-C.; Chen, M.-S. On Socio-Spatial Group Query for Location-Based Social Networks. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’12, Beijing, China, 12–16 August 2012; ACM Press: Beijing, China, 2012; p. 949. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.-Y.; Yang, D.-N.; Huang, L.-H.; Lee, W.-C.; Chen, M.-S. Socio-Spatial Group Queries for Impromptu Activity Planning. IEEE Trans. Knowl. Data Eng. 2015, 28, 196–210. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Hu, H.; Xu, C.; Xu, J.; Lee, W.-C. Geo-social group queries with minimum acquaintance constraints. VLDB J. 2017, 26, 709–727. [Google Scholar] [CrossRef]
- Fang, Y.; Cheng, R.; Li, X.; Luo, S.; Hu, J. Effective Community Search over Large Spatial Graphs. Proc. VLDB Endow. 2017, 10, 709–720. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, B.; Ali, M.E.; Choudhury, F.M.; Apon, S.H.; Sellis, T.; Li, J. The Flexible Socio Spatial Group Queries. Proc. VLDB Endow. 2018, 12, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Liu, C.; Zhou, R.; Li, J.; Yang, X.; Wang, B. Maximum Co-Located Community Search in Large Scale Social Networks. Proc. VLDB Endow. 2018, 11, 1233–1246. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Wang, Z.; Cheng, R.; Li, X.; Luo, S.; Hu, J.; Chen, X. On Spatial-Aware Community Search. IEEE Trans. Knowl. Data Eng. 2019, 31, 783–798. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Y.; Qin, L.; Zhang, W.; Lin, X. When Engagement Meets Similarity. Proc. VLDB Endow. 2017, 10, 998–1009. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wu, D.; Xu, J.; Choi, B.; Su, W. Spatial-aware interest group queries in location-based social networks. Data Knowl. Eng. 2014, 92, 20–38. [Google Scholar] [CrossRef]
- Guo, T.; Cao, X.; Cong, G. Efficient Algorithms for Answering the M-Closest Keywords Query. In Proceedings of the Acm Sigmod International Conference, Melbourne, VIC, Australia, 31 May–4 June 2015; pp. 405–418. [Google Scholar]
- FeLipe, I.D.; Hristidis, V.; Rishe, N. Keyword Search on Spatial Databases. In Proceedings of the IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008. [Google Scholar]
- Zhang, Z.; Huang, X.; Xu, J.; Choi, B.; Shang, Z. Keyword-Centric Community Search. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; IEEE: Macao, China, 2019; pp. 422–433. [Google Scholar] [CrossRef]
- Fang, Y.; Cheng, R.; Luo, S.; Hu, J. Effective Community Search for Large Attributed Graphs. Proc. VLDB Endow. 2016, 9, 1233–1244. [Google Scholar] [CrossRef] [Green Version]
- Xin, H.; Lakshmanan, L. Attribute-Driven Community Search. Proc. VLDB Endow. 2017, 10, 949–960. [Google Scholar]
- Luo, J.; Cao, X.; Xie, X.; Qu, Q.; Xu, Z.; Jensen, C.S. Efficient Attribute-Constrained Co-Located Community Search. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; IEEE: Dallas, TX, USA, 2020; pp. 1201–1212. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Zhou, R.; Xu, J.; Li, J. Finding Effective Geo-Social Group for Impromptu Activities with Diverse Demands. In Proceedings of the KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, 6–10 July 2020. [Google Scholar]
- Liu, Q.; Zhu, Y.; Zhao, M.; Huang, X.; Xu, J.; Gao, Y. VAC: Vertex-Centric Attributed Community Search. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; IEEE: Dallas, TX, USA, 2020; pp. 937–948. [Google Scholar] [CrossRef]
- Lee, T.-Q.; Park, Y. A Time-Based Recommender System Using Implicit Feed-back. In CSREA EEE; Citeseer: Princeton, NJ, USA, 2006; pp. 309–315. [Google Scholar]
- Rafeh, R.; Bahrehmand, A. An Adaptive Approach to Dealing with Unstable Behaviour of Users in Collaborative Filtering Systems. J. Inf. Sci. 2012, 38, 205–221. [Google Scholar] [CrossRef]
- Sun, B.; Dong, L. Dynamic Model Adaptive to User Interest Drift Based on Cluster and Nearest Neighbors. IEEE Access 2017, 5, 1682–1691. [Google Scholar] [CrossRef]
- Feng, H.; Tian, J.; Wang, H.J.; Li, M. Personalized Recommendations Based on Time-Weighted Overlapping Community Detection. Inf. Manage. 2015, 52, 789–800. [Google Scholar] [CrossRef]
- Li, R.-H.; Yu, J.X.; Mao, R. Efficient Core Maintenance in Large Dynamic Graphs. IEEE Trans. Knowl. Data Eng. 2014, 26, 2453–2465. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Qu, B.; Yang, J.; Cudre-Mauroux, P. Revisiting User Mobility and Social Relationships in LBSNs: A Hypergraph Embedding Approach. In Proceedings of the 2019 World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019. [Google Scholar]
- Lancichinetti, A.; Fortunato, S.; Kertesz, J. Detecting the Overlapping and Hierarchical Community Structure of Complex Networks. New J. Phys. 2009, 11, 033015. [Google Scholar] [CrossRef]

| Notation | Meaning |
|---|---|
| a graph with vertex set and edge set | |
| is a subgraph of , and and are the vertex set and edge set of , respectively | |
| the degree of vertex in | |
| AvgDegree() | the average degree of nodes in graph |
| a check-in timestamp | |
| text attribute set of node | |
| attribute weight set of node , | |
| size of attribute set | |
| union of attribute sets and without duplicate attributes | |
| attribute weight vector of | |
| size of attribute set | |
| position of node , and , are ’s latitude and longitude coordinates | |
| check-in coordinates of node at , and are ’s latitude and longitude at | |
| the textual similarity score of node and | |
| the spatial similarity score of node and | |
| the similarity score of node and | |
| the graph score of containing | |
| the time decay factor | |
| the balance factor of different type of attribute scores |
| Step | ||||
|---|---|---|---|---|
| Step 1 | ||||
| Step 2 | ||||
| Step 3 | ||||
| Step 4 | ||||
| Step 5 |
| Time Effective Window | 10% Window | 20% Window | 30% Window | 40% Window | 50% Window |
|---|---|---|---|---|---|
| TWC | 0.115 | 0.237 | 0.478 | 0.686 | 0.814 |
| ACQ | 0.006 | 0.065 | 0.126 | 0.208 | 0.325 |
| ATC | 0.063 | 0.097 | 0.158 | 0.197 | 0.305 |
| VAC | 0.084 | 0.105 | 0.178 | 0.186 | 0.317 |
| TWOD | 0.075 | 0.122 | 0.207 | 0.297 | 0.496 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhong, Y. Time-Weighted Community Search Based on Interest. Appl. Sci. 2022, 12, 7077. https://doi.org/10.3390/app12147077
Liu J, Zhong Y. Time-Weighted Community Search Based on Interest. Applied Sciences. 2022; 12(14):7077. https://doi.org/10.3390/app12147077
Chicago/Turabian StyleLiu, Jing, and Yong Zhong. 2022. "Time-Weighted Community Search Based on Interest" Applied Sciences 12, no. 14: 7077. https://doi.org/10.3390/app12147077
APA StyleLiu, J., & Zhong, Y. (2022). Time-Weighted Community Search Based on Interest. Applied Sciences, 12(14), 7077. https://doi.org/10.3390/app12147077





