Bond Graph-Based Approach to Modeling Variable-Speed Gearboxes with Multi-Type Clutches
Abstract
:1. Introduction
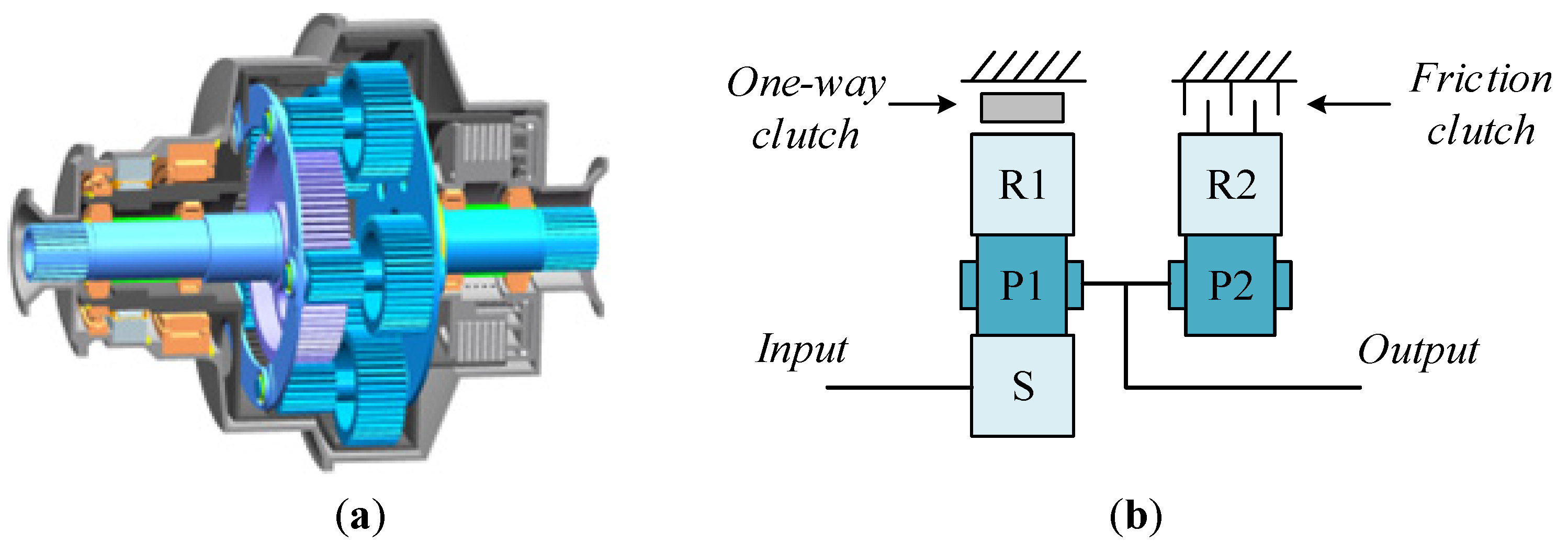
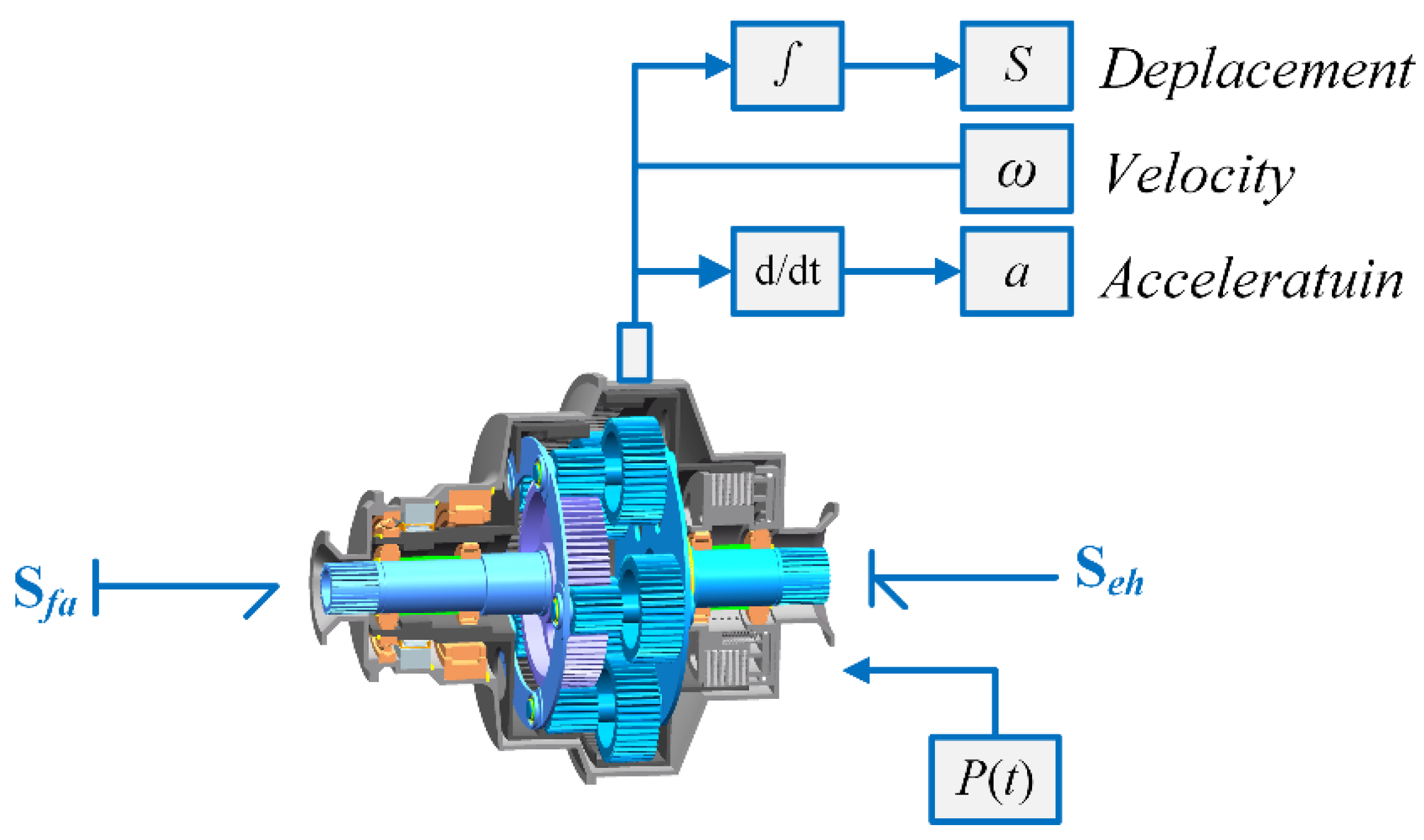
2. Research Object
3. BG Models of PGTs
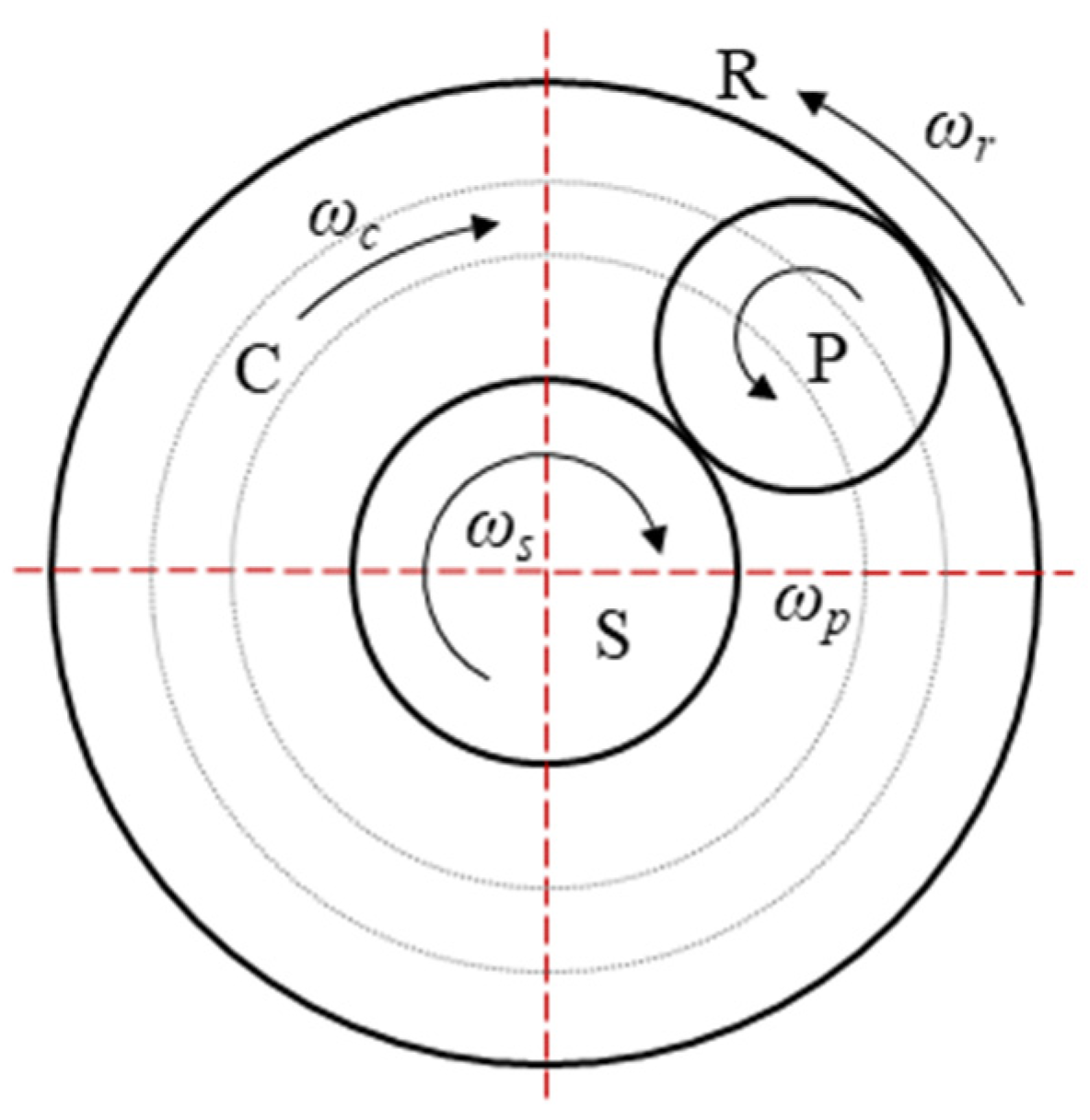
3.1. Single-Pinion PGT
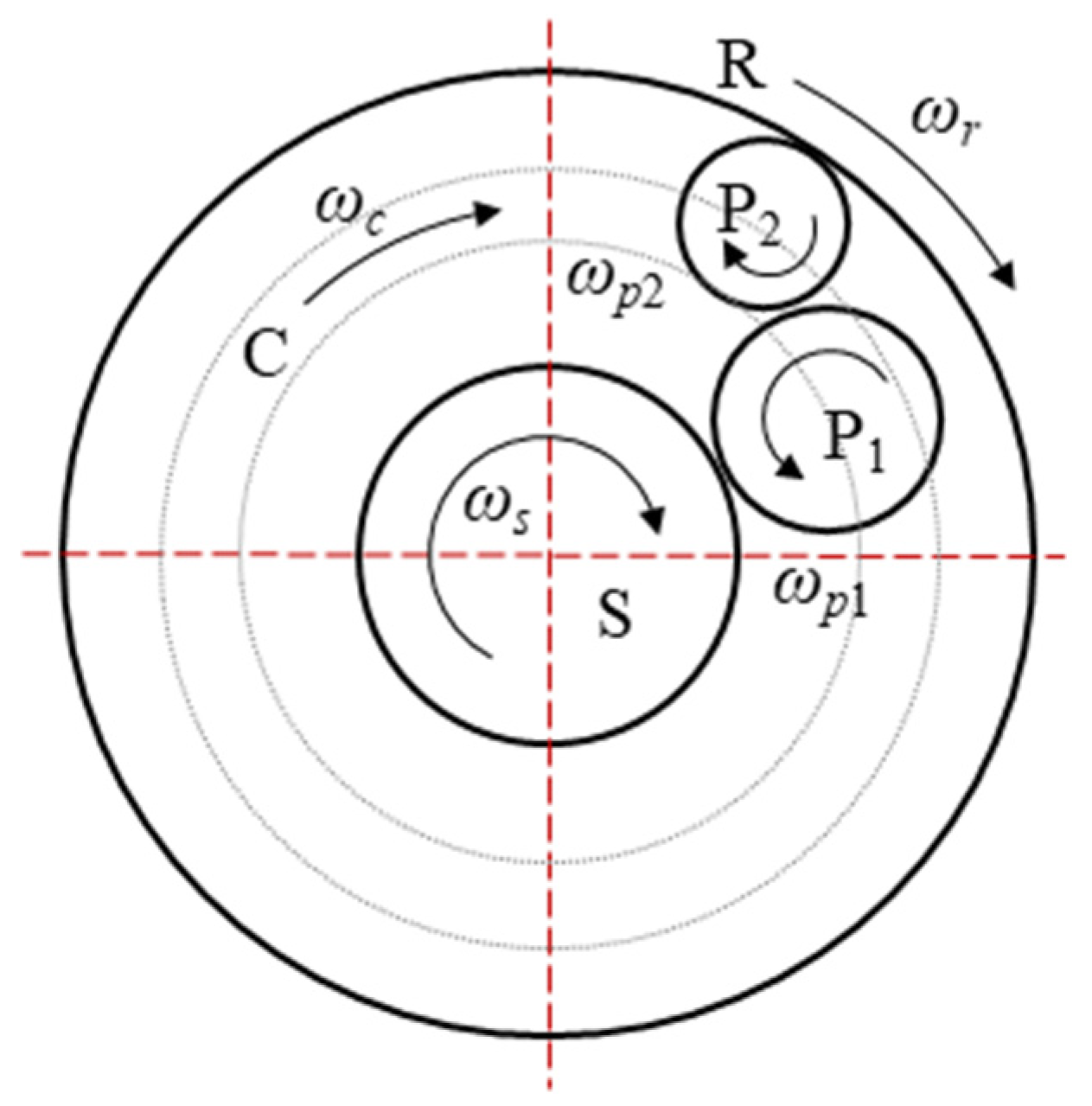
3.2. Double-Pinion PGT
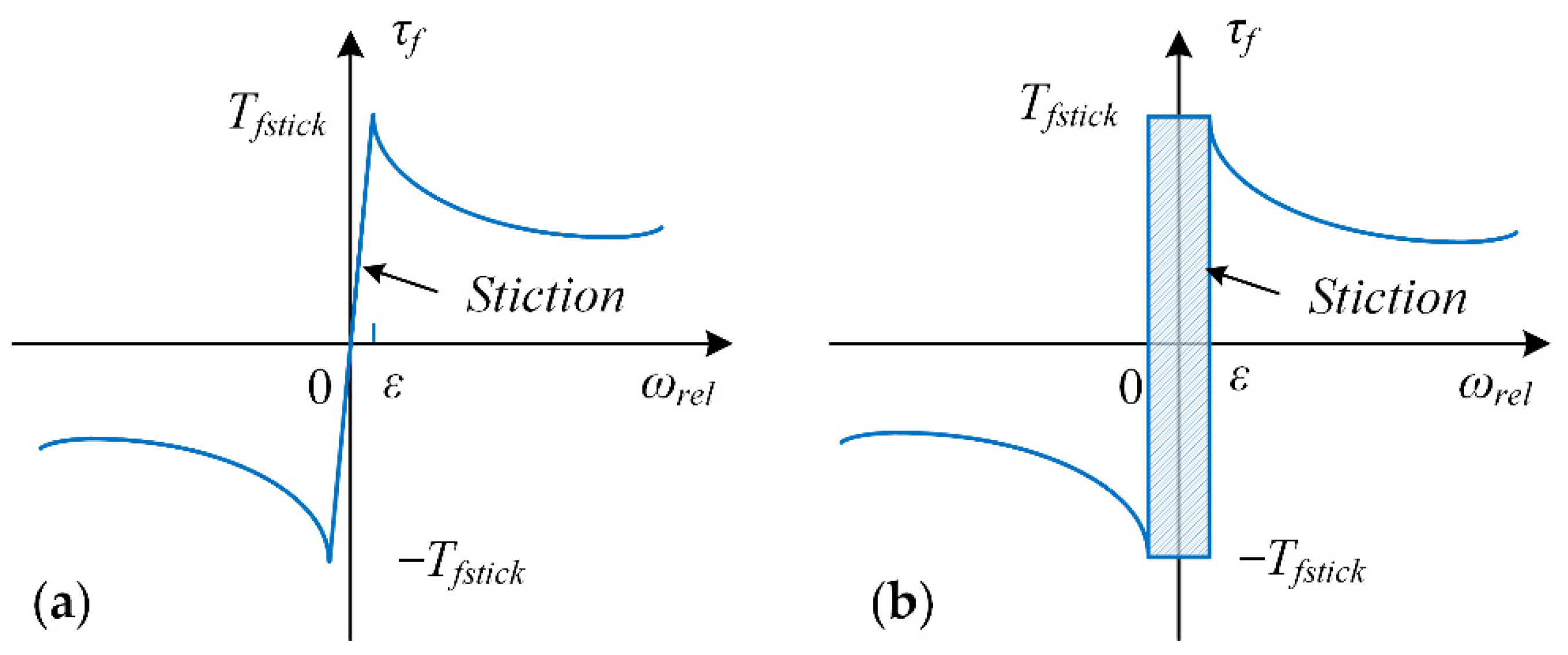
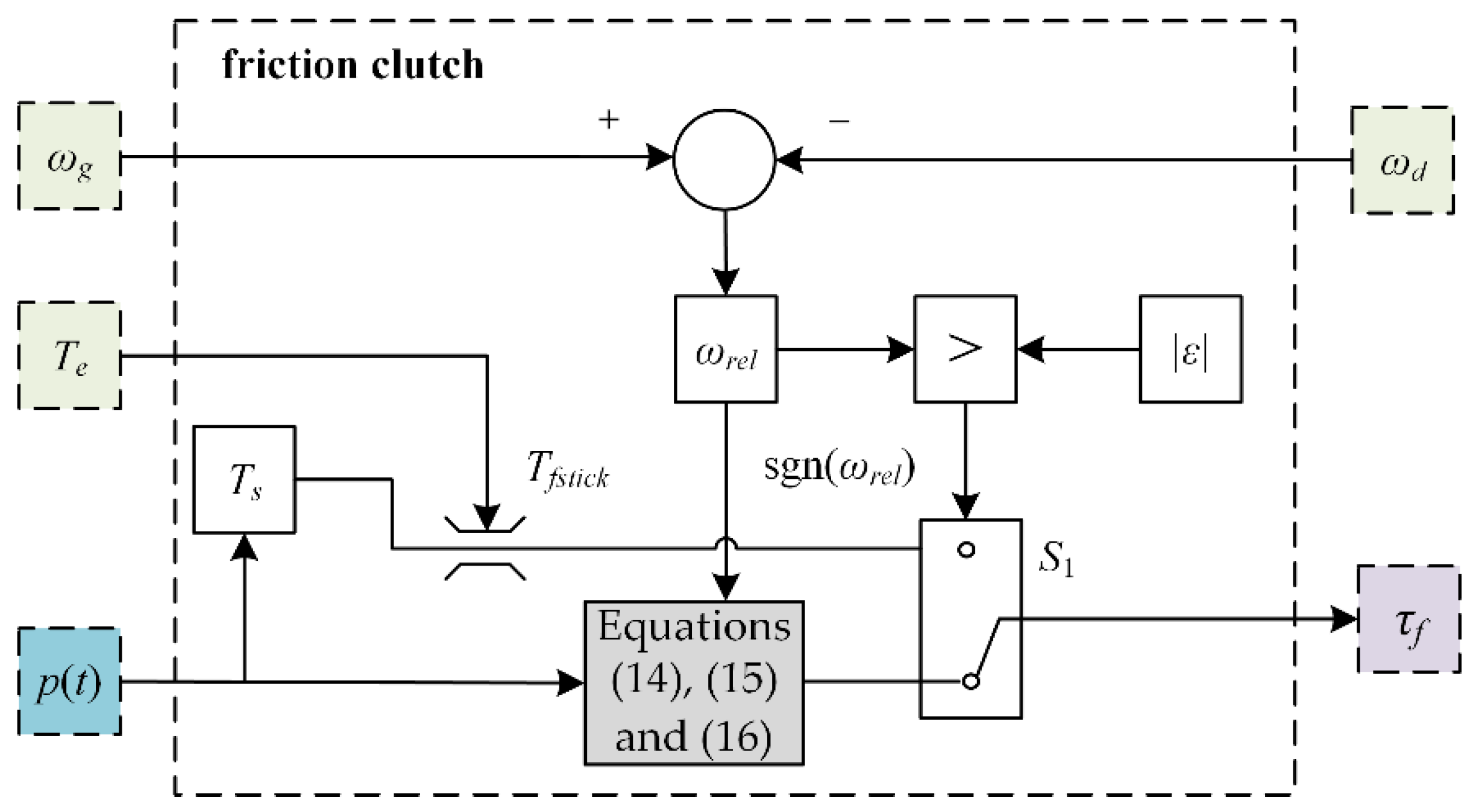
4. The Friction Clutch Model
4.1. The Karnopp Friction Model
4.2. The Friction Model for Hydraulic Clutches
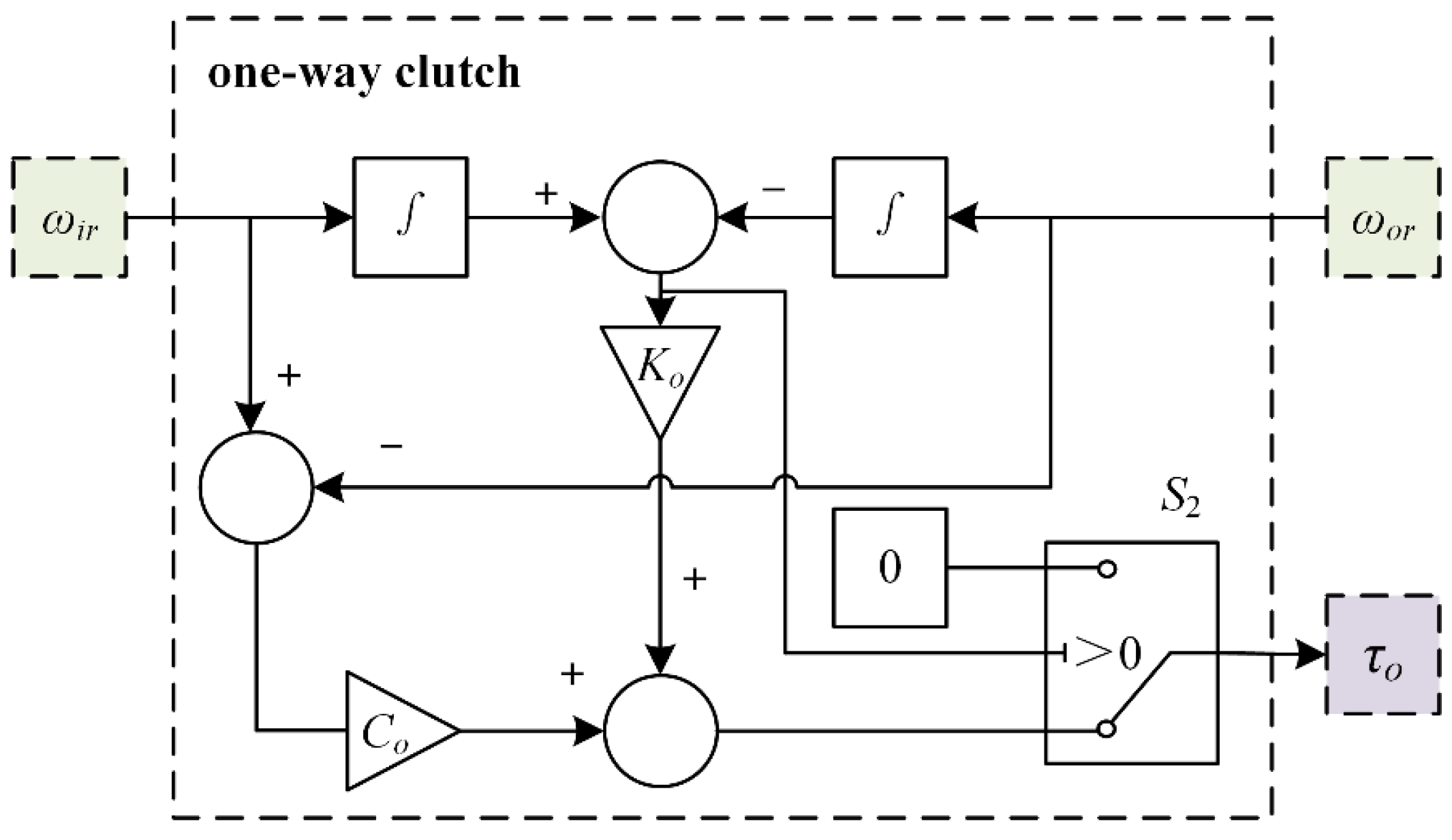
5. The One-Way Clutch Model
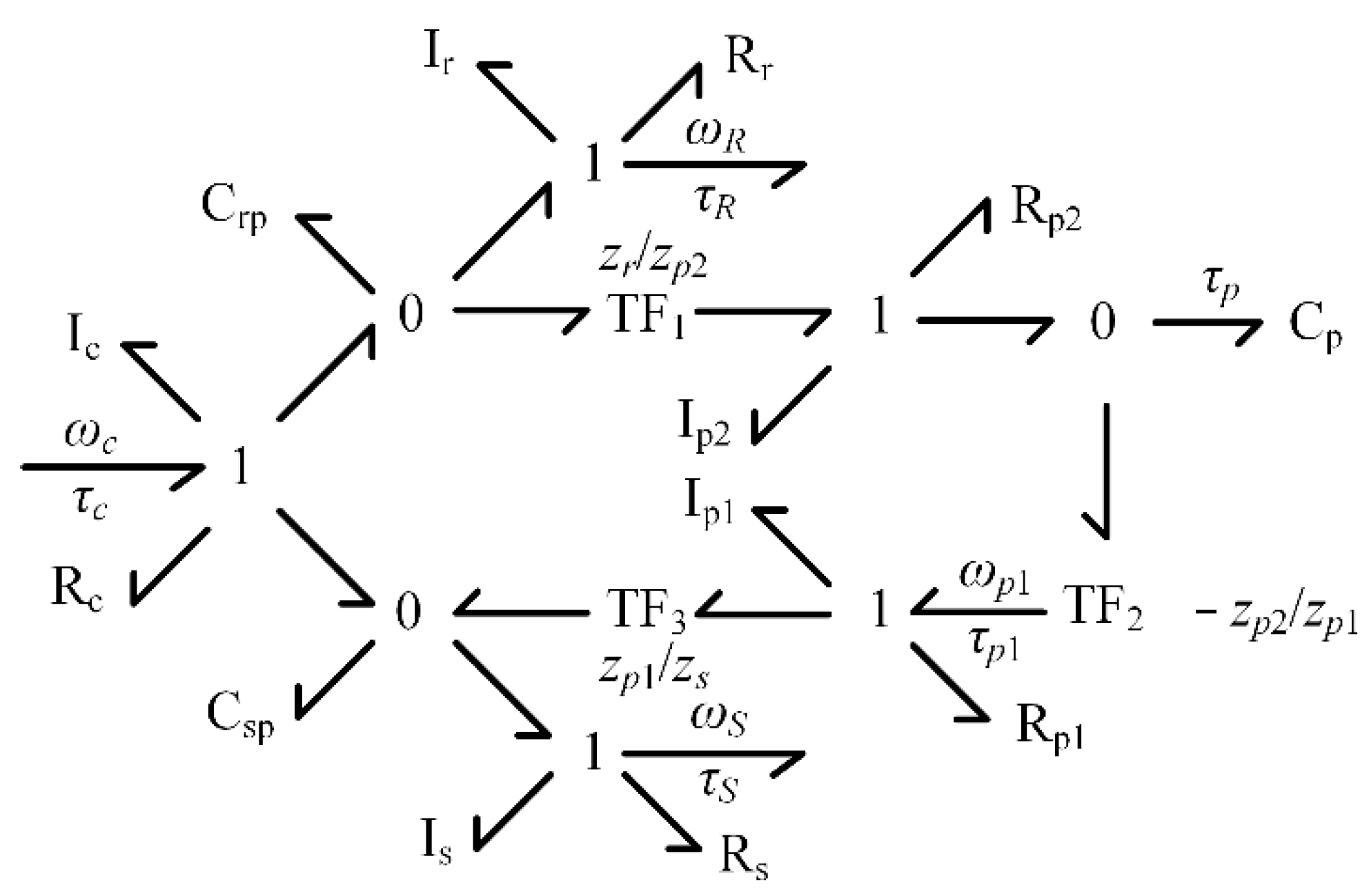
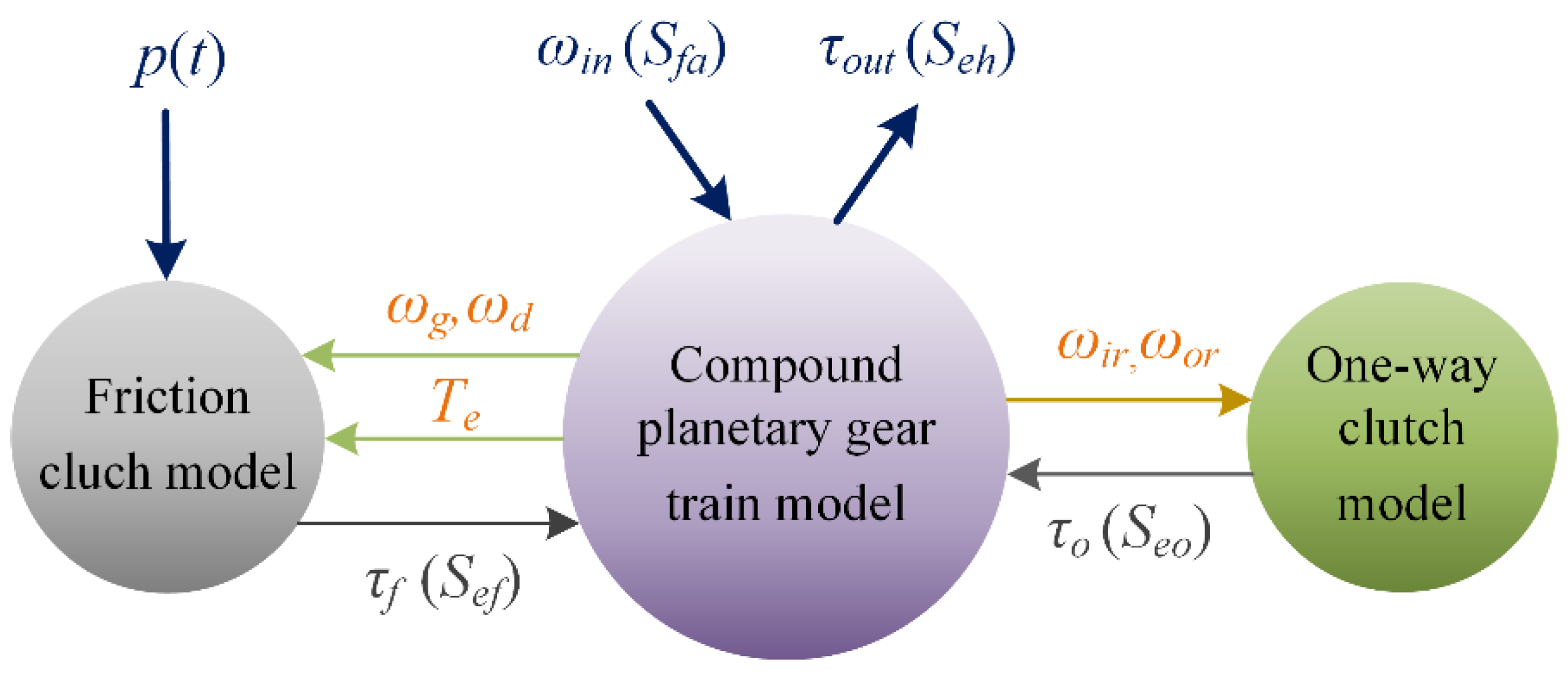
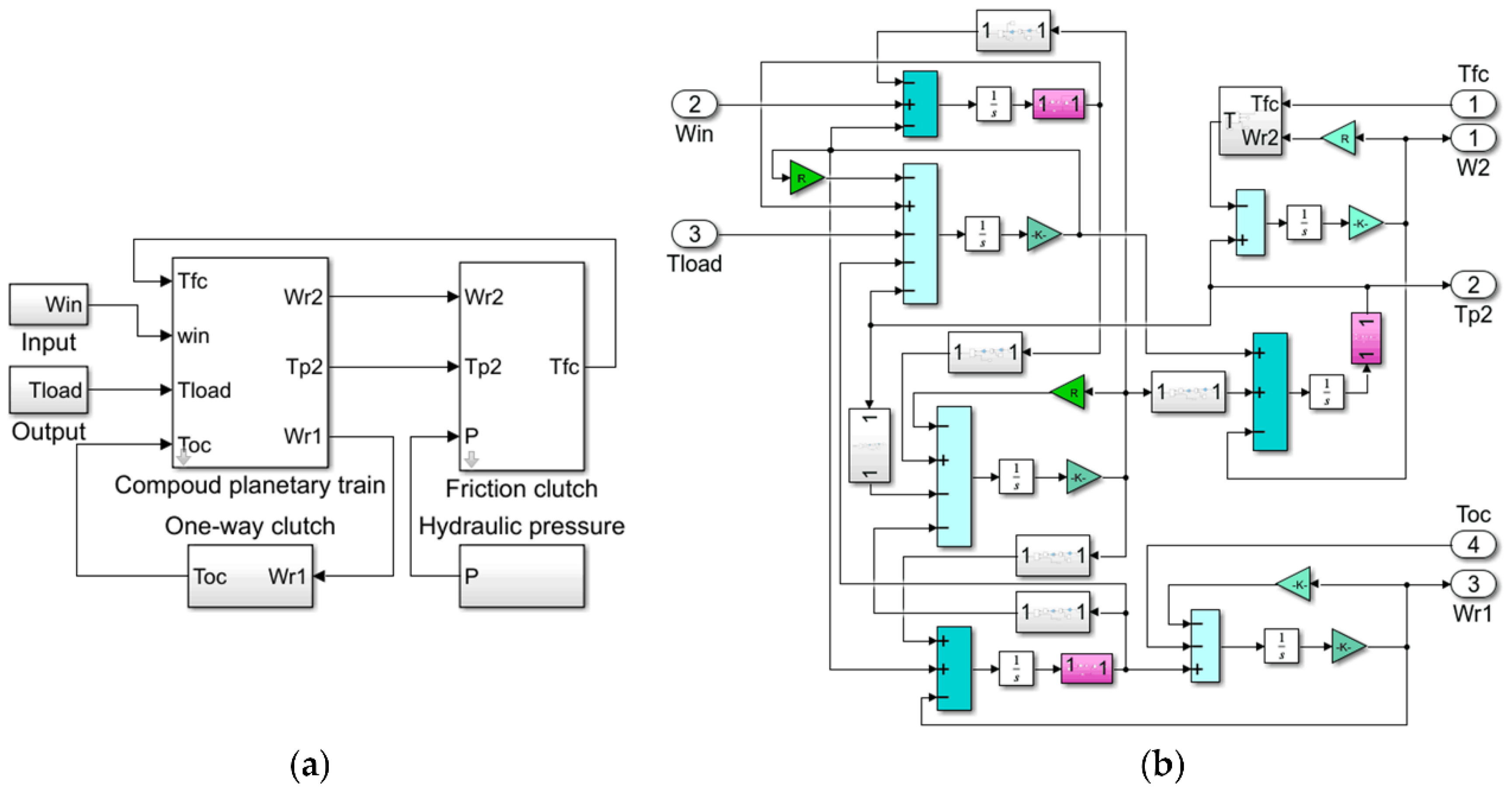
6. Coupling the Clutch Models to the PGT Model
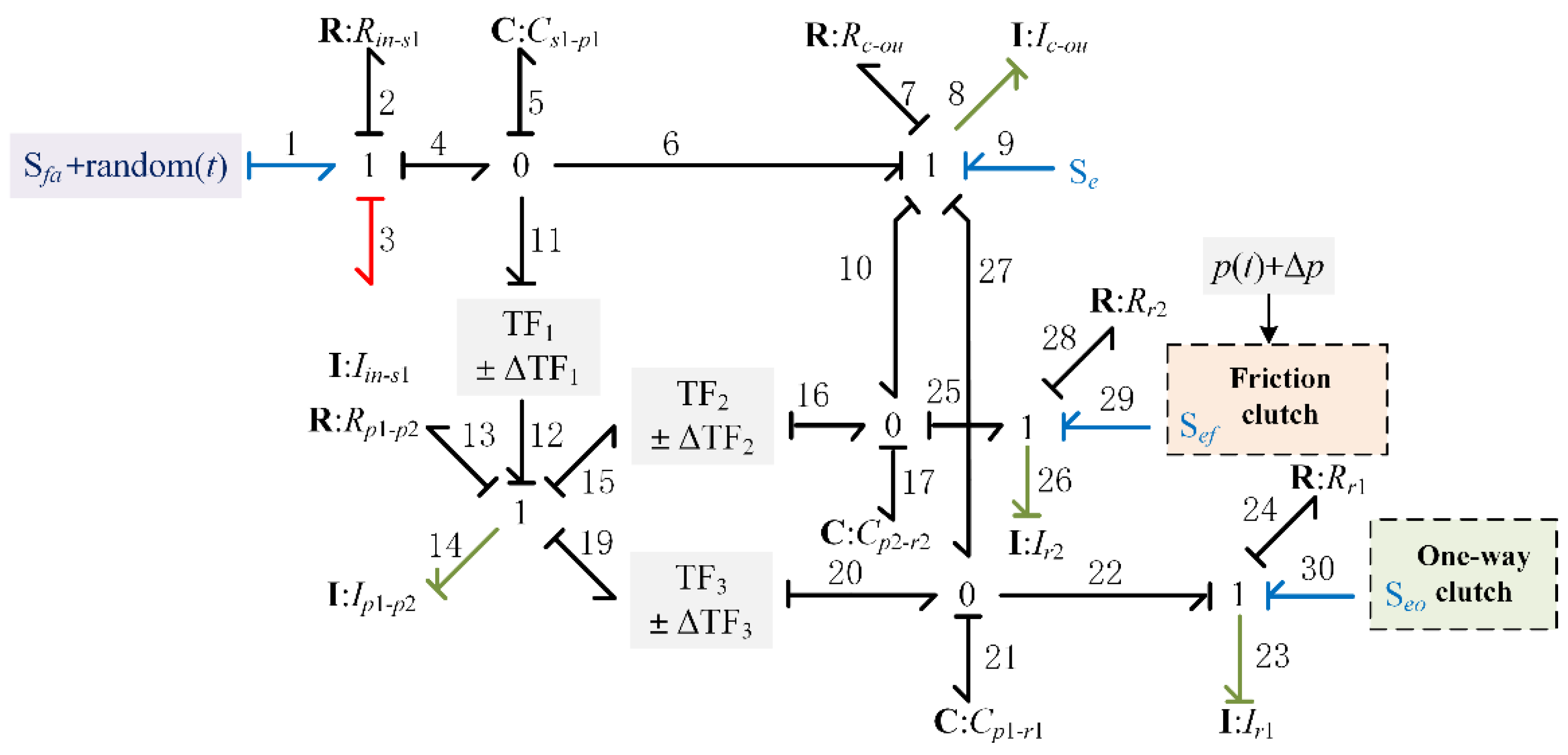
7. UncBG Model of a Variable-Speed Gearbox
7.1. Uncertain Factors
7.2. UncBG Model
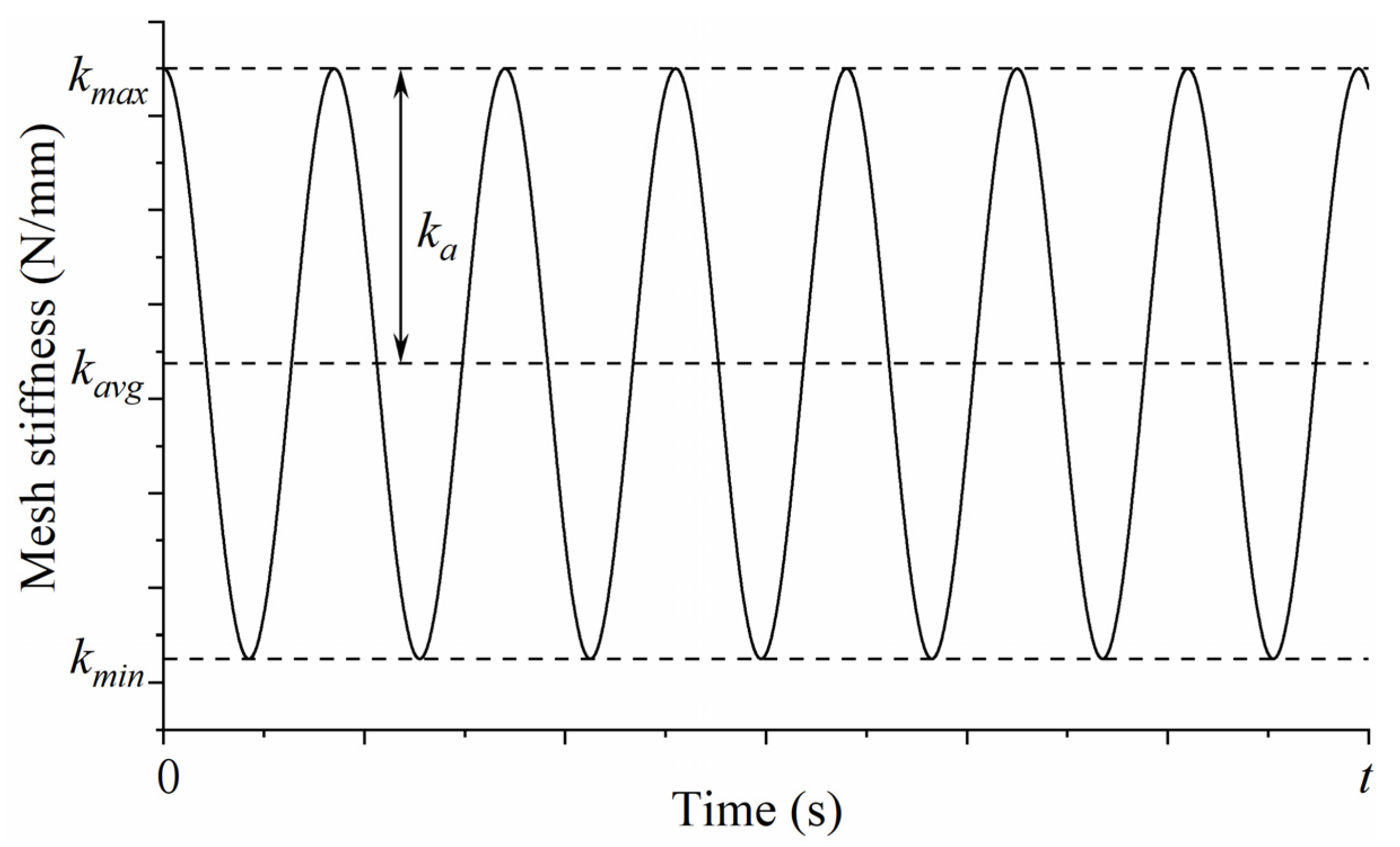
- The variable rigidity of each C-element in the BG model is considered. In this step, the uncertainty caused by the time-varying meshing stiffness k(t) is introduced into the BG model. Before that, the meshing stiffness in the meshing line direction must be the torsional stiffness in the circumferential direction, which is expressed as follows (where i, j represents a pair of meshing gears, while rb is the base circle radius):
- According to the structural characteristics of the compound PGT, different fluctuations (0.02–0.05%) are set for each TF element, for simulating the influence of manufacturing and assembly errors on the system’s response:
- Considering the speed fluctuation of the engine, a random signal is added to the working speed for simulating uncertain factors; the amplitude of the random signal is set to 0.2% of the working speed:
- In the form of harmonics, the driving hydraulic pressure of the friction clutch is increased by 2%, to represent the uncertainty of the driving hydraulic pressure (where th is the time at which the hydraulic pressure completes the loading process, and Th is the period of the hydraulic fluctuation):
8. Modeling and Numerical Verification of the Variable-Speed Gearbox
8.1. UncBG Model of a Double-Row Double Planetary Gearbox
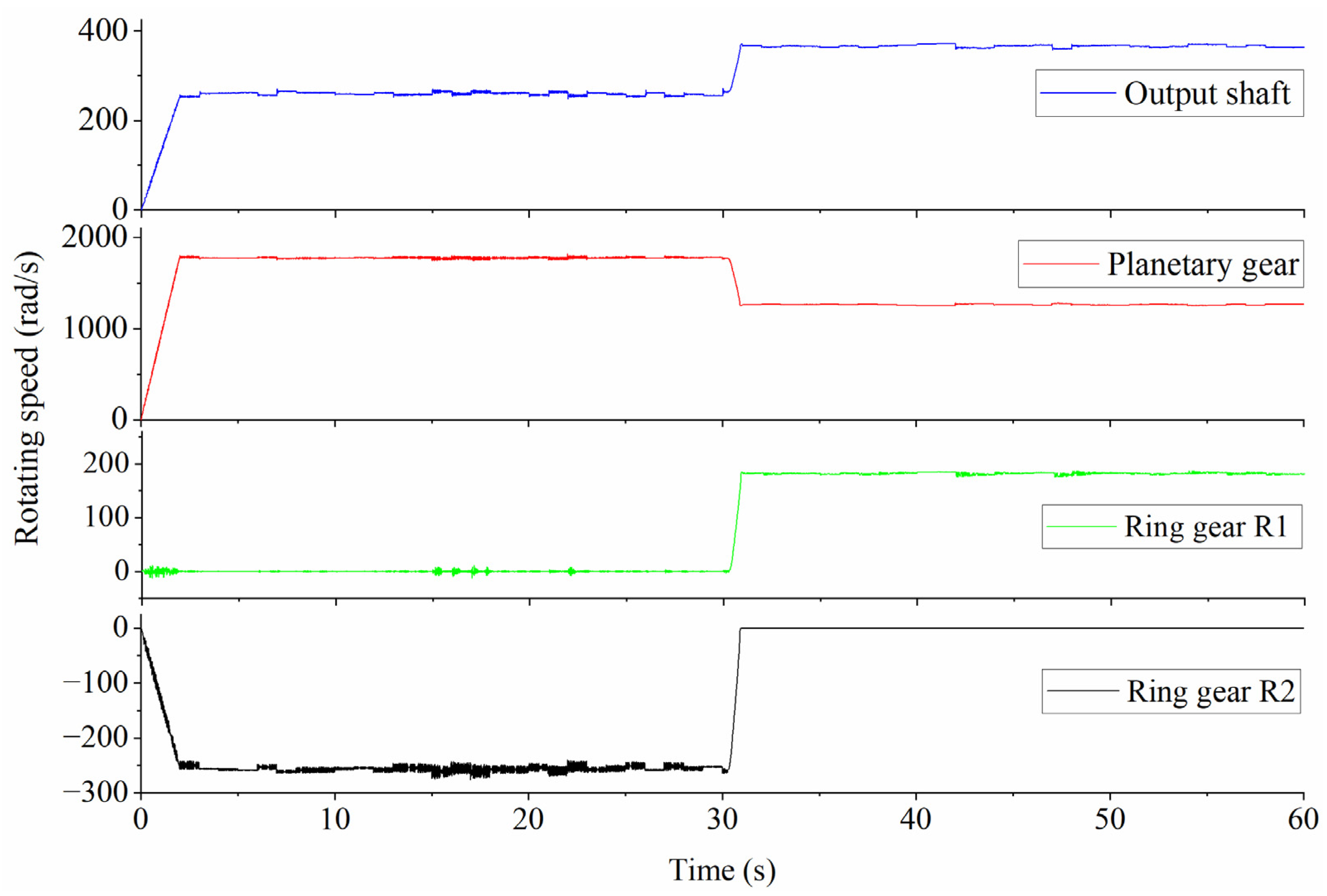
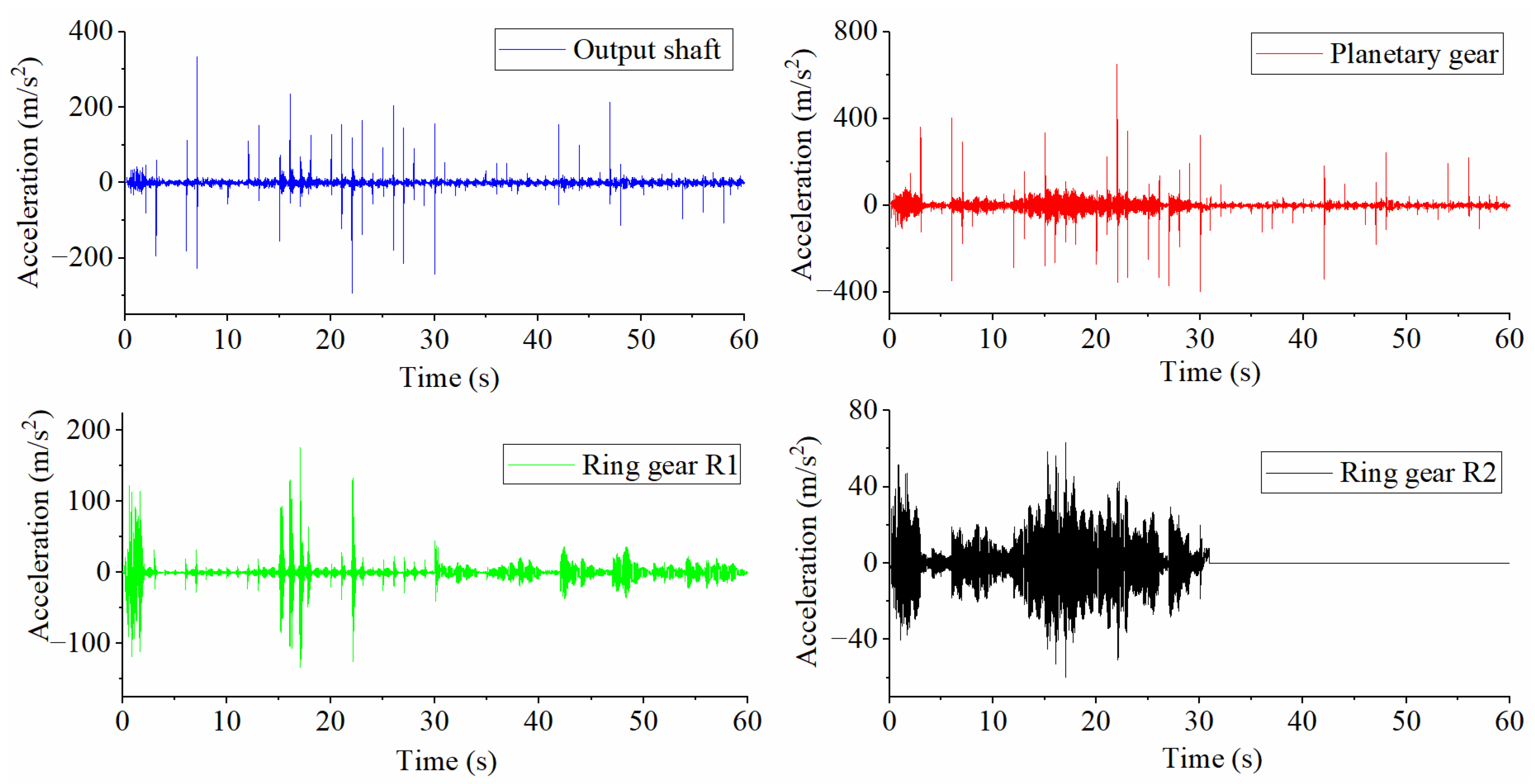
8.2. Results and Discussion
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Borutzky, W. Bond Graph Methodology: Development and Analysis of Multidisciplinary Dynamic System Models; Springer Science and Business Media: London, UK, 2010. [Google Scholar]
- Yao, W.; Chen, X.; Luo, W.; Van Tooren, M.; Guo, J. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Progr. Aeronaut. Sci. 2011, 47, 450–479. [Google Scholar] [CrossRef]
- Drewniak, J.; Kopeć, J.; Zawiślak, S. Graph models of automobile gears-kinematics. Int. J. Appl. Mech. Eng. 2014, 19, 563–573. [Google Scholar] [CrossRef] [Green Version]
- Deur, J.; Ivanović, V.; Assadian, F.; Kuang, M.; Tseng, E.H.; Hrovat, D. Bond graph modeling of automotive transmissions and drivelines. IFAC Proc. 2012, 45, 427–432. [Google Scholar] [CrossRef] [Green Version]
- Vangheluwe, H.; Lara, J.D.; Mosterman, P.J. An introduction to multi-paradigm modelling and simulation. In Proceedings of the 2002 AI, Simulation and Planning in High Autonomy Systems conference (AIS’2002), Lisboa, Portugal, 7–10 April 2002; pp. 9–20. [Google Scholar]
- Boudon, B.; Malburet, F.; Carmona, J.C. Simulation of a helicopter’s main gearbox semiactive suspension with bond graphs. Multibody Syst. Dyn. 2017, 40, 375–405. [Google Scholar] [CrossRef] [Green Version]
- Barjuei, E.S.; Toxiri, S.; Medrano-Cerda, G.A.; Caldwell, D.G.; Ortiz, J. Bond Graph Modeling of An Exoskeleton Actuator. In Proceedings of the 10th Computer Science and Electronic Engineering (CEEC 2018), Colchester, UK, 19–21 September 2018; pp. 101–106. [Google Scholar] [CrossRef]
- Deur, J.; Asgari, J.; Hrovat, D. Modeling of an automotive planetary gear set based on karnopp model for clutch friction. In Proceedings of the ASME 2003 International Mechanical Engineering Congress and Exposition (IMECE 2003), Washington, DC, USA, 15–21 November 2003; pp. 903–910. [Google Scholar] [CrossRef]
- Deur, J.; Asgari, J.; Hrovat, D.; Kovač, P. Modeling and analysis of automatic transmission engagement dynamics-linear case. J. Dyn. Syst. Meas. Control. 2006, 128, 263–277. [Google Scholar] [CrossRef]
- Deur, J.; Asgari, J.; Hrovat, D.; Kovač, P. Modeling and analysis of automatic transmission engagement dynamics-nonlinear case. J. Dyn. Syst. Meas. Control. 2006, 128, 251–262. [Google Scholar] [CrossRef]
- Ranogajec, V.; Deur, J.; Coric, M. Bond graph analysis of automatic transmission shifts including potential of extra clutch control. SAE Int. J. Engines. 2016, 9, 1929–1945. [Google Scholar] [CrossRef]
- Ivanovic, V.; Tseng, H.E. Bond graph based approach for modeling of automatic transmission dynamics. SAE Int. J. Engines 2017, 10, 1999–2014. [Google Scholar] [CrossRef]
- Ranogajec, V.; Ivanović, V.; Deur, J.; Tseng, H.E. Optimization-based assessment of automatic transmission double-transition shift controls. Control Eng. Pract. 2018, 76, 155–166. [Google Scholar] [CrossRef]
- Liu, J.; Yu, L.; Zeng, Q.; Li, Q. Synthesis of multi-row and multi-speed planetary gear mechanism for automatic transmission. Mech. Mach. Theor. 2018, 128, 616–627. [Google Scholar] [CrossRef]
- Li, X.T.; Wang, A.L. A modularization method of dynamic system modeling for multiple planetary gear trains transmission gearbox. Mech. Mach. Theor. 2019, 136, 162–177. [Google Scholar] [CrossRef]
- Jouilel, N.; Radouani, M.; El Fahime, B. Wind Turbine’s Gearbox Aided Design Approach Using Bond Graph Methodology and Monte Carlo Simulation. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 8, 89–101. [Google Scholar] [CrossRef]
- Mir-Haidari, S.E.; Behdinan, K. On the vibration transfer path analysis of aero-engines using bond graph theory. Aerosp. Sci. Technol. 2019, 95, 105516. [Google Scholar] [CrossRef]
- Tan, W.Z.; Wu, J.M.; Ni, D.; Yan, H.Z.; Xiang, E.M.; Liu, S.Q. Dynamic modeling and simulation of double-planetary gearbox based on bond graph. Math. Probl. Eng. 2021, 2021, 3964808. [Google Scholar] [CrossRef]
- Bao, H.Y.; Huang, W.; Lu, F.X. Investigation of engagement characteristics of a multi-disc wet friction clutch. Tribol. Int. 2021, 159, 106940. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Miran Fashandi, S.A. Modeling and simulation of a two-shaft gas turbine propulsion system containing a frictional plate–Type clutch. Proc. Inst. Mech. Eng. M J. Eng. Marit. Environ. 2019, 233, 502–514. [Google Scholar] [CrossRef]
- Karnopp, D.C. Computer simulation of stick-slip friction in mechanical dynamic systems. J. Dyn. Syst. Meas. Control. 1985, 107, 100–103. [Google Scholar] [CrossRef]
- Tustin, A. The effects of backlash and of speed dependent friction on the stability of closed-cycle control systems. J. Inst. Electr. Eng. IIA Autom. Regul. Servo Mech. 1974, 94, 143–151. [Google Scholar] [CrossRef]
- Armstrong-Helouvry, B. Stick-slip arising from Stribeck friction. Proc. ICRA 1990, 2, 1377–1382. [Google Scholar] [CrossRef]
- Iqbal, S.; Al-Bender, F.; Ompusunggu, A.P.; Pluymers, B.; Desmet, W. Modeling and analysis of wet friction clutch engagement dynamics. Mech. Syst. Signal Process. 2015, 60–61, 420–436. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Liu, Y.; Zhang, W. Modeling and experimental research on engaging characteristics of wet clutch. Ind. Lubr. Tribol. 2019, 71, 94–101. [Google Scholar] [CrossRef]
- Natsumeda, S.; Miyoshi, T. Numerical simulation of engagement of paper based wet clutch facing. J. Tribol. 1994, 116, 232–237. [Google Scholar] [CrossRef]
- Liu, Z.H.; Yan, H.Z.; Cao, Y.M.; Lai, Y. Bifurcation and chaos analysis of the spur gear transmission system for one-way clutch, two-shaft assembly. Shock Vib. 2017, 2017, 8621514. [Google Scholar] [CrossRef] [Green Version]
- Ke, Z.; Wei, W.; Liu, C. The dynamic wedging and friction characteristics of one-way clutch under transient loads from stator. Tribol. Int. 2020, 152, 106568. [Google Scholar] [CrossRef]
- Mockensturm, E.M.; Balaji, R. Piece-wise linear dynamic systems with one-way clutches. J. Vib. Acoust. 2005, 127, 475–482. [Google Scholar] [CrossRef]
- Ding, H. Periodic responses of a pulley–belt system with one-way clutch under inertia excitation. J. Sound Vib. 2015, 353, 308–326. [Google Scholar] [CrossRef]
- Snyder, C.A.; Robuck, M.; Wilkerson, J.; Nordstrom, C. Summary of the large civil tiltrotor (LCTR2) engine gearbox study. In Proceedings of the International Power Lift Conference 2010, Proceedings of the International Power Lift Conference 2010, Philadelphia, PA, USA, 5–7 October 2010; pp. 416–431. [Google Scholar]
- Stevens, M.A.; Lewicki, D.G.; Handschuh, R.F. Concepts for multi-speed rotorcraft drive system—Status of design and testing at NASA GRC. In Proceedings of the American Helicopter Society (AHS) 71st Annual Forum, Virginia Beach, VI, USA, 5–7 May 2015. [Google Scholar]
- Stevens, M.A.; Handschuh, R.F.; Lewicki, D.G. Offset Compound Gear Inline Two-Speed Drive. U.S. Patent 8,091,445, 10 January 2012. [Google Scholar]
- Jawad, A.; Dantan, J.; Sabri, V.; Beaucaire, P.; Gayton, N. A statistical tolerance analysis approach for over-constrained mechanism based on optimization and Monte Carlo simulation. Comput. Aid. Des. 2012, 44, 132–142. [Google Scholar] [CrossRef] [Green Version]
- Kam, C.S.; Dauphin-Tanguy, G. Bond graph models of structured parameter uncertainties. J. Franklin Inst. 2005, 342, 379–399. [Google Scholar] [CrossRef]



| Generalized Variables | Mechanical Variables | ||
|---|---|---|---|
| Meaning | Symbol | Meaning | Symbol |
| effort variable | e | torque | τ |
| flow variable | f | angular velocity | ω |
| generalized displacement | q | angular displacement | θ |
| generalized momentum | p | moment of inertia | J |
| Parameter | Value | Unit |
|---|---|---|
| rs: Sun base circle radius | 108.75 | mm |
| rp1: Planet P1 base circle radius | 22.5 | mm |
| rp2: Planet P2 base circle radius | 57.35 | mm |
| rr1: Ring R1 base circle radius | 153.75 | mm |
| rr2: Ring R2 base circle radius | 185 | mm |
| M: modulus | 2.5 | mm |
| Js: Sun inertia | 0.0358 | kg·m2 |
| Jp: Panetary inertia | 0.0033 | kg·m2 |
| Jr1: Ring R1 inertia | 0.1825 | kg·m2 |
| Jr2: Ring R2 inertia | 0.3243 | kg·m2 |
| Jc: Carrier inertia | 0.0326 | kg·m2 |
| Subsystem | Parameter | Value | Unit |
|---|---|---|---|
| Engine | Input speed Sfa | 628 | rad/s |
| Rotor | Load torque Se | 2670/3765.5 | Nm |
| Friction clutch | Hydraulic pressure Pmax | 0.8 | MPa |
| Exponential curve factor b | 14 | / | |
| Number of friction plates Nf | 6 | / | |
| Inner radius of friction plate ri | 77.5 | mm | |
| Outer radius of friction plate ro | 110 | mm | |
| Piston cavity area Ap | 0.028 | m2 | |
| Dynamic friction coefficient μc | 0.1 | / | |
| Stribeck coefficient δ | 0.02 | ||
| Static friction coefficient μs | 0.12 | / | |
| One-way clutch | Torsional stiffness Ko | 2.8 × 105 | Nm/rad |
| Torsional damping coefficient Co | 0.01 | Nm·s/rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yan, H.; Liu, S.; Zhang, Y.; Tan, W. Bond Graph-Based Approach to Modeling Variable-Speed Gearboxes with Multi-Type Clutches. Appl. Sci. 2022, 12, 6181. https://doi.org/10.3390/app12126181
Wu J, Yan H, Liu S, Zhang Y, Tan W. Bond Graph-Based Approach to Modeling Variable-Speed Gearboxes with Multi-Type Clutches. Applied Sciences. 2022; 12(12):6181. https://doi.org/10.3390/app12126181
Chicago/Turabian StyleWu, Jiangming, Hongzhi Yan, Shuangqi Liu, Yin Zhang, and Wuzhong Tan. 2022. "Bond Graph-Based Approach to Modeling Variable-Speed Gearboxes with Multi-Type Clutches" Applied Sciences 12, no. 12: 6181. https://doi.org/10.3390/app12126181
APA StyleWu, J., Yan, H., Liu, S., Zhang, Y., & Tan, W. (2022). Bond Graph-Based Approach to Modeling Variable-Speed Gearboxes with Multi-Type Clutches. Applied Sciences, 12(12), 6181. https://doi.org/10.3390/app12126181





